test-bench-apa300ml/index.org

Amplifier Piezoelectric Actuator APA300ML - Test Bench

• Introduction
• Model of an Amplified Piezoelectric Actuator and Sensor
• Test-Bench Description
• Measurement Procedure
  • Introduction
  • Stroke Measurement
  • Stiffness Measurement
  • Hysteresis measurement
  • Piezoelectric Actuator Constant
  • Piezoelectric Sensor Constant
  • Capacitance Measurement
  • Dynamical Behavior
  • Compare the results obtained for all 7 APA300ML
• Measurement Results

Introduction   ignore

The goal of this test bench is to extract all the important parameters of the Amplified Piezoelectric Actuator APA300ML.

This include:

• Stroke
• Stiffness
• Hysteresis
• Gain from the applied voltage $V_a$ to the generated Force $F_a$
• Gain from the sensor stack strain $\delta L$ to the generated voltage $V_s$
• Dynamical behavior

Model of an Amplified Piezoelectric Actuator and Sensor

Consider a schematic of the Amplified Piezoelectric Actuator in Figure fig:apa_model_schematic.

Amplified Piezoelectric Actuator Schematic

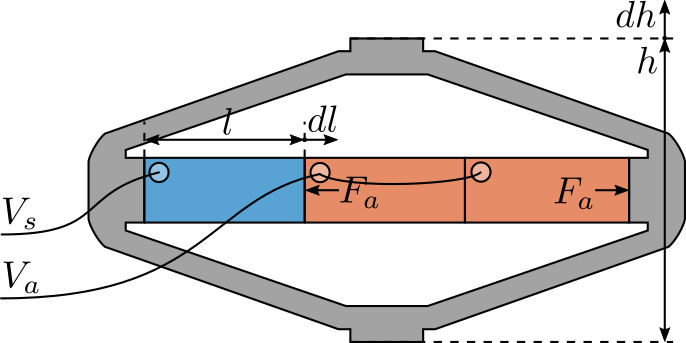
A voltage $V_a$ applied to the actuator stacks will induce an actuator force $F_a$:

\begin{equation} F_a = g_a \cdot V_a \end{equation}

A change of length $dl$ of the sensor stack will induce a voltage $V_s$:

\begin{equation} V_s = g_s \cdot dl \end{equation}

We wish here to experimental measure $g_a$ and $g_s$.

The block-diagram model of the piezoelectric actuator is then as shown in Figure fig:apa-model-simscape-schematic.

  \begin{tikzpicture}
    \node[block={2.0cm}{2.0cm}, align=center] (model) at (0,0){Simscape\\Model};
    \node[block, left=1.0 of model] (ga){$g_a(s)$};
    \node[block, right=1.0 of model] (gs){$g_s(s)$};

    \draw[<-] (ga.west) -- node[midway, above]{$V_a$} node[midway, below]{$[V]$} ++(-1.0, 0);
    \draw[->] (ga.east) --node[midway, above]{$F_a$} node[midway, below]{$[N]$} (model.west);
    \draw[->] (model.east) --node[midway, above]{$dl$} node[midway, below]{$[m]$} (gs.west);
    \draw[->] (gs.east) -- node[midway, above]{$V_s$} node[midway, below]{$[V]$} ++(1.0, 0);
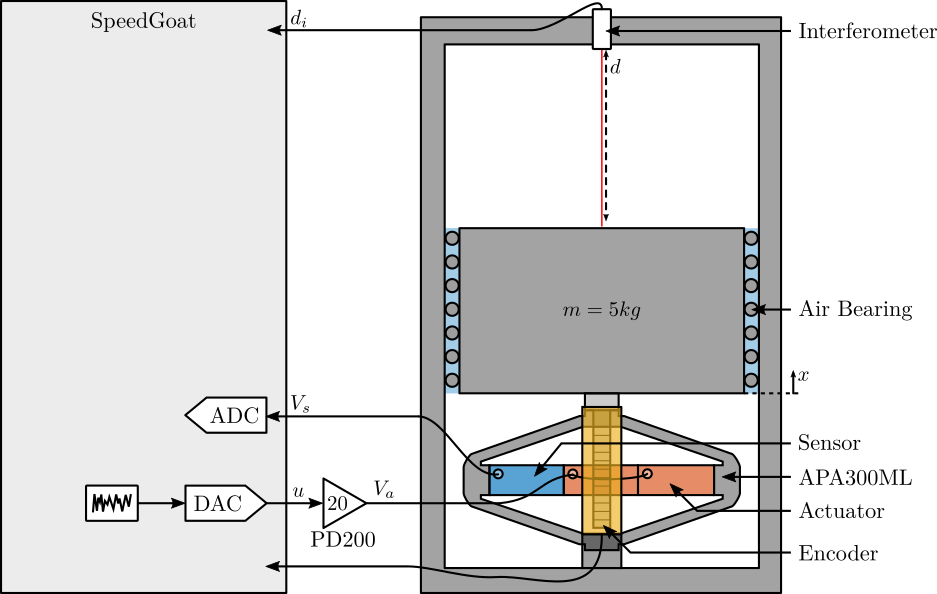
  \end{tikzpicture}

Model of the APA with Simscape/Simulink

Test-Bench Description

Here are the documentation of the equipment used for this test bench:

• Voltage Amplifier: PD200
• Amplified Piezoelectric Actuator: APA300ML
• DAC/ADC: Speedgoat IO313
• Encoder: Renishaw Vionic and used Ruler
• Interferometer: Attocube IDS3010

Schematic of the Test Bench

Measurement Procedure

Introduction   ignore

Stroke Measurement

Using the PD200 amplifier, output a voltage: \[ V_a = 65 + 85 \sin(2\pi \cdot t) \] To have a quasi-static excitation between -80 and 150V.

As the gain of the PD200 amplifier is 20, the DAC output voltage should be: \[ V_{dac}(t) = 3.25 + 4.25\sin(2\pi \cdot t) \]

Verify that the voltage offset is zero!

Measure the output vertical displacement $d$ using the interferometer.

Then, plot $d$ as a function of $V_a$, and perform a linear regression. Conclude on the obtained stroke.

Stiffness Measurement

Add some (known) weight $\delta m g$ on the suspended mass and measure the deflection $\delta d$. This can be tested when the piezoelectric stacks are open-circuit.

As the stiffness will be around $k \approx 10^6 N/m$, an added mass of $m \approx 100g$ will induce a static deflection of $\approx 1\mu m$ which should be large enough for a precise measurement using the interferometer.

Then the obtained stiffness is:

\begin{equation} k = \frac{\delta m g}{\delta d} \end{equation}

Hysteresis measurement

Supply a quasi static sinusoidal excitation $V_a$ at different voltages.

The offset should be 65V, and the sin amplitude can range from 1V up to 85V.

For each excitation amplitude, the vertical displacement $d$ of the mass is measured.

Then, $d$ is plotted as a function of $V_a$ for all the amplitudes.

Piezoelectric Actuator Constant

Using the measurement test-bench, it is rather easy the determine the static gain between the applied voltage $V_a$ to the induced displacement $d$. Use a quasi static (1Hz) excitation signal $V_a$ on the piezoelectric stack and measure the vertical displacement $d$. Perform a linear regression to obtain:

\begin{equation} d = g_{d/V_a} \cdot V_a \end{equation}

Using the Simscape model of the APA, it is possible to determine the static gain between the actuator force $F_a$ to the induced displacement $d$:

\begin{equation} d = g_{d/F_a} \cdot F_a \end{equation}

From the two gains, it is then easy to determine $g_a$:

\begin{equation} g_a = \frac{F_a}{V_a} = \frac{F_a}{d} \cdot \frac{d}{V_a} = \frac{g_{d/V_a}}{g_{d/F_a}} \end{equation}

Piezoelectric Sensor Constant

From a quasi static (1Hz) excitation of the piezoelectric stack, measure the gain from $V_a$ to $V_s$:

\begin{equation} V_s = g_{V_s/V_a} V_a \end{equation}

Using the simscape model, compute the static gain from the actuator force $F_a$ to the strain of the sensor stack $dl$:

\begin{equation} dl = g_{dl/F_a} F_a \end{equation}

Then, the static gain from the sensor stack strain $dl$ to the general voltage $V_s$ is:

\begin{equation} g_s = \frac{V_s}{dl} = \frac{V_s}{V_a} \cdot \frac{V_a}{F_a} \cdot \frac{F_a}{dl} = \frac{g_{V_s/V_a}}{g_a \cdot g_{dl/F_a}} \end{equation}

Alternatively, we could impose an external force to add strain in the APA that should be equally present in all the 3 stacks and equal to 1/5 of the vertical strain. This external force can be some weight added, or a piezo in parallel.

Capacitance Measurement

Measure the capacitance of the 3 stacks individually using a precise multi-meter.

Dynamical Behavior

Perform a system identification from $V_a$ to the measured displacement $d$ by the interferometer and by the encoder, and to the general voltage $V_s$.

This can be performed using different excitation signals.

This can also be performed with and without the encoder fixed to the APA.

Compare the results obtained for all 7 APA300ML

Compare all the obtained parameters for all the test APA.

Measurement Results