phd-nass-rotating-3dof-model/rotating_frame.org

Control in a rotating frame

• Goal of this note
• System
  • System description
  • Equations
  • Analysis
• Analytical Computation of forces for the NASS
  • Euler and Coriolis forces
  • Spring Softening Effect
• Control Strategies
  • Measurement in the fixed reference frame
    • QUESTION Is the loop gain is changing with the angle ?
  • Measurement in the rotating frame
• Effect of the rotating Speed
  • Use realistic parameters for the mass of the sample and stiffness of the X-Y stage
  • Check if the plant is changing a lot when we are not turning to when we are turning at the maximum speed (60rpm)
• Effect of the X-Y stage stiffness
  • At full speed, check how the coupling changes with the stiffness of the actuators

Goal of this note

The control objective is to stabilize the position of a rotating object with respect to a non-rotating frame.

The actuators are also rotating with the object.

We want to compare the two different approach:

• the measurement is made in the fixed frame
• the measurement is made in the rotating frame

System

<<sec:system>>

System description

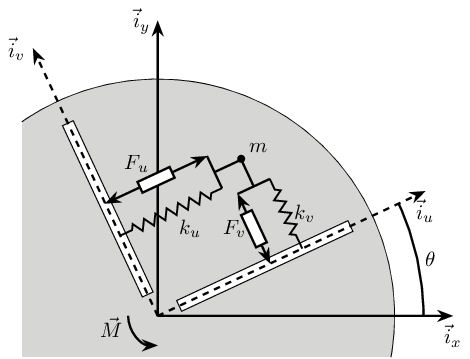
The system consists of one 2 degree of freedom translation stage on top of a spindle (figure fig:rotating_frame_2dof).

The control inputs are the forces applied in the translation stage ($F_u$ and $F_v$). As the translation stage is rotating around the Z axis due to the spindle, the forces are applied along $u$ and $v$.

The measurement is either the $x-y$ displacement of the object located on top of the translation stage or the $u-v$ displacement of the actuators.

Schematic of the mecanical system

In the following block diagram:

• $G$ is the transfer function from the forces applied in the actuators to the measurement
• $K$ is the controller to design
• $J$ is a Jacobian matrix usually used to change the reference frame

Indices $x$ and $y$ corresponds to signals in the fixed reference frame (along $\vec{i}_x$ and $\vec{i}_y$):

• $D_x$ is the measured position of the sample
• $r_x$ is the reference signal which corresponds to the wanted $D_x$
• $\epsilon_x$ is the position error

Indices $u$ and $v$ corresponds to signals in the rotating reference frame ($\vec{i}_u$ and $\vec{i}_v$):

• $F_u$ and $F_v$ are forces applied by the actuators
• $\epsilon_u$ and $\epsilon_v$ are position error of the sample along $\vec{i}_u$ and $\vec{i}_v$

Equations

<<sec:equations>>

Based on the figure fig:rotating_frame_2dof, we can write the equations of motion of the system.

Let's express the kinetic energy $T$ and the potential energy $V$ of the mass $m$:

\begin{align} T & = \frac{1}{2} m \left( \dot{x}^2 + \dot{y}^2 \right) \\ V & = \frac{1}{2} k \left( x^2 + y^2 \right) \end{align}

The Lagrangian is the kinetic energy minus the potential energy.

\begin{equation} L = T-V = \frac{1}{2} m \left( \dot{x}^2 + \dot{y}^2 \right) - \frac{1}{2} k \left( x^2 + y^2 \right) \end{equation}

The partial derivatives of the Lagrangian with respect to the variables $(x, y)$ are:

\begin{align*} \frac{\partial L}{\partial x} & = -kx \\ \frac{\partial L}{\partial y} & = -ky \\ \frac{d}{dt}\frac{\partial L}{\partial \dot{x}} & = m\ddot{x} \\ \frac{d}{dt}\frac{\partial L}{\partial \dot{y}} & = m\ddot{y} \end{align*}

The external forces applied to the mass are:

\begin{align*} F_{\text{ext}, x} &= F_u \cos{\theta} - F_v \sin{\theta}\\ F_{\text{ext}, y} &= F_u \sin{\theta} + F_v \cos{\theta} \end{align*}

By appling the Lagrangian equations, we obtain:

\begin{align} m\ddot{x} + kx = F_u \cos{\theta} - F_v \sin{\theta}\\ m\ddot{y} + ky = F_u \sin{\theta} + F_v \cos{\theta} \end{align}

We then change coordinates from $(x, y)$ to $(d_x, d_y, \theta)$.

\begin{align*} x & = d_u \cos{\theta} - d_v \sin{\theta}\\ y & = d_u \sin{\theta} + d_v \cos{\theta} \end{align*}

We obtain:

\begin{align*} \ddot{x} & = \ddot{d_u} \cos{\theta} - 2\dot{d_u}\dot{\theta}\sin{\theta} - d_u\ddot{\theta}\sin{\theta} - d_u\dot{\theta}^2 \cos{\theta} - \ddot{d_v} \sin{\theta} - 2\dot{d_v}\dot{\theta}\cos{\theta} - d_v\ddot{\theta}\cos{\theta} + d_v\dot{\theta}^2 \sin{\theta} \\ \ddot{y} & = \ddot{d_u} \sin{\theta} + 2\dot{d_u}\dot{\theta}\cos{\theta} + d_u\ddot{\theta}\cos{\theta} - d_u\dot{\theta}^2 \sin{\theta} + \ddot{d_v} \cos{\theta} - 2\dot{d_v}\dot{\theta}\sin{\theta} - d_v\ddot{\theta}\sin{\theta} - d_v\dot{\theta}^2 \cos{\theta} \\ \end{align*}

By injecting the previous result into the Lagrangian equation eq:lagrangian_eq_inertial, we obtain:

\begin{align*} m \ddot{d_u} \cos{\theta} - 2m\dot{d_u}\dot{\theta}\sin{\theta} - m d_u\ddot{\theta}\sin{\theta} - m d_u\dot{\theta}^2 \cos{\theta} -m \ddot{d_v} \sin{\theta} - 2m\dot{d_v}\dot{\theta}\cos{\theta} - m d_v\ddot{\theta}\cos{\theta} + m d_v\dot{\theta}^2 \sin{\theta} + k d_u \cos{\theta} - k d_v \sin{\theta} = F_u \cos{\theta} - F_v \sin{\theta} \\ m \ddot{d_u} \sin{\theta} + 2m\dot{d_u}\dot{\theta}\cos{\theta} + m d_u\ddot{\theta}\cos{\theta} - m d_u\dot{\theta}^2 \sin{\theta} + m \ddot{d_v} \cos{\theta} - 2m\dot{d_v}\dot{\theta}\sin{\theta} - m d_v\ddot{\theta}\sin{\theta} - m d_v\dot{\theta}^2 \cos{\theta} + k d_u \sin{\theta} + k d_v \cos{\theta} = F_u \sin{\theta} + F_v \cos{\theta} \end{align*}

Which is equivalent to:

\begin{align*} m \ddot{d_u} - 2m\dot{d_u}\dot{\theta}\frac{\sin{\theta}}{\cos{\theta}} - m d_u\ddot{\theta}\frac{\sin{\theta}}{\cos{\theta}} - m d_u\dot{\theta}^2 -m \ddot{d_v} \frac{\sin{\theta}}{\cos{\theta}} - 2m\dot{d_v}\dot{\theta} - m d_v\ddot{\theta} + m d_v\dot{\theta}^2 \frac{\sin{\theta}}{\cos{\theta}} + k d_u - k d_v \frac{\sin{\theta}}{\cos{\theta}} = F_u - F_v \frac{\sin{\theta}}{\cos{\theta}} \\ m \ddot{d_u} + 2m\dot{d_u}\dot{\theta}\frac{\cos{\theta}}{\sin{\theta}} + m d_u\ddot{\theta}\frac{\cos{\theta}}{\sin{\theta}} - m d_u\dot{\theta}^2 + m \ddot{d_v} \frac{\cos{\theta}}{\sin{\theta}} - 2m\dot{d_v}\dot{\theta} - m d_v\ddot{\theta} - m d_v\dot{\theta}^2 \frac{\cos{\theta}}{\sin{\theta}} + k d_u + k d_v \frac{\cos{\theta}}{\sin{\theta}} = F_u + F_v \frac{\cos{\theta}}{\sin{\theta}} \end{align*}

We can then subtract and add the previous equations to obtain the following equations:

\begin{align*} m \ddot{d_u} + (k - m\dot{\theta}^2) d_u &= F_u + 2 m\dot{d_v}\dot{\theta} + m d_v\ddot{\theta} \\ m \ddot{d_v} + (k - m\dot{\theta}^2) d_v &= F_v - 2 m\dot{d_u}\dot{\theta} - m d_u\ddot{\theta} \\ \end{align*}

Analysis

We obtain two differential equations that are coupled through:

• Euler forces: $m d_v \ddot{\theta}$
• Coriolis forces: $2 m \dot{d_v} \dot{\theta}$

Without the coupling terms, each equation is the equation of a one degree of freedom mass-spring system with mass $m$ and stiffness $k-d_u m\dot{\theta}^2$. Thus, the term $-d_u m\dot{\theta}^2$ acts like a negative stiffness (due to centrifugal forces).

Analytical Computation of forces for the NASS

For the NASS, the Euler forces should be less of a problem as $\ddot{\theta}$ should be very small when conducting an experiment.

First we will determine the value for Euler and Coriolis forces during regular experiment.

Euler and Coriolis forces

Let's define the parameters for the NASS.

  mlight = 35; % [kg]
  mheavy = 85; % [kg]

  wlight = 2*pi; % [rad/s]
  wheavy = 2*pi/60; % [rad/s]

  wdot = 1; % [rad/s2]

  d = 0.1; % [m]
  ddot = 0.2; % [m/s]

We then compute the corresponding values of the Coriolis and Euler forces, and the obtained values are displayed in table tab:euler_coriolis.

	Light	Heavy
Coriolis	44.0 N	1.8 N
Euler	3.5 N	8.5 N

Euler and Coriolis forces for the NASS

Spring Softening Effect

The values for the spring softening effect are displayed in table tab:spring_softening. This is definitely negligible when using piezoelectric actuators. It may not be the case when using voice coil actuators.

	Light	Heavy
Spring Soft.	3.5 N/m	8.5 N/m

Spring Softening effect

Control Strategies

<<sec:control_strategies>>

Measurement in the fixed reference frame

First, let's consider a measurement in the fixed referenced frame.

The transfer function from actuator $[F_u, F_v]$ to sensor $[D_x, D_y]$ is then $G(\theta)$.

Then the measurement is subtracted to the reference signal $[r_x, r_y]$ to obtain the position error in the fixed reference frame $[\epsilon_x, \epsilon_y]$.

The position error $[\epsilon_x, \epsilon_y]$ is then express in the rotating frame corresponding to the actuators $[\epsilon_u, \epsilon_v]$.

Finally, the control low $K$ links the position errors $[\epsilon_u, \epsilon_v]$ to the actuator forces $[F_u, F_v]$.

The block diagram is shown on figure fig:control_measure_fixed_2dof.

Control with a measure from fixed frame

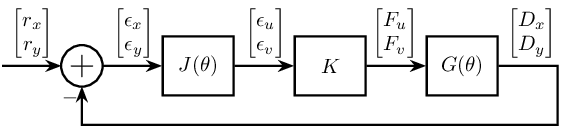
The loop gain is then $L = G(\theta) K J(\theta)$.

QUESTION Is the loop gain is changing with the angle ?

Is \[ G(\theta) J(\theta) = G(\theta_0) J(\theta_0) \] ?

Measurement in the rotating frame

Let's consider that the measurement is in the rotating reference frame.

The corresponding block diagram is shown figure fig:control_measure_rotating_2dof

Control with a measure from rotating frame

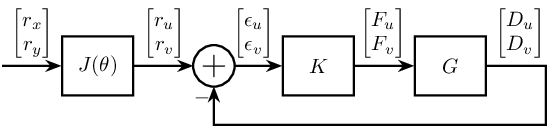
The loop gain is $L = G K$.

Effect of the rotating Speed

<<sec:effect_rot_speed>>

TODO Use realistic parameters for the mass of the sample and stiffness of the X-Y stage

TODO Check if the plant is changing a lot when we are not turning to when we are turning at the maximum speed (60rpm)

Effect of the X-Y stage stiffness

<<sec:effect_stiffness>>

TODO At full speed, check how the coupling changes with the stiffness of the actuators