nass-micro-station-measurements/static-to-dynamic/index.org

• Static measurement of the translation stage
  • ZIP file containing the data and matlab files
  • Notes
  • Data Pre-processing
  • Matlab - Data Import
  • Data - Plot
  • Translate to time domain
  • Compute the PSD
• Static Measurement of the spindle
  • ZIP file containing the data and matlab files

#+TITLE:Static Measurements

The goal here is to analyze the static measurement on the station (guiding error of each stage) and convert them to dynamic disturbances that can be use in the model of the micro-station.

The report by H-P van der Kleij on the static measurement of the ID31 station is available here.

Static measurement of the translation stage

<<sec:static_ty>>

ZIP file containing the data and matlab files   ignore

All the files (data and Matlab scripts) are accessible here.

Notes

• 5530: Straightness Plot: Yz
• Filename: r:\home\PDMU\PEL\Measurement_library\ID31\ID31_u_station\TY\12_12_2018\linear deviation _tyz_401_points.txt
• Acquisition date: 09/01/2019 13:49:42
• Current date: 08/03/2019 08:46:35
• Measurement Type: STRAIGHTNESS vertical
• Travel Mode: Bidirectional
• Number of Target Positions: 401
• Number of total data pairs: 2406
• Number of total data runs:6
• Position Value Units: millimeters
• Error Value Units: micrometers

Environmental Data	Min	Max	Avg
Air Temp (C)	024,57	024,61	024,59
Air Prs (mm)	742,56	743,29	742,83
Air Hmd (%)	024,00	024,00	024,00
MT1 Temp (C)			020,00
MT2 Temp (C)	024,40	024,44	024,42
MT3 Temp (C)	024,32	024,36	024,34

In a very schematic way, the measurement is explained on figure fig:guiding_error. The positioning error $d$ is measure as a function of $x$. Because the measurement is done in a static way, the dynamics of the station (represented by the mass-spring-damper system on the schematic) does not play a role in the measure.

The obtained data corresponds to the guiding errors.

Schematic of the measurement

Data Pre-processing

  sed 's/\t/  /g;s/\,/./g' "mat/linear_deviation_tyz_401_points.txt" > mat/data_tyz.txt

  head "mat/data_tyz.txt"

Run	Pos	TargetValue	ErrorValue
1	1	-4.5E+00	7.5377892E+00
1	2	-4.4775E+00	7.5422246E+00
1	3	-4.455E+00	7.5655617E+00
1	4	-4.4325E+00	7.5149518E+00
1	5	-4.41E+00	7.4886377E+00
1	6	-4.3875E+00	7.437007E+00
1	7	-4.365E+00	7.4449354E+00
1	8	-4.3425E+00	7.3937387E+00
1	9	-4.32E+00	7.3287468E+00

Matlab - Data Import

  filename = 'mat/data_tyz.txt';
  fileID = fopen(filename);
  data = cell2mat(textscan(fileID,'%f  %f  %f  %f', 'collectoutput', 1,'headerlines',1));
  fclose(fileID);

Data - Plot

First, we plot the straightness error as a function of the position (figure fig:raw_data_tyz).

  figure;
  hold on;
  for i=1:data(end, 1)
    plot(data(data(:, 1) == i, 3), data(data(:, 1) == i, 4), '-k');
  end
  hold off;
  xlabel('Target Value [mm]'); ylabel('Error Value [$\mu m$]');

  <<plt-matlab>>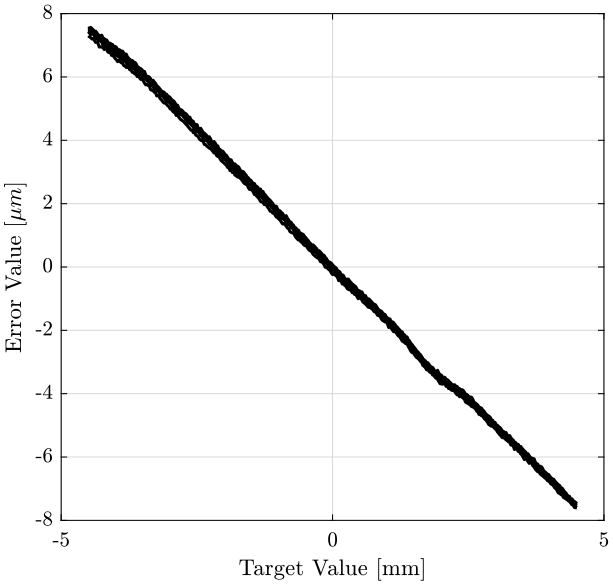

Time domain Data

Then, we compute mean value of each position, and we remove this mean value from the data. The results are shown on figure fig:processed_data_tyz.

  mean_pos = zeros(sum(data(:, 1)==1), 1);
  for i=1:sum(data(:, 1)==1)
    mean_pos(i) = mean(data(data(:, 2)==i, 4));
  end

  figure;
  hold on;
  for i=1:data(end, 1)
    filt = data(:, 1) == i;
    plot(data(filt, 3), data(filt, 4) - mean_pos, '-k');
  end
  hold off;
  xlabel('Target Value [mm]'); ylabel('Error Value [$\mu m$]');

  <<plt-matlab>>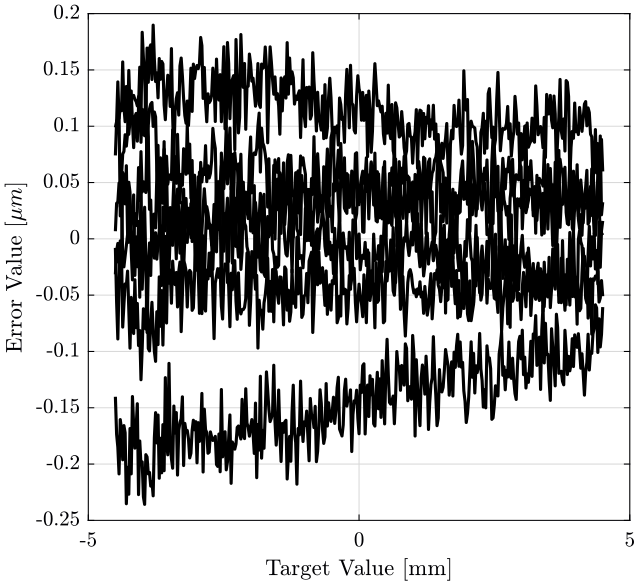

caption

Translate to time domain

We here make the assumptions that, during a scan with the translation stage, the Z motion of the translation stage will follow the guiding error measured.

We then create a time vector $t$ from 0 to 1 second that corresponds to a typical scan, and we plot the guiding error as a function of the time on figure fig:time_domain_tyz.

  t = linspace(0, 1, length(data(data(:, 1)==1, 4)));

  figure;
  hold on;
  plot(t, data(data(:, 1) == 1, 4) - mean_pos, '-k');
  hold off;
  xlabel('Time [s]'); ylabel('Error Value [um]');

  <<plt-matlab>>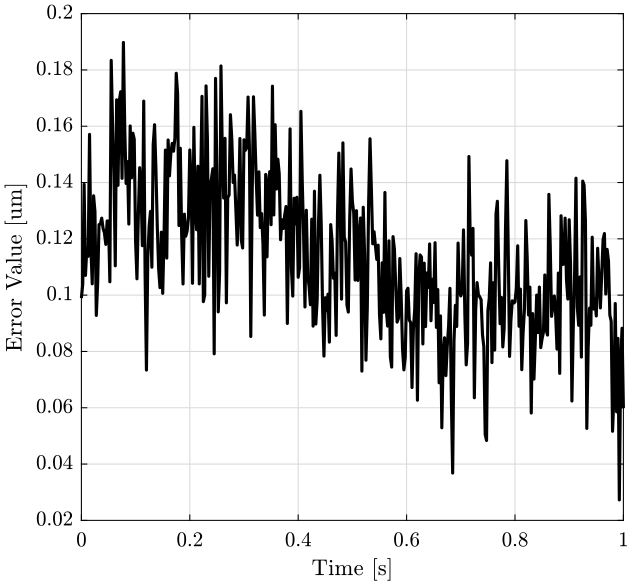

caption

Compute the PSD

We first compute some parameters that will be used for the PSD computation.

  dt = t(2)-t(1);

  Fs = 1/dt; % [Hz]

  win = hanning(ceil(1*Fs));

We remove the mean position from the data.

  x = data(data(:, 1) == 1, 4) - mean_pos;

And finally, we compute the power spectral density of the displacement obtained in the time domain.

The result is shown on figure fig:psd_tyz.

  [pxx, f] = pwelch(x, win, [], [], Fs);

  pxx_t = zeros(length(pxx), data(end, 1));

  for i=1:data(end, 1)
    x = data(data(:, 1) == i, 4) - mean_pos;
    [pxx, f] = pwelch(x, win, [], [], Fs);
    pxx_t(:, i) = pxx;
  end

  figure;
  hold on;
  plot(f, sqrt(mean(pxx_t, 2)), 'k-');
  hold off;
  xlabel('Frequency (Hz)');
  ylabel('Amplitude Spectral Density $\left[\frac{m}{\sqrt{Hz}}\right]$');
  set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log');

  <<plt-matlab>>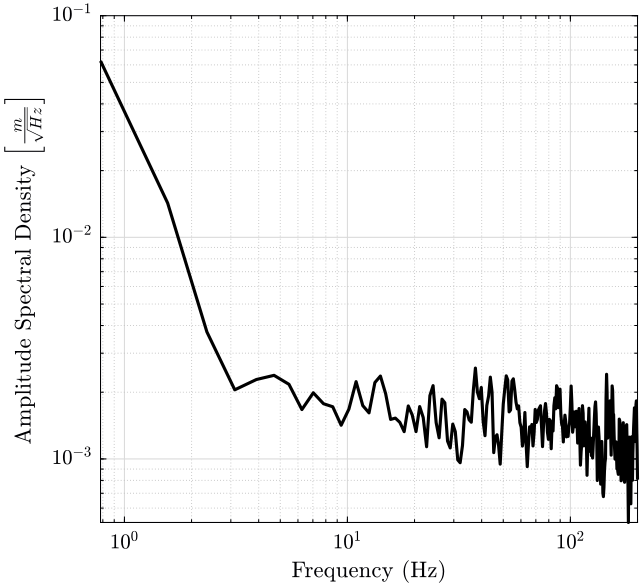

PSD of the Z motion when scanning with Ty at 1Hz

TODO Static Measurement of the spindle

<<sec:spindle_static>>

ZIP file containing the data and matlab files   ignore

All the files (data and Matlab scripts) are accessible here.