50 KiB
Sensor Fusion Paper - Matlab Computation
- Introduction
- ZIP file containing the data and matlab files
- Definition of the plant
- Multiplicative input uncertainty
- Specifications and performance weights
- Upper bounds on the norm of the complementary filters for NP, RS and RP
- H-Infinity synthesis of complementary filters
- Complementary filters using analytical formula
- Comparison of complementary filters
- Controller Analysis
- Nominal Stability and Nominal Performance
- Robust Stability and Robust Performance
- Pre-filter
- Matlab Functions
Introduction ignore
The control architecture studied here is shown on figure fig:sf_arch_class_prefilter where:
- $G^{\prime}$ is the plant to control
- $K = G^{-1} H_L^{-1}$ is the controller used with $G$ a model of the plant
- $H_L$ and $H_H$ are complementary filters ($H_L + H_H = 1$)
- $K_r$ is a pre-filter that can be added

Here is the outline of the matlab analysis for this control architecture:
- Section sec:plant: The plant model $G$ is defined
- Section sec:uncertainty: The plant uncertainty set $\Pi_I$ is defined using the multiplicative input uncertainty: $\Pi_I: \ G^\prime = G (1 + w_I \Delta)$. Thus the weight $w_I$ is defined such that the true system dynamics is included in the set $\Pi_I$
- Section sec:specifications: From the specifications on performance that are expressed in terms of upper bounds of $S$ and $T$, performance weights $w_S$ and $w_T$ are derived such that the goal is to obtain $|S| < \frac{1}{|w_S|}$ and $|T| < \frac{1}{|w_T|}, \ \forall \omega$
- Section sec:upper_bounds_filters: Upper bounds on the magnitude of the complementary filters $|H_L|$ and $|H_H|$ are defined in order to ensure Nominal Performance (NP), Robust Stability (RS) and Robust Performance (RP)
- Section sec:h_infinity: $H_L$ and $H_H$ are synthesize using the $\mathcal{H}_\infty$ synthesis such that $|H_L|$ and $|H_H|$ are within the specified bounds and such that $H_L + H_H = 1$ (complementary property)
- Section sec:analytical_formula: Analytical formulas of complementary filters are used
- Section sec:comp_filters: The obtained complementary filters using the $\mathcal{H}_\infty$ synthesis and the analytical formula are compared
- Section sec:controller_analysis: The obtain controller $K = G^{-1} H_H^{-1}$ is analyzed
- Section sec:nominal_stability_performance: The Nominal Stability (NS) and Nominal Performance conditions are verified
- Section sec:robustness_analysis: Robust Stability and Robust Performance conditions are studied
- Section sec:pre_filter: A pre-filter that is used to limit the input usage due to the change of the reference is added
ZIP file containing the data and matlab files ignore
All the files (data and Matlab scripts) are accessible here.
Definition of the plant
<<sec:plant>>
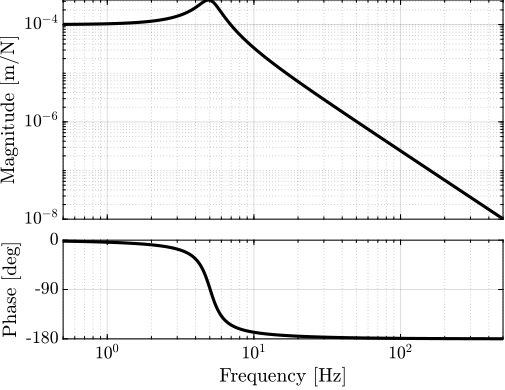
The studied system consists of a solid positioned on top of a motorized uni-axial soft suspension.
The absolute position $x$ of the solid is measured using an inertial sensor and a force $F$ can be applied to the mass using a voice coil actuator.
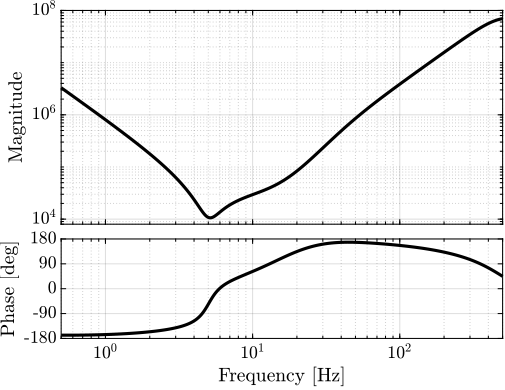
The model of the system is represented on figure fig:mech_sys_alone where the mass of the solid is $m = 10\ [kg]$, the stiffness of the suspension is $k = 10^4\ [N/m]$ and the damping of the system is $c = 10^2\ [N/(m/s)]$.

The plant $G$ is defined on matlab and its bode plot is shown on figure fig:bode_plot_mech_sys.
m = 10; % mass [kg]
k = 1e4; % stiffness [N/m]
c = 1e2; % damping [N/(m/s)]
G = 1/(m*s^2 + c*s + k);Multiplicative input uncertainty
<<sec:uncertainty>> We choose to use the multiplicative input uncertainty to model the plant uncertainty:
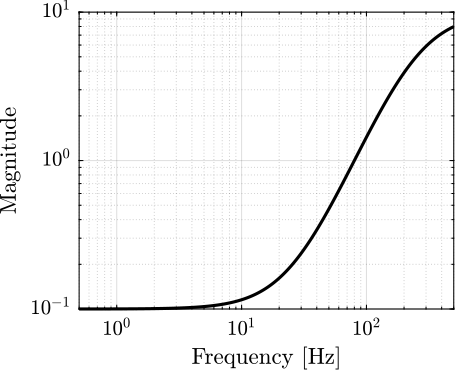
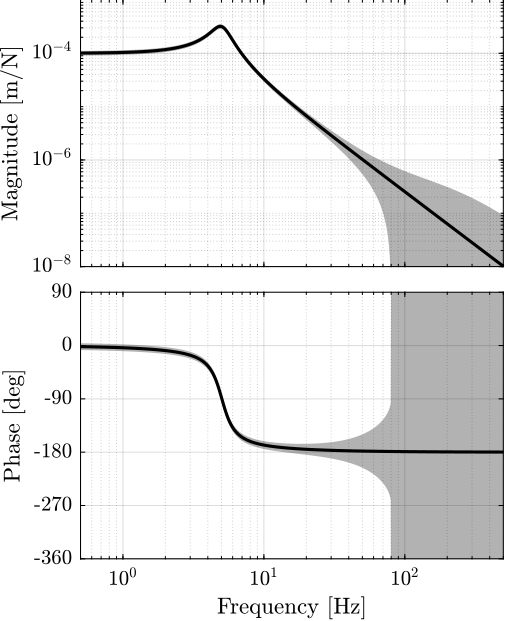
\begin{equation} \Pi_I: \ G^\prime(s) = G(s) (1 + w_I(s) \Delta(s)),\text{ with } |\Delta(j\omega)| < 1 \ \forall \omega \end{equation}The uncertainty weight is shown in figure fig:bode_wi.
wI = createWeight('n', 2, 'w0', 2*pi*80, 'G0', 0.1, 'G1', 10, 'Gc', 1);Elements in the uncertainty set $\Pi_I$ are computed and their bode plot is shown on figure fig:plant_uncertainty_bode_plot.
Specifications and performance weights
<<sec:specifications>>
The control objective is to isolate the displacement $x$ of the mass from the ground motion $w$.
The specifications are described below:
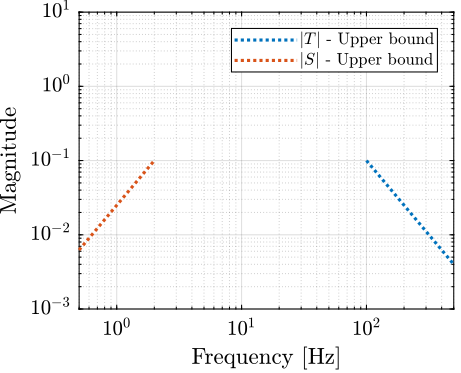
- at least a factor $10$ of disturbance rejection at $2\ \text{Hz}$ and with a slope of $2$ below $2\ \text{Hz}$ until a rejection of $10^3$
- the noise attenuation should be at least $10$ above $100\ \text{Hz}$ and with a slope of $-2$ above
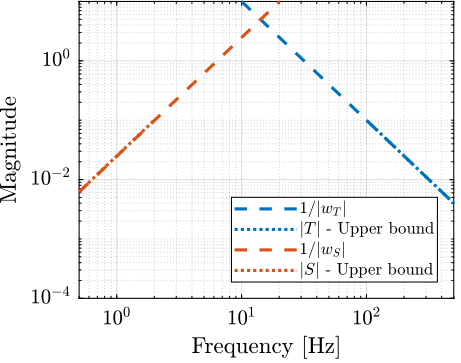
These specifications can be represented as upper bounds on the closed loop transfer functions $S$ and $T$ (see figure fig:bode_requirements).
We now define two weights, $w_S(s)$ and $w_T(s)$ such that $1/|w_S|$ and $1/|w_T|$ are lower than the previously defined upper bounds. Then, the performance specifications are satisfied if the following condition is valid: \[ \big|S(j\omega)\big| < \frac{1}{|w_S(j\omega)|} ; \quad \big|T(j\omega)\big| < \frac{1}{|w_T(j\omega)|}, \quad \forall \omega \]
The weights are defined as follow. They magnitude is compared with the upper bounds on $S$ and $T$ on figure fig:compare_weights_upper_bounds_S_T.
wS = 1600/(s+0.13)^2;
wT = 1000*((s/(2*pi*1000)))^2;Upper bounds on the norm of the complementary filters for NP, RS and RP
<<sec:upper_bounds_filters>>
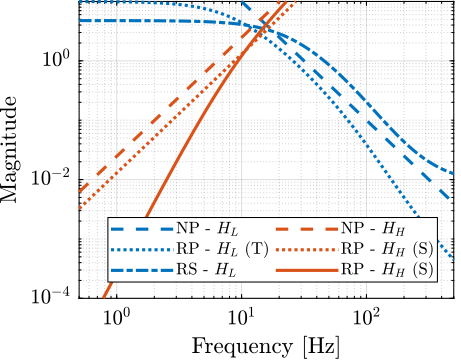
Now that we have defined $w_I$, $w_S$ and $w_T$, we can derive conditions for Nominal Performance, Robust Stability and Robust Performance ($j\omega$ is omitted here for readability):
\begin{align*} \text{NP} &\Leftrightarrow |H_H| < \frac{1}{|w_S|} \text{ and } |H_L| < \frac{1}{|w_T|} \quad \forall \omega \\ \text{RS} &\Leftrightarrow |H_L| < \frac{1}{|w_I| (2 + |w_I|)} \quad \forall \omega \\ \text{RP for } S &\Leftarrow |H_H| < \frac{1 + |w_I|}{|w_S| (2 + |w_I|)} \quad \forall \omega \\ \text{RP for } T &\Leftrightarrow |H_L| < \frac{1}{|w_T| (1 + |w_I|) + |w_I|} \quad \forall \omega \end{align*}These conditions are upper bounds on the complementary filters used for control.
We plot these conditions on figure fig:weights_NP_RS_RP.
H-Infinity synthesis of complementary filters
<<sec:h_infinity>>
We here synthesize the complementary filters using the $\mathcal{H}_\infty$ synthesis. The goal is to specify upper bounds on the norms of $H_L$ and $H_H$ while ensuring their complementary property ($H_L + H_H = 1$).
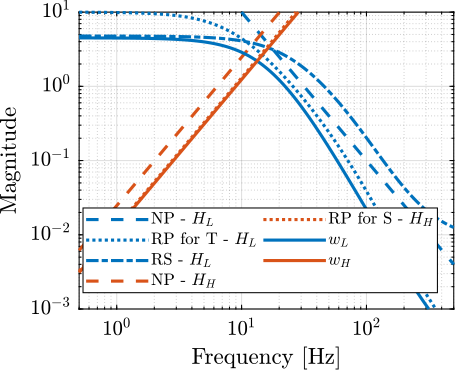
In order to do so, we use the generalized plant shown on figure fig:sf_hinf_filters_plant_b where $w_L$ and $w_H$ weighting transfer functions that will be used to shape $H_L$ and $H_H$ respectively.

The $\mathcal{H}_\infty$ synthesis applied on this generalized plant will give a transfer function $H_L$ (figure fig:sf_hinf_filters_b) such that the $\mathcal{H}_\infty$ norm of the transfer function from $w$ to $[z_H,\ z_L]$ is less than one: \[ \left\| \begin{array}{c} H_L w_L \\ (1 - H_L) w_H \end{array} \right\|_\infty < 1 \]
Thus, if the above condition is verified, we can define $H_H = 1 - H_L$ and we have that: \[ \left\| \begin{array}{c} H_L w_L \\ H_H w_H \end{array} \right\|_\infty < 1 \] Which is almost (with an maximum error of $\sqrt{2}$) equivalent to:
\begin{align*} |H_L| &< \frac{1}{|w_L|}, \quad \forall \omega \\ |H_H| &< \frac{1}{|w_H|}, \quad \forall \omega \end{align*}We then see that $w_L$ and $w_H$ can be used to shape both $H_L$ and $H_H$ while ensuring (by definition of $H_H = 1 - H_L$) their complementary property.

Thus, if we choose $w_L$ and $w_H$ such that $1/|w_L|$ and $1/|w_H|$ lie below the upper bounds of figure fig:weights_NP_RS_RP, we will ensure the NP, RS and RP of the controlled system.
Depending if we are interested only in NP, RS or RP, we can adjust the weights $w_L$ and $w_H$.
omegab = 2*pi*9;
wH = (omegab)^2/(s + omegab*sqrt(1e-5))^2;
omegab = 2*pi*28;
wL = (s + omegab/(4.5)^(1/3))^3/(s*(1e-4)^(1/3) + omegab)^3;We define the generalized plant $P$ on matlab.
P = [0 wL;
wH -wH;
1 0];
And we do the $\mathcal{H}_\infty$ synthesis using the hinfsyn command.
[Hl_hinf, ~, gamma, ~] = hinfsyn(P, 1, 1,'TOLGAM', 0.001, 'METHOD', 'ric', 'DISPLAY', 'on');[Hl_hinf, ~, gamma, ~] = hinfsyn(P, 1, 1,'TOLGAM', 0.001, 'METHOD', 'ric', 'DISPLAY', 'on');
Test bounds: 0.0000 < gamma <= 1.7285
gamma hamx_eig xinf_eig hamy_eig yinf_eig nrho_xy p/f
1.729 4.1e+01 8.4e-12 1.8e-01 0.0e+00 0.0000 p
0.864 3.9e+01 -5.8e-02# 1.8e-01 0.0e+00 0.0000 f
1.296 4.0e+01 8.4e-12 1.8e-01 0.0e+00 0.0000 p
1.080 4.0e+01 8.5e-12 1.8e-01 0.0e+00 0.0000 p
0.972 3.9e+01 -4.2e-01# 1.8e-01 0.0e+00 0.0000 f
1.026 4.0e+01 8.5e-12 1.8e-01 0.0e+00 0.0000 p
0.999 3.9e+01 8.5e-12 1.8e-01 0.0e+00 0.0000 p
0.986 3.9e+01 -1.2e+00# 1.8e-01 0.0e+00 0.0000 f
0.993 3.9e+01 -8.2e+00# 1.8e-01 0.0e+00 0.0000 f
0.996 3.9e+01 8.5e-12 1.8e-01 0.0e+00 0.0000 p
0.994 3.9e+01 8.5e-12 1.8e-01 0.0e+00 0.0000 p
0.993 3.9e+01 -3.2e+01# 1.8e-01 0.0e+00 0.0000 f
Gamma value achieved: 0.9942
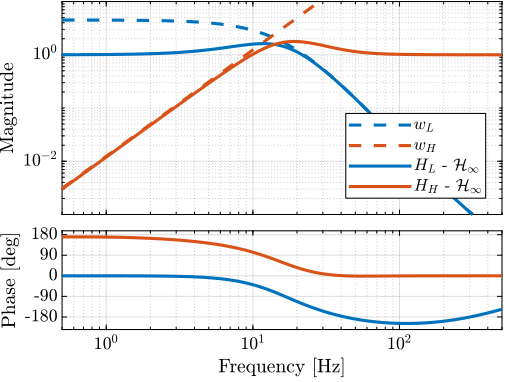
We then define the high pass filter $H_H = 1 - H_L$. The bode plot of both $H_L$ and $H_H$ is shown on figure fig:hinf_filters_results.
Hh_hinf = 1 - Hl_hinf;TODO Complementary filters using analytical formula
<<sec:analytical_formula>>
- The problem here is that the High pass filter gain goes to zero at high frequency, and when inverted, it will go to infinity.
We here use analytical formula for the complementary filters $H_L$ and $H_H$.
The first two formulas that are used to generate complementary filters are:
\begin{align*} H_L(s) &= \frac{(1+\alpha) (\frac{s}{\omega_0})+1}{\left((\frac{s}{\omega_0})+1\right) \left((\frac{s}{\omega_0})^2 + \alpha (\frac{s}{\omega_0}) + 1\right)}\\ H_H(s) &= \frac{(\frac{s}{\omega_0})^2 \left((\frac{s}{\omega_0})+1+\alpha\right)}{\left((\frac{s}{\omega_0})+1\right) \left((\frac{s}{\omega_0})^2 + \alpha (\frac{s}{\omega_0}) + 1\right)} \end{align*}where:
- $\omega_0$ is the blending frequency in rad/s.
-
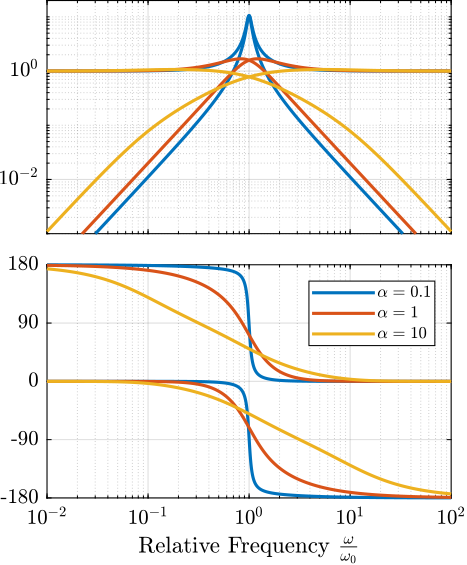
$\alpha$ is used to change the shape of the filters:
- Small values for $\alpha$ will produce high magnitude of the filters $|H_L(j\omega)|$ and $|H_H(j\omega)|$ near $\omega_0$ but smaller value for $|H_L(j\omega)|$ above $\approx 1.5 \omega_0$ and for $|H_H(j\omega)|$ below $\approx 0.7 \omega_0$
- A large $\alpha$ will do the opposite
This is illustrated on figure fig:comp_filters_param_alpha. As it is usually wanted to have the $\| S \|_\infty < 2$, $\alpha$ between $0.5$ and $1$ gives a good trade-off between the performance and the robustness. The slope of those filters at high and low frequencies is $-2$ and $2$ respectively for $H_L$ and $H_H$.
The parameters $\alpha$ and $\omega_0$ are chosen in order to have that the complementary filters stay below the defined upper bounds.
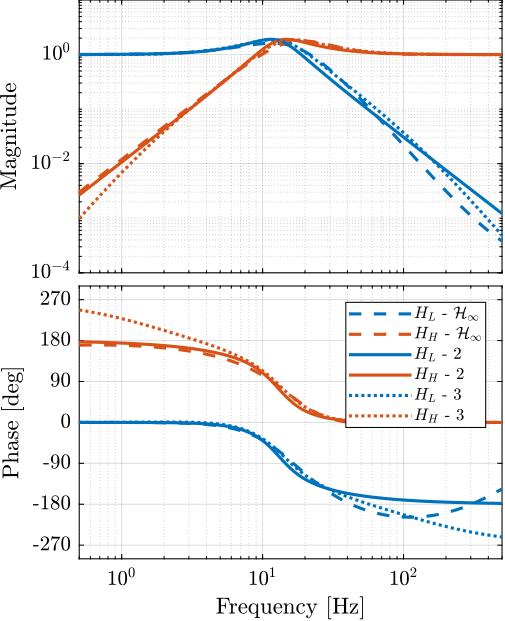
The obtained complementary filters are shown on figure fig:complementary_filters_second_order. The Robust Performance is not fulfilled for $T$, and we see that the RP condition as a slop of $-3$. We thus have to use different formula for the complementary filters here.
w0 = 2*pi*13;
alpha = 0.8;
Hh2_ana = (s/w0)^2*((s/w0)+1+alpha)/(((s/w0)+1)*((s/w0)^2 + alpha*(s/w0) + 1));
Hl2_ana = ((1+alpha)*(s/w0)+1)/(((s/w0)+1)*((s/w0)^2 + alpha*(s/w0) + 1));The following formula gives complementary filters with slopes of $-3$ and $3$:
\begin{align*} H_L(s) &= \frac{\left(1+(\alpha+1)(\beta+1)\right) (\frac{s}{\omega_0})^2 + (1+\alpha+\beta)(\frac{s}{\omega_0}) + 1}{\left(\frac{s}{\omega_0} + 1\right) \left( (\frac{s}{\omega_0})^2 + \alpha (\frac{s}{\omega_0}) + 1 \right) \left( (\frac{s}{\omega_0})^2 + \beta (\frac{s}{\omega_0}) + 1 \right)}\\ H_H(s) &= \frac{(\frac{s}{\omega_0})^3 \left( (\frac{s}{\omega_0})^2 + (1+\alpha+\beta) (\frac{s}{\omega_0}) + (1+(\alpha+1)(\beta+1)) \right)}{\left(\frac{s}{\omega_0} + 1\right) \left( (\frac{s}{\omega_0})^2 + \alpha (\frac{s}{\omega_0}) + 1 \right) \left( (\frac{s}{\omega_0})^2 + \beta (\frac{s}{\omega_0}) + 1 \right)} \end{align*}The parameters are:
- $\omega_0$ is the blending frequency in rad/s
- $\alpha$ and $\beta$ that are used to change the shape of the filters similarly to the parameter $\alpha$ for the second order complementary filters
The filters are defined below and the result is shown on figure fig:complementary_filters_third_order where we can see that the complementary filters are below the defined upper bounds.
alpha = 1;
beta = 10;
w0 = 2*pi*14;
Hh3_ana = (s/w0)^3 * ((s/w0)^2 + (1+alpha+beta)*(s/w0) + (1+(alpha+1)*(beta+1)))/((s/w0 + 1)*((s/w0)^2+alpha*(s/w0)+1)*((s/w0)^2+beta*(s/w0)+1));
Hl3_ana = ((1+(alpha+1)*(beta+1))*(s/w0)^2 + (1+alpha+beta)*(s/w0) + 1)/((s/w0 + 1)*((s/w0)^2+alpha*(s/w0)+1)*((s/w0)^2+beta*(s/w0)+1));Comparison of complementary filters
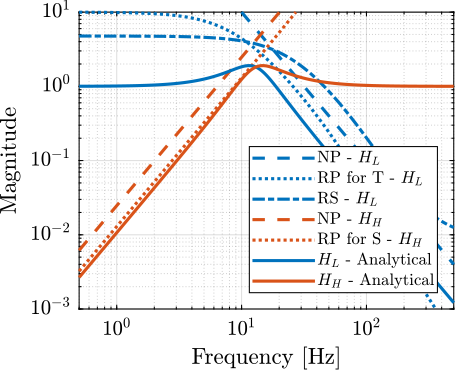
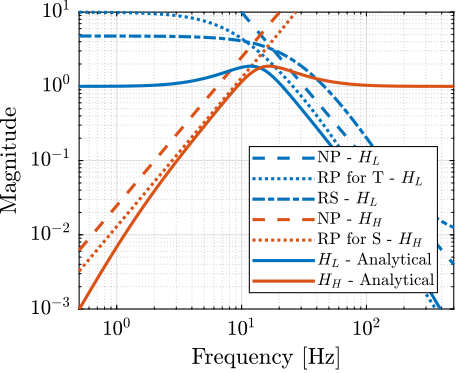
<<sec:comp_filters>> The generated complementary filters using $\mathcal{H}_\infty$ and the analytical formulas are compared on figure fig:comp_hinf_analytical.
Although they are very close to each other, there is some difference to note here:
- the analytical formula provides a very simple way to generate the complementary filters (and thus the controller), they could even be used to tune the controller online using the parameters $\alpha$ and $\omega_0$. However, these formula have the property that $|H_H|$ and $|H_L|$ are symmetrical with the frequency $\omega_0$ which may not be desirable.
- while the $\mathcal{H}_\infty$ synthesis of the complementary filters is not as straightforward as using the analytical formula, it provides a more optimized procedure to obtain the complementary filters
The complementary filters obtained with the $\mathcal{H}_\infty$ will be used for further analysis.
Controller Analysis
<<sec:controller_analysis>>
The controller $K$ is computed from the plant model $G$ and the low pass filter $H_H$: \[ K = G^{-1} H_H^{-1} \]
As this is not proper and thus realizable, a second order low pass filter is added with a crossover frequency much larger than the control bandwidth.
omega = 2*pi*500;
K = 1/(Hh_hinf*G) * 1/((1+s/omega)*(1+s/omega+(s/omega)^2));zpk(K)
ans =
4.961e12 (s+9.915e04) (s^2 + 5s + 500) (s^2 + 284.6s + 2.135e04) (s^2 + 130.5s + 9887)
--------------------------------------------------------------------------------------------------
(s+9.914e04) (s+6283) (s^2 + 0.3576s + 0.03198) (s^2 + 413.8s + 6.398e04) (s^2 + 6283s + 3.948e07)
Continuous-time zero/pole/gain model.
The bode plot of the controller is shown on figure fig:bode_plot_controller:
- two integrator are present at low frequency
- the resonance of the plant at $3.5\ \text{Hz}$ is inverted (notched)
- a lead is added at $10\ \text{Hz}$
Nominal Stability and Nominal Performance
<<sec:nominal_stability_performance>>
The nominal stability of the system is first checked with the allmargin matlab command.
allmargin(K*G*Hl_hinf)allmargin(K*G*Hl_hinf)
ans =
struct with fields:
GainMargin: 3.86196691340257
GMFrequency: 225.992831144248
PhaseMargin: 34.0890006269983
PMFrequency: 88.3632737129296
DelayMargin: 0.0067331740287082
DMFrequency: 88.3632737129296
Stable: 1
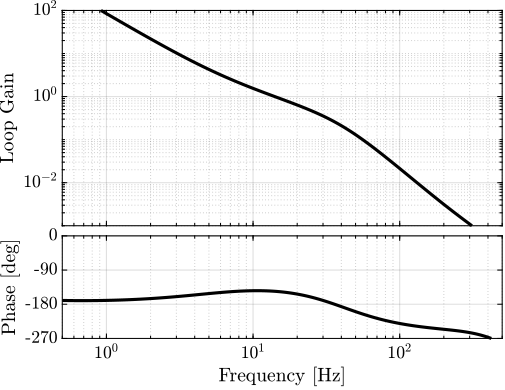
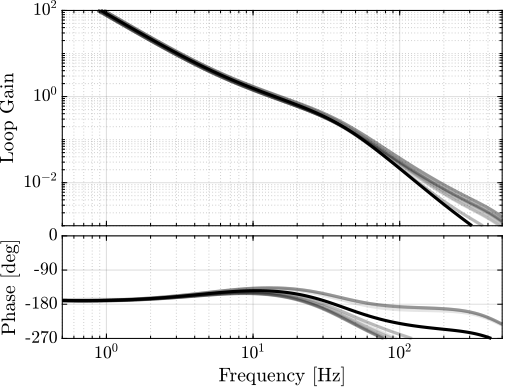
The system is stable and the stability margins are good.
The bode plot of the loop gain $L = K*G*H_L$ is shown on figure fig:bode_plot_loop_gain.
In order to check the Nominal Performance of the system, we compute the sensibility and the complementary sensibility transfer functions.
S = 1/(K*G*Hl_hinf + 1);
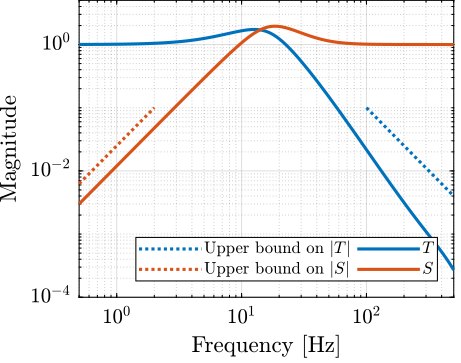
T = K*G*Hl_hinf/(K*G*Hl_hinf + 1);We then compare their norms with the upper bounds on the performance of the system (figure fig:verification_NP). As expected, we guarantee the Nominal Performance of the system.
Robust Stability and Robust Performance
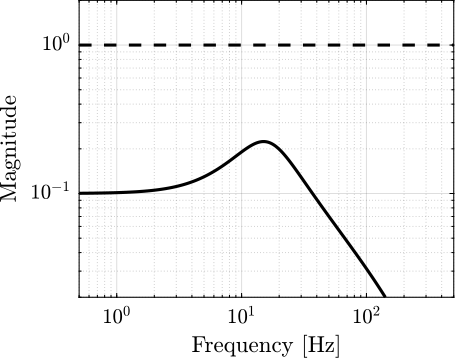
<<sec:robustness_analysis>> In order to verify the Robust stability of the system, we can use the following equivalence: \[ \text{RS} \Leftrightarrow \left| w_I T \right| < 1 \quad \forall \omega \]
This is shown on figure fig:robust_stability.
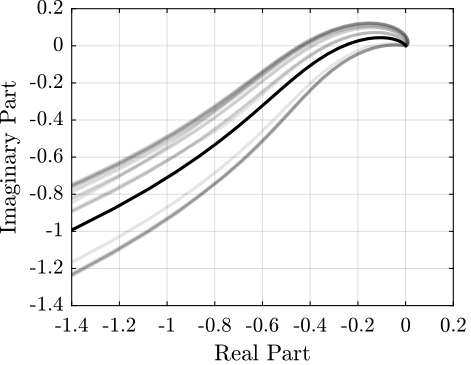
To check Robust Stability, we can also look at the loop gain of the uncertain system (figure fig:loop_gain_robustness) or the Nyquist plot (figure fig:nyquist_robustness).
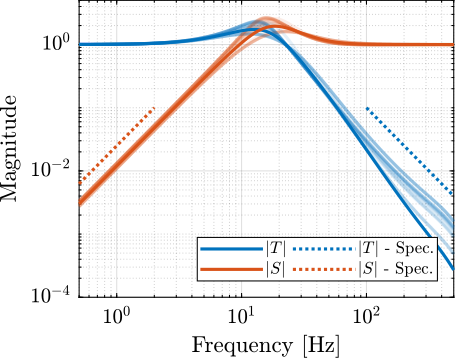
The Robust Performance is verified by plotting $|S|$ and $|T|$ for the uncertain system along side the upper bounds defined for performance. This is shown on figure fig:robust_performance_result and we can indeed confirmed that the robust performance property of the system is valid.
Pre-filter
<<sec:pre_filter>>
For now, we have not specified any performance requirements on the input usage due to change of reference. Do limit the input usage due to change of reference, we can use a pre-filter $K_r$ as shown on figure fig:sf_arch_class_prefilter.
If we want a response time of 0.01 second, we can choose a first order low pass filter with a crossover frequency at $1/0.01 = 100\ \text{Hz}$ as defined below.
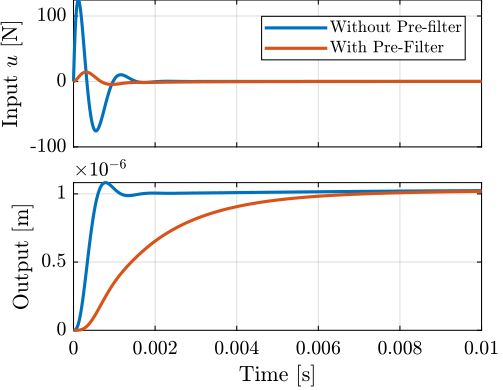
Kr = 1/(1+s/2/pi/100);We then run a simulation for a step of $1\mu m$ for the system without and with the pre-filter $K_r$ (figure fig:u_and_y_with_Kr). This confirms that a pre-filter can be used to limit the input usage due to change of reference using this architecture.
t = linspace(0, 0.01, 500);
opts = stepDataOptions;
opts.StepAmplitude = 1e-6;
u = step((K)/(1+G*K*Hl_hinf), t, opts);
uf = step((Kr*K)/(1+G*K*Hl_hinf), t, opts);
y = step((K*G)/(1+G*K*Hl_hinf), t, opts);
yf = step((Kr*G*K)/(1+G*K*Hl_hinf), t, opts);Matlab Functions
<<sec:matlab_functions>>
createWeight
<<sec:createWeight>>
This Matlab function is accessible here.
function [W] = createWeight(args)
% createWeight -
%
% Syntax: [in_data] = createWeight(in_data)
%
% Inputs:
% - n - Weight Order
% - G0 - Low frequency Gain
% - G1 - High frequency Gain
% - Gc - Gain of W at frequency w0
% - w0 - Frequency at which |W(j w0)| = Gc
%
% Outputs:
% - W - Generated Weight
arguments
args.n (1,1) double {mustBeInteger, mustBePositive} = 1
args.G0 (1,1) double {mustBeNumeric, mustBePositive} = 0.1
args.G1 (1,1) double {mustBeNumeric, mustBePositive} = 10
args.Gc (1,1) double {mustBeNumeric, mustBePositive} = 1
args.w0 (1,1) double {mustBeNumeric, mustBePositive} = 1
end
mustBeBetween(args.G0, args.Gc, args.G1);
s = tf('s');
W = (((1/args.w0)*sqrt((1-(args.G0/args.Gc)^(2/args.n))/(1-(args.Gc/args.G1)^(2/args.n)))*s + (args.G0/args.Gc)^(1/args.n))/((1/args.G1)^(1/args.n)*(1/args.w0)*sqrt((1-(args.G0/args.Gc)^(2/args.n))/(1-(args.Gc/args.G1)^(2/args.n)))*s + (1/args.Gc)^(1/args.n)))^args.n;
end
% Custom validation function
function mustBeBetween(a,b,c)
if ~((a > b && b > c) || (c > b && b > a))
eid = 'createWeight:inputError';
msg = 'Gc should be between G0 and G1.';
throwAsCaller(MException(eid,msg))
end
end
plotMagUncertainty
<<sec:plotMagUncertainty>>
This Matlab function is accessible here.
function [p] = plotMagUncertainty(W, freqs, args)
% plotMagUncertainty -
%
% Syntax: [p] = plotMagUncertainty(W, freqs, args)
%
% Inputs:
% - W - Multiplicative Uncertainty Weight
% - freqs - Frequency Vector [Hz]
% - args - Optional Arguments:
% - G
% - color_i
% - opacity
%
% Outputs:
% - p - Plot Handle
arguments
W
freqs double {mustBeNumeric, mustBeNonnegative}
args.G = tf(1)
args.color_i (1,1) double {mustBeInteger, mustBeNonnegative} = 0
args.opacity (1,1) double {mustBeNumeric, mustBeNonnegative} = 0.3
args.DisplayName char = ''
end
% Get defaults colors
colors = get(groot, 'defaultAxesColorOrder');
p = patch([freqs flip(freqs)], ...
[abs(squeeze(freqresp(args.G, freqs, 'Hz'))).*(1 + abs(squeeze(freqresp(W, freqs, 'Hz')))); ...
flip(abs(squeeze(freqresp(args.G, freqs, 'Hz'))).*max(1 - abs(squeeze(freqresp(W, freqs, 'Hz'))), 1e-6))], 'w', ...
'DisplayName', args.DisplayName);
if args.color_i == 0
p.FaceColor = [0; 0; 0];
else
p.FaceColor = colors(args.color_i, :);
end
p.EdgeColor = 'none';
p.FaceAlpha = args.opacity;
end
plotPhaseUncertainty
<<sec:plotPhaseUncertainty>>
This Matlab function is accessible here.
function [p] = plotPhaseUncertainty(W, freqs, args)
% plotPhaseUncertainty -
%
% Syntax: [p] = plotPhaseUncertainty(W, freqs, args)
%
% Inputs:
% - W - Multiplicative Uncertainty Weight
% - freqs - Frequency Vector [Hz]
% - args - Optional Arguments:
% - G
% - color_i
% - opacity
%
% Outputs:
% - p - Plot Handle
arguments
W
freqs double {mustBeNumeric, mustBeNonnegative}
args.G = tf(1)
args.color_i (1,1) double {mustBeInteger, mustBeNonnegative} = 0
args.opacity (1,1) double {mustBeNumeric, mustBePositive} = 0.3
args.DisplayName char = ''
end
% Get defaults colors
colors = get(groot, 'defaultAxesColorOrder');
% Compute Phase Uncertainty
Dphi = 180/pi*asin(abs(squeeze(freqresp(W, freqs, 'Hz'))));
Dphi(abs(squeeze(freqresp(W, freqs, 'Hz'))) > 1) = 360;
% Compute Plant Phase
G_ang = 180/pi*angle(squeeze(freqresp(args.G, freqs, 'Hz')));
p = patch([freqs flip(freqs)], [G_ang+Dphi; flip(G_ang-Dphi)], 'w', ...
'DisplayName', args.DisplayName);
if args.color_i == 0
p.FaceColor = [0; 0; 0];
else
p.FaceColor = colors(args.color_i, :);
end
p.EdgeColor = 'none';
p.FaceAlpha = args.opacity;
end