test-bench-vionic/index.org

Encoder Renishaw Vionic - Test Bench

• Introduction
• Encoder Model
• Test-Bench Description
• Measurement procedure
• Measurement Results
  • Noise Measurement
    • Analysis

Introduction   ignore

You can find below the document of:

• Vionic Encoder
• Linear Scale

We would like to characterize the encoder measurement system.

In particular, we would like to measure:

• Power Spectral Density of the measurement noise
• Bandwidth of the sensor
• Linearity of the sensor

Picture of the Vionic Encoder

Encoder Model

The Encoder is characterized by its dynamics $G_m(s)$ from the "true" displacement $y$ to measured displacement $y_m$. Ideally, this dynamics is constant over a wide frequency band with very small phase drop.

It is also characterized by its measurement noise $n$ that can be described by its Power Spectral Density (PSD).

The model of the encoder is shown in Figure fig:encoder-model-schematic.

  \begin{tikzpicture}
    \node[block] (G) at (0,0){$G_m(s)$};
    \node[addb, left=0.8 of G] (add){};

    \draw[<-] (add.west) -- ++(-1.0, 0) node[above right]{$y$};
    \draw[->] (add.east) -- (G.west);
    \draw[->] (G.east) -- ++(1.0, 0) node[above left]{$y_m$};
    \draw[<-] (add.north) -- ++(0, 0.6) node[below right](n){$n$};

    \begin{scope}[on background layer]
      \node[fit={(add.west|-G.south) (n.north-|G.east)}, inner sep=8pt, draw, dashed, fill=black!20!white] (P) {};
      \node[below left] at (P.north east) {Encoder};
    \end{scope}
  \end{tikzpicture}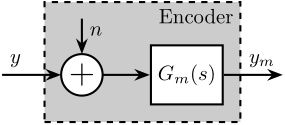

Model of the Encoder

Characteristics	Manual	Specifications
Range	Ruler length	> 200 [um]
Resolution	2.5 [nm]	< 50 [nm rms]
Sub-Divisional Error	$< \pm 15\,nm$
Bandwidth	To be checked	> 5 [kHz]

Expected interpolation errors for the Vionic Encoder

Test-Bench Description

To measure the noise $n$ of the encoder, one can rigidly fix the head and the ruler together such that no motion should be measured. Then, the measured signal $y_m$ corresponds to the noise $n$.

In order to measure the linearity, we have to compare the measured displacement with a reference sensor with a known linearity. An interferometer or capacitive sensor should work fine. An actuator should also be there so impose a displacement.

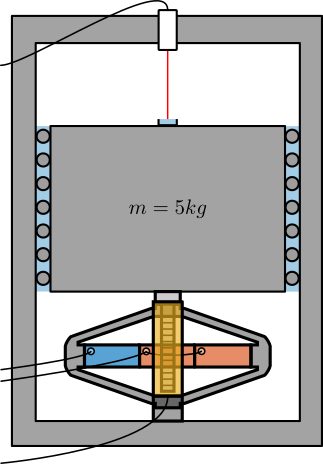
One idea is to use the test-bench shown in Figure fig:test_bench_encoder_calibration.

The APA300ML is used to excite the mass in a broad bandwidth. The motion is measured at the same time by the Vionic Encoder and by an interferometer (most likely an Attocube).

As the interferometer has a very large bandwidth, we should be able to estimate the bandwidth of the encoder is it is less than the Nyquist frequency (~ 5kHz).

Schematic of the test bench

To measure the noise of the sensor, we can also simply measure the output signal when the relative motion between the encoder and the ruler is null. This can be done by clamping the two as done in the mounting strut tool (Figure fig:test_bench_measure_noise).

Mounting Strut test bench as a clamping method to measure the encoder noise.

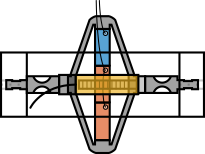
Measurement procedure

Measurement Results

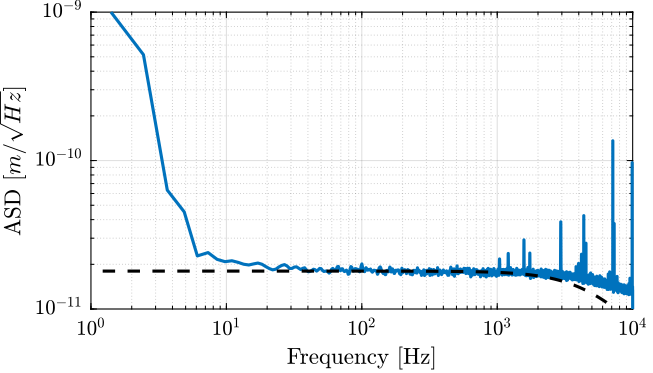
Noise Measurement

Analysis   ignore

load('noise_meas_100s_20kHz.mat', 't', 'x');
x = x - mean(x);

figure;
hold on;
plot(t, 1e9*x, '.', 'DisplayName', 'Raw');
plot(t, 1e9*lsim(1/(1 + s/2/pi/500), x, t), 'DisplayName', 'LPF - 500Hz')
hold off;
xlabel('Time [s]');
ylabel('Displacement [nm]');
legend('location', 'northeast');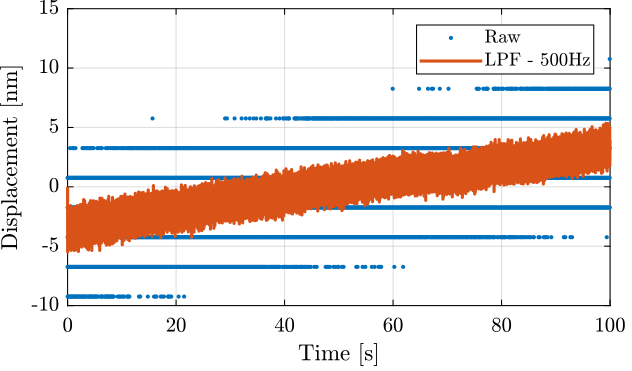

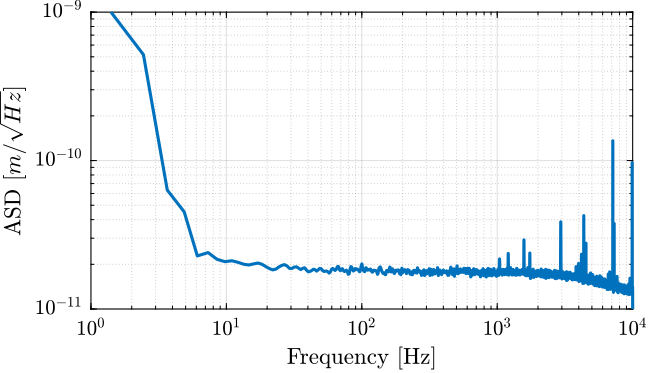
Time domain measurement (raw data and low pass filtered data)

Amplitude Spectral Density of the measured signal

Let's create a transfer function that approximate the measured noise of the encoder.

Gn_e = 1.8e-11/(1 + s/2/pi/5e3);

Measured ASD of the noise and modelled one