15 KiB
Encoder Renishaw Vionic - Test Bench
This report is also available as a pdf.
Introduction ignore
You can find below the documentation of:
In this document, we wish to characterize the performances of the encoder measurement system. In particular, we would like to measure:
- the measurement noise
- the linearity of the sensor
- the bandwidth of the sensor
This document is structured as follow:
- Section sec:vionic_expected_performances: the expected performance of the Vionic encoder system are described
- Section sec:encoder_model: a simple model of the encoder is developed
- Section sec:noise_measurement: the noise of the encoder is measured and a model of the noise is identified
- Section sec:linearity_measurement: the linearity of the sensor is estimated
Expected Performances
<<sec:vionic_expected_performances>>
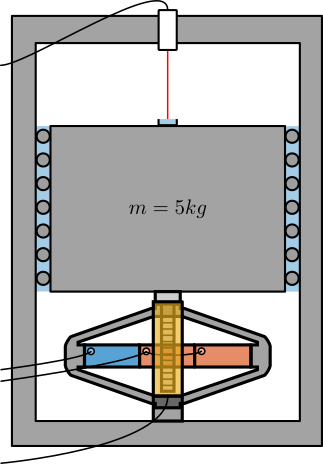
The Vionic encoder is shown in Figure fig:encoder_vionic.

From the Renishaw website:
The VIONiC encoder features the third generation of Renishaw's unique filtering optics that average the contributions from many scale periods and effectively filter out non-periodic features such as dirt. The nominally square-wave scale pattern is also filtered to leave a pure sinusoidal fringe field at the detector. Here, a multiple finger structure is employed, fine enough to produce photocurrents in the form of four symmetrically phased signals. These are combined to remove DC components and produce sine and cosine signal outputs with high spectral purity and low offset while maintaining bandwidth to beyond 500 kHz.
Fully integrated advanced dynamic signal conditioning, Auto Gain , Auto Balance and Auto Offset Controls combine to ensure ultra-low Sub-Divisional Error (SDE) of typically $<\pm 15\, nm$.
This evolution of filtering optics, combined with carefully-selected electronics, provide incremental signals with wide bandwidth achieving a maximum speed of 12 m/s with the lowest positional jitter (noise) of any encoder in its class. Interpolation is within the readhead, with fine resolution versions being further augmented by additional noise-reducing electronics to achieve jitter of just 1.6 nm RMS.
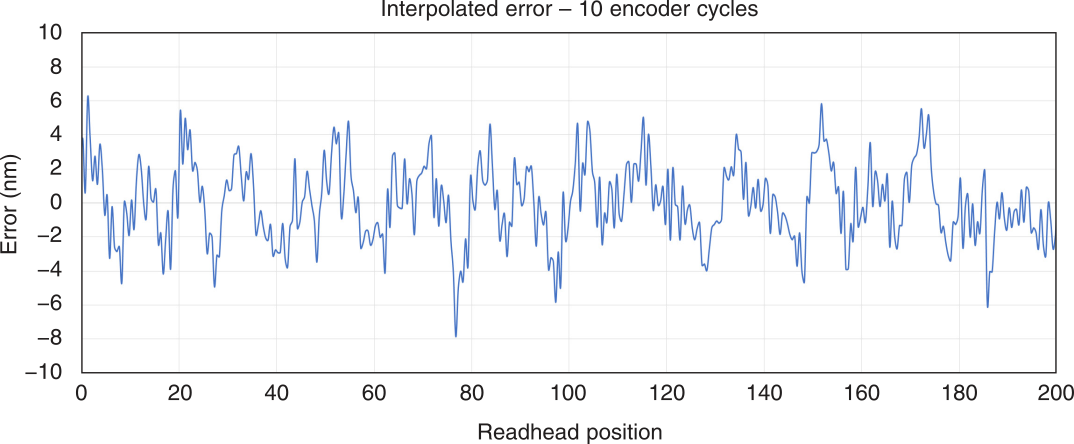
The expected interpolation errors (non-linearity) is shown in Figure fig:vionic_expected_noise.
The characteristics as advertise in the manual as well as our specifications are shown in Table tab:vionic_characteristics.
| Characteristics | Manual | Specification |
|---|---|---|
| Time Delay | < 0.5 ms | |
| Bandwidth | > 500 kHz | > 5 kHz |
| Noise | < 1.6 nm rms | < 50 nm rms |
| Linearity | < +/- 15 nm | |
| Range | Ruler length | > 200 um |
Encoder Model
<<sec:encoder_model>>
The Encoder is characterized by its dynamics $G_m(s)$ from the "true" displacement $y$ to measured displacement $y_m$. Ideally, this dynamics is constant over a wide frequency band with very small phase drop.
It is also characterized by its measurement noise $n$ that can be described by its Power Spectral Density (PSD) $\Gamma_n(\omega)$.
The model of the encoder is shown in Figure fig:encoder-model-schematic.
\begin{tikzpicture}
\node[block] (G) at (0,0){$G_m(s)$};
\node[addb, left=0.8 of G] (add){};
\draw[<-] (add.west) -- ++(-1.0, 0) node[above right]{$y$};
\draw[->] (add.east) -- (G.west);
\draw[->] (G.east) -- ++(1.0, 0) node[above left]{$y_m$};
\draw[<-] (add.north) -- ++(0, 0.6) node[below right](n){$n$};
\begin{scope}[on background layer]
\node[fit={(add.west|-G.south) (n.north-|G.east)}, inner sep=8pt, draw, dashed, fill=black!20!white] (P) {};
\node[below left] at (P.north east) {Encoder};
\end{scope}
\end{tikzpicture}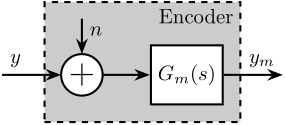
We can also use a transfer function $G_n(s)$ to shape a noise $\tilde{n}$ with unity ASD as shown in Figure fig:vionic_expected_noise.
\begin{tikzpicture}
\node[block] (G) at (0,0){$G_m(s)$};
\node[addb, left=0.8 of G] (add){};
\node[block, above=0.5 of add] (Gn) {$G_n(s)$};
\draw[<-] (add.west) -- ++(-1.0, 0) node[above right]{$y$};
\draw[->] (add.east) -- (G.west);
\draw[->] (G.east) -- ++(1.0, 0) node[above left]{$y_m$};
\draw[->] (Gn.south) -- (add.north) node[above right]{$n$};
\draw[<-] (Gn.north) -- ++(0, 0.6) node[below right](n){$\tilde{n}$};
\begin{scope}[on background layer]
\node[fit={(Gn.west|-G.south) (n.north-|G.east)}, inner sep=8pt, draw, dashed, fill=black!20!white] (P) {};
\node[below left] at (P.north east) {Encoder};
\end{scope}
\end{tikzpicture}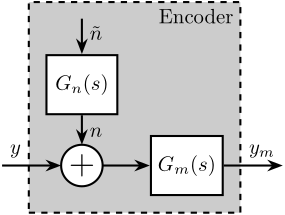
Noise Measurement
<<sec:noise_measurement>>
Test Bench
To measure the noise $n$ of the encoder, one can rigidly fix the head and the ruler together such that no motion should be measured. Then, the measured signal $y_m$ corresponds to the noise $n$.
TODO Thermal drifts
- picture of the setup
- long thermal drifts
- once stabilize, look at the noise
- compute low frequency ASD (may still be thermal drifts of the mechanics and not noise)
Time Domain signals
First we load the data.
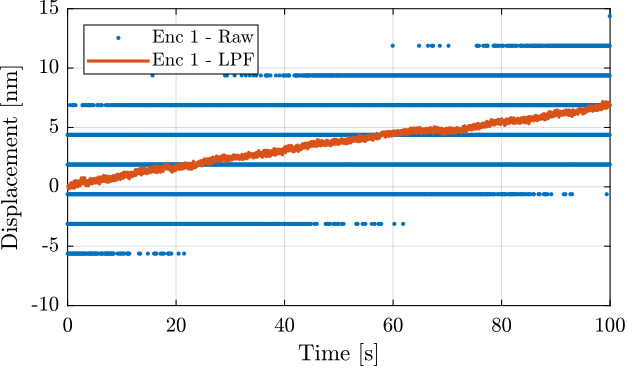
The raw measured data as well as the low pass filtered data (using a first order low pass filter with a cut-off at 10Hz) are shown in Figure fig:vionic_noise_raw_lpf.
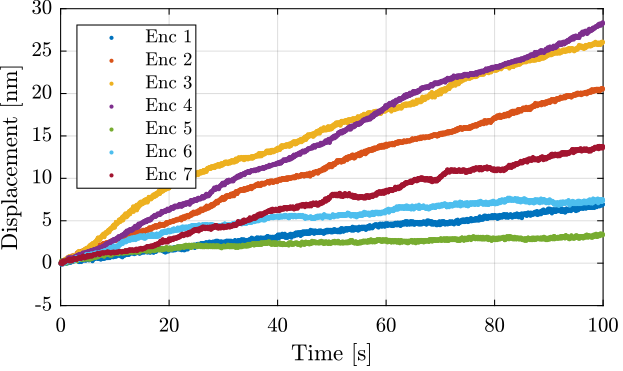
The time domain data for all the encoders are compared in Figure fig:vionic_noise_time.
Noise Spectral Density
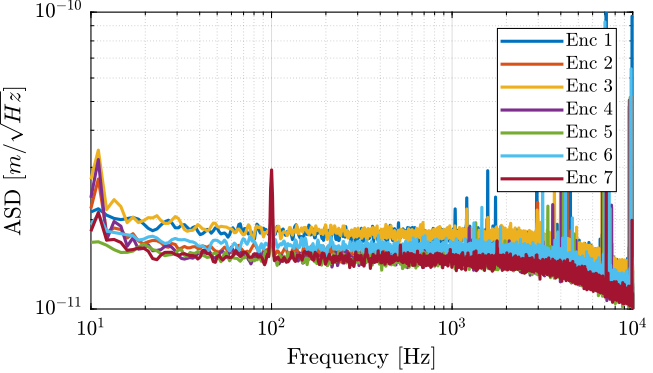
The amplitude spectral density is computed and shown in Figure fig:vionic_noise_asd.
Noise Model
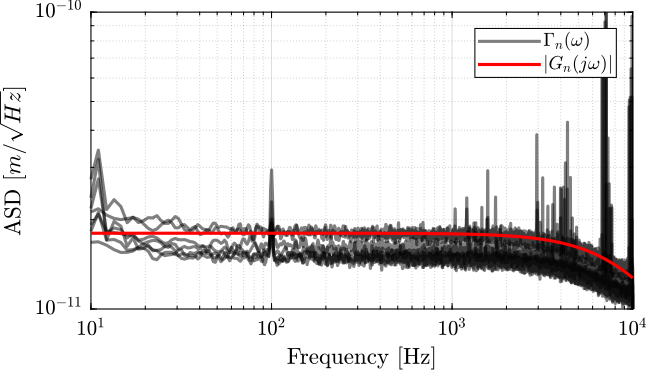
Let's create a transfer function that approximate the measured noise of the encoder.
Gn_e = 1.8e-11/(1 + s/2/pi/1e4);The amplitude of the transfer function and the measured ASD are shown in Figure fig:vionic_noise_asd_model.
Validity of the noise model
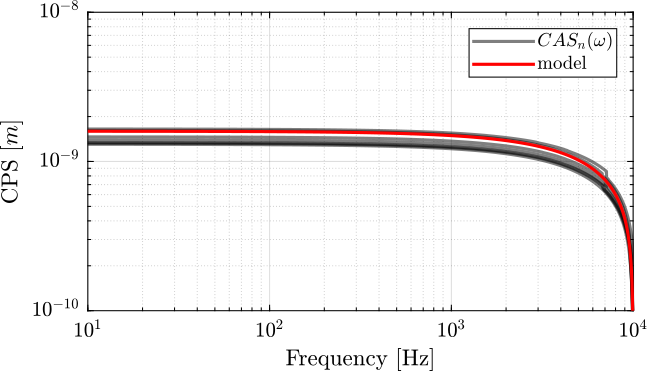
The cumulative amplitude spectrum is now computed and shown in Figure fig:vionic_noise_cas_model.
We can see that the Root Mean Square value of the measurement noise is $\approx 1.6 \, nm$ as advertise in the datasheet.
Linearity Measurement
<<sec:linearity_measurement>>
Test Bench
In order to measure the linearity, we have to compare the measured displacement with a reference sensor with a known linearity. An interferometer or capacitive sensor should work fine. An actuator should also be there so impose a displacement.
One idea is to use the test-bench shown in Figure fig:test_bench_encoder_calibration.
The APA300ML is used to excite the mass in a broad bandwidth. The motion is measured at the same time by the Vionic Encoder and by an interferometer (most likely an Attocube).
As the interferometer has a very large bandwidth, we should be able to estimate the bandwidth of the encoder if it is less than the Nyquist frequency that can be around 10kHz.