test-bench-vionic/test-bench-vionic.org

Encoder Renishaw Vionic - Test Bench

• Introduction
• Encoder Model
• Noise Measurement
  • Test Bench
  • Results
• Linearity Measurement
  • Test Bench
  • Results
• Dynamical Measurement
  • Test Bench
  • Results

---

This report is also available as a pdf.

---

Introduction   ignore

You can find below the document of:

• Vionic Encoder
• Linear Scale

We would like to characterize the encoder measurement system.

In particular, we would like to measure:

• Power Spectral Density of the measurement noise
• Bandwidth of the sensor
• Linearity of the sensor

• 1: 2YA275
• 2: 2YA274
• 3: 2YA273
• 4: 2YA270
• 5: 2YA272
• 6: 2YA271
• 7: 2YJ313

Encoder Model

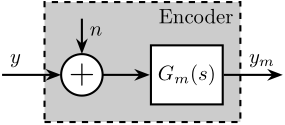
The Encoder is characterized by its dynamics $G_m(s)$ from the "true" displacement $y$ to measured displacement $y_m$. Ideally, this dynamics is constant over a wide frequency band with very small phase drop.

It is also characterized by its measurement noise $n$ that can be described by its Power Spectral Density (PSD).

The model of the encoder is shown in Figure fig:encoder-model-schematic.

  \begin{tikzpicture}
    \node[block] (G) at (0,0){$G_m(s)$};
    \node[addb, left=0.8 of G] (add){};

    \draw[<-] (add.west) -- ++(-1.0, 0) node[above right]{$y$};
    \draw[->] (add.east) -- (G.west);
    \draw[->] (G.east) -- ++(1.0, 0) node[above left]{$y_m$};
    \draw[<-] (add.north) -- ++(0, 0.6) node[below right](n){$n$};

    \begin{scope}[on background layer]
      \node[fit={(add.west|-G.south) (n.north-|G.east)}, inner sep=8pt, draw, dashed, fill=black!20!white] (P) {};
      \node[below left] at (P.north east) {Encoder};
    \end{scope}
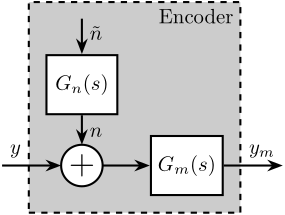
  \end{tikzpicture}

Model of the Encoder

We can also use a transfer function $G_n(s)$ to shape a noise $\tilde{n}$ with unity ASD as shown in Figure fig:vionic_expected_noise.

  \begin{tikzpicture}
    \node[block] (G) at (0,0){$G_m(s)$};
    \node[addb, left=0.8 of G] (add){};
    \node[block, above=0.5 of add] (Gn) {$G_n(s)$};

    \draw[<-] (add.west) -- ++(-1.0, 0) node[above right]{$y$};
    \draw[->] (add.east) -- (G.west);
    \draw[->] (G.east) -- ++(1.0, 0) node[above left]{$y_m$};
    \draw[->] (Gn.south) -- (add.north) node[above right]{$n$};
    \draw[<-] (Gn.north) -- ++(0, 0.6) node[below right](n){$\tilde{n}$};

    \begin{scope}[on background layer]
      \node[fit={(Gn.west|-G.south) (n.north-|G.east)}, inner sep=8pt, draw, dashed, fill=black!20!white] (P) {};
      \node[below left] at (P.north east) {Encoder};
    \end{scope}
  \end{tikzpicture}

Characteristics	Manual	Specifications
Range	Ruler length	> 200 [um]
Resolution	2.5 [nm]	< 50 [nm rms]
Sub-Divisional Error	$< \pm 15\,nm$
Bandwidth	To be checked	> 5 [kHz]

Expected interpolation errors for the Vionic Encoder

Noise Measurement

<<sec:noise_measurement>>

Test Bench

To measure the noise $n$ of the encoder, one can rigidly fix the head and the ruler together such that no motion should be measured. Then, the measured signal $y_m$ corresponds to the noise $n$.

Results

First we load the data.

%% Load Data
enc1 = load('noise_meas_100s_20kHz_1.mat', 't', 'x');
enc2 = load('noise_meas_100s_20kHz_2.mat', 't', 'x');
enc3 = load('noise_meas_100s_20kHz_3.mat', 't', 'x');
enc4 = load('noise_meas_100s_20kHz_4.mat', 't', 'x');
enc6 = load('noise_meas_100s_20kHz_6.mat', 't', 'x');
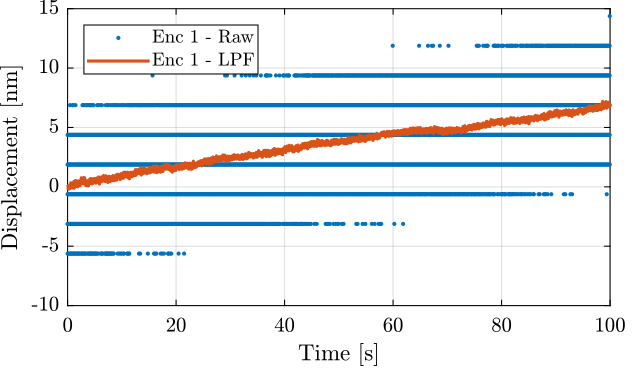
enc7 = load('noise_meas_100s_20kHz_7.mat', 't', 'x');

The raw measured data as well as the low pass filtered data (using a first order low pass filter with a cut-off at 10Hz) are shown in Figure fig:vionic_noise_raw_lpf.

Time domain measurement (raw data and low pass filtered data with first order 10Hz LPF)

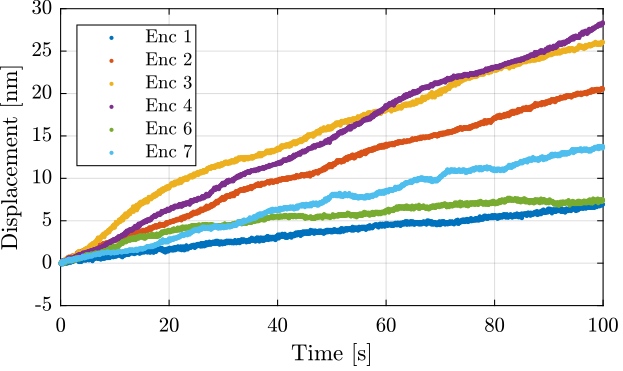
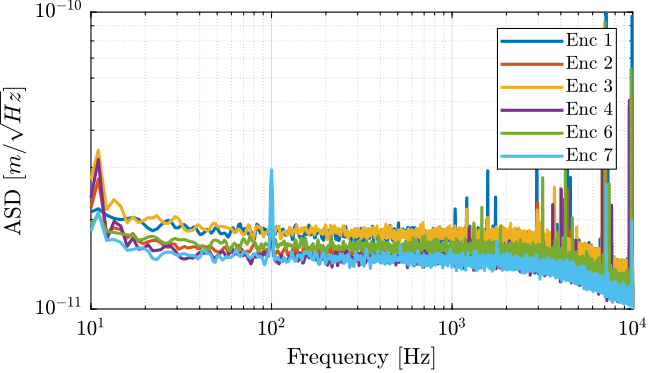
The time domain data for all the encoders are compared in Figure fig:vionic_noise_time.

Comparison of the time domain measurement

The amplitude spectral density is computed and shown in Figure fig:vionic_noise_asd.

Amplitude Spectral Density of the measured signal

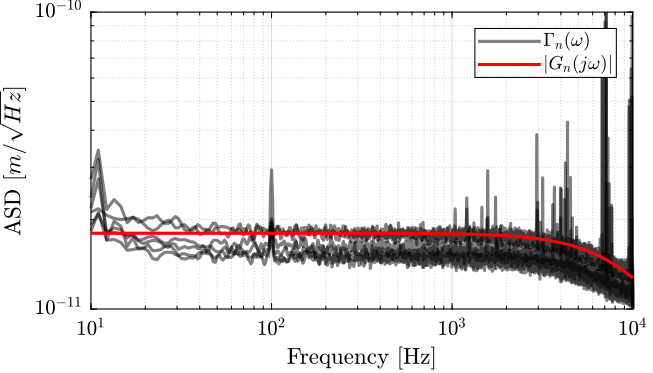
Let's create a transfer function that approximate the measured noise of the encoder.

Gn_e = 1.8e-11/(1 + s/2/pi/1e4);

The amplitude of the transfer function and the measured ASD are shown in Figure fig:vionic_noise_asd_model.

Measured ASD of the noise and modelled one

Linearity Measurement

<<sec:linearity_measurement>>

Test Bench

In order to measure the linearity, we have to compare the measured displacement with a reference sensor with a known linearity. An interferometer or capacitive sensor should work fine. An actuator should also be there so impose a displacement.

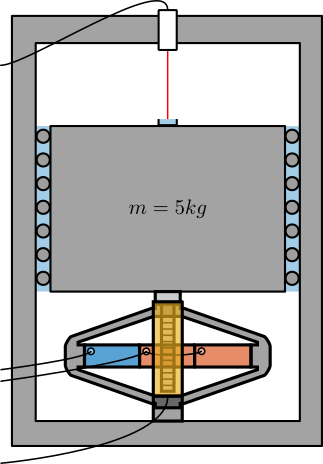
One idea is to use the test-bench shown in Figure fig:test_bench_encoder_calibration.

The APA300ML is used to excite the mass in a broad bandwidth. The motion is measured at the same time by the Vionic Encoder and by an interferometer (most likely an Attocube).

As the interferometer has a very large bandwidth, we should be able to estimate the bandwidth of the encoder if it is less than the Nyquist frequency that can be around 10kHz.

Schematic of the test bench

Results

Dynamical Measurement

<<sec:dynamical_measurement>>

Test Bench

Results