23 KiB
Measurement of Piezoelectric Amplifiers
- Introduction
- Effect of a change of capacitance
- Effect of a change in Voltage level
- Comparison PI / Cedrat
- Impedance Measurement
- Effect of filters configuration on the PI-E505 dynamics
Introduction ignore
The following two voltage amplifiers are tested:
The piezoelectric actuator under test is an APA95ML from Cedrat technology (doc). It contains three stacks with a capacitance of $5 \mu F$ each that can be connected independently to the amplifier.
This document is divided into the following sections:
- Section sec:effect_change_capacitance: The effect of a change in load capacitance on the amplifier dynamics is studied
- Section sec:effect_change_voltage: The effect on the voltage level on the amplifier dynamics is studied
- Section sec:comp_pi_cedrat: The dynamics of the E-505 and LA75B are compared
- Section sec:impedance_meas: The output impedance of both amplifiers are measured
- Section sec:pi_e505_filters: The effect of the internal filters of the E-505 on its dynamics is studied
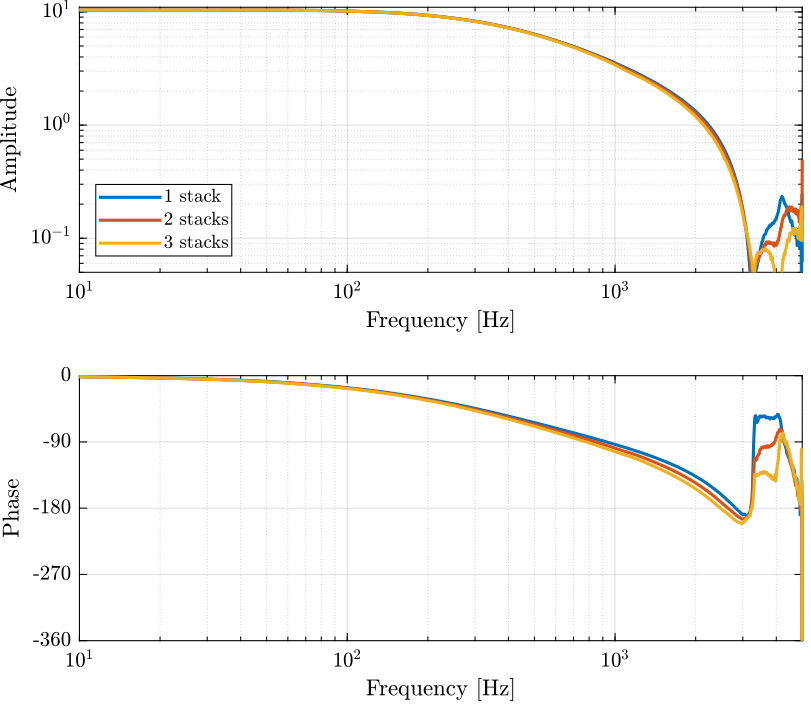
Effect of a change of capacitance
<<sec:effect_change_capacitance>>
Cedrat Technology
Load Data
piezo1 = load('cedrat_la75b_med_1_stack.mat', 't', 'V_in', 'V_out');
piezo2 = load('cedrat_la75b_med_2_stack.mat', 't', 'V_in', 'V_out');
piezo3 = load('cedrat_la75b_med_3_stack.mat', 't', 'V_in', 'V_out');Compute Coherence and Transfer functions
Ts = 1e-4;
win = hann(ceil(0.1/Ts));
[tf_1, f] = tfestimate(piezo1.V_in, piezo1.V_out, win, [], [], 1/Ts);
[co_1, ~] = mscohere(piezo1.V_in, piezo1.V_out, win, [], [], 1/Ts);
[tf_2, ~] = tfestimate(piezo2.V_in, piezo2.V_out, win, [], [], 1/Ts);
[co_2, ~] = mscohere(piezo2.V_in, piezo2.V_out, win, [], [], 1/Ts);
[tf_3, ~] = tfestimate(piezo3.V_in, piezo3.V_out, win, [], [], 1/Ts);
[co_3, ~] = mscohere(piezo3.V_in, piezo3.V_out, win, [], [], 1/Ts);We remove the phase delay due to the time delay of the ADC/DAC:
angle_delay = 180/pi*angle(squeeze(freqresp(exp(-s*Ts), f, 'Hz')));PI
piezo1 = load('pi_505_high.mat', 't', 'V_in', 'V_out');
piezo2 = load('pi_505_high_2_stacks.mat', 't', 'V_in', 'V_out');
piezo3 = load('pi_505_high_3_stacks.mat', 't', 'V_in', 'V_out'); Ts = 1e-4;
win = hann(ceil(0.1/Ts));
[tf_1, f] = tfestimate(piezo1.V_in, piezo1.V_out, win, [], [], 1/Ts);
[co_1, ~] = mscohere(piezo1.V_in, piezo1.V_out, win, [], [], 1/Ts);
[tf_2, ~] = tfestimate(piezo2.V_in, piezo2.V_out, win, [], [], 1/Ts);
[co_2, ~] = mscohere(piezo2.V_in, piezo2.V_out, win, [], [], 1/Ts);
[tf_3, ~] = tfestimate(piezo3.V_in, piezo3.V_out, win, [], [], 1/Ts);
[co_3, ~] = mscohere(piezo3.V_in, piezo3.V_out, win, [], [], 1/Ts);We remove the phase delay due to the time delay of the ADC/DAC:
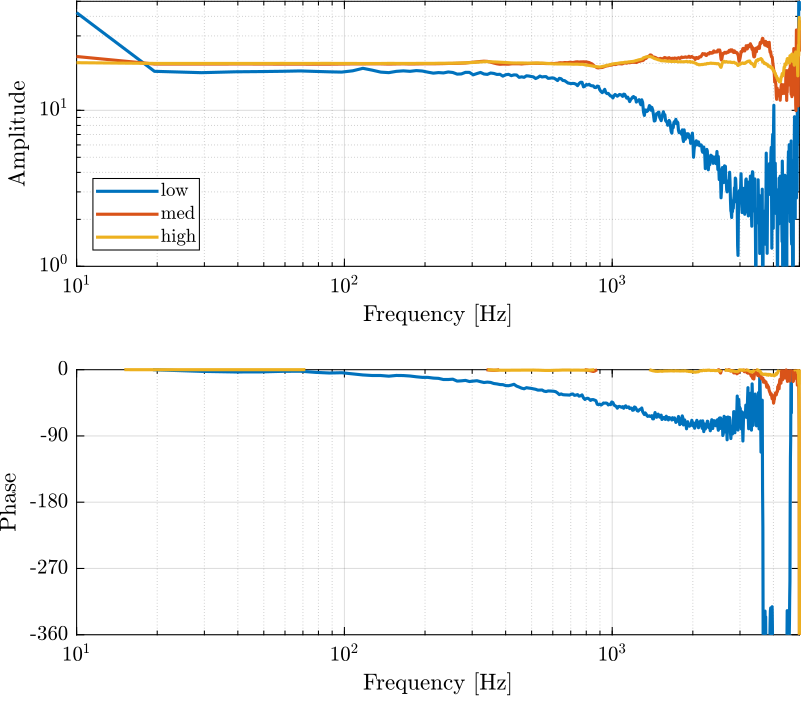
angle_delay = 180/pi*angle(squeeze(freqresp(exp(-s*Ts), f, 'Hz')));Effect of a change in Voltage level
<<sec:effect_change_voltage>>
Cedrat Technology
hi = load('cedrat_la75b_high_1_stack.mat', 't', 'V_in', 'V_out');
me = load('cedrat_la75b_med_1_stack.mat', 't', 'V_in', 'V_out');
lo = load('cedrat_la75b_low_1_stack.mat', 't', 'V_in', 'V_out'); Ts = 1e-4;
win = hann(ceil(0.1/Ts));
[tf_hi, f] = tfestimate(hi.V_in, hi.V_out, win, [], [], 1/Ts);
[co_hi, ~] = mscohere(hi.V_in, hi.V_out, win, [], [], 1/Ts);
[tf_me, ~] = tfestimate(me.V_in, me.V_out, win, [], [], 1/Ts);
[co_me, ~] = mscohere(me.V_in, me.V_out, win, [], [], 1/Ts);
[tf_lo, ~] = tfestimate(lo.V_in, lo.V_out, win, [], [], 1/Ts);
[co_lo, ~] = mscohere(lo.V_in, lo.V_out, win, [], [], 1/Ts);We remove the phase delay due to the time delay of the ADC/DAC:
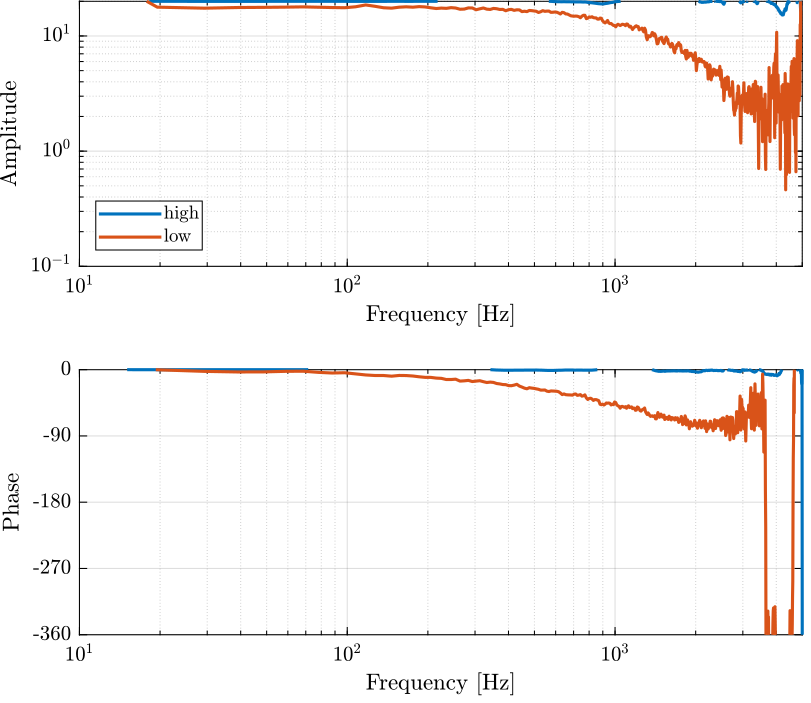
angle_delay = 180/pi*angle(squeeze(freqresp(exp(-s*Ts), f, 'Hz')));PI
hi = load('pi_505_high.mat', 't', 'V_in', 'V_out');
lo = load('pi_505_low.mat', 't', 'V_in', 'V_out'); Ts = 1e-4;
win = hann(ceil(0.1/Ts));
[tf_hi, f] = tfestimate(hi.V_in, hi.V_out, win, [], [], 1/Ts);
[co_hi, ~] = mscohere(hi.V_in, hi.V_out, win, [], [], 1/Ts);
[tf_lo, ~] = tfestimate(lo.V_in, lo.V_out, win, [], [], 1/Ts);
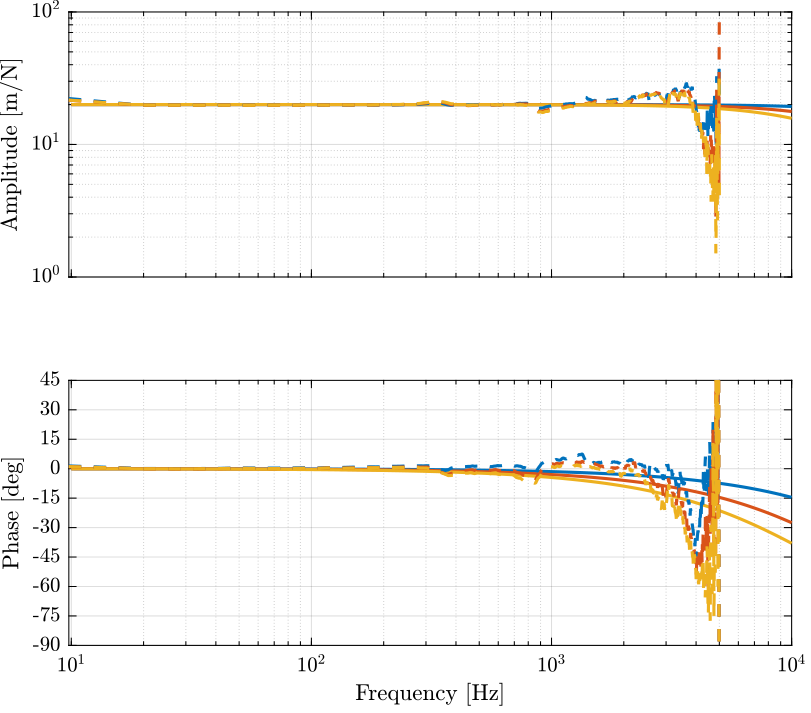
[co_lo, ~] = mscohere(lo.V_in, lo.V_out, win, [], [], 1/Ts);Comparison PI / Cedrat
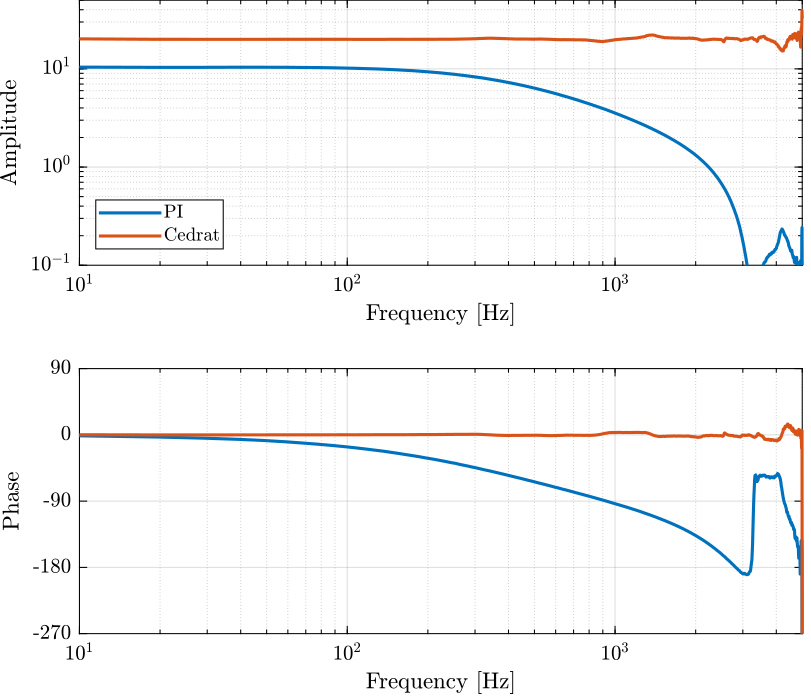
<<sec:comp_pi_cedrat>>
Results
ce_results = load('cedrat_la75b_high_1_stack.mat', 't', 'V_in', 'V_out');
pi_results = load('pi_505_high.mat', 't', 'V_in', 'V_out'); Ts = 1e-4;
win = hann(ceil(0.1/Ts));
[tf_ce, f] = tfestimate(ce_results.V_in, ce_results.V_out, win, [], [], 1/Ts);
[tf_pi, ~] = tfestimate(pi_results.V_in, pi_results.V_out, win, [], [], 1/Ts);We remove the phase delay due to the time delay of the ADC/DAC:
angle_delay = 180/pi*angle(squeeze(freqresp(exp(-s*Ts), f, 'Hz')));Impedance Measurement
<<sec:impedance_meas>>
Introduction ignore
The goal is to experimentally measure the output impedance of the voltage amplifiers.
To do so, the output voltage is first measure without any load ($V$). It is then measure when a 10Ohm load is used ($V^\prime$).
The load ($R = 10\Omega$) and the internal resistor ($R_i$) form a voltage divider, and thus: \[ V^\prime = \frac{R}{R + R_i} V \]
From the two values of voltage, the internal resistor value can be computed: \[ R_i = R \frac{V - V^\prime}{V^\prime} \]
Cedrat Technology
Compute Impedance
R = 10; % Resistive Load used [Ohm]
V = 0.998; % Output Voltage without any load [V]
Vp = 0.912; % Output Voltage with resistice load [V] R * (V - Vp)/Vp;0.94298
R = 47; % Resistive Load used [Ohm]
V = 4.960; % Output Voltage without any load [V]
Vp = 4.874; % Output Voltage with resistice load [V] R * (V - Vp)/Vp;0.8293
Effect of Impedance on the phase drop
C_1 = 5e-6; % Capacitance in [F]
C_2 = 10e-6; % Capacitance in [F]
C_3 = 15e-6; % Capacitance in [F]
Ri = R * (V - Vp)/Vp; % Internal resistance [Ohm]
G0 = 20;
G_1 = G0/(1+Ri*C_1*s);
G_2 = G0/(1+Ri*C_2*s);
G_3 = G0/(1+Ri*C_3*s);PI
R = 10; % Resistive Load used [Ohm]
V = 1.059; % Output Voltage without any load [V]
Vp = 0.828; % Output Voltage with resistice load [V] R * (V - Vp)/Vp2.7899
R = 10; % Resistive Load used [Ohm]
V = 2.092; % Output Voltage without any load [V]
Vp = 1.637; % Output Voltage with resistice load [V] R * (V - Vp)/Vp2.7795
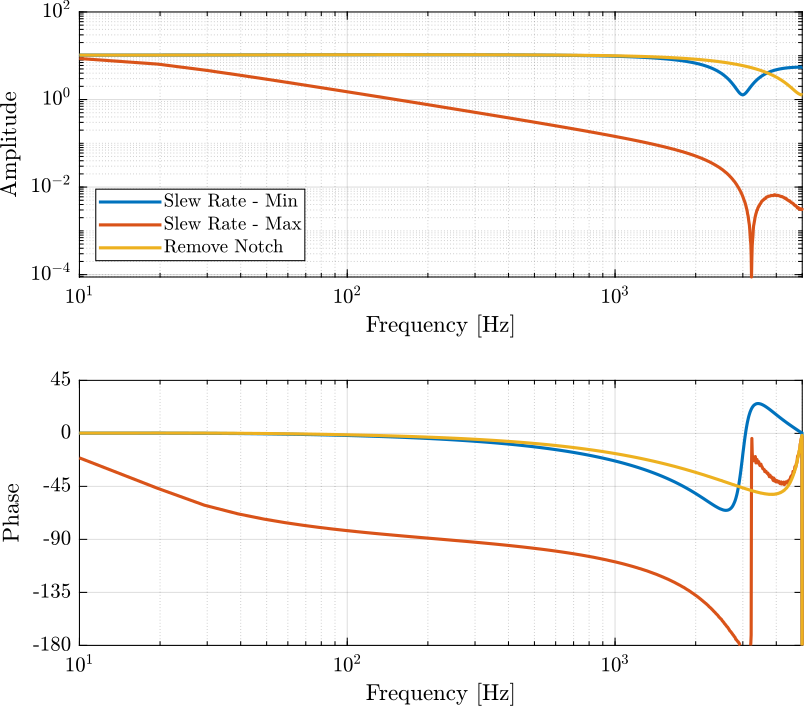
Effect of filters configuration on the PI-E505 dynamics
<<sec:pi_e505_filters>>
PI
Three measurements are done:
- Slew Rate limitation at maximum
- Slew Rate limitation at minimum
- Notch Filter at maximum frequency
pi_sr_min = load('pi_slew_rate_min.mat');
pi_sr_max = load('pi_slew_rate_max.mat');
pi_sr_max_notch = load('pi_slew_rate_max_notch_high.mat');
pi_sr_load = load('pi_slew_rate_max_notch_high_2stacks.mat'); Ts = 1e-4;
win = hann(ceil(0.1/Ts));
[tf_sr_min, f] = tfestimate(pi_sr_min.V_in, pi_sr_min.V_out, win, [], [], 1/Ts);
[tf_sr_max, ~] = tfestimate(pi_sr_max.V_in, pi_sr_max.V_out, win, [], [], 1/Ts);
[tf_sr_max_notch, ~] = tfestimate(pi_sr_max_notch.V_in, pi_sr_max_notch.V_out, win, [], [], 1/Ts);
[tf_sr_load, ~] = tfestimate(pi_sr_load.V_in, pi_sr_load.V_out, win, [], [], 1/Ts); angle_delay = 180/pi*angle(squeeze(freqresp(exp(-s*Ts), f, 'Hz')));Transfer function of the Voltage Amplifier
The identified transfer function still seems to match the one of a notch filter at 5kHz.
w_nf = 2*pi*5e3; % Notch Filter Frequency [rad/s]
G = 10.5*(s^2 + 2*w_nf*0.12*s + w_nf^2)/(s^2 + 2*w_nf*s + w_nf^2);With Load
R = 2.78; % Output Impedance [Ohm]
C = 9e-6; % Load capacitance [F]
G_amp = 10/(1 + s*R*C);