37 KiB
Flexible Joints - Test Bench
- Introduction
- Flexible Joints
- Dimensions
- Measurement Test Bench - Bending Stiffness
- Error budget
- First Measurements
- Bending Stiffness Measurement
This report is also available as a pdf.
Introduction ignore
In this document, we present a test-bench that has been developed in order to measure the bending stiffness of flexible joints.
It is structured as follow:
- Section sec:flexible_joints: the geometry of the flexible joints and the expected stiffness and stroke are presented
- Section sec:test_bench_desc: the measurement bench is presented
- Section sec:error_budget: an error budget is performed in order to estimate the accuracy of the measured stiffness
- Section sec:first_measurements: first measurements are performed
- Section sec:bending_stiffness_meas: the bending stiffness of the flexible joints are measured
Flexible Joints
<<sec:flexible_joints>>
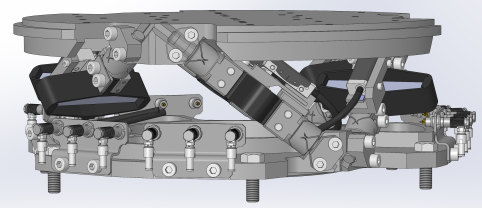
The flexible joints that are going to be measured in this document have been design to be used with a Nano-Hexapod (Figure fig:nano_hexapod).
Ideally, these flexible joints would behave as perfect ball joints, that is to say:
- no bending and torsional stiffnesses
- infinite shear and axial stiffnesses
- un-limited bending and torsional stroke
- no friction, no backlash
The real characteristics of the flexible joints will influence the dynamics of the Nano-Hexapod. Using a multi-body dynamical model of the nano-hexapod, the specifications in term of stiffness and stroke of the flexible joints have been determined and summarized in Table tab:flexible_joints_specs.
| Specification | FEM | |
|---|---|---|
| Axial Stiffness | > 100 [N/um] | 94 |
| Shear Stiffness | > 1 [N/um] | 13 |
| Bending Stiffness | < 100 [Nm/rad] | 5 |
| Torsion Stiffness | < 500 [Nm/rad] | 260 |
| Bending Stroke | > 1 [mrad] | 24.5 |
| Torsion Stroke | > 5 [urad] |
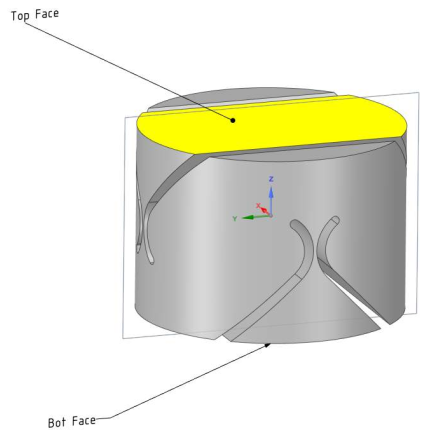
Then, the classical geometry of a flexible ball joint shown in Figure fig:flexible_joint_fem_geometry has been optimized in order to meet the requirements. This has been done using a Finite Element Software and the obtained joint's characteristics are summarized in Table tab:flexible_joints_specs.
The obtained geometry are defined in the drawings of the flexible joints. The material is a special kind of stainless steel called "F16PH"..
Dimensions
Measurements
Few notes:
- dirt inside: 3,10,12,13
- strange surface quality: 15,16
- Strange shape: 5
| Num | X1 | X2 | Y1 | Y2 |
|---|---|---|---|---|
| 1 | 224 | 214 | 223 | 226 |
| 2 | 237 | 224 | 229 | 231 |
| 3 | 239 | 231 | 234 | 230 |
| 4 | 229 | 232 | 233 | 227 |
| 5 | 228 | 228 | 225 | 212 |
| 6 | 224 | 220 | 220 | 221 |
| 7 | 228 | 226 | 206 | 207 |
| 8 | 224 | 223 | 230 | 224 |
| 9 | 228 | 233 | 223 | 231 |
| 10 | 235 | 231 | 228 | 230 |
| 11 | 211 | 204 | 197 | 207 |
| 12 | 225 | 226 | 227 | 226 |
| 13 | 231 | 220 | 215 | 228 |
| 14 | 224 | 221 | 216 | 224 |
| 15 | 220 | 221 | 209 | 214 |
| 16 | 230 | 229 | 213 | 210 |
Analysis
mean(data(:,2:end))
std(data(:,2:end))
std(data(:,2:end)')Measurement Test Bench - Bending Stiffness
<<sec:test_bench_desc>>
Introduction ignore
The most important characteristic of the flexible joint that we want to measure is its bending stiffness $k_{R_x} \approx k_{R_y}$.
To do so, we have to apply a torque $T_x$ on the flexible joint and measure its angular deflection $\theta_x$. The stiffness is then
\begin{equation} k_{R_x} = \frac{T_x}{\theta_x} \end{equation}As it is quite difficult to apply a pure torque, a force will be applied instead. The application point of the force should far enough from the flexible part such that the obtained bending is much larger than the displacement in shear.
The working principle of the bench is schematically shown in Figure fig:test_bench_principle. One part of the flexible joint is fixed. On the mobile part, a force $F_x$ is applied which is equivalent to a torque applied on the flexible joint center. The induced rotation is measured with a displacement sensor $d_x$.

This test-bench will be used to have a first approximation of the bending stiffnesss and stroke of the flexible joints. Another test-bench, better engineered will be used to measure the flexible joint's characteristics with better accuracy.
Flexible joint Geometry
The flexible joint used for the Nano-Hexapod is shown in Figure fig:flexible_joint_geometry. Its bending stiffness is foreseen to be $k_{R_y}\approx 5\,\frac{Nm}{rad}$ and its stroke $\theta_{y,\text{max}}\approx 25\,mrad$.
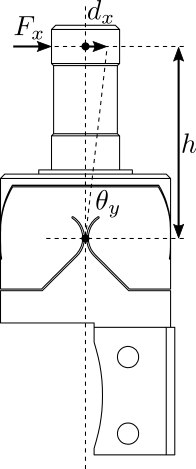
The height between the flexible point (center of the joint) and the point where external forces are applied is $h = 20\,mm$.
Let's define the parameters on Matlab.
kRx = 5; % Bending Stiffness [Nm/rad]
Rxmax = 25e-3; % Bending Stroke [rad]
h = 20e-3; % Height [m]Required external applied force
The bending $\theta_y$ of the flexible joint due to the force $F_x$ is:
\begin{equation} \theta_y = \frac{M_y}{k_{R_y}} = \frac{F_x h}{k_{R_y}} \end{equation}Therefore, the applied force to test the full range of the flexible joint is:
\begin{equation} F_{x,\text{max}} = \frac{k_{R_y} \theta_{y,\text{max}}}{h} \end{equation}Fxmax = kRx*Rxmax/h; % Force to induce maximum stroke [N]And we obtain:
\begin{equation} F_{x,max} = 6.2\, [N] \end{equation}
The measurement range of the force sensor should then be higher than $6.2\,N$.
Required actuator stroke and sensors range
The flexible joint is designed to allow a bending motion of $\pm 25\,mrad$. The corresponding stroke at the location of the force sensor is: \[ d_{x,\text{max}} = h \tan(R_{x,\text{max}}) \]
dxmax = h*tan(Rxmax);\begin{equation} d_{max} = 0.5\, [mm] \end{equation}
In order to test the full range of the flexible joint, the stroke of the translation stage used to move the force sensor should be higher than $0.5\,mm$. Similarly, the measurement range of the displacement sensor should also be higher than $0.5\,mm$.
Test Bench
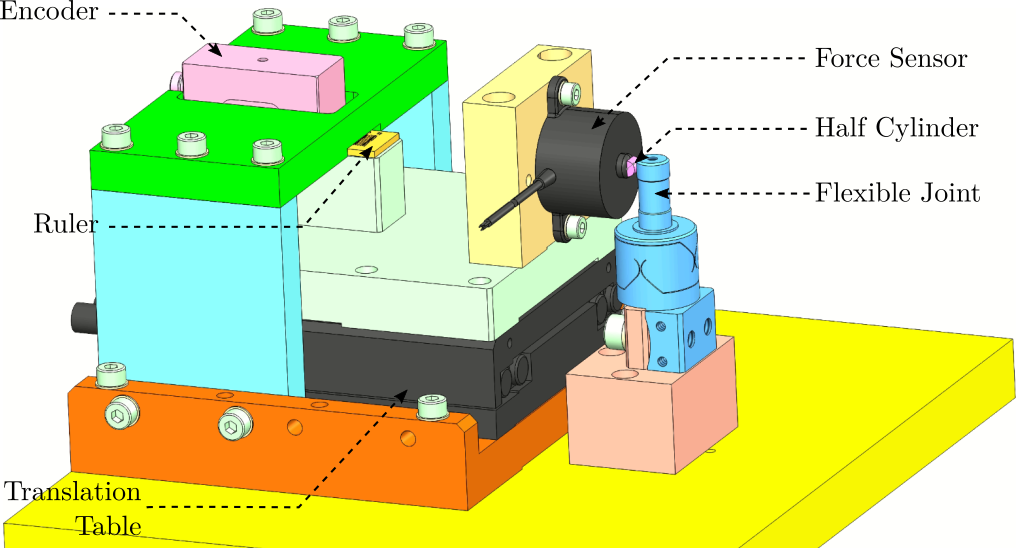
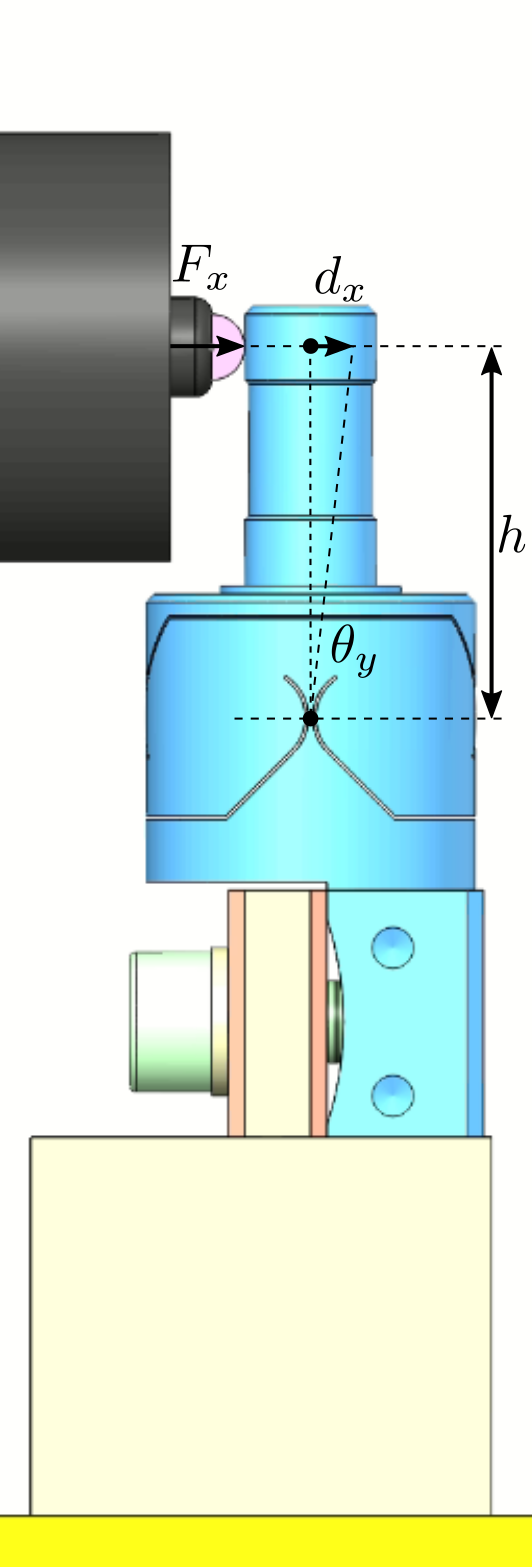
A CAD view of the measurement bench is shown in Figure fig:test_bench_flex_overview.
Here are the different elements used in this bench:
- Translation Stage: V-408
- Load Cells: FC2231-0000-0010-L
- Encoder: Renishaw Resolute 1nm
Both the measured force and displacement are acquired at the same time using a Speedgoat machine.
A side view of the bench with the important quantities are shown in Figure fig:test_bench_flex_side.
Error budget
<<sec:error_budget>>
Introduction ignore
Many things can impact the accuracy of the measured bending stiffness such as:
- Errors in the force and displacement measurement
- Shear effects
- Deflection of the Force sensor
- Errors in the geometry of the bench
In this section, we wish to estimate the attainable accuracy with the current bench, and identified the limiting factors.
Finite Element Model
From the Finite Element Model, the stiffness and stroke of the flexible joint have been computed and summarized in Tables tab:axial_shear_characteristics and tab:bending_torsion_characteristics.
| Stiffness [N/um] | Max Force [N] | Stroke [um] | |
|---|---|---|---|
| Axial | 94 | 469 | 5 |
| Shear | 13 | 242 | 19 |
| Stiffness [Nm/rad] | Max Torque [Nmm] | Stroke [mrad] | |
|---|---|---|---|
| Bending | 5 | 118 | 24 |
| Torsional | 260 | 1508 | 6 |
Setup
The setup is schematically represented in Figure fig:test_bench_flex_side_bis.
The force is applied on top of the flexible joint with a distance $h$ with the joint's center. The displacement of the flexible joint is also measured at the same height.
The height between the joint's center and the force application point is:
h = 25e-3; % Height [m]
Effect of Bending
The torque applied is:
\begin{equation} M_y = F_x \cdot h \end{equation}The flexible joint is experiencing a rotation $\theta_y$ due to the torque $M_y$:
\begin{equation} \theta_y = \frac{M_y}{k_{R_y}} = \frac{F_x \cdot h}{k_{R_y}} \end{equation}This rotation is then measured by the displacement sensor. The measured displacement is:
\begin{equation} D_b = h \tan(\theta_y) = h \tan\left( \frac{F_x \cdot h}{k_{R_y}} \right) \label{eq:bending_stiffness_formula} \end{equation}Computation of the bending stiffness
From equation eqref:eq:bending_stiffness_formula, we can compute the bending stiffness:
\begin{equation} k_{R_y} = \frac{F_x \cdot h}{\tan^{-1}\left( \frac{D_b}{h} \right)} \end{equation}For small displacement, we have
\begin{equation} \boxed{k_{R_y} \approx h^2 \frac{F_x}{d_x}} \end{equation}And therefore, to precisely measure $k_{R_y}$, we need to:
- precisely measure the motion $d_x$
- precisely measure the applied force $F_x$
- precisely now the height of the force application point $h$
Estimation error due to force and displacement sensors accuracy
The maximum error on the measured displacement with the encoder is 40 nm. This quite negligible compared to the measurement range of 0.5 mm.
The accuracy of the force sensor is around 1% and therefore, we should expect to have an accuracy on the measured stiffness of at most 1%.
Estimation error due to Shear
The effect of Shear on the measured displacement is simply:
\begin{equation} D_s = \frac{F_x}{k_s} \end{equation}The measured displacement will be the effect of shear + effect of bending
\begin{equation} d_x = D_b + D_s = h \tan\left( \frac{F_x \cdot h}{k_{R_y}} \right) + \frac{F_x}{k_s} \approx F_x \left( \frac{h^2}{k_{R_y}} + \frac{1}{k_s} \right) \end{equation}The estimated bending stiffness $k_{\text{est}}$ will then be:
\begin{equation} k_{\text{est}} = h^2 \frac{F_x}{d_x} \approx k_{R_y} \frac{1}{1 + \frac{k_{R_y}}{k_s h^2}} \end{equation}The measurement error due to Shear is 0.1 %
Estimation error due to force sensor compression
The measured displacement is not done directly at the joint's location. The force sensor compression will then induce an error on the joint's stiffness.
The force sensor stiffness $k_F$ is estimated to be around:
kF = 50/0.05e-3; % [N/m]k_F = 1.0e+06 [N/m]
The measured displacement will be the sum of the displacement induced by the bending and by the compression of the force sensor:
\begin{equation} d_x = D_b + \frac{F_x}{k_F} = h \tan\left( \frac{F_x \cdot h}{k_{R_y}} \right) + \frac{F_x}{k_F} \approx F_x \left( \frac{h^2}{k_{R_y}} + \frac{1}{k_F} \right) \end{equation}The estimated bending stiffness $k_{\text{est}}$ will then be:
\begin{equation} k_{\text{est}} = h^2 \frac{F_x}{d_x} \approx k_{R_y} \frac{1}{1 + \frac{k_{R_y}}{k_F h^2}} \end{equation}The measurement error due to height estimation errors is 0.8 %
Estimation error due to height estimation error
Let's consider an error in the estimation of the height from the application of the force to the joint's center:
\begin{equation} h_{\text{est}} = h (1 + \epsilon) \end{equation}The computed bending stiffness will be:
\begin{equation} k_\text{est} \approx h_{\text{est}}^2 \frac{F_x}{d_x} \end{equation}And the stiffness estimation error is:
\begin{equation} \frac{k_{\text{est}}}{k_{R_y}} = (1 + \epsilon)^2 \end{equation}h_err = 0.2e-3; % Height estimation error [m]The measurement error due to height estimation errors of 0.2 [mm] is 1.6 %
Conclusion
Based on the above analysis, we should expect no better than few percent of accuracy using the current test-bench. This is well enough for a first estimation of the bending stiffness of the flexible joints.
Another measurement bench allowing better accuracy will be developed.
First Measurements
<<sec:first_measurements>>
Introduction ignore
- Section sec:test_meas_probe:
- Section sec:meas_probe_stiffness:
Agreement between the probe and the encoder
<<sec:test_meas_probe>>
Introduction ignore
- Load Cells: FC2231-0000-0010-L (and XFL212R)
- Encoder: Renishaw Resolute 1nm
- Displacement Probe: Millimar C1216 electronics and Millimar 1318 probe
Setup ignore
The measurement setup is made such that the probe measured the translation table displacement. It should then measure the same displacement as the encoder. Using this setup, we should be able to compare the probe and the encoder.
Results ignore
Let's load the measurements.
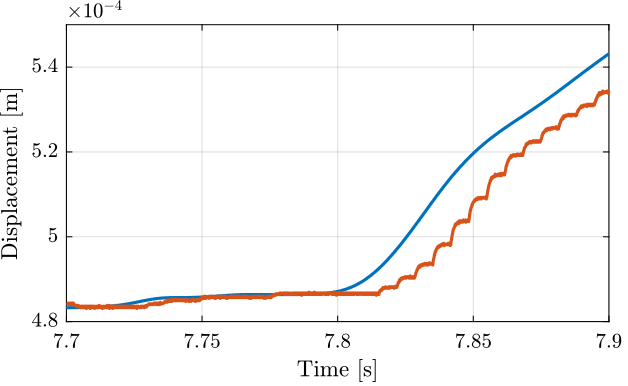
load('meas_probe_against_encoder.mat', 't', 'd', 'dp', 'F')The time domain measured displacement by the probe and by the encoder is shown in Figure fig:comp_encoder_probe_time.
If we zoom, we see that there is some delay between the encoder and the probe (Figure fig:comp_encoder_probe_time_zoom).
This delay is estimated using the finddelay command.
The time delay is approximately 15.8 [ms]
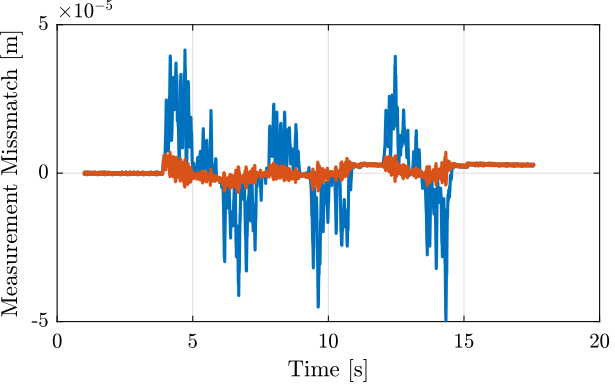
The measured mismatch between the encoder and the probe with and without compensating for the time delay are shown in Figure fig:comp_encoder_probe_mismatch.
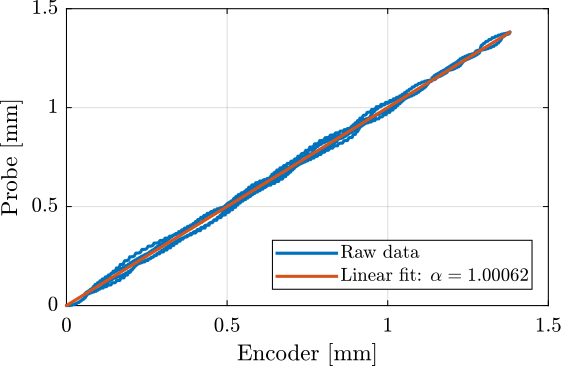
Finally, the displacement of the probe is shown as a function of the displacement of the encoder and a linear fit is made (Figure fig:comp_encoder_probe_linear_fit).
From the measurement, it is shown that the probe is well calibrated. However, there is some time delay of tens of milliseconds that could induce some measurement errors.
Measurement of the Millimar 1318 probe stiffness
<<sec:meas_probe_stiffness>>
Introduction ignore
- Translation Stage: V-408
- Load Cell: FC2231-0000-0010-L
- Encoder: Renishaw Resolute 1nm
- Displacement Probe: Millimar C1216 electronics and Millimar 1318 probe
Results ignore
Let's load the measurement results.
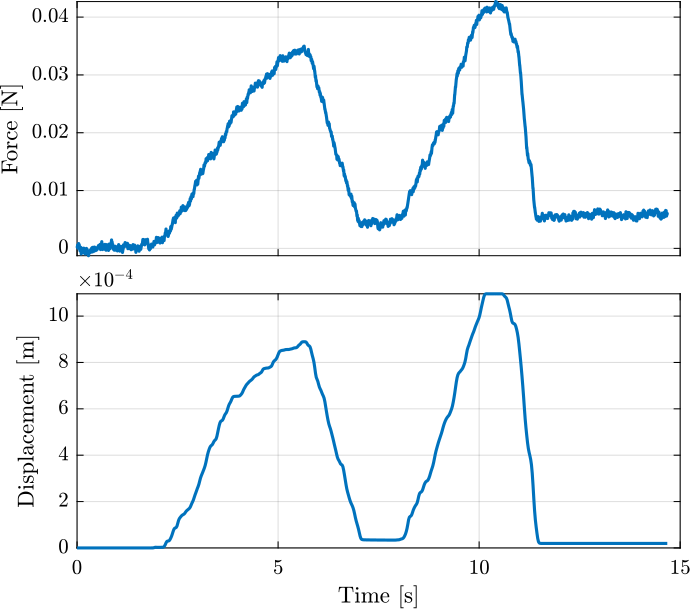
load('meas_stiff_probe.mat', 't', 'd', 'dp', 'F')The time domain measured force and displacement are shown in Figure fig:mahr_time_domain.
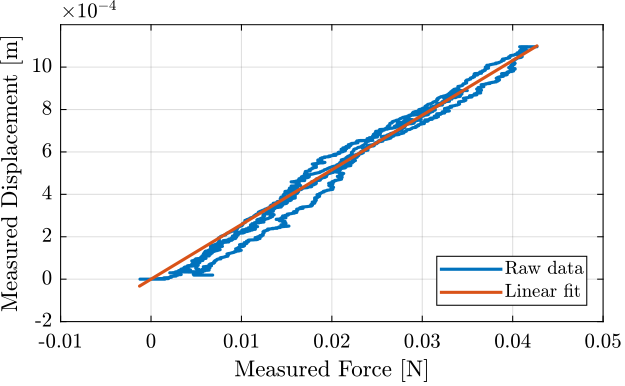
Now we can estimate the stiffness with a linear fit.
This is very close to the 0.04 [N/mm] written in the Millimar 1318 probe datasheet.
And compare the linear fit with the raw measurement data (Figure fig:mahr_stiffness_f_d_plot).
The Millimar 1318 probe has a stiffness of $\approx 0.04\,[N/mm]$.
Bending Stiffness Measurement
<<sec:bending_stiffness_meas>>
Results
load('meas_stiff_flex_12_x.mat', 't', 'd', 'F');d = d(t > 5.35 & t < 14.0);
F = F(t > 5.35 & t < 14.0);
t = t(t > 5.35 & t < 14.0);
d = d - d(1);
F = F - F(1);
t = t - t(1);ta = [0.05, 1.13];
tb = [5.75, 7.2];
d_l = [d(t > ta(1) & t < ta(2)); d(t > tb(1) & t < tb(2))];
F_l = [F(t > ta(1) & t < ta(2)); F(t > tb(1) & t < tb(2))];
d_l = d_l - d_l(1);
F_l = F_l - F_l(1);Stiffness is 5.579 [Nm/rad]
Results - Y
load('meas_stiff_flex_12_y.mat', 't', 'd', 'F');%% Automatic Zero of the force
F = F - mean(F(t > 0.9 & t < 1.1));
%% Start measurement at t = 1.0 s
d = d(t > 1.0);
F = F(t > 1.0);
t = t(t > 1.0); t = t - t(1);t_l = [5.58, 6.75]; % Time of flexible joint's linear region
t_s = [6.9, 7.24]; % Time of stop's linear regionBending Stiffness is 5.5 [Nm/rad]
Bending Stroke is 17.9 [mrad]
Results - X
load('meas_stiff_flex_12_x.mat', 't', 'd', 'F');%% Automatic Zero of the force
F = F - mean(F(t > 0.9 & t < 1.1));
%% Start measurement at t = 1.0 s
d = d(t > 1.0);
F = F(t > 1.0);
t = t(t > 1.0); t = t - t(1);t_l = [4.365, 5.47]; % Time of flexible joint's linear region
t_s = [5.65, 6.09]; % Time of stop's linear regionBending Stiffness is 5.7 [Nm/rad]
Bending Stroke is 17.9 [mrad]
Results - XY
load('meas_stiff_flex_12_xy.mat', 't', 'd', 'F');%% Automatic Zero of the force
F = F - mean(F(t > 0.9 & t < 1.1));
%% Start measurement at t = 1.0 s
d = d(t > 1.0);
F = F(t > 1.0);
t = t(t > 1.0); t = t - t(1);t_l = [4.99, 6.5]; % Time of flexible joint's linear region
t_s = [6.8, 7.10]; % Time of stop's linear regionBending Stiffness is 5.6 [Nm/rad]
Bending Stroke is 23.1 [mrad]