168 KiB
Nano-Hexapod - Test Bench
- Introduction
- Encoders fixed to the Struts
- Introduction
- Identification of the dynamics
- Comparison with the Simscape Model
- Introduction
- Load measured FRF
- Dynamics from Actuator to Force Sensors
- Dynamics from Actuator to Encoder
- Effect of a change in bending damping of the joints
- Effect of a change in damping factor of the APA
- Effect of a change in stiffness damping coef of the APA
- Effect of a change in mass damping coef of the APA
- Using Flexible model
- Flexible model + encoders fixed to the plates
- Integral Force Feedback
- Modal Analysis
- Accelerometers fixed on the top platform
- Encoders fixed to the plates
- Functions
This report is also available as a pdf.
Introduction ignore
This document is dedicated to the experimental study of the nano-hexapod shown in Figure fig:picture_bench_granite_nano_hexapod.
Here are the documentation of the equipment used for this test bench (lots of them are shwon in Figure fig:picture_bench_granite_overview):
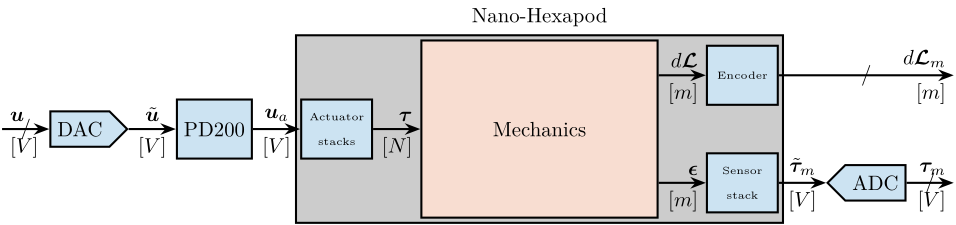
In Figure fig:nano_hexapod_signals is shown a block diagram of the experimental setup. When possible, the notations are consistent with this diagram and summarized in Table tab:list_signals.
\definecolor{instrumentation}{rgb}{0, 0.447, 0.741}
\definecolor{mechanics}{rgb}{0.8500, 0.325, 0.098}
\begin{tikzpicture}
% Blocs
\node[block={4.0cm}{3.0cm}, fill=mechanics!20!white] (nano_hexapod) {Mechanics};
\coordinate[] (inputF) at (nano_hexapod.west);
\coordinate[] (outputL) at ($(nano_hexapod.south east)!0.8!(nano_hexapod.north east)$);
\coordinate[] (outputF) at ($(nano_hexapod.south east)!0.2!(nano_hexapod.north east)$);
\node[block, left= 0.8 of inputF, fill=instrumentation!20!white, align=center] (F_stack) {\tiny Actuator \\ \tiny stacks};
\node[block, left= 0.8 of F_stack, fill=instrumentation!20!white] (PD200) {PD200};
\node[DAC, left= 0.8 of PD200, fill=instrumentation!20!white] (F_DAC) {DAC};
\node[block, right=0.8 of outputF, fill=instrumentation!20!white, align=center] (Fm_stack){\tiny Sensor \\ \tiny stack};
\node[ADC, right=0.8 of Fm_stack,fill=instrumentation!20!white] (Fm_ADC) {ADC};
\node[block, right=0.8 of outputL, fill=instrumentation!20!white] (encoder) {\tiny Encoder};
% Connections and labels
\draw[->] ($(F_DAC.west)+(-0.8,0)$) node[above right]{$\bm{u}$} node[below right]{$[V]$} -- node[sloped]{$/$} (F_DAC.west);
\draw[->] (F_DAC.east) -- node[midway, above]{$\tilde{\bm{u}}$}node[midway, below]{$[V]$} (PD200.west);
\draw[->] (PD200.east) -- node[midway, above]{$\bm{u}_a$}node[midway, below]{$[V]$} (F_stack.west);
\draw[->] (F_stack.east) -- (inputF) node[above left]{$\bm{\tau}$}node[below left]{$[N]$};
\draw[->] (outputF) -- (Fm_stack.west) node[above left]{$\bm{\epsilon}$} node[below left]{$[m]$};
\draw[->] (Fm_stack.east) -- node[midway, above]{$\tilde{\bm{\tau}}_m$}node[midway, below]{$[V]$} (Fm_ADC.west);
\draw[->] (Fm_ADC.east) -- node[sloped]{$/$} ++(0.8, 0)coordinate(end) node[above left]{$\bm{\tau}_m$}node[below left]{$[V]$};
\draw[->] (outputL) -- (encoder.west) node[above left]{$d\bm{\mathcal{L}}$} node[below left]{$[m]$};
\draw[->] (encoder.east) -- node[sloped]{$/$} (encoder-|end) node[above left]{$d\bm{\mathcal{L}}_m$}node[below left]{$[m]$};
% Nano-Hexapod
\begin{scope}[on background layer]
\node[fit={(F_stack.west|-nano_hexapod.south) (Fm_stack.east|-nano_hexapod.north)}, fill=black!20!white, draw, inner sep=2pt] (system) {};
\node[above] at (system.north) {Nano-Hexapod};
\end{scope}
\end{tikzpicture}| Unit | Matlab | Vector | Elements | |
|---|---|---|---|---|
| Control Input (wanted DAC voltage) | [V] |
u |
$\bm{u}$ | $u_i$ |
| DAC Output Voltage | [V] |
u |
$\tilde{\bm{u}}$ | $\tilde{u}_i$ |
| PD200 Output Voltage | [V] |
ua |
$\bm{u}_a$ | $u_{a,i}$ |
| Actuator applied force | [N] |
tau |
$\bm{\tau}$ | $\tau_i$ |
| Strut motion | [m] |
dL |
$d\bm{\mathcal{L}}$ | $d\mathcal{L}_i$ |
| Encoder measured displacement | [m] |
dLm |
$d\bm{\mathcal{L}}_m$ | $d\mathcal{L}_{m,i}$ |
| Force Sensor strain | [m] |
epsilon |
$\bm{\epsilon}$ | $\epsilon_i$ |
| Force Sensor Generated Voltage | [V] |
taum |
$\tilde{\bm{\tau}}_m$ | $\tilde{\tau}_{m,i}$ |
| Measured Generated Voltage | [V] |
taum |
$\bm{\tau}_m$ | $\tau_{m,i}$ |
| Motion of the top platform | [m,rad] |
dX |
$d\bm{\mathcal{X}}$ | $d\mathcal{X}_i$ |
| Metrology measured displacement | [m,rad] |
dXm |
$d\bm{\mathcal{X}}_m$ | $d\mathcal{X}_{m,i}$ |
This document is divided in the following sections:
- Section sec:encoders_struts: the encoders are fixed to the struts
- Section sec:encoders_plates: the encoders are fixed to the plates
Encoders fixed to the Struts
<<sec:encoders_struts>>
Introduction
In this section, the encoders are fixed to the struts.
It is divided in the following sections:
- Section sec:enc_struts_plant_id: the transfer function matrix from the actuators to the force sensors and to the encoders is experimentally identified.
- Section sec:enc_struts_comp_simscape: the obtained FRF matrix is compared with the dynamics of the simscape model
- Section sec:enc_struts_iff: decentralized Integral Force Feedback (IFF) is applied and its performances are evaluated.
- Section sec:enc_struts_modal_analysis: a modal analysis of the nano-hexapod is performed
Identification of the dynamics
<<sec:enc_struts_plant_id>>
Introduction ignore
Load Measurement Data
%% Load Identification Data
meas_data_lf = {};
for i = 1:6
meas_data_lf(i) = {load(sprintf('mat/frf_data_exc_strut_%i_noise_lf.mat', i), 't', 'Va', 'Vs', 'de')};
meas_data_hf(i) = {load(sprintf('mat/frf_data_exc_strut_%i_noise_hf.mat', i), 't', 'Va', 'Vs', 'de')};
endSpectral Analysis - Setup
%% Setup useful variables
% Sampling Time [s]
Ts = (meas_data_lf{1}.t(end) - (meas_data_lf{1}.t(1)))/(length(meas_data_lf{1}.t)-1);
% Sampling Frequency [Hz]
Fs = 1/Ts;
% Hannning Windows
win = hanning(ceil(1*Fs));
% And we get the frequency vector
[~, f] = tfestimate(meas_data_lf{1}.Va, meas_data_lf{1}.de, win, [], [], 1/Ts);
i_lf = f < 250; % Points for low frequency excitation
i_hf = f > 250; % Points for high frequency excitationDVF Plant
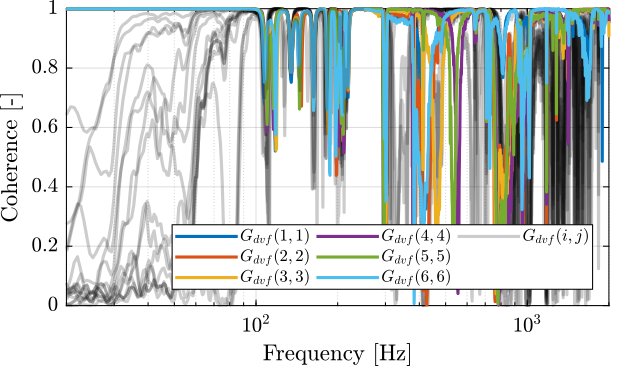
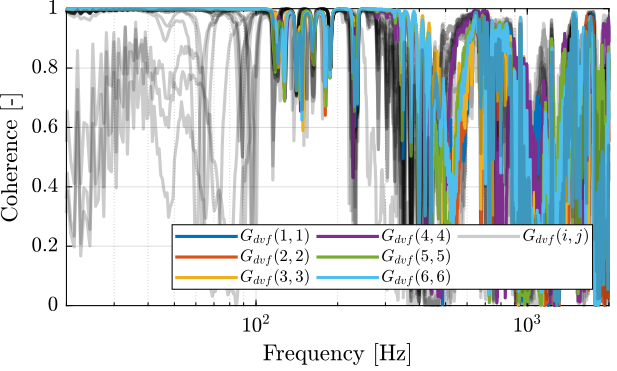
First, let's compute the coherence from the excitation voltage and the displacement as measured by the encoders (Figure fig:enc_struts_dvf_coh).
%% Coherence
coh_dvf = zeros(length(f), 6, 6);
for i = 1:6
coh_dvf_lf = mscohere(meas_data_lf{i}.Va, meas_data_lf{i}.de, win, [], [], 1/Ts);
coh_dvf_hf = mscohere(meas_data_hf{i}.Va, meas_data_hf{i}.de, win, [], [], 1/Ts);
coh_dvf(:,:,i) = [coh_dvf_lf(i_lf, :); coh_dvf_hf(i_hf, :)];
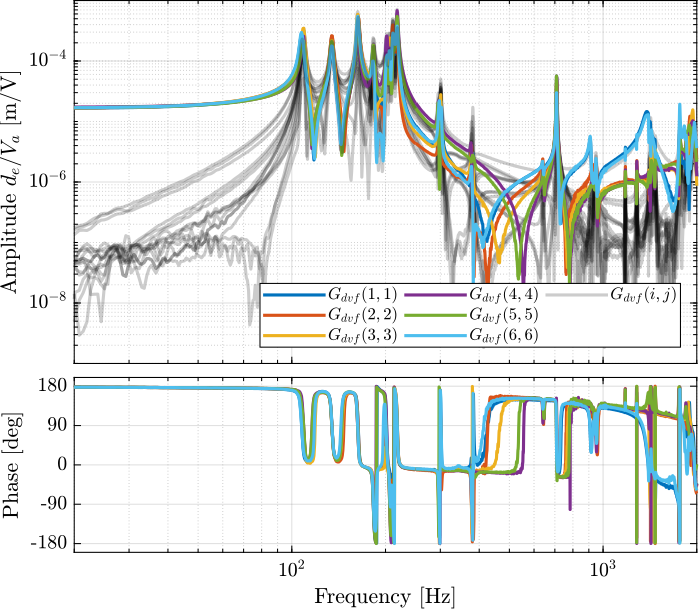
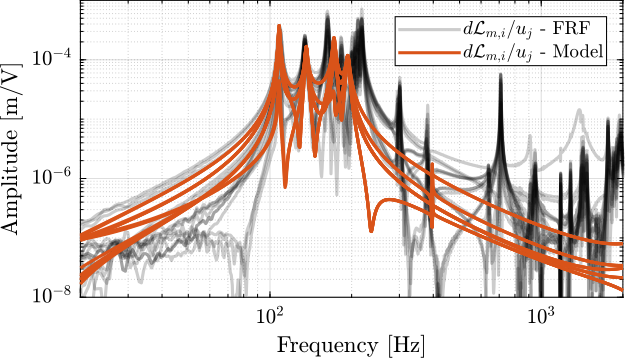
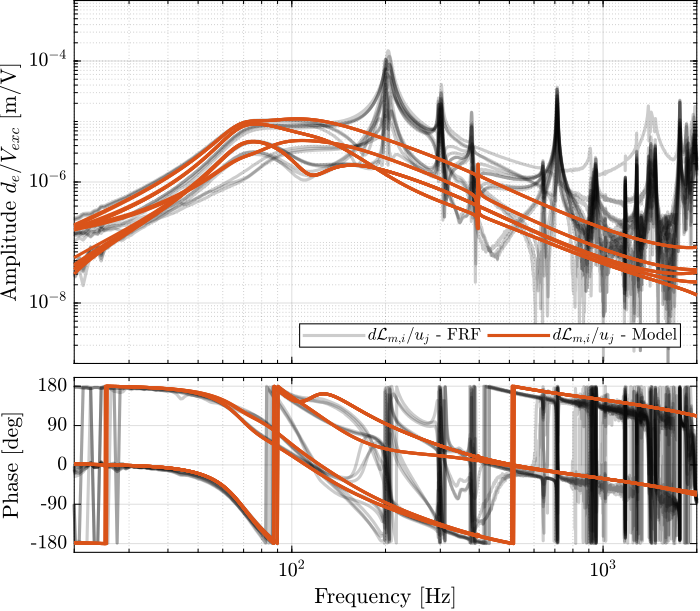
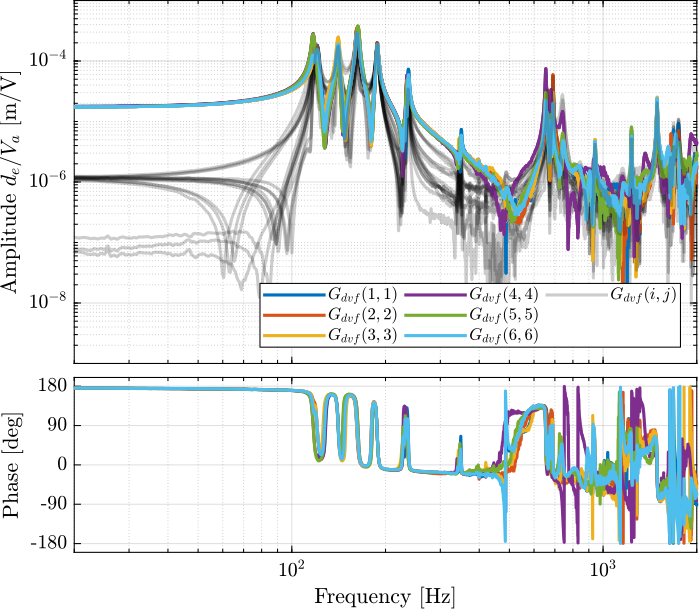
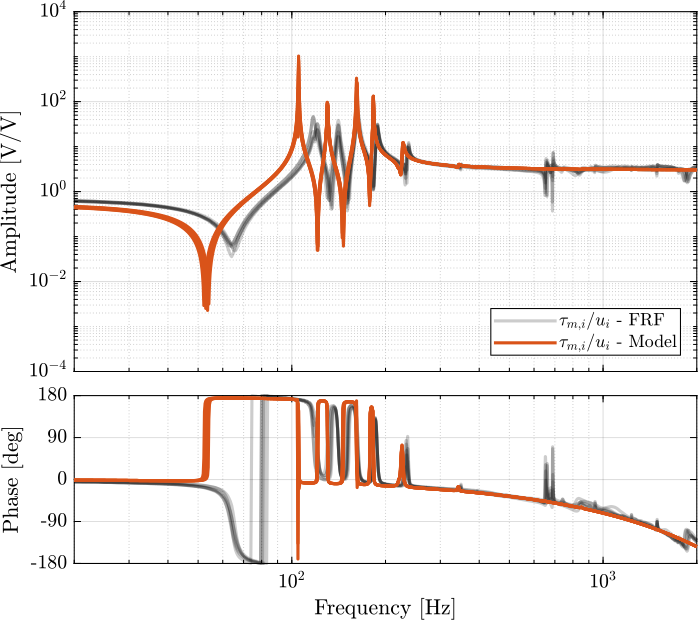
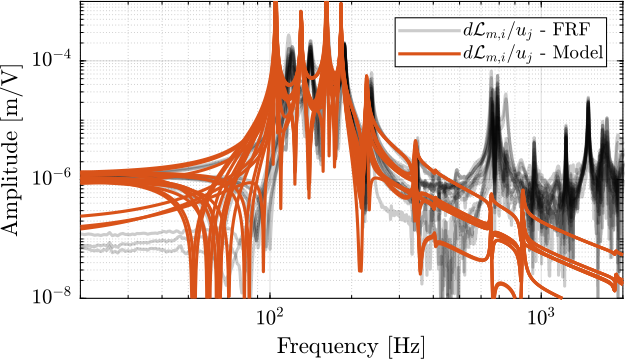
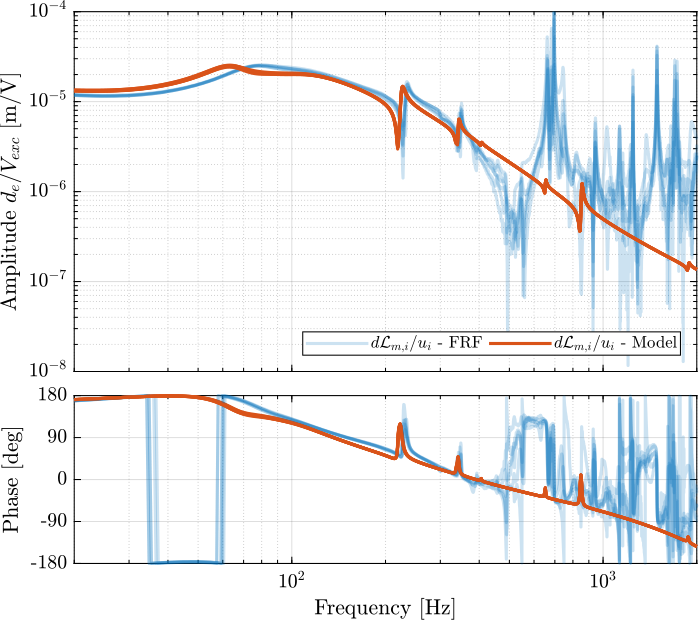
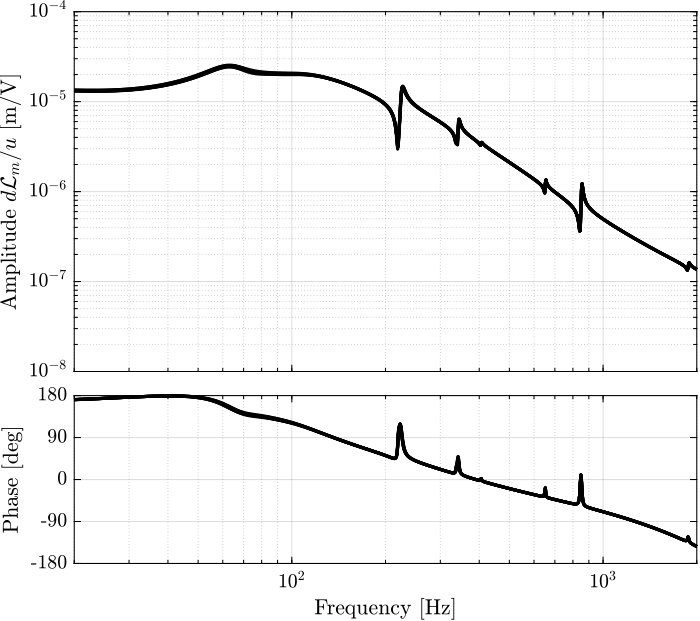
endThen the 6x6 transfer function matrix is estimated (Figure fig:enc_struts_dvf_frf).
%% DVF Plant (transfer function from u to dLm)
G_dvf = zeros(length(f), 6, 6);
for i = 1:6
G_dvf_lf = tfestimate(meas_data_lf{i}.Va, meas_data_lf{i}.de, win, [], [], 1/Ts);
G_dvf_hf = tfestimate(meas_data_hf{i}.Va, meas_data_hf{i}.de, win, [], [], 1/Ts);
G_dvf(:,:,i) = [G_dvf_lf(i_lf, :); G_dvf_hf(i_hf, :)];
endIFF Plant
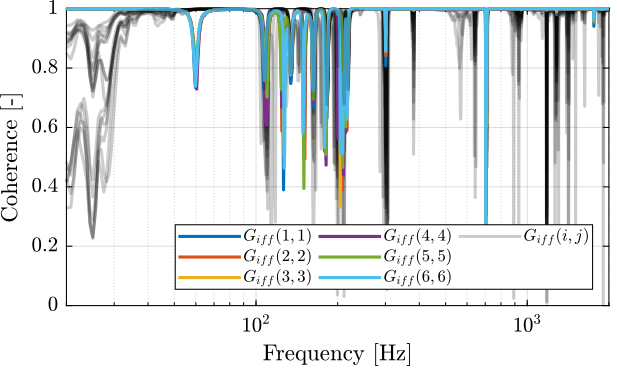
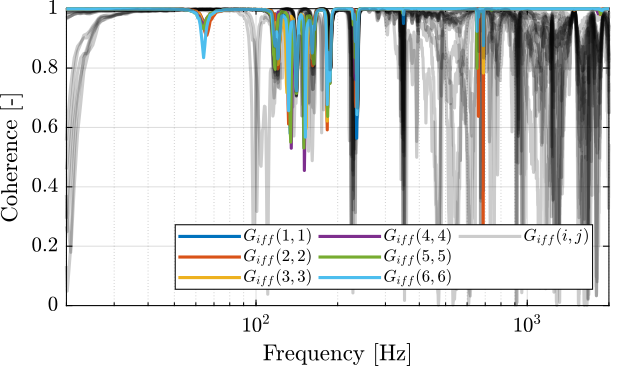
First, let's compute the coherence from the excitation voltage and the displacement as measured by the encoders (Figure fig:enc_struts_iff_coh).
%% Coherence for the IFF plant
coh_iff = zeros(length(f), 6, 6);
for i = 1:6
coh_iff_lf = mscohere(meas_data_lf{i}.Va, meas_data_lf{i}.Vs, win, [], [], 1/Ts);
coh_iff_hf = mscohere(meas_data_hf{i}.Va, meas_data_hf{i}.Vs, win, [], [], 1/Ts);
coh_iff(:,:,i) = [coh_iff_lf(i_lf, :); coh_iff_hf(i_hf, :)];
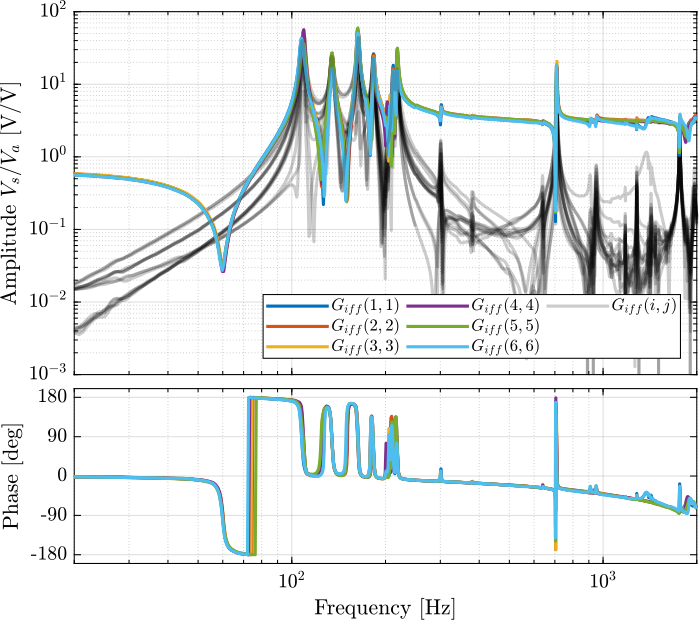
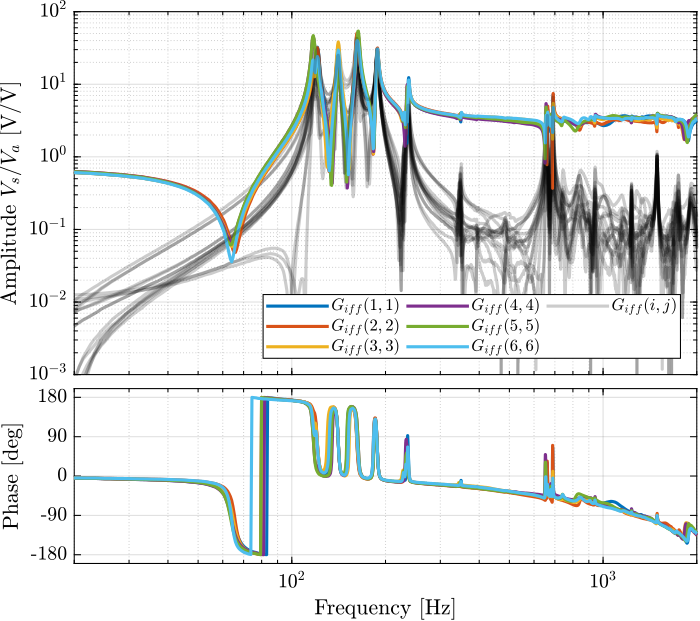
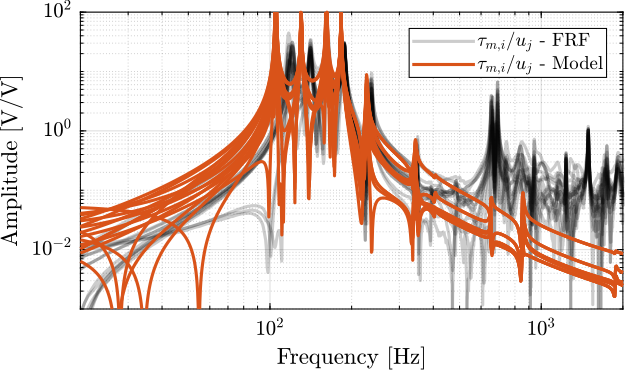
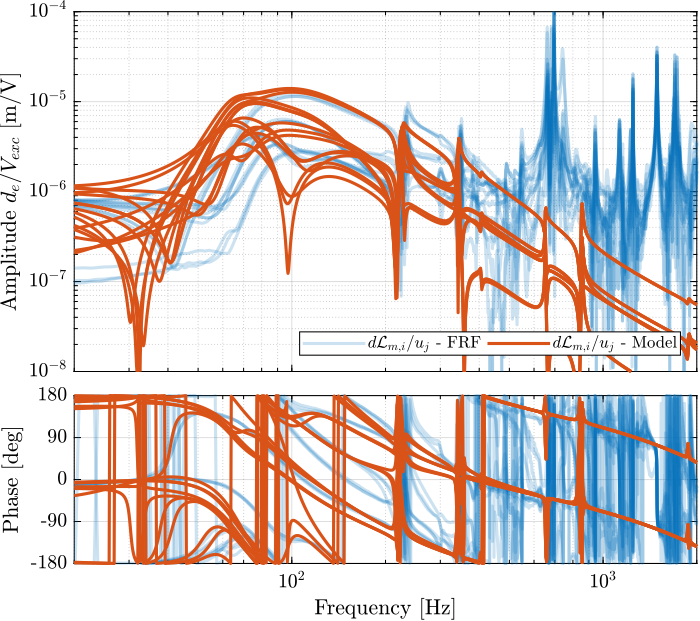
endThen the 6x6 transfer function matrix is estimated (Figure fig:enc_struts_iff_frf).
%% IFF Plant
G_iff = zeros(length(f), 6, 6);
for i = 1:6
G_iff_lf = tfestimate(meas_data_lf{i}.Va, meas_data_lf{i}.Vs, win, [], [], 1/Ts);
G_iff_hf = tfestimate(meas_data_hf{i}.Va, meas_data_hf{i}.Vs, win, [], [], 1/Ts);
G_iff(:,:,i) = [G_iff_lf(i_lf, :); G_iff_hf(i_hf, :)];
endSave Identified Plants
save('matlab/mat/identified_plants_enc_struts.mat', 'f', 'Ts', 'G_iff', 'G_dvf')Comparison with the Simscape Model
<<sec:enc_struts_comp_simscape>>
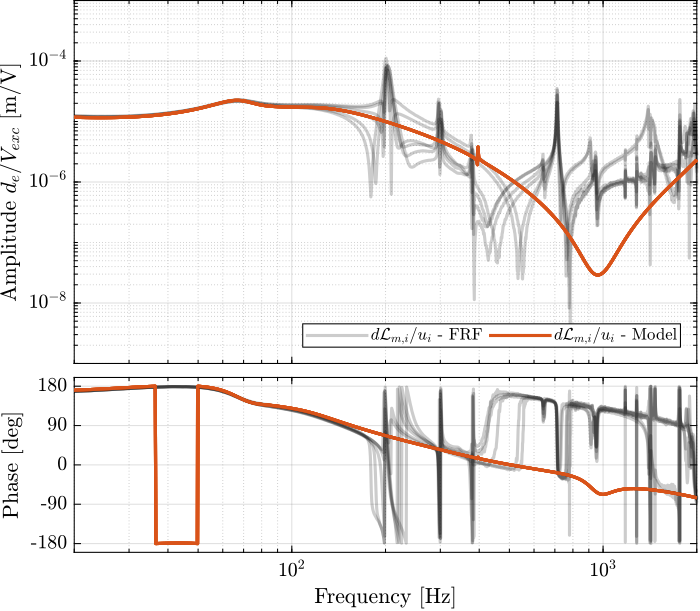
Introduction ignore
In this section, the measured dynamics is compared with the dynamics estimated from the Simscape model.
Load measured FRF
%% Load data
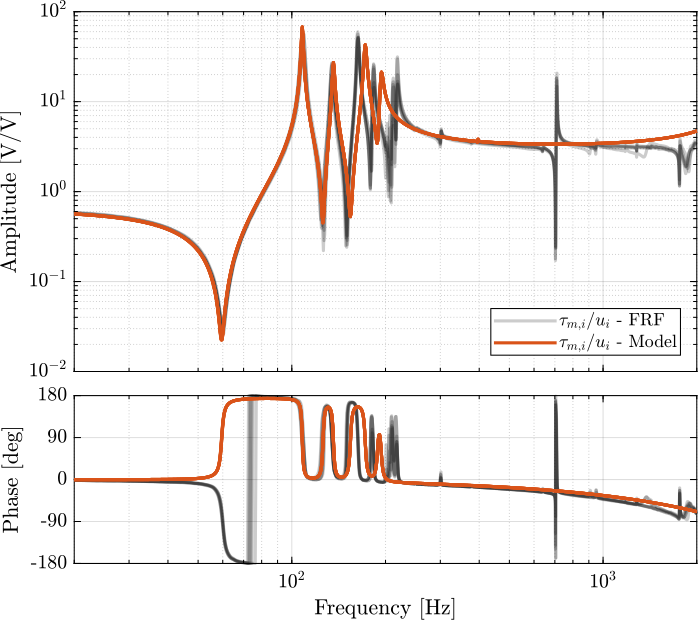
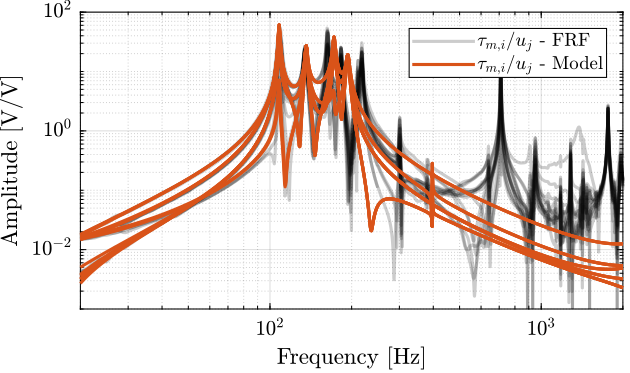
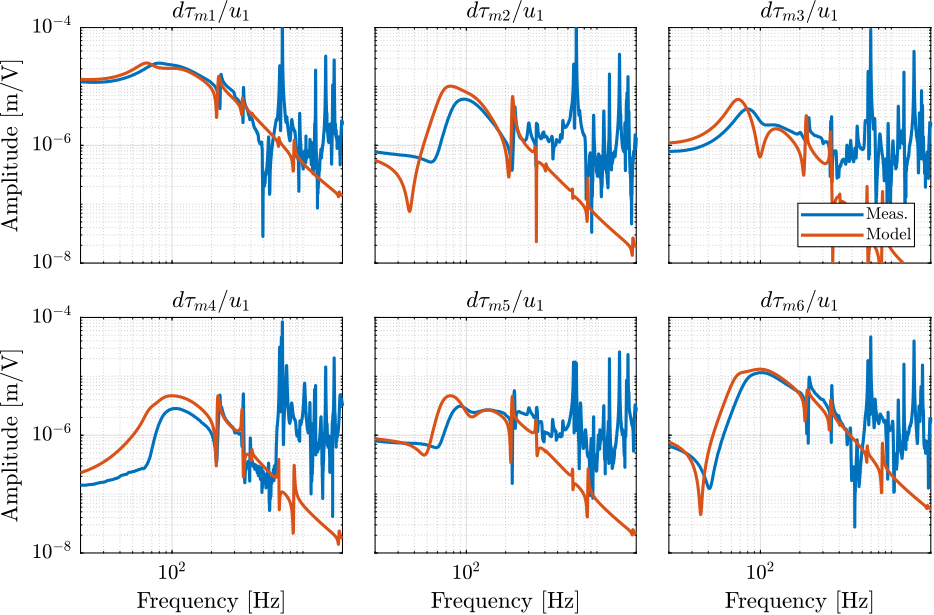
load('identified_plants_enc_struts.mat', 'f', 'Ts', 'G_iff', 'G_dvf')Dynamics from Actuator to Force Sensors
%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'struts', ...
'actuator_type', '2dof');%% Identify the IFF Plant (transfer function from u to taum)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dum'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors
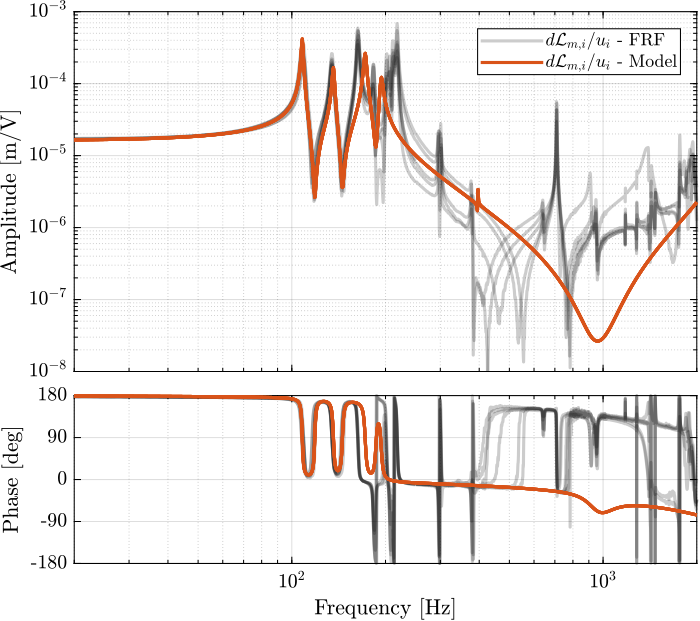
Giff = exp(-s*Ts)*linearize(mdl, io, 0.0, options);Dynamics from Actuator to Encoder
%% Initialization of the Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'struts', ...
'actuator_type', 'flexible');%% Identify the DVF Plant (transfer function from u to dLm)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Encoders
Gdvf = exp(-s*Ts)*linearize(mdl, io, 0.0, options);Effect of a change in bending damping of the joints
%% Tested bending dampings [Nm/(rad/s)]
cRs = [1e-3, 5e-3, 1e-2, 5e-2, 1e-1];%% Identify the DVF Plant (transfer function from u to dLm)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % EncodersThen the identification is performed for all the values of the bending damping.
%% Idenfity the transfer function from actuator to encoder for all bending dampins
Gs = {zeros(length(cRs), 1)};
for i = 1:length(cRs)
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'struts', ...
'actuator_type', 'flexible', ...
'flex_bot_cRx', cRs(i), ...
'flex_bot_cRy', cRs(i), ...
'flex_top_cRx', cRs(i), ...
'flex_top_cRy', cRs(i));
G = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
G.InputName = {'Va1', 'Va2', 'Va3', 'Va4', 'Va5', 'Va6'};
G.OutputName = {'dL1', 'dL2', 'dL3', 'dL4', 'dL5', 'dL6'};
Gs(i) = {G};
end- Could be nice
- Actual damping is very small
Effect of a change in damping factor of the APA
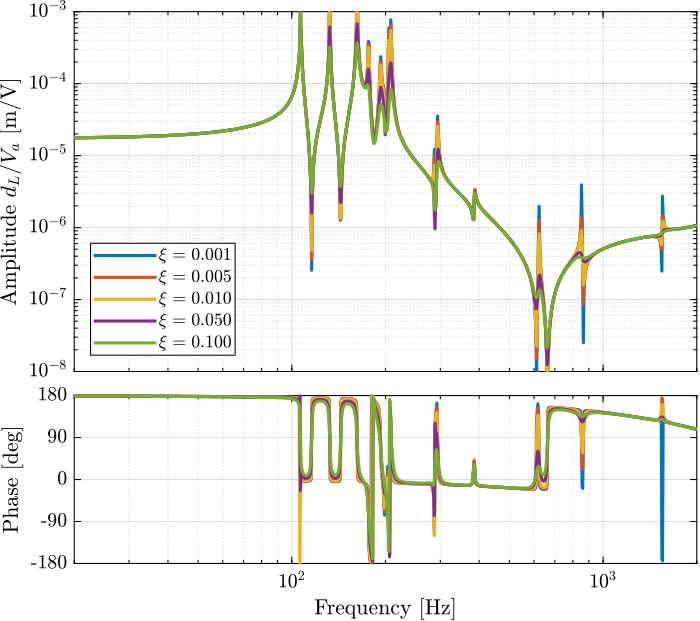
%% Tested bending dampings [Nm/(rad/s)]
xis = [1e-3, 5e-3, 1e-2, 5e-2, 1e-1];%% Identify the DVF Plant (transfer function from u to dLm)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Encoders%% Idenfity the transfer function from actuator to encoder for all bending dampins
Gs = {zeros(length(xis), 1)};
for i = 1:length(xis)
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'struts', ...
'actuator_type', 'flexible', ...
'actuator_xi', xis(i));
G = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
G.InputName = {'Va1', 'Va2', 'Va3', 'Va4', 'Va5', 'Va6'};
G.OutputName = {'dL1', 'dL2', 'dL3', 'dL4', 'dL5', 'dL6'};
Gs(i) = {G};
endDamping factor $\xi$ has a large impact on the damping of the "spurious resonances" at 200Hz and 300Hz.
Why is the damping factor does not change the damping of the first peak?
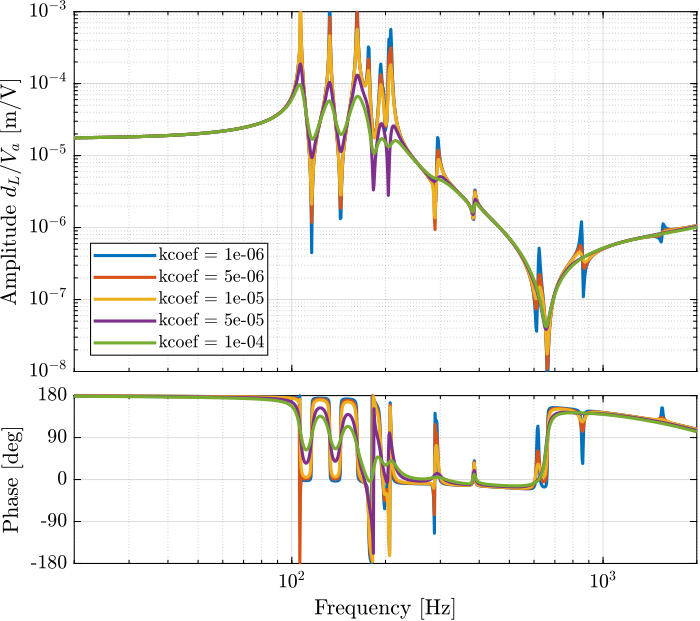
Effect of a change in stiffness damping coef of the APA
m_coef = 1e1;%% Tested bending dampings [Nm/(rad/s)]
k_coefs = [1e-6, 5e-6, 1e-5, 5e-5, 1e-4];%% Identify the DVF Plant (transfer function from u to dLm)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Encoders%% Idenfity the transfer function from actuator to encoder for all bending dampins
Gs = {zeros(length(k_coefs), 1)};
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'struts', ...
'actuator_type', 'flexible');
for i = 1:length(k_coefs)
k_coef = k_coefs(i);
G = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
G.InputName = {'Va1', 'Va2', 'Va3', 'Va4', 'Va5', 'Va6'};
G.OutputName = {'dL1', 'dL2', 'dL3', 'dL4', 'dL5', 'dL6'};
Gs(i) = {G};
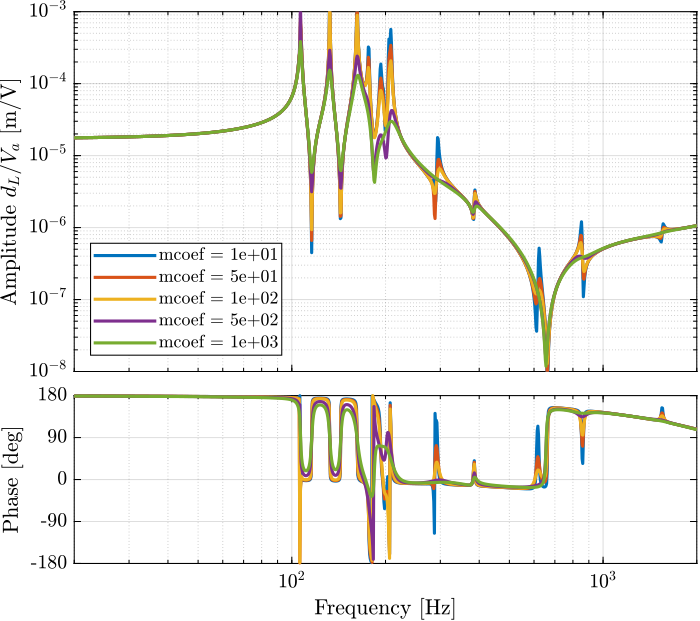
endEffect of a change in mass damping coef of the APA
k_coef = 1e-6;%% Tested bending dampings [Nm/(rad/s)]
m_coefs = [1e1, 5e1, 1e2, 5e2, 1e3];%% Identify the DVF Plant (transfer function from u to dLm)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Encoders%% Idenfity the transfer function from actuator to encoder for all bending dampins
Gs = {zeros(length(m_coefs), 1)};
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'struts', ...
'actuator_type', 'flexible');
for i = 1:length(m_coefs)
m_coef = m_coefs(i);
G = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
G.InputName = {'Va1', 'Va2', 'Va3', 'Va4', 'Va5', 'Va6'};
G.OutputName = {'dL1', 'dL2', 'dL3', 'dL4', 'dL5', 'dL6'};
Gs(i) = {G};
endTODO Using Flexible model
d_aligns = [[-0.05, -0.3, 0];
[ 0, 0.5, 0];
[-0.1, -0.3, 0];
[ 0, 0.3, 0];
[-0.05, 0.05, 0];
[0, 0, 0]]*1e-3;d_aligns = zeros(6,3);
% d_aligns(1,:) = [-0.05, -0.3, 0]*1e-3;
d_aligns(2,:) = [ 0, 0.3, 0]*1e-3;%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'struts', ...
'actuator_type', 'flexible', ...
'actuator_d_align', d_aligns);Why do we have smaller resonances when using flexible APA? On the test bench we have the same resonance as the 2DoF model. Could it be due to the compliance in other dof of the flexible model?
%% Identify the DVF Plant (transfer function from u to dLm)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Encoders
Gdvf = exp(-s*Ts)*linearize(mdl, io, 0.0, options);%% Identify the IFF Plant (transfer function from u to taum)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dum'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors
Giff = exp(-s*Ts)*linearize(mdl, io, 0.0, options);Flexible model + encoders fixed to the plates
%% Identify the IFF Plant (transfer function from u to taum)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensorsd_aligns = [[-0.05, -0.3, 0];
[ 0, 0.5, 0];
[-0.1, -0.3, 0];
[ 0, 0.3, 0];
[-0.05, 0.05, 0];
[0, 0, 0]]*1e-3;%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'struts', ...
'actuator_type', 'flexible', ...
'actuator_d_align', d_aligns);Gdvf_struts = exp(-s*Ts)*linearize(mdl, io, 0.0, options);%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'plates', ...
'actuator_type', 'flexible', ...
'actuator_d_align', d_aligns);Gdvf_plates = exp(-s*Ts)*linearize(mdl, io, 0.0, options);Integral Force Feedback
<<sec:enc_struts_iff>>
Introduction ignore
Identification of the IFF Plant
%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'struts', ...
'actuator_type', '2dof');%% Identify the IFF Plant (transfer function from u to taum)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dum'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors
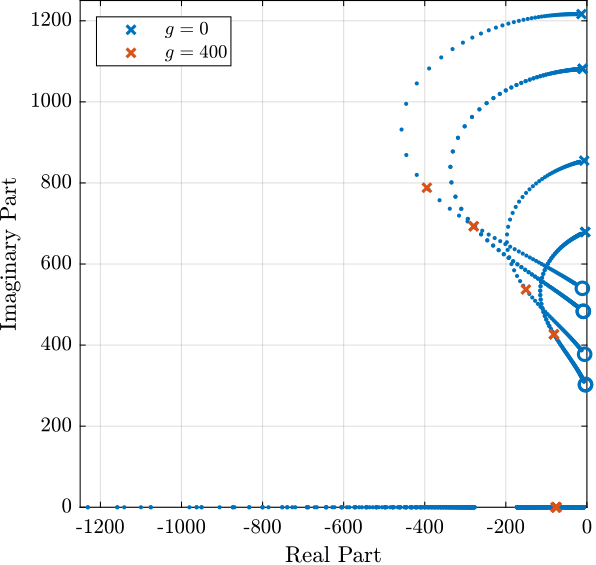
Giff = exp(-s*Ts)*linearize(mdl, io, 0.0, options);Root Locus and Decentralized Loop gain
%% IFF Controller
Kiff_g1 = -(1/(s + 2*pi*40))*... % Low pass filter (provides integral action above 40Hz)
(s/(s + 2*pi*30))*... % High pass filter to limit low frequency gain
(1/(1 + s/2/pi/500))*... % Low pass filter to be more robust to high frequency resonances
eye(6); % Diagonal 6x6 controllerThen the "optimal" IFF controller is:
%% IFF controller with Optimal gain
Kiff = g*Kiff_g1;save('matlab/mat/Kiff.mat', 'Kiff')Multiple Gains - Simulation
%% Tested IFF gains
iff_gains = [4, 10, 20, 40, 100, 200, 400];%% Initialize the Simscape model in closed loop
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'struts', ...
'actuator_type', '2dof', ...
'controller_type', 'iff');%% Identify the (damped) transfer function from u to dLm for different values of the IFF gain
Gd_iff = {zeros(1, length(iff_gains))};
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Strut Displacement (encoder)
for i = 1:length(iff_gains)
Kiff = iff_gains(i)*Kiff_g1*eye(6); % IFF Controller
Gd_iff(i) = {exp(-s*Ts)*linearize(mdl, io, 0.0, options)};
isstable(Gd_iff{i})
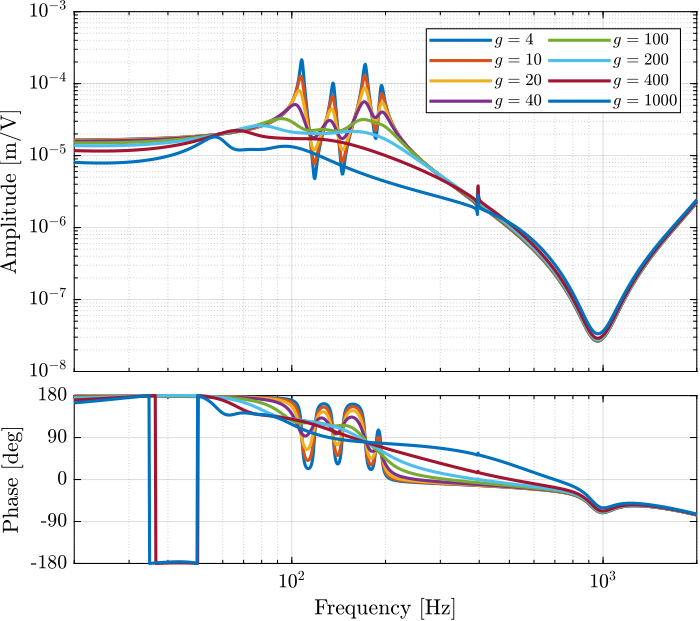
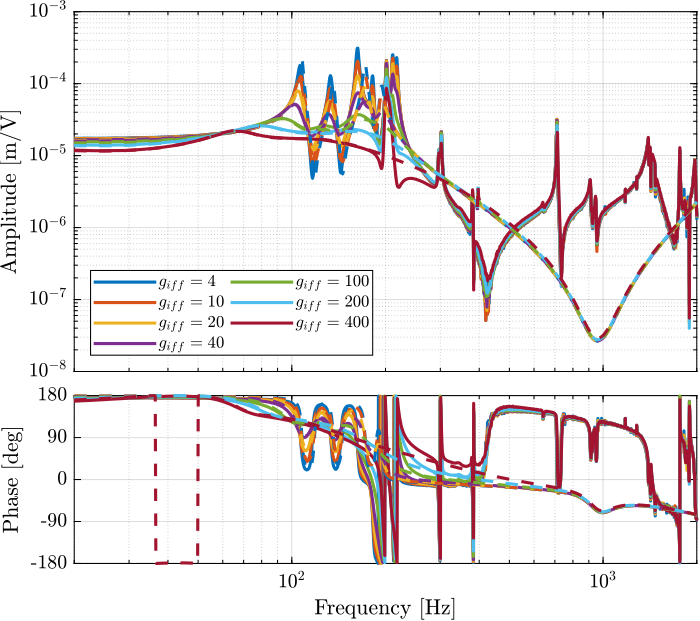
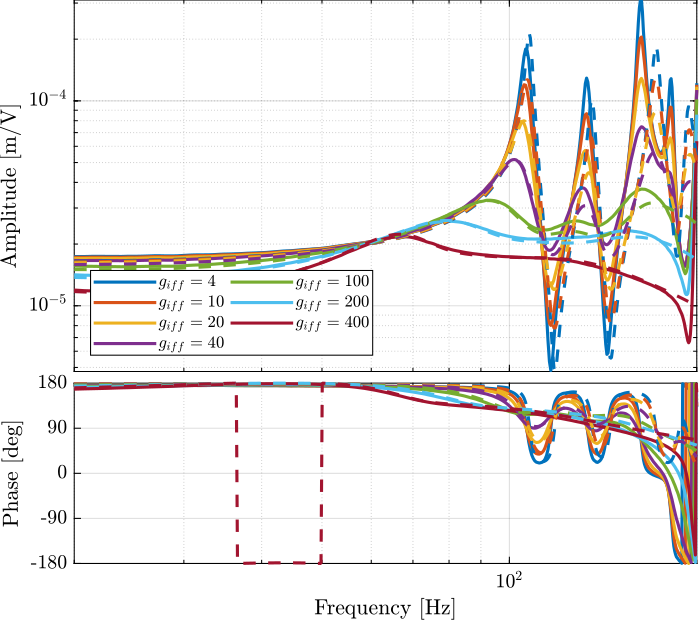
endExperimental Results - Gains
Introduction ignore
Let's look at the damping introduced by IFF as a function of the IFF gain and compare that with the results obtained using the Simscape model.
Load Data
%% Load Identification Data
meas_iff_gains = {};
for i = 1:length(iff_gains)
meas_iff_gains(i) = {load(sprintf('mat/iff_strut_1_noise_g_%i.mat', iff_gains(i)), 't', 'Vexc', 'Vs', 'de', 'u')};
endSpectral Analysis - Setup
%% Setup useful variables
% Sampling Time [s]
Ts = (meas_iff_gains{1}.t(end) - (meas_iff_gains{1}.t(1)))/(length(meas_iff_gains{1}.t)-1);
% Sampling Frequency [Hz]
Fs = 1/Ts;
% Hannning Windows
win = hanning(ceil(1*Fs));
% And we get the frequency vector
[~, f] = tfestimate(meas_iff_gains{1}.Vexc, meas_iff_gains{1}.de, win, [], [], 1/Ts);DVF Plant
%% DVF Plant (transfer function from u to dLm)
G_iff_gains = {};
for i = 1:length(iff_gains)
G_iff_gains{i} = tfestimate(meas_iff_gains{i}.Vexc, meas_iff_gains{i}.de(:,1), win, [], [], 1/Ts);
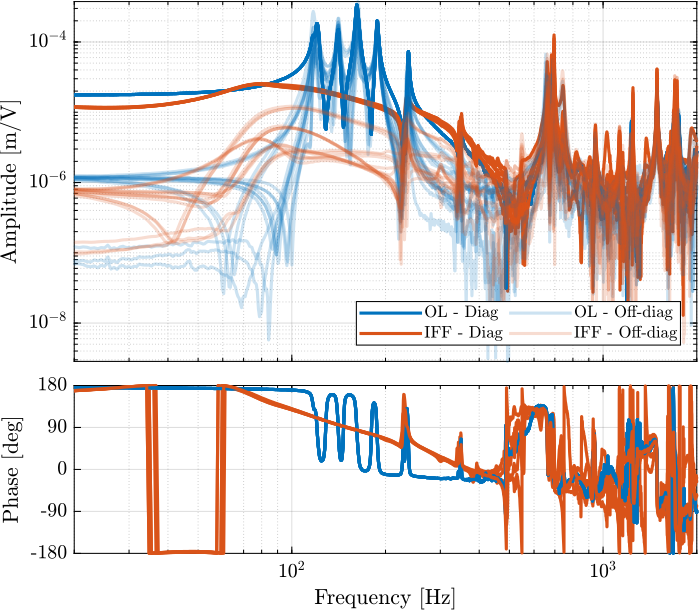
endThe IFF control strategy is very effective for the damping of the suspension modes. It however does not damp the modes at 200Hz, 300Hz and 400Hz (flexible modes of the APA). This is very logical.
Also, the experimental results and the models obtained from the Simscape model are in agreement.
Experimental Results - Comparison of the un-damped and fully damped system
Experimental Results - Damped Plant with Optimal gain
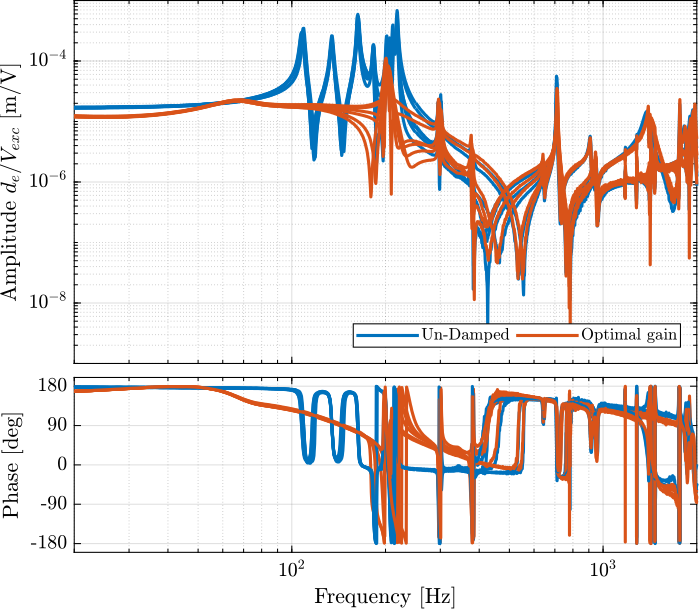
Introduction ignore
Let's now look at the $6 \times 6$ damped plant with the optimal gain $g = 400$.
Load Data
%% Load Identification Data
meas_iff_struts = {};
for i = 1:6
meas_iff_struts(i) = {load(sprintf('mat/iff_strut_%i_noise_g_400.mat', i), 't', 'Vexc', 'Vs', 'de', 'u')};
endSpectral Analysis - Setup
%% Setup useful variables
% Sampling Time [s]
Ts = (meas_iff_struts{1}.t(end) - (meas_iff_struts{1}.t(1)))/(length(meas_iff_struts{1}.t)-1);
% Sampling Frequency [Hz]
Fs = 1/Ts;
% Hannning Windows
win = hanning(ceil(1*Fs));
% And we get the frequency vector
[~, f] = tfestimate(meas_iff_struts{1}.Vexc, meas_iff_struts{1}.de, win, [], [], 1/Ts);DVF Plant
%% DVF Plant (transfer function from u to dLm)
G_iff_opt = {};
for i = 1:6
G_iff_opt{i} = tfestimate(meas_iff_struts{i}.Vexc, meas_iff_struts{i}.de, win, [], [], 1/Ts);
endWith the IFF control strategy applied and the optimal gain used, the suspension modes are very well damped. Remains the undamped flexible modes of the APA (200Hz, 300Hz, 400Hz), and the modes of the plates (700Hz).
The Simscape model and the experimental results are in very good agreement.
Modal Analysis
<<sec:enc_struts_modal_analysis>>
Introduction ignore
Several 3-axis accelerometers are fixed on the top platform of the nano-hexapod as shown in Figure fig:compliance_vertical_comp_iff.
The top platform is then excited using an instrumented hammer as shown in Figure fig:hammer_excitation_compliance_meas.
Effectiveness of the IFF Strategy - Compliance
In this section, we wish to estimated the effectiveness of the IFF strategy concerning the compliance.
The top plate is excited vertically using the instrumented hammer two times:
- no control loop is used
- decentralized IFF is used
The data is loaded.
frf_ol = load('Measurement_Z_axis.mat'); % Open-Loop
frf_iff = load('Measurement_Z_axis_damped.mat'); % IFFThe mean vertical motion of the top platform is computed by averaging all 5 accelerometers.
%% Multiply by 10 (gain in m/s^2/V) and divide by 5 (number of accelerometers)
d_frf_ol = 10/5*(frf_ol.FFT1_H1_4_1_RMS_Y_Mod + frf_ol.FFT1_H1_7_1_RMS_Y_Mod + frf_ol.FFT1_H1_10_1_RMS_Y_Mod + frf_ol.FFT1_H1_13_1_RMS_Y_Mod + frf_ol.FFT1_H1_16_1_RMS_Y_Mod)./(2*pi*frf_ol.FFT1_H1_16_1_RMS_X_Val).^2;
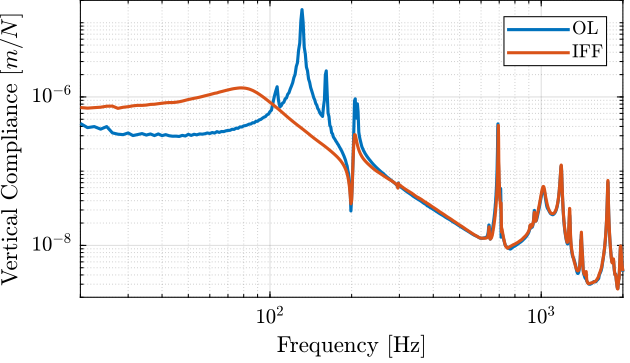
d_frf_iff = 10/5*(frf_iff.FFT1_H1_4_1_RMS_Y_Mod + frf_iff.FFT1_H1_7_1_RMS_Y_Mod + frf_iff.FFT1_H1_10_1_RMS_Y_Mod + frf_iff.FFT1_H1_13_1_RMS_Y_Mod + frf_iff.FFT1_H1_16_1_RMS_Y_Mod)./(2*pi*frf_iff.FFT1_H1_16_1_RMS_X_Val).^2;The vertical compliance (magnitude of the transfer function from a vertical force applied on the top plate to the vertical motion of the top plate) is shown in Figure fig:compliance_vertical_comp_iff.
From Figure fig:compliance_vertical_comp_iff, it is clear that the IFF control strategy is very effective in damping the suspensions modes of the nano-hexapode. It also has the effect of degrading (slightly) the vertical compliance at low frequency.
It also seems some damping can be added to the modes at around 205Hz which are flexible modes of the struts.
Comparison with the Simscape Model
Let's now compare the measured vertical compliance with the vertical compliance as estimated from the Simscape model.
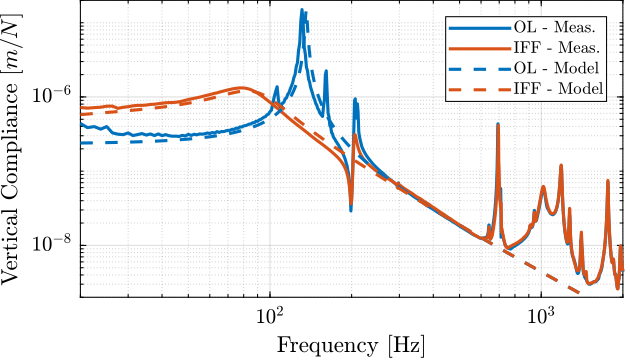
The transfer function from a vertical external force to the absolute motion of the top platform is identified (with and without IFF) using the Simscape model.
The comparison is done in Figure fig:compliance_vertical_comp_model_iff. Again, the model is quite accurate!
Obtained Mode Shapes
Then, several excitation are performed using the instrumented Hammer and the mode shapes are extracted.
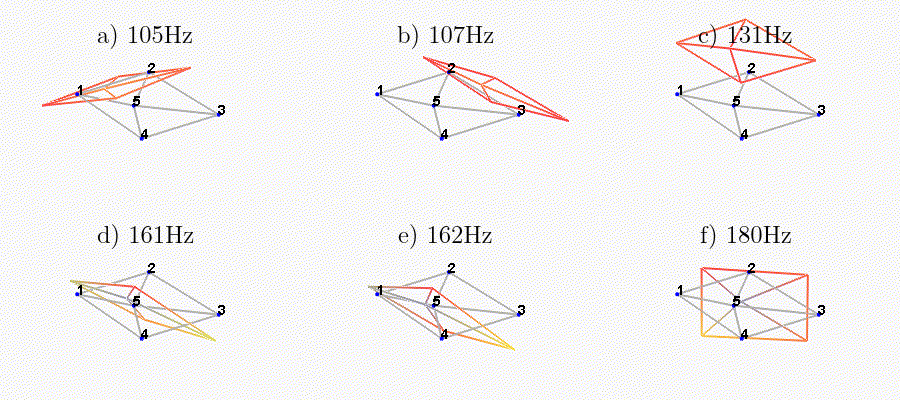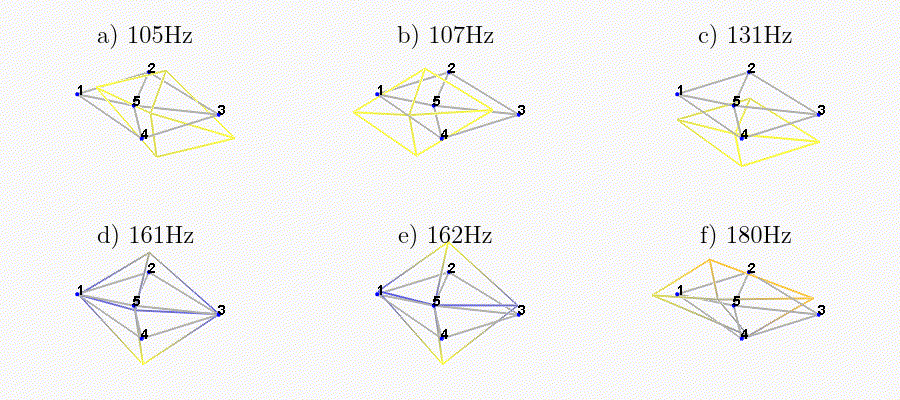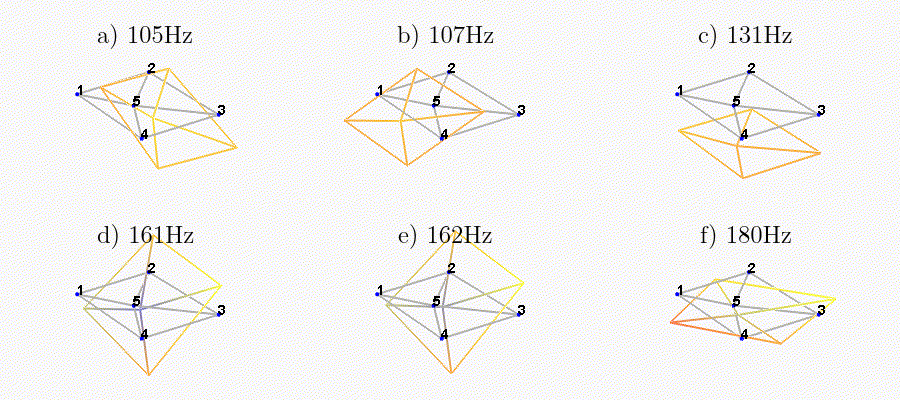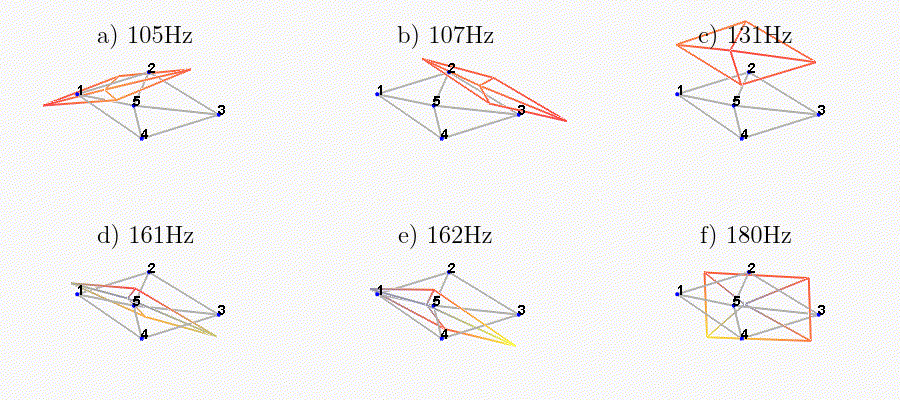
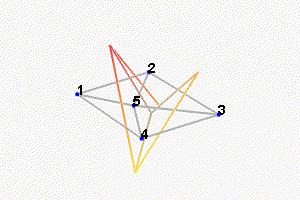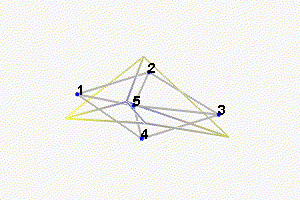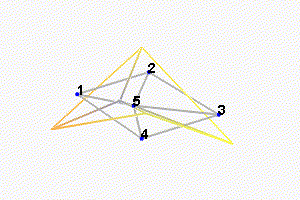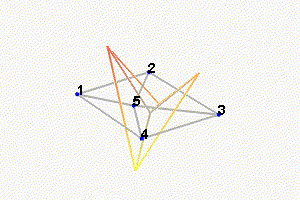
We can observe the mode shapes of the first 6 modes that are the suspension modes (the plate is behaving as a solid body) in Figure fig:mode_shapes_annotated.
Then, there is a mode at 692Hz which corresponds to a flexible mode of the top plate (Figure fig:mode_shapes_flexible_annotated).
The obtained modes are summarized in Table tab:description_modes.
| Mode | Freq. [Hz] | Description |
|---|---|---|
| 1 | 105 | Suspension Mode: Y-translation |
| 2 | 107 | Suspension Mode: X-translation |
| 3 | 131 | Suspension Mode: Z-translation |
| 4 | 161 | Suspension Mode: Y-tilt |
| 5 | 162 | Suspension Mode: X-tilt |
| 6 | 180 | Suspension Mode: Z-rotation |
| 7 | 692 | (flexible) Membrane mode of the top platform |
Accelerometers fixed on the top platform
Experimental Identification
%% Load Identification Data
meas_acc = {};
for i = 1:6
meas_acc(i) = {load(sprintf('mat/meas_acc_top_plat_strut_%i.mat', i), 't', 'Va', 'de', 'Am')};
end%% Setup useful variables
% Sampling Time [s]
Ts = (meas_acc{1}.t(end) - (meas_acc{1}.t(1)))/(length(meas_acc{1}.t)-1);
% Sampling Frequency [Hz]
Fs = 1/Ts;
% Hannning Windows
win = hanning(ceil(1*Fs));
% And we get the frequency vector
[~, f] = tfestimate(meas_acc{1}.Va, meas_acc{1}.de, win, [], [], 1/Ts);The sensibility of the accelerometers are $0.1 V/g \approx 0.01 V/(m/s^2)$.
%% Compute the 6x6 transfer function matrix
G_acc = zeros(length(f), 6, 6);
for i = 1:6
G_acc(:,:,i) = tfestimate(meas_acc{i}.Va, 1/0.01*meas_acc{i}.Am, win, [], [], 1/Ts);
endLocation and orientation of accelerometers
Opm = [ 0.047, -0.112, 10e-3;
0.047, -0.112, 10e-3;
-0.113, 0.011, 10e-3;
-0.113, 0.011, 10e-3;
0.040, 0.113, 10e-3;
0.040, 0.113, 10e-3]';
Osm = [-1, 0, 0;
0, 0, 1;
0, -1, 0;
0, 0, 1;
-1, 0, 0;
0, 0, 1]';COM
Hbm = -15e-3;
M = getTransformationMatrixAcc(Opm-[0;0;Hbm], Osm);
J = getJacobianNanoHexapod(Hbm);G_acc_CoM = zeros(size(G_acc));
for i = 1:length(f)
G_acc_CoM(i, :, :) = inv(M)*squeeze(G_acc(i, :, :))*inv(J');
endCOK
Hbm = -42.3e-3;
M = getTransformationMatrixAcc(Opm-[0;0;Hbm], Osm);
J = getJacobianNanoHexapod(Hbm);G_acc_CoK = zeros(size(G_acc));
for i = 1:length(f)
G_acc_CoK(i, :, :) = inv(M)*squeeze(G_acc(i, :, :))*inv(J');
endComp with the Simscape Model
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'struts', ...
'actuator_type', 'flexible', ...
'MO_B', -42.3e-3);%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Relative Motion Outputs
G = linearize(mdl, io, 0.0, options);
G.InputName = {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};
G.OutputName = {'D1', 'D2', 'D3', 'D4', 'D5', 'D6'};Then use the Jacobian matrices to obtain the "cartesian" centralized plant.
Gc = inv(n_hexapod.geometry.J)*...
G*...
inv(n_hexapod.geometry.J');Encoders fixed to the plates
<<sec:encoders_plates>>
Introduction ignore
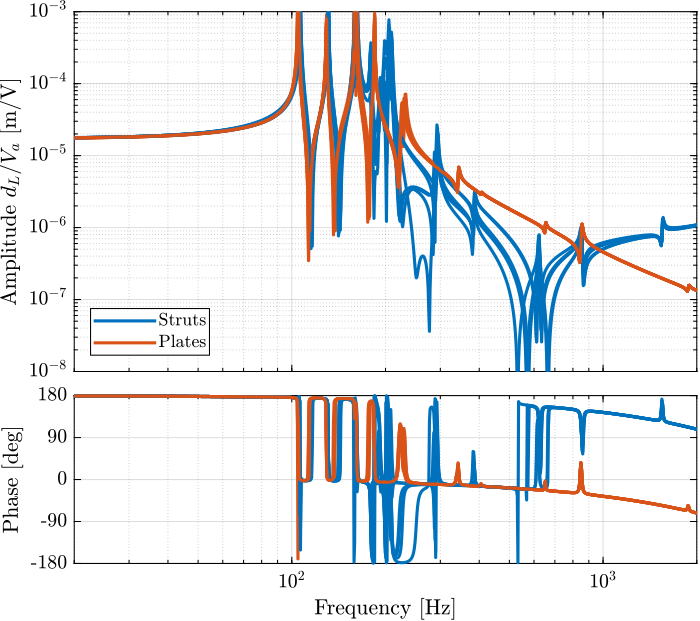
In this section, the encoders are fixed to the plates rather than to the struts as shown in Figure fig:enc_fixed_to_struts.
It is structured as follow:
- Section sec:enc_plates_plant_id: The dynamics of the nano-hexapod is identified
- Section sec:enc_plates_comp_simscape: The identified dynamics is compared with the Simscape model
- Section sec:enc_plates_iff: The Integral Force Feedback (IFF) control strategy is applied and the dynamics of the damped nano-hexapod is identified and compare with the Simscape model
- Section sec:hac_iff_struts: The High Authority Control (HAC) in the frame of the struts is developed
- Section sec:hac_iff_struts_ref_track: Some reference tracking tests are performed in order to experimentally validate the HAC-LAC control strategy.
Identification of the dynamics
<<sec:enc_plates_plant_id>>
Introduction ignore
Load Measurement Data
%% Load Identification Data
meas_data_lf = {};
for i = 1:6
meas_data_lf(i) = {load(sprintf('mat/frf_exc_strut_%i_enc_plates_noise.mat', i), 't', 'Va', 'Vs', 'de')};
endSpectral Analysis - Setup
%% Setup useful variables
% Sampling Time [s]
Ts = (meas_data_lf{1}.t(end) - (meas_data_lf{1}.t(1)))/(length(meas_data_lf{1}.t)-1);
% Sampling Frequency [Hz]
Fs = 1/Ts;
% Hannning Windows
win = hanning(ceil(1*Fs));
% And we get the frequency vector
[~, f] = tfestimate(meas_data_lf{1}.Va, meas_data_lf{1}.de, win, [], [], 1/Ts);DVF Plant
First, let's compute the coherence from the excitation voltage and the displacement as measured by the encoders (Figure fig:enc_plates_dvf_coh).
%% Coherence
coh_dvf = zeros(length(f), 6, 6);
for i = 1:6
coh_dvf(:, :, i) = mscohere(meas_data_lf{i}.Va, meas_data_lf{i}.de, win, [], [], 1/Ts);
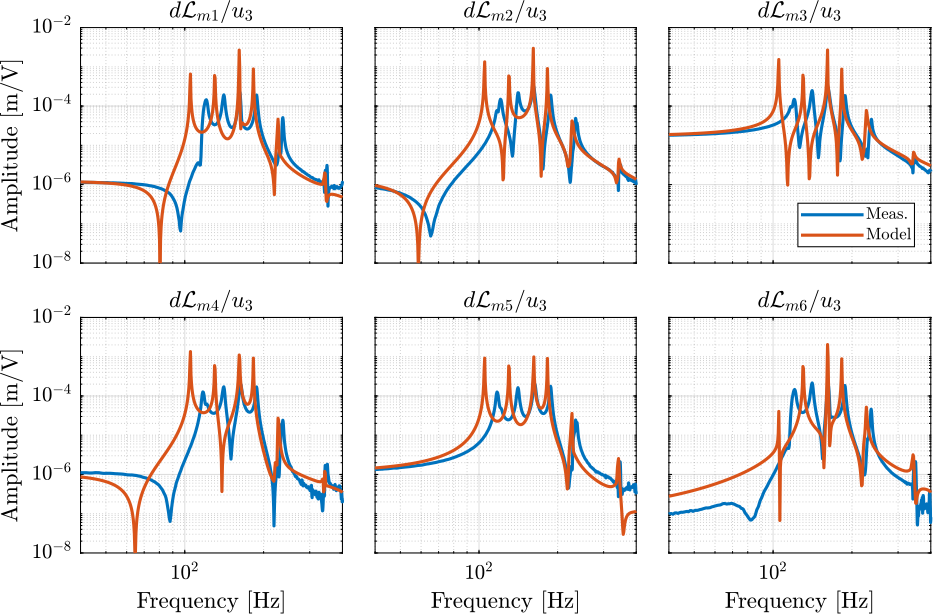
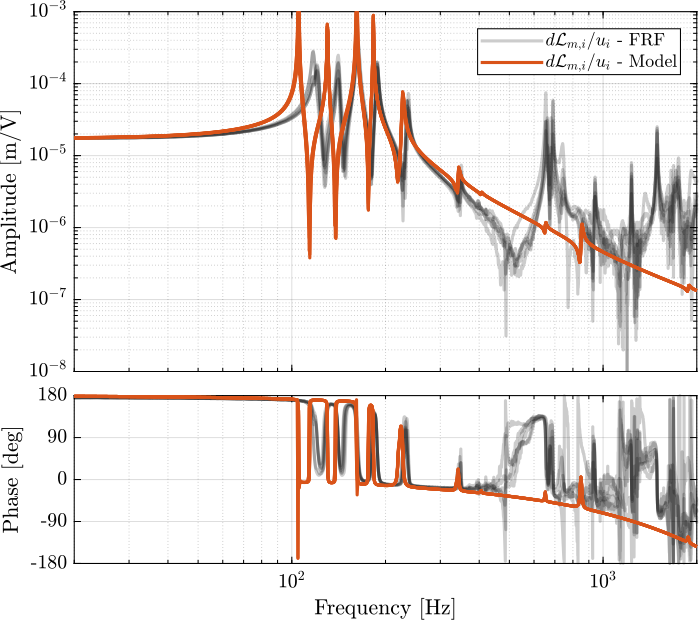
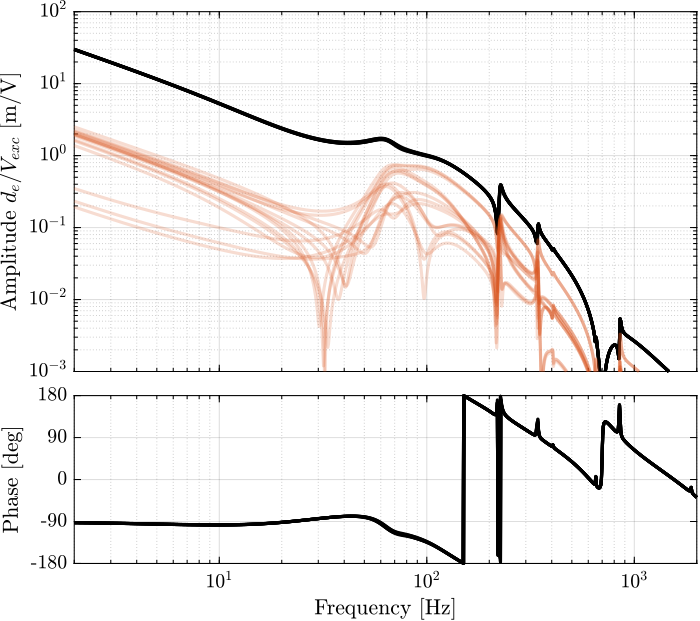
endThen the 6x6 transfer function matrix is estimated (Figure fig:enc_plates_dvf_frf).
%% DVF Plant (transfer function from u to dLm)
G_dvf = zeros(length(f), 6, 6);
for i = 1:6
G_dvf(:,:,i) = tfestimate(meas_data_lf{i}.Va, meas_data_lf{i}.de, win, [], [], 1/Ts);
endIFF Plant
First, let's compute the coherence from the excitation voltage and the displacement as measured by the encoders (Figure fig:enc_plates_iff_coh).
%% Coherence for the IFF plant
coh_iff = zeros(length(f), 6, 6);
for i = 1:6
coh_iff(:,:,i) = mscohere(meas_data_lf{i}.Va, meas_data_lf{i}.Vs, win, [], [], 1/Ts);
endThen the 6x6 transfer function matrix is estimated (Figure fig:enc_plates_iff_frf).
%% IFF Plant
G_iff = zeros(length(f), 6, 6);
for i = 1:6
G_iff(:,:,i) = tfestimate(meas_data_lf{i}.Va, meas_data_lf{i}.Vs, win, [], [], 1/Ts);
endSave Identified Plants
save('matlab/mat/identified_plants_enc_plates.mat', 'f', 'Ts', 'G_iff', 'G_dvf')Comparison with the Simscape Model
<<sec:enc_plates_comp_simscape>>
Introduction ignore
In this section, the measured dynamics is compared with the dynamics estimated from the Simscape model.
Load measured FRF
%% Load data
load('identified_plants_enc_plates.mat', 'f', 'Ts', 'G_iff', 'G_dvf')Dynamics from Actuator to Force Sensors
%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'plates', ...
'actuator_type', 'flexible');%% Identify the IFF Plant (transfer function from u to taum)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dum'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors
Giff = exp(-s*Ts)*linearize(mdl, io, 0.0, options);Dynamics from Actuator to Encoder
%% Initialization of the Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'plates', ...
'actuator_type', 'flexible');%% Identify the DVF Plant (transfer function from u to dLm)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Encoders
Gdvf = exp(-s*Ts)*linearize(mdl, io, 0.0, options);Integral Force Feedback
<<sec:enc_plates_iff>>
Introduction ignore
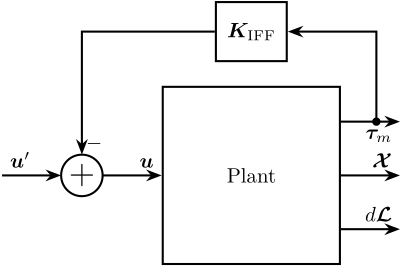
\begin{tikzpicture}
% Blocs
\node[block={3.0cm}{3.0cm}] (P) {Plant};
\coordinate[] (inputF) at ($(P.south west)!0.5!(P.north west)$);
\coordinate[] (outputF) at ($(P.south east)!0.8!(P.north east)$);
\coordinate[] (outputX) at ($(P.south east)!0.5!(P.north east)$);
\coordinate[] (outputL) at ($(P.south east)!0.2!(P.north east)$);
\node[block, above=0.4 of P] (Kiff) {$\bm{K}_\text{IFF}$};
\node[addb={+}{}{-}{}{}, left= of inputF] (addF) {};
% Connections and labels
\draw[->] (outputF) -- ++(1, 0) node[below left]{$\bm{\tau}_m$};
\draw[->] (outputL) -- ++(1, 0) node[above left]{$d\bm{\mathcal{L}}$};
\draw[->] (outputX) -- ++(1, 0) node[above left]{$\bm{\mathcal{X}}$};
\draw[->] ($(outputF) + (0.6, 0)$)node[branch]{} |- (Kiff.east);
\draw[->] (Kiff.west) -| (addF.north);
\draw[->] (addF.east) -- (inputF) node[above left]{$\bm{u}$};
\draw[<-] (addF.west) -- ++(-1, 0) node[above right]{$\bm{u}^\prime$};
\end{tikzpicture}Identification of the IFF Plant
%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'plates', ...
'actuator_type', '2dof');%% Identify the IFF Plant (transfer function from u to taum)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors
Giff = exp(-s*Ts)*linearize(mdl, io, 0.0, options);Effect of IFF on the plant - Simscape Model
load('Kiff.mat', 'Kiff')%% Identify the (damped) transfer function from u to dLm for different values of the IFF gain
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Plate Displacement (encoder)%% Initialize the Simscape model in closed loop
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'plates', ...
'actuator_type', 'flexible');Gd_ol = exp(-s*Ts)*linearize(mdl, io, 0.0, options);%% Initialize the Simscape model in closed loop
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'plates', ...
'actuator_type', 'flexible', ...
'controller_type', 'iff');Gd_iff = exp(-s*Ts)*linearize(mdl, io, 0.0, options);1
Experimental Results - Damped Plant with Optimal gain
Introduction ignore
Let's now look at the $6 \times 6$ damped plant with the optimal gain $g = 400$.
Load Data
%% Load Identification Data
meas_iff_plates = {};
for i = 1:6
meas_iff_plates(i) = {load(sprintf('mat/frf_exc_iff_strut_%i_enc_plates_noise.mat', i), 't', 'Va', 'Vs', 'de', 'u')};
endSpectral Analysis - Setup
%% Setup useful variables
% Sampling Time [s]
Ts = (meas_iff_plates{1}.t(end) - (meas_iff_plates{1}.t(1)))/(length(meas_iff_plates{1}.t)-1);
% Sampling Frequency [Hz]
Fs = 1/Ts;
% Hannning Windows
win = hanning(ceil(1*Fs));
% And we get the frequency vector
[~, f] = tfestimate(meas_iff_plates{1}.Va, meas_iff_plates{1}.de, win, [], [], 1/Ts);Simscape Model
load('Kiff.mat', 'Kiff')%% Initialize the Simscape model in closed loop
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'plates', ...
'actuator_type', 'flexible', ...
'controller_type', 'iff');%% Identify the (damped) transfer function from u to dLm for different values of the IFF gain
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Plate Displacement (encoder)Gd_iff_opt = exp(-s*Ts)*linearize(mdl, io, 0.0, options);DVF Plant
%% IFF Plant
G_enc_iff_opt = zeros(length(f), 6, 6);
for i = 1:6
G_enc_iff_opt(:,:,i) = tfestimate(meas_iff_plates{i}.Va, meas_iff_plates{i}.de, win, [], [], 1/Ts);
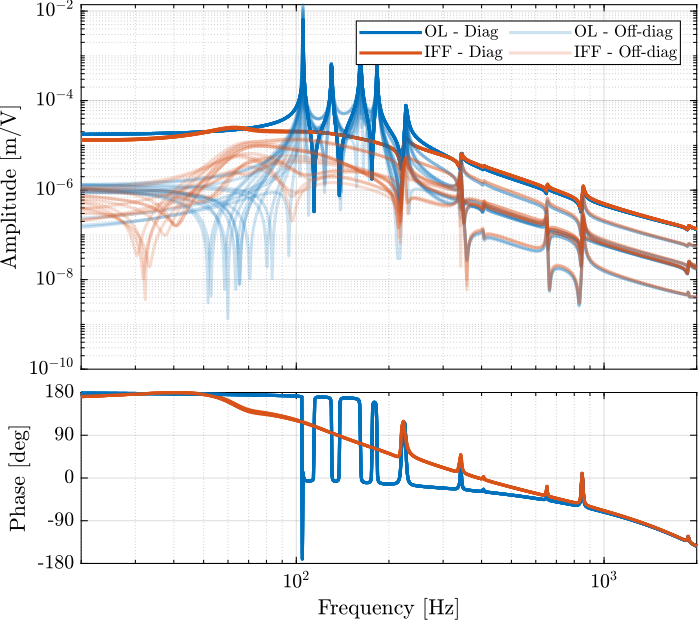
endEffect of IFF on the plant - FRF
Save Damped Plant
save('matlab/mat/damped_plant_enc_plates.mat', 'f', 'Ts', 'G_enc_iff_opt')HAC Control - Frame of the struts
<<sec:hac_iff_struts>>
Introduction ignore
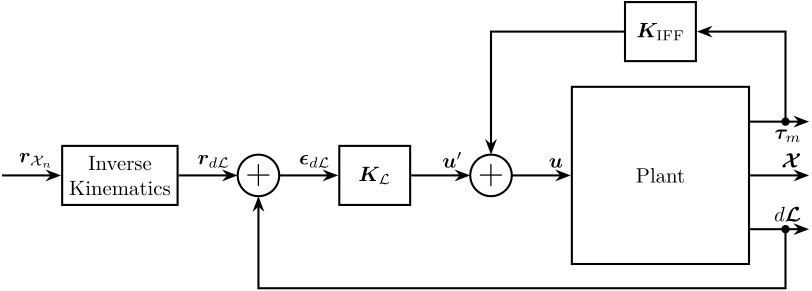
In a first approximation, the Jacobian matrix can be used instead of using the inverse kinematic equations.
\begin{tikzpicture}
% Blocs
\node[block={3.0cm}{3.0cm}] (P) {Plant};
\coordinate[] (inputF) at ($(P.south west)!0.5!(P.north west)$);
\coordinate[] (outputF) at ($(P.south east)!0.8!(P.north east)$);
\coordinate[] (outputX) at ($(P.south east)!0.5!(P.north east)$);
\coordinate[] (outputL) at ($(P.south east)!0.2!(P.north east)$);
\node[block, above=0.4 of P] (Kiff) {$\bm{K}_\text{IFF}$};
\node[addb, left= of inputF] (addF) {};
\node[block, left= of addF] (K) {$\bm{K}_\mathcal{L}$};
\node[addb, left= of K] (subr) {};
\node[block, align=center, left= of subr] (J) {Inverse\\Kinematics};
% Connections and labels
\draw[->] (outputF) -- ++(1, 0) node[below left]{$\bm{\tau}_m$};
\draw[->] ($(outputF) + (0.6, 0)$)node[branch]{} |- (Kiff.east);
\draw[->] (Kiff.west) -| (addF.north);
\draw[->] (addF.east) -- (inputF) node[above left]{$\bm{u}$};
\draw[->] (outputL) -- ++(1, 0) node[above left]{$d\bm{\mathcal{L}}$};
\draw[->] ($(outputL) + (0.6, 0)$)node[branch]{} -- ++(0, -1) -| (subr.south);
\draw[->] (subr.east) -- (K.west) node[above left]{$\bm{\epsilon}_{d\mathcal{L}}$};
\draw[->] (K.east) -- (addF.west) node[above left]{$\bm{u}^\prime$};
\draw[->] (outputX) -- ++(1, 0) node[above left]{$\bm{\mathcal{X}}$};
\draw[->] (J.east) -- (subr.west) node[above left]{$\bm{r}_{d\mathcal{L}}$};
\draw[<-] (J.west)node[above left]{$\bm{r}_{\mathcal{X}_n}$} -- ++(-1, 0);
\end{tikzpicture}Simscape Model
Let's start with the Simscape model and the damped plant.
Apply HAC control and verify the system is stable.
Then, try the control strategy on the real plant.
load('Kiff.mat', 'Kiff')%% Initialize the Simscape model in closed loop
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'plates', ...
'actuator_type', 'flexible', ...
'controller_type', 'iff');%% Identify the (damped) transfer function from u to dLm for different values of the IFF gain
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Plate Displacement (encoder)Gd_iff_opt = exp(-s*Ts)*linearize(mdl, io, 0.0, options);isstable(Gd_iff_opt)1
HAC Controller
Let's try to have 100Hz bandwidth:
%% Lead
a = 2; % Amount of phase lead / width of the phase lead / high frequency gain
wc = 2*pi*100; % Frequency with the maximum phase lead [rad/s]
H_lead = (1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));
%% Low Pass filter
H_lpf = 1/(1 + s/2/pi/200);
%% Notch
gm = 0.02;
xi = 0.3;
wn = 2*pi*700;
H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);Khac_iff_struts = -(1/(2.87e-5)) * ... % Gain
H_lead * ... % Lead
H_notch * ... % Notch
(2*pi*100/s) * ... % Integrator
eye(6); % 6x6 Diagonalsave('matlab/mat/Khac_iff_struts.mat', 'Khac_iff_struts')Lhac_iff_struts = Khac_iff_struts*Gd_iff_opt;Experimental Loop Gain
Verification of the Stability using the Simscape model
%% Initialize the Simscape model in closed loop
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'plates', ...
'actuator_type', 'flexible', ...
'controller_type', 'hac-iff-struts');Gd_iff_hac_opt = linearize(mdl, io, 0.0, options);isstable(Gd_iff_hac_opt)1
Reference Tracking
<<sec:hac_iff_struts_ref_track>>
Introduction ignore
Load
load('Khac_iff_struts.mat', 'Khac_iff_struts')Y-Z Scans
Generate the Scan
Rx_yz = generateYZScanTrajectory(...
'y_tot', 4e-6, ...
'z_tot', 8e-6, ...
'n', 5, ...
'Ts', 1e-3, ...
'ti', 2, ...
'tw', 0.5, ...
'ty', 2, ...
'tz', 1);figure;
hold on;
plot(Rx_yz(:,1), Rx_yz(:,3), ...
'DisplayName', 'Y motion')
plot(Rx_yz(:,1), Rx_yz(:,4), ...
'DisplayName', 'Z motion')
hold off;
xlabel('Time [s]');
ylabel('Displacement [m]');
legend('location', 'northeast');figure;
plot(Rx_yz(:,3), Rx_yz(:,4));
xlabel('y [m]'); ylabel('z [m]');Reference Signal for the Strut lengths
Let's use the Jacobian to estimate the wanted strut length as a function of time.
dL_ref = [n_hexapod.geometry.J*Rx_yz(:, 2:7)']';figure;
hold on;
for i=1:6
plot(Rx_yz(:,1), dL_ref(:, i))
end
xlabel('Time [s]'); ylabel('Displacement [m]');Time domain simulation with 2DoF model
%% Initialize the Simscape model in closed loop
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '2dof', ...
'flex_top_type', '3dof', ...
'motion_sensor_type', 'plates', ...
'actuator_type', '2dof', ...
'controller_type', 'hac-iff-struts');set_param(mdl,'StopTime', num2str(Rx_yz(end,1)))
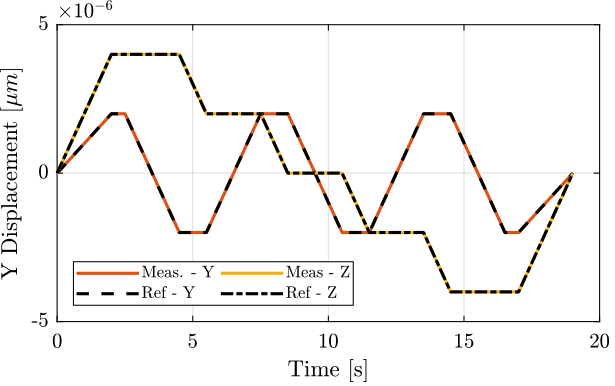
set_param(mdl,'SimulationCommand','start')out.X.Data = out.X.Data - out.X.Data(1,:);"NASS" reference path
Generate Path
ref_path = [ ...
0, 0, 0;
0, 0, 1; % N
0, 4, 1;
3, 0, 1;
3, 4, 1;
3, 4, 0;
4, 0, 0;
4, 0, 1; % A
4, 3, 1;
5, 4, 1;
6, 4, 1;
7, 3, 1;
7, 2, 1;
4, 2, 1;
4, 3, 1;
5, 4, 1;
6, 4, 1;
7, 3, 1;
7, 0, 1;
7, 0, 0;
8, 0, 0;
8, 0, 1; % S
11, 0, 1;
11, 2, 1;
8, 2, 1;
8, 4, 1;
11, 4, 1;
11, 4, 0;
12, 0, 0;
12, 0, 1; % S
15, 0, 1;
15, 2, 1;
12, 2, 1;
12, 4, 1;
15, 4, 1;
15, 4, 0;
];
% Center the trajectory arround zero
ref_path = ref_path - (max(ref_path) - min(ref_path))/2;
% Define the X-Y-Z cuboid dimensions containing the trajectory
X_max = 10e-6;
Y_max = 4e-6;
Z_max = 2e-6;
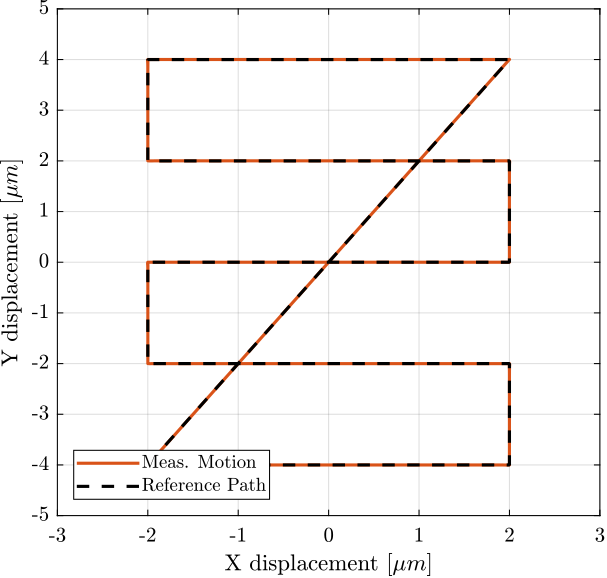
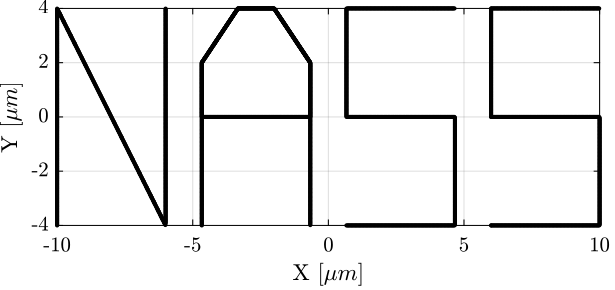
ref_path = ([X_max, Y_max, Z_max]./max(ref_path)).*ref_path; % [m]Rx_nass = generateXYZTrajectory('points', ref_path);figure;
plot(1e6*Rx_nass(Rx_nass(:,4)>0, 2), 1e6*Rx_nass(Rx_nass(:,4)>0, 3), 'k.')
xlabel('X [$\mu m$]');
ylabel('Y [$\mu m$]');
axis equal;
xlim(1e6*[min(Rx_nass(:,2)), max(Rx_nass(:,2))]);
ylim(1e6*[min(Rx_nass(:,3)), max(Rx_nass(:,3))]);figure;
plot3(Rx_nass(:,2), Rx_nass(:,3), Rx_nass(:,4), 'k-');
xlabel('x');
ylabel('y');
zlabel('z');figure;
hold on;
plot(Rx_nass(:,1), Rx_nass(:,2));
plot(Rx_nass(:,1), Rx_nass(:,3));
plot(Rx_nass(:,1), Rx_nass(:,4));
hold off;figure;
scatter(Rx_nass(:,2), Rx_nass(:,3), 1, Rx_nass(:,4), 'filled')
colormap winterSimscape Simulations
%% Initialize the Simscape model in closed loop
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '2dof', ...
'flex_top_type', '3dof', ...
'motion_sensor_type', 'plates', ...
'actuator_type', '2dof', ...
'controller_type', 'hac-iff-struts');set_param(mdl,'StopTime', num2str(Rx_nass(end,1)))
set_param(mdl,'SimulationCommand','start')out.X.Data = out.X.Data - out.X.Data(1,:);Save Reference paths
save('matlab/mat/reference_path.mat', 'Rx_yz', 'Rx_nass')Experimental Results
Feedforward (Open-Loop) Control
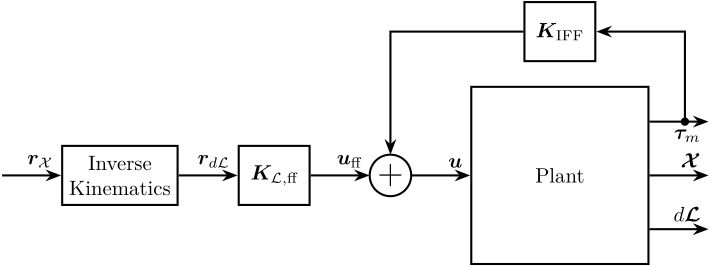
Introduction
\begin{tikzpicture}
% Blocs
\node[block={3.0cm}{3.0cm}] (P) {Plant};
\coordinate[] (inputF) at ($(P.south west)!0.5!(P.north west)$);
\coordinate[] (outputF) at ($(P.south east)!0.8!(P.north east)$);
\coordinate[] (outputX) at ($(P.south east)!0.5!(P.north east)$);
\coordinate[] (outputL) at ($(P.south east)!0.2!(P.north east)$);
\node[block, above=0.4 of P] (Kiff) {$\bm{K}_\text{IFF}$};
\node[addb, left= of inputF] (addF) {};
\node[block, left= of addF] (Kff) {$\bm{K}_{\mathcal{L},\text{ff}}$};
\node[block, align=center, left= of Kff] (J) {Inverse\\Kinematics};
% Connections and labels
\draw[->] (outputF) -- ++(1, 0) node[below left]{$\bm{\tau}_m$};
\draw[->] ($(outputF) + (0.6, 0)$)node[branch]{} |- (Kiff.east);
\draw[->] (Kiff.west) -| (addF.north);
\draw[->] (addF.east) -- (inputF) node[above left]{$\bm{u}$};
\draw[->] (outputL) -- ++(1, 0) node[above left]{$d\bm{\mathcal{L}}$};
\draw[->] (outputX) -- ++(1, 0) node[above left]{$\bm{\mathcal{X}}$};
\draw[->] (Kff.east) -- (addF.west) node[above left]{$\bm{u}_{\text{ff}}$};
\draw[->] (J.east) -- (Kff.west) node[above left]{$\bm{r}_{d\mathcal{L}}$};
\draw[<-] (J.west)node[above left]{$\bm{r}_{\mathcal{X}}$} -- ++(-1, 0);
\end{tikzpicture}Simple Feedforward Controller
Let's estimate the mean DC gain for the damped plant (diagonal elements:)
1.773e-05
The feedforward controller is then taken as the inverse of this gain (the minus sign is there manually added as it is "removed" by the abs function):
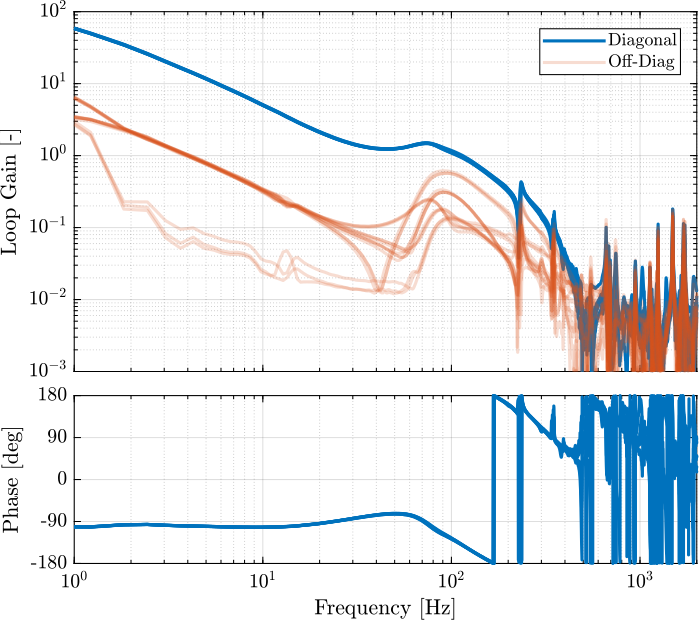
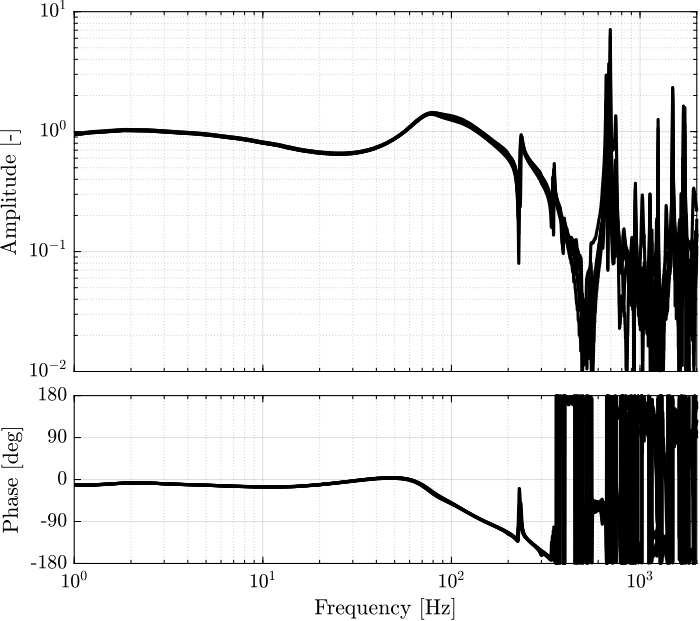
Kff_iff_L = -1/mean(diag(abs(squeeze(mean(G_enc_iff_opt(f>2 & f<4,:,:))))));The open-loop gain (feedforward controller times the damped plant) is shown in Figure fig:open_loop_gain_feedforward_iff_struts.
And save the feedforward controller for further use:
Kff_iff_L = zpk(Kff_iff_L)*eye(6);save('matlab/mat/feedforward_iff.mat', 'Kff_iff_L')Test with Simscape Model
load('reference_path.mat', 'Rx_yz');Feedback/Feedforward control in the frame of the struts
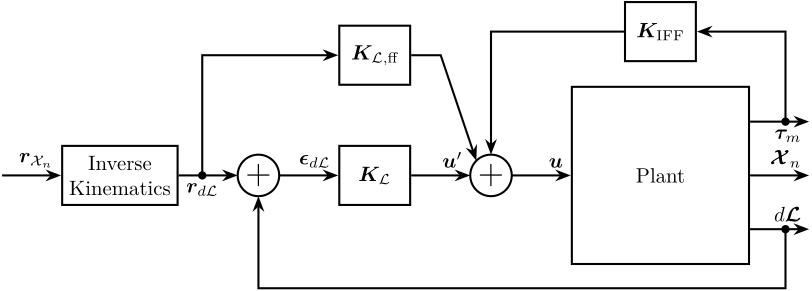
Introduction ignore
\begin{tikzpicture}
% Blocs
\node[block={3.0cm}{3.0cm}] (P) {Plant};
\coordinate[] (inputF) at ($(P.south west)!0.5!(P.north west)$);
\coordinate[] (outputF) at ($(P.south east)!0.8!(P.north east)$);
\coordinate[] (outputX) at ($(P.south east)!0.5!(P.north east)$);
\coordinate[] (outputL) at ($(P.south east)!0.2!(P.north east)$);
\node[block, above=0.4 of P] (Kiff) {$\bm{K}_\text{IFF}$};
\node[addb, left= of inputF] (addF) {};
\node[block, left= of addF] (K) {$\bm{K}_\mathcal{L}$};
\node[block, above= of K] (Kff) {$\bm{K}_{\mathcal{L},\text{ff}}$};
\node[addb, left= of K] (subr) {};
\node[block, align=center, left= of subr] (J) {Inverse\\Kinematics};
% Connections and labels
\draw[->] (outputF) -- ++(1, 0) node[below left]{$\bm{\tau}_m$};
\draw[->] ($(outputF) + (0.6, 0)$)node[branch]{} |- (Kiff.east);
\draw[->] (Kiff.west) -| (addF.north);
\draw[->] (addF.east) -- (inputF) node[above left]{$\bm{u}$};
\draw[->] (outputL) -- ++(1, 0) node[above left]{$d\bm{\mathcal{L}}$};
\draw[->] ($(outputL) + (0.6, 0)$)node[branch]{} -- ++(0, -1) -| (subr.south);
\draw[->] (subr.east) -- (K.west) node[above left]{$\bm{\epsilon}_{d\mathcal{L}}$};
\draw[->] (K.east) -- (addF.west) node[above left]{$\bm{u}^\prime$};
\draw[->] (outputX) -- ++(1, 0) node[above left]{$\bm{\mathcal{X}}_n$};
\draw[->] (J.east) -- (subr.west);
\draw[->] ($(J.east) + (0.4, 0)$)node[branch]{} node[below]{$\bm{r}_{d\mathcal{L}}$} |- (Kff.west);
\draw[->] (Kff.east) -- ++(0.5, 0) -- (addF.north west);
\draw[<-] (J.west)node[above left]{$\bm{r}_{\mathcal{X}_n}$} -- ++(-1, 0);
\end{tikzpicture}Functions
generateXYZTrajectory
<<sec:generateXYZTrajectory>>
Function description
function [ref] = generateXYZTrajectory(args)
% generateXYZTrajectory -
%
% Syntax: [ref] = generateXYZTrajectory(args)
%
% Inputs:
% - args
%
% Outputs:
% - ref - Reference SignalOptional Parameters
arguments
args.points double {mustBeNumeric} = zeros(2, 3) % [m]
args.ti (1,1) double {mustBeNumeric, mustBePositive} = 1 % Time to go to first point and after last point [s]
args.tw (1,1) double {mustBeNumeric, mustBePositive} = 0.5 % Time wait between each point [s]
args.tm (1,1) double {mustBeNumeric, mustBePositive} = 1 % Motion time between points [s]
args.Ts (1,1) double {mustBeNumeric, mustBePositive} = 1e-3 % Sampling Time [s]
endInitialize Time Vectors
time_i = 0:args.Ts:args.ti;
time_w = 0:args.Ts:args.tw;
time_m = 0:args.Ts:args.tm;XYZ Trajectory
% Go to initial position
xyz = (args.points(1,:))'*(time_i/args.ti);
% Wait
xyz = [xyz, xyz(:,end).*ones(size(time_w))];
% Scans
for i = 2:size(args.points, 1)
% Go to next point
xyz = [xyz, xyz(:,end) + (args.points(i,:)' - xyz(:,end))*(time_m/args.tm)];
% Wait a litle bit
xyz = [xyz, xyz(:,end).*ones(size(time_w))];
end
% End motion
xyz = [xyz, xyz(:,end) - xyz(:,end)*(time_i/args.ti)];Reference Signal
t = 0:args.Ts:args.Ts*(length(xyz) - 1);ref = zeros(length(xyz), 7);
ref(:, 1) = t;
ref(:, 2:4) = xyz';
generateYZScanTrajectory
<<sec:generateYZScanTrajectory>>
Function description
function [ref] = generateYZScanTrajectory(args)
% generateYZScanTrajectory -
%
% Syntax: [ref] = generateYZScanTrajectory(args)
%
% Inputs:
% - args
%
% Outputs:
% - ref - Reference SignalOptional Parameters
arguments
args.y_tot (1,1) double {mustBeNumeric} = 10e-6 % [m]
args.z_tot (1,1) double {mustBeNumeric} = 10e-6 % [m]
args.n (1,1) double {mustBeInteger, mustBePositive} = 10 % [-]
args.Ts (1,1) double {mustBeNumeric, mustBePositive} = 1e-4 % [s]
args.ti (1,1) double {mustBeNumeric, mustBePositive} = 1 % [s]
args.tw (1,1) double {mustBeNumeric, mustBePositive} = 1 % [s]
args.ty (1,1) double {mustBeNumeric, mustBePositive} = 1 % [s]
args.tz (1,1) double {mustBeNumeric, mustBePositive} = 1 % [s]
endInitialize Time Vectors
time_i = 0:args.Ts:args.ti;
time_w = 0:args.Ts:args.tw;
time_y = 0:args.Ts:args.ty;
time_z = 0:args.Ts:args.tz;Y and Z vectors
% Go to initial position
y = (time_i/args.ti)*(args.y_tot/2);
% Wait
y = [y, y(end)*ones(size(time_w))];
% Scans
for i = 1:args.n
if mod(i,2) == 0
y = [y, -(args.y_tot/2) + (time_y/args.ty)*args.y_tot];
else
y = [y, (args.y_tot/2) - (time_y/args.ty)*args.y_tot];
end
if i < args.n
y = [y, y(end)*ones(size(time_z))];
end
end
% Wait a litle bit
y = [y, y(end)*ones(size(time_w))];
% End motion
y = [y, y(end) - y(end)*time_i/args.ti];% Go to initial position
z = (time_i/args.ti)*(args.z_tot/2);
% Wait
z = [z, z(end)*ones(size(time_w))];
% Scans
for i = 1:args.n
z = [z, z(end)*ones(size(time_y))];
if i < args.n
z = [z, z(end) - (time_z/args.tz)*args.z_tot/(args.n-1)];
end
end
% Wait a litle bit
z = [z, z(end)*ones(size(time_w))];
% End motion
z = [z, z(end) - z(end)*time_i/args.ti];Reference Signal
t = 0:args.Ts:args.Ts*(length(y) - 1);ref = zeros(length(y), 7);
ref(:, 1) = t;
ref(:, 3) = y;
ref(:, 4) = z;
getTransformationMatrixAcc
<<sec:getTransformationMatrixAcc>>
Function description
function [M] = getTransformationMatrixAcc(Opm, Osm)
% getTransformationMatrixAcc -
%
% Syntax: [M] = getTransformationMatrixAcc(Opm, Osm)
%
% Inputs:
% - Opm - Nx3 (N = number of accelerometer measurements) X,Y,Z position of accelerometers
% - Opm - Nx3 (N = number of accelerometer measurements) Unit vectors representing the accelerometer orientation
%
% Outputs:
% - M - Transformation MatrixTransformation matrix from motion of the solid body to accelerometer measurements
Let's try to estimate the x-y-z acceleration of any point of the solid body from the acceleration/angular acceleration of the solid body expressed in $\{O\}$. For any point $p_i$ of the solid body (corresponding to an accelerometer), we can write:
\begin{equation} \begin{bmatrix} a_{i,x} \\ a_{i,y} \\ a_{i,z} \end{bmatrix} = \begin{bmatrix} \dot{v}_x \\ \dot{v}_y \\ \dot{v}_z \end{bmatrix} + p_i \times \begin{bmatrix} \dot{\omega}_x \\ \dot{\omega}_y \\ \dot{\omega}_z \end{bmatrix} \end{equation}We can write the cross product as a matrix product using the skew-symmetric transformation:
\begin{equation} \begin{bmatrix} a_{i,x} \\ a_{i,y} \\ a_{i,z} \end{bmatrix} = \begin{bmatrix} \dot{v}_x \\ \dot{v}_y \\ \dot{v}_z \end{bmatrix} + \underbrace{\begin{bmatrix} 0 & p_{i,z} & -p_{i,y} \\ -p_{i,z} & 0 & p_{i,x} \\ p_{i,y} & -p_{i,x} & 0 \end{bmatrix}}_{P_{i,[\times]}} \cdot \begin{bmatrix} \dot{\omega}_x \\ \dot{\omega}_y \\ \dot{\omega}_z \end{bmatrix} \end{equation}If we now want to know the (scalar) acceleration $a_i$ of the point $p_i$ in the direction of the accelerometer direction $\hat{s}_i$, we can just project the 3d acceleration on $\hat{s}_i$:
\begin{equation} a_i = \hat{s}_i^T \cdot \begin{bmatrix} a_{i,x} \\ a_{i,y} \\ a_{i,z} \end{bmatrix} = \hat{s}_i^T \cdot \begin{bmatrix} \dot{v}_x \\ \dot{v}_y \\ \dot{v}_z \end{bmatrix} + \left( \hat{s}_i^T \cdot P_{i,[\times]} \right) \cdot \begin{bmatrix} \dot{\omega}_x \\ \dot{\omega}_y \\ \dot{\omega}_z \end{bmatrix} \end{equation}Which is equivalent as a simple vector multiplication:
\begin{equation} a_i = \begin{bmatrix} \hat{s}_i^T & \hat{s}_i^T \cdot P_{i,[\times]} \end{bmatrix} \begin{bmatrix} \dot{v}_x \\ \dot{v}_y \\ \dot{v}_z \\ \dot{\omega}_x \\ \dot{\omega}_y \\ \dot{\omega}_z \end{bmatrix} = \begin{bmatrix} \hat{s}_i^T & \hat{s}_i^T \cdot P_{i,[\times]} \end{bmatrix} {}^O\vec{x} \end{equation}And finally we can combine the 6 (line) vectors for the 6 accelerometers to write that in a matrix form. We obtain Eq. eqref:eq:M_matrix.
The transformation from solid body acceleration ${}^O\vec{x}$ from sensor measured acceleration $\vec{a}$ is: \begin{equation} \label{eq:M_matrix} \vec{a} = _brace{\begin{bmatrix} \hat{s}_1^T & \hat{s}_1^T \cdot P_{1,[\times]} \\ \vdots & \vdots \\ \hat{s}_6^T & \hat{s}_6^T \cdot P_{6,[\times]} \end{bmatrix}}M {}^O\vec{x}
\end{equation}
with $\hat{s}_i$ the unit vector representing the measured direction of the i'th accelerometer expressed in frame $\{O\}$ and $P_{i,[\times]}$ the skew-symmetric matrix representing the cross product of the position of the i'th accelerometer expressed in frame $\{O\}$.
Let's define such matrix using matlab:
M = zeros(length(Opm), 6);
for i = 1:length(Opm)
Ri = [0, Opm(3,i), -Opm(2,i);
-Opm(3,i), 0, Opm(1,i);
Opm(2,i), -Opm(1,i), 0];
M(i, 1:3) = Osm(:,i)';
M(i, 4:6) = Osm(:,i)'*Ri;
endend
getJacobianNanoHexapod
<<sec:getJacobianNanoHexapod>>
Function description
function [J] = getJacobianNanoHexapod(Hbm)
% getJacobianNanoHexapod -
%
% Syntax: [J] = getJacobianNanoHexapod(Hbm)
%
% Inputs:
% - Hbm - Height of {B} w.r.t. {M} [m]
%
% Outputs:
% - J - Jacobian MatrixTransformation matrix from motion of the solid body to accelerometer measurements
Fa = [[-86.05, -74.78, 22.49],
[ 86.05, -74.78, 22.49],
[ 107.79, -37.13, 22.49],
[ 21.74, 111.91, 22.49],
[-21.74, 111.91, 22.49],
[-107.79, -37.13, 22.49]]'*1e-3; % Ai w.r.t. {F} [m]
Mb = [[-28.47, -106.25, -22.50],
[ 28.47, -106.25, -22.50],
[ 106.25, 28.47, -22.50],
[ 77.78, 77.78, -22.50],
[-77.78, 77.78, -22.50],
[-106.25, 28.47, -22.50]]'*1e-3; % Bi w.r.t. {M} [m]
H = 95e-3; % Stewart platform height [m]
Fb = Mb + [0; 0; H]; % Bi w.r.t. {F} [m]
si = Fb - Fa;
si = si./vecnorm(si); % Normalize
Bb = Mb - [0; 0; Hbm];
J = [si', cross(Bb, si)'];