58 KiB
Nano-Hexapod - Test Bench
- Introduction
- Encoders fixed to the Struts
- Encoders fixed to the plates
This report is also available as a pdf.
Introduction ignore
This document is dedicated to the experimental study of the nano-hexapod shown in Figure fig:picture_bench_granite_nano_hexapod.

Here are the documentation of the equipment used for this test bench (lots of them are shwon in Figure fig:picture_bench_granite_overview):

In Figure fig:nano_hexapod_signals is shown a block diagram of the experimental setup. When possible, the notations are consistent with this diagram and summarized in Table tab:list_signals.
\definecolor{instrumentation}{rgb}{0, 0.447, 0.741}
\definecolor{mechanics}{rgb}{0.8500, 0.325, 0.098}
\begin{tikzpicture}
% Blocs
\node[block={4.0cm}{3.0cm}, fill=mechanics!20!white] (nano_hexapod) {Mechanics};
\coordinate[] (inputF) at (nano_hexapod.west);
\coordinate[] (outputL) at ($(nano_hexapod.south east)!0.8!(nano_hexapod.north east)$);
\coordinate[] (outputF) at ($(nano_hexapod.south east)!0.2!(nano_hexapod.north east)$);
\node[block, left= 0.8 of inputF, fill=instrumentation!20!white, align=center] (F_stack) {\tiny Actuator \\ \tiny stacks};
\node[block, left= 0.8 of F_stack, fill=instrumentation!20!white] (PD200) {PD200};
\node[DAC, left= 0.8 of PD200, fill=instrumentation!20!white] (F_DAC) {DAC};
\node[block, right=0.8 of outputF, fill=instrumentation!20!white, align=center] (Fm_stack){\tiny Sensor \\ \tiny stack};
\node[ADC, right=0.8 of Fm_stack,fill=instrumentation!20!white] (Fm_ADC) {ADC};
\node[block, right=0.8 of outputL, fill=instrumentation!20!white] (encoder) {\tiny Encoder};
% Connections and labels
\draw[->] ($(F_DAC.west)+(-0.8,0)$) node[above right]{$\bm{u}$} node[below right]{$[V]$} -- node[sloped]{$/$} (F_DAC.west);
\draw[->] (F_DAC.east) -- node[midway, above]{$\tilde{\bm{u}}$}node[midway, below]{$[V]$} (PD200.west);
\draw[->] (PD200.east) -- node[midway, above]{$\bm{u}_a$}node[midway, below]{$[V]$} (F_stack.west);
\draw[->] (F_stack.east) -- (inputF) node[above left]{$\bm{\tau}$}node[below left]{$[N]$};
\draw[->] (outputF) -- (Fm_stack.west) node[above left]{$\bm{\epsilon}$} node[below left]{$[m]$};
\draw[->] (Fm_stack.east) -- node[midway, above]{$\tilde{\bm{\tau}}_m$}node[midway, below]{$[V]$} (Fm_ADC.west);
\draw[->] (Fm_ADC.east) -- node[sloped]{$/$} ++(0.8, 0)coordinate(end) node[above left]{$\bm{\tau}_m$}node[below left]{$[V]$};
\draw[->] (outputL) -- (encoder.west) node[above left]{$d\bm{\mathcal{L}}$} node[below left]{$[m]$};
\draw[->] (encoder.east) -- node[sloped]{$/$} (encoder-|end) node[above left]{$d\bm{\mathcal{L}}_m$}node[below left]{$[m]$};
% Nano-Hexapod
\begin{scope}[on background layer]
\node[fit={(F_stack.west|-nano_hexapod.south) (Fm_stack.east|-nano_hexapod.north)}, fill=black!20!white, draw, inner sep=2pt] (system) {};
\node[above] at (system.north) {Nano-Hexapod};
\end{scope}
\end{tikzpicture}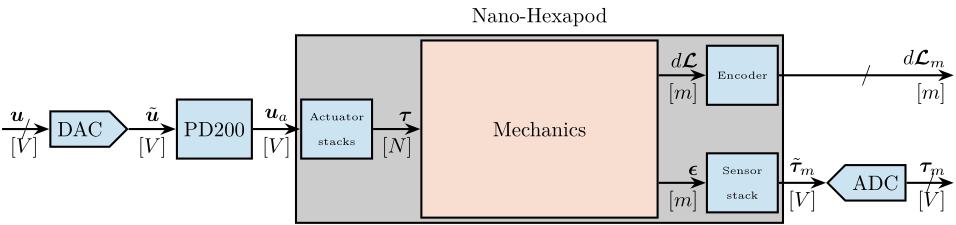
| Unit | Matlab | Vector | Elements | |
|---|---|---|---|---|
| Control Input (wanted DAC voltage) | [V] |
u |
$\bm{u}$ | $u_i$ |
| DAC Output Voltage | [V] |
u |
$\tilde{\bm{u}}$ | $\tilde{u}_i$ |
| PD200 Output Voltage | [V] |
ua |
$\bm{u}_a$ | $u_{a,i}$ |
| Actuator applied force | [N] |
tau |
$\bm{\tau}$ | $\tau_i$ |
| Strut motion | [m] |
dL |
$d\bm{\mathcal{L}}$ | $d\mathcal{L}_i$ |
| Encoder measured displacement | [m] |
dLm |
$d\bm{\mathcal{L}}_m$ | $d\mathcal{L}_{m,i}$ |
| Force Sensor strain | [m] |
epsilon |
$\bm{\epsilon}$ | $\epsilon_i$ |
| Force Sensor Generated Voltage | [V] |
taum |
$\tilde{\bm{\tau}}_m$ | $\tilde{\tau}_{m,i}$ |
| Measured Generated Voltage | [V] |
taum |
$\bm{\tau}_m$ | $\tau_{m,i}$ |
| Motion of the top platform | [m,rad] |
dX |
$d\bm{\mathcal{X}}$ | $d\mathcal{X}_i$ |
| Metrology measured displacement | [m,rad] |
dXm |
$d\bm{\mathcal{X}}_m$ | $d\mathcal{X}_{m,i}$ |
This document is divided in the following sections:
- Section sec:encoders_struts: the encoders are fixed to the struts
- Section sec:encoders_plates: the encoders are fixed to the plates
Encoders fixed to the Struts
<<sec:encoders_struts>>
Introduction
In this section, the encoders are fixed to the struts.
It is divided in the following sections:
- Section sec:enc_struts_plant_id: the transfer function matrix from the actuators to the force sensors and to the encoders is experimentally identified.
- Section sec:enc_struts_comp_simscape: the obtained FRF matrix is compared with the dynamics of the simscape model
- Section sec:enc_struts_iff: decentralized Integral Force Feedback (IFF) is applied and its performances are evaluated.
- Section sec:enc_struts_modal_analysis: a modal analysis of the nano-hexapod is performed
Identification of the dynamics
<<sec:enc_struts_plant_id>>
Load Data
%% Load Identification Data
meas_data_lf = {};
for i = 1:6
meas_data_lf(i) = {load(sprintf('mat/frf_data_exc_strut_%i_noise_lf.mat', i), 't', 'Va', 'Vs', 'de')};
meas_data_hf(i) = {load(sprintf('mat/frf_data_exc_strut_%i_noise_hf.mat', i), 't', 'Va', 'Vs', 'de')};
endSpectral Analysis - Setup
%% Setup useful variables
% Sampling Time [s]
Ts = (meas_data_lf{1}.t(end) - (meas_data_lf{1}.t(1)))/(length(meas_data_lf{1}.t)-1);
% Sampling Frequency [Hz]
Fs = 1/Ts;
% Hannning Windows
win = hanning(ceil(1*Fs));
% And we get the frequency vector
[~, f] = tfestimate(meas_data_lf{1}.Va, meas_data_lf{1}.de, win, [], [], 1/Ts);
i_lf = f < 250; % Points for low frequency excitation
i_hf = f > 250; % Points for high frequency excitationDVF Plant
First, let's compute the coherence from the excitation voltage and the displacement as measured by the encoders (Figure fig:enc_struts_dvf_coh).
%% Coherence
coh_dvf_lf = zeros(length(f), 6, 6);
coh_dvf_hf = zeros(length(f), 6, 6);
for i = 1:6
coh_dvf_lf(:, :, i) = mscohere(meas_data_lf{i}.Va, meas_data_lf{i}.de, win, [], [], 1/Ts);
coh_dvf_hf(:, :, i) = mscohere(meas_data_hf{i}.Va, meas_data_hf{i}.de, win, [], [], 1/Ts);
end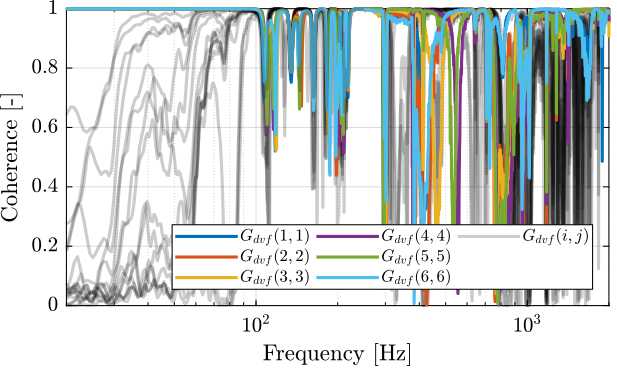
Then the 6x6 transfer function matrix is estimated (Figure fig:enc_struts_dvf_frf).
%% DVF Plant (transfer function from u to dLm)
G_dvf_lf = zeros(length(f), 6, 6);
G_dvf_hf = zeros(length(f), 6, 6);
for i = 1:6
G_dvf_lf(:, :, i) = tfestimate(meas_data_lf{i}.Va, meas_data_lf{i}.de, win, [], [], 1/Ts);
G_dvf_hf(:, :, i) = tfestimate(meas_data_hf{i}.Va, meas_data_hf{i}.de, win, [], [], 1/Ts);
end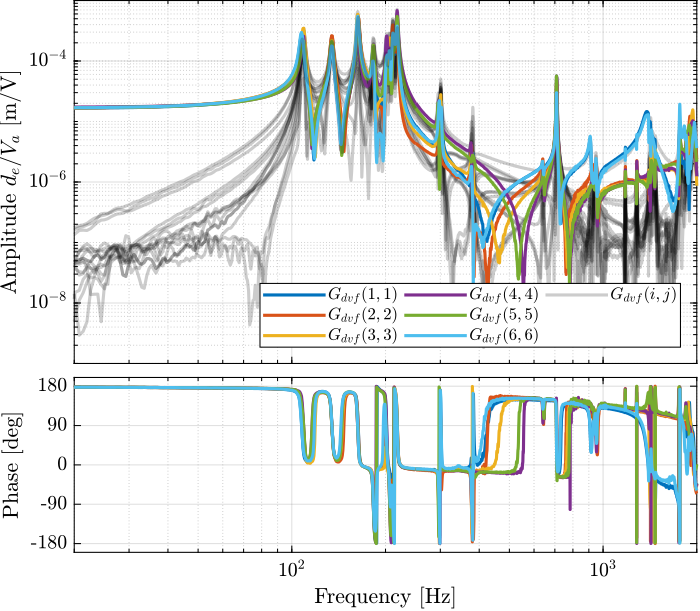
IFF Plant
First, let's compute the coherence from the excitation voltage and the displacement as measured by the encoders (Figure fig:enc_struts_iff_coh).
%% Coherence for the IFF plant
coh_iff_lf = zeros(length(f), 6, 6);
coh_iff_hf = zeros(length(f), 6, 6);
for i = 1:6
coh_iff_lf(:, :, i) = mscohere(meas_data_lf{i}.Va, meas_data_lf{i}.Vs, win, [], [], 1/Ts);
coh_iff_hf(:, :, i) = mscohere(meas_data_hf{i}.Va, meas_data_hf{i}.Vs, win, [], [], 1/Ts);
end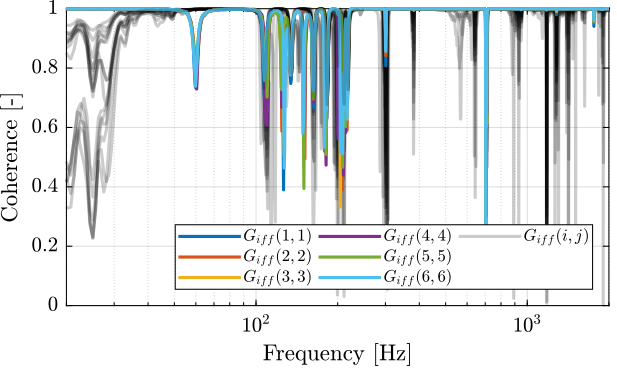
Then the 6x6 transfer function matrix is estimated (Figure fig:enc_struts_iff_frf).
%% IFF Plant
G_iff_lf = zeros(length(f), 6, 6);
G_iff_hf = zeros(length(f), 6, 6);
for i = 1:6
G_iff_lf(:, :, i) = tfestimate(meas_data_lf{i}.Va, meas_data_lf{i}.Vs, win, [], [], 1/Ts);
G_iff_hf(:, :, i) = tfestimate(meas_data_hf{i}.Va, meas_data_hf{i}.Vs, win, [], [], 1/Ts);
end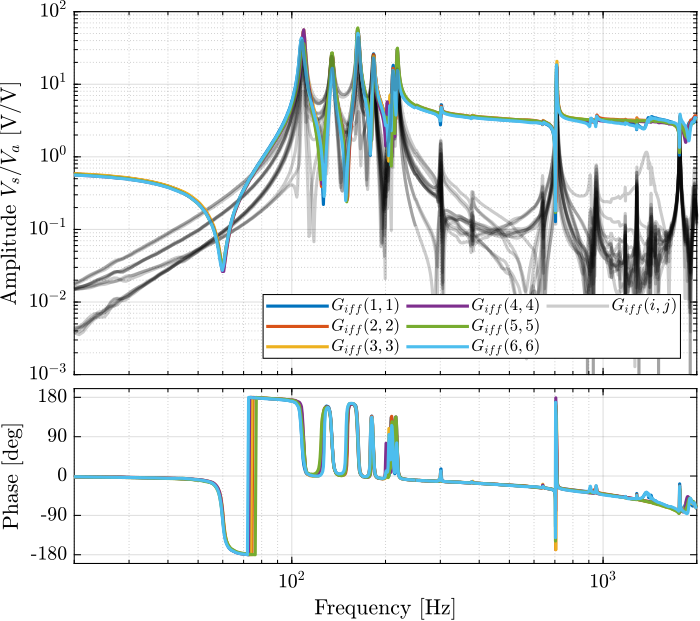
Comparison with the Simscape Model
<<sec:enc_struts_comp_simscape>>
Introduction ignore
In this section, the measured dynamics is compared with the dynamics estimated from the Simscape model.
Dynamics from Actuator to Force Sensors
%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'struts', ...
'actuator_type', '2dof');%% Identify the IFF Plant (transfer function from u to taum)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors
Giff = exp(-s*Ts)*linearize(mdl, io, 0.0, options);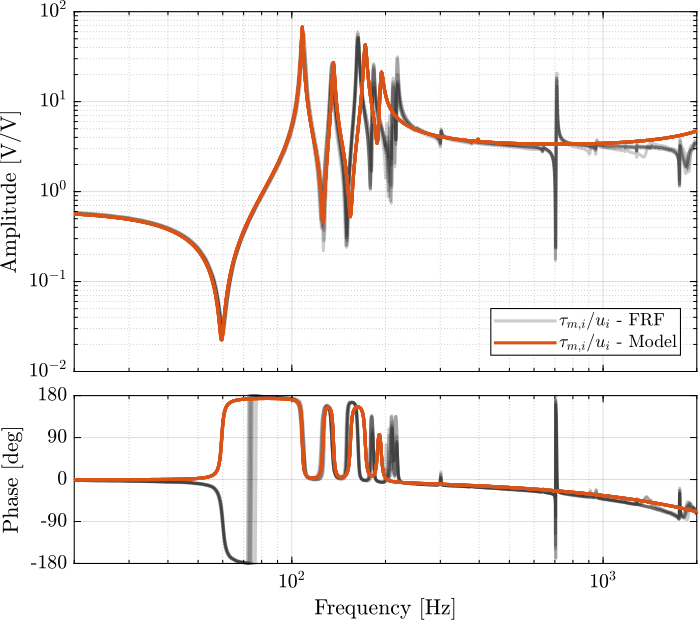
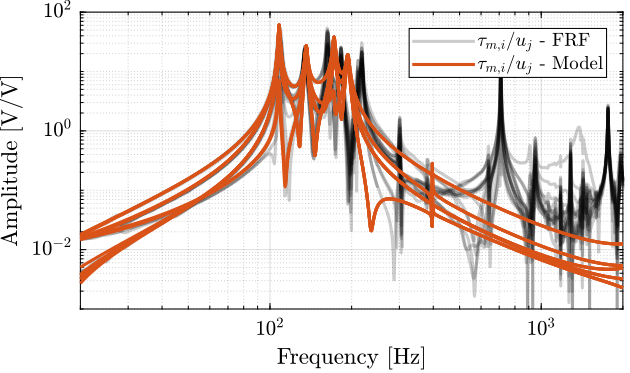
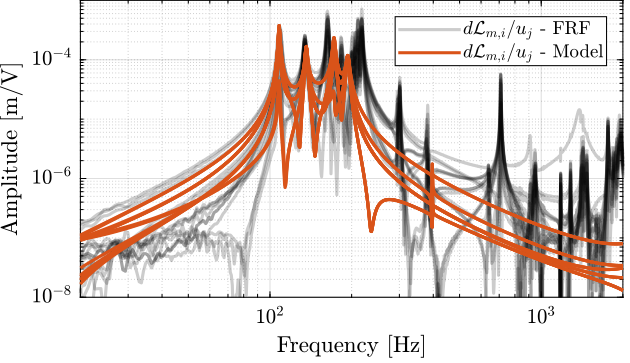
Dynamics from Actuator to Encoder
%% Initialization of the Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'struts', ...
'actuator_type', '2dof');%% Identify the DVF Plant (transfer function from u to dLm)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Encoders
Gdvf = exp(-s*Ts)*linearize(mdl, io, 0.0, options);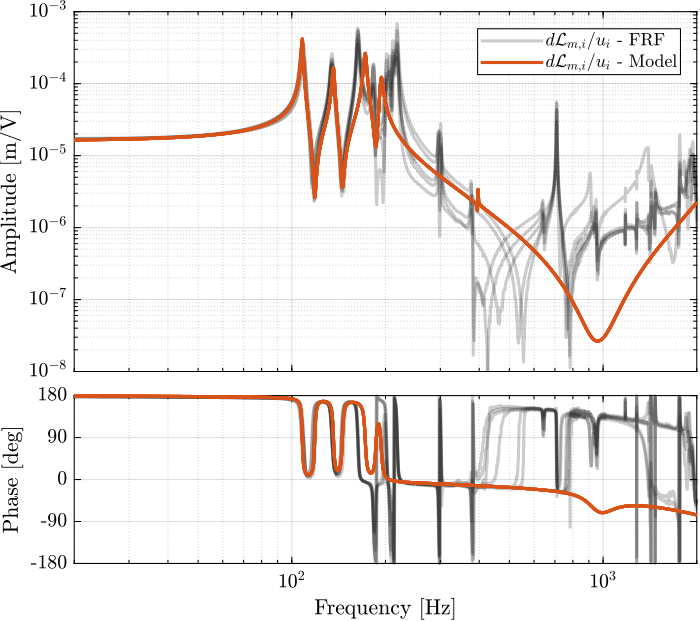
Integral Force Feedback
<<sec:enc_struts_iff>>
Root Locus and Decentralized Loop gain
%% IFF Controller
Kiff_g1 = (1/(s + 2*pi*40))*... % Low pass filter (provides integral action above 40Hz)
(s/(s + 2*pi*30))*... % High pass filter to limit low frequency gain
(1/(1 + s/2/pi/500))*... % Low pass filter to be more robust to high frequency resonances
eye(6); % Diagonal 6x6 controller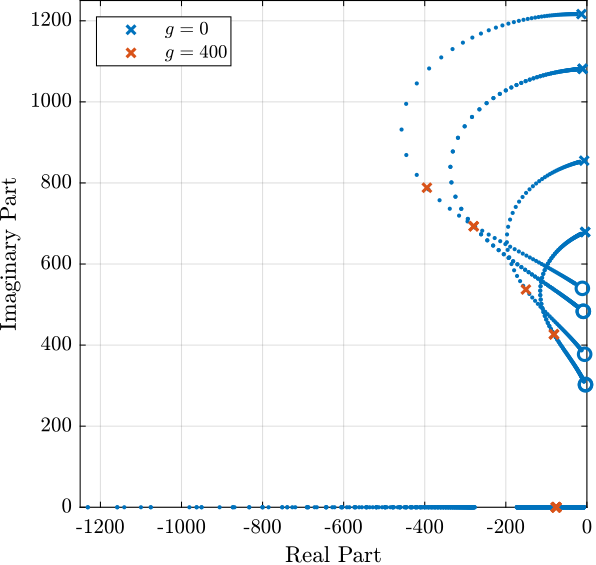
Then the "optimal" IFF controller is:
%% IFF controller with Optimal gain
Kiff = g*Kiff_g1;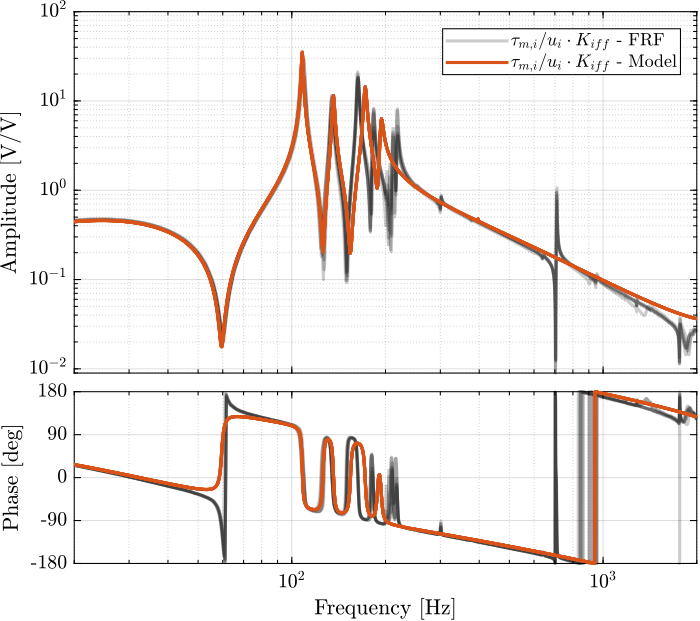
Multiple Gains - Simulation
%% Tested IFF gains
iff_gains = [4, 10, 20, 40, 100, 200, 400];%% Initialize the Simscape model in closed loop
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
'flex_top_type', '4dof', ...
'motion_sensor_type', 'struts', ...
'actuator_type', '2dof', ...
'controller_type', 'iff');%% Identify the (damped) transfer function from u to dLm for different values of the IFF gain
Gd_iff = {zeros(1, length(iff_gains))};
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Strut Displacement (encoder)
for i = 1:length(iff_gains)
Kiff = iff_gains(i)*Kiff_g1*eye(6); % IFF Controller
Gd_iff(i) = {exp(-s*Ts)*linearize(mdl, io, 0.0, options)};
isstable(Gd_iff{i})
end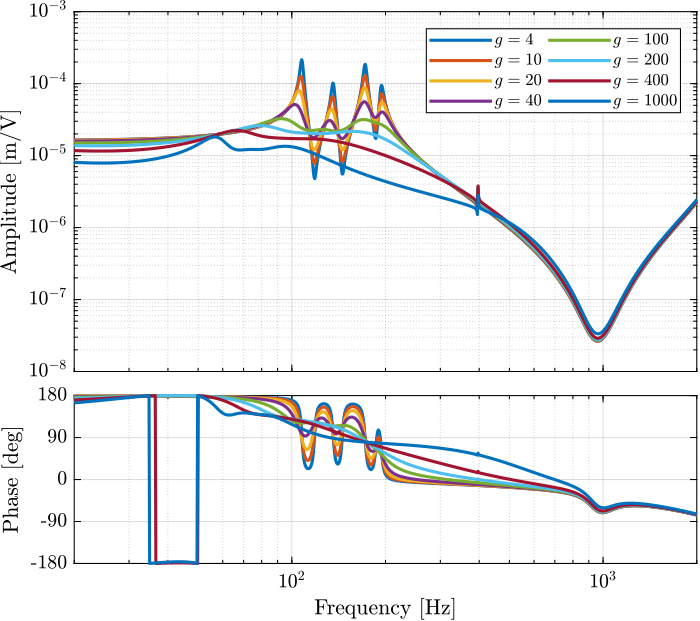
Experimental Results - Gains
Introduction ignore
Let's look at the damping introduced by IFF as a function of the IFF gain and compare that with the results obtained using the Simscape model.
Load Data
%% Load Identification Data
meas_iff_gains = {};
for i = 1:length(iff_gains)
meas_iff_gains(i) = {load(sprintf('mat/iff_strut_1_noise_g_%i.mat', iff_gains(i)), 't', 'Vexc', 'Vs', 'de', 'u')};
endSpectral Analysis - Setup
%% Setup useful variables
% Sampling Time [s]
Ts = (meas_iff_gains{1}.t(end) - (meas_iff_gains{1}.t(1)))/(length(meas_iff_gains{1}.t)-1);
% Sampling Frequency [Hz]
Fs = 1/Ts;
% Hannning Windows
win = hanning(ceil(1*Fs));
% And we get the frequency vector
[~, f] = tfestimate(meas_iff_gains{1}.Vexc, meas_iff_gains{1}.de, win, [], [], 1/Ts);DVF Plant
%% DVF Plant (transfer function from u to dLm)
G_iff_gains = {};
for i = 1:length(iff_gains)
G_iff_gains{i} = tfestimate(meas_iff_gains{i}.Vexc, meas_iff_gains{i}.de(:,1), win, [], [], 1/Ts);
end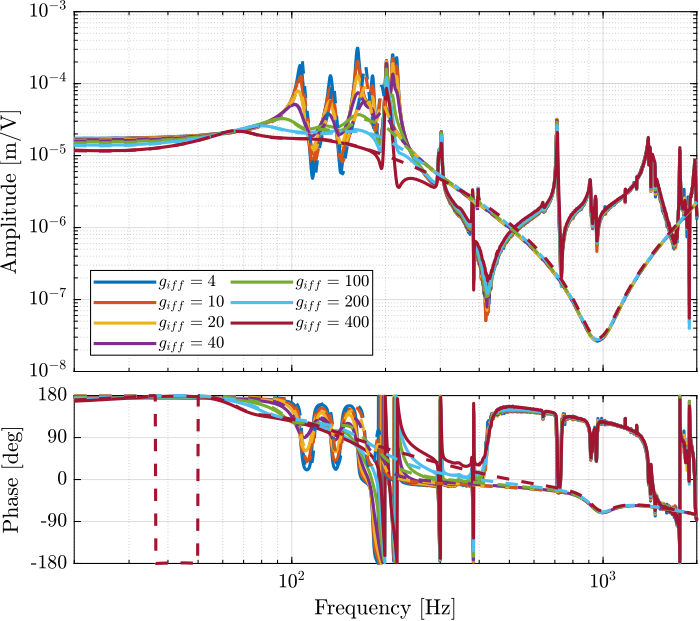
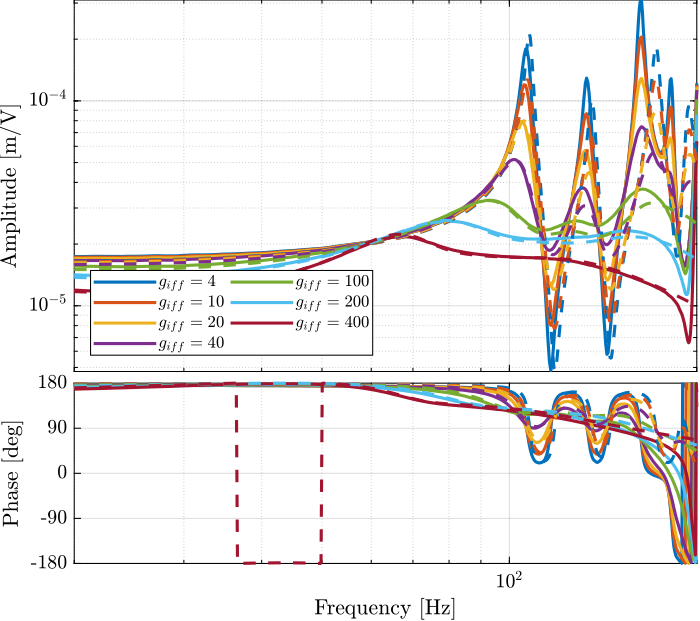
The IFF control strategy is very effective for the damping of the suspension modes. It however does not damp the modes at 200Hz, 300Hz and 400Hz (flexible modes of the APA). This is very logical.
Also, the experimental results and the models obtained from the Simscape model are in agreement.
Experimental Results - Comparison of the un-damped and fully damped system
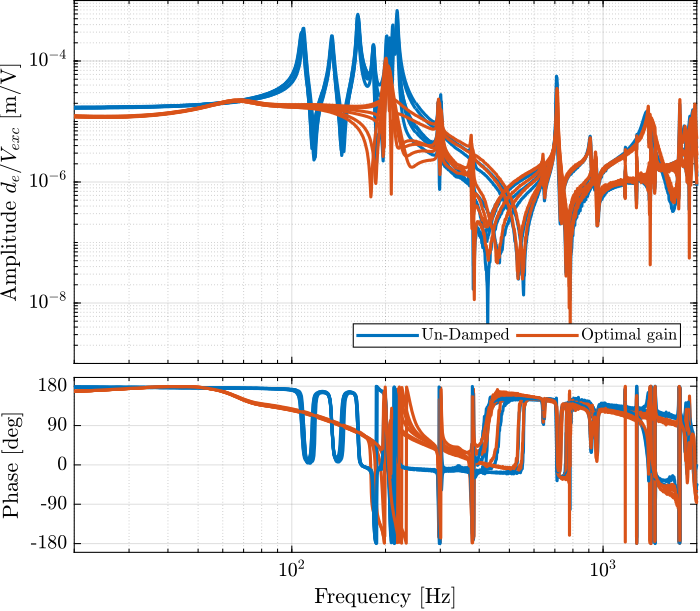
A series of modes at around 205Hz are also damped.
Are these damped modes at 205Hz additional "suspension" modes or flexible modes of the struts?
Experimental Results - Damped Plant with Optimal gain
Introduction ignore
Let's now look at the $6 \times 6$ damped plant with the optimal gain $g = 400$.
Load Data
%% Load Identification Data
meas_iff_struts = {};
for i = 1:6
meas_iff_struts(i) = {load(sprintf('mat/iff_strut_%i_noise_g_400.mat', i), 't', 'Vexc', 'Vs', 'de', 'u')};
endSpectral Analysis - Setup
%% Setup useful variables
% Sampling Time [s]
Ts = (meas_iff_struts{1}.t(end) - (meas_iff_struts{1}.t(1)))/(length(meas_iff_struts{1}.t)-1);
% Sampling Frequency [Hz]
Fs = 1/Ts;
% Hannning Windows
win = hanning(ceil(1*Fs));
% And we get the frequency vector
[~, f] = tfestimate(meas_iff_struts{1}.Vexc, meas_iff_struts{1}.de, win, [], [], 1/Ts);DVF Plant
%% DVF Plant (transfer function from u to dLm)
G_iff_opt = {};
for i = 1:6
G_iff_opt{i} = tfestimate(meas_iff_struts{i}.Vexc, meas_iff_struts{i}.de, win, [], [], 1/Ts);
end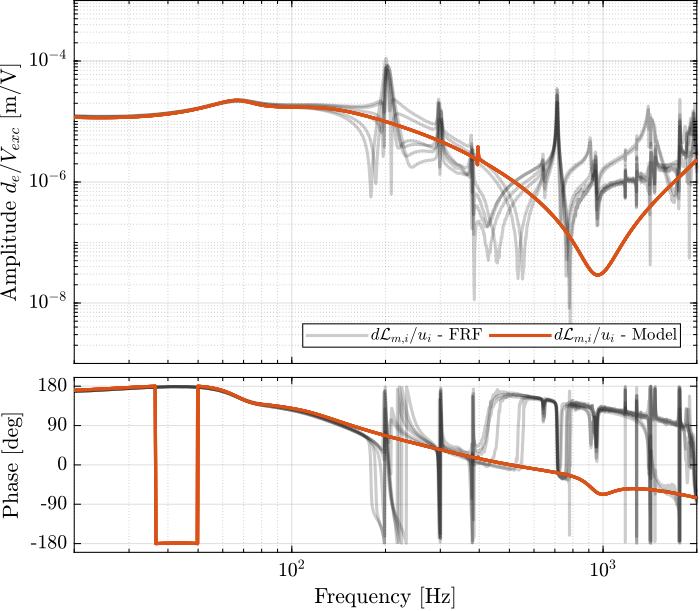
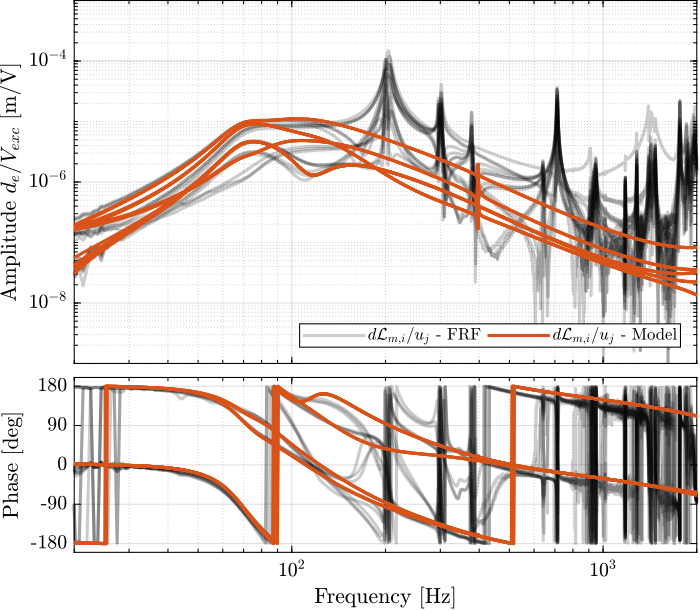
With the IFF control strategy applied and the optimal gain used, the suspension modes are very well damped. Remains the undamped flexible modes of the APA (200Hz, 300Hz, 400Hz), and the modes of the plates (700Hz).
The Simscape model and the experimental results are in very good agreement.
Modal Analysis
<<sec:enc_struts_modal_analysis>>
Introduction ignore
Several 3-axis accelerometers are fixed on the top platform of the nano-hexapod as shown in Figure fig:compliance_vertical_comp_iff.

The top platform is then excited using an instrumented hammer as shown in Figure fig:hammer_excitation_compliance_meas.

Effectiveness of the IFF Strategy - Compliance
In this section, we wish to estimated the effectiveness of the IFF strategy concerning the compliance.
The top plate is excited vertically using the instrumented hammer two times:
- no control loop is used
- decentralized IFF is used
The data is loaded.
frf_ol = load('Measurement_Z_axis.mat'); % Open-Loop
frf_iff = load('Measurement_Z_axis_damped.mat'); % IFFThe mean vertical motion of the top platform is computed by averaging all 5 accelerometers.
%% Multiply by 10 (gain in m/s^2/V) and divide by 5 (number of accelerometers)
d_frf_ol = 10/5*(frf_ol.FFT1_H1_4_1_RMS_Y_Mod + frf_ol.FFT1_H1_7_1_RMS_Y_Mod + frf_ol.FFT1_H1_10_1_RMS_Y_Mod + frf_ol.FFT1_H1_13_1_RMS_Y_Mod + frf_ol.FFT1_H1_16_1_RMS_Y_Mod)./(2*pi*frf_ol.FFT1_H1_16_1_RMS_X_Val).^2;
d_frf_iff = 10/5*(frf_iff.FFT1_H1_4_1_RMS_Y_Mod + frf_iff.FFT1_H1_7_1_RMS_Y_Mod + frf_iff.FFT1_H1_10_1_RMS_Y_Mod + frf_iff.FFT1_H1_13_1_RMS_Y_Mod + frf_iff.FFT1_H1_16_1_RMS_Y_Mod)./(2*pi*frf_iff.FFT1_H1_16_1_RMS_X_Val).^2;The vertical compliance (magnitude of the transfer function from a vertical force applied on the top plate to the vertical motion of the top plate) is shown in Figure fig:compliance_vertical_comp_iff.
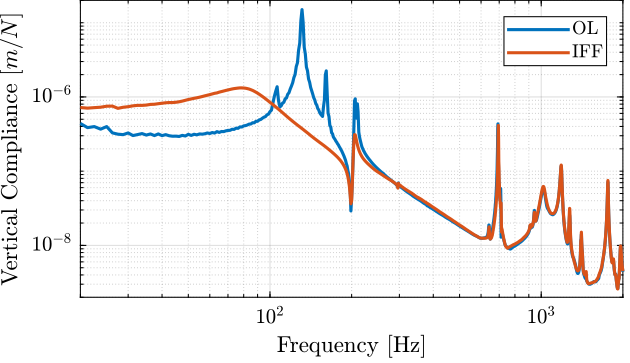
From Figure fig:compliance_vertical_comp_iff, it is clear that the IFF control strategy is very effective in damping the suspensions modes of the nano-hexapode. It also has the effect of degrading (slightly) the vertical compliance at low frequency.
It also seems some damping can be added to the modes at around 205Hz which are flexible modes of the struts.
Comparison with the Simscape Model
Let's now compare the measured vertical compliance with the vertical compliance as estimated from the Simscape model.
The transfer function from a vertical external force to the absolute motion of the top platform is identified (with and without IFF) using the Simscape model.
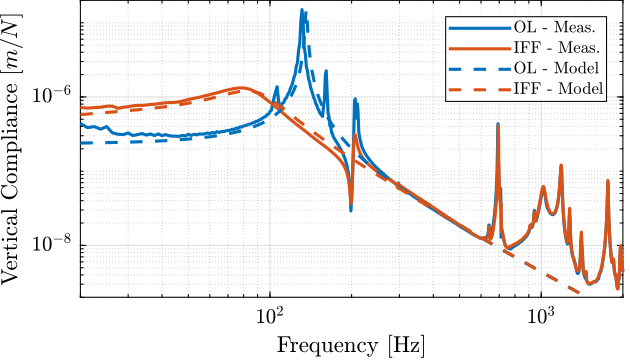
The comparison is done in Figure fig:compliance_vertical_comp_model_iff. Again, the model is quite accurate!
Obtained Mode Shapes
Then, several excitation are performed using the instrumented Hammer and the mode shapes are extracted.
We can observe the mode shapes of the first 6 modes that are the suspension modes (the plate is behaving as a solid body) in Figure fig:mode_shapes_annotated.
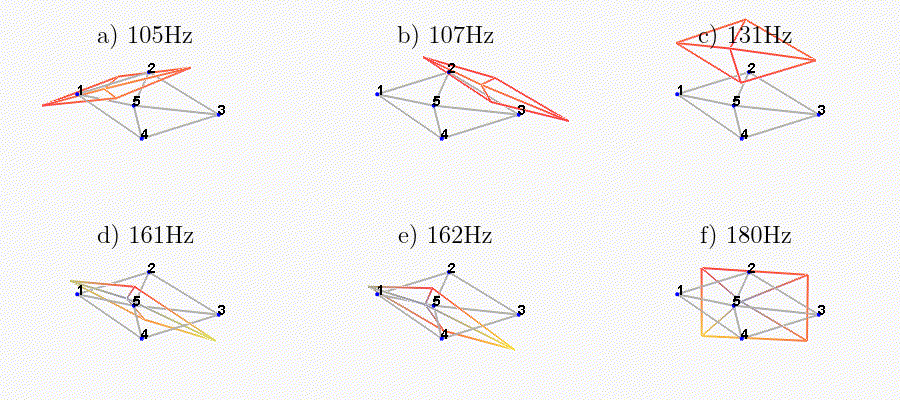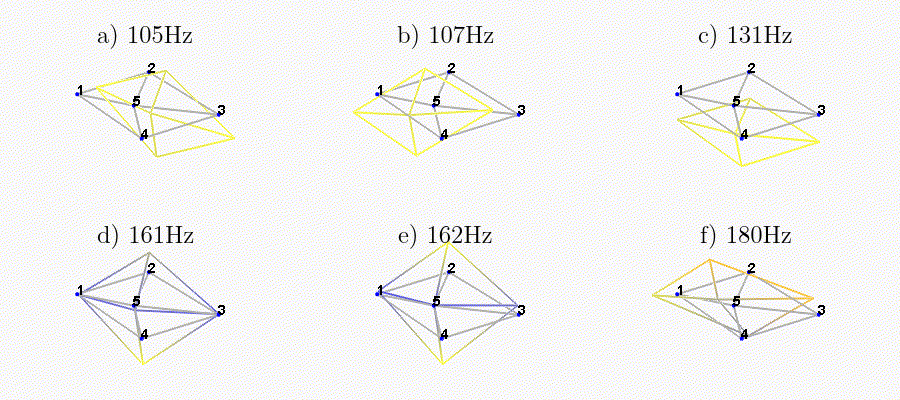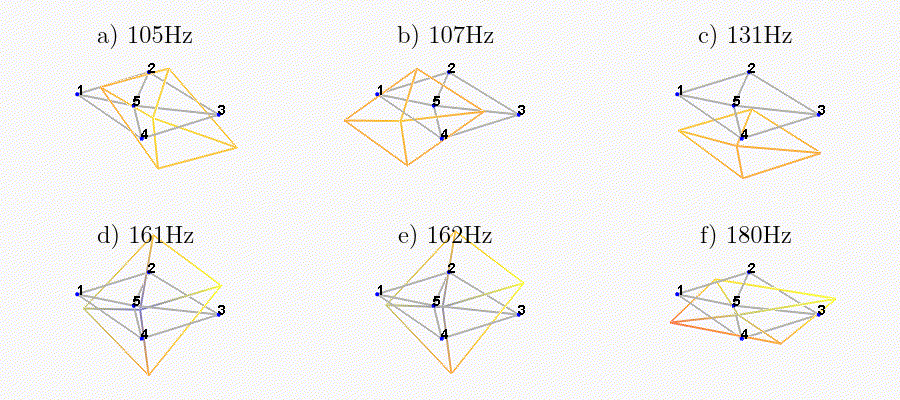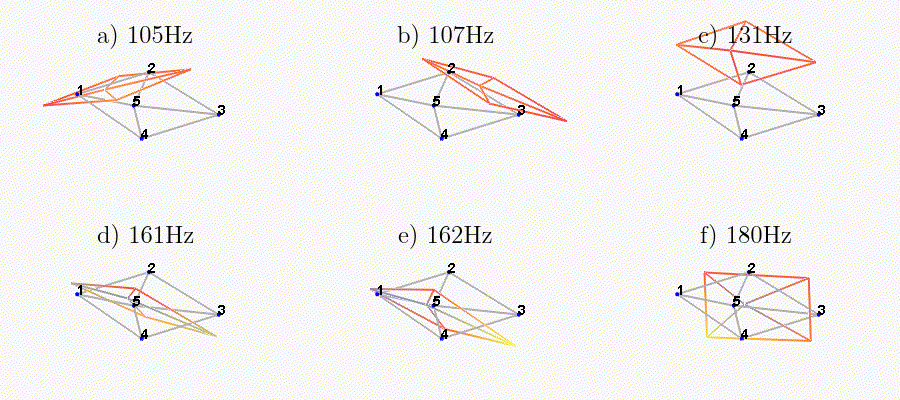
Then, there is a mode at 692Hz which corresponds to a flexible mode of the top plate (Figure fig:mode_shapes_annotated).
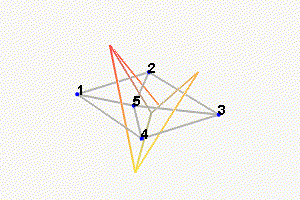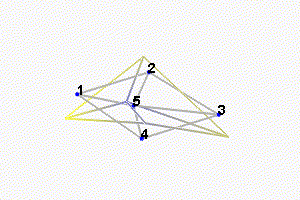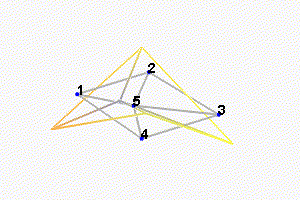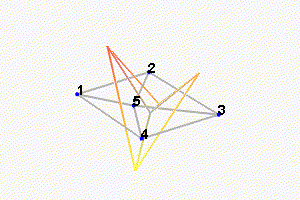
The obtained modes are summarized in Table tab:description_modes.
| Mode | Freq. [Hz] | Description |
|---|---|---|
| 1 | 105 | Suspension Mode: Y-translation |
| 2 | 107 | Suspension Mode: X-translation |
| 3 | 131 | Suspension Mode: Z-translation |
| 4 | 161 | Suspension Mode: Y-tilt |
| 5 | 162 | Suspension Mode: X-tilt |
| 6 | 180 | Suspension Mode: Z-rotation |
| 7 | 692 | (flexible) Membrane mode of the top platform |
Encoders fixed to the plates
<<sec:encoders_plates>>