24 KiB
Test Bench APA95ML
- Introduction
- Setup
- Run Experiment and Save Data
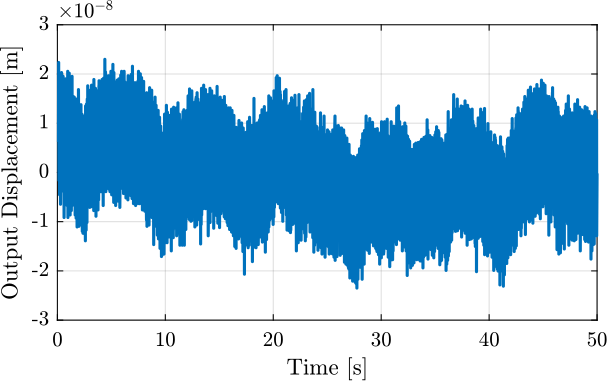
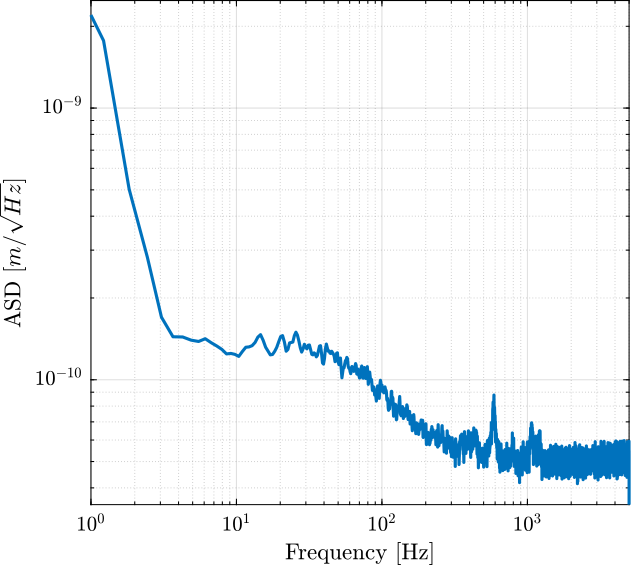
- Huddle Test
- Transfer Function Estimation using the DAC as the driver
- Transfer Function Estimation using the PI Amplifier
- Transfer function from force actuator to force sensor
- IFF Tests
Setup
Parameters
Ts = 1e-4;Filter White Noise
Glpf = 1/(1 + s/2/pi/500);
Gz = c2d(Glpf, Ts, 'tustin');Run Experiment and Save Data
Load Data
data = SimulinkRealTime.utils.getFileScopeData('data/apa95ml.dat').data;Save Data
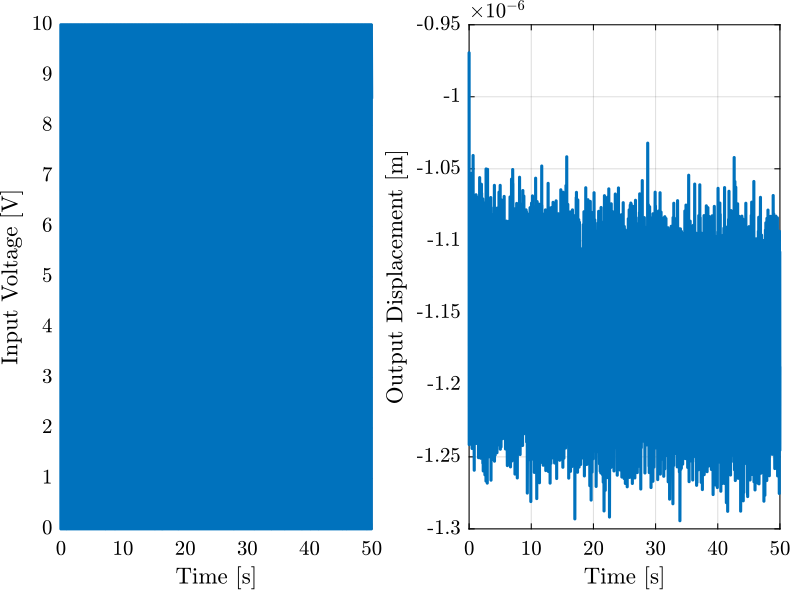
u = data(:, 1); % Input Voltage [V]
y = data(:, 2); % Output Displacement [m]
t = data(:, 3); % Time [s] save('./mat/huddle_test.mat', 't', 'u', 'y', 'Glpf');Huddle Test
Transfer Function Estimation using the DAC as the driver
Introduction ignore
Results presented in this sections are wrong as the ADC cannot deliver enought current to the piezoelectric actuator.
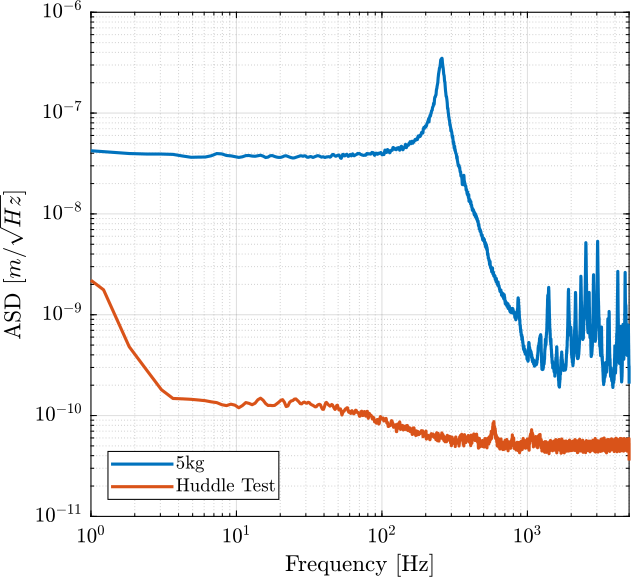
Comparison of the PSD with Huddle Test
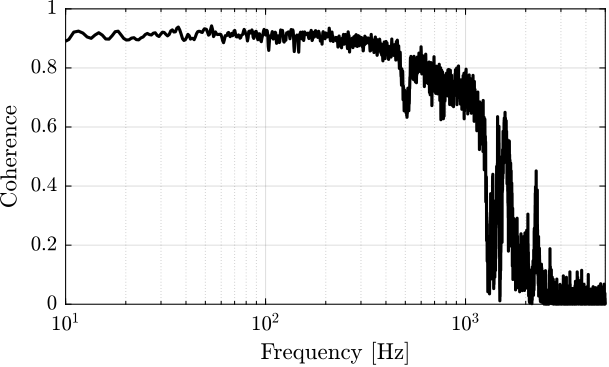
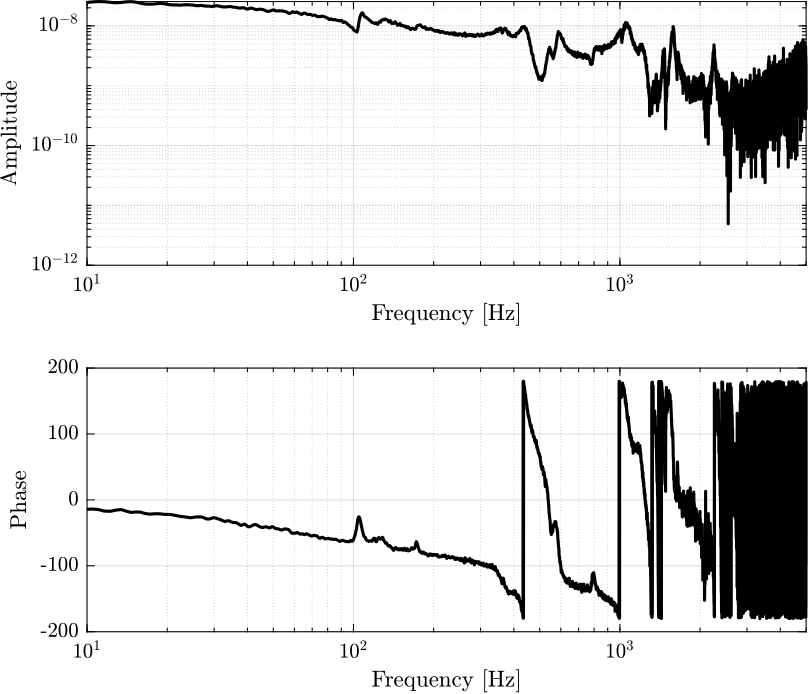
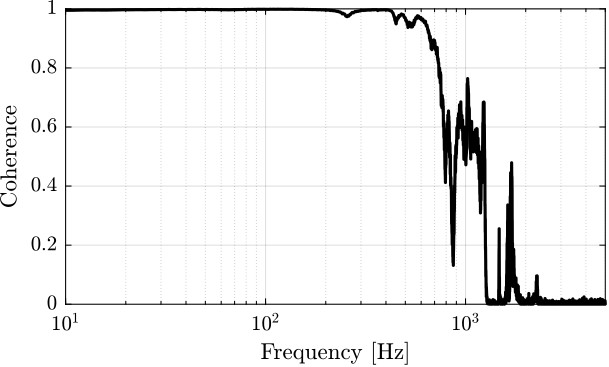
Compute TF estimate and Coherence
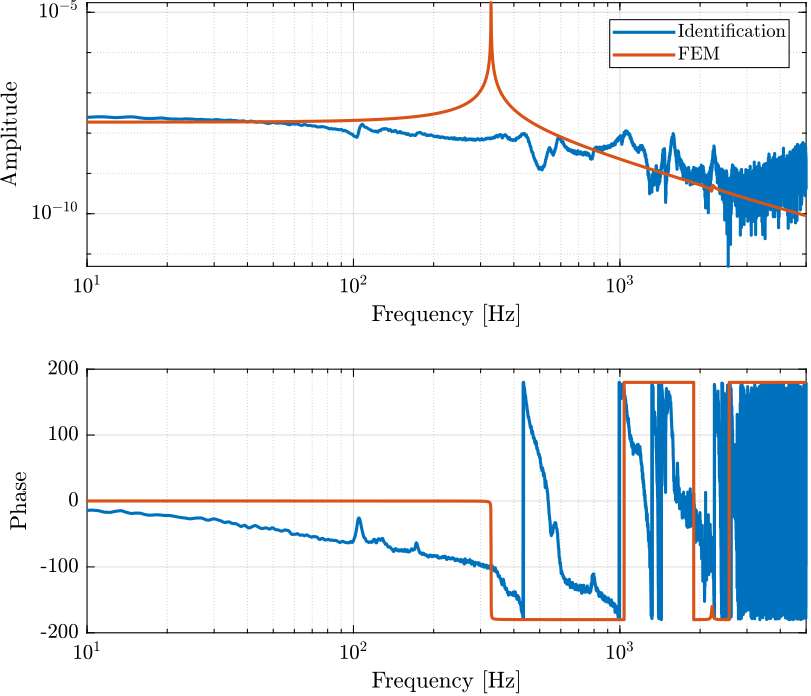
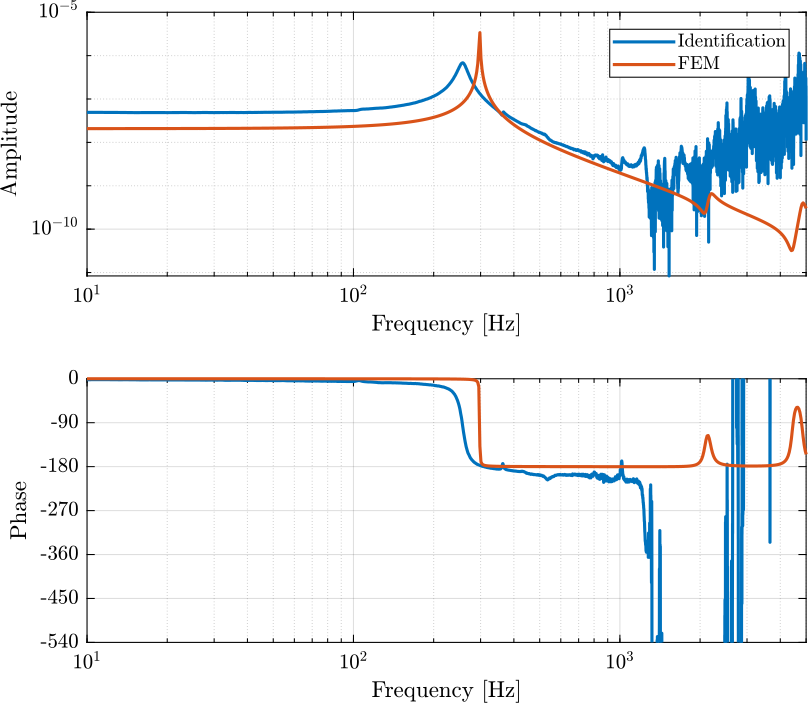
Comparison with the FEM model
Conclusion ignore
The problem comes from the fact that the piezo is driven directly by the DAC that cannot deliver enought current. In the next section, a current amplifier is used.
Transfer Function Estimation using the PI Amplifier
Load Data
ht = load('./mat/huddle_test.mat', 't', 'u', 'y');
load('./mat/apa95ml_5kg_Amp_E505.mat', 't', 'u', 'um', 'y'); u = 10*(u - mean(u)); % Input Voltage of Piezo [V]
um = 10*(um - mean(um)); % Monitor [V]
y = y - mean(y); % Mass displacement [m]
ht.u = 10*(ht.u - mean(ht.u));
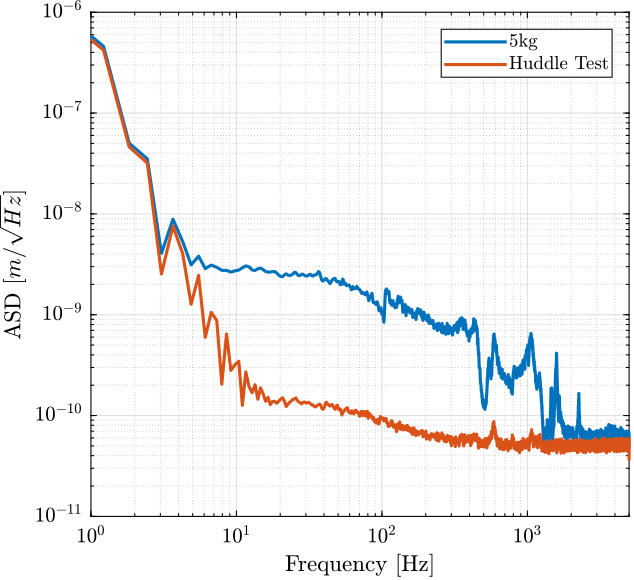
ht.y = ht.y - mean(ht.y);Comparison of the PSD with Huddle Test
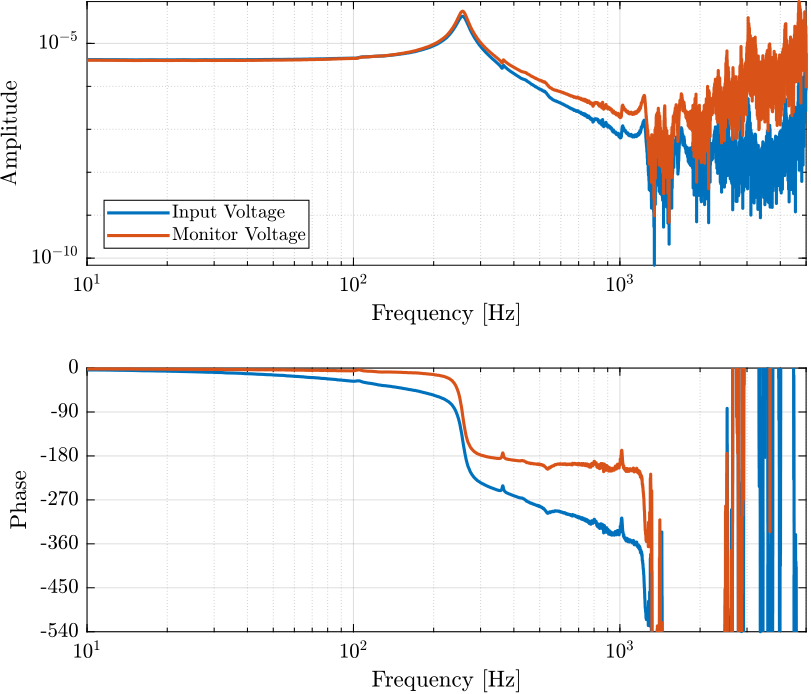
Compute TF estimate and Coherence
Transfer function from force actuator to force sensor
Introduction ignore
Two measurements are performed:
- Speedgoat DAC => Voltage Amplifier (x20) => 1 Piezo Stack => … => 2 Stacks as Force Sensor (parallel) => Speedgoat ADC
- Speedgoat DAC => Voltage Amplifier (x20) => 2 Piezo Stacks (parallel) => … => 1 Stack as Force Sensor => Speedgoat ADC
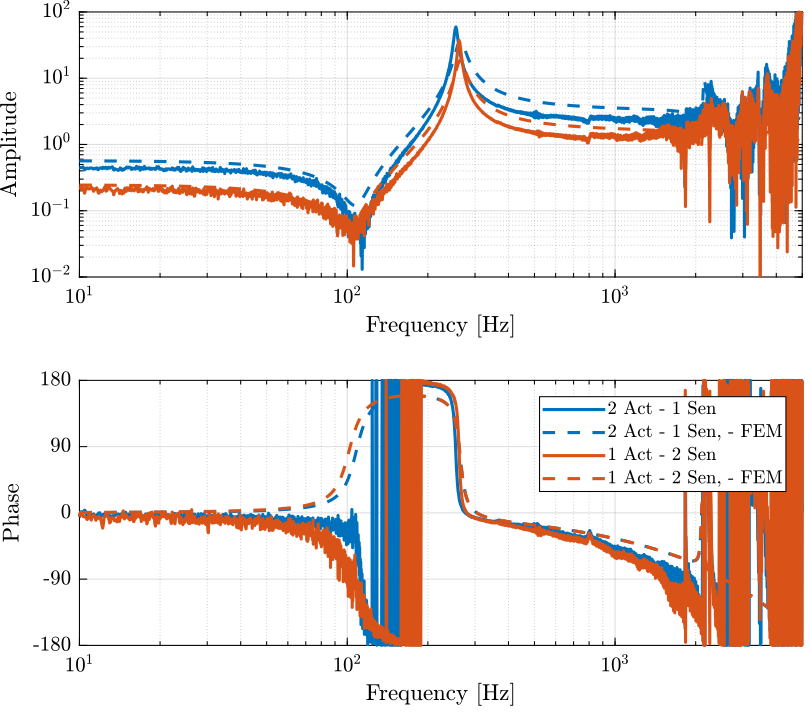
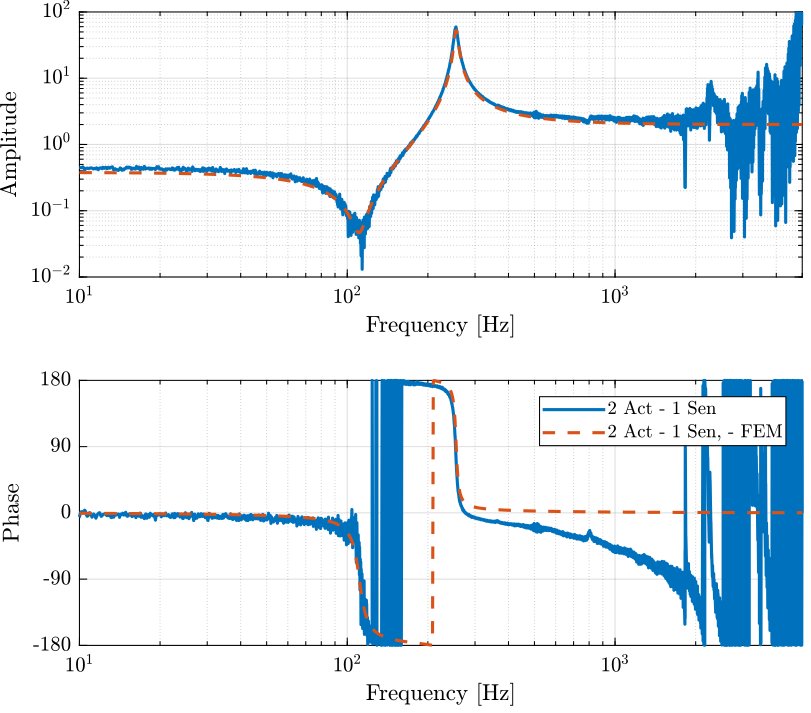
The obtained dynamics from force actuator to force sensor are compare with the FEM model.
Load Data ignore
The data are loaded:
a_ss = load('mat/apa95ml_5kg_1a_2s.mat', 't', 'u', 'y', 'v');
aa_s = load('mat/apa95ml_5kg_2a_1s.mat', 't', 'u', 'y', 'v');
load('mat/G_force_sensor_5kg.mat', 'G');Adjust gain ignore
Let's use the amplifier gain to obtain the true voltage applied to the actuator stack(s)
The parameters of the piezoelectric stacks are defined below:
d33 = 3e-10; % Strain constant [m/V]
n = 80; % Number of layers per stack
eT = 1.6e-8; % Permittivity under constant stress [F/m]
sD = 2e-11; % Elastic compliance under constant electric displacement [m2/N]
ka = 235e6; % Stack stiffness [N/m]From the FEM, we construct the transfer function from DAC voltage to ADC voltage.
Gfem_aa_s = exp(-s/1e4)*20*(2*d33*n*ka)*(G(3,1)+G(3,2))*d33/(eT*sD*n);
Gfem_a_ss = exp(-s/1e4)*20*( d33*n*ka)*(G(3,1)+G(2,1))*d33/(eT*sD*n);Compute TF estimate and Coherence ignore
The transfer function from input voltage to output voltage are computed and shown in Figure fig:bode_plot_force_sensor_voltage_comp_fem.
Ts = a_ss.t(end)/(length(a_ss.t)-1);
Fs = 1/Ts;
win = hann(ceil(10/Ts));
[tf_a_ss, f] = tfestimate(a_ss.u, a_ss.v, win, [], [], 1/Ts);
[coh_a_ss, ~] = mscohere( a_ss.u, a_ss.v, win, [], [], 1/Ts);
[tf_aa_s, f] = tfestimate(aa_s.u, aa_s.v, win, [], [], 1/Ts);
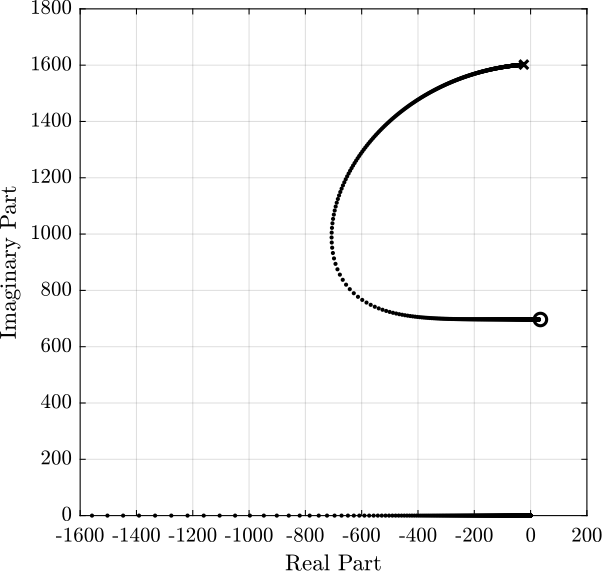
[coh_aa_s, ~] = mscohere( aa_s.u, aa_s.v, win, [], [], 1/Ts);System Identification
IFF Tests
Load Data
iff_g10 = load('./mat/apa95ml_iff_g10_res.mat', 'u', 't', 'y', 'v');
iff_g100 = load('./mat/apa95ml_iff_g100_res.mat', 'u', 't', 'y', 'v');
iff_of = load('./mat/apa95ml_iff_off_res.mat', 'u', 't', 'y', 'v'); Ts = 1e-4;
win = hann(ceil(10/Ts));
[tf_iff_g10, f] = tfestimate(iff_g10.u, iff_g10.y, win, [], [], 1/Ts);
[co_iff_g10, ~] = mscohere(iff_g10.u, iff_g10.y, win, [], [], 1/Ts);
[tf_iff_g100, f] = tfestimate(iff_g100.u, iff_g100.y, win, [], [], 1/Ts);
[co_iff_g100, ~] = mscohere(iff_g100.u, iff_g100.y, win, [], [], 1/Ts);
[tf_iff_of, ~] = tfestimate(iff_of.u, iff_of.y, win, [], [], 1/Ts);
[co_iff_of, ~] = mscohere(iff_of.u, iff_of.y, win, [], [], 1/Ts); figure;
hold on;
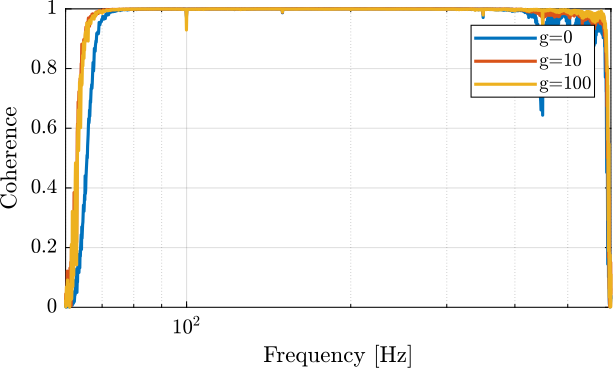
plot(f, co_iff_of, '-', 'DisplayName', 'g=0')
plot(f, co_iff_g10, '-', 'DisplayName', 'g=10')
plot(f, co_iff_g100, '-', 'DisplayName', 'g=100')
set(gca, 'Xscale', 'log'); set(gca, 'Yscale', 'lin');
ylabel('Coherence'); xlabel('Frequency [Hz]');
hold off;
legend();
xlim([60, 600]) figure;
ax1 = subplot(2, 1, 1);
hold on;
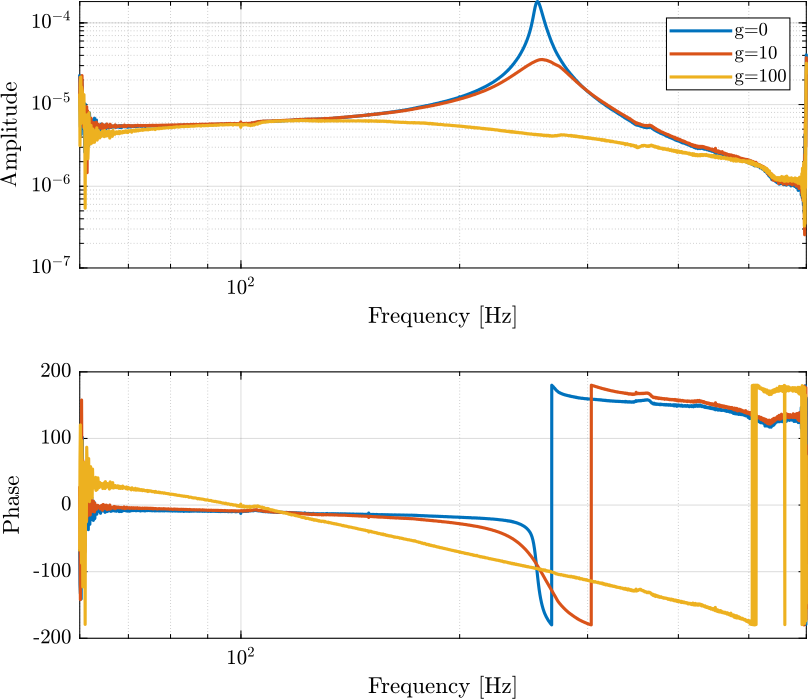
plot(f, abs(tf_iff_of), '-', 'DisplayName', 'g=0')
plot(f, abs(tf_iff_g10), '-', 'DisplayName', 'g=10')
plot(f, abs(tf_iff_g100), '-', 'DisplayName', 'g=100')
set(gca, 'Xscale', 'log'); set(gca, 'Yscale', 'log');
ylabel('Amplitude'); xlabel('Frequency [Hz]');
hold off;
legend();
ax2 = subplot(2, 1, 2);
hold on;
plot(f, 180/pi*angle(-tf_iff_of), '-')
plot(f, 180/pi*angle(-tf_iff_g10), '-')
plot(f, 180/pi*angle(-tf_iff_g100), '-')
set(gca, 'Xscale', 'log'); set(gca, 'Yscale', 'lin');
ylabel('Phase'); xlabel('Frequency [Hz]');
hold off;
linkaxes([ax1,ax2], 'x');
xlim([60, 600]);