11 KiB
11 KiB
SVD Control
Simscape Model
Simulink
open('gravimeter.slx') %% Name of the Simulink File
mdl = 'gravimeter';
%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F1'], 1, 'openinput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/F2'], 1, 'openinput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/F3'], 1, 'openinput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/Acc_side'], 1, 'openoutput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/Acc_side'], 2, 'openoutput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/Acc_top'], 1, 'openoutput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/Acc_top'], 2, 'openoutput'); io_i = io_i + 1;
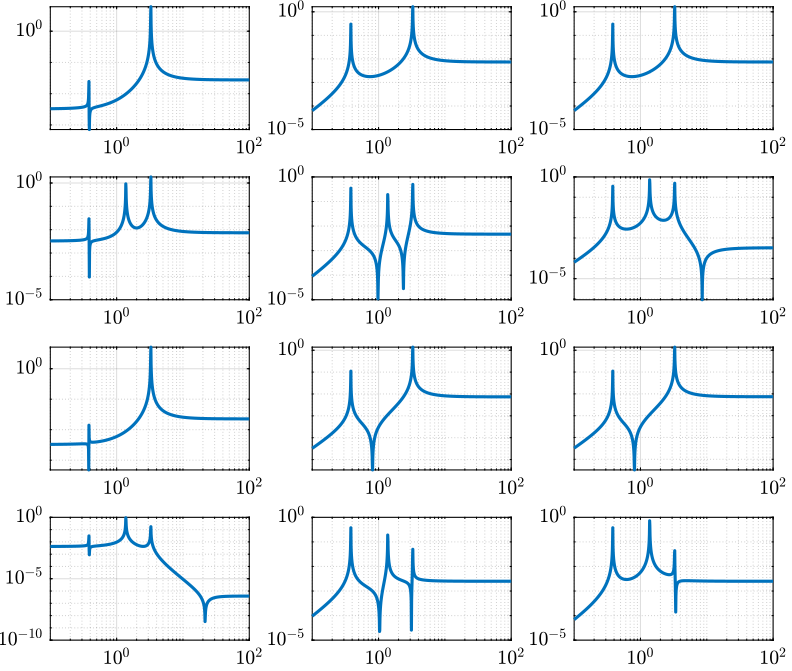
G = linearize(mdl, io); freqs = logspace(-1, 2, 1000);
figure;
for in_i = 1:3
for out_i = 1:4
subplot(4, 3, 3*(out_i-1)+in_i);
plot(freqs, abs(squeeze(freqresp(G(out_i,in_i)/s^2, freqs, 'Hz'))), '-');
set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log');
end
endMatlab Code
clc;
% close all
g = 100000;
w0 = 2*pi*.5; % MinusK BM1 tablle
l = 0.5; %[m]
la = 1; %[m]
h = 1.7; %[m]
ha = 1.7;% %[m]
m = 400; %[kg]
k = 15e3;%[N/m]
kv = k;
kh = 15e3;
I = 115;%[kg m^2]
% c = 0.06;
% l = 0.4719; %[m]
% la = .477; %[m]
% h = 1.8973; %[m]
% ha = 1.9060;% %[m]
% m = 98.1421; %[kg]
% k = 14512;%[N/m]
% I = 28.5372;%[kg m^2]
cv = 0.03;
ch = 0.03;
%% System definition
[Fr, x1, z1, x2, z2, wx, wz, x12, z12, PHIwx, PHIwz,xsum,zsum,xdelta,zdelta,rot]...
= modelGeneration(m,I,k,h,ha,l,la,cv,ch,kv,kh);
%% Bode options
P = bodeoptions;
P.FreqUnits = 'Hz';
P.MagUnits = 'abs';
P.MagScale = 'log';
P.Grid = 'on';
P.PhaseWrapping = 'on';
P.Xlim = [1e-1,1e2];
%P.PhaseVisible = 'off';
w = 2*pi*logspace(-1,2,1000);
%% curves points
% slide 4
F_sl4 = [2e-1 4e-1 7e-1 1 2 3 5];
Amp_sl4 = [ 1 2 4 2.5 1 7e-1 7e-1];
F_sl4_phase = [2e-1 4e-1 7e-1 1 ];
Phase_sl4 = (180/pi).*[0 0 -0.5 -1.7];
%slide 6
F_sl6 = [2e-1 4e-1 1 2 3 5];
Amp_sl6 = [1 1 6e-1 2e-1 3e-1 3e-1];
F_sl6_phase = [2e-1 4e-1 1 ];
Phase_sl6 = (180/pi).*[0 0 0 ];
%slide 9
F_sl9 = [2.5e-1 4e-1 6e-1 1 1.7 2.2 3 5 10];
Amp_sl9 = [3 6 1 5e-1 1 2 7e-1 2.5e-1 7e-2];
Phase_sl9 = (180/pi)*[0 -1 -pi 0 -1 -1.5 -pi -pi -pi];
% slide 14
F_sl14 = [ 2e-1 4e-1 6e-1 8e-1 1 2 3 5 10];
Amp_sl14 = [9e-1 1.5 1.2 0.35 .3 1.2 .3 .1 5e-2];
F_sl14_phase = [ 2e-1 4e-1 6e-1 8e-1 ];
Phase_sl14 = (180/pi).*[0 0 -1.7 -2];
%rotation
F_rot = [1e-1 2e-1 4e-1 5e-1 7e-1 1 2 3 6.5 10 20];
Amp_rot = [7e-8 2.2e-7 3e-7 1e-7 2e-8 9e-9 3e-8 9e-9 1e-9 4e-10 8e-11];
%% Plots
% %slide 3
% figure
% loglog(Fr,abs(x2).^.5,Fr,abs(x1).^.5,Fr,abs(xsum).^.5,Fr,abs(xdelta).^.5)
% xlabel('Frequency [Hz]');ylabel('Acceleration [m/s^2/rtHz]')
% legend('Top sensor','Bottom sensor','Half sum','Half difference');
% title('Horizontal')
% xlim([7e-2 1e1]);
%slide 4
figure
subplot 211
loglog(Fr, abs(x12)./abs(x1));hold on;
loglog(F_sl4,Amp_sl4,'*');
xlabel('Frequency [Hz]');ylabel('Amplitude [-]');
title('X direction Top/bottom sensor');
xlim([7e-2 1e1]);
subplot 212
semilogx(Fr, (180/pi).*angle(x12./abs(x1)));hold on;
loglog(F_sl4_phase,Phase_sl4,'*');
xlabel('Frequency [Hz]');ylabel('Phase [deg]');
xlim([7e-2 1e1]);
%slide 6
figure
subplot 211
loglog(Fr, abs(z12)./abs(z1));hold on;
loglog(F_sl6,Amp_sl6,'*');
xlabel('Frequency [Hz]');ylabel('Amplitude [-]');
title('Z direction Top/bottom sensor');
xlim([7e-2 1e1]);
subplot 212
semilogx(Fr, (180/pi).*angle(z12./abs(z1)));hold on;
loglog(F_sl6_phase,Phase_sl6,'*');
xlabel('Frequency [Hz]');ylabel('Phase [deg]');
xlim([7e-2 1e1]);ylim([-180 180]);
% %slide 6
% figure
% loglog(Fr,abs(z2).^.5,Fr,abs(z1).^.5,Fr,abs(zsum).^.5,Fr,abs(zdelta).^.5)
% xlabel('Frequency [Hz]');ylabel('Acceleration [m/s^2/rtHz]')
% legend('Top sensor','Bottom sensor','Half sum','Half difference');
% title('Vertical')
% xlim([7e-2 1e1]);
%slide 9
figure
subplot 211
loglog(Fr, abs(PHIwx)./abs(wx));hold on;
loglog(F_sl9,Amp_sl9,'*');
xlabel('Frequency [Hz]');ylabel('Amplitude [-]');
title('X direction bottom/ground sensor');
xlim([7e-2 1e1]);
ylim([0.01 10]);
subplot 212
semilogx(Fr, (180/pi).*angle(PHIwx./abs(wx)));hold on;
loglog(F_sl9,Phase_sl9,'*');
xlabel('Frequency [Hz]');ylabel('Phase [deg]');
xlim([7e-2 1e1]);
% %slide 8
% figure
% loglog(Fr,abs(wx).^.5,Fr,abs(x1).^.5,'-.',Fr,abs(x2).^.5,'.');
% grid on;xlabel('Frequency [Hz]');
% ylabel('ASD [m/s^2/rtHz]');
% xlim([7e-2 1e1]);
% legend('Ground','Bottom sensor','Top sensor');
% title('Horizontal');
%
% %slide 13
% figure
% loglog(Fr,abs(wz).^.5,Fr,abs(z1).^.5,'-.',Fr,abs(z2).^.5,'.');
% grid on;xlabel('Frequency [Hz]');
% ylabel('ASD [m/s^2/rtHz]');
% xlim([7e-2 1e1]);
% legend('Ground','Bottom sensor','Top sensor');
% title('Vertical');
%slide 14
figure
subplot 211
loglog(Fr, abs(PHIwz)./abs(wz));hold on;
loglog(F_sl14,Amp_sl14,'*');
xlabel('Frequency [Hz]');ylabel('Amplitude [-]');
title('Z direction bottom/ground sensor');
xlim([7e-2 1e1]);
ylim([0.01 10]);
subplot 212
semilogx(Fr, (180/pi).*angle(PHIwz./abs(wz)));hold on;
loglog(F_sl14_phase,Phase_sl14,'*');
xlabel('Frequency [Hz]');ylabel('Phase [deg]');
xlim([7e-2 1e1]);
%rotation
figure
loglog(Fr,abs(rot).^.5./((2*pi*Fr').^2),F_rot,Amp_rot,'*');
xlabel('Frequency [Hz]');ylabel('Rotation [rad/rtHz]')
xlim([7e-2 1e1]);Model Generation
function [Fr, x1, z1, x2, z2, wx, wz, x12, z12, PHIwx, PHIwz,xsum,zsum,xdelta,zdelta,rot] = modelGeneration(m,I,k,h,ha,l,la,dampv,damph,kv,kh)
%% generation of the state space model
M = [m 0 0
0 m 0
0 0 I];
%Jacobian of the bottom sensor
Js1 = [1 0 h/2
0 1 -l/2];
%Jacobian of the top sensor
Js2 = [1 0 -h/2
0 1 0];
%Jacobian of the actuators
Ja = [1 0 ha/2 %Left horizontal actuator
%1 0 h/2 %Right horizontal actuator
0 1 -la/2 %Left vertical actuator
0 1 la/2]; %Right vertical actuator
Jah = [1 0 ha/2];
Jav = [0 1 -la/2 %Left vertical actuator
0 1 la/2]; %Right vertical actuator
Jta = Ja';
Jtah = Jah';
Jtav = Jav';
K = kv*Jtav*Jav + kh*Jtah*Jah;
C = dampv*kv*Jtav*Jav+damph*kh*Jtah*Jah;
E = [1 0 0
0 1 0
0 0 1]; %projecting ground motion in the directions of the legs
AA = [zeros(3) eye(3)
-M\K -M\C];
BB = [zeros(3,6)
M\Jta M\(k*Jta*E)];
CC = [[Js1;Js2] zeros(4,3);
zeros(2,6)
(Js1+Js2)./2 zeros(2,3)
(Js1-Js2)./2 zeros(2,3)
(Js1-Js2)./(2*h) zeros(2,3)];
DD = [zeros(4,6)
zeros(2,3) eye(2,3)
zeros(6,6)];
system_dec = ss(AA,BB,CC,DD);
%input = three actuators and three ground motions
%output = the bottom sensor; the top sensor; the ground motion; the half
%sum; the half difference; the rotation
%% Injecting ground motion in the system to have the output
Fr = logspace(-2,3,1e3);
w=2*pi*Fr*1i;
%fit of the ground motion data in m/s^2/rtHz
Fr_ground_x = [0.07 0.1 0.15 0.3 0.7 0.8 0.9 1.2 5 10];
n_ground_x1 = [4e-7 4e-7 2e-6 1e-6 5e-7 5e-7 5e-7 1e-6 1e-5 3.5e-5];
Fr_ground_v = [0.07 0.08 0.1 0.11 0.12 0.15 0.25 0.6 0.8 1 1.2 1.6 2 6 10];
n_ground_v1 = [7e-7 7e-7 7e-7 1e-6 1.2e-6 1.5e-6 1e-6 9e-7 7e-7 7e-7 7e-7 1e-6 2e-6 1e-5 3e-5];
n_ground_x = interp1(Fr_ground_x,n_ground_x1,Fr,'linear');
n_ground_v = interp1(Fr_ground_v,n_ground_v1,Fr,'linear');
% figure
% loglog(Fr,abs(n_ground_v),Fr_ground_v,n_ground_v1,'*');
% xlabel('Frequency [Hz]');ylabel('ASD [m/s^2 /rtHz]');
% return
%converting into PSD
n_ground_x = (n_ground_x).^2;
n_ground_v = (n_ground_v).^2;
%Injecting ground motion in the system and getting the outputs
system_dec_f = (freqresp(system_dec,abs(w)));
PHI = zeros(size(Fr,2),12,12);
for p = 1:size(Fr,2)
Sw=zeros(6,6);
Iact = zeros(3,3);
Sw(4,4) = n_ground_x(p);
Sw(5,5) = n_ground_v(p);
Sw(6,6) = n_ground_v(p);
Sw(1:3,1:3) = Iact;
PHI(p,:,:) = (system_dec_f(:,:,p))*Sw(:,:)*(system_dec_f(:,:,p))';
end
x1 = PHI(:,1,1);
z1 = PHI(:,2,2);
x2 = PHI(:,3,3);
z2 = PHI(:,4,4);
wx = PHI(:,5,5);
wz = PHI(:,6,6);
x12 = PHI(:,1,3);
z12 = PHI(:,2,4);
PHIwx = PHI(:,1,5);
PHIwz = PHI(:,2,6);
xsum = PHI(:,7,7);
zsum = PHI(:,8,8);
xdelta = PHI(:,9,9);
zdelta = PHI(:,10,10);
rot = PHI(:,11,11);