svd-control/index.org

SVD Control

• Gravimeter - Simscape Model
  • Simscape Model - Parameters
  • System Identification - Without Gravity
  • System Identification - With Gravity
  • Analytical Model
    • Parameters
    • generation of the state space model
    • Comparison with the Simscape Model
    • Analysis
    • Control Section
    • Greshgorin radius
    • Injecting ground motion in the system to have the output
• Gravimeter - Functions
  • align
  • pzmap_testCL
• Stewart Platform - Simscape Model
  • Jacobian
  • Simscape Model
  • Identification of the plant
  • Obtained Dynamics
  • Real Approximation of $G$ at the decoupling frequency
  • Verification of the decoupling using the "Gershgorin Radii"
  • Decoupled Plant
  • Diagonal Controller
  • Centralized Control
  • SVD Control
  • Results

Gravimeter - Simscape Model

Simscape Model - Parameters

  open('gravimeter.slx')

Parameters

  l  = 0.5; % Length of the mass [m]
  la = 0.5; % Position of Act. [m]

  h  = 1.7; % Height of the mass [m]
  ha = 1.7; % Position of Act. [m]

  m = 400; % Mass [kg]
  I = 115; % Inertia [kg m^2]

  k = 15e3; % Actuator Stiffness [N/m]
  c = 0.03; % Actuator Damping [N/(m/s)]

  deq = 0.2; % Length of the actuators [m]

  g = 0; % Gravity [m/s2]

System Identification - Without Gravity

  %% Name of the Simulink File
  mdl = 'gravimeter';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/F1'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/F2'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/F3'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_side'], 1, 'openoutput'); io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_side'], 2, 'openoutput'); io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_top'], 1, 'openoutput'); io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_top'], 2, 'openoutput'); io_i = io_i + 1;

  G = linearize(mdl, io);
  G.InputName  = {'F1', 'F2', 'F3'};
  G.OutputName = {'Ax1', 'Az1', 'Ax2', 'Az2'};

pole(G)
ans =
      -0.000473481142385801 +      21.7596190728632i
      -0.000473481142385801 -      21.7596190728632i
      -7.49842879459177e-05 +       8.6593576906982i
      -7.49842879459177e-05 -       8.6593576906982i
      -5.15386867925747e-06 +      2.27025295182755i
      -5.15386867925747e-06 -      2.27025295182755i

The plant as 6 states as expected (2 translations + 1 rotation)

  size(G)

State-space model with 4 outputs, 3 inputs, and 6 states.

Open Loop Transfer Function from 3 Actuators to 4 Accelerometers

System Identification - With Gravity

  g = 9.80665; % Gravity [m/s2]

  Gg = linearize(mdl, io);
  Gg.InputName  = {'F1', 'F2', 'F3'};
  Gg.OutputName = {'Ax1', 'Az1', 'Ax2', 'Az2'};

We can now see that the system is unstable due to gravity.

pole(G)
ans =
          -10.9848275341276 +                     0i
           10.9838836405193 +                     0i
      -7.49855396089326e-05 +      8.65962885769976i
      -7.49855396089326e-05 -      8.65962885769976i
      -6.68819341967921e-06 +      0.83296042226902i
      -6.68819341967921e-06 -      0.83296042226902i

Open Loop Transfer Function from 3 Actuators to 4 Accelerometers with an without gravity

Analytical Model

Parameters

Control parameters

  g = 1e5;
  g_svd = 1e5;

System parameters

  l  = 0.5; % Length of the mass [m]
  la = 0.5; % Position of Act. [m]

  h  = 1.7; % Height of the mass [m]
  ha = 1.7; % Position of Act. [m]

  m = 400; % Mass [kg]
  I = 115; % Inertia [kg m^2]

  k = 15e3; % Actuator Stiffness [N/m]
  c = 0.03; % Actuator Damping [N/(m/s)]

Bode options.

  P = bodeoptions;
  P.FreqUnits = 'Hz';
  P.MagUnits = 'abs';
  P.MagScale = 'log';
  P.Grid = 'on';
  P.PhaseWrapping = 'on';
  P.Title.FontSize = 14;
  P.XLabel.FontSize = 14;
  P.YLabel.FontSize = 14;
  P.TickLabel.FontSize = 12;
  P.Xlim = [1e-1,1e2];
  P.MagLowerLimMode = 'manual';
  P.MagLowerLim= 1e-3;
  %P.PhaseVisible = 'off';

Frequency vector.

  w = 2*pi*logspace(-1,2,1000); % [rad/s]

generation of the state space model

  M = [m 0 0
       0 m 0
       0 0 I];

  %Jacobian of the bottom sensor
  Js1 = [1 0 h/2
         0 1 -l/2];
  %Jacobian of the top sensor
  Js2 = [1 0 -h/2
         0 1 0];

  %Jacobian of the actuators
  Ja = [1 0 ha/2 %Left horizontal actuator
                 %1 0 h/2 %Right horizontal actuator
        0 1 -la/2 %Left vertical actuator
        0 1 la/2]; %Right vertical actuator
  Jta = Ja';
  K = k*Jta*Ja;
  C = c*Jta*Ja;

  E = [1 0 0
       0 1 0
       0 0 1]; %projecting ground motion in the directions of the legs

  AA = [zeros(3) eye(3)
        -M\K -M\C];

  BB = [zeros(3,6)
        M\Jta M\(k*Jta*E)];

  % BB = [zeros(3,3)
  %     M\Jta ];
  %
  % CC = [Ja zeros(3)];
  % DD = zeros(3,3);

  CC = [[Js1;Js2] zeros(4,3);
        zeros(2,6)
        (Js1+Js2)./2 zeros(2,3)
        (Js1-Js2)./2 zeros(2,3)
        (Js1-Js2)./(2*h) zeros(2,3)];

  DD = [zeros(4,6)
        zeros(2,3) eye(2,3)
        zeros(6,6)];

  system_dec = ss(AA,BB,CC,DD);

• Input = three actuators and three ground motions
• Output = the bottom sensor; the top sensor; the ground motion; the half sum; the half difference; the rotation

  size(system_dec)

State-space model with 12 outputs, 6 inputs, and 6 states.

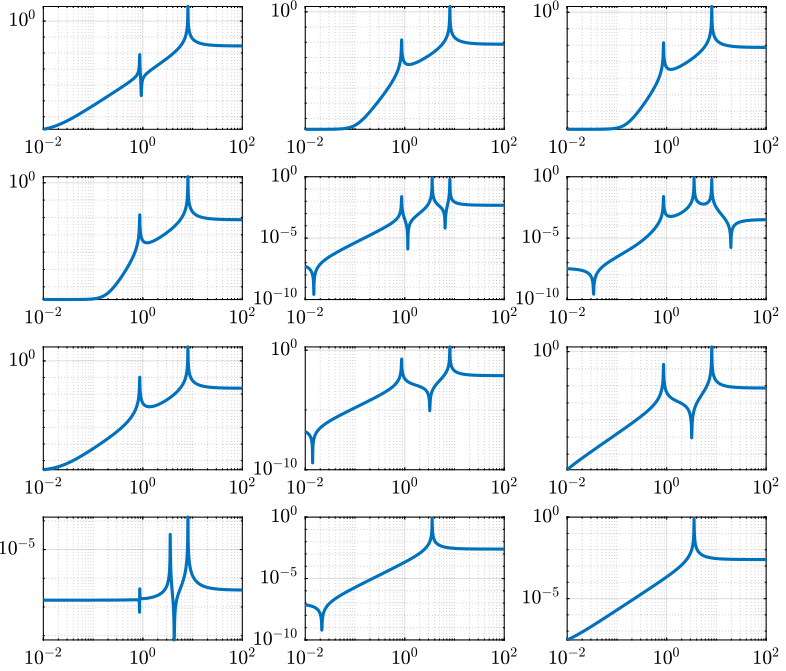
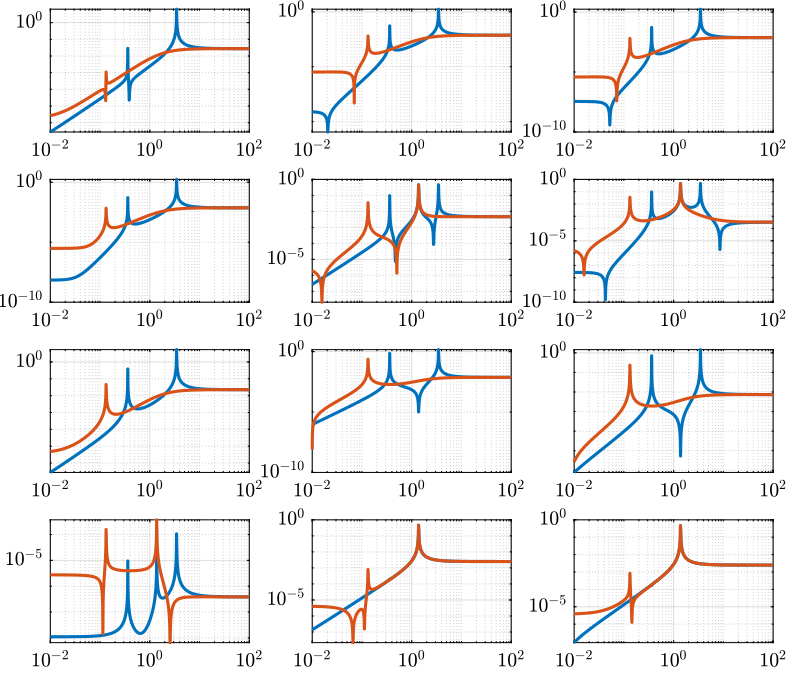
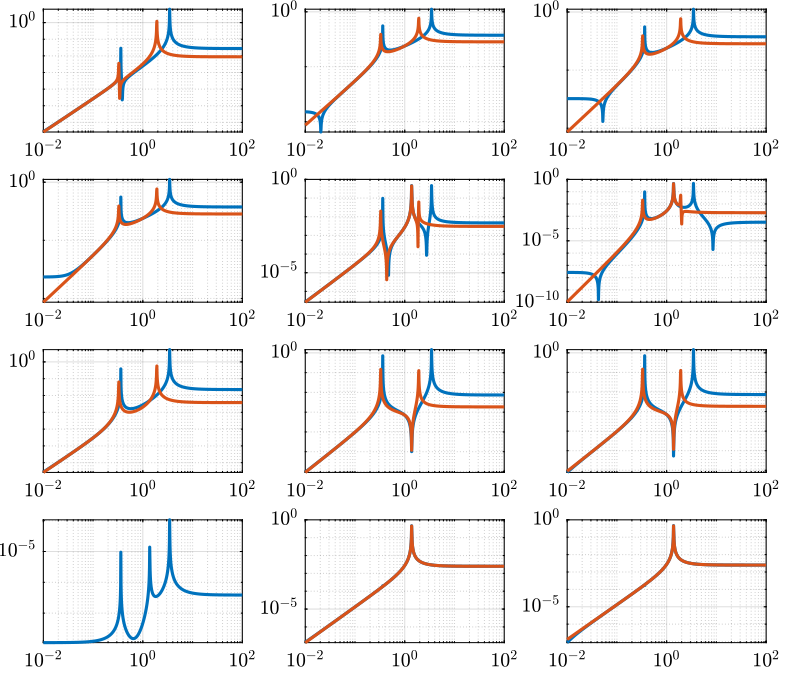
Comparison with the Simscape Model

Comparison of the analytical and the Simscape models

Analysis

  % figure
  % bode(system_dec,P);
  % return

  %% svd decomposition
  % system_dec_freq = freqresp(system_dec,w);
  % S = zeros(3,length(w));
  % for m = 1:length(w)
  %     S(:,m) = svd(system_dec_freq(1:4,1:3,m));
  % end
  % figure
  % loglog(w./(2*pi), S);hold on;
  % % loglog(w./(2*pi), abs(Val(1,:)),w./(2*pi), abs(Val(2,:)),w./(2*pi), abs(Val(3,:)));
  % xlabel('Frequency [Hz]');ylabel('Singular Value [-]');
  % legend('\sigma_1','\sigma_2','\sigma_3');%,'\sigma_4','\sigma_5','\sigma_6');
  % ylim([1e-8 1e-2]);
  %
  % %condition number
  % figure
  % loglog(w./(2*pi), S(1,:)./S(3,:));hold on;
  % % loglog(w./(2*pi), abs(Val(1,:)),w./(2*pi), abs(Val(2,:)),w./(2*pi), abs(Val(3,:)));
  % xlabel('Frequency [Hz]');ylabel('Condition number [-]');
  % % legend('\sigma_1','\sigma_2','\sigma_3');%,'\sigma_4','\sigma_5','\sigma_6');
  %
  % %performance indicator
  % system_dec_svd = freqresp(system_dec(1:4,1:3),2*pi*10);
  % [U,S,V] = svd(system_dec_svd);
  % H_svd_OL = -eye(3,4);%-[zpk(-2*pi*10,-2*pi*40,40/10) 0 0 0; 0 10*zpk(-2*pi*40,-2*pi*200,40/200) 0 0; 0 0 zpk(-2*pi*2,-2*pi*10,10/2) 0];% - eye(3,4);%
  % H_svd = pinv(V')*H_svd_OL*pinv(U);
  % % system_dec_control_svd_ = feedback(system_dec,g*pinv(V')*H*pinv(U));
  %
  % OL_dec = g_svd*H_svd*system_dec(1:4,1:3);
  % OL_freq = freqresp(OL_dec,w); % OL = G*H
  % CL_system = feedback(eye(3),-g_svd*H_svd*system_dec(1:4,1:3));
  % CL_freq = freqresp(CL_system,w); % CL = (1+G*H)^-1
  % % CL_system_2 = feedback(system_dec,H);
  % % CL_freq_2 = freqresp(CL_system_2,w); % CL = G/(1+G*H)
  % for i = 1:size(w,2)
  %     OL(:,i) = svd(OL_freq(:,:,i));
  %     CL (:,i) = svd(CL_freq(:,:,i));
  %     %CL2 (:,i) = svd(CL_freq_2(:,:,i));
  % end
  %
  % un = ones(1,length(w));
  % figure
  % loglog(w./(2*pi),OL(3,:)+1,'k',w./(2*pi),OL(3,:)-1,'b',w./(2*pi),1./CL(1,:),'r--',w./(2*pi),un,'k:');hold on;%
  % % loglog(w./(2*pi), 1./(CL(2,:)),w./(2*pi), 1./(CL(3,:)));
  % % semilogx(w./(2*pi), 1./(CL2(1,:)),w./(2*pi), 1./(CL2(2,:)),w./(2*pi), 1./(CL2(3,:)));
  % xlabel('Frequency [Hz]');ylabel('Singular Value [-]');
  % legend('GH \sigma_{inf} +1 ','GH \sigma_{inf} -1','S 1/\sigma_{sup}');%,'\lambda_1','\lambda_2','\lambda_3');
  %
  % figure
  % loglog(w./(2*pi),OL(1,:)+1,'k',w./(2*pi),OL(1,:)-1,'b',w./(2*pi),1./CL(3,:),'r--',w./(2*pi),un,'k:');hold on;%
  % % loglog(w./(2*pi), 1./(CL(2,:)),w./(2*pi), 1./(CL(3,:)));
  % % semilogx(w./(2*pi), 1./(CL2(1,:)),w./(2*pi), 1./(CL2(2,:)),w./(2*pi), 1./(CL2(3,:)));
  % xlabel('Frequency [Hz]');ylabel('Singular Value [-]');
  % legend('GH \sigma_{sup} +1 ','GH \sigma_{sup} -1','S 1/\sigma_{inf}');%,'\lambda_1','\lambda_2','\lambda_3');

Control Section

  system_dec_10Hz = freqresp(system_dec,2*pi*10);
  system_dec_0Hz = freqresp(system_dec,0);

  system_decReal_10Hz = pinv(align(system_dec_10Hz));
  [Ureal,Sreal,Vreal] = svd(system_decReal_10Hz(1:4,1:3));
  normalizationMatrixReal = abs(pinv(Ureal)*system_dec_0Hz(1:4,1:3)*pinv(Vreal'));

  [U,S,V] = svd(system_dec_10Hz(1:4,1:3));
  normalizationMatrix = abs(pinv(U)*system_dec_0Hz(1:4,1:3)*pinv(V'));

  H_dec = ([zpk(-2*pi*5,-2*pi*30,30/5) 0 0 0
            0 zpk(-2*pi*4,-2*pi*20,20/4) 0 0
            0 0 0 zpk(-2*pi,-2*pi*10,10)]);
  H_cen_OL = [zpk(-2*pi,-2*pi*10,10) 0 0; 0 zpk(-2*pi,-2*pi*10,10) 0;
              0 0 zpk(-2*pi*5,-2*pi*30,30/5)];
  H_cen = pinv(Jta)*H_cen_OL*pinv([Js1; Js2]);
  % H_svd_OL = -[1/normalizationMatrix(1,1) 0 0 0
  %     0 1/normalizationMatrix(2,2) 0 0
  %     0 0 1/normalizationMatrix(3,3) 0];
  % H_svd_OL_real = -[1/normalizationMatrixReal(1,1) 0 0 0
  %     0 1/normalizationMatrixReal(2,2) 0 0
  %     0 0 1/normalizationMatrixReal(3,3) 0];
  H_svd_OL = -[1/normalizationMatrix(1,1)*zpk(-2*pi*10,-2*pi*60,60/10) 0 0 0
               0 1/normalizationMatrix(2,2)*zpk(-2*pi*5,-2*pi*30,30/5) 0 0
               0 0 1/normalizationMatrix(3,3)*zpk(-2*pi*2,-2*pi*10,10/2) 0];
  H_svd_OL_real = -[1/normalizationMatrixReal(1,1)*zpk(-2*pi*10,-2*pi*60,60/10) 0 0 0
                    0 1/normalizationMatrixReal(2,2)*zpk(-2*pi*5,-2*pi*30,30/5) 0 0
                    0 0 1/normalizationMatrixReal(3,3)*zpk(-2*pi*2,-2*pi*10,10/2) 0];
  % H_svd_OL_real = -[zpk(-2*pi*10,-2*pi*40,40/10) 0 0 0; 0 10*zpk(-2*pi*10,-2*pi*100,100/10) 0 0; 0 0 zpk(-2*pi*2,-2*pi*10,10/2) 0];%-eye(3,4);
  % H_svd_OL = -[zpk(-2*pi*10,-2*pi*40,40/10) 0 0 0; 0 zpk(-2*pi*4,-2*pi*20,4/20) 0 0; 0 0 zpk(-2*pi*2,-2*pi*10,10/2) 0];% - eye(3,4);%
  H_svd = pinv(V')*H_svd_OL*pinv(U);
  H_svd_real = pinv(Vreal')*H_svd_OL_real*pinv(Ureal);

  OL_dec = g*H_dec*system_dec(1:4,1:3);
  OL_cen = g*H_cen_OL*pinv([Js1; Js2])*system_dec(1:4,1:3)*pinv(Jta);
  OL_svd = 100*H_svd_OL*pinv(U)*system_dec(1:4,1:3)*pinv(V');
  OL_svd_real = 100*H_svd_OL_real*pinv(Ureal)*system_dec(1:4,1:3)*pinv(Vreal');

  % figure
  % bode(OL_dec,w,P);title('OL Decentralized');
  % figure
  % bode(OL_cen,w,P);title('OL Centralized');

  figure
  bode(g*system_dec(1:4,1:3),w,P);
  title('gain * Plant');

  figure
  bode(OL_svd,OL_svd_real,w,P);
  title('OL SVD');
  legend('SVD of Complex plant','SVD of real approximation of the complex plant')

  figure
  bode(system_dec(1:4,1:3),pinv(U)*system_dec(1:4,1:3)*pinv(V'),P);

  CL_dec = feedback(system_dec,g*H_dec,[1 2 3],[1 2 3 4]);
  CL_cen = feedback(system_dec,g*H_cen,[1 2 3],[1 2 3 4]);
  CL_svd = feedback(system_dec,100*H_svd,[1 2 3],[1 2 3 4]);
  CL_svd_real = feedback(system_dec,100*H_svd_real,[1 2 3],[1 2 3 4]);

  pzmap_testCL(system_dec,H_dec,g,[1 2 3],[1 2 3 4])
  title('Decentralized control');

  pzmap_testCL(system_dec,H_cen,g,[1 2 3],[1 2 3 4])
  title('Centralized control');

  pzmap_testCL(system_dec,H_svd,100,[1 2 3],[1 2 3 4])
  title('SVD control');

  pzmap_testCL(system_dec,H_svd_real,100,[1 2 3],[1 2 3 4])
  title('Real approximation SVD control');

  P.Ylim = [1e-8 1e-3];
  figure
  bodemag(system_dec(1:4,1:3),CL_dec(1:4,1:3),CL_cen(1:4,1:3),CL_svd(1:4,1:3),CL_svd_real(1:4,1:3),P);
  title('Motion/actuator')
  legend('Control OFF','Decentralized control','Centralized control','SVD control','SVD control real appr.');

  P.Ylim = [1e-5 1e1];
  figure
  bodemag(system_dec(1:4,4:6),CL_dec(1:4,4:6),CL_cen(1:4,4:6),CL_svd(1:4,4:6),CL_svd_real(1:4,4:6),P);
  title('Transmissibility');
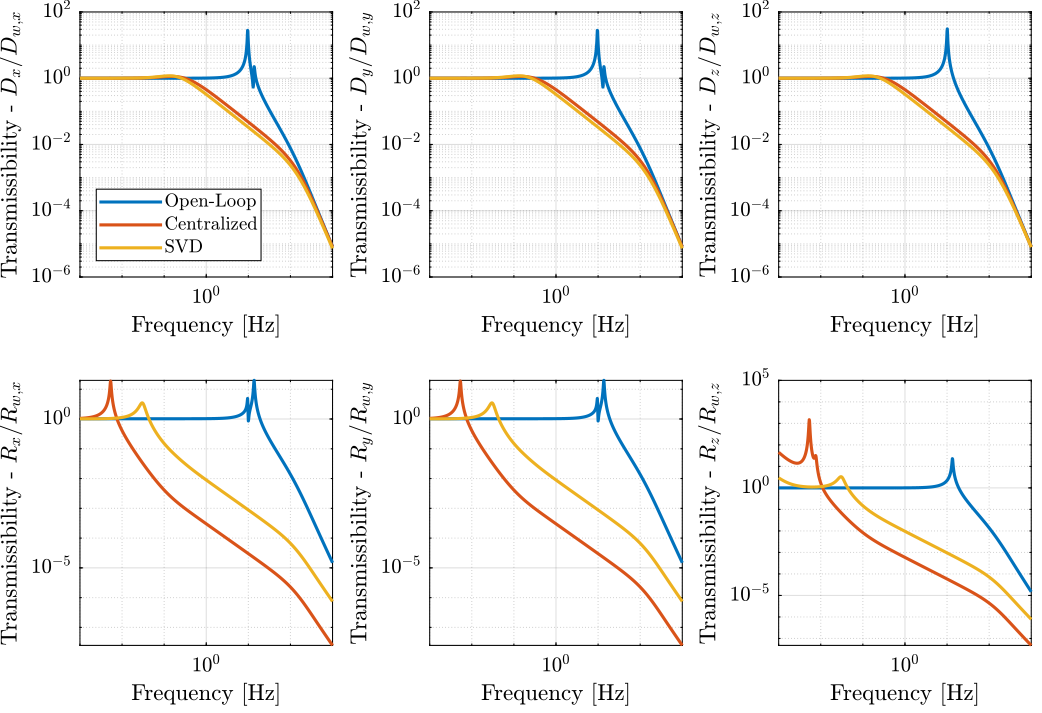
  legend('Control OFF','Decentralized control','Centralized control','SVD control','SVD control real appr.');

  figure
  bodemag(system_dec([7 9],4:6),CL_dec([7 9],4:6),CL_cen([7 9],4:6),CL_svd([7 9],4:6),CL_svd_real([7 9],4:6),P);
  title('Transmissibility from half sum and half difference in the X direction');
  legend('Control OFF','Decentralized control','Centralized control','SVD control','SVD control real appr.');

  figure
  bodemag(system_dec([8 10],4:6),CL_dec([8 10],4:6),CL_cen([8 10],4:6),CL_svd([8 10],4:6),CL_svd_real([8 10],4:6),P);
  title('Transmissibility from half sum and half difference in the Z direction');
  legend('Control OFF','Decentralized control','Centralized control','SVD control','SVD control real appr.');

Greshgorin radius

  system_dec_freq = freqresp(system_dec,w);
  x1 = zeros(1,length(w));
  z1 = zeros(1,length(w));
  x2 = zeros(1,length(w));
  S1 = zeros(1,length(w));
  S2 = zeros(1,length(w));
  S3 = zeros(1,length(w));

  for t = 1:length(w)
      x1(t) = (abs(system_dec_freq(1,2,t))+abs(system_dec_freq(1,3,t)))/abs(system_dec_freq(1,1,t));
      z1(t) = (abs(system_dec_freq(2,1,t))+abs(system_dec_freq(2,3,t)))/abs(system_dec_freq(2,2,t));
      x2(t) = (abs(system_dec_freq(3,1,t))+abs(system_dec_freq(3,2,t)))/abs(system_dec_freq(3,3,t));
      system_svd = pinv(Ureal)*system_dec_freq(1:4,1:3,t)*pinv(Vreal');
      S1(t) = (abs(system_svd(1,2))+abs(system_svd(1,3)))/abs(system_svd(1,1));
      S2(t) = (abs(system_svd(2,1))+abs(system_svd(2,3)))/abs(system_svd(2,2));
      S2(t) = (abs(system_svd(3,1))+abs(system_svd(3,2)))/abs(system_svd(3,3));
  end

  limit = 0.5*ones(1,length(w));

  figure
  loglog(w./(2*pi),x1,w./(2*pi),z1,w./(2*pi),x2,w./(2*pi),limit,'--');
  legend('x_1','z_1','x_2','Limit');
  xlabel('Frequency [Hz]');
  ylabel('Greshgorin radius [-]');

  figure
  loglog(w./(2*pi),S1,w./(2*pi),S2,w./(2*pi),S3,w./(2*pi),limit,'--');
  legend('S1','S2','S3','Limit');
  xlabel('Frequency [Hz]');
  ylabel('Greshgorin radius [-]');
  % set(gcf,'color','w')

Injecting ground motion in the system to have the output

  Fr = logspace(-2,3,1e3);
  w=2*pi*Fr*1i;
  %fit of the ground motion data in m/s^2/rtHz
  Fr_ground_x = [0.07 0.1 0.15 0.3 0.7 0.8 0.9 1.2 5 10];
  n_ground_x1 = [4e-7 4e-7 2e-6 1e-6 5e-7 5e-7 5e-7 1e-6 1e-5 3.5e-5];
  Fr_ground_v = [0.07 0.08 0.1 0.11 0.12 0.15 0.25 0.6 0.8 1 1.2 1.6 2 6 10];
  n_ground_v1 = [7e-7 7e-7 7e-7 1e-6 1.2e-6 1.5e-6 1e-6 9e-7 7e-7 7e-7 7e-7 1e-6 2e-6 1e-5 3e-5];

  n_ground_x = interp1(Fr_ground_x,n_ground_x1,Fr,'linear');
  n_ground_v = interp1(Fr_ground_v,n_ground_v1,Fr,'linear');
  % figure
  % loglog(Fr,abs(n_ground_v),Fr_ground_v,n_ground_v1,'*');
  % xlabel('Frequency [Hz]');ylabel('ASD [m/s^2 /rtHz]');
  % return

  %converting into PSD
  n_ground_x = (n_ground_x).^2;
  n_ground_v = (n_ground_v).^2;

  %Injecting ground motion in the system and getting the outputs
  system_dec_f = (freqresp(system_dec,abs(w)));
  PHI = zeros(size(Fr,2),12,12);
  for p = 1:size(Fr,2)
      Sw=zeros(6,6);
      Iact = zeros(3,3);
      Sw(4,4) = n_ground_x(p);
      Sw(5,5) = n_ground_v(p);
      Sw(6,6) = n_ground_v(p);
      Sw(1:3,1:3) = Iact;
      PHI(p,:,:) = (system_dec_f(:,:,p))*Sw(:,:)*(system_dec_f(:,:,p))';
  end
  x1 = PHI(:,1,1);
  z1 = PHI(:,2,2);
  x2 = PHI(:,3,3);
  z2 = PHI(:,4,4);
  wx = PHI(:,5,5);
  wz = PHI(:,6,6);
  x12 = PHI(:,1,3);
  z12 = PHI(:,2,4);
  PHIwx = PHI(:,1,5);
  PHIwz = PHI(:,2,6);
  xsum = PHI(:,7,7);
  zsum = PHI(:,8,8);
  xdelta = PHI(:,9,9);
  zdelta = PHI(:,10,10);
  rot = PHI(:,11,11);

Gravimeter - Functions

align

<<sec:align>>

This Matlab function is accessible here.

  function [A] = align(V)
  %A!ALIGN(V) returns a constat matrix A which is the real alignment of the
  %INVERSE of the complex input matrix V
  %from Mohit slides

      if (nargin ==0) || (nargin > 1)
          disp('usage: mat_inv_real = align(mat)')
          return
      end

      D = pinv(real(V'*V));
      A = D*real(V'*diag(exp(1i * angle(diag(V*D*V.'))/2)));


  end

pzmap_testCL

<<sec:pzmap_testCL>>

This Matlab function is accessible here.

  function [] = pzmap_testCL(system,H,gain,feedin,feedout)
  % evaluate and plot the pole-zero map for the closed loop system for
  % different values of the gain

      [~, n] = size(gain);
      [m1, n1, ~] = size(H);
      [~,n2] = size(feedin);

      figure
      for i = 1:n
          %     if n1 == n2
          system_CL = feedback(system,gain(i)*H,feedin,feedout);

          [P,Z] = pzmap(system_CL);
          plot(real(P(:)),imag(P(:)),'x',real(Z(:)),imag(Z(:)),'o');hold on
          xlabel('Real axis (s^{-1})');ylabel('Imaginary Axis (s^{-1})');
          %         clear P Z
          %     else
          %         system_CL = feedback(system,gain(i)*H(:,1+(i-1)*m1:m1+(i-1)*m1),feedin,feedout);
          %
          %         [P,Z] = pzmap(system_CL);
          %         plot(real(P(:)),imag(P(:)),'x',real(Z(:)),imag(Z(:)),'o');hold on
          %         xlabel('Real axis (s^{-1})');ylabel('Imaginary Axis (s^{-1})');
          %         clear P Z
          %     end
      end
      str = {strcat('gain = ' , num2str(gain(1)))};  % at the end of first loop, z being loop output
      str = [str , strcat('gain = ' , num2str(gain(1)))]; % after 2nd loop
      for i = 2:n
          str = [str , strcat('gain = ' , num2str(gain(i)))]; % after 2nd loop
          str = [str , strcat('gain = ' , num2str(gain(i)))]; % after 2nd loop
      end
      legend(str{:})
  end

Stewart Platform - Simscape Model

Jacobian

First, the position of the "joints" (points of force application) are estimated and the Jacobian computed.

  open('stewart_platform/drone_platform_jacobian.slx');

  sim('drone_platform_jacobian');

  Aa = [a1.Data(1,:);
        a2.Data(1,:);
        a3.Data(1,:);
        a4.Data(1,:);
        a5.Data(1,:);
        a6.Data(1,:)]';

  Ab = [b1.Data(1,:);
        b2.Data(1,:);
        b3.Data(1,:);
        b4.Data(1,:);
        b5.Data(1,:);
        b6.Data(1,:)]';

  As = (Ab - Aa)./vecnorm(Ab - Aa);

  l = vecnorm(Ab - Aa)';

  J = [As' , cross(Ab, As)'];

  save('./jacobian.mat', 'Aa', 'Ab', 'As', 'l', 'J');

Simscape Model

  open('stewart_platform/drone_platform.slx');

Definition of spring parameters

  kx = 50; % [N/m]
  ky = 50;
  kz = 50;

  cx = 0.025; % [Nm/rad]
  cy = 0.025;
  cz = 0.025;

We load the Jacobian.

  load('./jacobian.mat', 'Aa', 'Ab', 'As', 'l', 'J');

Identification of the plant

The dynamics is identified from forces applied by each legs to the measured acceleration of the top platform.

  %% Name of the Simulink File
  mdl = 'drone_platform';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/Dw'],              1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/u'],               1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Inertial Sensor'], 1, 'openoutput'); io_i = io_i + 1;

  G = linearize(mdl, io);
  G.InputName  = {'Dwx', 'Dwy', 'Dwz', 'Rwx', 'Rwy', 'Rwz', ...
                  'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};
  G.OutputName = {'Ax', 'Ay', 'Az', 'Arx', 'Ary', 'Arz'};

There are 24 states (6dof for the bottom platform + 6dof for the top platform).

  size(G)

State-space model with 6 outputs, 12 inputs, and 24 states.

  % G = G*blkdiag(inv(J), eye(6));
  % G.InputName  = {'Dw1', 'Dw2', 'Dw3', 'Dw4', 'Dw5', 'Dw6', ...
  %                 'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};

Thanks to the Jacobian, we compute the transfer functions in the frame of the legs and in an inertial frame.

  Gx = G*blkdiag(eye(6), inv(J'));
  Gx.InputName  = {'Dwx', 'Dwy', 'Dwz', 'Rwx', 'Rwy', 'Rwz', ...
                   'Fx', 'Fy', 'Fz', 'Mx', 'My', 'Mz'};

  Gl = J*G;
  Gl.OutputName  = {'A1', 'A2', 'A3', 'A4', 'A5', 'A6'};

Obtained Dynamics

Stewart Platform Plant from forces applied by the legs to the acceleration of the platform

Stewart Platform Plant from torques applied by the legs to the angular acceleration of the platform

Stewart Platform Plant from forces applied by the legs to displacement of the legs

Transmissibility

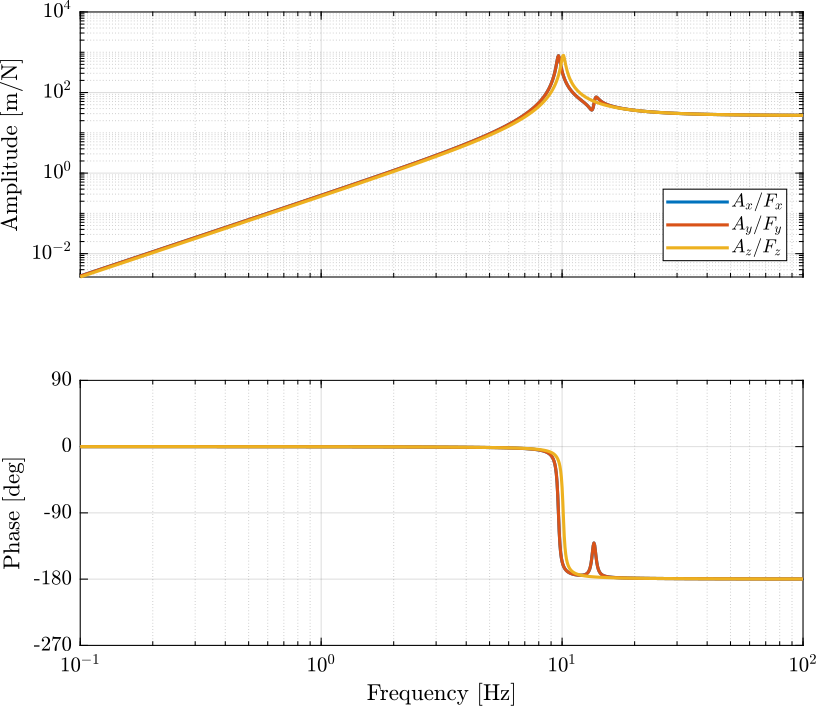
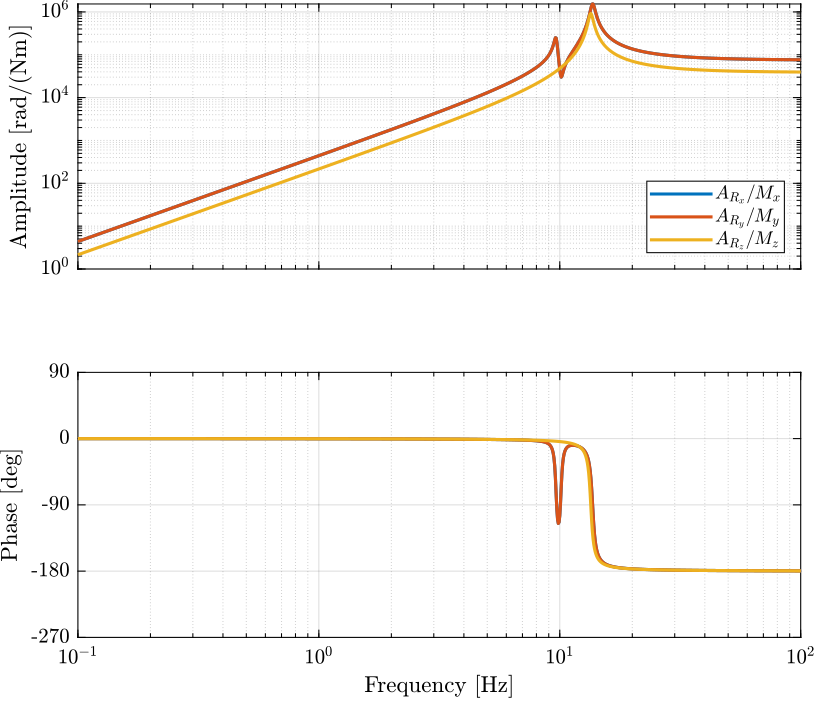
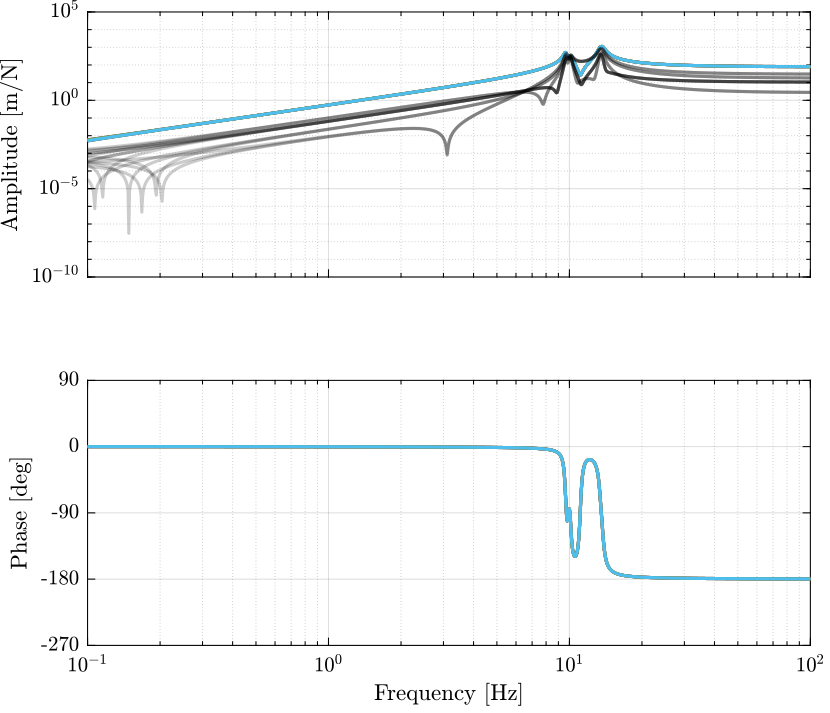
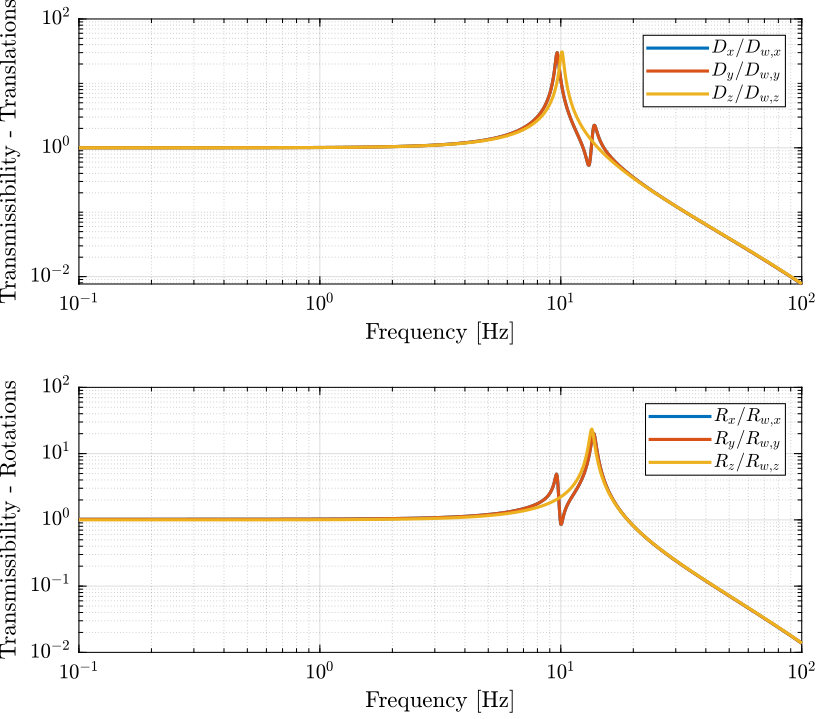
Real Approximation of $G$ at the decoupling frequency

Let's compute a real approximation of the complex matrix $H_1$ which corresponds to the the transfer function $G_c(j\omega_c)$ from forces applied by the actuators to the measured acceleration of the top platform evaluated at the frequency $\omega_c$.

  wc = 2*pi*20; % Decoupling frequency [rad/s]

  Gc = G({'Ax', 'Ay', 'Az', 'Arx', 'Ary', 'Arz'}, ...
         {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'}); % Transfer function to find a real approximation

  H1 = evalfr(Gc, j*wc);

The real approximation is computed as follows:

  D = pinv(real(H1'*H1));
  H1 = inv(D*real(H1'*diag(exp(j*angle(diag(H1*D*H1.'))/2))));

Verification of the decoupling using the "Gershgorin Radii"

First, the Singular Value Decomposition of $H_1$ is performed: \[ H_1 = U \Sigma V^H \]

  [U,S,V] = svd(H1);

Then, the "Gershgorin Radii" is computed for the plant $G_c(s)$ and the "SVD Decoupled Plant" $G_d(s)$: \[ G_d(s) = U^T G_c(s) V \]

This is computed over the following frequencies.

  freqs = logspace(-2, 2, 1000); % [Hz]

Gershgorin Radii for the coupled plant:

  Gr_coupled = zeros(length(freqs), size(Gc,2));

  H = abs(squeeze(freqresp(Gc, freqs, 'Hz')));
  for out_i = 1:size(Gc,2)
      Gr_coupled(:, out_i) = squeeze((sum(H(out_i,:,:)) - H(out_i,out_i,:))./H(out_i, out_i, :));
  end

Gershgorin Radii for the decoupled plant using SVD:

  Gd = U'*Gc*V;
  Gr_decoupled = zeros(length(freqs), size(Gd,2));

  H = abs(squeeze(freqresp(Gd, freqs, 'Hz')));
  for out_i = 1:size(Gd,2)
      Gr_decoupled(:, out_i) = squeeze((sum(H(out_i,:,:)) - H(out_i,out_i,:))./H(out_i, out_i, :));
  end

Gershgorin Radii for the decoupled plant using the Jacobian:

  Gj = Gc*inv(J');
  Gr_jacobian = zeros(length(freqs), size(Gj,2));

  H = abs(squeeze(freqresp(Gj, freqs, 'Hz')));

  for out_i = 1:size(Gj,2)
      Gr_jacobian(:, out_i) = squeeze((sum(H(out_i,:,:)) - H(out_i,out_i,:))./H(out_i, out_i, :));
  end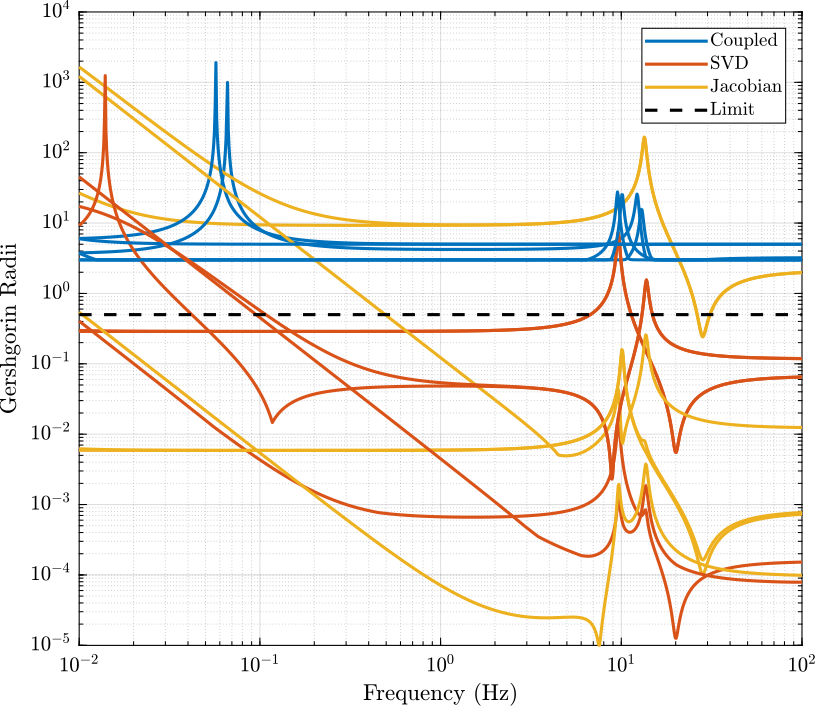

Gershgorin Radii of the Coupled and Decoupled plants

Decoupled Plant

Let's see the bode plot of the decoupled plant $G_d(s)$. \[ G_d(s) = U^T G_c(s) V \]

Decoupled Plant using SVD

Decoupled Plant using the Jacobian

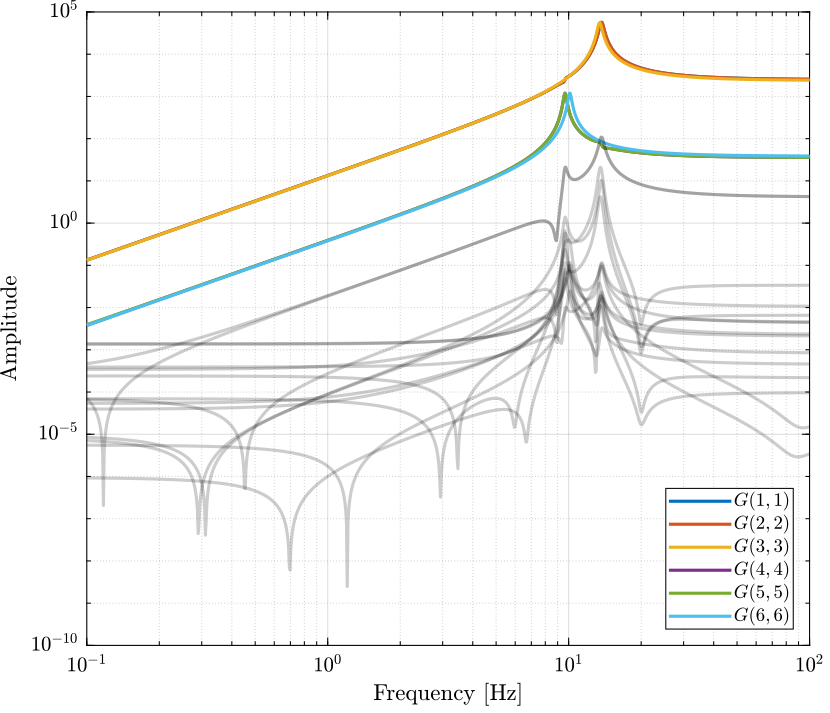
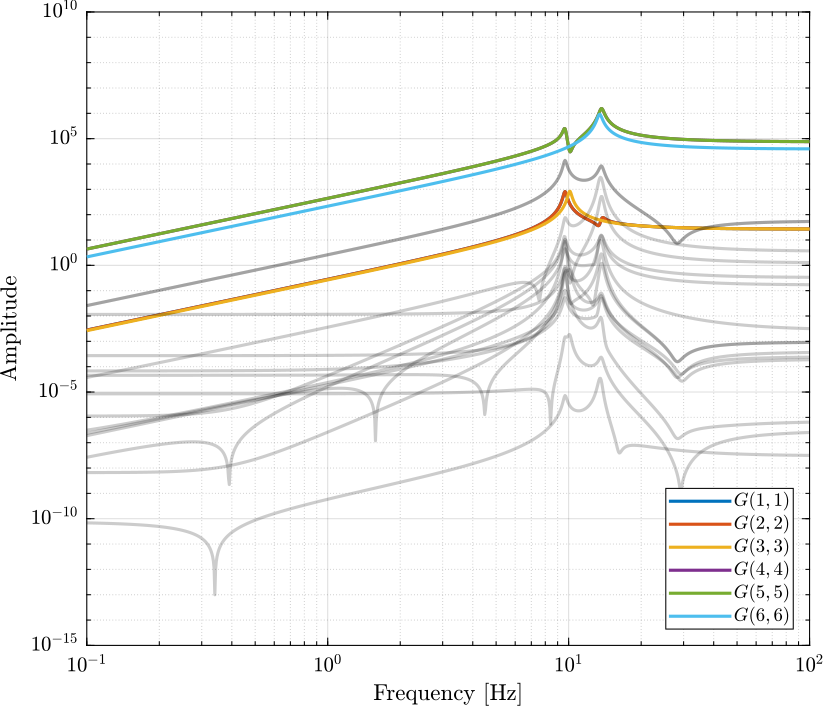
Diagonal Controller

The controller $K$ is a diagonal controller consisting a low pass filters with a crossover frequency $\omega_c$ and a DC gain $C_g$.

  wc = 2*pi*0.1; % Crossover Frequency [rad/s]
  C_g = 50; % DC Gain

  K = eye(6)*C_g/(s+wc);

Centralized Control

The control diagram for the centralized control is shown below.

The controller $K_c$ is "working" in an cartesian frame. The Jacobian is used to convert forces in the cartesian frame to forces applied by the actuators.

  \begin{tikzpicture}
    \node[block={2cm}{1.5cm}] (G) {$G$};
    \node[block, below right=0.6 and -0.5 of G] (K) {$K_c$};
    \node[block, below left= 0.6 and -0.5 of G] (J) {$J^{-T}$};

    % Inputs of the controllers
    \coordinate[] (inputd) at ($(G.south west)!0.75!(G.north west)$);
    \coordinate[] (inputu) at ($(G.south west)!0.25!(G.north west)$);

    % Connections and labels
    \draw[<-] (inputd) -- ++(-0.8, 0) node[above right]{$D_w$};
    \draw[->] (G.east) -- ++(2.0, 0)  node[above left]{$a$};
    \draw[->] ($(G.east)+(1.4, 0)$)node[branch]{} |- (K.east);
    \draw[->] (K.west) -- (J.east) node[above right]{$\mathcal{F}$};
    \draw[->] (J.west) -- ++(-0.6, 0) |- (inputu) node[above left]{$\tau$};
  \end{tikzpicture}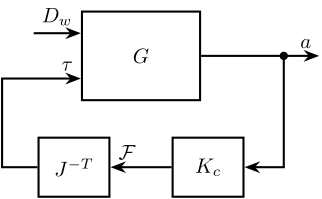

  G_cen = feedback(G, inv(J')*K, [7:12], [1:6]);

SVD Control

The SVD control architecture is shown below. The matrices $U$ and $V$ are used to decoupled the plant $G$.

  \begin{tikzpicture}
    \node[block={2cm}{1.5cm}] (G) {$G$};
    \node[block, below right=0.6 and 0 of G] (U) {$U^{-1}$};
    \node[block, below=0.6 of G] (K) {$K_{\text{SVD}}$};
    \node[block, below left= 0.6 and 0 of G] (V) {$V^{-T}$};

    % Inputs of the controllers
    \coordinate[] (inputd) at ($(G.south west)!0.75!(G.north west)$);
    \coordinate[] (inputu) at ($(G.south west)!0.25!(G.north west)$);

    % Connections and labels
    \draw[<-] (inputd) -- ++(-0.8, 0) node[above right]{$D_w$};
    \draw[->] (G.east) -- ++(2.5, 0) node[above left]{$a$};
    \draw[->] ($(G.east)+(2.0, 0)$) node[branch]{} |- (U.east);
    \draw[->] (U.west) -- (K.east);
    \draw[->] (K.west) -- (V.east);
    \draw[->] (V.west) -- ++(-0.6, 0) |- (inputu) node[above left]{$\tau$};
  \end{tikzpicture}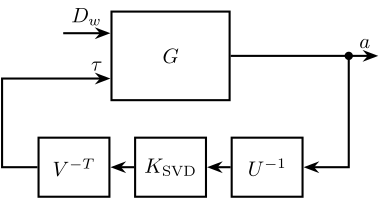

SVD Control

  G_svd = feedback(G, pinv(V')*K*pinv(U), [7:12], [1:6]);

Results

Let's first verify the stability of the closed-loop systems:

  isstable(G_cen)

ans =
  logical
   1

  isstable(G_svd)

ans =
  logical
   1

The obtained transmissibility in Open-loop, for the centralized control as well as for the SVD control are shown in Figure fig:stewart_platform_simscape_cl_transmissibility.

Obtained Transmissibility