svd-control/index.org

Diagonal control using the SVD and the Jacobian Matrix

• Introduction
• Gravimeter - Simscape Model
  • Introduction
  • Gravimeter Model - Parameters
  • System Identification
  • Decoupling using the Jacobian
  • Decoupling using the SVD
  • Verification of the decoupling using the "Gershgorin Radii"
  • Verification of the decoupling using the "Relative Gain Array"
  • Obtained Decoupled Plants
  • Diagonal Controller
  • Closed-Loop system Performances
  • Robustness to a change of actuator position
  • Combined / comparison of K and M decoupling
    • Introduction
    • Decoupling of the mass matrix
    • Decoupling of the stiffness matrix
    • Combined decoupling of the mass and stiffness matrices
    • Conclusion
  • SVD decoupling performances
• Stewart Platform - Simscape Model
  • Introduction
  • Simscape Model - Parameters
  • Identification of the plant
  • Decoupling using the Jacobian
  • Decoupling using the SVD
  • Verification of the decoupling using the "Gershgorin Radii"
  • Verification of the decoupling using the "Relative Gain Array"
  • Obtained Decoupled Plants
  • Diagonal Controller
  • Closed-Loop system Performances

Introduction   ignore

In this document, the use of the Jacobian matrix and the Singular Value Decomposition to render a physical plant diagonal dominant is studied. Then, a diagonal controller is used.

These two methods are tested on two plants:

• In Section sec:gravimeter on a 3-DoF gravimeter
• In Section sec:stewart_platform on a 6-DoF Stewart platform

Gravimeter - Simscape Model

<<sec:gravimeter>>

Introduction

In this part, diagonal control using both the SVD and the Jacobian matrices are applied on a gravimeter model:

• Section sec:gravimeter_model: the model is described and its parameters are defined.
• Section sec:gravimeter_identification: the plant dynamics from the actuators to the sensors is computed from a Simscape model.
• Section sec:gravimeter_jacobian_decoupling: the plant is decoupled using the Jacobian matrices.
• Section sec:gravimeter_svd_decoupling: the Singular Value Decomposition is performed on a real approximation of the plant transfer matrix and further use to decouple the system.
• Section sec:gravimeter_gershgorin_radii: the effectiveness of the decoupling is computed using the Gershorin radii
• Section sec:gravimeter_rga: the effectiveness of the decoupling is computed using the Relative Gain Array
• Section sec:gravimeter_decoupled_plant: the obtained decoupled plants are compared
• Section sec:gravimeter_diagonal_control: the diagonal controller is developed
• Section sec:gravimeter_closed_loop_results: the obtained closed-loop performances for the two methods are compared

Gravimeter Model - Parameters

<<sec:gravimeter_model>>

The model of the gravimeter is schematically shown in Figure fig:gravimeter_model.

Model of the gravimeter

Model of the struts

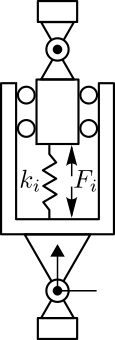
The parameters used for the simulation are the following:

  l  = 1.0; % Length of the mass [m]
  h  = 1.7; % Height of the mass [m]

  la = l/2; % Position of Act. [m]
  ha = h/2; % Position of Act. [m]

  m = 400; % Mass [kg]
  I = 115; % Inertia [kg m^2]

  k = 15e3; % Actuator Stiffness [N/m]
  c = 2e1; % Actuator Damping [N/(m/s)]

  deq = 0.2; % Length of the actuators [m]

  g = 0; % Gravity [m/s2]

System Identification

<<sec:gravimeter_identification>>

  %% Name of the Simulink File
  mdl = 'gravimeter';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/F1'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/F2'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/F3'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_side'], 1, 'openoutput'); io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_side'], 2, 'openoutput'); io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_top'], 1, 'openoutput'); io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_top'], 2, 'openoutput'); io_i = io_i + 1;

  G = linearize(mdl, io);
  G.InputName  = {'F1', 'F2', 'F3'};
  G.OutputName = {'Ax1', 'Ay1', 'Ax2', 'Ay2'};

The inputs and outputs of the plant are shown in Figure fig:gravimeter_plant_schematic.

More precisely there are three inputs (the three actuator forces):

\begin{equation} \bm{\tau} = \begin{bmatrix}\tau_1 \\ \tau_2 \\ \tau_2 \end{bmatrix} \end{equation}

And 4 outputs (the two 2-DoF accelerometers):

\begin{equation} \bm{a} = \begin{bmatrix} a_{1x} \\ a_{1y} \\ a_{2x} \\ a_{2y} \end{bmatrix} \end{equation}

Schematic of the gravimeter plant

We can check the poles of the plant:

-0.12243+13.551i

-0.12243-13.551i

-0.05+8.6601i

-0.05-8.6601i

-0.0088785+3.6493i

-0.0088785-3.6493i

As expected, the plant as 6 states (2 translations + 1 rotation)

  size(G)

State-space model with 4 outputs, 3 inputs, and 6 states.

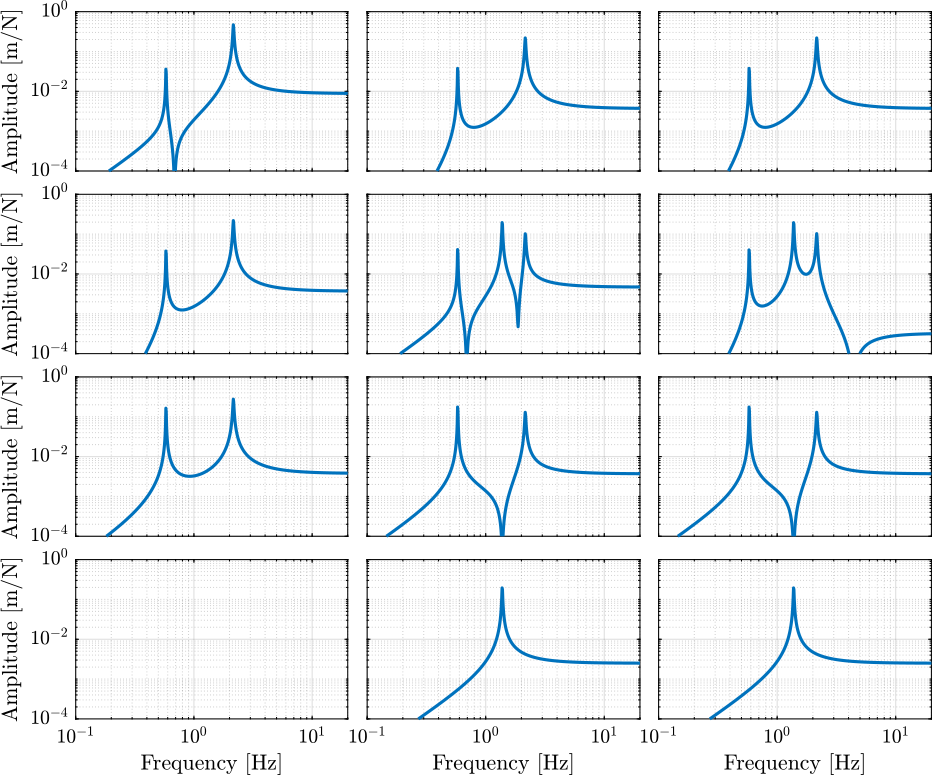
The bode plot of all elements of the plant are shown in Figure fig:open_loop_tf.

Open Loop Transfer Function from 3 Actuators to 4 Accelerometers

Decoupling using the Jacobian

<<sec:gravimeter_jacobian_decoupling>>

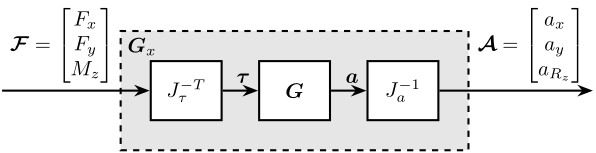
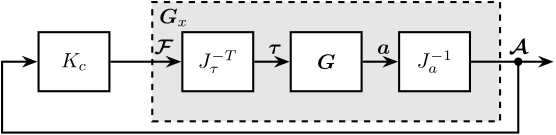
Consider the control architecture shown in Figure fig:gravimeter_decouple_jacobian.

The Jacobian matrix $J_{\tau}$ is used to transform forces applied by the three actuators into forces/torques applied on the gravimeter at its center of mass:

\begin{equation} \begin{bmatrix} \tau_1 \\ \tau_2 \\ \tau_3 \end{bmatrix} = J_{\tau}^{-T} \begin{bmatrix} F_x \\ F_y \\ M_z \end{bmatrix} \end{equation}

The Jacobian matrix $J_{a}$ is used to compute the vertical acceleration, horizontal acceleration and rotational acceleration of the mass with respect to its center of mass:

\begin{equation} \begin{bmatrix} a_x \\ a_y \\ a_{R_z} \end{bmatrix} = J_{a}^{-1} \begin{bmatrix} a_{x1} \\ a_{y1} \\ a_{x2} \\ a_{y2} \end{bmatrix} \end{equation}

We thus define a new plant as defined in Figure fig:gravimeter_decouple_jacobian. \[ \bm{G}_x(s) = J_a^{-1} \bm{G}(s) J_{\tau}^{-T} \]

$\bm{G}_x(s)$ correspond to the $3 \times 3$transfer function matrix from forces and torques applied to the gravimeter at its center of mass to the absolute acceleration of the gravimeter's center of mass (Figure fig:gravimeter_decouple_jacobian).

Decoupled plant $\bm{G}_x$ using the Jacobian matrix $J$

The Jacobian corresponding to the sensors and actuators are defined below:

  Ja = [1 0 -h/2
        0 1  l/2
        1 0  h/2
        0 1  0];

  Jt = [1 0 -ha
        0 1  la
        0 1 -la];

And the plant $\bm{G}_x$ is computed:

  Gx = pinv(Ja)*G*pinv(Jt');
  Gx.InputName  = {'Fx', 'Fy', 'Mz'};
  Gx.OutputName  = {'Dx', 'Dy', 'Rz'};

size(Gx)
State-space model with 3 outputs, 3 inputs, and 6 states.

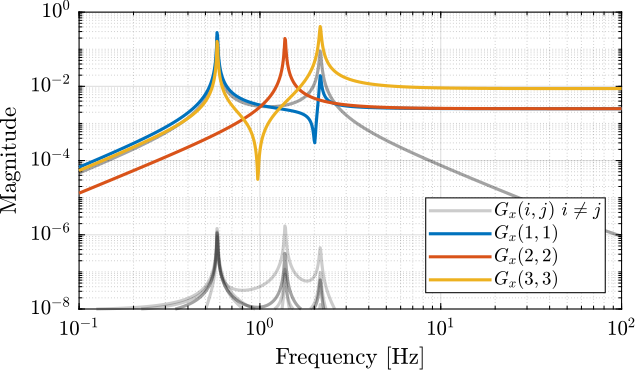
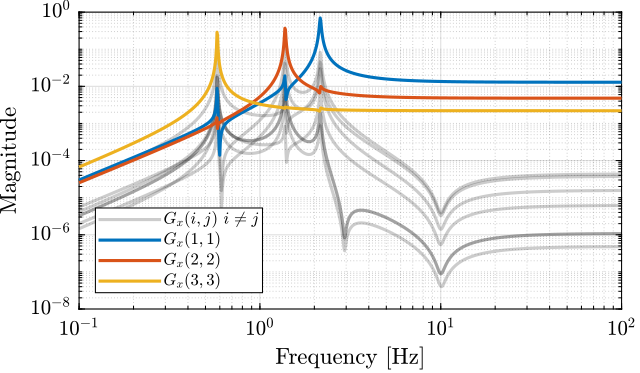
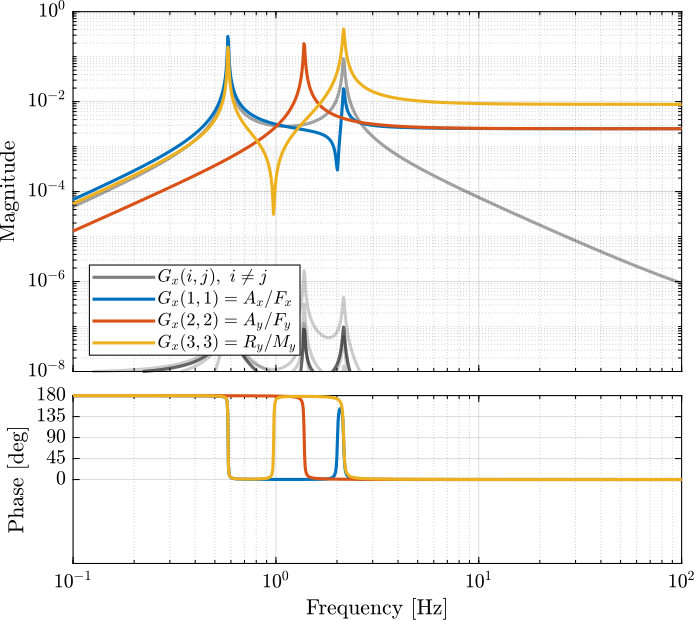
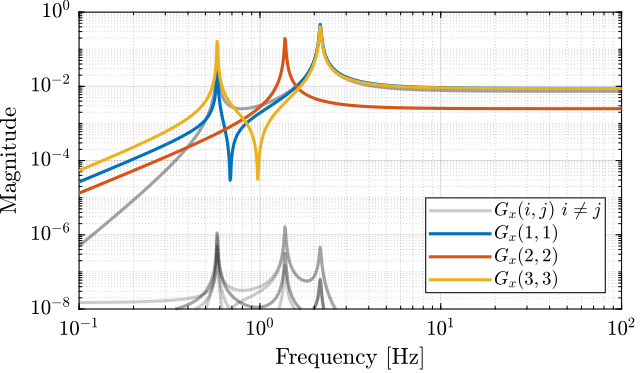
The diagonal and off-diagonal elements of $G_x$ are shown in Figure fig:gravimeter_jacobian_plant.

Diagonal and off-diagonal elements of $G_x$

Decoupling using the SVD

<<sec:gravimeter_svd_decoupling>>

In order to decouple the plant using the SVD, first a real approximation of the plant transfer function matrix as the crossover frequency is required.

Let's compute a real approximation of the complex matrix $H_1$ which corresponds to the the transfer function $G(j\omega_c)$ from forces applied by the actuators to the measured acceleration of the top platform evaluated at the frequency $\omega_c$.

  wc = 2*pi*10; % Decoupling frequency [rad/s]

  H1 = evalfr(G, j*wc);

The real approximation is computed as follows:

  D = pinv(real(H1'*H1));
  H1 = pinv(D*real(H1'*diag(exp(j*angle(diag(H1*D*H1.'))/2))));

0.0092	-0.0039	0.0039
-0.0039	0.0048	0.00028
-0.004	0.0038	-0.0038
8.4e-09	0.0025	0.0025

Real approximate of $G$ at the decoupling frequency $\omega_c$

Now, the Singular Value Decomposition of $H_1$ is performed: \[ H_1 = U \Sigma V^H \]

  [U,S,V] = svd(H1);

-0.78	0.26	-0.53	-0.2
0.4	0.61	-0.04	-0.68
0.48	-0.14	-0.85	0.2
0.03	0.73	0.06	0.68

$U$ matrix

-0.79	0.11	-0.6
0.51	0.67	-0.54
-0.35	0.73	0.59

$V$ matrix

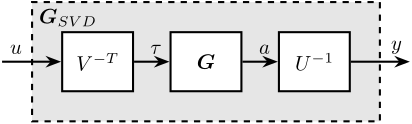
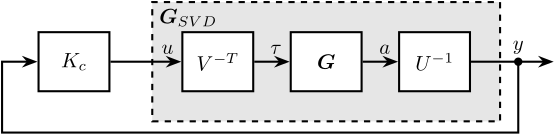
The obtained matrices $U$ and $V$ are used to decouple the system as shown in Figure fig:gravimeter_decouple_svd.

Decoupled plant $\bm{G}_{SVD}$ using the Singular Value Decomposition

The decoupled plant is then: \[ \bm{G}_{SVD}(s) = U^{-1} \bm{G}(s) V^{-H} \]

  Gsvd = inv(U)*G*inv(V');

size(Gsvd)
State-space model with 4 outputs, 3 inputs, and 6 states.

The 4th output (corresponding to the null singular value) is discarded, and we only keep the $3 \times 3$ plant:

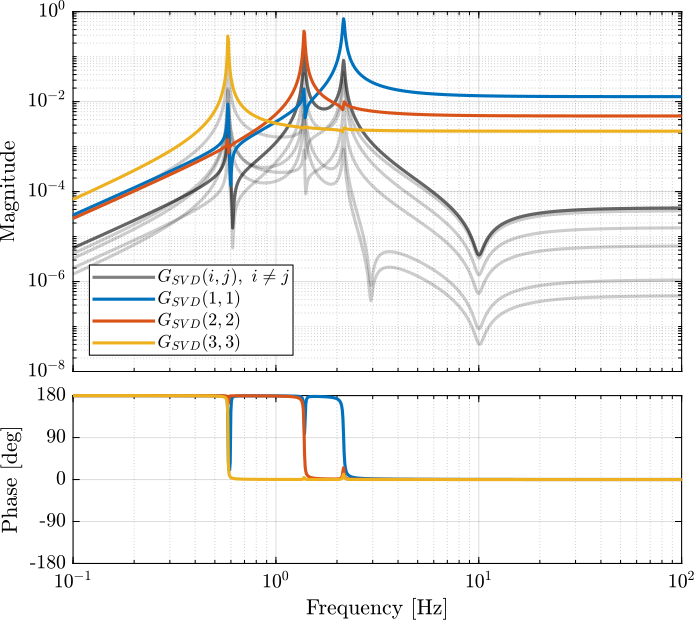
  Gsvd = Gsvd(1:3, 1:3);

The diagonal and off-diagonal elements of the "SVD" plant are shown in Figure fig:gravimeter_svd_plant.

Diagonal and off-diagonal elements of $G_{svd}$

Verification of the decoupling using the "Gershgorin Radii"

<<sec:gravimeter_gershgorin_radii>>

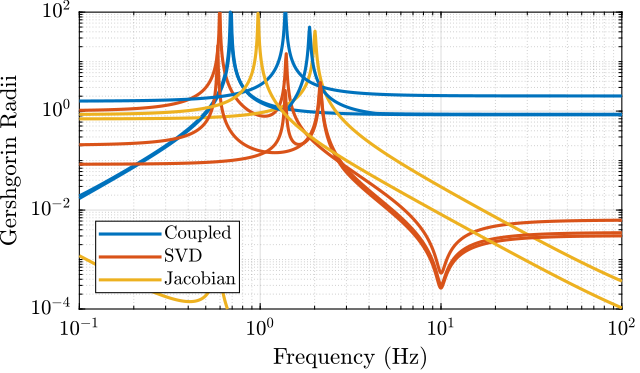
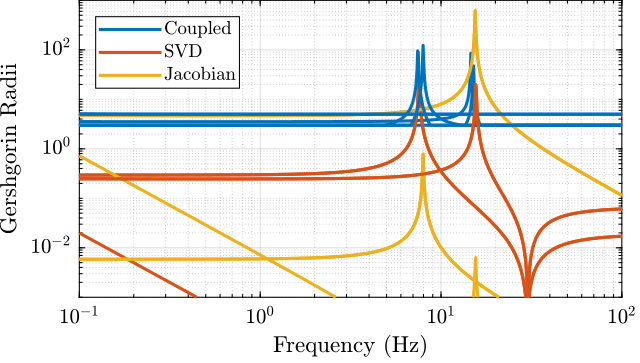
The "Gershgorin Radii" is computed for the coupled plant $G(s)$, for the "Jacobian plant" $G_x(s)$ and the "SVD Decoupled Plant" $G_{SVD}(s)$:

The "Gershgorin Radii" of a matrix $S$ is defined by: \[ \zeta_i(j\omega) = \frac{\sum\limits_{j\neq i}|S_{ij}(j\omega)|}{|S_{ii}(j\omega)|} \]

Gershgorin Radii of the Coupled and Decoupled plants

Verification of the decoupling using the "Relative Gain Array"

<<sec:gravimeter_rga>>

The relative gain array (RGA) is defined as:

\begin{equation} \Lambda\big(G(s)\big) = G(s) \times \big( G(s)^{-1} \big)^T \end{equation}

where $\times$ denotes an element by element multiplication and $G(s)$ is an $n \times n$ square transfer matrix.

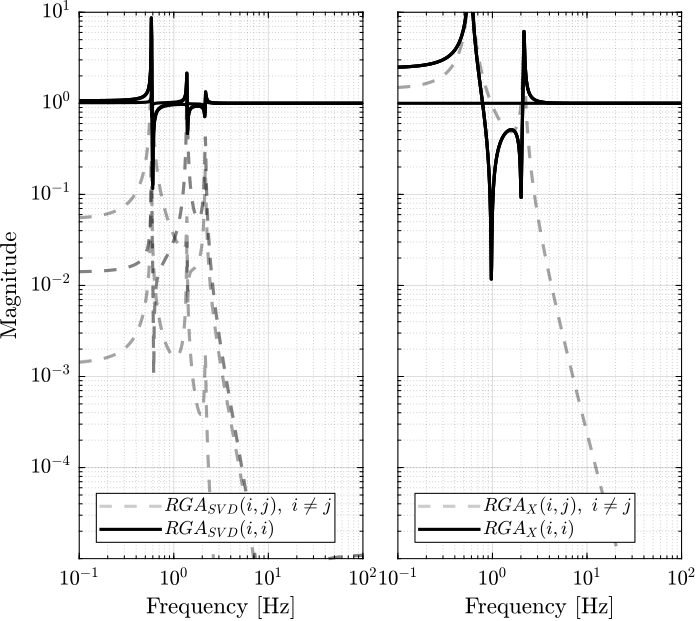
The obtained RGA elements are shown in Figure fig:gravimeter_rga.

Obtained norm of RGA elements for the SVD decoupled plant and the Jacobian decoupled plant

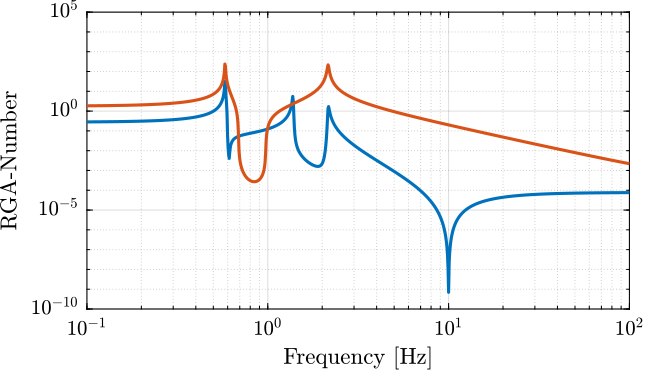
The RGA-number is also a measure of diagonal dominance:

\begin{equation} \text{RGA-number} = \| \Lambda(G) - I \|_\text{sum} \end{equation}

RGA-Number for the Gravimeter

Obtained Decoupled Plants

<<sec:gravimeter_decoupled_plant>>

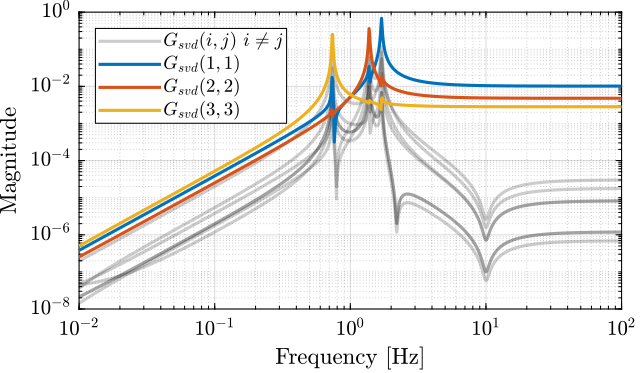
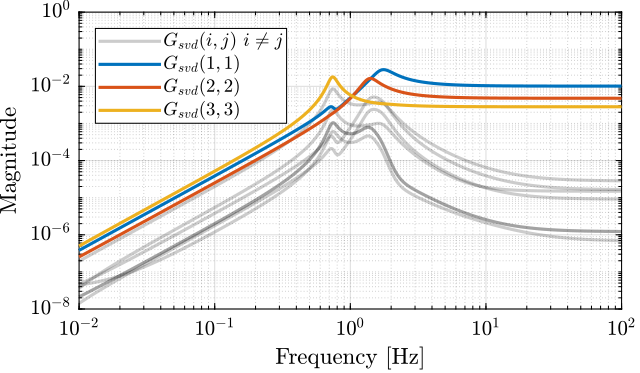
The bode plot of the diagonal and off-diagonal elements of $G_{SVD}$ are shown in Figure fig:gravimeter_decoupled_plant_svd.

Decoupled Plant using SVD

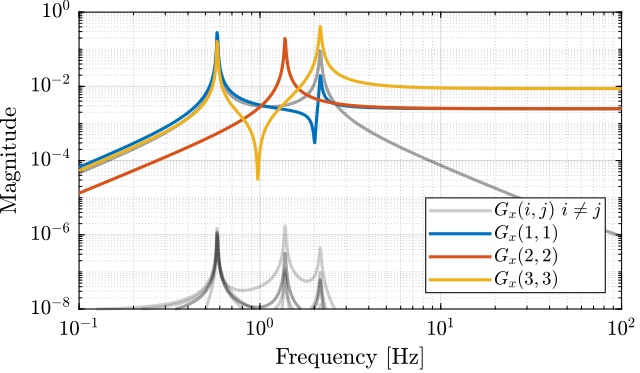
Similarly, the bode plots of the diagonal elements and off-diagonal elements of the decoupled plant $G_x(s)$ using the Jacobian are shown in Figure fig:gravimeter_decoupled_plant_jacobian.

Gravimeter Platform Plant from forces (resp. torques) applied by the legs to the acceleration (resp. angular acceleration) of the platform as well as all the coupling terms between the two (non-diagonal terms of the transfer function matrix)

Diagonal Controller

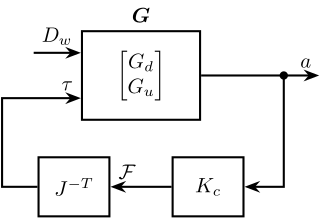
<<sec:gravimeter_diagonal_control>> The control diagram for the centralized control is shown in Figure fig:centralized_control_gravimeter.

The controller $K_c$ is "working" in an cartesian frame. The Jacobian is used to convert forces in the cartesian frame to forces applied by the actuators.

Control Diagram for the Centralized control

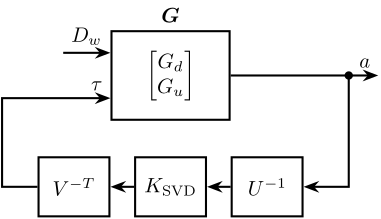
The SVD control architecture is shown in Figure fig:svd_control_gravimeter. The matrices $U$ and $V$ are used to decoupled the plant $G$.

Control Diagram for the SVD control

We choose the controller to be a low pass filter: \[ K_c(s) = \frac{G_0}{1 + \frac{s}{\omega_0}} \]

$G_0$ is tuned such that the crossover frequency corresponding to the diagonal terms of the loop gain is equal to $\omega_c$

  wc = 2*pi*10;  % Crossover Frequency [rad/s]
  w0 = 2*pi*0.1; % Controller Pole [rad/s]

  K_cen = diag(1./diag(abs(evalfr(Gx, j*wc))))*(1/abs(evalfr(1/(1 + s/w0), j*wc)))/(1 + s/w0);
  L_cen = K_cen*Gx;
  G_cen = feedback(G, pinv(Jt')*K_cen*pinv(Ja));

  K_svd = diag(1./diag(abs(evalfr(Gsvd, j*wc))))*(1/abs(evalfr(1/(1 + s/w0), j*wc)))/(1 + s/w0);
  L_svd = K_svd*Gsvd;
  U_inv = inv(U);
  G_svd = feedback(G, inv(V')*K_svd*U_inv(1:3, :));

The obtained diagonal elements of the loop gains are shown in Figure fig:gravimeter_comp_loop_gain_diagonal.

Comparison of the diagonal elements of the loop gains for the SVD control architecture and the Jacobian one

Closed-Loop system Performances

<<sec:gravimeter_closed_loop_results>>

Let's first verify the stability of the closed-loop systems:

  isstable(G_cen)

ans =
  logical
   1

  isstable(G_svd)

ans =
  logical
   1

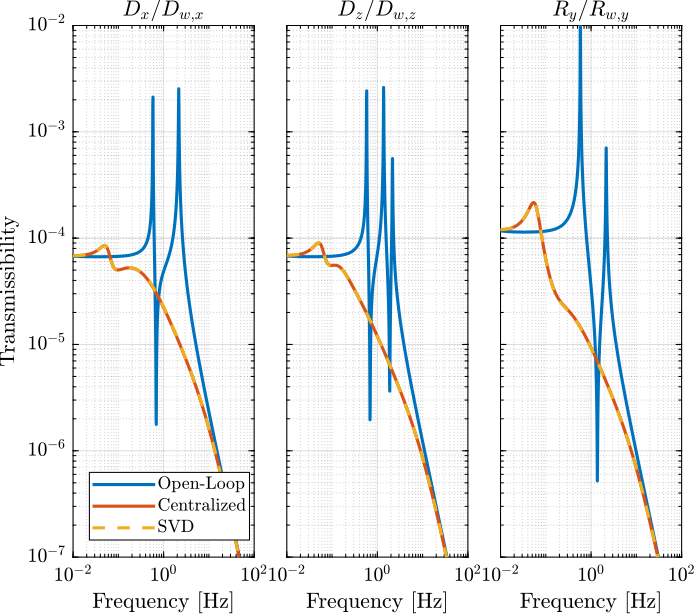
The obtained transmissibility in Open-loop, for the centralized control as well as for the SVD control are shown in Figure fig:gravimeter_platform_simscape_cl_transmissibility.

Obtained Transmissibility

Obtain coupling terms of the transmissibility matrix

Robustness to a change of actuator position

Let say we change the position of the actuators:

  la = l/2*0.7; % Position of Act. [m]
  ha = h/2*0.7; % Position of Act. [m]

The new plant is computed, and the centralized and SVD control architectures are applied using the previsouly computed Jacobian matrices and $U$ and $V$ matrices.

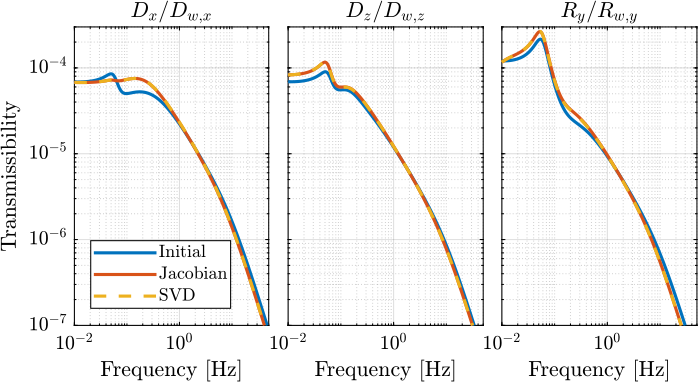
The closed-loop system are still stable, and their

Transmissibility for the initial CL system and when the position of actuators are changed

Combined / comparison of K and M decoupling

Introduction   ignore

If we want to decouple the system at low frequency (determined by the stiffness matrix), we have to compute the Jacobians at a point where the stiffness matrix is diagonal. A displacement (resp. rotation) of the mass at this particular point should induce a pure force (resp. torque) on the same point due to stiffnesses in the system. This can be verified by geometrical computations.

If we want to decouple the system at high frequency (determined by the mass matrix), we have tot compute the Jacobians at the Center of Mass of the suspended solid. Similarly to the stiffness analysis, when considering only the inertia effects (neglecting the stiffnesses), a force (resp. torque) applied at this point (the center of mass) should induce a pure acceleration (resp. angular acceleration).

Ideally, we would like to have a decoupled mass matrix and stiffness matrix at the same time. To do so, the actuators (springs) should be positioned such that the stiffness matrix is diagonal when evaluated at the CoM of the solid.

Decoupling of the mass matrix

Choice of {O} such that the Mass Matrix is Diagonal

  la = l/2; % Position of Act. [m]
  ha = h/2; % Position of Act. [m]

  %% Name of the Simulink File
  mdl = 'gravimeter';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/F1'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/F2'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/F3'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_side'], 1, 'openoutput'); io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_side'], 2, 'openoutput'); io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_top'], 1, 'openoutput'); io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_top'], 2, 'openoutput'); io_i = io_i + 1;

  G = linearize(mdl, io);
  G.InputName  = {'F1', 'F2', 'F3'};
  G.OutputName = {'Ax1', 'Ay1', 'Ax2', 'Ay2'};

Decoupling at the CoM (Mass decoupled)

  JMa = [1 0 -h/2
         0 1  l/2
         1 0  h/2
         0 1  0];

  JMt = [1 0 -ha
         0 1  la
         0 1 -la];

  GM = pinv(JMa)*G*pinv(JMt');
  GM.InputName  = {'Fx', 'Fy', 'Mz'};
  GM.OutputName  = {'Dx', 'Dy', 'Rz'};

Diagonal and off-diagonal elements of the decoupled plant

Decoupling of the stiffness matrix

Choice of {O} such that the Stiffness Matrix is Diagonal

Decoupling at the point where K is diagonal (x = 0, y = -h/2 from the schematic {O} frame):

  JKa = [1 0  0
         0 1 -l/2
         1 0 -h
         0 1  0];

  JKt = [1 0  0
         0 1 -la
         0 1  la];

And the plant $\bm{G}_x$ is computed:

  GK = pinv(JKa)*G*pinv(JKt');
  GK.InputName  = {'Fx', 'Fy', 'Mz'};
  GK.OutputName  = {'Dx', 'Dy', 'Rz'};

Diagonal and off-diagonal elements of the decoupled plant

Combined decoupling of the mass and stiffness matrices

Ideal location of the actuators such that both the mass and stiffness matrices are diagonal

To do so, the actuator position should be modified

  la = l/2; % Position of Act. [m]
  ha = 0; % Position of Act. [m]

  %% Name of the Simulink File
  mdl = 'gravimeter';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/F1'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/F2'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/F3'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_side'], 1, 'openoutput'); io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_side'], 2, 'openoutput'); io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_top'], 1, 'openoutput'); io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Acc_top'], 2, 'openoutput'); io_i = io_i + 1;

  G = linearize(mdl, io);
  G.InputName  = {'F1', 'F2', 'F3'};
  G.OutputName = {'Ax1', 'Ay1', 'Ax2', 'Ay2'};

  JMa = [1 0 -h/2
         0 1  l/2
         1 0  h/2
         0 1  0];

  JMt = [1 0 -ha
         0 1  la
         0 1 -la];

  GKM = pinv(JMa)*G*pinv(JMt');
  GKM.InputName  = {'Fx', 'Fy', 'Mz'};
  GKM.OutputName  = {'Dx', 'Dy', 'Rz'};

Diagonal and off-diagonal elements of the decoupled plant

Conclusion

Ideally, the mechanical system should be designed in order to have a decoupled stiffness matrix at the CoM of the solid.

If not the case, the system can either be decoupled as low frequency if the Jacobian are evaluated at a point where the stiffness matrix is decoupled. Or it can be decoupled at high frequency if the Jacobians are evaluated at the CoM.

SVD decoupling performances

As the SVD is applied on a real approximation of the plant dynamics at a frequency $\omega_0$, it is foreseen that the effectiveness of the decoupling depends on the validity of the real approximation.

Let's do the SVD decoupling on a plant that is mostly real (low damping) and one with a large imaginary part (larger damping).

Start with small damping, the obtained diagonal and off-diagonal terms are shown in Figure fig:gravimeter_svd_low_damping.

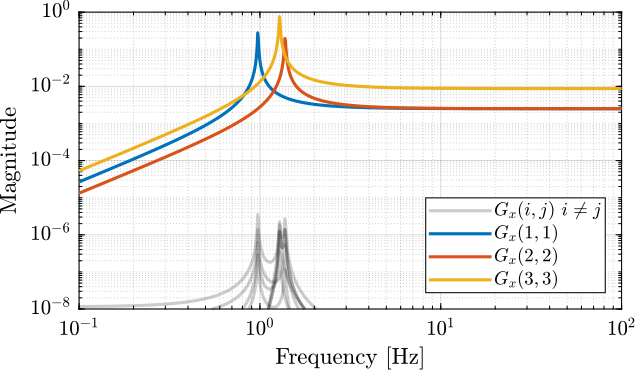
  c = 2e1; % Actuator Damping [N/(m/s)]

Diagonal and off-diagonal term when decoupling with SVD on the gravimeter with small damping

Now take a larger damping, the obtained diagonal and off-diagonal terms are shown in Figure fig:gravimeter_svd_high_damping.

  c = 5e2; % Actuator Damping [N/(m/s)]

Diagonal and off-diagonal term when decoupling with SVD on the gravimeter with high damping

Stewart Platform - Simscape Model

<<sec:stewart_platform>>

Introduction   ignore

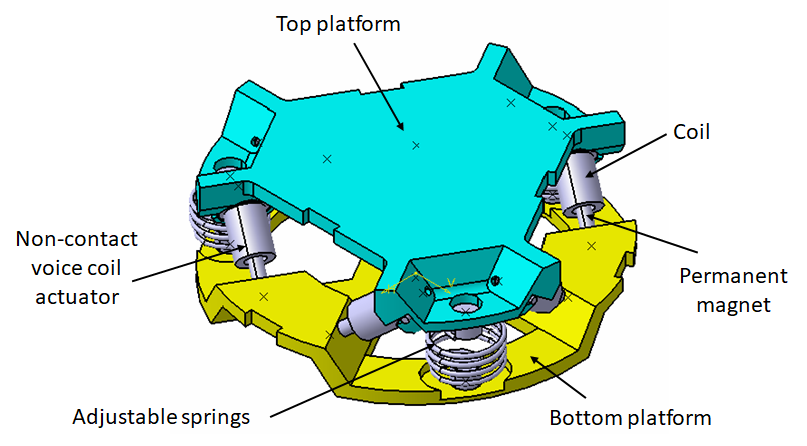
In this analysis, we wish to applied SVD control to the Stewart Platform shown in Figure fig:SP_assembly.

Some notes about the system:

• 6 voice coils actuators are used to control the motion of the top platform.
• the motion of the top platform is measured with a 6-axis inertial unit (3 acceleration + 3 angular accelerations)
• the control objective is to isolate the top platform from vibrations coming from the bottom platform

Stewart Platform CAD View

The analysis of the SVD/Jacobian control applied to the Stewart platform is performed in the following sections:

• Section sec:stewart_simscape: The parameters of the Simscape model of the Stewart platform are defined
• Section sec:stewart_identification: The plant is identified from the Simscape model and the system coupling is shown
• Section sec:stewart_jacobian_decoupling: The plant is first decoupled using the Jacobian
• Section sec:stewart_svd_decoupling: The decoupling is performed thanks to the SVD. To do so a real approximation of the plant is computed.
• Section sec:stewart_gershorin_radii: The effectiveness of the decoupling with the Jacobian and SVD are compared using the Gershorin Radii
• Section sec:stewart_rga:
• Section sec:stewart_decoupled_plant: The dynamics of the decoupled plants are shown
• Section sec:stewart_diagonal_control: A diagonal controller is defined to control the decoupled plant
• Section sec:stewart_closed_loop_results: Finally, the closed loop system properties are studied

Simscape Model - Parameters

<<sec:stewart_simscape>>

  open('drone_platform.slx');

Definition of spring parameters:

  kx = 0.5*1e3/3; % [N/m]
  ky = 0.5*1e3/3;
  kz = 1e3/3;

  cx = 0.025; % [Nm/rad]
  cy = 0.025;
  cz = 0.025;

We suppose the sensor is perfectly positioned.

  sens_pos_error = zeros(3,1);

Gravity:

  g = 0;

We load the Jacobian (previously computed from the geometry):

  load('jacobian.mat', 'Aa', 'Ab', 'As', 'l', 'J');

We initialize other parameters:

  U = eye(6);
  V = eye(6);
  Kc = tf(zeros(6));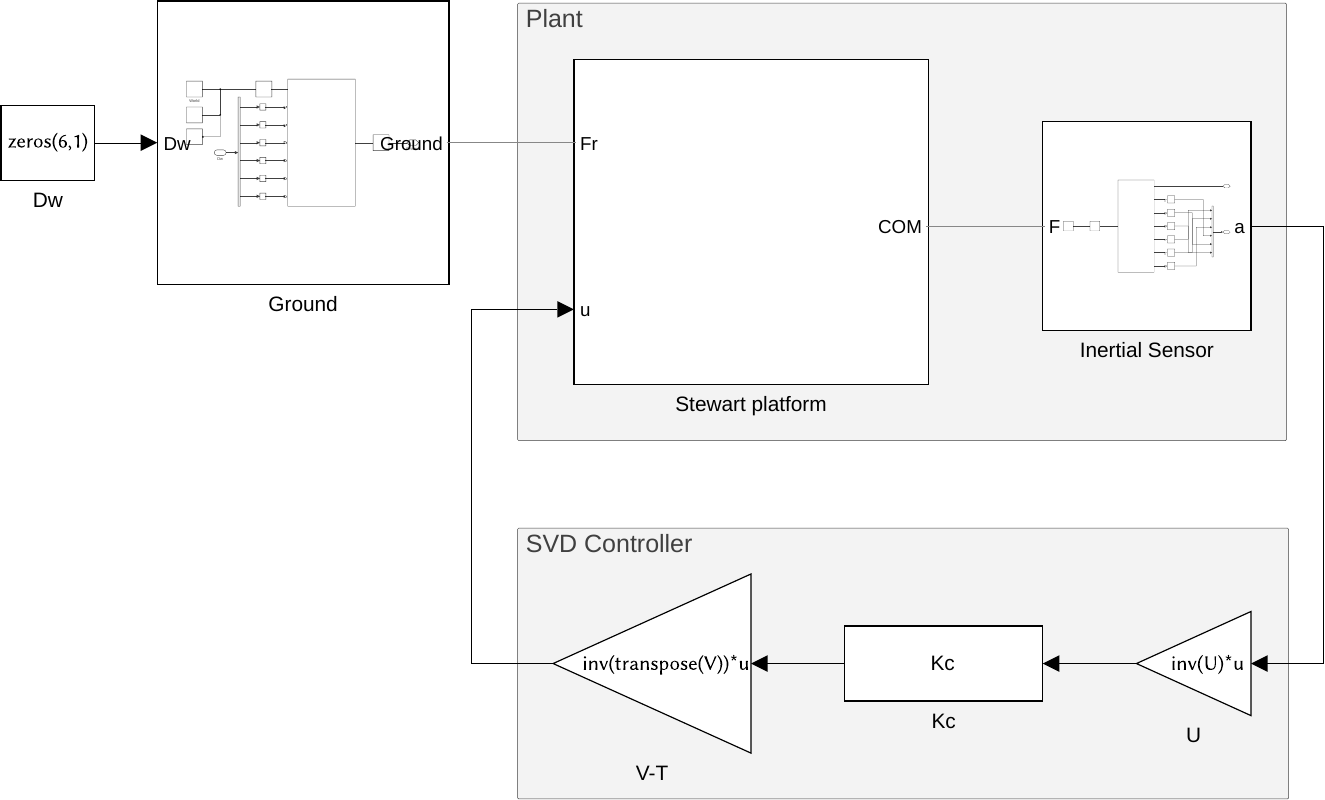

General view of the Simscape Model

Simscape model of the Stewart platform

Identification of the plant

<<sec:stewart_identification>>

The plant shown in Figure fig:stewart_platform_plant is identified from the Simscape model.

The inputs are:

• $D_w$ translation and rotation of the bottom platform (with respect to the center of mass of the top platform)
• $\tau$ the 6 forces applied by the voice coils

The outputs are the 6 accelerations measured by the inertial unit.

Considered plant $\bm{G} = \begin{bmatrix}G_d\\G_u\end{bmatrix}$. $D_w$ is the translation/rotation of the support, $\tau$ the actuator forces, $a$ the acceleration/angular acceleration of the top platform

  %% Name of the Simulink File
  mdl = 'drone_platform';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/Dw'],              1, 'openinput');  io_i = io_i + 1; % Ground Motion
  io(io_i) = linio([mdl, '/V-T'],             1, 'openinput');  io_i = io_i + 1; % Actuator Forces
  io(io_i) = linio([mdl, '/Inertial Sensor'], 1, 'openoutput'); io_i = io_i + 1; % Top platform acceleration

  G = linearize(mdl, io);
  G.InputName  = {'Dwx', 'Dwy', 'Dwz', 'Rwx', 'Rwy', 'Rwz', ...
                  'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};
  G.OutputName = {'Ax', 'Ay', 'Az', 'Arx', 'Ary', 'Arz'};

  % Plant
  Gu = G(:, {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'});
  % Disturbance dynamics
  Gd = G(:, {'Dwx', 'Dwy', 'Dwz', 'Rwx', 'Rwy', 'Rwz'});

There are 24 states (6dof for the bottom platform + 6dof for the top platform).

  size(G)

State-space model with 6 outputs, 12 inputs, and 24 states.

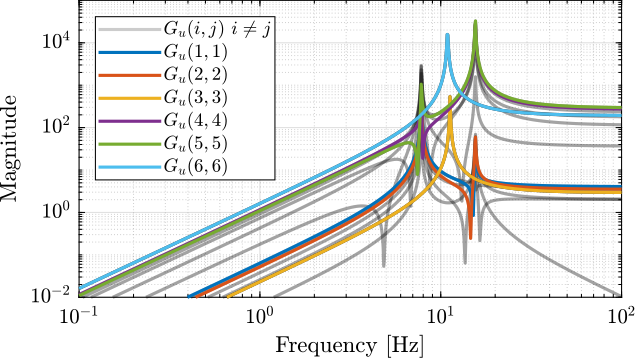
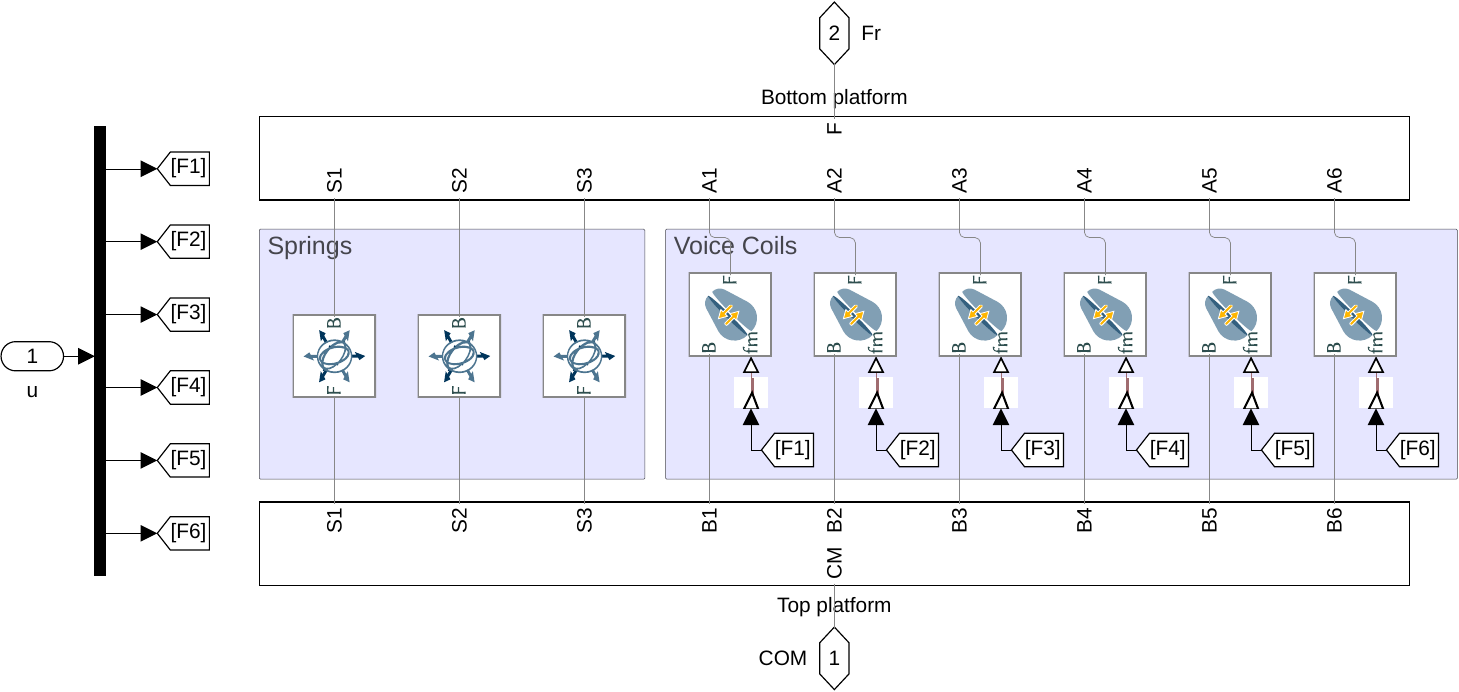
The elements of the transfer matrix $\bm{G}$ corresponding to the transfer function from actuator forces $\tau$ to the measured acceleration $a$ are shown in Figure fig:stewart_platform_coupled_plant.

One can easily see that the system is strongly coupled.

Magnitude of all 36 elements of the transfer function matrix $G_u$

Decoupling using the Jacobian

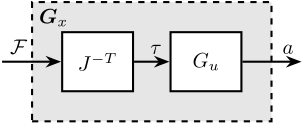
<<sec:stewart_jacobian_decoupling>> Consider the control architecture shown in Figure fig:plant_decouple_jacobian. The Jacobian matrix is used to transform forces/torques applied on the top platform to the equivalent forces applied by each actuator.

The Jacobian matrix is computed from the geometry of the platform (position and orientation of the actuators).

0.811	0.0	0.584	-0.018	-0.008	0.025
-0.406	-0.703	0.584	-0.016	-0.012	-0.025
-0.406	0.703	0.584	0.016	-0.012	0.025
0.811	0.0	0.584	0.018	-0.008	-0.025
-0.406	-0.703	0.584	0.002	0.019	0.025
-0.406	0.703	0.584	-0.002	0.019	-0.025

Computed Jacobian Matrix

Decoupled plant $\bm{G}_x$ using the Jacobian matrix $J$

We define a new plant: \[ G_x(s) = G(s) J^{-T} \]

$G_x(s)$ correspond to the transfer function from forces and torques applied to the top platform to the absolute acceleration of the top platform.

  Gx = Gu*inv(J');
  Gx.InputName  = {'Fx', 'Fy', 'Fz', 'Mx', 'My', 'Mz'};

Decoupling using the SVD

<<sec:stewart_svd_decoupling>>

In order to decouple the plant using the SVD, first a real approximation of the plant transfer function matrix as the crossover frequency is required.

Let's compute a real approximation of the complex matrix $H_1$ which corresponds to the the transfer function $G_u(j\omega_c)$ from forces applied by the actuators to the measured acceleration of the top platform evaluated at the frequency $\omega_c$.

  wc = 2*pi*30; % Decoupling frequency [rad/s]

  H1 = evalfr(Gu, j*wc);

The real approximation is computed as follows:

  D = pinv(real(H1'*H1));
  H1 = inv(D*real(H1'*diag(exp(j*angle(diag(H1*D*H1.'))/2))));

4.4	-2.1	-2.1	4.4	-2.4	-2.4
-0.2	-3.9	3.9	0.2	-3.8	3.8
3.4	3.4	3.4	3.4	3.4	3.4
-367.1	-323.8	323.8	367.1	43.3	-43.3
-162.0	-237.0	-237.0	-162.0	398.9	398.9
220.6	-220.6	220.6	-220.6	220.6	-220.6

Real approximate of $G$ at the decoupling frequency $\omega_c$

Note that the plant $G_u$ at $\omega_c$ is already an almost real matrix. This can be seen on the Bode plots where the phase is close to 1. This can be verified below where only the real value of $G_u(\omega_c)$ is shown

4.4	-2.1	-2.1	4.4	-2.4	-2.4
-0.2	-3.9	3.9	0.2	-3.8	3.8
3.4	3.4	3.4	3.4	3.4	3.4
-367.1	-323.8	323.8	367.1	43.3	-43.3
-162.0	-237.0	-237.0	-162.0	398.9	398.9
220.6	-220.6	220.6	-220.6	220.6	-220.6

Real part of $G$ at the decoupling frequency $\omega_c$

Now, the Singular Value Decomposition of $H_1$ is performed: \[ H_1 = U \Sigma V^H \]

  [U,~,V] = svd(H1);

-0.005	7e-06	6e-11	-3e-06	-1	0.1
-7e-06	-0.005	-9e-09	-5e-09	-0.1	-1
4e-08	-2e-10	-6e-11	-1	3e-06	-3e-07
-0.002	-1	-5e-06	2e-10	0.0006	0.005
1	-0.002	-1e-08	2e-08	-0.005	0.0006
-4e-09	5e-06	-1	6e-11	-2e-09	-1e-08

Obtained matrix $U$

-0.2	0.5	-0.4	-0.4	-0.6	-0.2
-0.3	0.5	0.4	-0.4	0.5	0.3
-0.3	-0.5	-0.4	-0.4	0.4	-0.4
-0.2	-0.5	0.4	-0.4	-0.5	0.3
0.6	-0.06	-0.4	-0.4	0.1	0.6
0.6	0.06	0.4	-0.4	-0.006	-0.6

Obtained matrix $V$

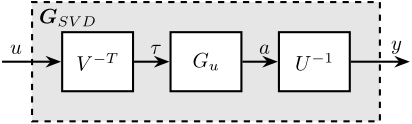
The obtained matrices $U$ and $V$ are used to decouple the system as shown in Figure fig:plant_decouple_svd.

Decoupled plant $\bm{G}_{SVD}$ using the Singular Value Decomposition

The decoupled plant is then: \[ G_{SVD}(s) = U^{-1} G_u(s) V^{-H} \]

  Gsvd = inv(U)*Gu*inv(V');

Verification of the decoupling using the "Gershgorin Radii"

<<sec:stewart_gershorin_radii>>

The "Gershgorin Radii" is computed for the coupled plant $G(s)$, for the "Jacobian plant" $G_x(s)$ and the "SVD Decoupled Plant" $G_{SVD}(s)$:

The "Gershgorin Radii" of a matrix $S$ is defined by: \[ \zeta_i(j\omega) = \frac{\sum\limits_{j\neq i}|S_{ij}(j\omega)|}{|S_{ii}(j\omega)|} \]

This is computed over the following frequencies.

Gershgorin Radii of the Coupled and Decoupled plants

Verification of the decoupling using the "Relative Gain Array"

<<sec:stewart_rga>>

The relative gain array (RGA) is defined as:

\begin{equation} \Lambda\big(G(s)\big) = G(s) \times \big( G(s)^{-1} \big)^T \end{equation}

where $\times$ denotes an element by element multiplication and $G(s)$ is an $n \times n$ square transfer matrix.

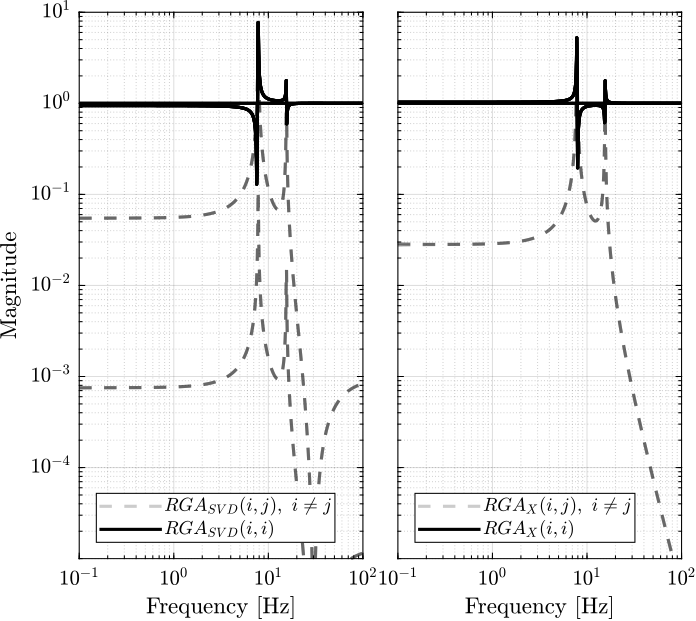
The obtained RGA elements are shown in Figure fig:simscape_model_rga.

Obtained norm of RGA elements for the SVD decoupled plant and the Jacobian decoupled plant

Obtained Decoupled Plants

<<sec:stewart_decoupled_plant>>

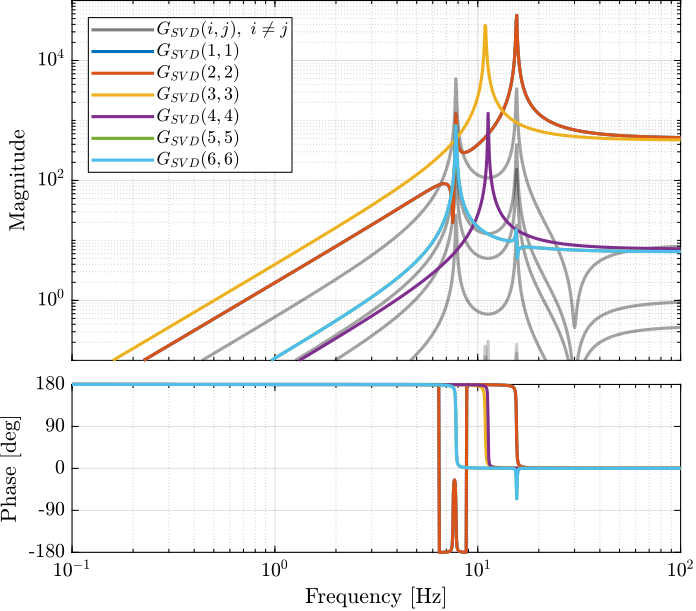
The bode plot of the diagonal and off-diagonal elements of $G_{SVD}$ are shown in Figure fig:simscape_model_decoupled_plant_svd.

Decoupled Plant using SVD

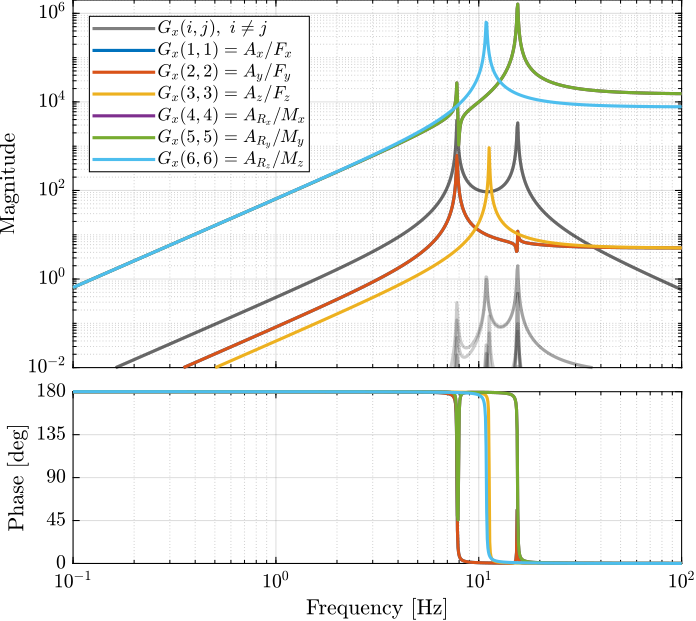
Similarly, the bode plots of the diagonal elements and off-diagonal elements of the decoupled plant $G_x(s)$ using the Jacobian are shown in Figure fig:simscape_model_decoupled_plant_jacobian.

Stewart Platform Plant from forces (resp. torques) applied by the legs to the acceleration (resp. angular acceleration) of the platform as well as all the coupling terms between the two (non-diagonal terms of the transfer function matrix)

Diagonal Controller

<<sec:stewart_diagonal_control>> The control diagram for the centralized control is shown in Figure fig:centralized_control.

The controller $K_c$ is "working" in an cartesian frame. The Jacobian is used to convert forces in the cartesian frame to forces applied by the actuators.

Control Diagram for the Centralized control

The SVD control architecture is shown in Figure fig:svd_control. The matrices $U$ and $V$ are used to decoupled the plant $G$.

Control Diagram for the SVD control

We choose the controller to be a low pass filter: \[ K_c(s) = \frac{G_0}{1 + \frac{s}{\omega_0}} \]

$G_0$ is tuned such that the crossover frequency corresponding to the diagonal terms of the loop gain is equal to $\omega_c$

  wc = 2*pi*80;  % Crossover Frequency [rad/s]
  w0 = 2*pi*0.1; % Controller Pole [rad/s]

  K_cen = diag(1./diag(abs(evalfr(Gx, j*wc))))*(1/abs(evalfr(1/(1 + s/w0), j*wc)))/(1 + s/w0);
  L_cen = K_cen*Gx;
  G_cen = feedback(G, pinv(J')*K_cen, [7:12], [1:6]);

  K_svd = diag(1./diag(abs(evalfr(Gsvd, j*wc))))*(1/abs(evalfr(1/(1 + s/w0), j*wc)))/(1 + s/w0);
  L_svd = K_svd*Gsvd;
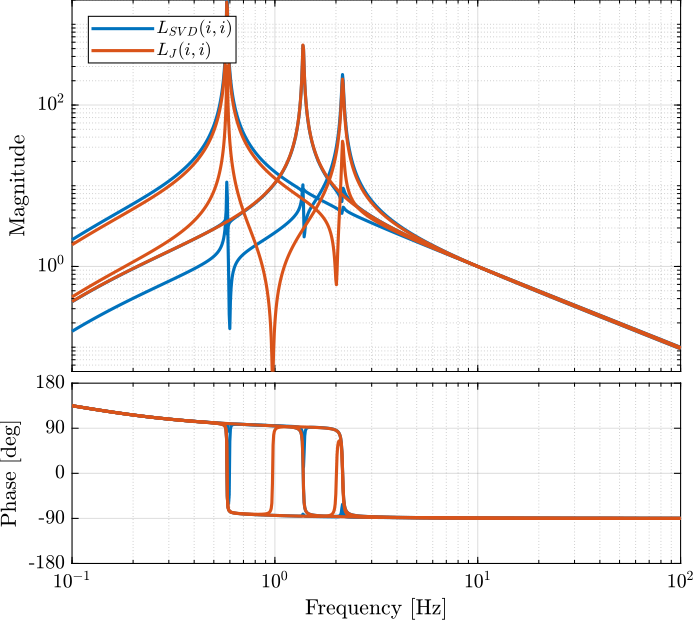
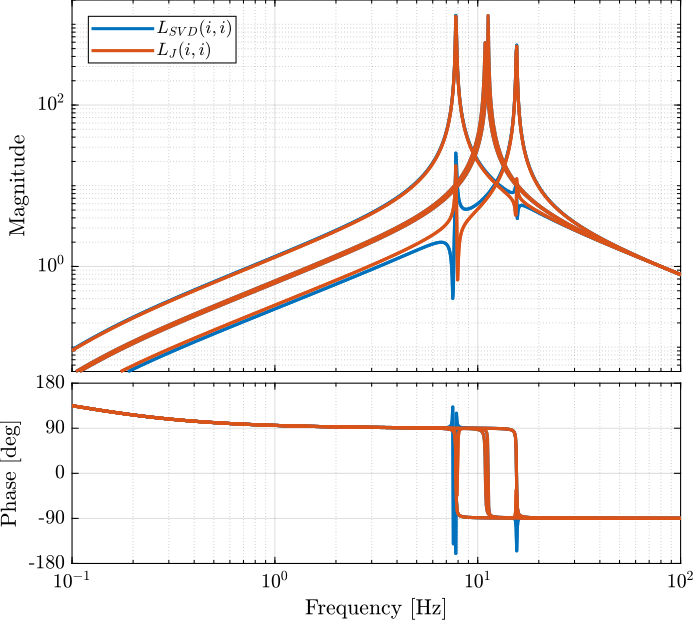
  G_svd = feedback(G, inv(V')*K_svd*inv(U), [7:12], [1:6]);

The obtained diagonal elements of the loop gains are shown in Figure fig:stewart_comp_loop_gain_diagonal.

Comparison of the diagonal elements of the loop gains for the SVD control architecture and the Jacobian one

Closed-Loop system Performances

<<sec:stewart_closed_loop_results>>

Let's first verify the stability of the closed-loop systems:

  isstable(G_cen)

ans =
  logical
   1

  isstable(G_svd)

ans =
  logical
   1

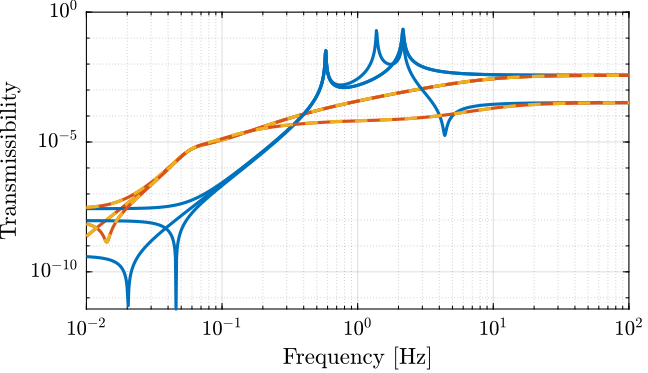
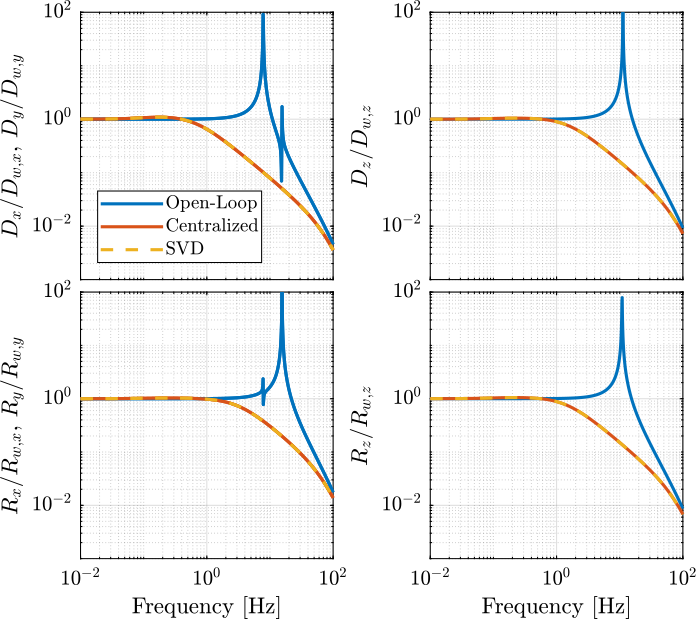
The obtained transmissibility in Open-loop, for the centralized control as well as for the SVD control are shown in Figure fig:stewart_platform_simscape_cl_transmissibility.

Obtained Transmissibility