tdehaeze/stewart-simscape
1
0
Fork 0
Code Issues Pull Requests Releases Wiki Activity
4d47a51d9f
stewart-simscape/simscape-model.org

24 KiB
Raw Blame History

Stewart Platform - Simscape Model

Introduction   ignore

Stewart platforms are generated in multiple steps.

We define 4 important frames:

  • $\{F\}$: Frame fixed to the Fixed base and located at the center of its bottom surface. This is used to fix the Stewart platform to some support.
  • $\{M\}$: Frame fixed to the Moving platform and located at the center of its top surface. This is used to place things on top of the Stewart platform.
  • $\{A\}$: Frame fixed to the fixed base. It defined the center of rotation of the moving platform.
  • $\{B\}$: Frame fixed to the moving platform. The motion of the moving platforms and forces applied to it are defined with respect to this frame $\{B\}$.

Then, we define the location of the spherical joints:

  • $\bm{a}_{i}$ are the position of the spherical joints fixed to the fixed base
  • $\bm{b}_{i}$ are the position of the spherical joints fixed to the moving platform

We define the rest position of the Stewart platform:

  • For simplicity, we suppose that the fixed base and the moving platform are parallel and aligned with the vertical axis at their rest position.
  • Thus, to define the rest position of the Stewart platform, we just have to defined its total height $H$. $H$ corresponds to the distance from the bottom of the fixed base to the top of the moving platform.

From $\bm{a}_{i}$ and $\bm{b}_{i}$, we can determine the length and orientation of each strut:

  • $l_{i}$ is the length of the strut
  • ${}^{A}\hat{\bm{s}}_{i}$ is the unit vector align with the strut

The position of the Spherical joints can be done using various methods:

  • Cubic configuration
  • Geometrical
  • Definition them by hand
  • These methods should be easily scriptable and corresponds to specific functions that returns ${}^{F}\bm{a}_{i}$ and ${}^{M}\bm{b}_{i}$. The input of these functions are the parameters corresponding to the wanted geometry. We need also to know the height of the platform.

For Simscape, we need:

  • The position of the frame $\{A\}$ with respect to the frame $\{F\}$: ${}^{F}\bm{O}_{A}$
  • The position of the frame $\{B\}$ with respect to the frame $\{M\}$: ${}^{M}\bm{O}_{B}$
  • The position and orientation of each spherical joint fixed to the fixed base: ${}^{F}\bm{a}_{i}$ and ${}^{F}\bm{R}_{a_{i}}$
  • The position and orientation of each spherical joint fixed to the moving platform: ${}^{M}\bm{b}_{i}$ and ${}^{M}\bm{R}_{b_{i}}$
  • The rest length of each strut: $l_{i}$
  • The stiffness and damping of each actuator: $k_{i}$ and $c_{i}$

Procedure

The procedure is the following:

  1. Choose $H$
  2. Choose ${}^{F}\bm{O}_{A}$ and ${}^{M}\bm{O}_{B}$
  3. Choose $\bm{a}_{i}$ and $\bm{b}_{i}$, probably by specifying ${}^{F}\bm{a}_{i}$ and ${}^{M}\bm{b}_{i}$
  4. Choose $k_{i}$ and $c_{i}$

Matlab Code

Simscape Model 

  open('stewart_platform.slx')

Define the Height of the Platform 

  %% 1. Height of the platform. Location of {F} and {M}
  H = 90e-3; % [m]
  FO_M = [0; 0; H];

Define the location of {A} and {B} 

  %% 2. Location of {A} and {B}
  FO_A = [0; 0; 100e-3] + FO_M;% [m,m,m]
  MO_B = [0; 0; 100e-3];% [m,m,m]

Define the position of $a_{i}$ and $b_{i}$ 

  %% 3. Position of ai and bi
  Fa = zeros(3, 6); % Fa_i is the i'th vector of Fa
  Mb = zeros(3, 6); % Mb_i is the i'th vector of Mb
  Aa = Fa - repmat(FO_A, [1, 6]);
  Bb = Mb - repmat(MO_B, [1, 6]);

  Ab = Bb - repmat(-MO_B-FO_M+FO_A, [1, 6]);
  Ba = Aa - repmat( MO_B+FO_M-FO_A, [1, 6]);

  As = (Ab - Aa)./vecnorm(Ab - Aa); % As_i is the i'th vector of As
  l = vecnorm(Ab - Aa);

  Bs = (Bb - Ba)./vecnorm(Bb - Ba);

  FRa = zeros(3,3,6);
  MRb = zeros(3,3,6);

  for i = 1:6
    FRa(:,:,i) = [cross([0;1;0],As(:,i)) , cross(As(:,i), cross([0;1;0], As(:,i))) , As(:,i)];
    FRa(:,:,i) = FRa(:,:,i)./vecnorm(FRa(:,:,i));

    MRb(:,:,i) = [cross([0;1;0],Bs(:,i)) , cross(Bs(:,i), cross([0;1;0], Bs(:,i))) , Bs(:,i)];
    MRb(:,:,i) = MRb(:,:,i)./vecnorm(MRb(:,:,i));
  end

Define the dynamical properties of each strut 

  %% 4. Stiffness and Damping of each strut
  Ki = 1e6*ones(6,1);
  Ci = 1e2*ones(6,1);

Old Introduction   ignore

First, geometrical parameters are defined:

  • ${}^A\bm{a}_i$ - Position of the joints fixed to the fixed base w.r.t $\{A\}$
  • ${}^A\bm{b}_i$ - Position of the joints fixed to the mobile platform w.r.t $\{A\}$
  • ${}^B\bm{b}_i$ - Position of the joints fixed to the mobile platform w.r.t $\{B\}$
  • $H$ - Total height of the mobile platform

These parameter are enough to determine all the kinematic properties of the platform like the Jacobian, stroke, stiffness, … These geometrical parameters can be generated using different functions: initializeCubicConfiguration for cubic configuration or initializeGeneralConfiguration for more general configuration.

A function computeGeometricalProperties is then used to compute:

  • $\bm{J}_f$ - Jacobian matrix for the force location
  • $\bm{J}_d$ - Jacobian matrix for displacement estimation
  • $\bm{R}_m$ - Rotation matrices to position the leg vectors

Then, geometrical parameters are computed for all the mechanical elements with the function initializeMechanicalElements:

  • Shape of the platforms

    • External Radius
    • Internal Radius
    • Density
    • Thickness

  • Shape of the Legs

    • Radius
    • Size of ball joint
    • Density

Other Parameters are defined for the Simscape simulation:

  • Sample mass, volume and position (initializeSample function)
  • Location of the inertial sensor
  • Location of the point for the differential measurements
  • Location of the Jacobian point for velocity/displacement computation

Cubic Configuration

To define the cubic configuration, we need to define 4 parameters:

  • The size of the cube
  • The location of the cube
  • The position of the plane joint the points $a_{i}$
  • The position of the plane joint the points $b_{i}$

To do so, we specify the following parameters:

  • $H_{C}$ the height of the useful part of the cube
  • ${}^{F}O_{C}$ the position of the center of the cube with respect to $\{F\}$
  • ${}^{F}H_{A}$: the height of the plane joining the points $a_{i}$ with respect to the frame $\{F\}$
  • ${}^{M}H_{B}$: the height of the plane joining the points $b_{i}$ with respect to the frame $\{B\}$

We define the parameters

  Hc = 60e-3; % [m]
  FOc = 50e-3; % [m]
  FHa = 15e-3; % [m]
  MHb = 15e-3; % [m]

We define the useful points of the cube with respect to the Cube's center. ${}^{C}C$ are the 6 vertices of the cubes expressed in a frame {C} which is located at the center of the cube and aligned with {F} and {M}.

  sx = [ 2; -1; -1];
  sy = [ 0;  1; -1];
  sz = [ 1;  1;  1];

  R = [sx, sy, sz]./vecnorm([sx, sy, sz]);

  L = Hc*sqrt(3);

  Cc = R'*[[0;0;L],[L;0;L],[L;0;0],[L;L;0],[0;L;0],[0;L;L]] - [0;0;1.5*Hc];

  CCf = [Cc(:,1), Cc(:,3), Cc(:,3), Cc(:,5), Cc(:,5), Cc(:,1)]; % CCf(:,i) corresponds to the bottom cube's vertice corresponding to the i'th leg
  CCm = [Cc(:,2), Cc(:,2), Cc(:,4), Cc(:,4), Cc(:,6), Cc(:,6)]; % CCm(:,i) corresponds to the top cube's vertice corresponding to the i'th leg

We can compute the vector of each leg ${}^{C}\hat{\bm{s}}_{i}$ (unit vector from ${}^{C}C_{f}$ to ${}^{C}C_{m}$).

  CSi = (CCm - CCf)./vecnorm(CCm - CCf);

We now which to compute the position of the joints $a_{i}$ and $b_{i}$.

  Fa = zeros(3, 6); % Fa_i is the i'th vector of Fa
  Mb = zeros(3, 6); % Mb_i is the i'th vector of Mb
  Fa = CCf + [0; 0; FOc] + ((FHa-(FOc-Hc/2))./CSi(3,:)).*CSi;
  Mb = CCf + [0; 0; FOc-H] + ((H-MHb-(FOc-Hc/2))./CSi(3,:)).*CSi; % TODO

initializeCubicConfiguration

<<sec:initializeCubicConfiguration>>

Function description 

  function [stewart] = initializeCubicConfiguration(opts_param)

Optional Parameters

Default values for opts.

  opts = struct(...
      'H_tot', 90,  ... % Total height of the Hexapod [mm]
      'L',     110, ... % Size of the Cube [mm]
      'H',     40,  ... % Height between base joints and platform joints [mm]
      'H0',    75   ... % Height between the corner of the cube and the plane containing the base joints [mm]
      );

Populate opts with input parameters

  if exist('opts_param','var')
      for opt = fieldnames(opts_param)'
          opts.(opt{1}) = opts_param.(opt{1});
      end
  end

Cube Creation 

  points = [0, 0, 0; ...
            0, 0, 1; ...
            0, 1, 0; ...
            0, 1, 1; ...
            1, 0, 0; ...
            1, 0, 1; ...
            1, 1, 0; ...
            1, 1, 1];
  points = opts.L*points;

We create the rotation matrix to rotate the cube

  sx = cross([1, 1, 1], [1 0 0]);
  sx = sx/norm(sx);

  sy = -cross(sx, [1, 1, 1]);
  sy = sy/norm(sy);

  sz = [1, 1, 1];
  sz = sz/norm(sz);

  R = [sx', sy', sz']';

We use to rotation matrix to rotate the cube

  cube = zeros(size(points));
  for i = 1:size(points, 1)
    cube(i, :) = R * points(i, :)';
  end

Vectors of each leg 

  leg_indices = [3, 4; ...
                 2, 4; ...
                 2, 6; ...
                 5, 6; ...
                 5, 7; ...
                 3, 7];

Vectors are:

  legs = zeros(6, 3);
  legs_start = zeros(6, 3);

  for i = 1:6
    legs(i, :) = cube(leg_indices(i, 2), :) - cube(leg_indices(i, 1), :);
    legs_start(i, :) = cube(leg_indices(i, 1), :);
  end

Verification of Height of the Stewart Platform

If the Stewart platform is not contained in the cube, throw an error.

  Hmax = cube(4, 3) - cube(2, 3);
  if opts.H0 < cube(2, 3)
    error(sprintf('H0 is not high enought. Minimum H0 = %.1f', cube(2, 3)));
  else if opts.H0 + opts.H > cube(4, 3)
    error(sprintf('H0+H is too high. Maximum H0+H = %.1f', cube(4, 3)));
    error('H0+H is too high');
  end

Determinate the location of the joints

We now determine the location of the joints on the fixed platform w.r.t the fixed frame $\{A\}$. $\{A\}$ is fixed to the bottom of the base.

  Aa = zeros(6, 3);
  for i = 1:6
    t = (opts.H0-legs_start(i, 3))/(legs(i, 3));
    Aa(i, :) = legs_start(i, :) + t*legs(i, :);
  end

And the location of the joints on the mobile platform with respect to $\{A\}$.

  Ab = zeros(6, 3);
  for i = 1:6
    t = (opts.H0+opts.H-legs_start(i, 3))/(legs(i, 3));
    Ab(i, :) = legs_start(i, :) + t*legs(i, :);
  end

And the location of the joints on the mobile platform with respect to $\{B\}$.

  Bb = zeros(6, 3);
  Bb = Ab - (opts.H0 + opts.H_tot/2 + opts.H/2)*[0, 0, 1];
  h = opts.H0 + opts.H/2 - opts.H_tot/2;
  Aa = Aa - h*[0, 0, 1];
  Ab = Ab - h*[0, 0, 1];

Returns Stewart Structure 

  stewart = struct();
  stewart.Aa = Aa;
  stewart.Ab = Ab;
  stewart.Bb = Bb;
  stewart.H_tot = opts.H_tot;
end

initializeGeneralConfiguration

Function description

The initializeGeneralConfiguration function takes one structure that contains configurations for the hexapod and returns one structure representing the Hexapod.

  function [stewart] = initializeGeneralConfiguration(opts_param)

Optional Parameters

Default values for opts.

  opts = struct(...
      'H_tot',   90, ... % Height of the platform [mm]
      'H_joint', 15, ... % Height of the joints [mm]
      'H_plate', 10, ... % Thickness of the fixed and mobile platforms [mm]
      'R_bot',  100, ... % Radius where the legs articulations are positionned [mm]
      'R_top',  80,  ... % Radius where the legs articulations are positionned [mm]
      'a_bot',  10,  ... % Angle Offset [deg]
      'a_top',  40,  ... % Angle Offset [deg]
      'da_top', 0    ... % Angle Offset from 0 position [deg]
      );

Populate opts with input parameters

  if exist('opts_param','var')
      for opt = fieldnames(opts_param)'
          opts.(opt{1}) = opts_param.(opt{1});
      end
  end

Geometry Description

/tdehaeze/stewart-simscape/media/commit/4d47a51d9fe288e72b302e1f915231207639c94a/figs/stewart_bottom_plate.png
Schematic of the bottom plates with all the parameters

Compute Aa and Ab

We compute $[a_1, a_2, a_3, a_4, a_5, a_6]^T$ and $[b_1, b_2, b_3, b_4, b_5, b_6]^T$.

  Aa = zeros(6, 3); % [mm]
  Ab = zeros(6, 3); % [mm]
  Bb = zeros(6, 3); % [mm]
  for i = 1:3
      Aa(2*i-1,:) = [opts.R_bot*cos( pi/180*(120*(i-1) - opts.a_bot) ), ...
                     opts.R_bot*sin( pi/180*(120*(i-1) - opts.a_bot) ), ...
                     opts.H_plate+opts.H_joint];
      Aa(2*i,:)   = [opts.R_bot*cos( pi/180*(120*(i-1) + opts.a_bot) ), ...
                     opts.R_bot*sin( pi/180*(120*(i-1) + opts.a_bot) ), ...
                     opts.H_plate+opts.H_joint];

      Ab(2*i-1,:) = [opts.R_top*cos( pi/180*(120*(i-1) + opts.da_top - opts.a_top) ), ...
                     opts.R_top*sin( pi/180*(120*(i-1) + opts.da_top - opts.a_top) ), ...
                     opts.H_tot - opts.H_plate - opts.H_joint];
      Ab(2*i,:)   = [opts.R_top*cos( pi/180*(120*(i-1) + opts.da_top + opts.a_top) ), ...
                     opts.R_top*sin( pi/180*(120*(i-1) + opts.da_top + opts.a_top) ), ...
                     opts.H_tot - opts.H_plate - opts.H_joint];
  end

  Bb = Ab - opts.H_tot*[0,0,1];

Returns Stewart Structure 

  stewart = struct();
  stewart.Aa = Aa;
  stewart.Ab = Ab;
  stewart.Bb = Bb;
  stewart.H_tot = opts.H_tot;
end

computeGeometricalProperties

Function description 

  function [stewart] = computeGeometricalProperties(stewart, opts_param)

Optional Parameters

Default values for opts.

  opts = struct(...
      'Jd_pos', [0, 0, 30], ... % Position of the Jacobian for displacement estimation from the top of the mobile platform [mm]
      'Jf_pos', [0, 0, 30]  ... % Position of the Jacobian for force location from the top of the mobile platform [mm]
      );

Populate opts with input parameters

  if exist('opts_param','var')
      for opt = fieldnames(opts_param)'
          opts.(opt{1}) = opts_param.(opt{1});
      end
  end

Rotation matrices

We initialize $l_i$ and $\hat{s}_i$

  leg_length = zeros(6, 1); % [mm]
  leg_vectors = zeros(6, 3);

We compute $b_i - a_i$, and then:

\begin{align*} l_i &= \left|b_i - a_i\right| \\ \hat{s}_i &= \frac{b_i - a_i}{l_i} \end{align*} 
  legs = stewart.Ab - stewart.Aa;

  for i = 1:6
      leg_length(i) = norm(legs(i,:));
      leg_vectors(i,:) = legs(i,:) / leg_length(i);
  end

We compute rotation matrices to have the orientation of the legs. The rotation matrix transforms the $z$ axis to the axis of the leg. The other axis are not important here.

  stewart.Rm = struct('R', eye(3));

  for i = 1:6
    sx = cross(leg_vectors(i,:), [1 0 0]);
    sx = sx/norm(sx);

    sy = -cross(sx, leg_vectors(i,:));
    sy = sy/norm(sy);

    sz = leg_vectors(i,:);
    sz = sz/norm(sz);

    stewart.Rm(i).R = [sx', sy', sz'];
  end

Jacobian matrices

Compute Jacobian Matrix

  Jd = zeros(6);

  for i = 1:6
    Jd(i, 1:3) = leg_vectors(i, :);
    Jd(i, 4:6) = cross(0.001*(stewart.Bb(i, :) - opts.Jd_pos), leg_vectors(i, :));
  end

  stewart.Jd = Jd;
  stewart.Jd_inv = inv(Jd);
  Jf = zeros(6);

  for i = 1:6
    Jf(i, 1:3) = leg_vectors(i, :);
    Jf(i, 4:6) = cross(0.001*(stewart.Bb(i, :) - opts.Jf_pos), leg_vectors(i, :));
  end

  stewart.Jf = Jf;
  stewart.Jf_inv = inv(Jf);
  end

initializeMechanicalElements

Function description 

  function [stewart] = initializeMechanicalElements(stewart, opts_param)

Optional Parameters

Default values for opts.

  opts = struct(...
      'thickness', 10, ... % Thickness of the base and platform [mm]
      'density',   1000, ... % Density of the material used for the hexapod [kg/m3]
      'k_ax',      1e8, ... % Stiffness of each actuator [N/m]
      'c_ax',      1000, ... % Damping of each actuator [N/(m/s)]
      'stroke',    50e-6  ... % Maximum stroke of each actuator [m]
      );

Populate opts with input parameters

  if exist('opts_param','var')
      for opt = fieldnames(opts_param)'
          opts.(opt{1}) = opts_param.(opt{1});
      end
  end

Bottom Plate

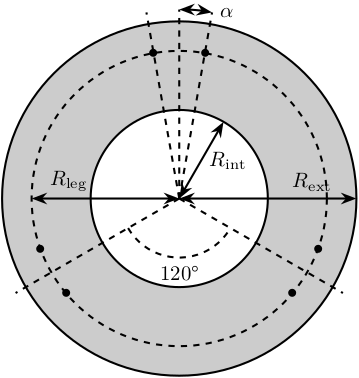
/tdehaeze/stewart-simscape/media/commit/4d47a51d9fe288e72b302e1f915231207639c94a/figs/stewart_bottom_plate.png
Schematic of the bottom plates with all the parameters

The bottom plate structure is initialized.

  BP = struct();

We defined its internal radius (if there is a hole in the bottom plate) and its outer radius.

  BP.Rint = 0;   % Internal Radius [mm]
  BP.Rext = 150; % External Radius [mm]

We define its thickness.

  BP.H = opts.thickness; % Thickness of the Bottom Plate [mm]

We defined the density of the material of the bottom plate.

  BP.density = opts.density; % Density of the material [kg/m3]

And its color.

  BP.color = [0.7 0.7 0.7]; % Color [RGB]

Then the profile of the bottom plate is computed and will be used by Simscape

  BP.shape = [BP.Rint BP.H; BP.Rint 0; BP.Rext 0; BP.Rext BP.H]; % [mm]

The structure is added to the stewart structure

  stewart.BP = BP;

Top Plate

The top plate structure is initialized.

  TP = struct();

We defined the internal and external radius of the top plate.

  TP.Rint = 0;   % [mm]
  TP.Rext = 100; % [mm]

The thickness of the top plate.

  TP.H = 10; % [mm]

The density of its material.

  TP.density = opts.density; % Density of the material [kg/m3]

Its color.

  TP.color = [0.7 0.7 0.7]; % Color [RGB]

Then the shape of the top plate is computed

  TP.shape = [TP.Rint TP.H; TP.Rint 0; TP.Rext 0; TP.Rext TP.H];

The structure is added to the stewart structure

  stewart.TP  = TP;

Legs

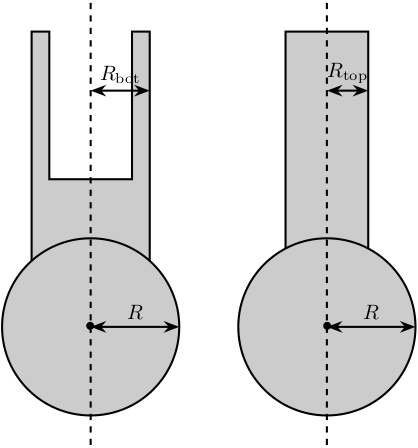
/tdehaeze/stewart-simscape/media/commit/4d47a51d9fe288e72b302e1f915231207639c94a/figs/stewart_legs.png
Schematic for the legs of the Stewart platform

The leg structure is initialized.

  Leg = struct();

The maximum Stroke of each leg is defined.

  Leg.stroke = opts.stroke; % [m]

The stiffness and damping of each leg are defined

  Leg.k_ax = opts.k_ax; % Stiffness of each leg [N/m]
  Leg.c_ax = opts.c_ax; % Damping of each leg [N/(m/s)]

The radius of the legs are defined

  Leg.Rtop = 10; % Radius of the cylinder of the top part of the leg[mm]
  Leg.Rbot = 12; % Radius of the cylinder of the bottom part of the leg [mm]

The density of its material.

  Leg.density = opts.density; % Density of the material used for the legs [kg/m3]

Its color.

  Leg.color = [0.5 0.5 0.5]; % Color of the top part of the leg [RGB]

The radius of spheres representing the ball joints are defined.

  Leg.R = 1.3*Leg.Rbot; % Size of the sphere at the extremity of the leg [mm]

We estimate the length of the legs.

  legs = stewart.Ab - stewart.Aa;
  Leg.lenght = norm(legs(1,:))/1.5;

Then the shape of the bottom leg is estimated

  Leg.shape.bot = ...
      [0        0; ...
       Leg.Rbot 0; ...
       Leg.Rbot Leg.lenght; ...
       Leg.Rtop Leg.lenght; ...
       Leg.Rtop 0.2*Leg.lenght; ...
       0        0.2*Leg.lenght];

The structure is added to the stewart structure

  stewart.Leg = Leg;

Ball Joints

/tdehaeze/stewart-simscape/media/commit/4d47a51d9fe288e72b302e1f915231207639c94a/figs/stewart_ball_joints.png
Schematic of the support for the ball joints

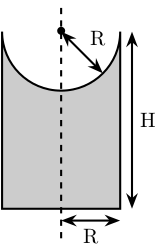
SP is the structure representing the support for the ball joints at the extremity of each leg.

The SP structure is initialized.

  SP = struct();

We can define its rotational stiffness and damping. For now, we use perfect joints.

  SP.k = 0; % [N*m/deg]
  SP.c = 0; % [N*m/deg]

Its height is defined

  SP.H = stewart.Aa(1, 3) - BP.H; % [mm]

Its radius is based on the radius on the sphere at the end of the legs.

  SP.R = Leg.R; % [mm]
  SP.section = [0    SP.H-SP.R;
                0    0;
                SP.R 0;
                SP.R SP.H];

The density of its material is defined.

  SP.density = opts.density; % [kg/m^3]

Its color is defined.

  SP.color = [0.7 0.7 0.7]; % [RGB]

The structure is added to the Hexapod structure

  stewart.SP  = SP;

initializeSample

Function description 

  function [] = initializeSample(opts_param)

Optional Parameters

Default values for opts.

  sample = struct( ...
      'radius',     100, ... % radius of the cylinder [mm]
      'height',     100, ... % height of the cylinder [mm]
      'mass',       10,  ... % mass of the cylinder [kg]
      'measheight', 50, ... % measurement point z-offset [mm]
      'offset',     [0, 0, 0],   ... % offset position of the sample [mm]
      'color',      [0.9 0.1 0.1] ...
      );

Populate opts with input parameters

  if exist('opts_param','var')
      for opt = fieldnames(opts_param)'
          sample.(opt{1}) = opts_param.(opt{1});
      end
  end

Save the Sample structure 

  save('./mat/sample.mat', 'sample');
  end