stewart-simscape/active-damping.org

Stewart Platform - Decentralized Active Damping

• Introduction
• Inertial Control
  • Introduction
  • Identification of the Dynamics
  • Effect of the Flexible Joint stiffness on the Dynamics
  • Obtained Damping
  • Conclusion
• Integral Force Feedback
  • Introduction
  • Identification of the Dynamics with perfect Joints
  • Effect of the Flexible Joint stiffness on the Dynamics
  • Obtained Damping
  • Conclusion
• Direct Velocity Feedback
  • Introduction
  • Identification of the Dynamics with perfect Joints
  • Effect of the Flexible Joint stiffness on the Dynamics
  • Obtained Damping
  • Conclusion

Introduction   ignore

The following decentralized active damping techniques are briefly studied:

• Inertial Control (proportional feedback of the absolute velocity): Section sec:active_damping_inertial
• Integral Force Feedback: Section sec:active_damping_iff
• Direct feedback of the relative velocity of each strut: Section sec:active_damping_dvf

Inertial Control

<<sec:active_damping_inertial>>

Introduction   ignore

Identification of the Dynamics

  stewart = initializeStewartPlatform();
  stewart = initializeFramesPositions(stewart, 'H', 90e-3, 'MO_B', 45e-3);
  stewart = generateGeneralConfiguration(stewart);
  stewart = computeJointsPose(stewart);
  stewart = initializeStrutDynamics(stewart);
  stewart = initializeJointDynamics(stewart, 'disable', true);
  stewart = initializeCylindricalPlatforms(stewart);
  stewart = initializeCylindricalStruts(stewart);
  stewart = computeJacobian(stewart);
  stewart = initializeStewartPose(stewart);

  %% Options for Linearized
  options = linearizeOptions;
  options.SampleTime = 0;

  %% Name of the Simulink File
  mdl = 'stewart_active_damping';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/F'],   1, 'openinput');  io_i = io_i + 1; % Actuator Force Inputs [N]
  io(io_i) = linio([mdl, '/Vm'],  1, 'openoutput'); io_i = io_i + 1; % Absolute velocity of each leg [m/s]

  %% Run the linearization
  G = linearize(mdl, io, options);
  G.InputName  = {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};
  G.OutputName = {'Vm1', 'Vm2', 'Vm3', 'Vm4', 'Vm5', 'Vm6'};

The transfer function from actuator forces to force sensors is shown in Figure fig:inertial_plant_coupling.

<<plt-matlab>>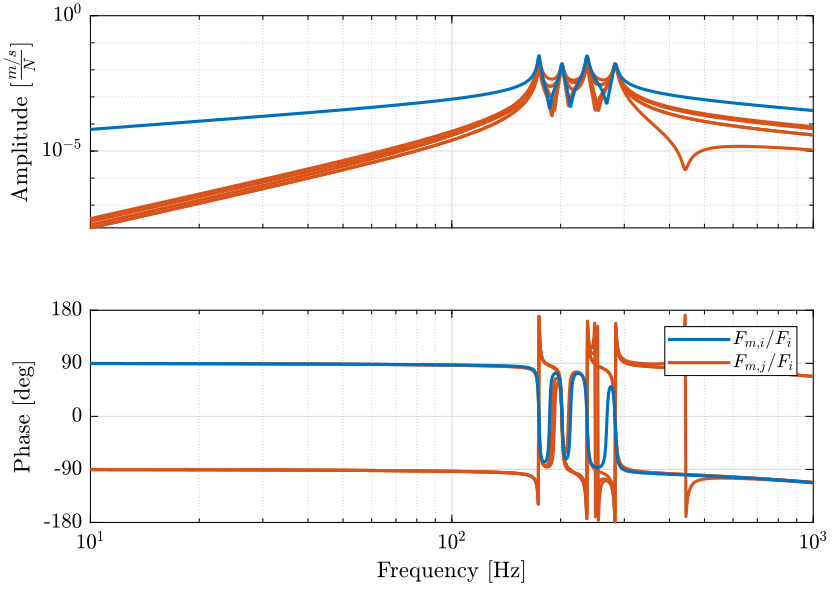

Transfer function from the Actuator force $F_{i}$ to the absolute velocity of the same leg $v_{m,i}$ and to the absolute velocity of the other legs $v_{m,j}$ with $i \neq j$ in grey (png, pdf)

Effect of the Flexible Joint stiffness on the Dynamics

We add some stiffness and damping in the flexible joints and we re-identify the dynamics.

  stewart = initializeJointDynamics(stewart);
  Gf = linearize(mdl, io, options);
  Gf.InputName  = {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};
  Gf.OutputName = {'Vm1', 'Vm2', 'Vm3', 'Vm4', 'Vm5', 'Vm6'};

The new dynamics from force actuator to force sensor is shown in Figure fig:inertial_plant_flexible_joint_decentralized.

<<plt-matlab>>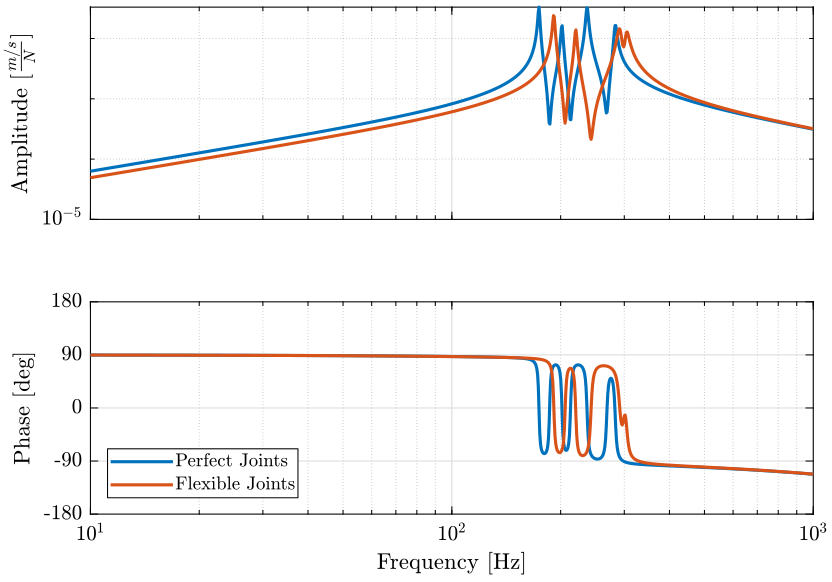

Transfer function from the Actuator force $F_{i}$ to the absolute velocity sensor $v_{m,i}$ (png, pdf)

Obtained Damping

The control is a performed in a decentralized manner. The $6 \times 6$ control is a diagonal matrix with pure proportional action on the diagonal: \[ K(s) = g

\begin{bmatrix} 1 & & 0 \\ & \ddots & \\ 0 & & 1 \end{bmatrix} \]

The root locus is shown in figure fig:root_locus_inertial_rot_stiffness and the obtained pole damping function of the control gain is shown in figure fig:pole_damping_gain_inertial_rot_stiffness.

<<plt-matlab>>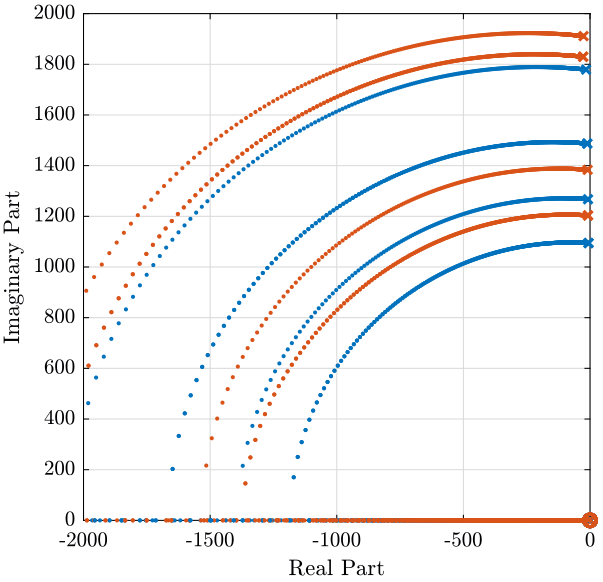

Root Locus plot with Decentralized Inertial Control when considering the stiffness of flexible joints (png, pdf)

<<plt-matlab>>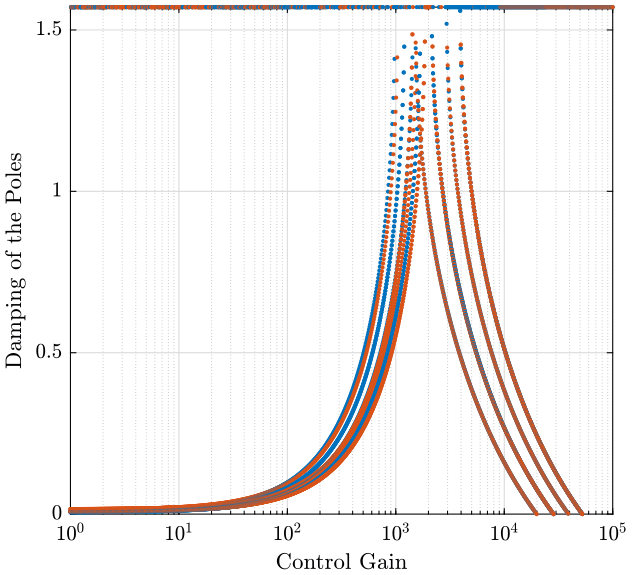

Damping of the poles with respect to the gain of the Decentralized Inertial Control when considering the stiffness of flexible joints (png, pdf)

Conclusion

Joint stiffness does increase the resonance frequencies of the system but does not change the attainable damping when using relative motion sensors.

Integral Force Feedback

<<sec:active_damping_iff>>

Introduction   ignore

Identification of the Dynamics with perfect Joints

We first initialize the Stewart platform without joint stiffness.

  stewart = initializeStewartPlatform();
  stewart = initializeFramesPositions(stewart, 'H', 90e-3, 'MO_B', 45e-3);
  stewart = generateGeneralConfiguration(stewart);
  stewart = computeJointsPose(stewart);
  stewart = initializeStrutDynamics(stewart);
  stewart = initializeAmplifiedStrutDynamics(stewart);
  stewart = initializeJointDynamics(stewart, 'disable', true);
  stewart = initializeCylindricalPlatforms(stewart);
  stewart = initializeCylindricalStruts(stewart);
  stewart = computeJacobian(stewart);
  stewart = initializeStewartPose(stewart);

And we identify the dynamics from force actuators to force sensors.

  %% Options for Linearized
  options = linearizeOptions;
  options.SampleTime = 0;

  %% Name of the Simulink File
  mdl = 'stewart_active_damping';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/F'],   1, 'openinput'); io_i = io_i + 1; % Actuator Force Inputs [N]
  io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensor Outputs [N]

  %% Run the linearization
  G = linearize(mdl, io, options);
  G.InputName  = {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};
  G.OutputName = {'Fm1', 'Fm2', 'Fm3', 'Fm4', 'Fm5', 'Fm6'};

The transfer function from actuator forces to force sensors is shown in Figure fig:iff_plant_coupling.

<<plt-matlab>>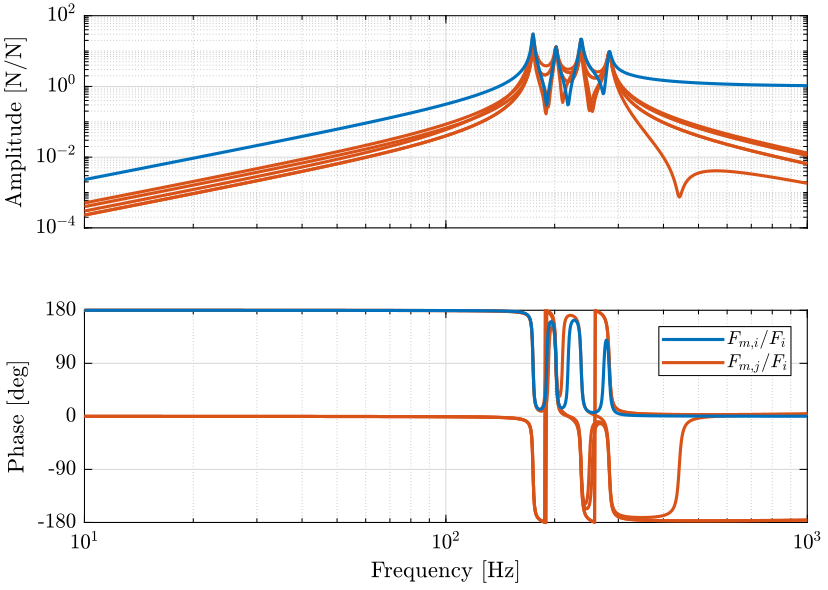

Transfer function from the Actuator force $F_{i}$ to the Force sensor of the same leg $F_{m,i}$ and to the force sensor of the other legs $F_{m,j}$ with $i \neq j$ in grey (png, pdf)

Effect of the Flexible Joint stiffness on the Dynamics

We add some stiffness and damping in the flexible joints and we re-identify the dynamics.

  stewart = initializeJointDynamics(stewart);
  Gf = linearize(mdl, io, options);
  Gf.InputName  = {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};
  Gf.OutputName = {'Fm1', 'Fm2', 'Fm3', 'Fm4', 'Fm5', 'Fm6'};

The new dynamics from force actuator to force sensor is shown in Figure fig:iff_plant_flexible_joint_decentralized.

<<plt-matlab>>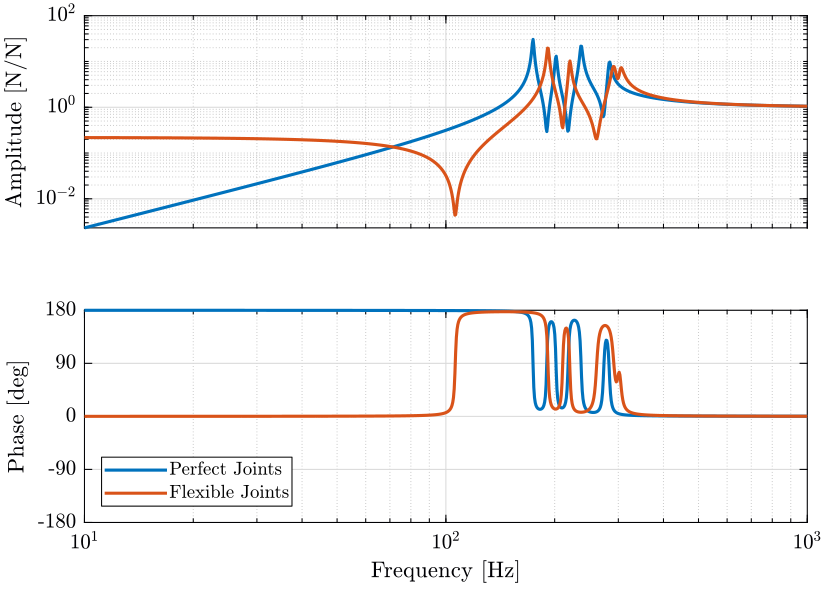

Transfer function from the Actuator force $F_{i}$ to the force sensor $F_{m,i}$ (png, pdf)

Obtained Damping

The control is a performed in a decentralized manner. The $6 \times 6$ control is a diagonal matrix with pure integration action on the diagonal: \[ K(s) = g

\begin{bmatrix} \frac{1}{s} & & 0 \\ & \ddots & \\ 0 & & \frac{1}{s} \end{bmatrix} \]

The root locus is shown in figure fig:root_locus_iff_rot_stiffness and the obtained pole damping function of the control gain is shown in figure fig:pole_damping_gain_iff_rot_stiffness.

<<plt-matlab>>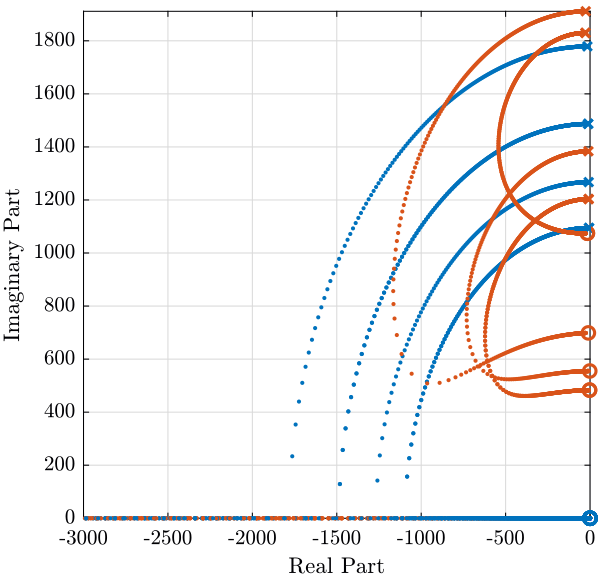

Root Locus plot with Decentralized Integral Force Feedback when considering the stiffness of flexible joints (png, pdf)

<<plt-matlab>>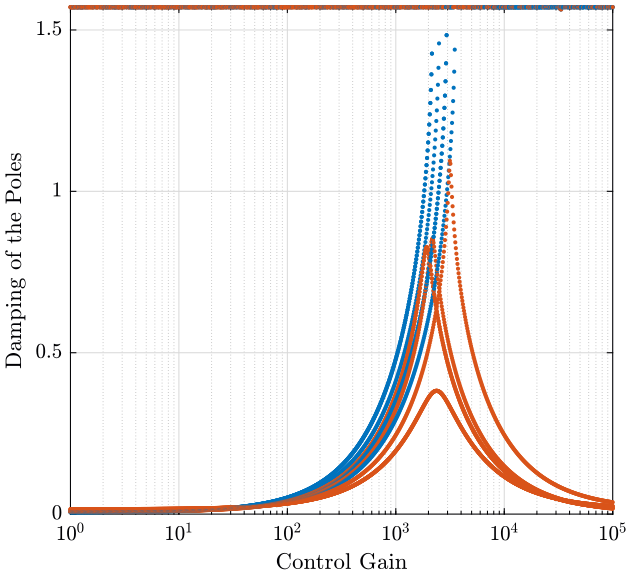

Damping of the poles with respect to the gain of the Decentralized Integral Force Feedback when considering the stiffness of flexible joints (png, pdf)

Conclusion

The joint stiffness has a huge impact on the attainable active damping performance when using force sensors. Thus, if Integral Force Feedback is to be used in a Stewart platform with flexible joints, the rotational stiffness of the joints should be minimized.

Direct Velocity Feedback

<<sec:active_damping_dvf>>

Introduction   ignore

Identification of the Dynamics with perfect Joints

We first initialize the Stewart platform without joint stiffness.

  stewart = initializeStewartPlatform();
  stewart = initializeFramesPositions(stewart, 'H', 90e-3, 'MO_B', 45e-3);
  stewart = generateGeneralConfiguration(stewart);
  stewart = computeJointsPose(stewart);
  stewart = initializeStrutDynamics(stewart);
  stewart = initializeJointDynamics(stewart, 'disable', true);
  stewart = initializeCylindricalPlatforms(stewart);
  stewart = initializeCylindricalStruts(stewart);
  stewart = computeJacobian(stewart);
  stewart = initializeStewartPose(stewart);

And we identify the dynamics from force actuators to force sensors.

  %% Options for Linearized
  options = linearizeOptions;
  options.SampleTime = 0;

  %% Name of the Simulink File
  mdl = 'stewart_active_damping';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/F'],   1, 'openinput'); io_i = io_i + 1; % Actuator Force Inputs [N]
  io(io_i) = linio([mdl, '/Dm'], 1, 'openoutput'); io_i = io_i + 1; % Relative Displacement Outputs [N]

  %% Run the linearization
  G = linearize(mdl, io, options);
  G.InputName  = {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};
  G.OutputName = {'Dm1', 'Dm2', 'Dm3', 'Dm4', 'Dm5', 'Dm6'};

The transfer function from actuator forces to relative motion sensors is shown in Figure fig:dvf_plant_coupling.

<<plt-matlab>>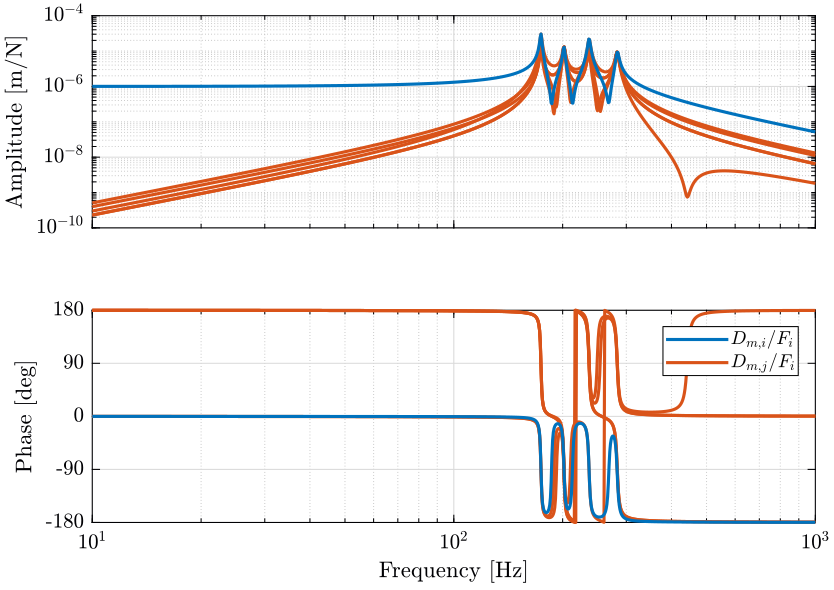

Transfer function from the Actuator force $F_{i}$ to the Relative Motion Sensor $D_{m,j}$ with $i \neq j$ (png, pdf)

Effect of the Flexible Joint stiffness on the Dynamics

We add some stiffness and damping in the flexible joints and we re-identify the dynamics.

  stewart = initializeJointDynamics(stewart);
  Gf = linearize(mdl, io, options);
  Gf.InputName  = {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};
  Gf.OutputName = {'Dm1', 'Dm2', 'Dm3', 'Dm4', 'Dm5', 'Dm6'};

The new dynamics from force actuator to relative motion sensor is shown in Figure fig:dvf_plant_flexible_joint_decentralized.

<<plt-matlab>>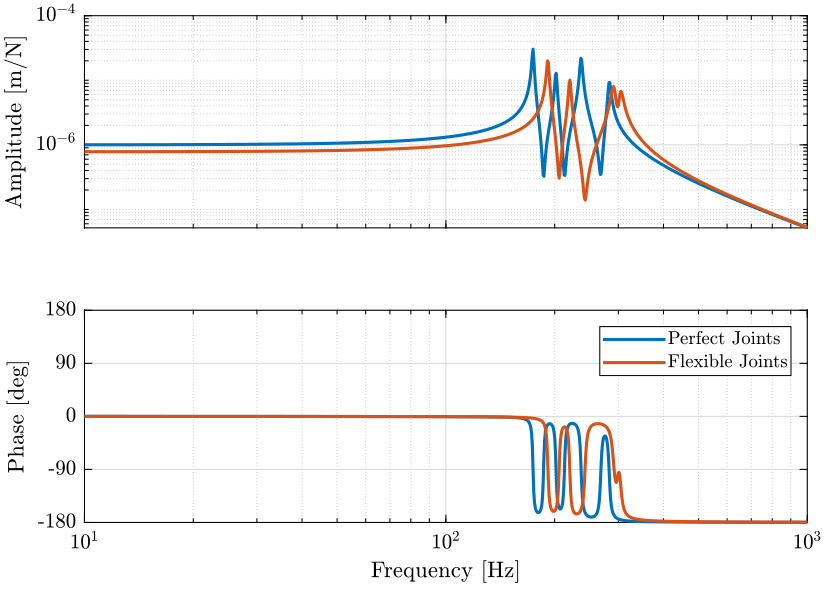

Transfer function from the Actuator force $F_{i}$ to the relative displacement sensor $D_{m,i}$ (png, pdf)

Obtained Damping

The control is a performed in a decentralized manner. The $6 \times 6$ control is a diagonal matrix with pure derivative action on the diagonal: \[ K(s) = g

\begin{bmatrix} s & & \\ & \ddots & \\ & & s \end{bmatrix} \]

The root locus is shown in figure fig:root_locus_dvf_rot_stiffness and the obtained pole damping function of the control gain is shown in figure fig:pole_damping_gain_dvf_rot_stiffness.

<<plt-matlab>>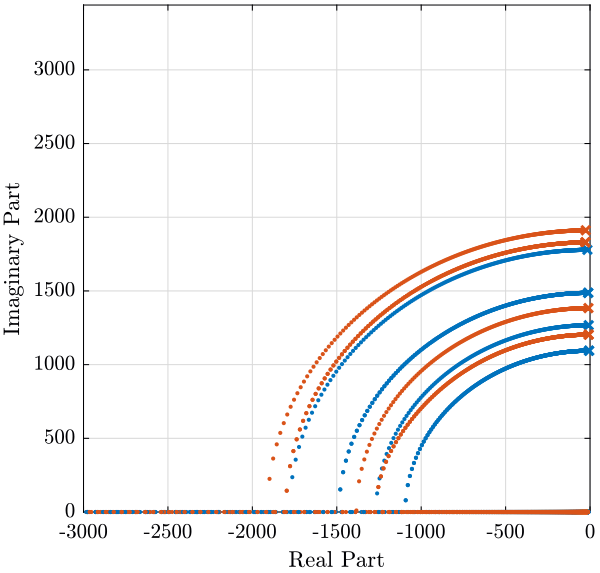

Root Locus plot with Direct Velocity Feedback when considering the Stiffness of flexible joints (png, pdf)

<<plt-matlab>>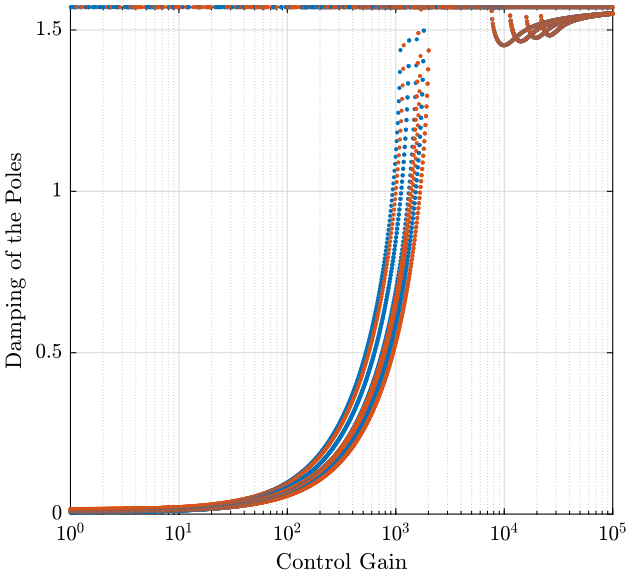

Damping of the poles with respect to the gain of the Direct Velocity Feedback when considering the Stiffness of flexible joints (png, pdf)

Conclusion

Joint stiffness does increase the resonance frequencies of the system but does not change the attainable damping when using relative motion sensors.