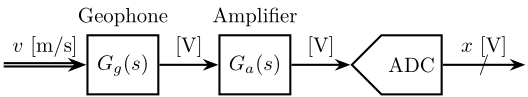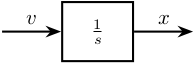spectral-analysis/index.org

Spectral Analysis using Matlab

• Introduction
• Spectral Analysis - Basics
  • ZIP file containing the data and matlab files
  • Introduction
  • Sensitivity of the instrumentation
  • Convert the time domain from volts to velocity
  • Power Spectral Density and Amplitude Spectral Density
  • Modification of a signal's Power Spectral Density when going through an LTI system
  • From PSD of the velocity to the PSD of the displacement
  • Cumulative Power/Amplitude Spectrum
• Time domain signal that approximate a PSD - TF technique
  • ZIP file containing the data and matlab files
  • Introduction
  • Signal's PSD
  • Transfer Function that approximate the ASD
  • Generated Time domain signal
  • Comparison of the Power Spectral Densities
  • Simulink
• Time domain signal that approximate a PSD - IFFT technique
  • ZIP file containing the data and matlab files
  • Introduction
  • Signal's PSD
  • Algorithm
  • Obtained Time Domain Signal
  • PSD Comparison
• Compute the Noise level and Signal level from PSD
  • ZIP file containing the data and matlab files
  • Introduction
  • Time Domain Signal
  • Estimation of the magnitude of a deterministic signal
  • Estimation of the noise level
• Further Notes
  • PSD of ADC quantization noise
• Bibliography

Introduction   ignore

This document presents the mathematics as well as the matlab scripts to do various spectral analysis on a measured signal.

Some matlab documentation about Spectral Analysis can be found here.

First, in section sec:spectral_analysis_basics, some basics of spectral analysis are presented.

In some cases, we want to generate a time domain signal with defined Power Spectral Density. Two methods are presented in sections sec:approximate_tf and sec:approximate_ifft.

Finally, some notes are done on how to compute the noise level and signal level from a given Power Spectral Density in section sec:compute_psd_levels.

Spectral Analysis - Basics

<<sec:spectral_analysis_basics>>

ZIP file containing the data and matlab files   ignore

All the files (data and Matlab scripts) are accessible here.

Introduction   ignore

In this section, the basics of spectral analysis is presented with the associated Matlab commands.

This include:

• how to compute the Power Spectral Density (PSD) and the Amplitude Spectral Density (ASD)
• how to take into account the sensitivity of the sensor and of the electronics
• how to compute the Cumulative Power Spectrum (CPS) and the Cumulative Amplitude Spectrum (CAS)

Sensitivity of the instrumentation

A typical measurement setup is shown in figure fig:velocity_to_voltage where we measure a physical signal which is here a velocity $v(t)$ using a geophone. The geophone has some dynamics that we represent with $G_g(s)$, its output a voltage. The output of the geophone is then amplified by a voltage amplifier with a transfer function $G_a(s)$.

Finally, the signal is discretised with an ADC and we obtain $x(k\Delta t)$.

To obtain the real physical quantity $v(t)$ as measured by the sensor from the obtained signal $x(k\Delta t)$, one have to know the sensitivity of the sensors and electronics used ($G_g(s)$ and $G_a(s)$).

Schematic of the instrumentation used for the measurement

Let's say, we know that the sensitivity of the geophone used is \[ G_g(s) = G_0 \frac{\frac{s}{2\pi f_0}}{1 + \frac{s}{2\pi f_0}} \quad \left[\frac{V}{m/s}\right] \]

The parameters are defined below.

  G0 = 88; % Sensitivity [V/(m/s)]
  f0 = 2; % Cut-off frequency [Hz]

  Gg = G0*(s/2/pi/f0)/(1+s/2/pi/f0);

And the dynamics of the amplifier in the bandwidth of interest is just a gain: $G_a(s) = 1000$.

  Ga = 1000;

Convert the time domain from volts to velocity

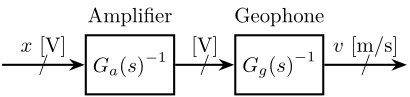
Let's here try to obtain the time domain signal $v(t)$ from the measurement $x$.

If ${G_a(s)}^{-1} {G_g(s)}^{-1}$ is proper, we can simulate this dynamical system to go from the voltage $x$ to the velocity $v$ as shown in figure fig:voltage_to_velocity.

If ${G_a(s)}^{-1} {G_g(s)}^{-1}$ is not proper, we add low pass filters at high frequency to make the system proper.

Schematic of the instrumentation used for the measurement

Let's load the measured $x$.

  data = load('mat/data_028.mat', 'data'); data = data.data;

  t = data(:, 3); % Time vector [s]
  x = data(:, 1)-mean(data(:, 1)); % The offset if removed (coming from the voltage amplifier) [v]

  dt = t(2)-t(1); % Sampling Time [s]
  Fs = 1/dt; % Sampling Frequency [Hz]

We simulate this system with matlab using the lsim command.

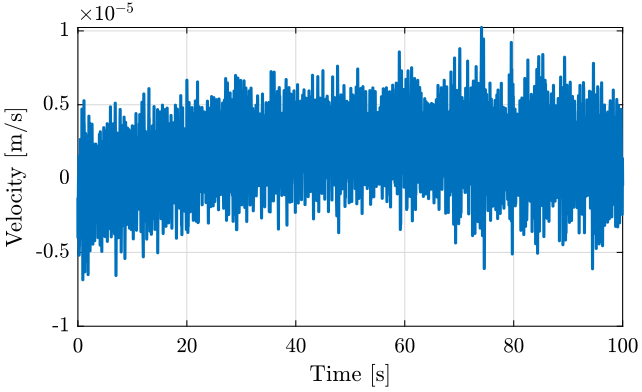
  v = lsim(inv(Gg*Ga), x, t);

And we plot the obtained velocity

  <<plt-matlab>>

Computed Velocity from the measured Voltage

Power Spectral Density and Amplitude Spectral Density

From the Matlab documentation:

The goal of spectral estimation is to describe the distribution (over frequency) of the power contained in a signal, based on a finite set of data.

We now have the velocity $v(t)\ [m/s]$ in the time domain.

The Power Spectral Density (PSD) $S_v(f)$ of the time domain $v(t)$ can be computed using the following equation: \[ S_v(f) = \frac{1}{f_s} \sum_{m=-\infty}^{\infty} R_{xx}(m) e^{-j 2 \pi m f / f_s} \ \left[\frac{(m/s)^2}{Hz}\right] \] where

• $f_s$ is the sampling frequency in Hz
• $R_{xx}$ is the autocorrelation

The PSD represents the distribution of the (average) signal power over frequency. $S_v(f)df$ is the infinitesimal power in the band $(f-df/2, f+df/2)$ and the total power in the signal is obtained by integrating these infinitesimal contributions.

To compute the Power Spectral Density with matlab, we use the pwelch function (documentation). The use of the pwelch function is: [pxx,w] = pwelch(x,window,noverlap,nfft, fs) with:

• x is the discrete time signal
• window is a window that is used to smooth the obtained PSD
• overlap can be used to have some overlap from section to section
• nfft specifies the number of FFT points for the PSD
• fs is the sampling frequency of the data x in Hertz

As explained in cite:schmid12_how_to_use_fft_matlab, it is recommended to use the pwelch function the following way:

First, define a window (preferably the hanning one) by specifying the averaging factor na.

  nx = length(v);
  na = 8;
  win = hanning(floor(nx/na));

Then, compute the power spectral density $S_v$ and the associated frequency vector $f$ with no overlap.

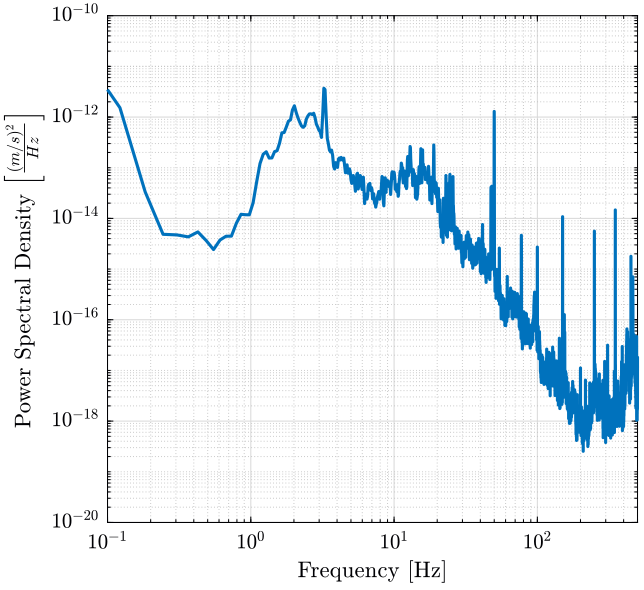
  [Sv, f] = pwelch(v, win, 0, [], Fs);

The obtained PSD is shown in figure fig:psd_velocity.

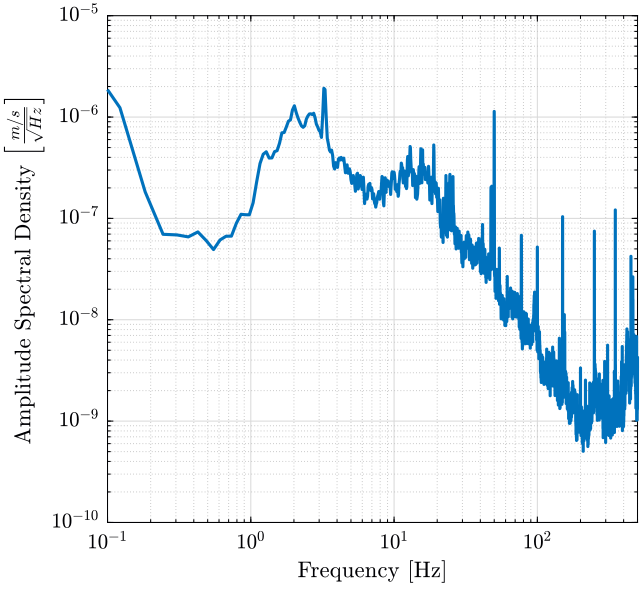
  <<plt-matlab>>

Power Spectral Density of the measured velocity

The Amplitude Spectral Density (ASD) is defined as the square root of the Power Spectral Density and is shown in figure fig:asd_velocity.

\begin{equation} \Gamma_{vv}(f) = \sqrt{S_{vv}(f)} \quad \left[ \frac{m/s}{\sqrt{Hz}} \right] \end{equation}

  <<plt-matlab>>

Power Spectral Density of the measured velocity

Modification of a signal's Power Spectral Density when going through an LTI system

Instead of computing the time domain velocity before computing the Power Spectral Density, we could have directly computed the PSD of the measured voltage $x$ and then take into account the sensitivity of the measurement devices to have the PSD of the velocity.

To do so, we use the fact that a signal $u$ with a PSD $S_{uu}$ going through a LTI system $G_(s)$ (figure fig:velocity_to_voltage_psd) will generate a signal $y$ with a PSD:

\begin{equation} S_{yy}(\omega) = \left|G(j\omega)\right|^2 S_{uu}(\omega) \end{equation}

Schematic of the instrumentation used for the measurement

Similarly, the ASD of $y$ is:

\begin{equation} \Gamma_{yy}(\omega) = \left|G(j\omega)\right| \Gamma_{uu}(\omega) \end{equation}

Thus, we could have computed the PSD of $x$ and then obtain the PSD of the velocity with: \[ S_{v}(\omega) = |G_a(j\omega) G_g(j\omega)|^{-1} S_{x}(\omega) \]

The PSD of $x$ is computed below.

  nx = length(x);
  na = 8;
  win = hanning(floor(nx/na));
  [Sx, f] = pwelch(x, win, 0, [], Fs);

And the PSD of $v$ is obtained with the below code.

  Svv = Sx.*squeeze(abs(freqresp(inv(Gg*Ga), f, 'Hz'))).^2;

The result is compare with the PSD computed from the $v$ signal obtained with the lsim command in figure fig:psd_velocity_lti_method.

  <<plt-matlab>>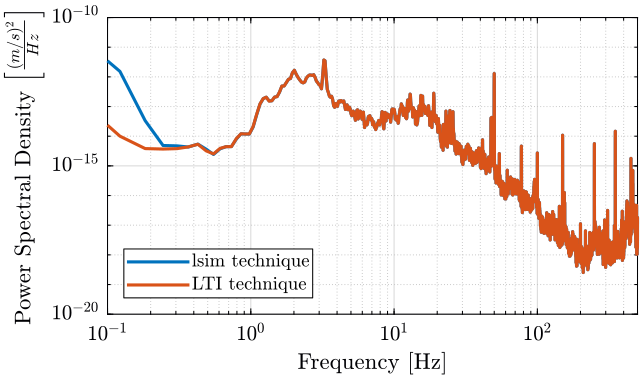

Obtain PSD of the velocity using the formula (png, pdf)

From PSD of the velocity to the PSD of the displacement

Similarly to what has been done in the last section, we can consider the displacement $d$ can be obtained from the velocity $v$ by going through an LTI system $1/s$ as shown in figure fig:velocity_to_displacement_psd.

Schematic of the instrumentation used for the measurement

We then have the relation between the PSD of $d$ and the PSD of $v$:

\begin{equation} S_{dd}(\omega) = \left|\frac{1}{j \omega}\right|^2 S_{vv}(\omega) \end{equation}

Using a frequency variable $f$ in Hz:

\begin{equation} S_{dd}(f) = \left| \frac{1}{j 2\pi f} \right|^2 S_{vv}(f) \end{equation}

For the Amplitude Spectral Density:

\begin{equation} \Gamma_{dd}(f) = \frac{1}{2\pi f} \Gamma_{vv}(f) \end{equation}

Note here that the PSD (and ASD) of one variable and its derivatives/integrals are equal at one particular frequency $f = 1\ rad/s \approx 0.16\ Hz$:

\begin{equation} S_{xx}(\omega = 1) = S_{vv}(\omega = 1) \end{equation}

With Matlab, the PSD of the displacement can be computed from the PSD of the velocity with the following code.

  Sd = Sv.*(1./(2*pi*f)).^2;

The obtained PSD of the displacement can be seen in figure fig:psd_velocity_displacement.

  <<plt-matlab>>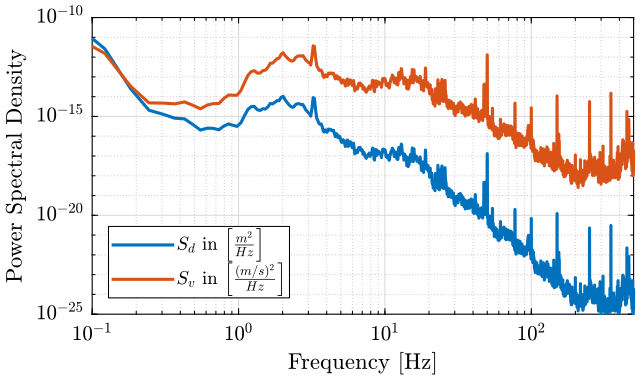

PSD of the Velocity and Displacement (png, pdf)

Cumulative Power/Amplitude Spectrum

The Cumulative Power Spectrum is the cumulative integral of the Power Spectral Density:

\begin{equation} CPS_v(f) = \int_0^f PSD_v(\nu) d\nu \quad [(m/s)^2] \end{equation}

It is also possible to integrate from high frequency to low frequency:

\begin{equation} CPS_v(f) = \int_f^\infty PSD_v(\nu) d\nu \quad [(m/s)^2] \end{equation}

The Cumulative Power Spectrum taken at frequency $f$ thus represent the power in the signal in the frequency band $0$ to $f$ or $f$ to $\infty$ depending on the above definition taken.

The choice of the integral direction depends on the shape of the PSD. If the power is mostly present at low frequencies, it is preferable to use equation eq:cps_inv.

The Cumulative Amplitude Spectrum is defined as the square root of the Cumulative Power Spectrum: \[ CAS_v(f) = \sqrt{CPS_v(f)} = \sqrt{\int_f^\infty PSD_v(\nu) d\nu} \quad [m/s] \]

The Root Mean Square value of the velocity corresponds to the Cumulative Amplitude Spectrum when integrated at all frequencies: \[ v_{\text{rms}} = \sqrt{\int_0^\infty PSD_v(\nu) d\nu} = CAS_v(0) \quad [m/s \ \text{rms}] \]

With Matlab, the Cumulative Power Spectrum can be computed with the below formulas and the results are shown in figure fig:cps_integral_comp.

  CPS_v  = cumtrapz(f, Sv); % Cumulative Power Spectrum from low to high frequencies
  CPS_vv = flip(-cumtrapz(flip(f), flip(Sv))); % Cumulative Power Spectrum from high to low frequencies

  figure;
  ax1 = subplot(1, 2, 1);
  hold on;
  plot(f, CPS_v);
  hold off;
  set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
  xlabel('Frequency [Hz]'); ylabel('Cumulative Power Spectrum [$(m/s)^2$]')

  ax2 = subplot(1, 2, 2);
  hold on;
  plot(f, CPS_vv);
  hold off;
  set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
  xlabel('Frequency [Hz]');

  linkaxes([ax1,ax2],'xy');
  xlim([0.1, 500]); ylim([1e-15, 1e-11]);

  <<plt-matlab>>

Cumulative Power Spectrum (png, pdf)

Time domain signal that approximate a PSD - TF technique

<<sec:approximate_tf>>

ZIP file containing the data and matlab files   ignore

All the files (data and Matlab scripts) are accessible here.

Introduction   ignore

Signal's PSD

We load the PSD of the signal we wish to replicate.

  load('./mat/dist_psd.mat', 'dist_f');

We remove the first value with very high PSD.

  dist_f.f = dist_f.f(3:end);
  dist_f.psd_gm = dist_f.psd_gm(3:end);

The PSD of the signal is shown on figure ref:fig:psd_ground_motion.

  <<plt-matlab>>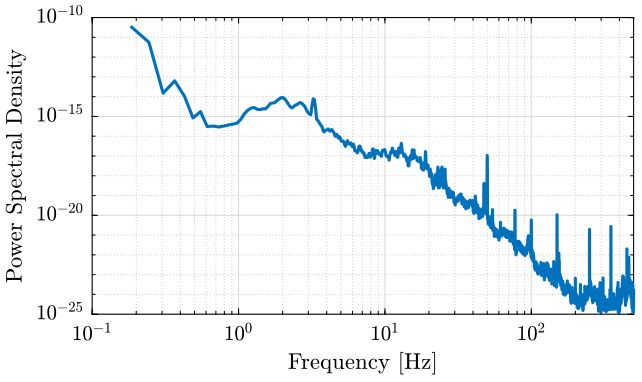

PSD of the signal (png, pdf)

Transfer Function that approximate the ASD

Using sisotool or any other tool, we create a transfer function $G$ such that its magnitude is close to the Amplitude Spectral Density $\Gamma_x = \sqrt{S_x}$: \[ |G(j\omega)| \approx \Gamma_x(\omega) \]

  G_gm = 0.002*(s^2 + 3.169*s + 27.74)/(s*(s+32.73)*(s+8.829)*(s+7.983)^2);

We compare the ASD $\Gamma_x(\omega)$ and the magnitude of the generated transfer function $|G(j\omega)|$ in figure /tdehaeze/spectral-analysis/src/commit/fec84e305f4da2267337e3a12298be9fd6aad762/.

  <<plt-matlab>>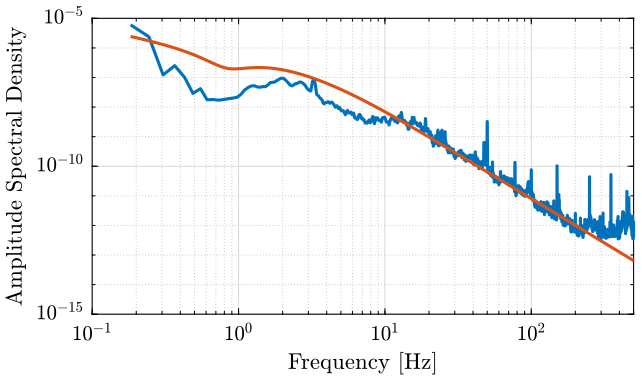

Comparison of the ASD and of the transfer function's magnitude (png, pdf)

Generated Time domain signal

We know that a signal $u$ going through a LTI system $G$ (figure fig:velocity_to_voltage_psd_bis) will have its ASD modified according to the following equation:

\begin{equation} \Gamma_{yy}(\omega) = \left|G(j\omega)\right| \Gamma_{uu}(\omega) \end{equation}

Schematic of the instrumentation used for the measurement

Thus, if we create a random signal with an ASD equal to one at all frequency and we pass this signal through the previously defined LTI transfer function G_gm, we should obtain a signal with an ASD that approximate the original ASD.

To obtain a random signal with an ASD equal to one, we use the following code.

  Fs = 2*dist_f.f(end); % Sampling Frequency [Hz]
  Ts = 1/Fs; % Sampling Time [s]

  t = 0:Ts:500; % Time Vector [s]
  u = sqrt(Fs/2)*randn(length(t), 1); % Signal with an ASD equal to one

We then use lsim to compute $y$ as shown in figure fig:velocity_to_voltage_psd_bis.

  y = lsim(G_gm, u, t);

The obtained time domain signal is shown in figure fig:time_domain_u.

  <<plt-matlab>>

Obtained time domain signal $y(t)$ (png, pdf)

Comparison of the Power Spectral Densities

We now compute the Power Spectral Density of the computed time domain signal $y$.

  nx = length(y);
  na = 16;
  win = hanning(floor(nx/na));

  [pxx, f] = pwelch(y, win, 0, [], Fs);

Finally, we compare the PSD of the original signal and the obtained signal on figure ref:fig:psd_comparison.

  <<plt-matlab>>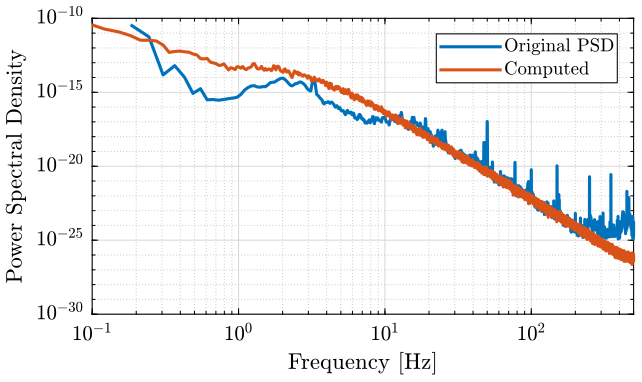

Comparison of the original PSD and the PSD of the computed time domain signal (png, pdf)

Simulink

One advantage of this technique is that it can be easily integrated into simulink.

The corresponding schematic is shown in figure fig:simulink_psd_generate where the block Band-Limited White Noise is used to generate a random signal with a PSD equal to one (parameter Noise Power is set to 1).

Then, the signal generated pass through the transfer function representing the wanted ASD.

Simulink Schematic

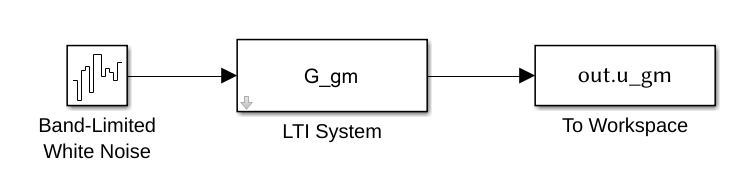
We simulate the system shown in figure fig:simulink_psd_generate.

  out = sim('matlab/generate_signal_psd.slx');

And we compute the PSD of the generated signal.

  nx = length(out.u_gm.Data);
  na = 8;
  win = hanning(floor(nx/na));

  [pxx, f] = pwelch(out.u_gm.Data, win, 0, [], 1e3);

Finally, we compare the PSD of the generated signal with the original PSD in figure fig:compare_psd_original_simulink.

  <<plt-matlab>>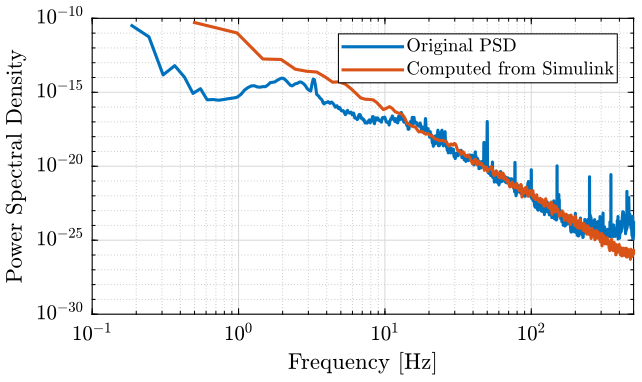

Comparison of the obtained signal's PSD and original PSD (png, pdf)

Time domain signal that approximate a PSD - IFFT technique

<<sec:approximate_ifft>>

ZIP file containing the data and matlab files   ignore

All the files (data and Matlab scripts) are accessible here.

Introduction   ignore

The technique comes from cite:preumont94_random_vibrat_spect_analy (section 12.11). It is used to compute a periodic signal that has any Power Spectral Density defined. It makes used of the Unversed Fast Fourier Transform (IFFT).

Signal's PSD

We load the PSD of the signal we wish to replicate.

  load('./mat/dist_psd.mat', 'dist_f');

We remove the first value with very high PSD.

  dist_f.f = dist_f.f(3:end);
  dist_f.psd_gm = dist_f.psd_gm(3:end);

The PSD of the signal is shown on figure ref:fig:psd_original.

  <<plt-matlab>>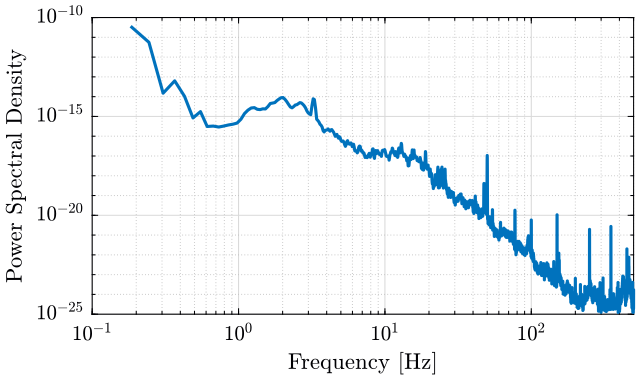

PSD of the original signal (png, pdf)

Algorithm

We define some parameters that will be used in the algorithm.

  Fs = 2*dist_f.f(end);    % Sampling Frequency of data is twice the maximum frequency of the PSD vector [Hz]
  N  = 2*length(dist_f.f); % Number of Samples match the one of the wanted PSD
  T0 = N/Fs;               % Signal Duration [s]
  df = 1/T0;               % Frequency resolution of the DFT [Hz]
                           % Also equal to (dist_f.f(2)-dist_f.f(1))

We then specify the wanted PSD.

  phi = dist_f.psd_gm;

We create amplitudes corresponding to wanted PSD.

  C = zeros(N/2,1);
  for i = 1:N/2
    C(i) = sqrt(phi(i)*df);
  end

Finally, we add some random phase to C.

  theta = 2*pi*rand(N/2,1); % Generate random phase [rad]

  Cx = [0 ; C.*complex(cos(theta),sin(theta))];
  Cx = [Cx; flipud(conj(Cx(2:end)))];;

Obtained Time Domain Signal

The time domain data is generated by an inverse FFT.

The ifft Matlab does not take into account the sampling frequency, thus we need to normalize the signal.

  u = N/sqrt(2)*ifft(Cx); % Normalisation of the IFFT
  t = linspace(0, T0, N+1); % Time Vector [s]

  <<plt-matlab>>

Obtained signal in the time domain (png, pdf)

PSD Comparison

We duplicate the time domain signal to have a longer signal and thus a more precise PSD result.

  u_rep = repmat(u, 10, 1);

We compute the PSD of the obtained signal with the following commands.

  nx = length(u_rep);
  na = 16;
  win = hanning(floor(nx/na));

  [pxx, f] = pwelch(u_rep, win, 0, [], Fs);

Finally, we compare the PSD of the original signal and the obtained signal on figure ref:fig:psd_comparison.

  <<plt-matlab>>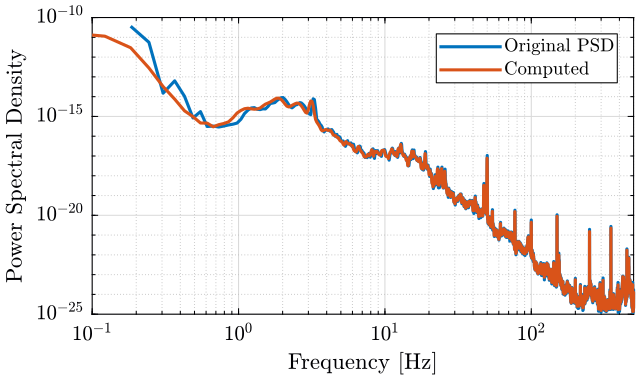

Comparison of the PSD of the original signal and the PSD of the obtained signal (png, pdf)

Compute the Noise level and Signal level from PSD

<<sec:compute_psd_levels>>

ZIP file containing the data and matlab files   ignore

All the files (data and Matlab scripts) are accessible here.

Introduction   ignore

We here make use of the Power Spectral Density to estimate either the noise level or the amplitude of a deterministic signal. Everything is explained in cite:schmid12_how_to_use_fft_matlab sections 5 and 6.

Time Domain Signal

Let's first define the number of sample and the sampling time.

  N  = 10000; % Number of Sample
  dt = 0.001; % Sampling Time [s]

  t = dt*(0:1:N-1)'; % Time vector [s]

We generate of signal that consist of:

• a white noise with an RMS value equal to anoi
• two sinusoidal signals

The parameters are defined below.

  asig = 0.1; % Amplitude of the signal [V]
  fsig = 10;  % Frequency of the signal [Hz]

  ahar = 0.5; % Amplitude of the harmonic [V]
  fhar = 50;  % Frequency of the harmonic [Hz]

  anoi = 1e-3; % RMS value of the noise

The signal $x$ is generated with the following code and is shown in figure fig:time_domain_x_zoom.

  x = anoi*randn(N, 1) + asig*sin((2*pi*fsig)*t) + ahar*sin((2*pi*fhar)*t);

  <<plt-matlab>>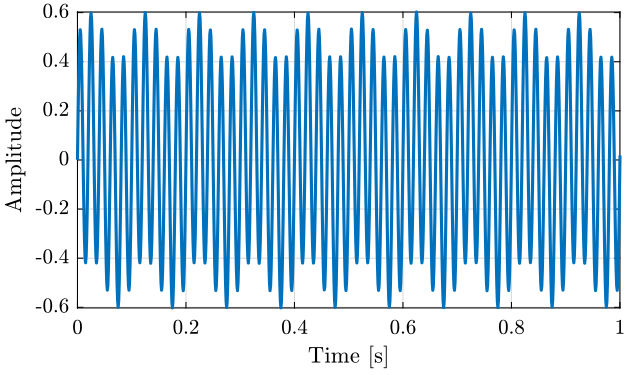

Time Domain Signal (png, pdf)

Estimation of the magnitude of a deterministic signal

Let's compute the PSD of the signal using the blackmanharris window.

  nx = length(x);
  na = 8;
  win = blackmanharris(floor(nx/na));

  [pxx, f] = pwelch(x, win, 0, [], 1/dt);

Normalization of the PSD.

  CG = sum(win)/(nx/na);
  NG = sum(win.^2)/(nx/na);
  fbin = f(2) - f(1);

  pxx_norm = pxx*(NG*fbin/CG^2);

We determine the frequency bins corresponding to the frequency of the signals.

  isig = round(fsig/fbin)+1;
  ihar = round(fhar/fbin)+1;

The theoretical RMS value of the signal is:

  srmt = asig/sqrt(2); % Theoretical value of signal magnitude

And we estimate the RMS value of the signal by either integrating the PSD around the frequency of the signal or by just taking the maximum value.

  srms = sqrt(sum(pxx(isig-5:isig+5)*fbin)); % Signal spectrum integrated
  srmsp = sqrt(pxx_norm(isig) * NG*fbin/CG^2); % Maximum read off spectrum

	Signal Magnitude [rms]
Theoretical	0.0707
Integrated	0.0707
Maximum	0.0529

We see that the integrated value gives a good approximate of the true RMS value whereas the maximum value give an poor approximate. This effect is called scallop loss. Thus, always the integrated method should be used.

Estimation of the noise level

The noise level can also be computed using the integration method.

The theoretical RMS noise value is.

  nth = anoi/sqrt(max(f)) % Theoretical value [V/sqrt(Hz)]

We can estimate this RMS value by integrating the PSD at frequencies where the power of the noise signal is above the power of the other signals.

  navg = sqrt(mean(pxx_norm([ihar+10:end]))) % pwelch output averaged

	test
Theoretical	4.472e-05
Average	4.337e-05

The estimate of the noise level is quite good.

Further Notes

PSD of ADC quantization noise

This is taken from here.

Let's note:

• $q$ is the corresponding value in [V] of the least significant bit (LSB)
• $\Delta V$ is the full range of the ADC in [V]
• $n$ is the number of ADC's bits
• $f_s$ is the sample frequency in [Hz]

Let's suppose that the ADC is ideal. The only noise comes from the quantization error. Interestingly, the noise amplitude is uniformly distributed.

The quantization noise can take a value between $\pm q/2$, and the probability density function is constant in this range (i.e., it’s a uniform distribution). Since the integral of the probability density function is equal to one, its value will be $1/q$ for $-q/2 < e < q/2$ (Fig. fig:probability_density_function_adc).

Probability density function $p(e)$ of the ADC error $e$

Now, we can calculate the time average power of the quantization noise as

\begin{equation} P_q = \int_{-q/2}^{q/2} e^2 p(e) de = \frac{q^2}{12} \end{equation}

The other important parameter of a noise source is the power spectral density (PSD), which indicates how the noise power spreads in different frequency bands. To find the power spectral density, we need to calculate the Fourier transform of the autocorrelation function of the noise.

Assuming that the noise samples are not correlated with one another, we can approximate the autocorrelation function with a delta function in the time domain. Since the Fourier transform of a delta function is equal to one, the power spectral density will be frequency independent. Therefore, the quantization noise is white noise with total power equal to $P_q = \frac{q^2}{12}$.

Thus, the two-sided PSD (from $\frac{-f_s}{2}$ to $\frac{f_s}{2}$), we should divide the noise power $P_q$ by $f_s$:

\begin{equation} \int_{-f_s/2}^{f_s/2} \Gamma(f) d f = f_s \Gamma = \frac{q^2}{12} \end{equation}

Finally:

\begin{equation} \begin{aligned} \Gamma &= \frac{q^2}{12 f_s} \\ &= \frac{\left(\frac{\Delta V}{2^n}\right)^2}{12 f_s} \text{ in } \left[ \frac{V^2}{Hz} \right] \end{aligned} \end{equation}

Bibliography   ignore

bibliographystyle:unsrt bibliography:ref.bib