88 KiB
Nano-Hexapod on top of a Spindle - Test Bench
Introduction ignore
Test-Bench Description
Introduction ignore
Alignment
Procedure:
- Align bottom sphere with the spindle rotation axis (~ 10um)
- Align top sphere with the spindle rotation axis (~ 10um)
Short Range metrology system
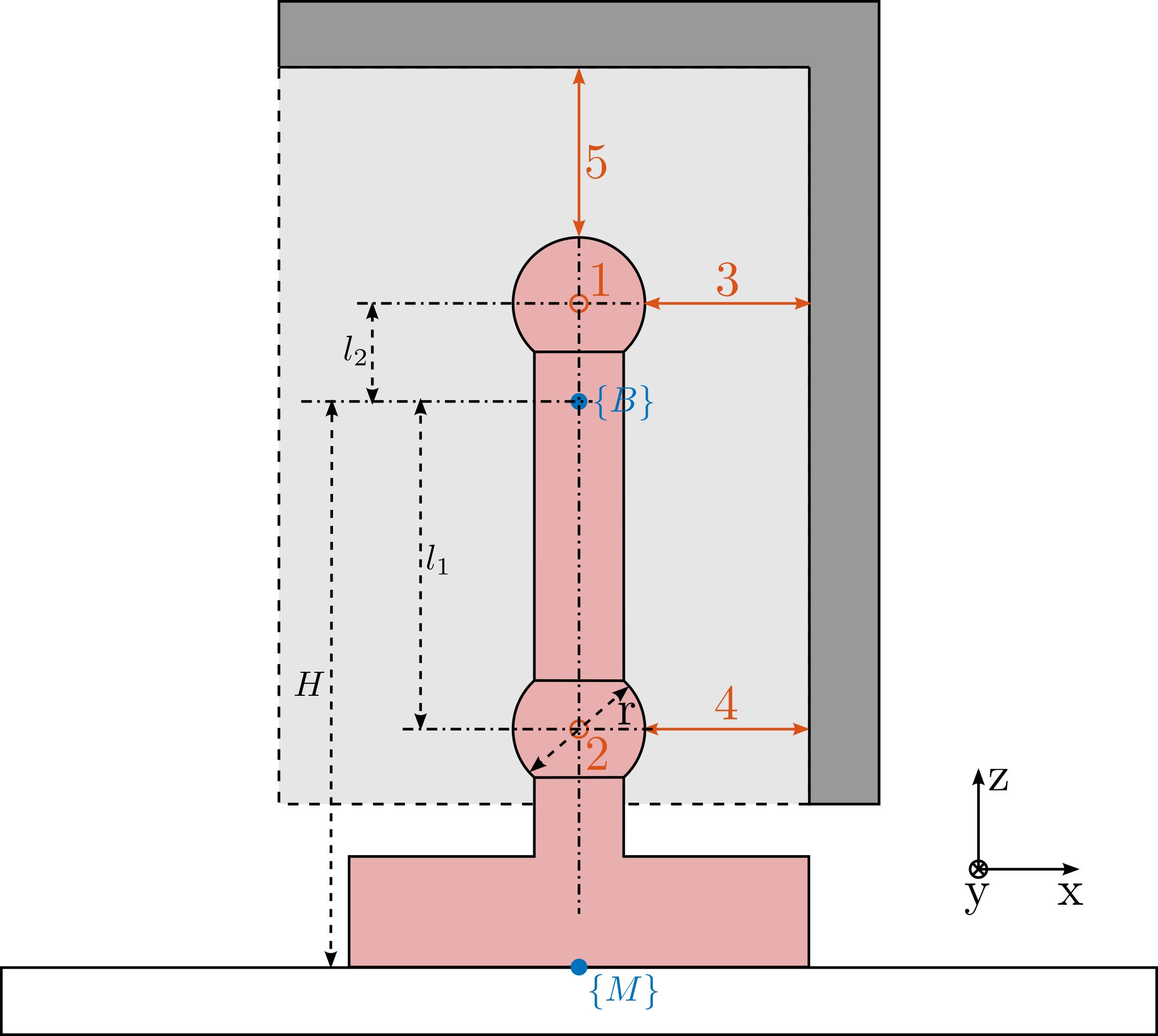
There are 5 interferometers pointing at 2 spheres as shown in Figure ref:fig:LION_metrology_interferometers.
| Value | |
|---|---|
| Sphere Diameter | 25.4mm |
| Distance between the spheres | 76.2mm |
Assumptions:
- Interferometers are perfectly positioned / oriented
- Sphere is perfect
Compute the Jacobian matrix:
- From pure X-Y-Z-Rx-Ry small motions, compute the effect on the 5 measured distances
- Compute the matrix
- Inverse the matrix
- Verify that it is working with simple example (for example using Solidworkds)
We have the following set of equations:
\begin{align} d_1 &= -D_y + l_2 R_x \\ d_2 &= -D_y - l_1 R_x \\ d_3 &= -D_x - l_2 R_y \\ d_4 &= -D_x + l_1 R_y \\ d_5 &= -D_z \end{align}That can be written as a linear transformation:
\begin{equation} \begin{bmatrix} d_1 \\ d_2 \\ d_3 \\ d_4 \\ d_5 \end{bmatrix} = \begin{bmatrix} 0 & -1 & 0 & l_2 & 0 \\ 0 & -1 & 0 & -l_1 & 0 \\ -1 & 0 & 0 & 0 & -l_2 \\ -1 & 0 & 0 & 0 & l_1 \\ 0 & 0 & -1 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} D_x \\ D_y \\ D_z \\ R_x \\ R_y \end{bmatrix} \end{equation}By inverting the matrix, we obtain the Jacobian relation:
\begin{equation} \begin{bmatrix} D_x \\ D_y \\ D_z \\ R_x \\ R_y \end{bmatrix} = \begin{bmatrix} 0 & -1 & 0 & l_2 & 0 \\ 0 & -1 & 0 & -l_1 & 0 \\ -1 & 0 & 0 & 0 & -l_2 \\ -1 & 0 & 0 & 0 & l_1 \\ 0 & 0 & -1 & 0 & 0 \end{bmatrix}^{-1} \cdot \begin{bmatrix} d_1 \\ d_2 \\ d_3 \\ d_4 \\ d_5 \end{bmatrix} \end{equation}%% Parameters
H = 150e-3;
l1 = (150-38-52)*1e-3;
l2 = (52+38+76.2-150)*1e-3;%% Transformation matrix
Hm = [ 0 -1 0 l2 0;
0 -1 0 -l1 0;
-1 0 0 0 -l2;
-1 0 0 0 l1;
0 0 -1 0 0];| d1 | d2 | d3 | d4 | d5 | |
|---|---|---|---|---|---|
| Dx | 0.0 | 0.0 | -0.79 | -0.21 | 0.0 |
| Dy | -0.79 | -0.21 | -0.0 | -0.0 | 0.0 |
| Dz | 0.0 | 0.0 | 0.0 | 0.0 | -1.0 |
| Rx | 13.12 | -13.12 | 0.0 | -0.0 | 0.0 |
| Ry | 0.0 | 0.0 | -13.12 | 13.12 | 0.0 |
Spindle errors
Introduction ignore
The spindle is rotated at 60rpm during 10 turns. The signal of all 5 interferometers are recorded.
data = load(sprintf('%s/spindle/mat/2022-12-20_15-47_sec_test.mat', data_dir));Errors in $D_x$ and $D_y$
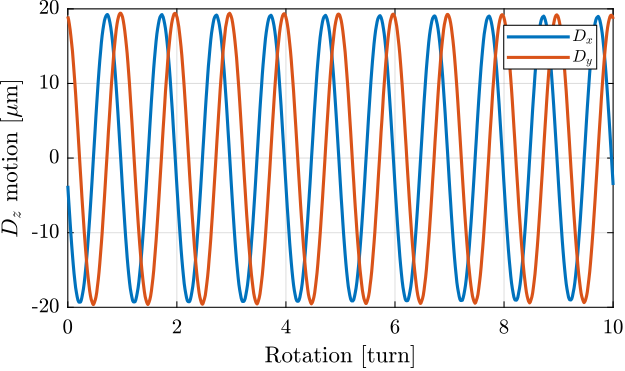
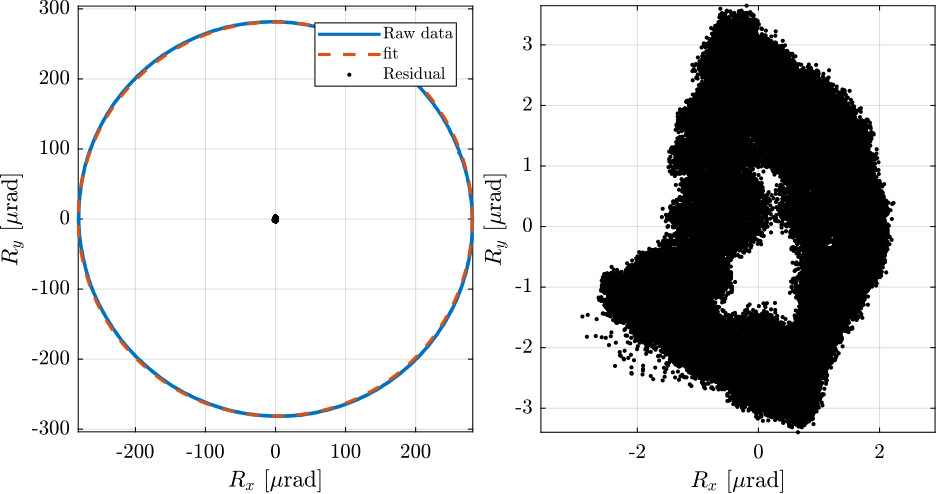
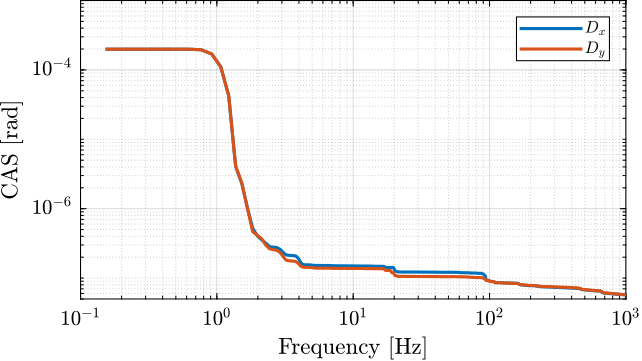
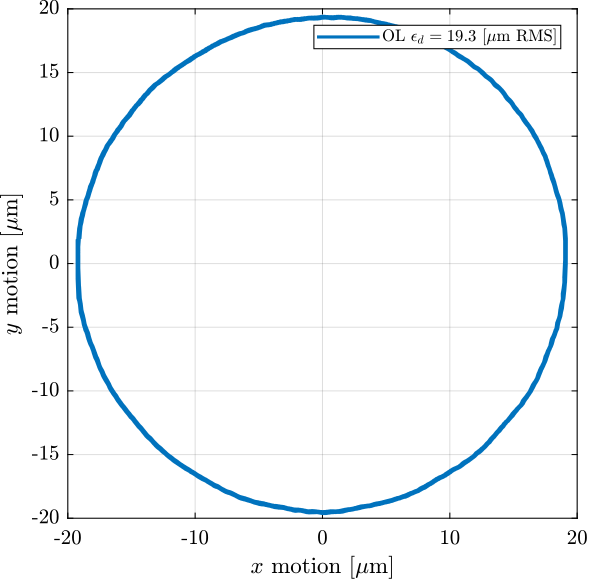
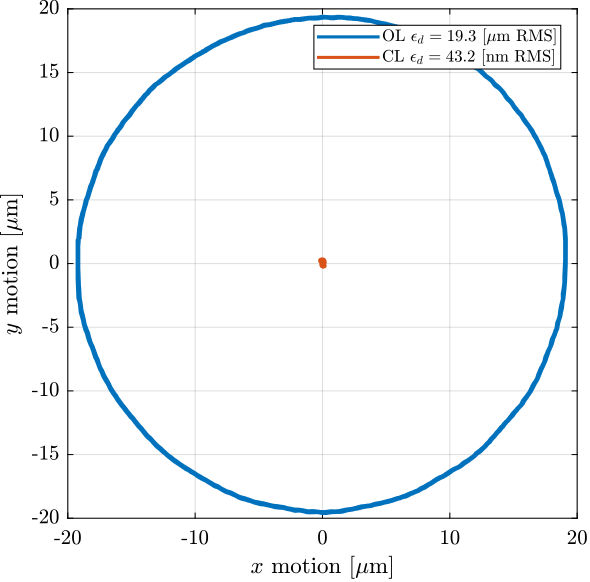
Because of the eccentricity of the reference surfaces (the spheres), we expect the motion in the X-Y plane to be a circle as a first approximation. We can first see that in Figure ref:fig:dx_dy_motion_rotation that shows the measured $D_x$ and $D_y$ motion as a function of the $R_z$ angle.
%% Circle Fit
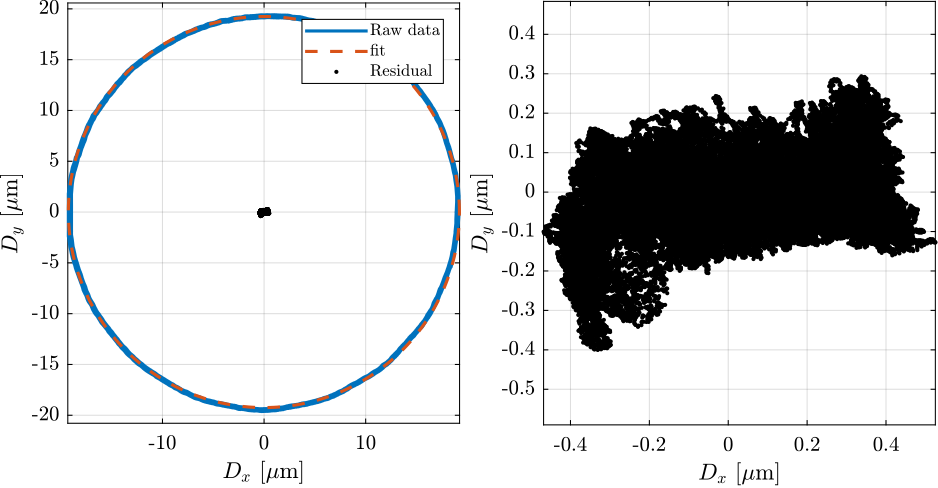
[xc,yc,R,a] = circlefit(data.Dx_int, data.Dy_int);A circle is fit, and the obtained radius of the circle (i.e. the excentricity) is estimated to be:
Error linked to excentricity = 19 um
The motion in the X-Y plane as well as the circle fit and the residual motion (circle fit subtracted from the measured motion) are shown in Figure ref:fig:dx_dy_spindle_rotation.
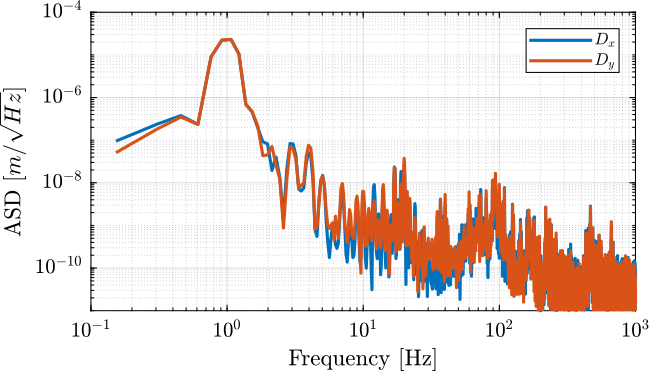
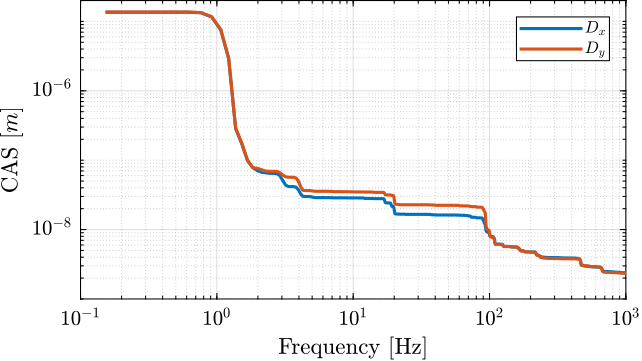
Let's now analyse the frequency content in the signal.
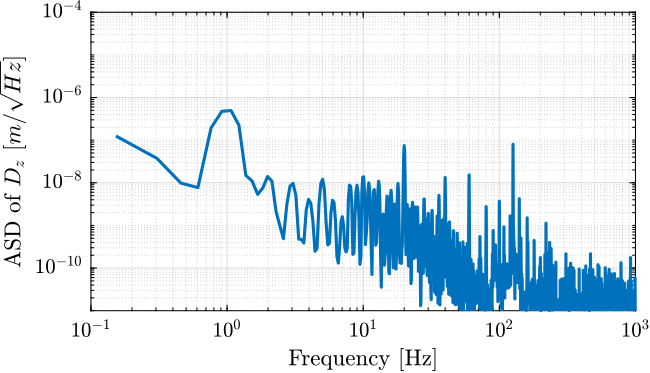
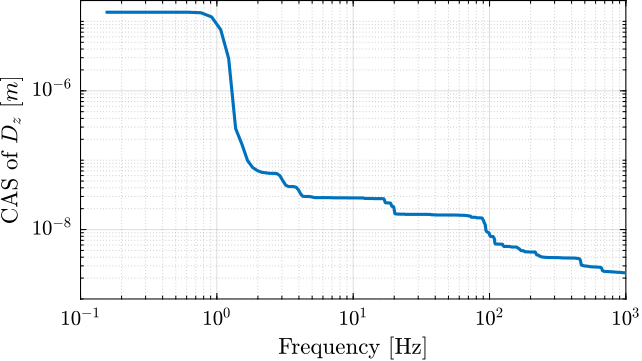
Errors in vertical motion $D_z$
The top interferometer is measuring the vertical motion of the sphere.
However, if the top sphere is not perfectly aligned with the spindle axis, there will also measure some vertical motion due to this excentricity.
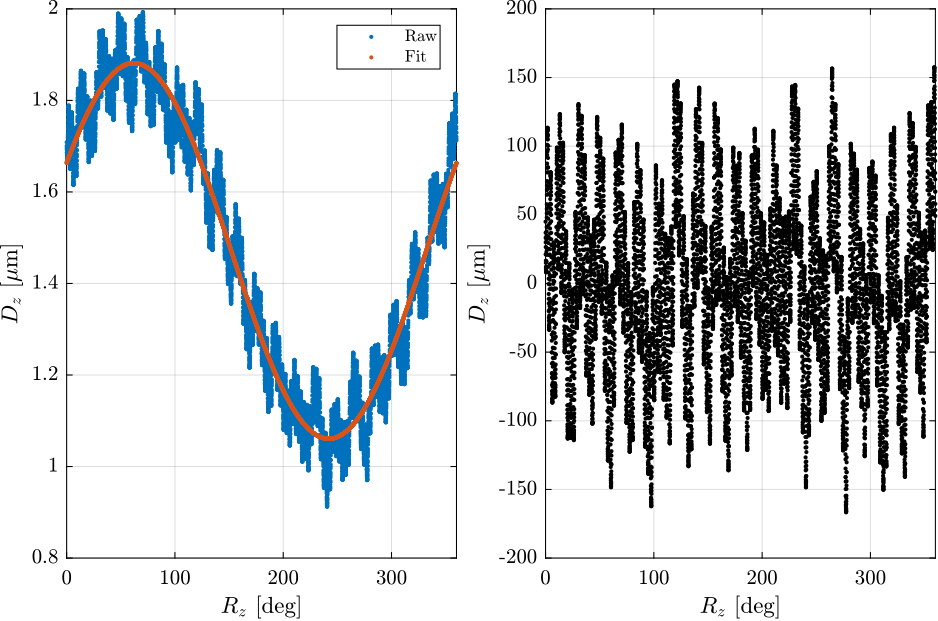
Let's fit a sinus with a period of one turn.
%% Fit Sinus with period of one turn
x1 = data.Rz(data.t<1);
y1 = data.Dz_int(data.t<1);
fit = @(b,x) b(1).*sin(x + b(2)) + b(3); % Function to fit
fcn = @(b) sum((fit(b,x1) - y1).^2); % Least-Squares cost function
s1 = fminsearch(fcn, [1e-6; 30; 1.5e-6]) % Minimise Least-SquaresErrors linked to excentricity = 410 [nm]
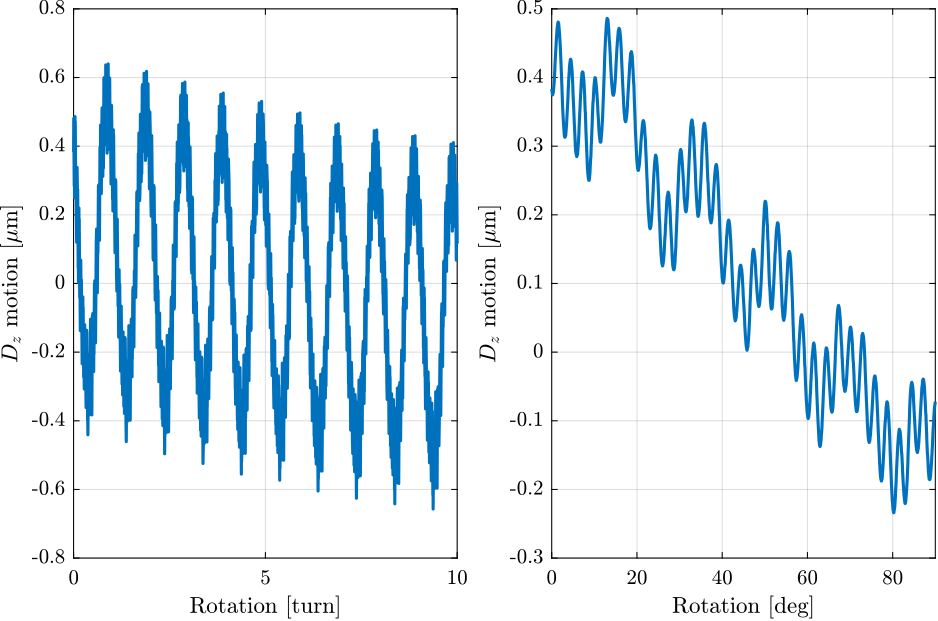
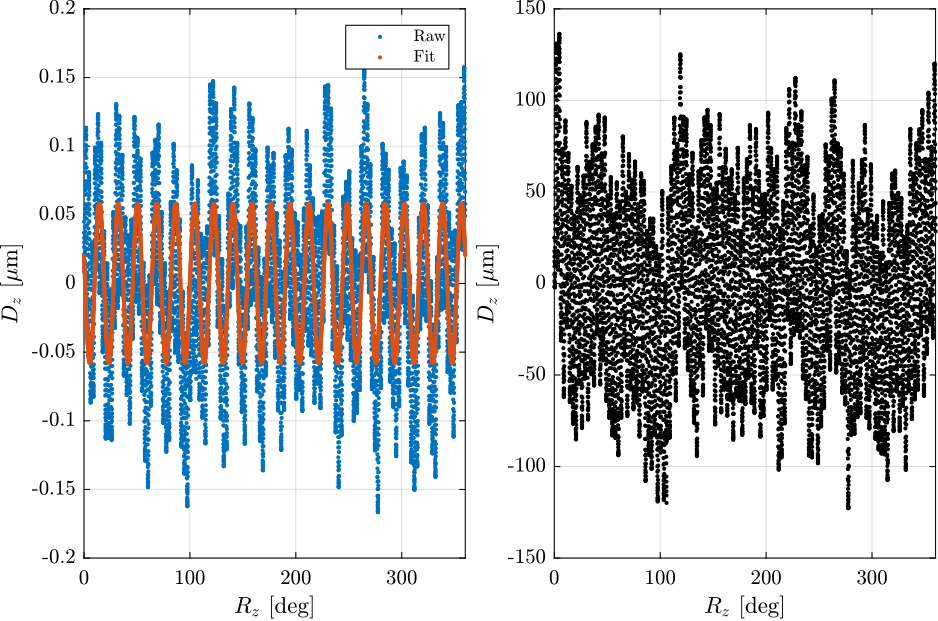
If we look at the remaining motion after removing the effect of the eccentricity (Figure ref:fig:dz_motion_rotation_excentricity, right), we can see a signal with 20 periods every turn. Let's fit this.
%% Fit Sinus with period of 18 degrees (one electrical period)
x2 = data.Rz(data.t<1)*20;
y2 = y1 - fit(s1, x1);
fit = @(b,x) b(1).*sin(x + b(2)) + b(3); % Function to fit
fcn = @(b) sum((fit(b,x2) - y2).^2); % Least-Squares cost function
s2 = fminsearch(fcn, [50e-9; 30; 0]) % Minimise Least-SquaresErrors linked to spindle motor = 58 [nm]
Let's look at the signal in the frequency domain.
On top of the peak at 1Hz (excentricity) and at 20Hz (number of pole pairs), we can observe a frequency of 126Hz (i.e. 126 periods per turn, approx 2.85 deg).
Could this be related to the air bearing system?
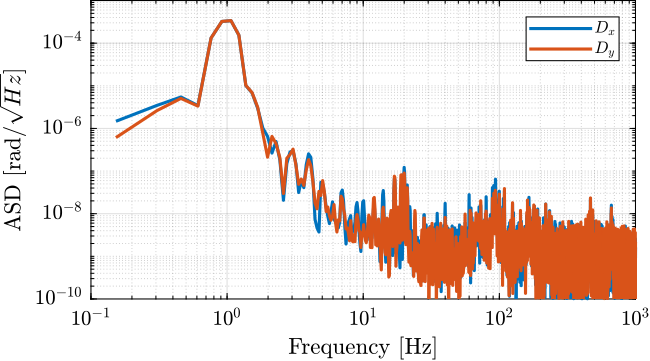
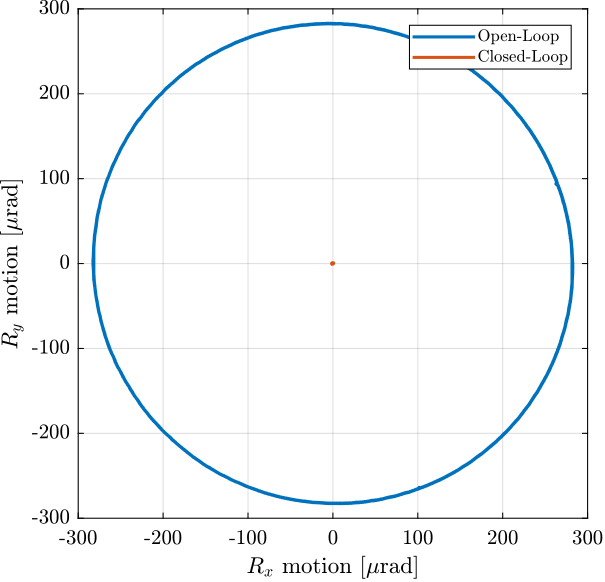
Angle errors in $R_x$ and $R_y$
Simscape Model
Introduction ignore
A 3D view of the Simscape model is shown in Figure ref:fig:simscape_model_spindle_bench. The Spindle is represented by a Bushing joint. Axial, radial and tilt stiffnesses are taken from the Spindle datasheet (see Table).
| Stiffness | Value | Unit |
|---|---|---|
| Axial | 402 | $N/\mu m$ |
| Radial | 226 | $N/\mu m$ |
| Tilt | 2380 | $Nm/mrad$ |
The metrology system consists of 5 distance measurements (represented by the red lines in Figure ref:fig:simscape_model_spindle_bench).
Simscape model parameters
The nano-hexapod is initialized.
%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('MO_B', 150e-3, ...
'actuator_type', '2dof', ...
'motion_sensor_type', 'plates');%% Initialize Spindle
spindle = struct();
%% Stiffnesses
spindle.kx = 226e6; % Radial stiffness in [N/m]
spindle.ky = 226e6; % Radial stiffness in [N/m]
spindle.kz = 402e6; % Axial stiffness in [N/m]
spindle.krx = 2.38e6; % Tilt stiffness in [Nm/rad]
spindle.kry = 2.38e6; % Tilt stiffness in [Nm/rad]
spindle.krz = 0; % Rotation stiffness in [Nm/rad]
%% Damping
spindle.cx = 1/(2*0.01)/(sqrt(spindle.kx*50)); % Radial damping in [N/(m/s)]
spindle.cy = 1/(2*0.01)/(sqrt(spindle.ky*50)); % Radial damping in [N/(m/s)]
spindle.cz = 1/(2*0.01)/(sqrt(spindle.kz*50)); % Axial damping in [N/(m/s)]
spindle.crx = 1/(2*0.01)/(sqrt(spindle.krx*50)); % Tilt damping in [Nm/(rad/s)]
spindle.cry = 1/(2*0.01)/(sqrt(spindle.kry*50)); % Tilt damping in [Nm/(rad/s)]
spindle.crz = 0; % Rotation damping in [Nm/(rad/s)]The Jacobian matrix that computes the $[x, y, z, R_x, R_y]$ motion of the sample from the 5 interferometers is defined below.
% Sensor Jacobian (Interferometers to Cartesian motion)
J_int_to_X_ = [ 0 0 -0.787401574803149 -0.212598425196851 0;
-0.78740157480315 -0.21259842519685 0 0 0;
0 0 0 0 -1;
13.1233595800525 -13.1233595800525 0 0 0;
0 0 -13.1233595800525 13.1233595800525 0];Control Architecture
Let's note:
- $d\mathcal{L}_m = [d_{\mathcal{L}_1},\ d_{\mathcal{L}_2},\ d_{\mathcal{L}_3},\ d_{\mathcal{L}_4},\ d_{\mathcal{L}_5},\ d_{\mathcal{L}_6}]$ the measurement of the 6 encoders fixed to the nano-hexapod
- $\bm{\tau}_m = [\tau_{m_1},\ \tau_{m_2},\ \tau_{m_3},\ \tau_{m_4},\ \tau_{m_5},\ \tau_{m_6}]$ the voltages measured by the 6 force sensors
- $\bm{u} = [u_1,\ u_2,\ u_3,\ u_4,\ u_5,\ u_6]$ the voltages send to the voltage amplifiers for the 6 piezoelectric actuators
- $R_z$ the spindle measured angle (encoder)
- $\bm{d}_m = [d_1,\ d_2,\ d_3,\ d_4,\ d_5]$ the distances measured by the 5 interferometers (see Figure ref:fig:LION_metrology_interferometers_bis)
Computation of the strut errors from the external metrology
The following frames are defined:
- $\{ W \}$: the frame that represents the wanted pose of the sample
- $\{ M \}$: the frame that represents the measured pose of the sample (estimated from the 5 interferometers and the spindle encoder)
- $\{ G \}$: the frame fixed to the granite and positioned at the sample's center
- $\{ H \}$: the frame fixed to the the spindle rotor, and positioned at the sample's center
We can express several homogeneous transformation matrices.
Frame fixed to the spindle rotor (centered on the sample's position), expressed in the frame of the granite:
\begin{equation} {}^{G}\bm{T}_H = \begin{bmatrix} cos(R_z) & -sin(R_z) & 0 & 0 \\ sin(R_z) & cos(R_z) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{equation}with $R_z$ the spindle encoder.
Wanted position expressed in the frame of the granite:
\begin{equation} {}^{G}\bm{T}_W = \begin{bmatrix} & & & r_{D_x} \\ & \bm{R}_x(r_{R_x}) \bm{R}_y(r_{R_y}) \bm{R}_z(r_{R_z}) & & r_{D_y} \\ & & & r_{D_z} \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{equation}with $\bm{R}(r_{R_x}, r_{R_y}, r_{R_z})$ representing the wanted orientation of the sample with respect to the granite. Typically, $r_{R_x} = 0$, $r_{R_y} = 0$ and $r_{R_z}$ corresponds to the spindle encoder $R_z$.
Measured position of the sample with respect to the granite:
\begin{equation} {}^{G}\bm{T}_M = \begin{bmatrix} & & & y_{D_x} \\ & \bm{R}_x(y_{R_x}) \bm{R}_y(y_{R_y}) \bm{R}_z(R_z) & & y_{D_y} \\ & & & y_{D_z} \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{equation}with $R_z$ the spindle encoder, and $[y_{D_x},\ y_{D_y},\ y_{D_z},\ y_{R_x},\ y_{R_y}]$ are obtained from the 5 interferometers:
\begin{equation} \begin{bmatrix} y_{D_x} \\ y_{D_y} \\ y_{D_z} \\ y_{R_x} \\ y_{R_y} \end{bmatrix} = \begin{bmatrix} 0 & -1 & 0 & l_2 & 0 \\ 0 & -1 & 0 & -l_1 & 0 \\ -1 & 0 & 0 & 0 & -l_2 \\ -1 & 0 & 0 & 0 & l_1 \\ 0 & 0 & -1 & 0 & 0 \end{bmatrix}^{-1} \cdot \begin{bmatrix} d_1 \\ d_2 \\ d_3 \\ d_4 \\ d_5 \end{bmatrix} \end{equation}In order to have the position error in the frame of the nano-hexapod, we have to compute ${}^M\bm{T}_W$:
\begin{align} {}^M\bm{T}_W &= {}^M\bm{T}_G \cdot {}^G\bm{T}_W \\ &= {{}^G\bm{T}_M}^{-1} \cdot {}^G\bm{T}_W \end{align}The inverse of the transformation matrix can be obtained by
\begin{equation} {}^B\bm{T}_A = {}^A\bm{T}_B^{-1} = \left[ \begin{array}{ccc|c} & & & \\ & {}^A\bm{R}_B^T & & -{}^A \bm{R}_B^T {}^A\bm{P}_{O_B} \\ & & & \cr \hline 0 & 0 & 0 & 1 \\ \end{array} \right] \end{equation}The position errors $\bm{\epsilon}_{\mathcal{X}} = [\epsilon_{D_x},\ \epsilon_{D_y},\ \epsilon_{D_z},\ \epsilon_{R_x},\ \epsilon_{R_y},\ \epsilon_{R_z}]$ expressed in a frame fixed to the nano-hexapod can be extracted from ${}^W\bm{T}_M$:
- $\epsilon_{D_x} = {}^M\bm{T}_W(1,4)$
- $\epsilon_{D_y} = {}^M\bm{T}_W(2,4)$
- $\epsilon_{D_z} = {}^M\bm{T}_W(3,4)$
- $\epsilon_{R_y} = \text{atan2}({}^M\bm{T}_W(1,3), \sqrt{{}^M\bm{T}_W(1,1)^2 + {}^M\bm{T}_W(1,2)^2})$
- $\epsilon_{R_x} = \text{atan2}(\frac{-{}^M\bm{T}_W(2,3)}{\cos(\epsilon_{R_y})}, \frac{{}^M\bm{T}_W(3,3)}{\cos(\epsilon_{R_y})})$
- $\epsilon_{R_z} = \text{atan2}(\frac{-{}^M\bm{T}_W(1,2)}{\cos(\epsilon_{R_y})}, \frac{{}^M\bm{T}_W(1,1)}{\cos(\epsilon_{R_y})})$
Finally, the strut errors $\bm{\epsilon}_{\mathcal{L}} = [\epsilon_{\matcal{L}_1},\ \epsilon_{\matcal{L}_2},\ \epsilon_{\matcal{L}_3},\ \epsilon_{\matcal{L}_4},\ \epsilon_{\matcal{L}_5},\ \epsilon_{\matcal{L}_6}]$ can be computed from:
\begin{equation} \bm{\epsilon}_\mathcal{L} = \bm{J} \cdot \bm{\epsilon}_\mathcal{X} \end{equation}IFF Plant
start_angle = 0; % [deg]options = linearizeOptions;
options.SampleTime = 0;
%% Identify the transfer function from u to taum
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
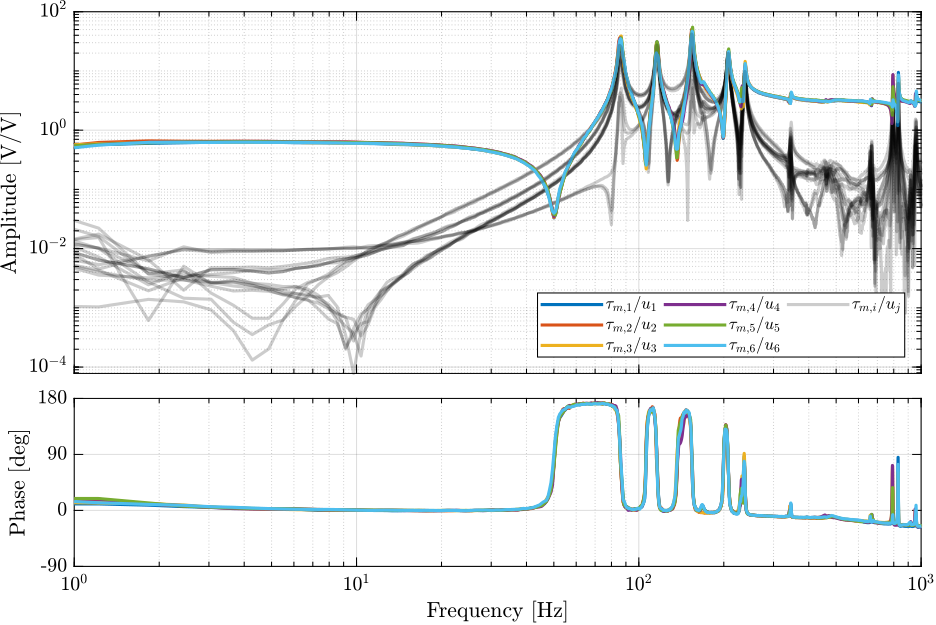
io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors
%% Perform the model extraction
G_iff = linearize(mdl, io, 0.0, options);DVF Plant
start_angle = 0; % [deg]options = linearizeOptions;
options.SampleTime = 0;
%% Identify the transfer function from u to taum
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
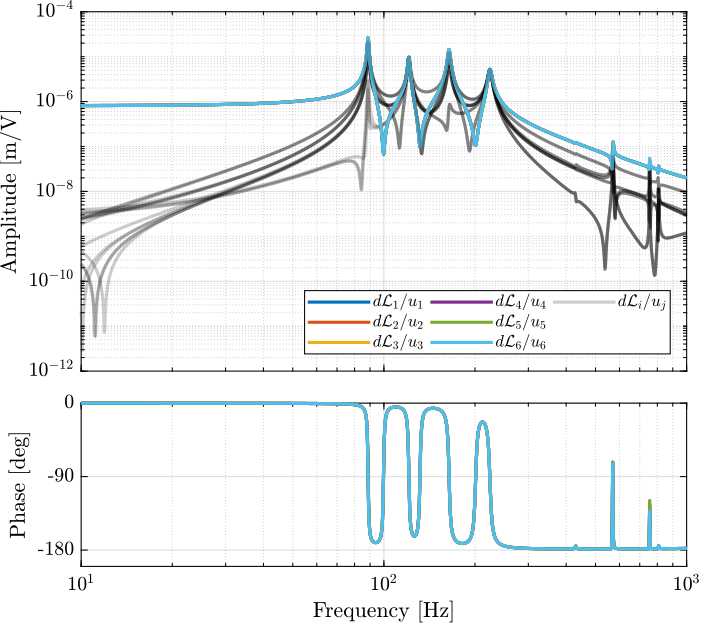
io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Encoders
%% Perform the model extraction
G_dvf = linearize(mdl, io, 0.0, options);HAC Plant
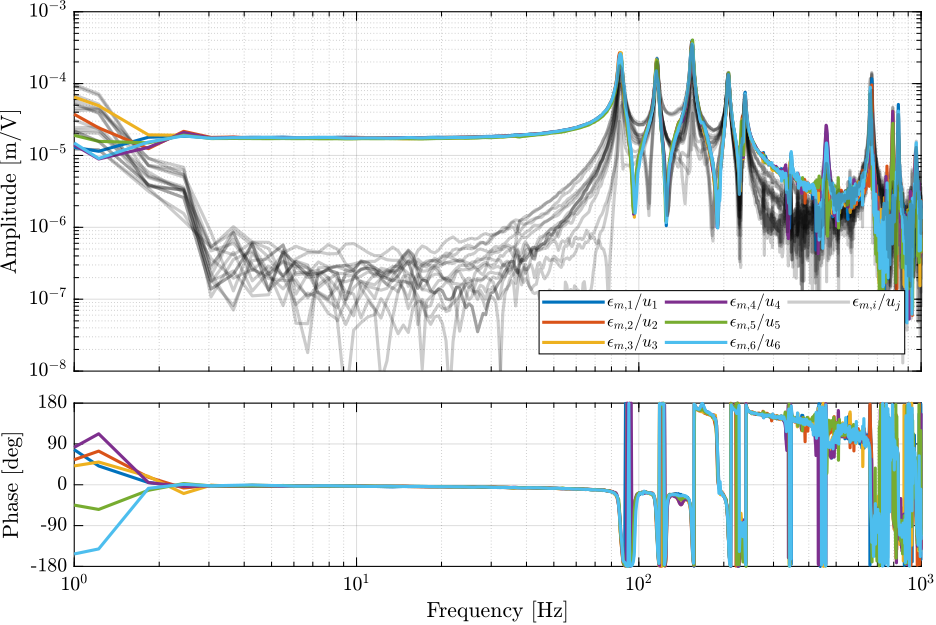
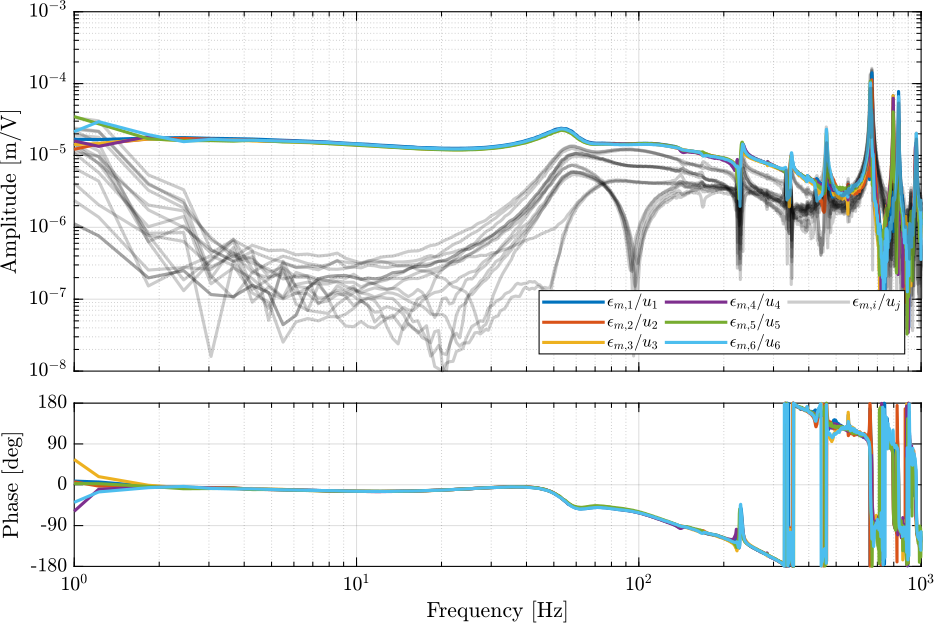
The transfer functions from the 6 actuator inputs to the 6 estimated strut errors are extracted from the Simscape model.
start_angle = 0; % [deg]options = linearizeOptions;
options.SampleTime = 0;
%% Identify the transfer function from u to taum
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/J_X_to_L'], 1, 'openoutput'); io_i = io_i + 1; % Estimated Strut Error
%% Perform the model extraction
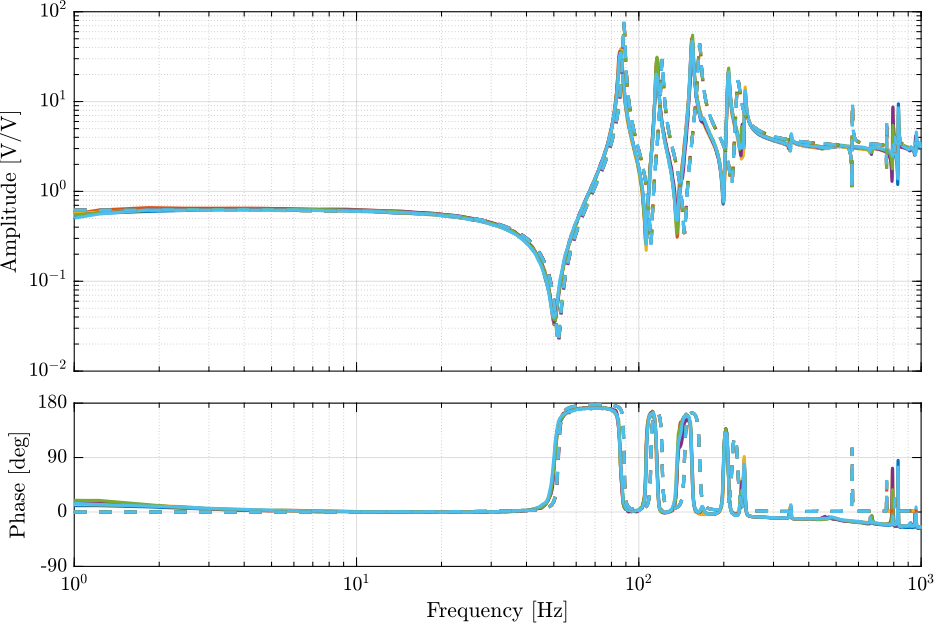
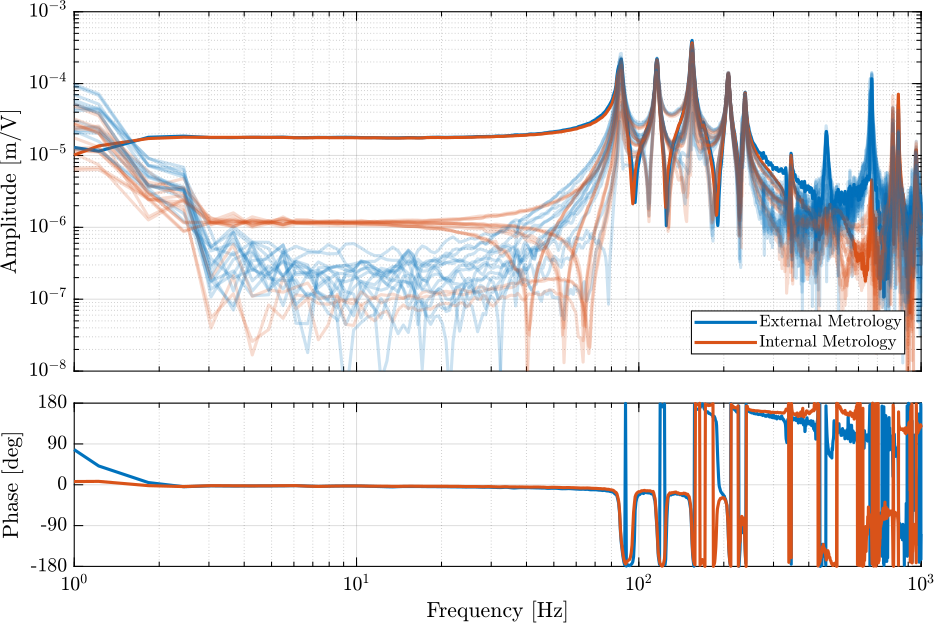
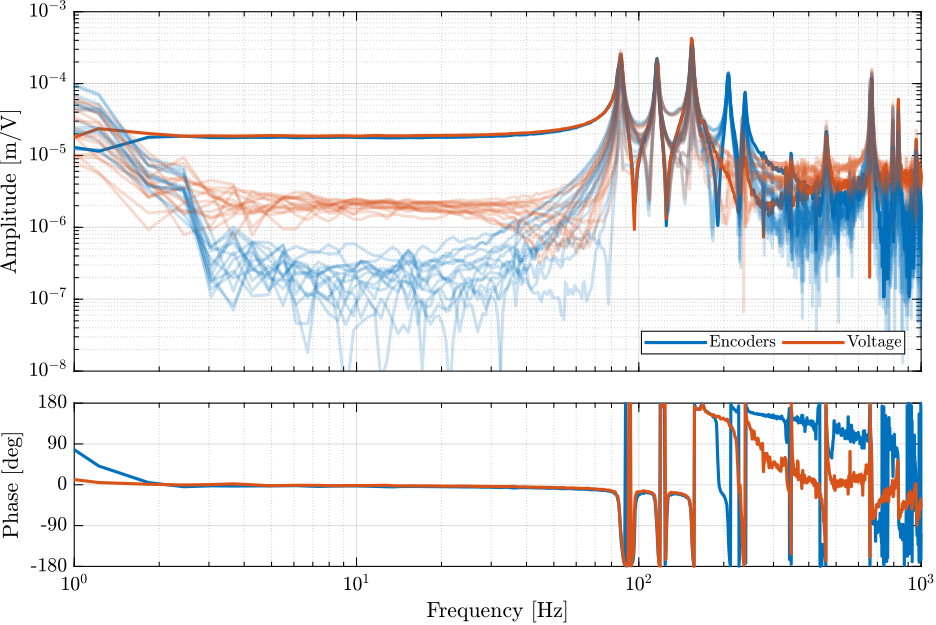
G = linearize(mdl, io, 0.0, options);The obtained transfer functions are shown in Figure ref:fig:simscape_model_hac_plant.
We can see that the system is well decoupled at low frequency (i.e. below the first resonance of the Nano-Hexapod).
Control Experiment
IFF Plant
IFF Controller
Open Loop Plant
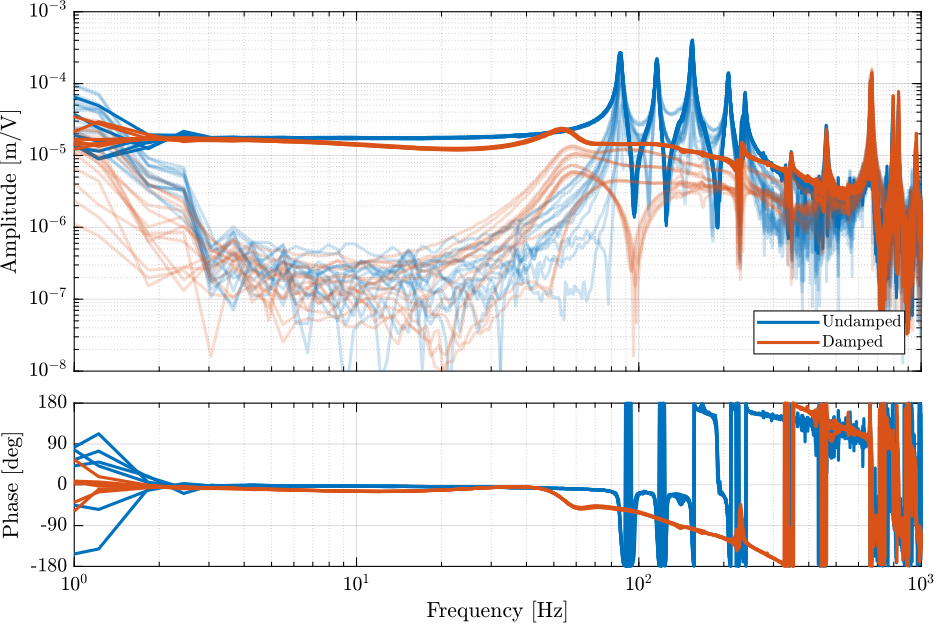
Damped Plant
HAC Controller
%% Lead to increase phase margin
a = 4; % Amount of phase lead / width of the phase lead / high frequency gain
wc = 2*pi*15; % Frequency with the maximum phase lead [rad/s]
H_lead = (1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));
%% Low Pass filter to increase robustness
H_lpf = 1/(1 + s/2/pi/60);
%% Notch at the top-plate resonance
gm = 0.02;
xi = 0.3;
wn = 2*pi*665;
H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);
%% Decentralized HAC
Khac_iff_struts = (8e3) * ... % Gain
H_notch * ... % Notch
H_lpf * ... % LPF
(2*pi*100/s) * ... % Integrator
eye(6); % 6x6 Diagonal