phd-test-bench-nano-hexapod/test-bench-nano-hexapod.org

Nano-Hexapod - Test Bench

• Introduction
• Mounting Procedure
  • Mounting Goals
  • Mounting Bench
  • Mounting Procedure
  • Nano-Hexapod Mounting
    • Introduction
    • Plates
    • Mounting Tool
    • Mounted Hexapod
• Encoders fixed to the struts
  • Introduction
  • Identification of the dynamics
    • Introduction
    • Load Measurement Data
    • Spectral Analysis - Setup
    • Transfer function from Actuator to Encoder
    • Transfer function from Actuator to Force Sensor
    • Save Identified Plants
  • Jacobian matrices and centralized plants
    • Introduction
    • Jacobian Matrices
    • Obtained Centralized plants
    • Centralized plant using the Force sensors
  • Comparison with the Simscape Model
    • Introduction
    • Simscape Model - Identification
    • Dynamics from Actuator to Force Sensors
    • Dynamics from Actuator to Encoder
    • Using Flexible model
  • Integral Force Feedback
    • Introduction
    • IFF Control Law and Optimal Gain
    • Effect of IFF on the transfer function from actuator to encoder - Simulations
    • Effect of IFF on the plant - Experimental Results
      • Introduction
      • Load Data
      • Spectral Analysis - Setup
      • DVF Plant
      • Experimental Results - Comparison of the un-damped and fully damped system
    • Experimental Results - Damped Plant with Optimal gain
      • Introduction
      • Load Data
      • Spectral Analysis - Setup
      • DVF Plant
    • Comparison with the Flexible model
    • Conclusion
  • Modal Analysis
    • Introduction
    • Obtained Mode Shapes
    • Nano-Hexapod Compliance - Effect of IFF
    • Comparison with the Simscape Model
  • Conclusion
• Encoders fixed to the plates
  • Introduction
  • Identification of the dynamics
    • Introduction
    • Data Loading and Spectral Analysis Setup
    • Transfer function from Actuator to Encoder
    • Transfer function from Actuator to Force Sensor
    • Save Identified Plants
  • Comparison with the Simscape Model
    • Introduction
    • Identification with the Simscape Model
    • Dynamics from Actuator to Force Sensors
    • Dynamics from Actuator to Encoder
    • Conclusion
  • Integral Force Feedback
    • Introduction
    • Effect of IFF on the plant - Simscape Model
    • Effect of IFF on the plant - FRF
    • Comparison of the measured FRF and the Simscape model
  • Effect of Payload mass on the Dynamics
    • Introduction
    • Measured Frequency Response Functions
    • Rigidification of the added payloads
    • Transfer function from Actuators to Encoders
    • Transfer function from Actuators to Force Sensors
    • Coupling of the transfer function from Actuator to Encoders
  • Comparison with the Simscape model
    • Introduction
    • System Identification
    • Transfer function from Actuators to Encoders
    • Transfer function from Actuators to Force Sensors
  • Integral Force Feedback Controller
    • Introduction
    • Robust IFF Controller
    • Estimated Damped Plant from the Simscape model
    • Compute the identified FRF with IFF
    • Comparison of the measured FRF and the Simscape model
    • Change of coupling with IFF
  • Un-Balanced mass
    • Introduction
    • Compute the identified FRF with IFF
    • Effect of an unbalanced payload
  • Conclusion
• Decentralized High Authority Control with Integral Force Feedback
  • Introduction
  • Reference Tracking - Trajectories
    • Introduction
    • Y-Z Scans
    • Tilt Scans
    • "NASS" reference path
  • First Basic High Authority Controller
    • Introduction
    • HAC Controller
    • Verification of the Stability using the Simscape model
    • Experimental Validation
    • Controller with increased stability margins
  • Interaction Analysis and Decoupling
    • Introduction
    • Parameters
    • No Decoupling (Decentralized)
    • Static Decoupling
    • Decoupling at the Crossover
    • SVD Decoupling
    • Dynamic decoupling
    • Jacobian Decoupling - Center of Stiffness
    • Jacobian Decoupling - Center of Mass
    • Decoupling Comparison
    • Decoupling Robustness
    • Conclusion
  • Robust High Authority Controller
    • Introduction
    • Using Jacobian evaluated at the center of stiffness
      • Decoupled Plant
      • SISO Controller Design
      • Obtained Loop Gain
      • Verification of the Stability
      • Save for further analysis
      • Sensitivity transfer function from the model
    • Using Singular Value Decomposition
      • Decoupled Plant
      • Controller Design
      • Loop Gain
      • Stability Verification
      • Save for further analysis
      • Measured Sensitivity Transfer Function
      • Sensitivity transfer function from the model
• Bibliography

---

This report is also available as a pdf.

---

Introduction   ignore

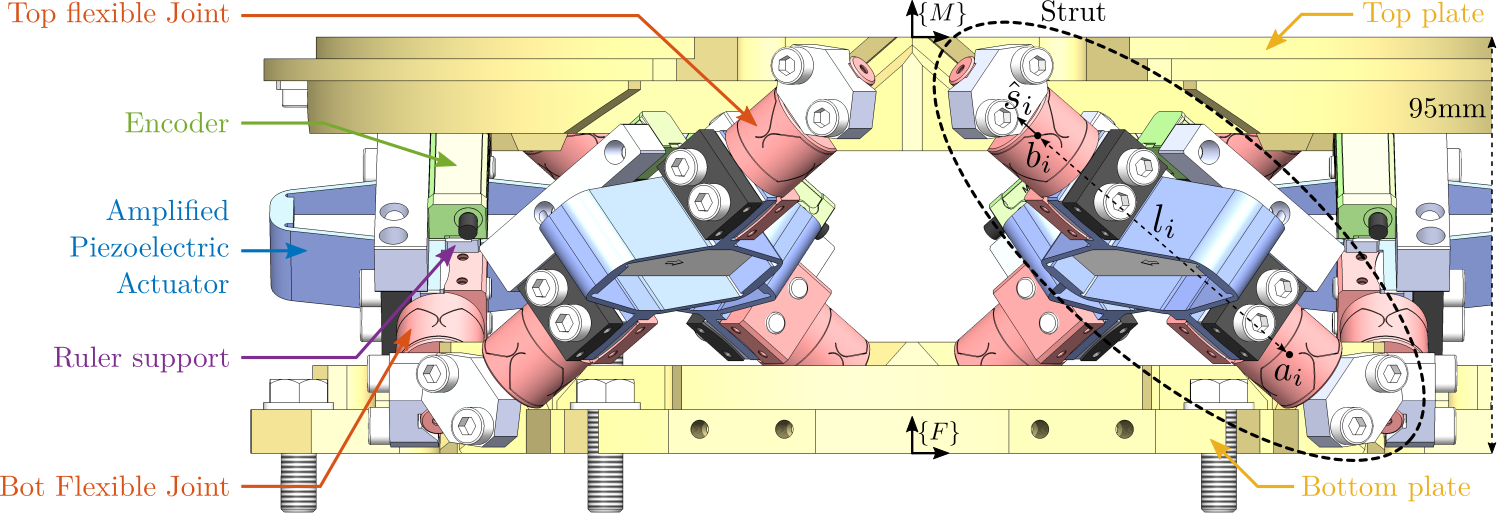
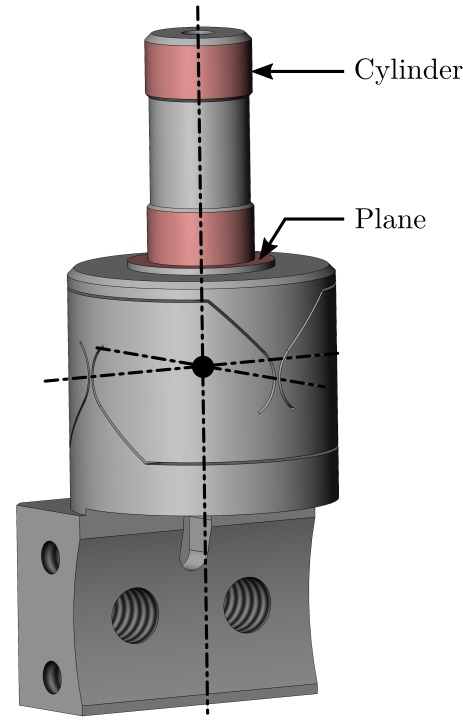
This document is dedicated to the experimental study of the nano-hexapod shown in Figure ref:fig:test_nhexa_picture_bench_granite_nano_hexapod.

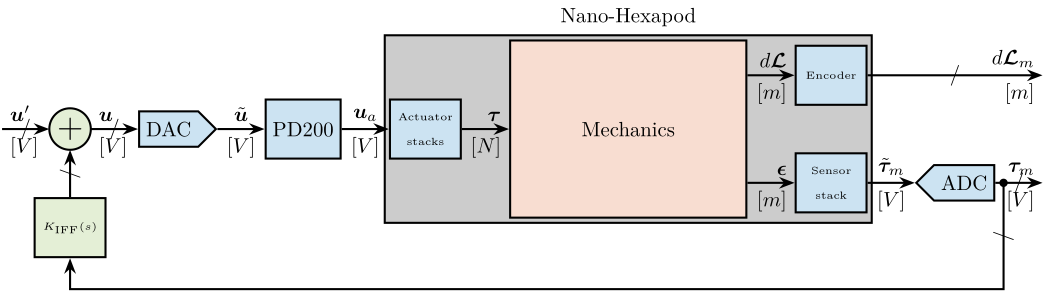
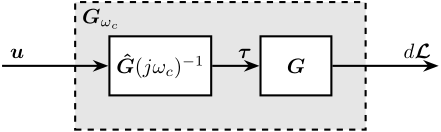
In Figure ref:fig:test_nhexa_nano_hexapod_signals is shown a block diagram of the experimental setup. When possible, the notations are consistent with this diagram and summarized in Table ref:tab:list_signals.

\definecolor{instrumentation}{rgb}{0, 0.447, 0.741}
\definecolor{mechanics}{rgb}{0.8500, 0.325, 0.098}

\begin{tikzpicture}
  % Blocs
  \node[block={4.0cm}{3.0cm}, fill=mechanics!20!white] (nano_hexapod) {Mechanics};
  \coordinate[] (inputF)  at (nano_hexapod.west);
  \coordinate[] (outputL) at ($(nano_hexapod.south east)!0.8!(nano_hexapod.north east)$);
  \coordinate[] (outputF) at ($(nano_hexapod.south east)!0.2!(nano_hexapod.north east)$);

  \node[block, left= 0.8 of inputF,  fill=instrumentation!20!white, align=center] (F_stack) {\tiny Actuator \\ \tiny stacks};
  \node[block, left= 0.8 of F_stack, fill=instrumentation!20!white] (PD200)   {PD200};
  \node[DAC,   left= 0.8 of PD200,   fill=instrumentation!20!white] (F_DAC)   {DAC};
  \node[block, right=0.8 of outputF, fill=instrumentation!20!white, align=center] (Fm_stack){\tiny Sensor \\ \tiny stack};
  \node[ADC,   right=0.8 of Fm_stack,fill=instrumentation!20!white] (Fm_ADC)  {ADC};
  \node[block, right=0.8 of outputL, fill=instrumentation!20!white] (encoder) {\tiny Encoder};

  % Connections and labels
  \draw[->] ($(F_DAC.west)+(-0.8,0)$) node[above right]{$\bm{u}$} node[below right]{$[V]$} -- node[sloped]{$/$} (F_DAC.west);
  \draw[->] (F_DAC.east)   -- node[midway, above]{$\tilde{\bm{u}}$}node[midway, below]{$[V]$} (PD200.west);
  \draw[->] (PD200.east)   -- node[midway, above]{$\bm{u}_a$}node[midway, below]{$[V]$} (F_stack.west);
  \draw[->] (F_stack.east) -- (inputF) node[above left]{$\bm{\tau}$}node[below left]{$[N]$};

  \draw[->] (outputF)       -- (Fm_stack.west) node[above left]{$\bm{\epsilon}$} node[below left]{$[m]$};
  \draw[->] (Fm_stack.east) -- node[midway, above]{$\tilde{\bm{\tau}}_m$}node[midway, below]{$[V]$} (Fm_ADC.west);
  \draw[->] (Fm_ADC.east)   -- node[sloped]{$/$} ++(0.8, 0)coordinate(end) node[above left]{$\bm{\tau}_m$}node[below left]{$[V]$};

  \draw[->] (outputL)      -- (encoder.west) node[above left]{$d\bm{\mathcal{L}}$} node[below left]{$[m]$};
  \draw[->] (encoder.east) -- node[sloped]{$/$} (encoder-|end) node[above left]{$d\bm{\mathcal{L}}_m$}node[below left]{$[m]$};

  % Nano-Hexapod
  \begin{scope}[on background layer]
    \node[fit={(F_stack.west|-nano_hexapod.south) (Fm_stack.east|-nano_hexapod.north)}, fill=black!20!white, draw, inner sep=2pt] (system) {};
    \node[above] at (system.north) {Nano-Hexapod};
  \end{scope}
\end{tikzpicture}

	Unit	Matlab	Vector	Elements
Control Input (wanted DAC voltage)	[V]	u	$\bm{u}$	$u_i$
DAC Output Voltage	[V]	u	$\tilde{\bm{u}}$	$\tilde{u}_i$
PD200 Output Voltage	[V]	ua	$\bm{u}_a$	$u_{a,i}$
Actuator applied force	[N]	tau	$\bm{\tau}$	$\tau_i$
Strut motion	[m]	dL	$d\bm{\mathcal{L}}$	$d\mathcal{L}_i$
Encoder measured displacement	[m]	dLm	$d\bm{\mathcal{L}}_m$	$d\mathcal{L}_{m,i}$
Force Sensor strain	[m]	epsilon	$\bm{\epsilon}$	$\epsilon_i$
Force Sensor Generated Voltage	[V]	taum	$\tilde{\bm{\tau}}_m$	$\tilde{\tau}_{m,i}$
Measured Generated Voltage	[V]	taum	$\bm{\tau}_m$	$\tau_{m,i}$
Motion of the top platform	[m,rad]	dX	$d\bm{\mathcal{X}}$	$d\mathcal{X}_i$
Metrology measured displacement	[m,rad]	dXm	$d\bm{\mathcal{X}}_m$	$d\mathcal{X}_{m,i}$

This document is divided in the following sections:

• Section ref:sec:test_nhexa_mounting: mounting of the nano-hexapod
• Section ref:sec:test_nhexa_encoders_struts: the dynamics of the nano-hexapod when the encoders are fixed to the struts is studied.
• Section ref:sec:test_nhexa_encoders_plates: the same is done when the encoders are fixed to the plates.
• Section ref:sec:test_nhexa_decentralized_hac_iff: a decentralized HAC-LAC strategy is studied and implemented.

Mounting Procedure

<<sec:test_nhexa_mounting>>

Mounting Goals

Fixation of the flexible points to the nano-hexapod plates

#+caption:Reference surfaces of the flexible joint interface with the plates

Mounting Bench

Mounting Procedure

1. Fix the bottom plate with the cylindrical tool
2. Put the top plate on the granite
3. Put the cylindrical tool and bottom plate on top of the top plate (Figure ref:fig:test_nhexa_mounting_tool_hexapod_bot_view). This position the bottom plate with respect to the top plate in X, Y, Z, Rx, Ry
4. Put the pin to position/fix the Rz. Now the two plates should be position and clamped together
5. Fix the 6 struts
6. Remove the pin and the tool
7. Put the nano-hexapod in place

Nano-Hexapod Mounting

<<sec:nano_hexapod_mounting>>

Introduction   ignore

Plates

Mounting Tool

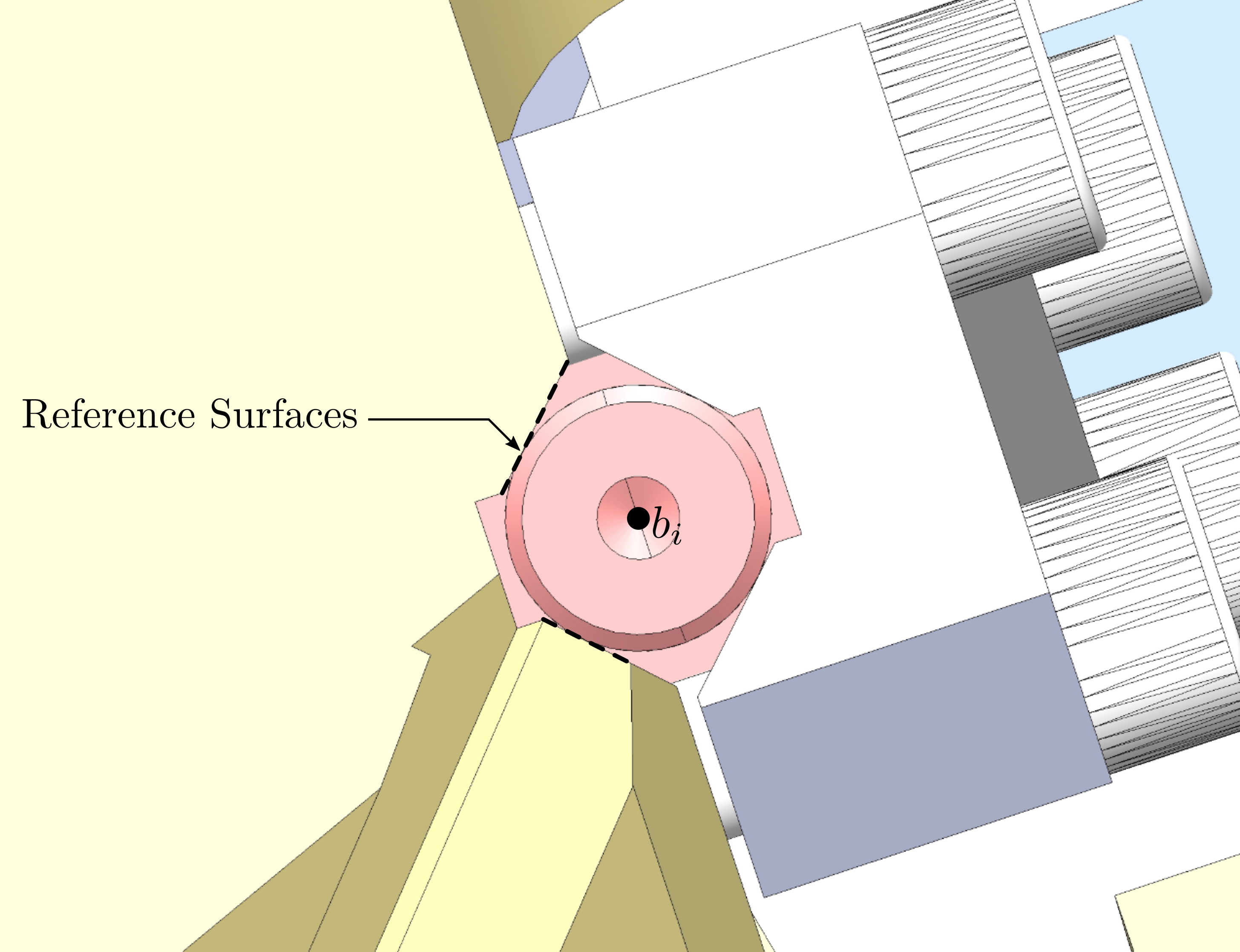
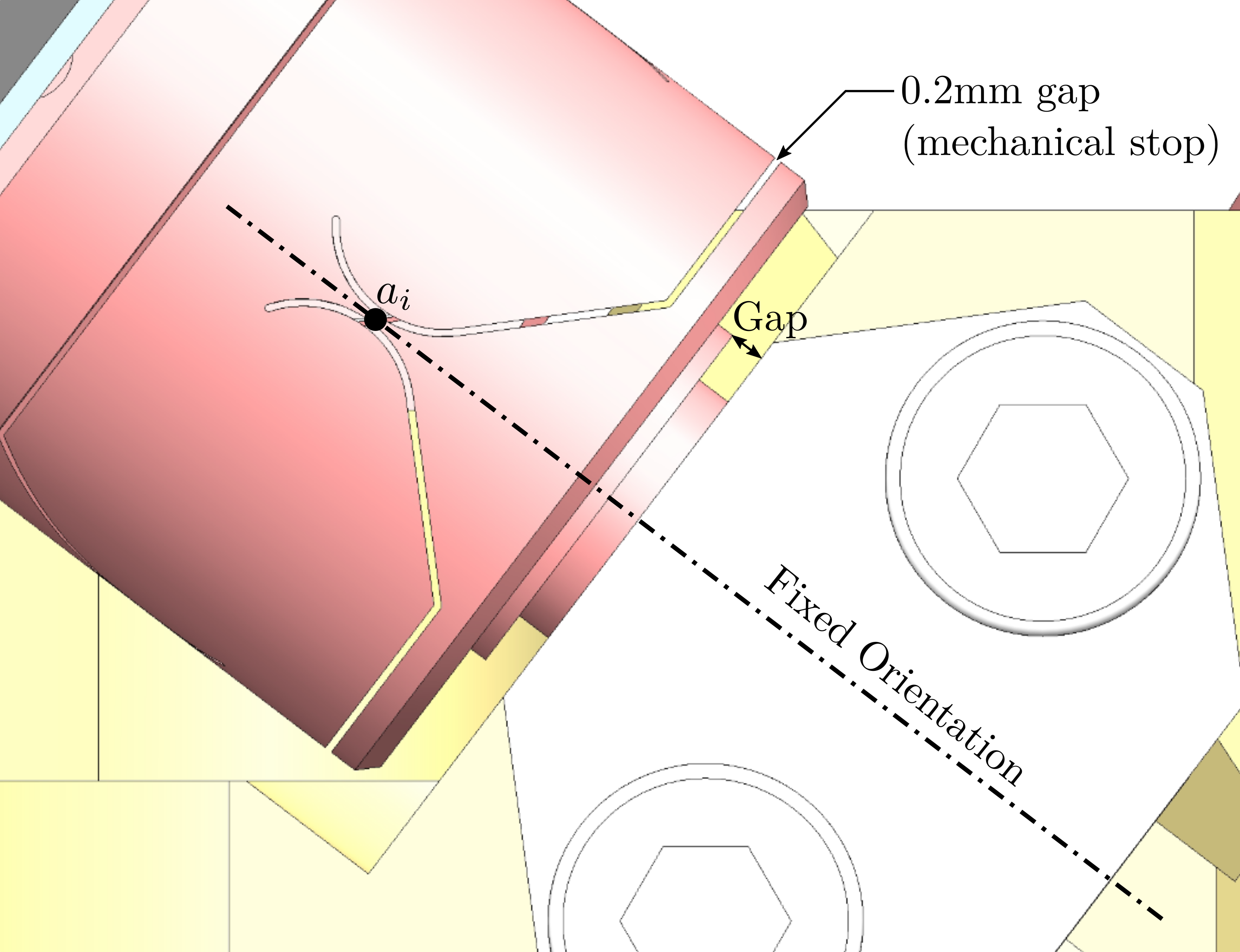
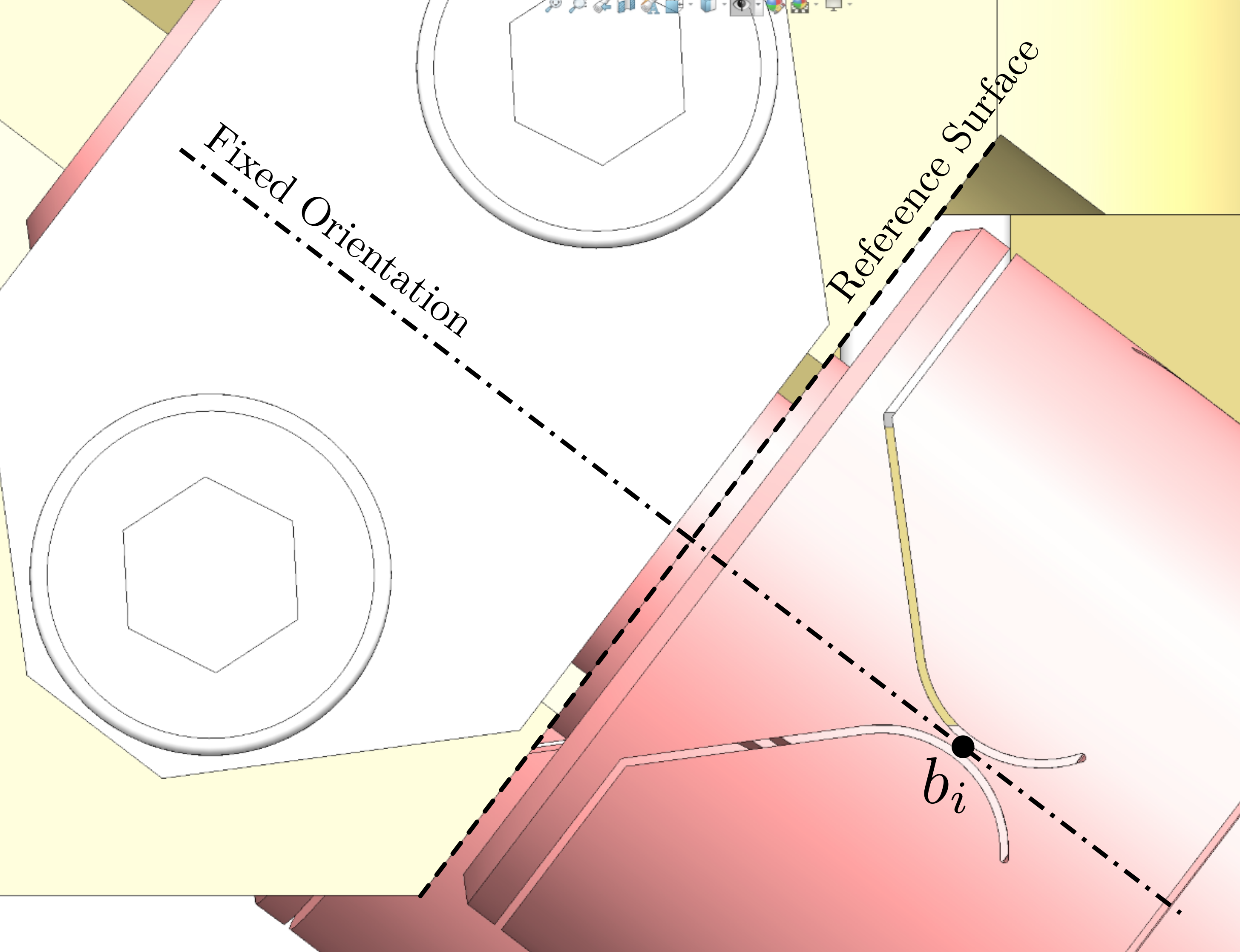
A mounting tool is used to position the top and bottom platforms. Then the struts can be mounted one by one. When all the struts are mounted, the "mounting tool" is disassembled and the nano-hexapod is considered to be mounted.

The main goal of this "mounting tool" is to position the "V" shapes of both plates such that they are coaxial.

The straightness is the diameter of the smallest cylinder containing all points of the axis.

Strut nb	Meas 1	Meas 2
1	7um	3um
2	11um	11um
3	15um	14um
4	6um	6um
5	7um	5um
6	6um	7um

Using the FARO arm, the coaxiality of the "V" shapes have been measured to better than $15\,\mu m$! This means that the two cylinders corresponding to the flexible joints are both within a perfect cylinder with a diameter of $15\,\mu m$. This is probably better than that, but we reached the limit of the FARO arm's precision.

Mounted Hexapod

Encoders fixed to the struts

<<sec:test_nhexa_encoders_struts>>

Introduction   ignore

In this section, the encoders are fixed to the struts.

It is divided in the following sections:

• Section ref:sec:test_nhexa_enc_struts_plant_id: the transfer function matrix from the actuators to the force sensors and to the encoders is experimentally identified.
• Section ref:sec:test_nhexa_enc_struts_comp_simscape: the obtained FRF matrix is compared with the dynamics of the simscape model
• Section ref:sec:test_nhexa_enc_struts_iff: decentralized Integral Force Feedback (IFF) is applied and its performances are evaluated.
• Section ref:sec:test_nhexa_enc_struts_modal_analysis: a modal analysis of the nano-hexapod is performed

Identification of the dynamics

<<sec:test_nhexa_enc_struts_plant_id>>

Introduction   ignore

Load Measurement Data

Two identifications are performed, one for low frequencies and one for higher frequencies.

%% Load Identification Data
meas_data_lf = {};

for i = 1:6
    meas_data_lf(i) = {load(sprintf('frf_data_exc_strut_%i_noise_lf.mat', i), 't', 'Va', 'Vs', 'de')};
    meas_data_hf(i) = {load(sprintf('frf_data_exc_strut_%i_noise_hf.mat', i), 't', 'Va', 'Vs', 'de')};
end

Spectral Analysis - Setup

The window used for the spectral analysis is defined as well as the frequency vector f.

%% Setup useful variables
% Sampling Time [s]
Ts = (meas_data_lf{1}.t(end) - (meas_data_lf{1}.t(1)))/(length(meas_data_lf{1}.t)-1);

% Sampling Frequency [Hz]
Fs = 1/Ts;

% Hannning Windows
win = hanning(ceil(1*Fs));

% And we get the frequency vector
[~, f] = tfestimate(meas_data_lf{1}.Va, meas_data_lf{1}.de, win, [], [], 1/Ts);

i_lf = f < 250; % Points for low frequency excitation
i_hf = f > 250; % Points for high frequency excitation

Transfer function from Actuator to Encoder

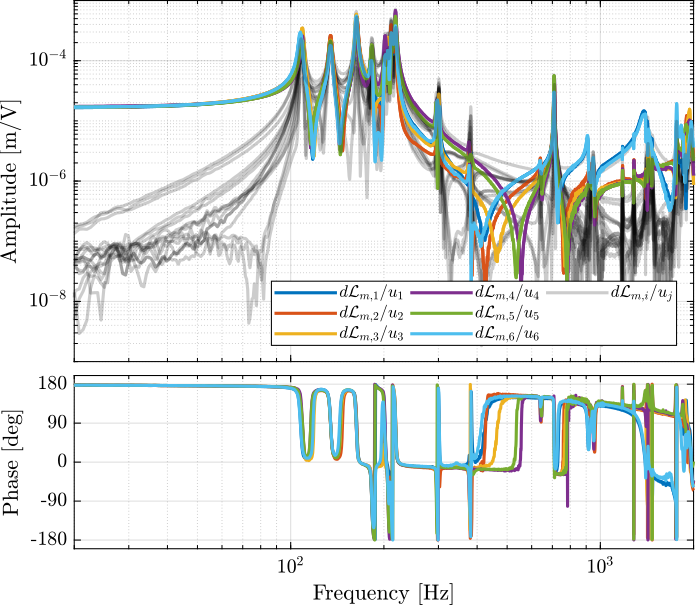
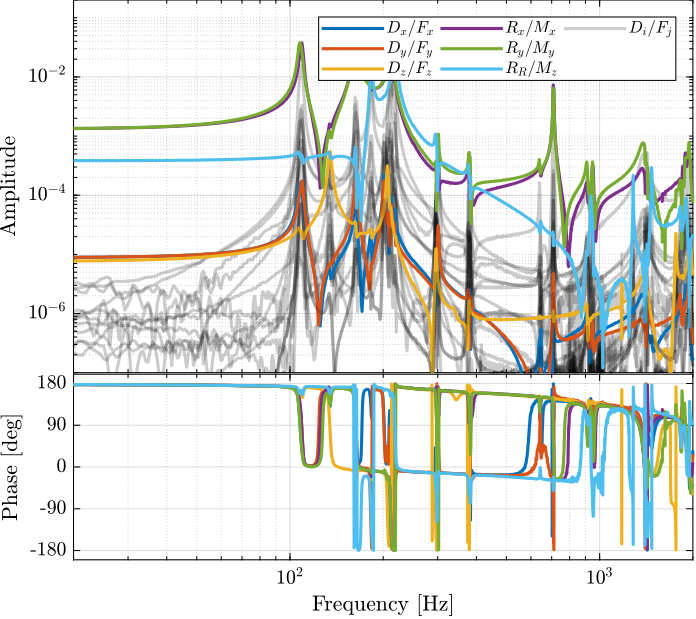
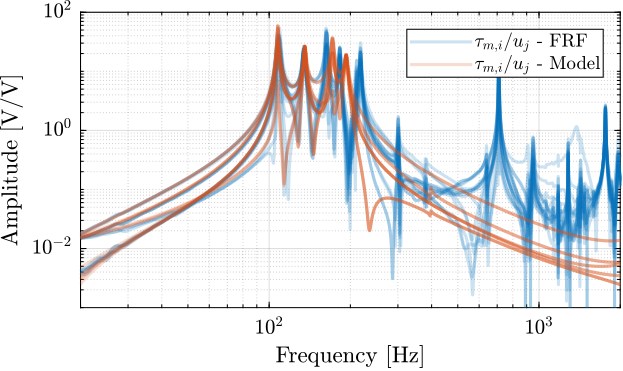
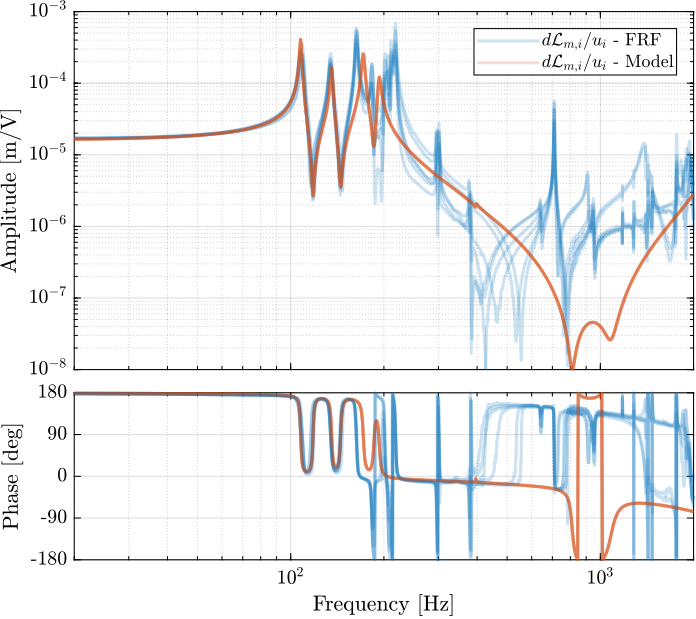
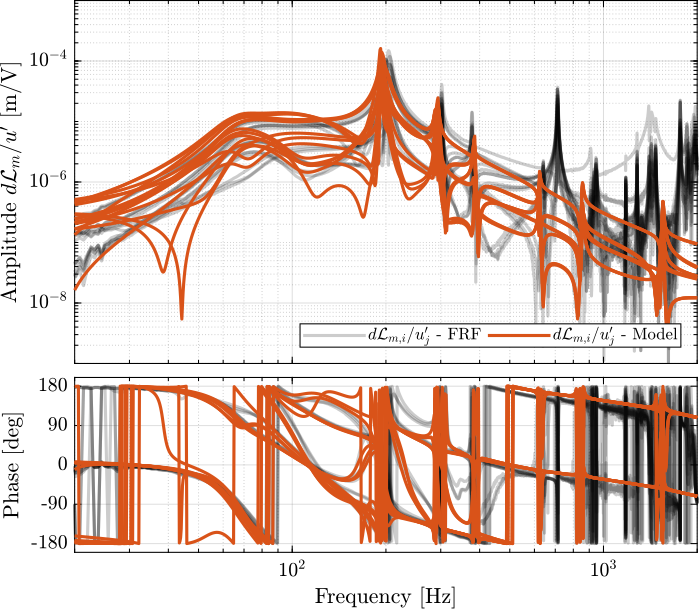
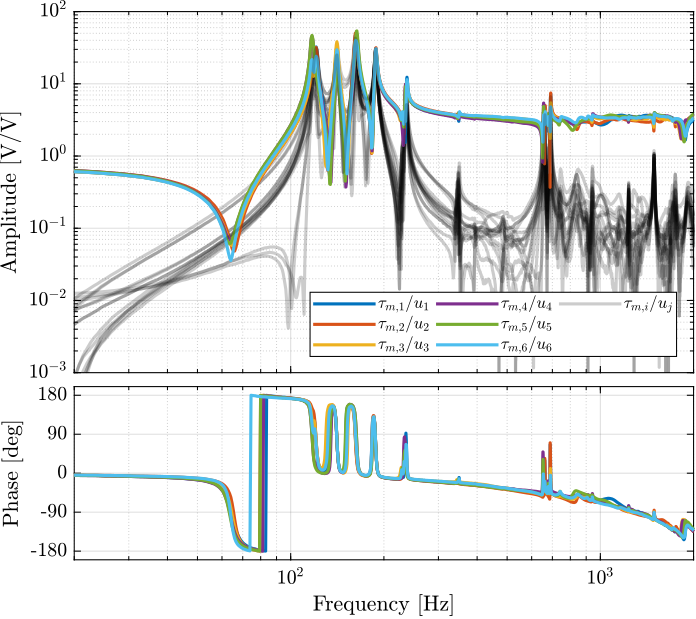
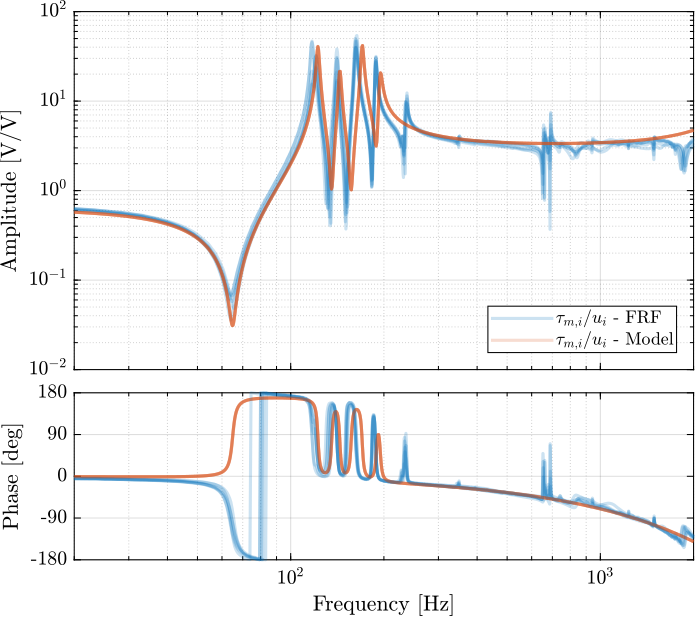
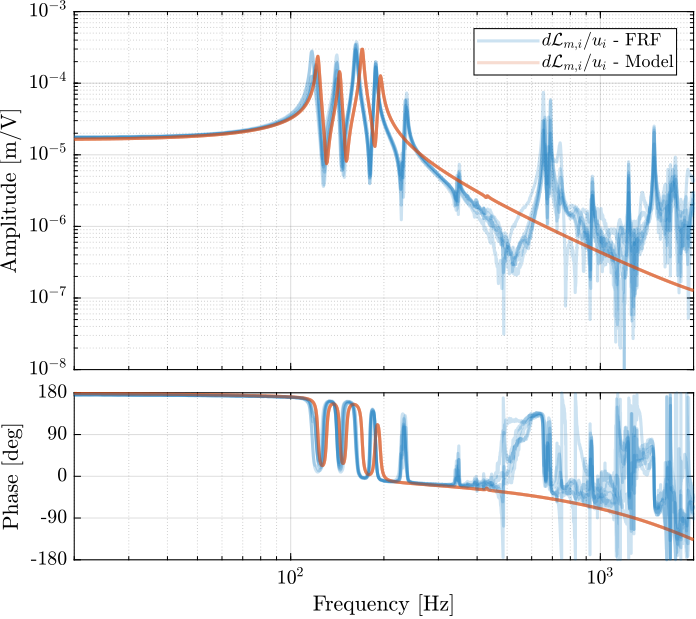
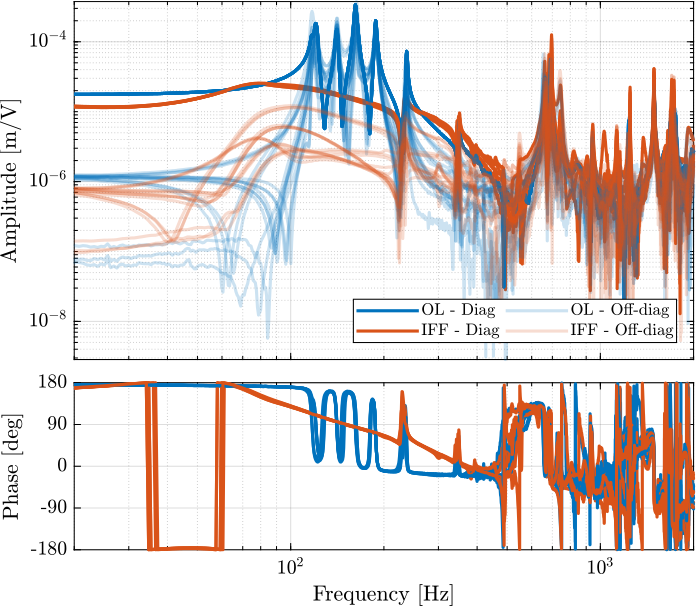
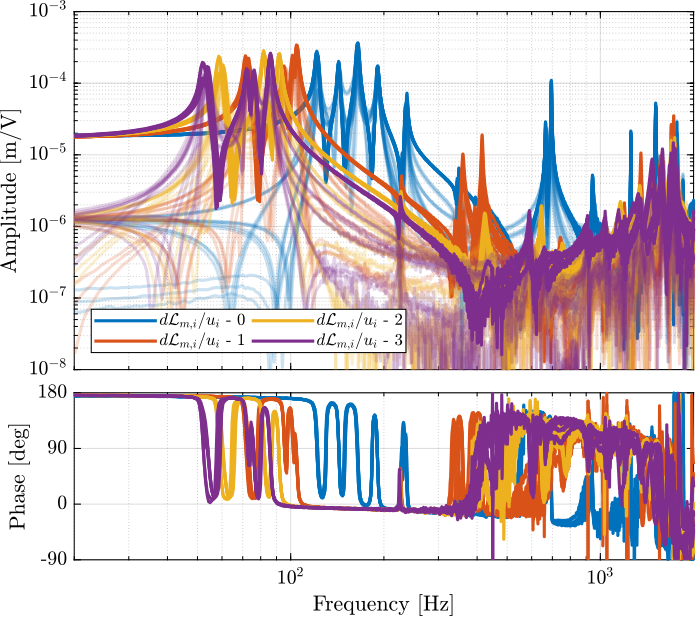
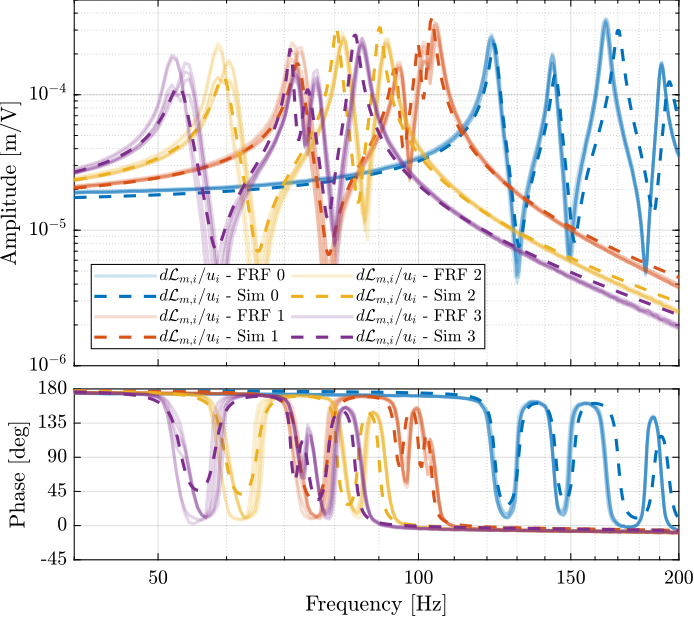
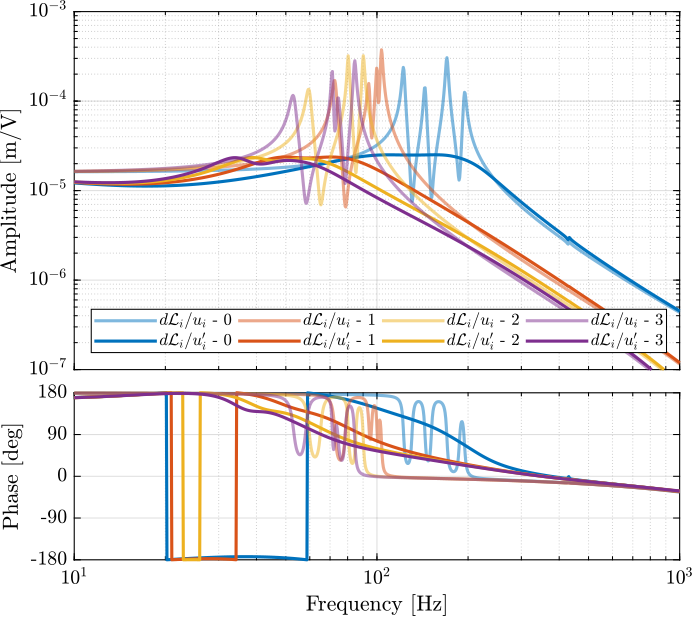
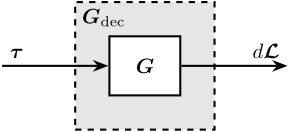
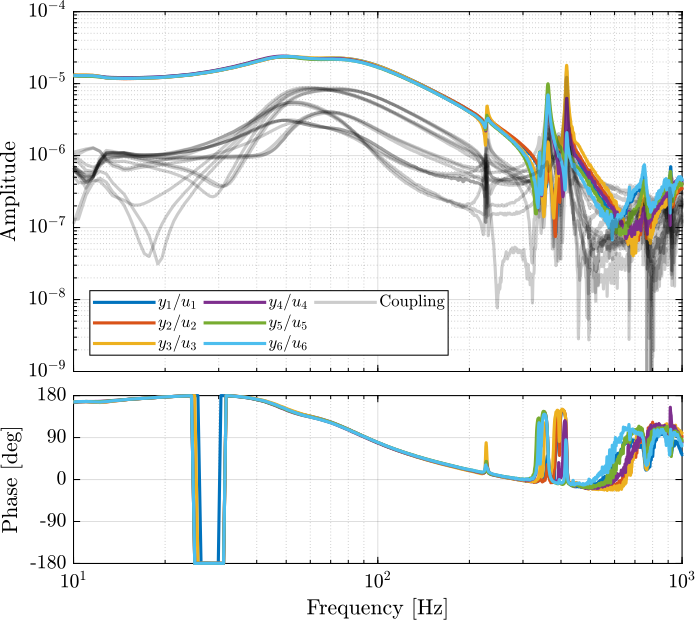
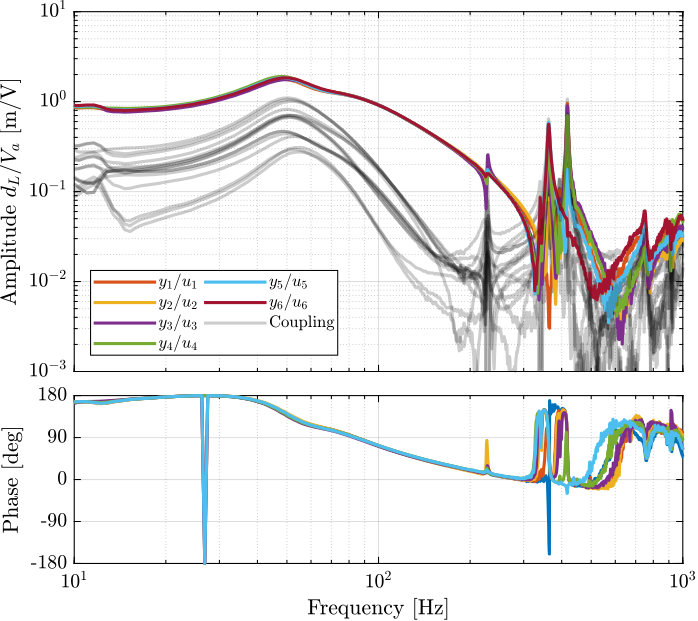
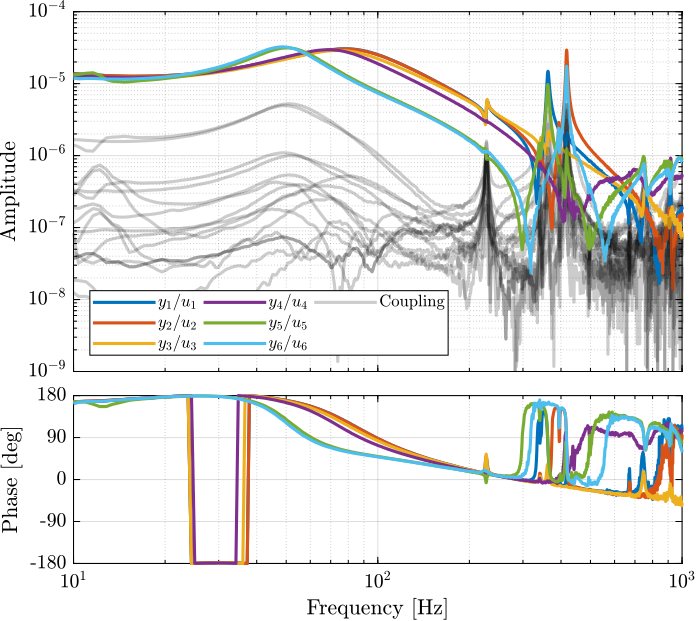
The 6x6 transfer function matrix from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ is estimated and shown in Figure ref:fig:test_nhexa_enc_struts_dvf_frf.

%% Transfer function from u to dLm
G_dL = zeros(length(f), 6, 6);

for i = 1:6
    G_dL_lf = tfestimate(meas_data_lf{i}.Va, meas_data_lf{i}.de, win, [], [], 1/Ts);
    G_dL_hf = tfestimate(meas_data_hf{i}.Va, meas_data_hf{i}.de, win, [], [], 1/Ts);
    G_dL(:,:,i) = [G_dL_lf(i_lf, :); G_dL_hf(i_hf, :)];
end

Measured FRF for the transfer function from $\bm{u}$ to $d\bm{\mathcal{L}_m}$

The low frequency gain of the transfer function from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ is close to diagonal. Then the coupling is quite large starting from the frequency of the first suspension mode (110Hz to 180Hz). Additional modes at 220Hz, 300Hz and 380Hz which are the modes of the struts are adding a lot of complexity in the plant and phase drops. Then there is a mode at 700Hz which correspond to a flexible mode of the top plate.

Transfer function from Actuator to Force Sensor

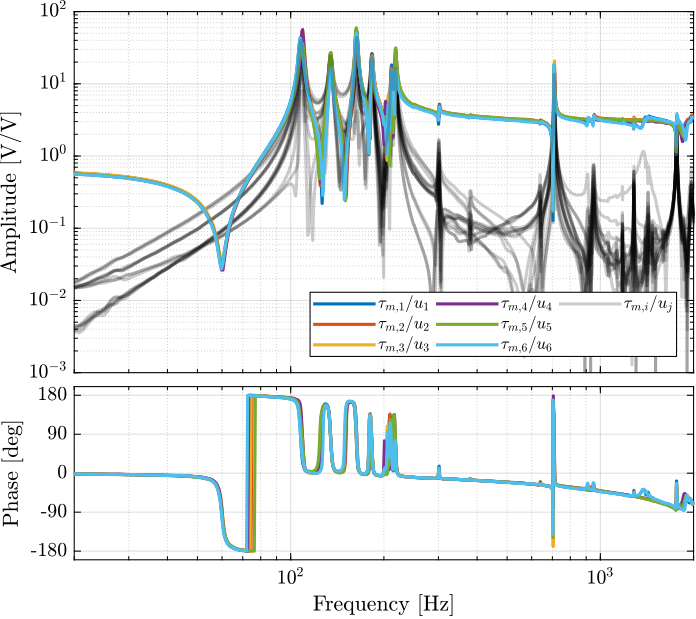
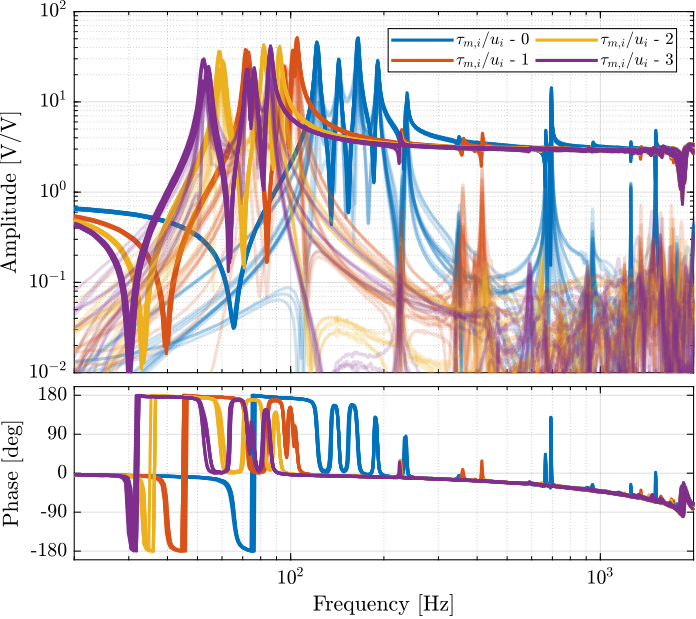
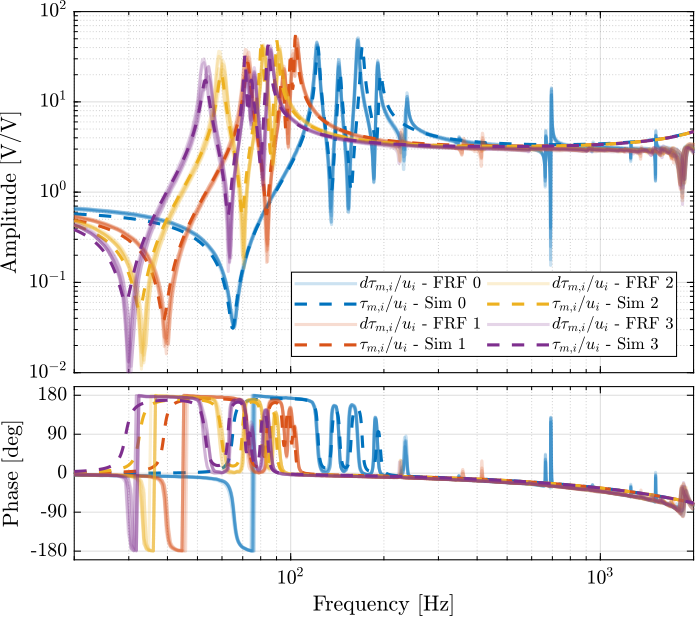
The 6x6 transfer function matrix from $\bm{u}$ to $\bm{\tau}_m$ is estimated and shown in Figure ref:fig:test_nhexa_enc_struts_iff_frf.

%% Transfer function from u to taum
G_tau = zeros(length(f), 6, 6);

for i = 1:6
    G_tau_lf = tfestimate(meas_data_lf{i}.Va, meas_data_lf{i}.Vs, win, [], [], 1/Ts);
    G_tau_hf = tfestimate(meas_data_hf{i}.Va, meas_data_hf{i}.Vs, win, [], [], 1/Ts);
    G_tau(:,:,i) = [G_tau_lf(i_lf, :); G_tau_hf(i_hf, :)];
end

Measured FRF for the transfer function from $\bm{u}$ to $\bm{\tau}_m$

The transfer function matrix from $\bm{u}$ to $\bm{\tau}_m$ in Figure ref:fig:test_nhexa_enc_struts_iff_frf has alternating poles and zeros as expected. The 4 suspensions modes have quite separated poles and zeros which indicates that is should be possible to add a good amount of damping to these modes using Integral Force Feedback.

Save Identified Plants

The identified plants are now saved for further analysis.

save('data_frf/identified_plants_enc_struts.mat', 'f', 'Ts', 'G_tau', 'G_dL')

Jacobian matrices and centralized plants

Introduction   ignore

The Jacobian is used to transform the excitation force in the cartesian frame as well as the displacements.

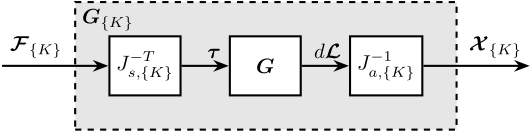
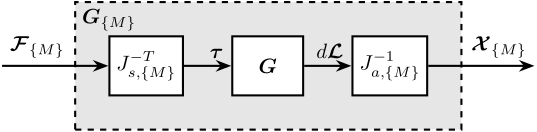
Consider the plant shown in Figure ref:fig:test_nhexa_schematic_jacobian_in_out with:

• $\bm{u}$ the 6 input voltages (going to the PD200 amplifier and then to the APA)
• $d\bm{\mathcal{L}}$ the relative motion sensor outputs (encoders)
• $\bm{\tau}_m$ the generated voltage of the force sensor stacks
• $J_a$ and $J_s$ the Jacobians for the actuators and sensors

\begin{tikzpicture}
  % Blocs
  \node[block={2.0cm}{2.0cm}] (P) {Plant};
  \coordinate[] (inputF)  at (P.west);
  \coordinate[] (outputL) at ($(P.south east)!0.8!(P.north east)$);
  \coordinate[] (outputF) at ($(P.south east)!0.2!(P.north east)$);

  \node[block, left= of inputF]   (Ja) {$\bm{J}^{-T}_a$};
  \node[block, right= of outputL] (Js) {$\bm{J}^{-1}_s$};
  \node[block, right= of outputF] (Jf) {$\bm{J}^{T}_a$};

  % Connections and labels
  \draw[->] ($(Ja.west)+(-1,0)$) -- (Ja.west) node[above left]{$\bm{\mathcal{F}}$};
  \draw[->] (Ja.east) -- (inputF)  node[above left]{$\bm{u}$};
  \draw[->] (outputL) -- (Js.west) node[above left]{$d\bm{\mathcal{L}}$};
  \draw[->] (Js.east) -- ++(1, 0) node[above left]{$d\bm{\mathcal{X}}$};
  \draw[->] (outputF) -- (Jf.west) node[above left]{$\bm{\tau}_m$};
  \draw[->] (Jf.east) -- ++(1, 0) node[above left]{$\bm{\mathcal{F}}_m$};
\end{tikzpicture}

Plant in the cartesian Frame

Jacobian Matrices

The Jacobian matrices (for the sensors and for the actuators) are estimated in two cases:

• when the point of interest is at 150mm above the top platform
• when the point of interest is at the "center of stiffness" (42mm below the top platform)

%% Initialize the Hexapod with the Interest point 150mm above the top platform
n_hexapod = initializeNanoHexapodFinal('MO_B', 150e-3, ...
                                       'motion_sensor_type', 'struts');

% Jacobian matrices
Ja_coi = n_hexapod.geometry.J;
Js_coi = n_hexapod.geometry.Js;

%% Initialize the Hexapod with Interest point at the Center of Stiffness
n_hexapod = initializeNanoHexapodFinal('MO_B', -42e-3, ...
                                       'motion_sensor_type', 'struts');

% Jacobian matrices
Ja_cok = n_hexapod.geometry.J;
Js_cok = n_hexapod.geometry.Js;

Obtained Centralized plants

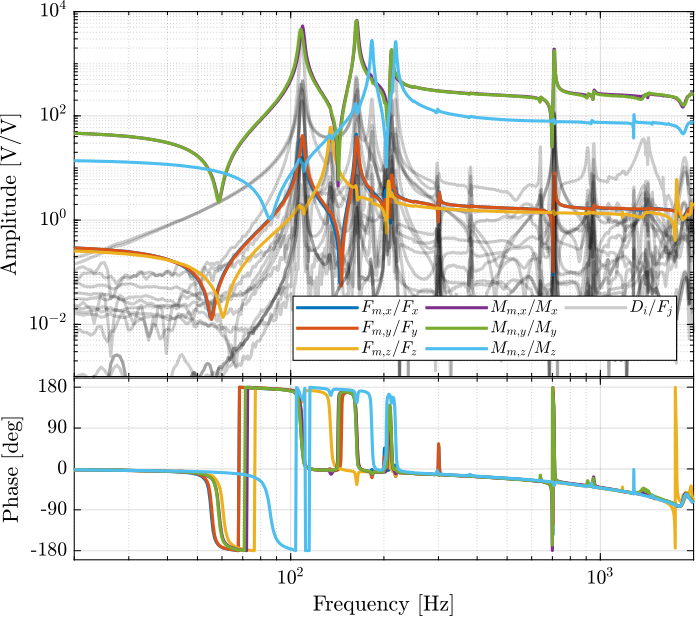
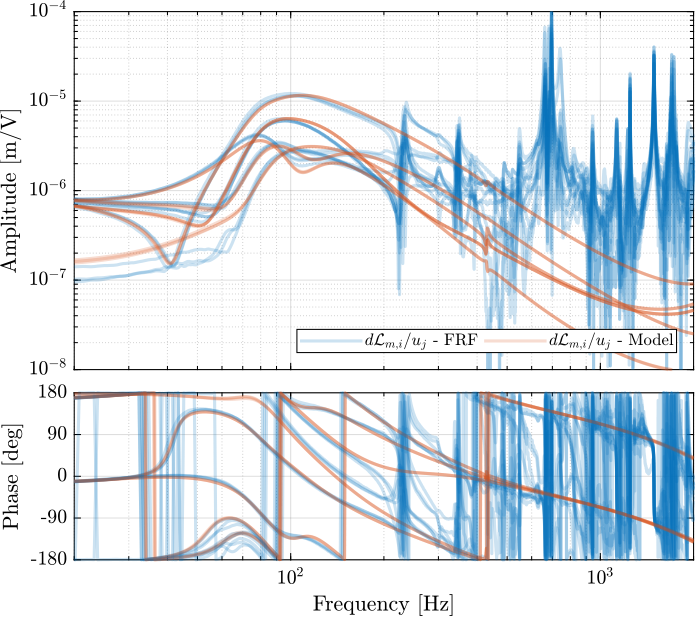
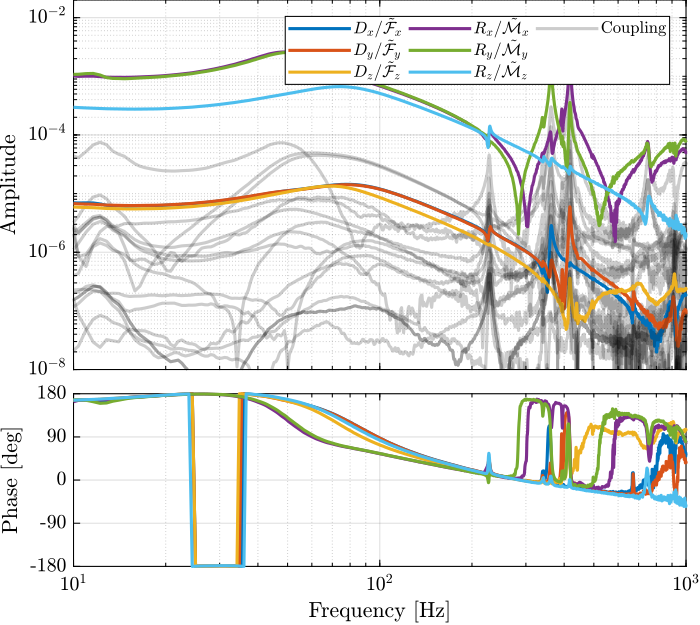
The transfer function matrices from $\bm{\mathcal{F}}$ to $d\bm{\mathcal{X}}$ are computed for both Jacobians and shown in Figures ref:fig:test_nhexa_enc_struts_cok_dvf_cart_frf (Center of Stiffness) and ref:fig:test_nhexa_enc_struts_coi_dvf_cart_frf (Point of Interest).

%% "Centralized" plant at the "center of stiffness"
G_dL_J_cok = permute(pagemtimes(inv(Js_cok), pagemtimes(permute(G_dL, [2 3 1]), inv(Ja_cok'))), [3 1 2]);

%% "Centralized" plant at the "point of interest"
G_dL_J_coi = permute(pagemtimes(inv(Js_coi), pagemtimes(permute(G_dL, [2 3 1]), inv(Ja_coi'))), [3 1 2]);

Bode plot of the transfer function from $\bm{\mathcal{F}}$ to $d\bm{\mathcal{X}}$ which is computed using the Jacobian matrices evaluted at the Center of Stiffness

Bode plot of the transfer function from $\bm{\mathcal{F}}$ to $d\bm{\mathcal{X}}$ which is computed using the Jacobian matrices evaluated at the Point of Interest

The centralized plant evaluated at the Center of Stiffness (Figure ref:fig:test_nhexa_enc_struts_cok_dvf_cart_frf) is presenting a good decoupling at low frequency which is not the case for the Centralized plant at the point of interest in Figure ref:fig:test_nhexa_enc_struts_coi_dvf_cart_frf.

Centralized plant using the Force sensors

The transfer function from $\bm{\mathcal{F}}$ to $\bm{\mathcal{F}}_m$ is computed using the Jacobian evaluated at the Center of Stiffness and shown in Figure ref:fig:test_nhexa_enc_struts_iff_cart_frf.

%% Computed Centralized plant: transfer function from F to Fm
G_tau_J = permute(pagemtimes(inv(Js_cok), pagemtimes(permute(G_tau, [2 3 1]), inv(Ja_cok'))), [3 1 2]);

From Figure ref:fig:test_nhexa_enc_struts_iff_cart_frf, we can well estimate the directions of the suspension modes:

• modes at 110Hz and 160Hz are horizontal translation/rotation modes
• mode at 135Hz is a pure vertical mode
• mode at 185Hz is a pure rotation mode around the vertical axis

Measured FRF for the IFF plant in the cartesian frame

Comparison with the Simscape Model

<<sec:test_nhexa_enc_struts_comp_simscape>>

Introduction   ignore

In this section, the measured dynamics is compared with the dynamics estimated from the Simscape model.

Simscape Model - Identification

Let's initialize the nano-hexapod using 2 DoF models for the APA.

%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
                                       'flex_top_type', '4dof', ...
                                       'motion_sensor_type', 'struts', ...
                                       'actuator_type', '2dof');

The Nano-hexapod is fixed on a rigid granite and no payload is fixed on top of the hexapod.

%% Nano-Hexapod is fixed on a rigid granite
support.type = 0;

%% No Payload on top of the Nano-Hexapod
payload.type = 0;

The transfer function matrix from $\bm{u}$ to $\bm{\tau}_m$ using the Simscape model is now extracted.

%% Identify the transfer function from u to taum
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'],  1, 'openinput');   io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/Fm'],  1, 'openoutput'); io_i = io_i + 1; % Force Sensors

%% Perform the model extraction
G_tau = exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options);

And the plant from $\bm{u}$ to $d\bm{\mathcal{L}}_m$.

%% Identify the DVF Plant (transfer function from u to dLm)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput');  io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Encoders

%% Perform the identification
G_dL = exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options);

Both transfer functions are saved for further use.

save('data_frf/simscape_plants_enc_struts.mat', 'G_tau', 'G_dL')

%% Load the Previsouly saved plants from the Simscape model
sim_ol = load('simscape_plants_enc_struts.mat', 'G_tau', 'G_dL');

Dynamics from Actuator to Force Sensors

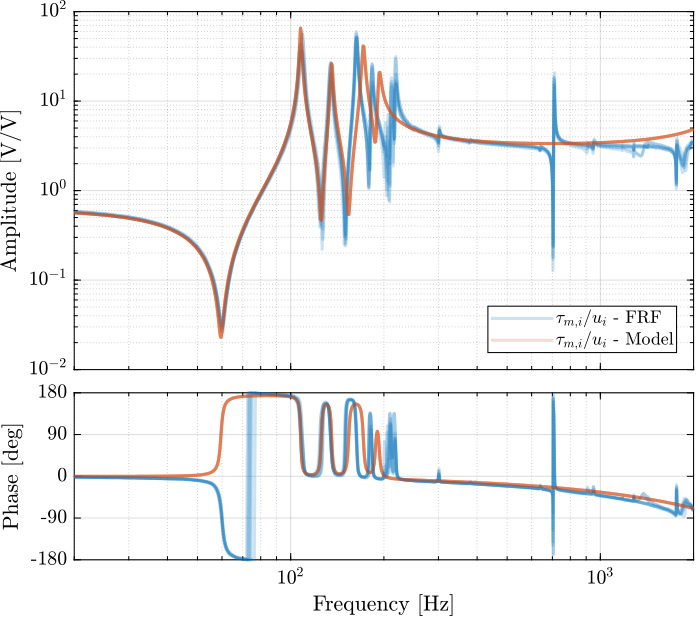
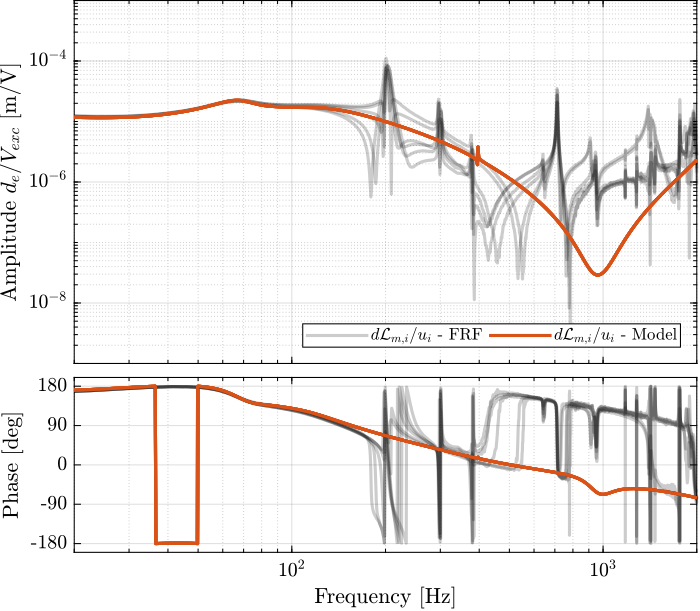
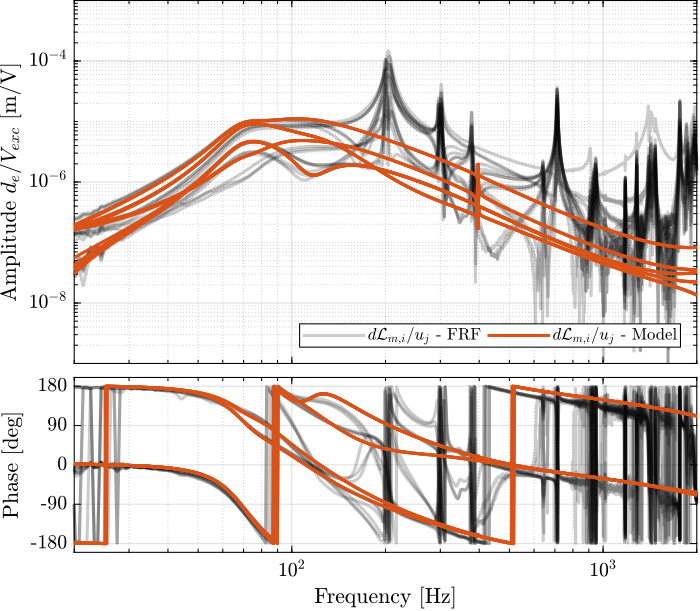
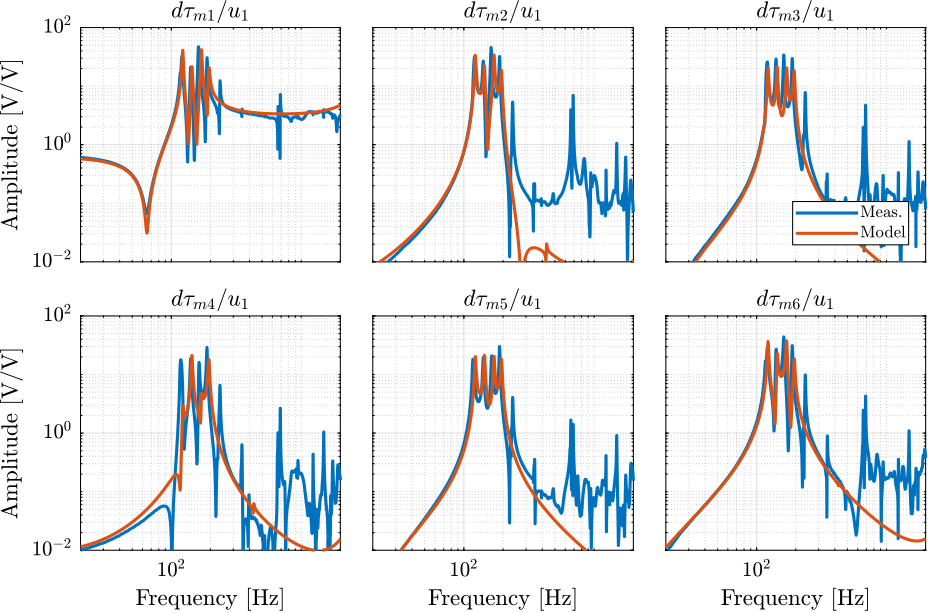
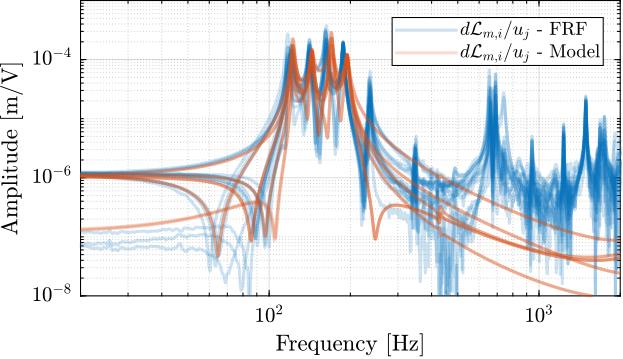
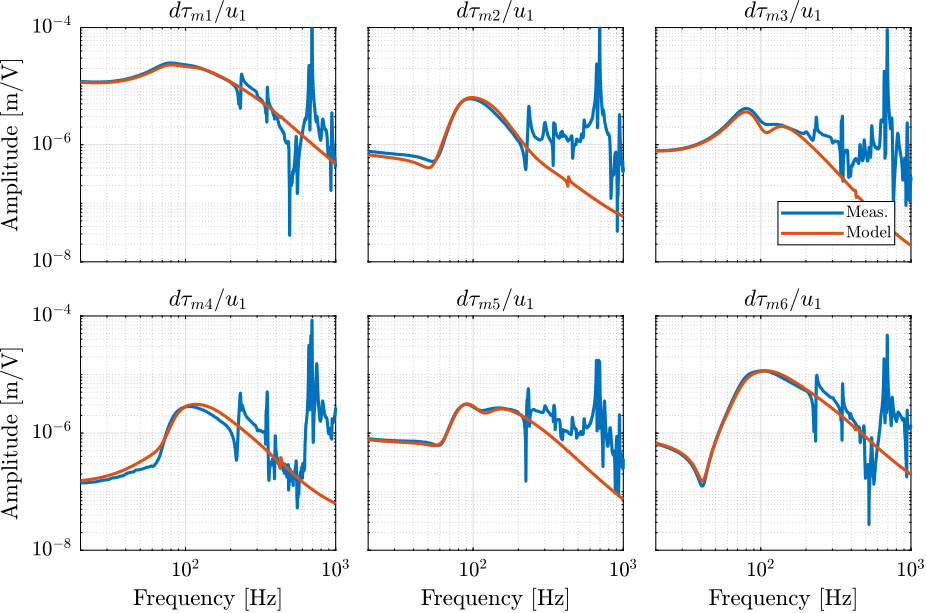
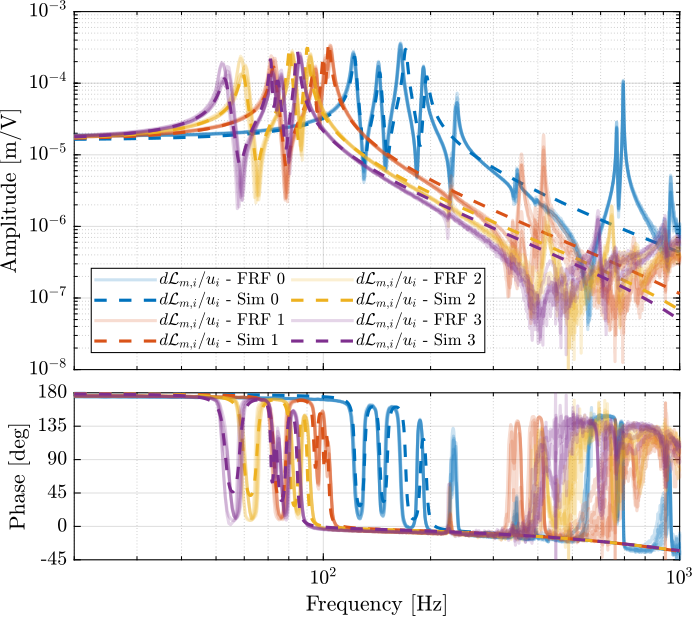
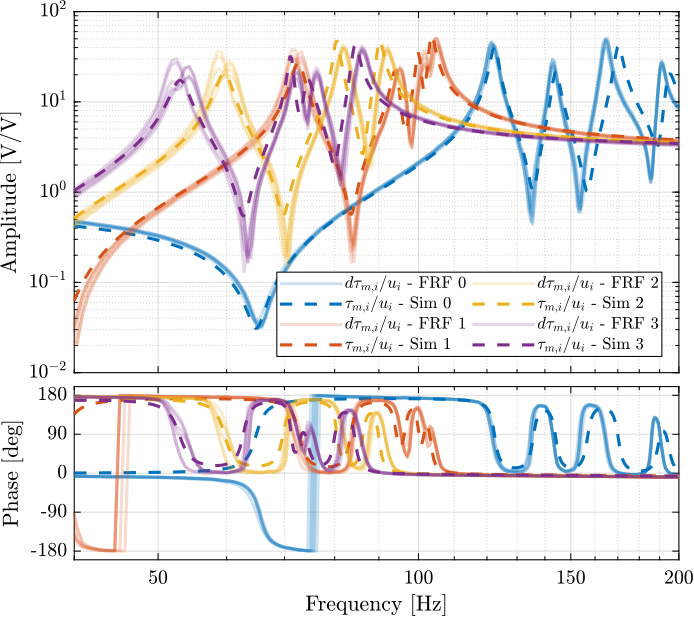
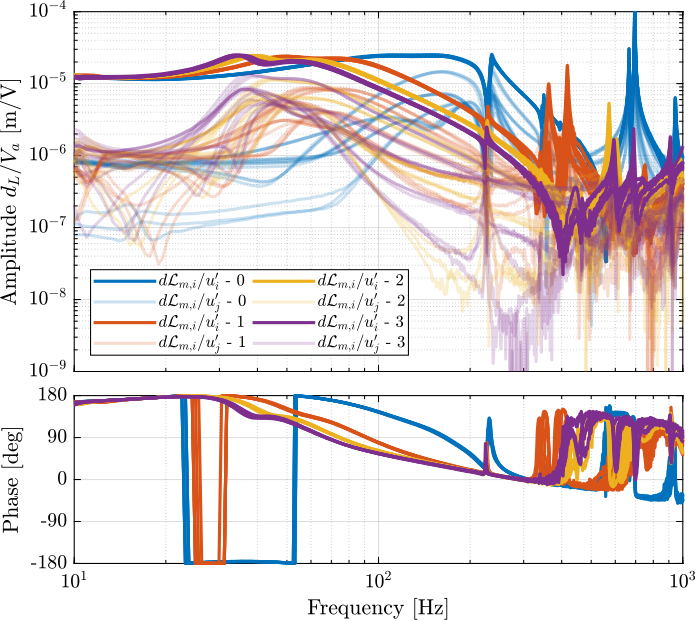
The comparison between the extracted model and the measurement is done in Figures ref:fig:test_nhexa_enc_struts_iff_comp_simscape (diagonal elements) and ref:fig:test_nhexa_enc_struts_iff_comp_offdiag_simscape (off-diagonal elements).

Comparison of the diagonal elements of the transfer function matrix from $\bm{u}$ to $\bm{\tau}_m$ - Simscape Model and measured FRF

Comparison of the off-diagonal elements of the transfer function matrix from $\bm{u}$ to $\bm{\tau}_m$ - Simscape Model and measured FRF

Dynamics from Actuator to Encoder

The comparison between the model is done in Figures ref:fig:test_nhexa_enc_struts_dvf_comp_simscape and ref:fig:test_nhexa_enc_struts_dvf_comp_offdiag_simscape.

Diagonal elements of the DVF Plant

Off diagonal elements of the DVF Plant

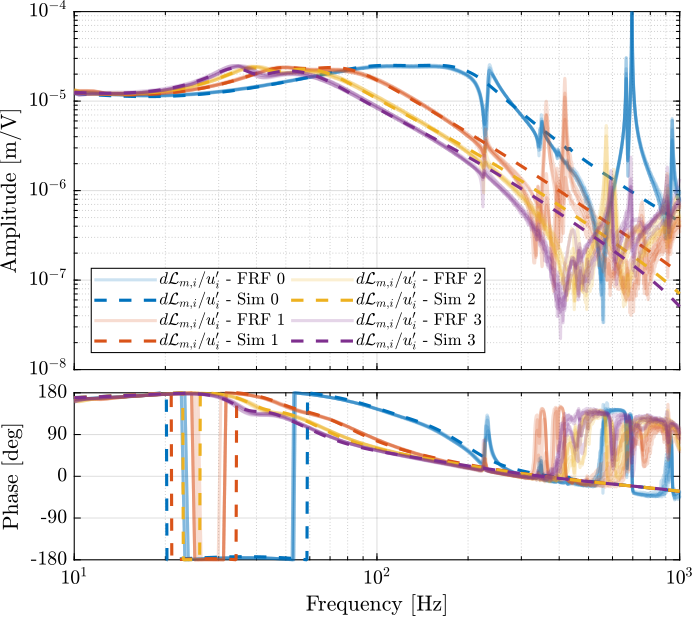
The Simscape model is quite accurately representing the system dynamics. Using 2dof models for the APA, we don't model the flexible modes of the APA. Similarly, the flexible modes of the top plate are not modelled. But up to 200Hz, the model is accurate.

Using Flexible model

In order to model flexible modes of the APA, flexible elements are used and some misalignment between the APA and the flexible joints is introduced.

These misalignments are estimated from measurements performed on each of the struts.

%% Misalignement between the APA and
d_aligns = [[-0.05,  -0.3,  0];
            [ 0,      0.5,  0];
            [-0.1,   -0.3,  0];
            [ 0,      0.3,  0];
            [-0.05,   0.05, 0];
            [0,       0,    0]]*1e-3;

The dynamics from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ is estimated.

%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
                                       'flex_top_type', '4dof', ...
                                       'motion_sensor_type', 'struts', ...
                                       'actuator_type', 'flexible', ...
                                       'actuator_d_align', d_aligns);

%% Identify the DVF Plant (transfer function from u to dLm)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'],  1, 'openinput');  io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dL'],  1, 'openoutput'); io_i = io_i + 1; % Encoders

sim_flex.G_dL = exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options);

The obtained diagonal elements are compared with the measurements in Figure ref:fig:test_nhexa_comp_frf_sim_enc_struts_modes. Modeling the APA as flexible elements can indeed yields to more accurate models. However this also adds a lot of states to the system, and time domain simulations can become realy long to perform.

Comparison of the measured transfer functions from $u_i$ to $d\mathcal{L}_{m,i}$ - Simscape model and measured FRF

Integral Force Feedback

<<sec:test_nhexa_enc_struts_iff>>

Introduction   ignore

In this section, the Integral Force Feedback (IFF) control strategy is applied to the nano-hexapod. The main goal of this to add damping to the nano-hexapod's modes.

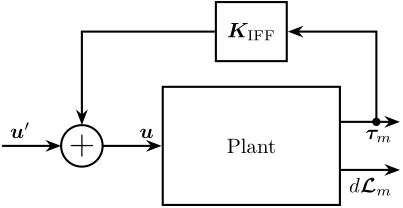
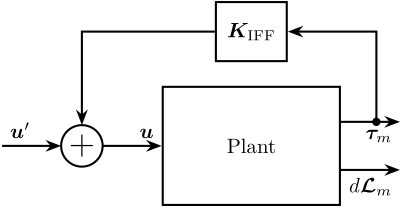
The control architecture is shown in Figure ref:fig:test_nhexa_control_architecture_iff_struts where $\bm{K}_\text{IFF}$ is a diagonal $6 \times 6$ controller.

The system as then a new input $\bm{u}^\prime$, and the transfer function from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ should be easier to control than the initial transfer function from $\bm{u}$ to $d\bm{\mathcal{L}}_m$.

\begin{tikzpicture}
  % Blocs
  \node[block={3.0cm}{2.0cm}] (P) {Plant};
  \coordinate[] (inputF) at ($(P.south west)!0.5!(P.north west)$);
  \coordinate[] (outputF) at ($(P.south east)!0.7!(P.north east)$);
  \coordinate[] (outputL) at ($(P.south east)!0.3!(P.north east)$);

  \node[block, above=0.4 of P] (Kiff) {$\bm{K}_\text{IFF}$};
  \node[addb, left= of inputF] (addF) {};

  % Connections and labels
  \draw[->] (outputF) -- ++(1, 0) node[below left]{$\bm{\tau}_m$};
  \draw[->] (outputL) -- ++(1, 0) node[below left]{$d\bm{\mathcal{L}}_m$};

  \draw[->] ($(outputF) + (0.6, 0)$)node[branch]{} |- (Kiff.east);
  \draw[->] (Kiff.west) -| (addF.north);
  \draw[->] (addF.east) -- (inputF) node[above left]{$\bm{u}$};
  \draw[<-] (addF.west) -- ++(-1, 0) node[above right]{$\bm{u}^\prime$};
\end{tikzpicture}

Integral Force Feedback Strategy

This section is structured as follow:

• Section ref:sec:test_nhexa_iff_struts_plant_id: Using the Simscape model (APA taken as 2DoF model), the transfer function from $\bm{u}$ to $\bm{\tau}_m$ is identified. Based on the obtained dynamics, the control law is developed and the optimal gain is estimated using the Root Locus.
• Section ref:sec:test_nhexa_iff_struts_effect_plant: Still using the Simscape model, the effect of the IFF gain on the the transfer function from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ is studied.
• Section ref:sec:test_nhexa_iff_struts_effect_plant_exp: The same is performed experimentally: several IFF gains are used and the damped plant is identified each time.
• Section ref:sec:test_nhexa_iff_struts_opt_gain: The damped model and the identified damped system are compared for the optimal IFF gain. It is found that IFF indeed adds a lot of damping into the system. However it is not efficient in damping the spurious struts modes.
• Section ref:sec:test_nhexa_iff_struts_comp_flex_model: Finally, a "flexible" model of the APA is used in the Simscape model and the optimally damped model is compared with the measurements.

IFF Control Law and Optimal Gain

<<sec:test_nhexa_iff_struts_plant_id>>

The IFF controller is defined as shown below:

%% IFF Controller
Kiff_g1 = -(1/(s + 2*pi*40))*...    % LPF: provides integral action above 40Hz
           (s/(s + 2*pi*30))*...    % HPF: limit low frequency gain
           (1/(1 + s/2/pi/500))*... % LPF: more robust to high frequency resonances
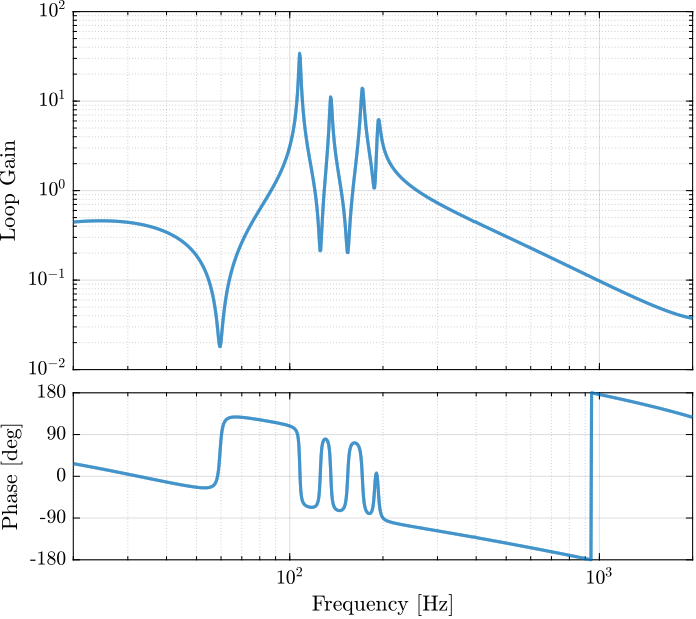
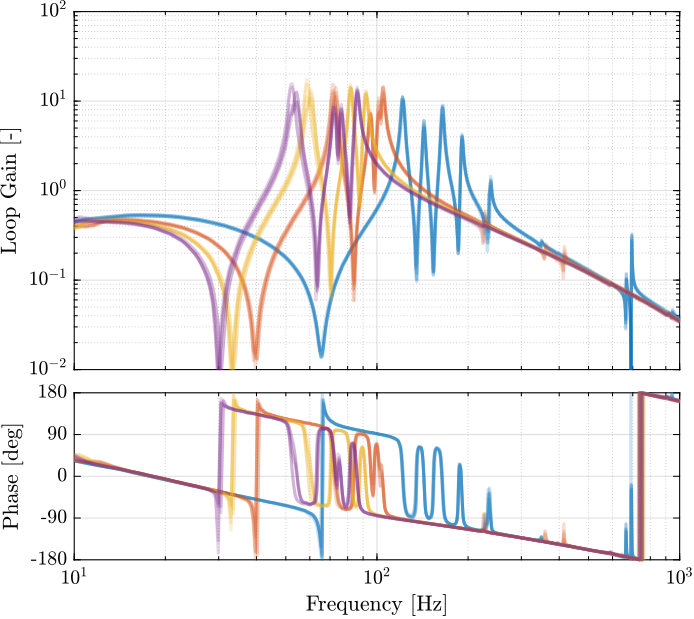
           eye(6);                  % Diagonal 6x6 controller

Then, the poles of the system are shown in the complex plane as a function of the controller gain (i.e. Root Locus plot) in Figure ref:fig:test_nhexa_enc_struts_iff_root_locus. A gain of $400$ is chosen as the "optimal" gain as it visually seems to be the gain that adds the maximum damping to all the suspension modes simultaneously.

Root Locus for the IFF control strategy

Then the "optimal" IFF controller is defined:

%% IFF controller with Optimal gain
Kiff = 400*Kiff_g1;

And it is saved for further use.

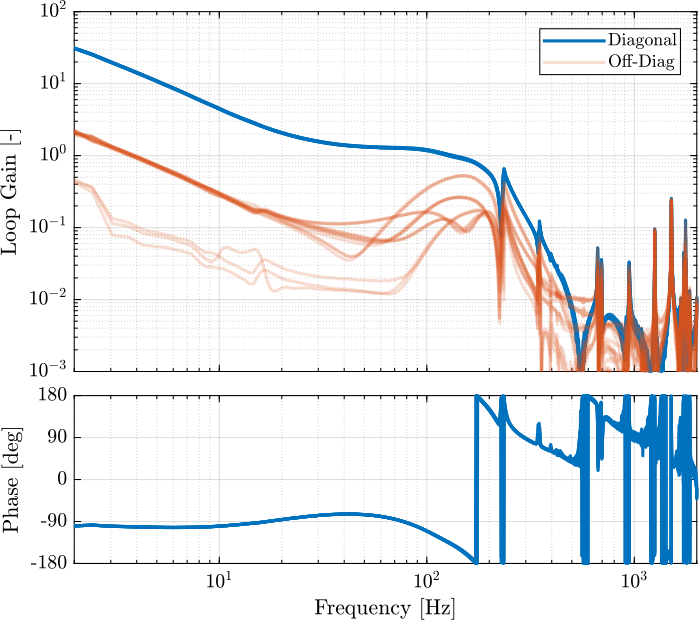
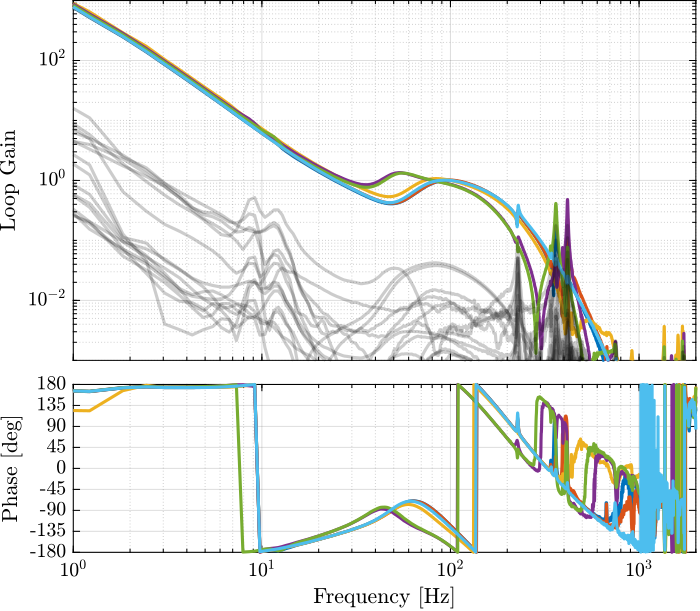
save('data_sim/Kiff_struts_no_payload.mat', 'Kiff')

The bode plots of the "diagonal" elements of the loop gain are shown in Figure ref:fig:test_nhexa_enc_struts_iff_opt_loop_gain. It is shown that the phase and gain margins are quite high and the loop gain is large around the resonances.

Bode plot of the "decentralized loop gain" $G_\text{iff}(i,i) \times K_\text{iff}(i,i)$

Effect of IFF on the transfer function from actuator to encoder - Simulations

<<sec:test_nhexa_iff_struts_effect_plant>>

Still using the Simscape model with encoders fixed to the struts and 2DoF APA, the IFF strategy is tested.

%% Initialize the Simscape model in closed loop
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
                                       'flex_top_type', '4dof', ...
                                       'motion_sensor_type', 'struts', ...
                                       'actuator_type', '2dof', ...
                                       'controller_type', 'iff');

The Nano-hexapod is fixed on a rigid granite and no payload is fixed on top of the hexapod.

%% Nano-Hexapod is fixed on a rigid granite
support.type = 0;

%% No Payload on top of the Nano-Hexapod
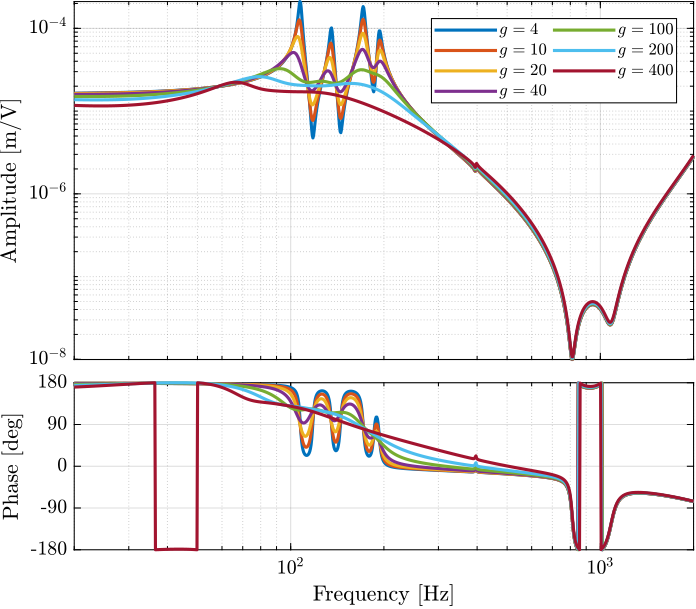
payload.type = 0;

The following IFF gains are tested:

%% Tested IFF gains
iff_gains = [4, 10, 20, 40, 100, 200, 400];

And the transfer functions from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ are identified for all the IFF gains.

%% Identify the (damped) transfer function from u to dLm for different values of the IFF gain
Gd_iff = {zeros(1, length(iff_gains))};

clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput');  io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Strut Displacement (encoder)

for i = 1:length(iff_gains)
    Kiff = iff_gains(i)*Kiff_g1*eye(6); % IFF Controller
    Gd_iff(i) = {exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options)};

    isstable(Gd_iff{i})
end

The obtained dynamics are shown in Figure ref:fig:test_nhexa_enc_struts_iff_gains_effect_dvf_plant.

Effect of the IFF gain $g$ on the transfer function from $\bm{\tau}$ to $d\bm{\mathcal{L}}_m$

Effect of IFF on the plant - Experimental Results

<<sec:test_nhexa_iff_struts_effect_plant_exp>>

Introduction   ignore

The IFF strategy is applied experimentally and the transfer function from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ is identified for all the defined values of the gain.

Load Data

First load the identification data.

%% Load Identification Data
meas_iff_gains = {};

for i = 1:length(iff_gains)
    meas_iff_gains(i) = {load(sprintf('iff_strut_1_noise_g_%i.mat', iff_gains(i)), 't', 'Vexc', 'de')};
end

Spectral Analysis - Setup

And define the useful variables that will be used for the identification using the tfestimate function.

%% Setup useful variables
% Sampling Time [s]
Ts = (meas_iff_gains{1}.t(end) - (meas_iff_gains{1}.t(1)))/(length(meas_iff_gains{1}.t)-1);

% Sampling Frequency [Hz]
Fs = 1/Ts;

% Hannning Windows
win = hanning(ceil(1*Fs));

% And we get the frequency vector
[~, f] = tfestimate(meas_iff_gains{1}.Vexc, meas_iff_gains{1}.de, win, [], [], 1/Ts);

DVF Plant

The transfer functions are estimated for all the values of the gain.

%% Transfer function from u to dLm
G_iff_gains = {};

for i = 1:length(iff_gains)
    G_iff_gains{i} = tfestimate(meas_iff_gains{i}.Vexc, meas_iff_gains{i}.de(:,1), win, [], [], 1/Ts);
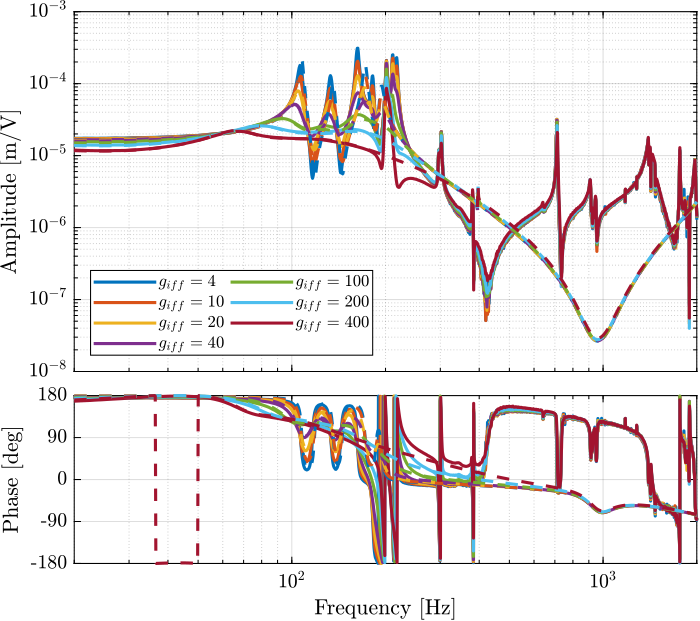
end

The obtained dynamics as shown in the bode plot in Figure ref:fig:test_nhexa_comp_iff_gains_dvf_plant. The dashed curves are the results obtained using the model, and the solid curves the results from the experimental identification.

Transfer function from $u$ to $d\mathcal{L}_m$ for multiple values of the IFF gain

The bode plot is then zoomed on the suspension modes of the nano-hexapod in Figure ref:fig:test_nhexa_comp_iff_gains_dvf_plant_zoom.

Transfer function from $u$ to $d\mathcal{L}_m$ for multiple values of the IFF gain (Zoom)

The IFF control strategy is very effective for the damping of the suspension modes. It however does not damp the modes at 200Hz, 300Hz and 400Hz (flexible modes of the APA).

Also, the experimental results and the models obtained from the Simscape model are in agreement concerning the damped system (up to the flexible modes).

Experimental Results - Comparison of the un-damped and fully damped system

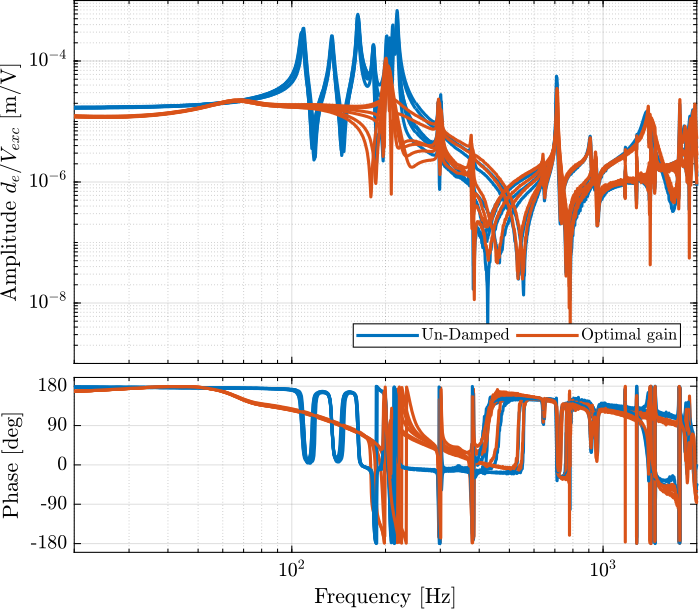
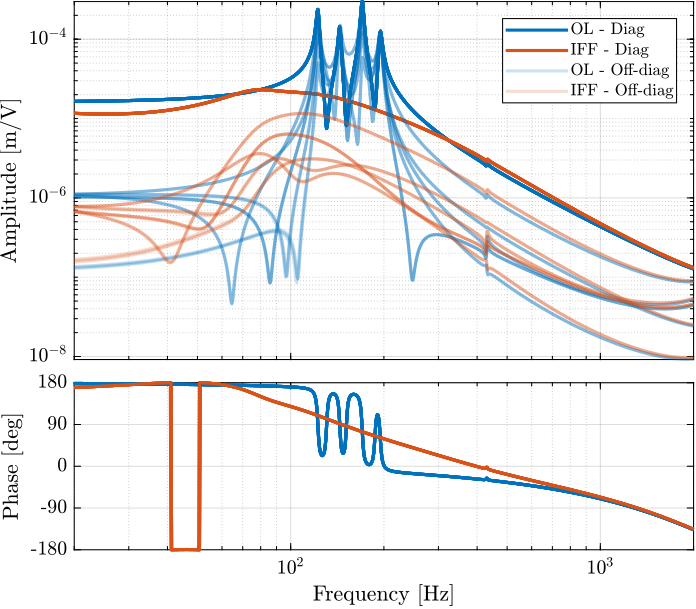
The un-damped and damped experimental plants are compared in Figure ref:fig:test_nhexa_comp_undamped_opt_iff_gain_diagonal (diagonal terms).

It is very clear that all the suspension modes are very well damped thanks to IFF. However, there is little to no effect on the flexible modes of the struts and of the plate.

Comparison of the diagonal elements of the tranfer function from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ without active damping and with optimal IFF gain

Experimental Results - Damped Plant with Optimal gain

<<sec:test_nhexa_iff_struts_opt_gain>>

Introduction   ignore

Let's now look at the $6 \times 6$ damped plant with the optimal gain $g = 400$.

Load Data

The experimental data are loaded.

%% Load Identification Data
meas_iff_struts = {};

for i = 1:6
    meas_iff_struts(i) = {load(sprintf('iff_strut_%i_noise_g_400.mat', i), 't', 'Vexc', 'Vs', 'de', 'u')};
end

Spectral Analysis - Setup

And the parameters useful for the spectral analysis are defined.

%% Setup useful variables
% Sampling Time [s]
Ts = (meas_iff_struts{1}.t(end) - (meas_iff_struts{1}.t(1)))/(length(meas_iff_struts{1}.t)-1);

% Sampling Frequency [Hz]
Fs = 1/Ts;

% Hannning Windows
win = hanning(ceil(1*Fs));

% And we get the frequency vector
[~, f] = tfestimate(meas_iff_struts{1}.Vexc, meas_iff_struts{1}.de, win, [], [], 1/Ts);

DVF Plant

Finally, the $6 \times 6$ plant is identified using the tfestimate function.

%% DVF Plant (transfer function from u to dLm)
G_iff_opt = {};

for i = 1:6
    G_iff_opt{i} = tfestimate(meas_iff_struts{i}.Vexc, meas_iff_struts{i}.de, win, [], [], 1/Ts);
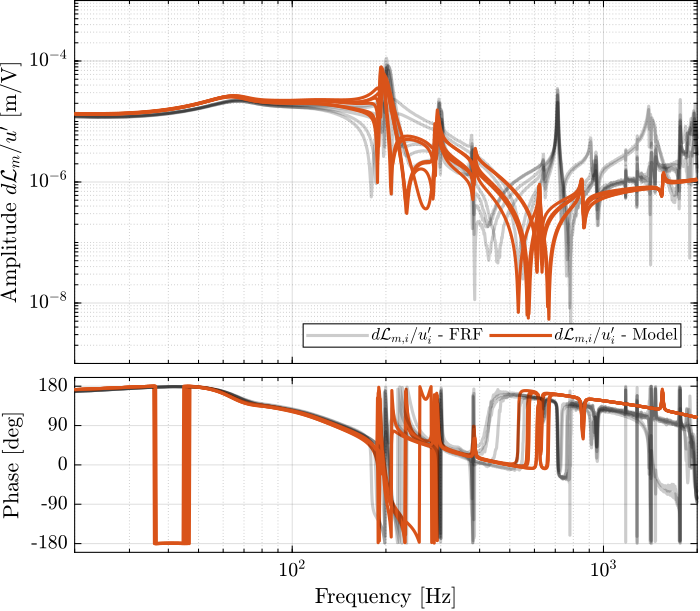
end

The obtained diagonal elements are compared with the model in Figure ref:fig:test_nhexa_damped_iff_plant_comp_diagonal.

Comparison of the diagonal elements of the transfer functions from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ with active damping (IFF) applied with an optimal gain $g = 400$

And all the off-diagonal elements are compared with the model in Figure ref:fig:test_nhexa_damped_iff_plant_comp_off_diagonal.

Comparison of the off-diagonal elements of the transfer functions from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ with active damping (IFF) applied with an optimal gain $g = 400$

With the IFF control strategy applied and the optimal gain used, the suspension modes are very well damped. Remains the un-damped flexible modes of the APA (200Hz, 300Hz, 400Hz), and the modes of the plates (700Hz).

The Simscape model and the experimental results are in very good agreement.

Comparison with the Flexible model

<<sec:test_nhexa_iff_struts_comp_flex_model>>

When using the 2-DoF model for the APA, the flexible modes of the struts were not modelled, and it was the main limitation of the model. Now, let's use a flexible model for the APA, and see if the obtained damped plant using the model is similar to the measured dynamics.

First, the nano-hexapod is initialized.

%% Estimated misalignement of the struts
d_aligns = [[-0.05,  -0.3,  0];
            [ 0,      0.5,  0];
            [-0.1,   -0.3,  0];
            [ 0,      0.3,  0];
            [-0.05,   0.05, 0];
            [0,       0,    0]]*1e-3;


%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
                                       'flex_top_type', '4dof', ...
                                       'motion_sensor_type', 'struts', ...
                                       'actuator_type', 'flexible', ...
                                       'actuator_d_align', d_aligns, ...
                                       'controller_type', 'iff');

And the "optimal" controller is loaded.

%% Optimal IFF controller
load('Kiff_struts_no_payload.mat', 'Kiff');

The transfer function from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ is identified using the Simscape model.

%% Linearized inputs/outputs
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'],  1, 'openinput');  io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dL'],  1, 'openoutput'); io_i = io_i + 1; % Strut Displacement (encoder)

%% Identification of the plant
Gd_iff = exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options);

The obtained diagonal elements are shown in Figure ref:fig:test_nhexa_enc_struts_iff_opt_damp_comp_flex_model_diag while the off-diagonal elements are shown in Figure ref:fig:test_nhexa_enc_struts_iff_opt_damp_comp_flex_model_off_diag.

Diagonal elements of the transfer function from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ - comparison of the measured FRF and the identified dynamics using the flexible model

Off-diagonal elements of the transfer function from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ - comparison of the measured FRF and the identified dynamics using the flexible model

Using flexible models for the APA, the agreement between the Simscape model of the nano-hexapod and the measured FRF is very good.

Only the flexible mode of the top-plate is not appearing in the model which is very logical as the top plate is taken as a solid body.

Conclusion

The decentralized Integral Force Feedback strategy applied on the nano-hexapod is very effective in damping all the suspension modes.

The Simscape model (especially when using a flexible model for the APA) is shown to be very accurate, even when IFF is applied.

Modal Analysis

<<sec:test_nhexa_enc_struts_modal_analysis>>

Introduction   ignore

Several 3-axis accelerometers are fixed on the top platform of the nano-hexapod as shown in Figure ref:fig:test_nhexa_compliance_vertical_comp_iff.

The top platform is then excited using an instrumented hammer as shown in Figure ref:fig:test_nhexa_hammer_excitation_compliance_meas.

From this experiment, the resonance frequencies and the associated mode shapes can be computed (Section ref:sec:test_nhexa_modal_analysis_mode_shapes). Then, in Section ref:sec:test_nhexa_compliance_effect_iff, the vertical compliance of the nano-hexapod is experimentally estimated. Finally, in Section ref:sec:test_nhexa_compliance_effect_iff_comp_model, the measured compliance is compare with the estimated one from the Simscape model.

Obtained Mode Shapes

<<sec:test_nhexa_modal_analysis_mode_shapes>>

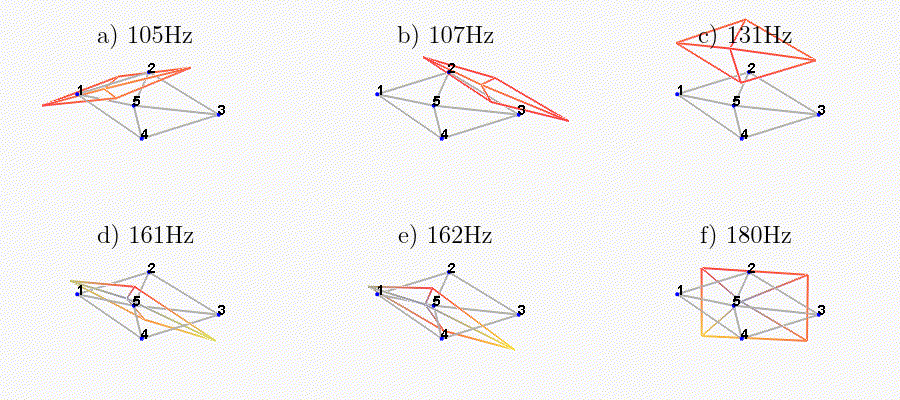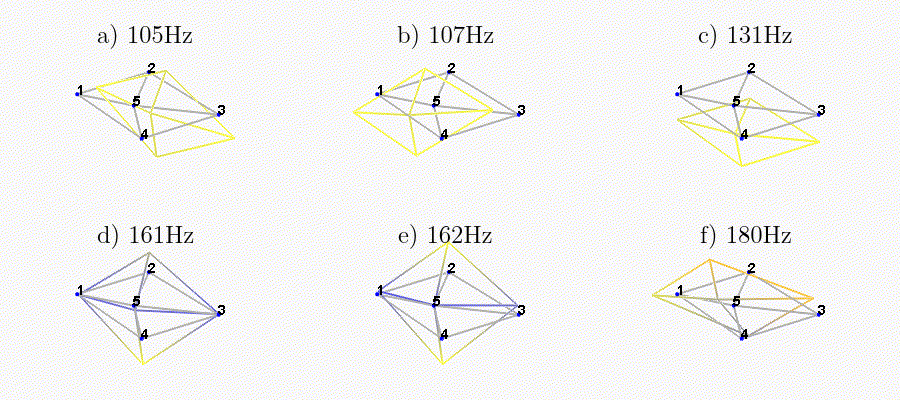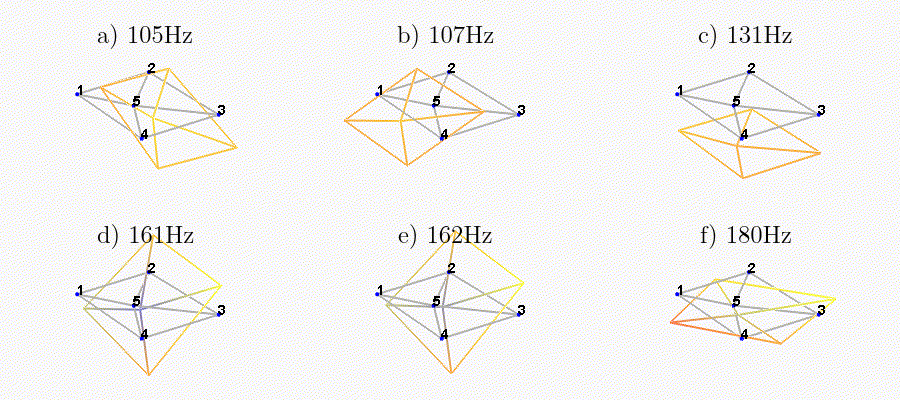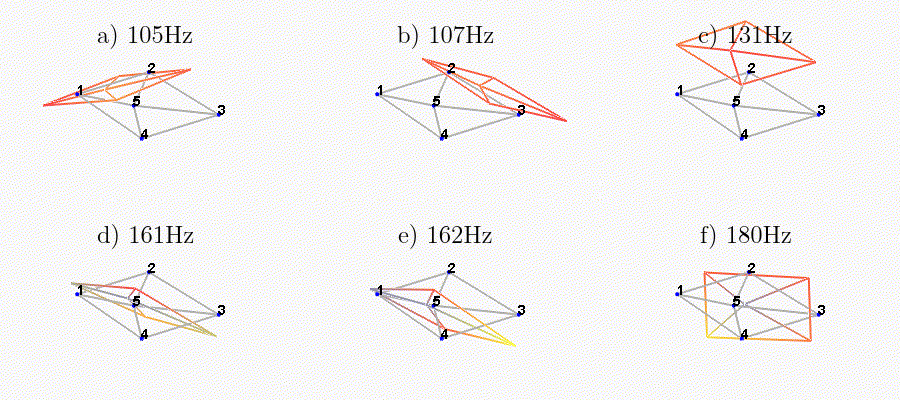
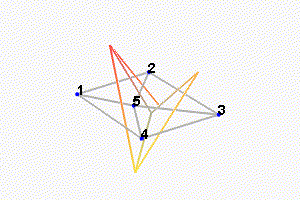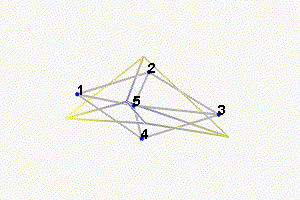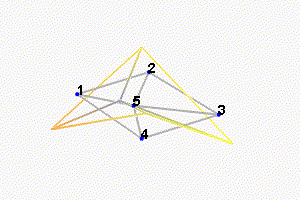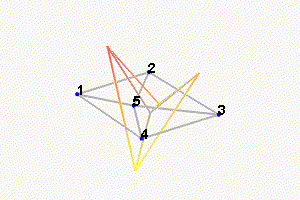
We can observe the mode shapes of the first 6 modes that are the suspension modes (the plate is behaving as a solid body) in Figure ref:fig:test_nhexa_mode_shapes_annotated.

Then, there is a mode at 692Hz which corresponds to a flexible mode of the top plate (Figure ref:fig:test_nhexa_mode_shapes_flexible_annotated).

The obtained modes are summarized in Table ref:tab:description_modes.

Mode	Freq. [Hz]	Description
1	105	Suspension Mode: Y-translation
2	107	Suspension Mode: X-translation
3	131	Suspension Mode: Z-translation
4	161	Suspension Mode: Y-tilt
5	162	Suspension Mode: X-tilt
6	180	Suspension Mode: Z-rotation
7	692	(flexible) Membrane mode of the top platform

Nano-Hexapod Compliance - Effect of IFF

<<sec:test_nhexa_compliance_effect_iff>>

In this section, we wish to estimate the effectiveness of the IFF strategy regarding the compliance.

The top plate is excited vertically using the instrumented hammer two times:

1. no control loop is used
2. decentralized IFF is used

The data are loaded.

frf_ol  = load('Measurement_Z_axis.mat'); % Open-Loop
frf_iff = load('Measurement_Z_axis_damped.mat'); % IFF

The mean vertical motion of the top platform is computed by averaging all 5 vertical accelerometers.

%% Multiply by 10 (gain in m/s^2/V) and divide by 5 (number of accelerometers)
d_frf_ol = 10/5*(frf_ol.FFT1_H1_4_1_RMS_Y_Mod + frf_ol.FFT1_H1_7_1_RMS_Y_Mod + frf_ol.FFT1_H1_10_1_RMS_Y_Mod + frf_ol.FFT1_H1_13_1_RMS_Y_Mod + frf_ol.FFT1_H1_16_1_RMS_Y_Mod)./(2*pi*frf_ol.FFT1_H1_16_1_RMS_X_Val).^2;
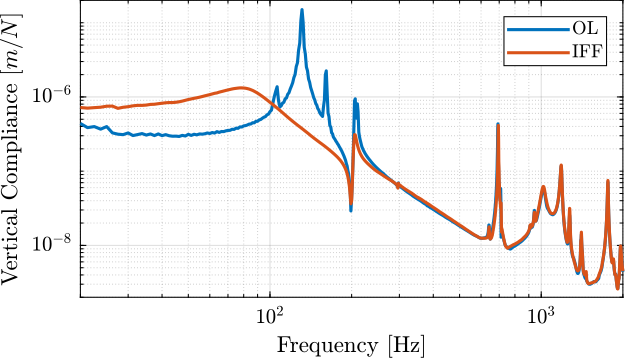
d_frf_iff = 10/5*(frf_iff.FFT1_H1_4_1_RMS_Y_Mod + frf_iff.FFT1_H1_7_1_RMS_Y_Mod + frf_iff.FFT1_H1_10_1_RMS_Y_Mod + frf_iff.FFT1_H1_13_1_RMS_Y_Mod + frf_iff.FFT1_H1_16_1_RMS_Y_Mod)./(2*pi*frf_iff.FFT1_H1_16_1_RMS_X_Val).^2;

The vertical compliance (magnitude of the transfer function from a vertical force applied on the top plate to the vertical motion of the top plate) is shown in Figure ref:fig:test_nhexa_compliance_vertical_comp_iff.

Measured vertical compliance with and without IFF

From Figure ref:fig:test_nhexa_compliance_vertical_comp_iff, it is clear that the IFF control strategy is very effective in damping the suspensions modes of the nano-hexapod. It also has the effect of (slightly) degrading the vertical compliance at low frequency.

It also seems some damping can be added to the modes at around 205Hz which are flexible modes of the struts.

Comparison with the Simscape Model

<<sec:test_nhexa_compliance_effect_iff_comp_model>>

Let's initialize the Simscape model such that it corresponds to the experiment.

%% Nano-Hexapod is fixed on a rigid granite
support.type = 0;

%% No Payload on top of the Nano-Hexapod
payload.type = 0;

%% Initialize Nano-Hexapod in Open Loop
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
                                       'flex_top_type', '4dof', ...
                                       'motion_sensor_type', 'struts', ...
                                       'actuator_type', '2dof');

And let's compare the measured vertical compliance with the vertical compliance as estimated from the Simscape model.

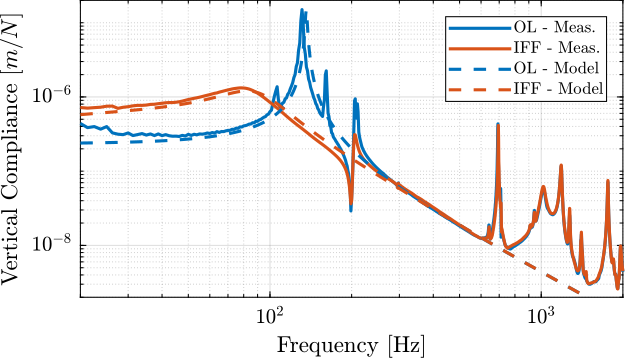
The transfer function from a vertical external force to the absolute motion of the top platform is identified (with and without IFF) using the Simscape model.

The comparison is done in Figure ref:fig:test_nhexa_compliance_vertical_comp_model_iff. Again, the model is quite accurate in predicting the (closed-loop) behavior of the system.

Measured vertical compliance with and without IFF

Conclusion

From the previous analysis, several conclusions can be drawn:

• Decentralized IFF is very effective in damping the "suspension" modes of the nano-hexapod (Figure ref:fig:test_nhexa_comp_undamped_opt_iff_gain_diagonal)
• Decentralized IFF does not damp the "spurious" modes of the struts nor the flexible modes of the top plate (Figure ref:fig:test_nhexa_comp_undamped_opt_iff_gain_diagonal)
• Even though the Simscape model and the experimentally measured FRF are in good agreement (Figures ref:fig:test_nhexa_enc_struts_iff_opt_damp_comp_flex_model_diag and ref:fig:test_nhexa_enc_struts_iff_opt_damp_comp_flex_model_off_diag), the obtain dynamics from the control inputs $\bm{u}$ and the encoders $d\bm{\mathcal{L}}_m$ is very difficult to control

Therefore, in the following sections, the encoders will be fixed to the plates. The goal is to be less sensitive to the flexible modes of the struts.

Encoders fixed to the plates

<<sec:test_nhexa_encoders_plates>>

Introduction   ignore

In this section, the encoders are fixed to the plates rather than to the struts as shown in Figure ref:fig:test_nhexa_enc_fixed_to_struts.

It is structured as follow:

• Section ref:sec:test_nhexa_enc_plates_plant_id: The dynamics of the nano-hexapod is identified.
• Section ref:sec:test_nhexa_enc_plates_comp_simscape: The identified dynamics is compared with the Simscape model.
• Section ref:sec:test_nhexa_enc_plates_iff: The Integral Force Feedback (IFF) control strategy is applied and the dynamics of the damped nano-hexapod is identified and compare with the Simscape model.

Identification of the dynamics

<<sec:test_nhexa_enc_plates_plant_id>>

Introduction   ignore

In this section, the dynamics of the nano-hexapod with the encoders fixed to the plates is identified.

First, the measurement data are loaded in Section ref:sec:test_nhexa_enc_plates_plant_id_setup, then the transfer function matrix from the actuators to the encoders are estimated in Section ref:sec:test_nhexa_enc_plates_plant_id_dvf. Finally, the transfer function matrix from the actuators to the force sensors is estimated in Section ref:sec:test_nhexa_enc_plates_plant_id_iff.

Data Loading and Spectral Analysis Setup

<<sec:test_nhexa_enc_plates_plant_id_setup>>

The actuators are excited one by one using a low pass filtered white noise. For each excitation, the 6 force sensors and 6 encoders are measured and saved.

%% Load Identification Data
meas_data = {};

for i = 1:6
    meas_data(i) = {load(sprintf('frf_exc_strut_%i_enc_plates_noise.mat', i), 't', 'Va', 'Vs', 'de')};
end

Transfer function from Actuator to Encoder

<<sec:test_nhexa_enc_plates_plant_id_dvf>>

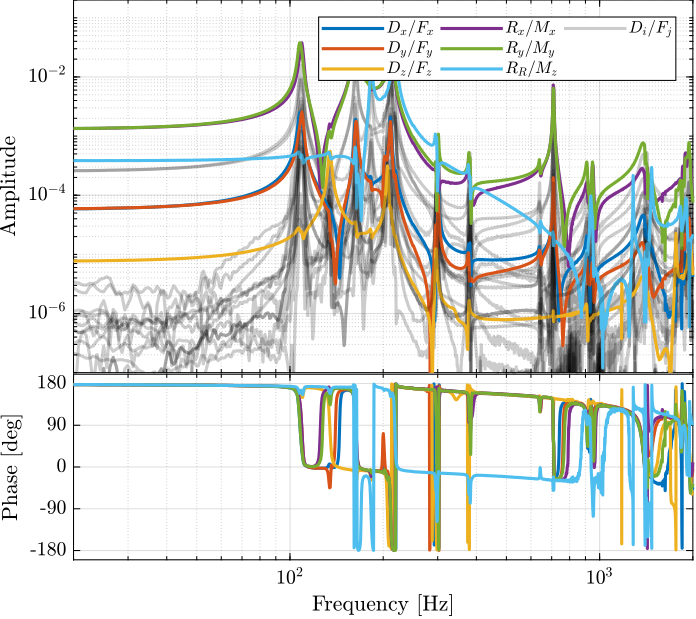
The 6x6 transfer function matrix from the excitation voltage $\bm{u}$ and the displacement $d\bm{\mathcal{L}}_m$ as measured by the encoders is estimated.

%% Transfer function from u to dLm
G_dL = zeros(length(f), 6, 6);

for i = 1:6
    G_dL(:,:,i) = tfestimate(meas_data{i}.Va, meas_data{i}.de, win, [], [], 1/Ts);
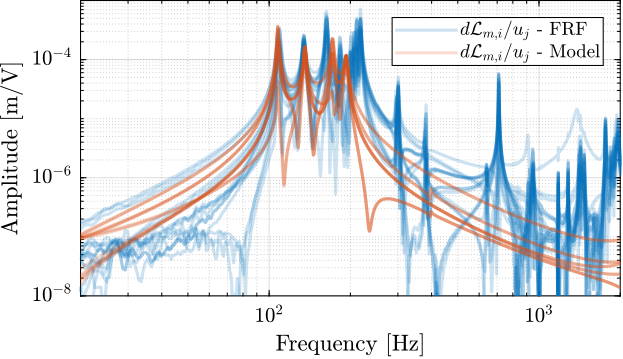
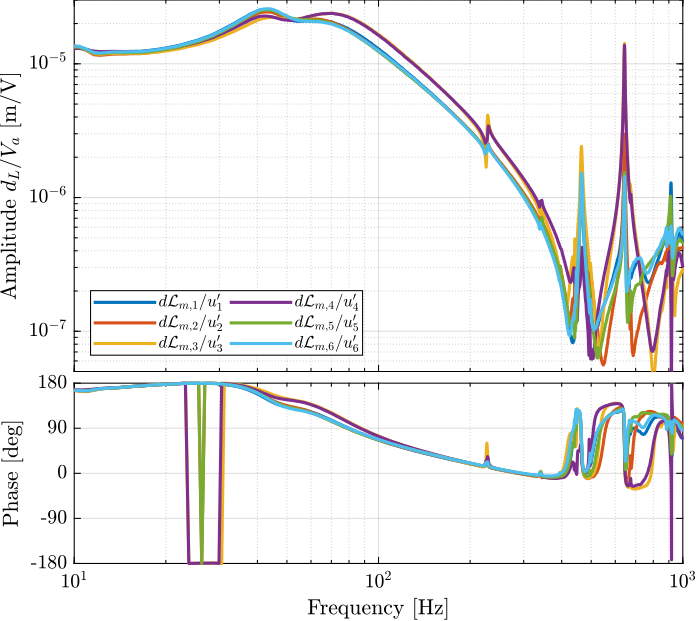
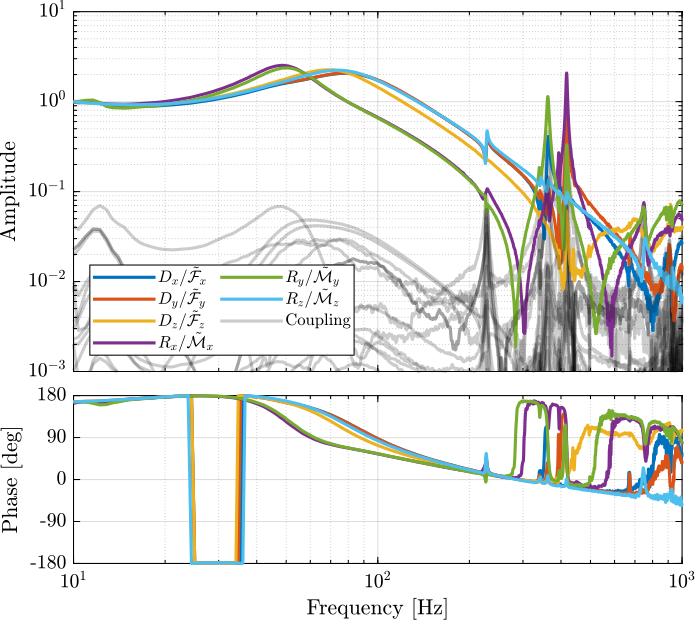
end

The diagonal and off-diagonal terms of this transfer function matrix are shown in Figure ref:fig:test_nhexa_enc_plates_dvf_frf.

Measured FRF for the transfer function from $\bm{u}$ to $d\bm{\mathcal{L}}_m$

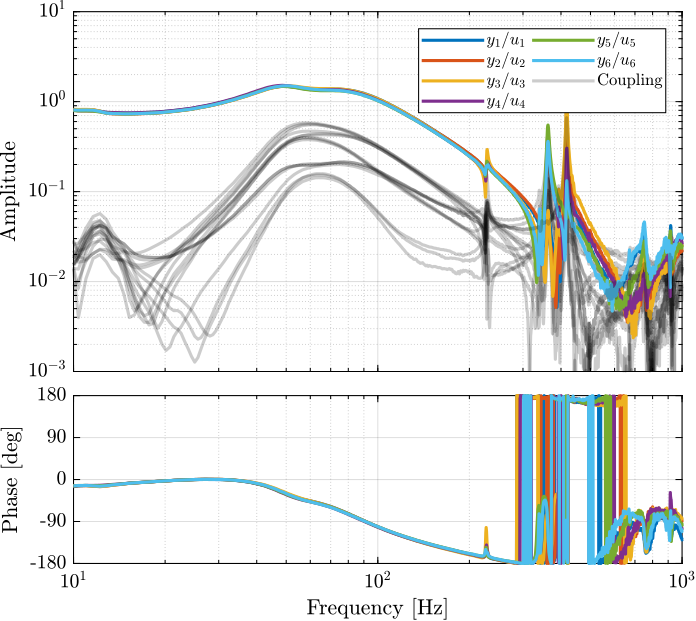
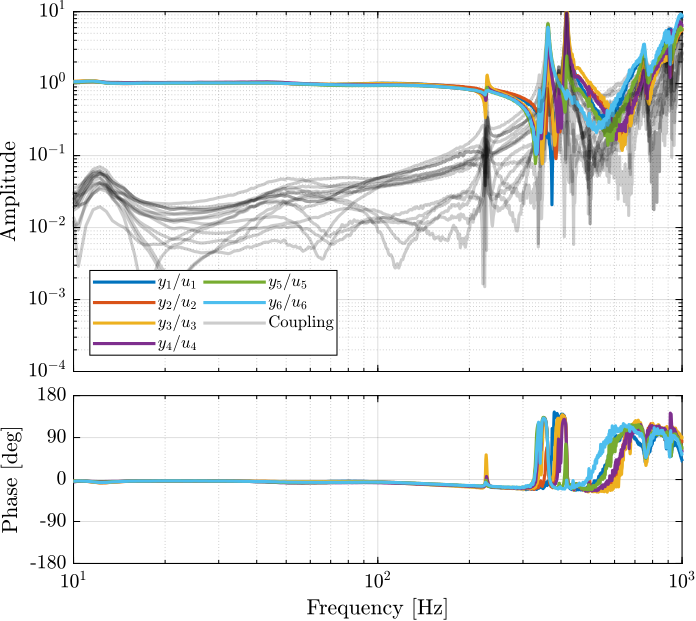
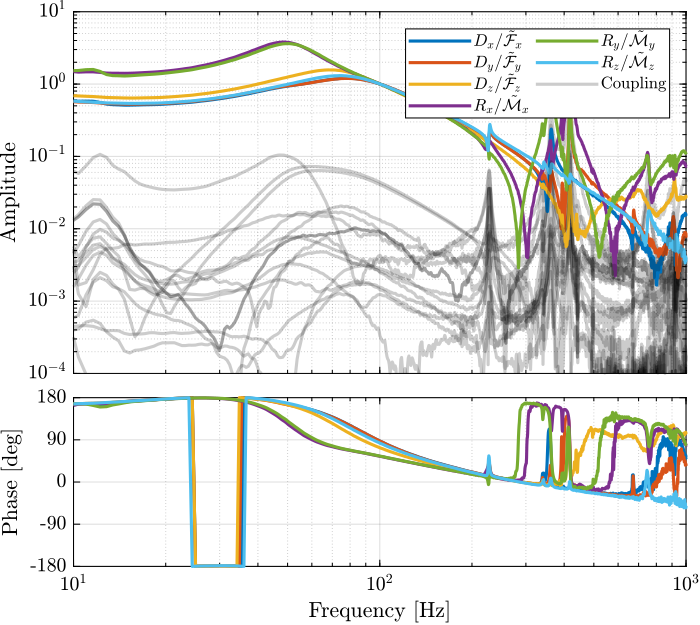
From Figure ref:fig:test_nhexa_enc_plates_dvf_frf, we can draw few conclusions on the transfer functions from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ when the encoders are fixed to the plates:

• the decoupling is rather good at low frequency (below the first suspension mode). The low frequency gain is constant for the off diagonal terms, whereas when the encoders where fixed to the struts, the low frequency gain of the off-diagonal terms were going to zero (Figure ref:fig:test_nhexa_enc_struts_dvf_frf).
• the flexible modes of the struts at 226Hz and 337Hz are indeed shown in the transfer functions, but their amplitudes are rather low.
• the diagonal terms have alternating poles and zeros up to at least 600Hz: the flexible modes of the struts are not affecting the alternating pole/zero pattern. This what not the case when the encoders were fixed to the struts (Figure ref:fig:test_nhexa_enc_struts_dvf_frf).

Transfer function from Actuator to Force Sensor

<<sec:test_nhexa_enc_plates_plant_id_iff>> Then the 6x6 transfer function matrix from the excitation voltage $\bm{u}$ and the voltage $\bm{\tau}_m$ generated by the Force senors is estimated.

%% IFF Plant
G_tau = zeros(length(f), 6, 6);

for i = 1:6
    G_tau(:,:,i) = tfestimate(meas_data{i}.Va, meas_data{i}.Vs, win, [], [], 1/Ts);
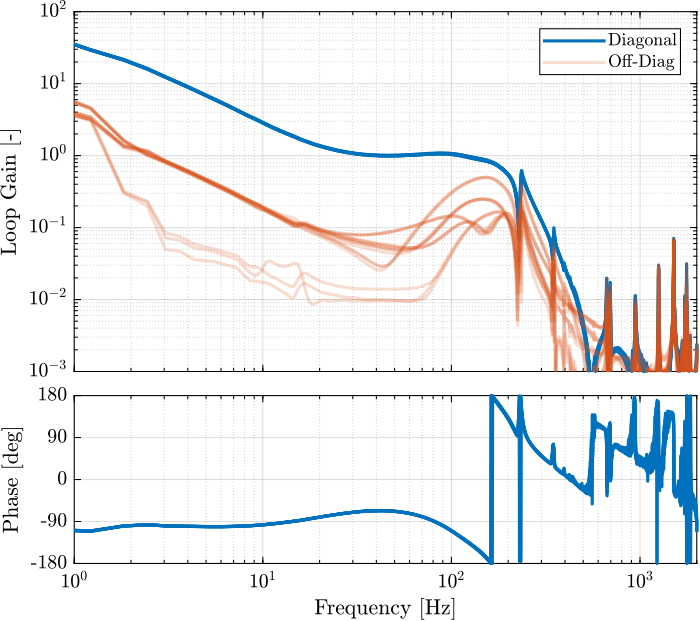
end

The bode plot of the diagonal and off-diagonal terms are shown in Figure ref:fig:test_nhexa_enc_plates_iff_frf.

Measured FRF for the IFF plant

It is shown in Figure ref:fig:test_nhexa_enc_plates_iff_comp_simscape_all that:

• The IFF plant has alternating poles and zeros
• The first flexible mode of the struts as 235Hz is appearing, and therefore is should be possible to add some damping to this mode using IFF
• The decoupling is quite good at low frequency (below the first model) as well as high frequency (above the last suspension mode, except near the flexible modes of the top plate)

Save Identified Plants

The identified dynamics is saved for further use.

save('data_frf/identified_plants_enc_plates.mat', 'f', 'Ts', 'G_tau', 'G_dL')

Comparison with the Simscape Model

<<sec:test_nhexa_enc_plates_comp_simscape>>

Introduction   ignore

In this section, the measured dynamics done in Section ref:sec:test_nhexa_enc_plates_plant_id is compared with the dynamics estimated from the Simscape model.

Identification with the Simscape Model

The nano-hexapod is initialized with the APA taken as 2dof models.

%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
                                       'flex_top_type', '4dof', ...
                                       'motion_sensor_type', 'plates', ...
                                       'actuator_type', '2dof');

support.type = 1; % On top of vibration table
payload.type = 0; % No Payload

Then the transfer function from $\bm{u}$ to $\bm{\tau}_m$ is identified using the Simscape model.

%% Identify the transfer function from u to taum
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput');   io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors

G_tau = exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options);

Now, the dynamics from the DAC voltage $\bm{u}$ to the encoders $d\bm{\mathcal{L}}_m$ is estimated using the Simscape model.

%% Identify the DVtransfer function from u to dLm
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'],  1, 'openinput');  io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Encoders

G_dL = exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options);

The identified dynamics is saved for further use.

save('data_frf/simscape_plants_enc_plates.mat', 'G_tau', 'G_dL');

Dynamics from Actuator to Force Sensors

The identified dynamics is compared with the measured FRF:

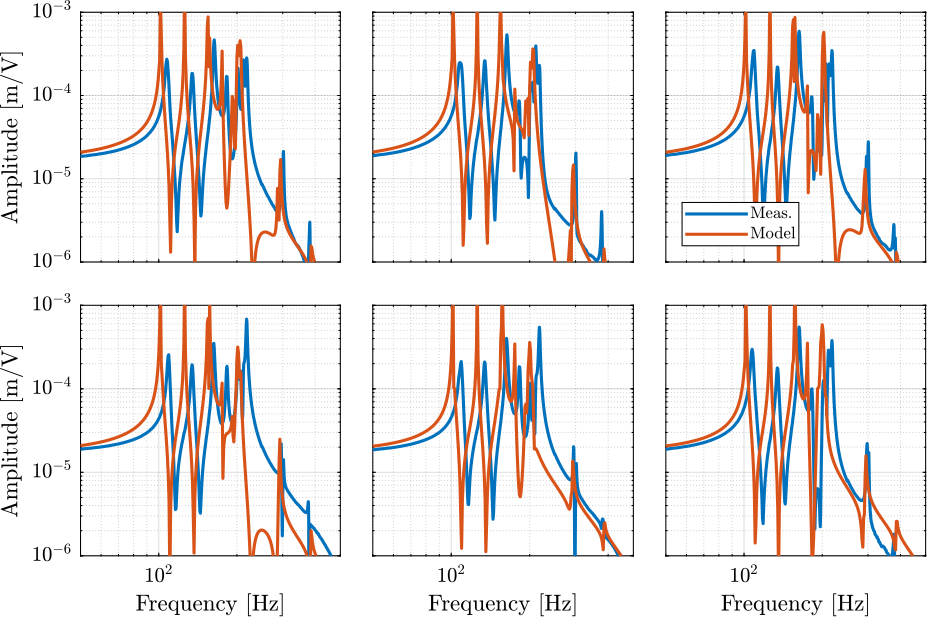
• Figure ref:fig:test_nhexa_enc_plates_iff_comp_simscape_all: the individual transfer function from $u_1$ (the DAC voltage for the first actuator) to the force sensors of all 6 struts are compared
• Figure ref:fig:test_nhexa_enc_plates_iff_comp_simscape: all the diagonal elements are compared
• Figure ref:fig:test_nhexa_enc_plates_iff_comp_offdiag_simscape: all the off-diagonal elements are compared

IFF Plant for the first actuator input and all the force senosrs

Diagonal elements of the IFF Plant

Off diagonal elements of the IFF Plant

Dynamics from Actuator to Encoder

The identified dynamics is compared with the measured FRF:

• Figure ref:fig:test_nhexa_enc_plates_dvf_comp_simscape_all: the individual transfer function from $u_3$ (the DAC voltage for the actuator number 3) to the six encoders
• Figure ref:fig:test_nhexa_enc_plates_dvf_comp_simscape: all the diagonal elements are compared
• Figure ref:fig:test_nhexa_enc_plates_dvf_comp_offdiag_simscape: all the off-diagonal elements are compared

DVF Plant for the first actuator input and all the encoders

Diagonal elements of the DVF Plant

Off diagonal elements of the DVF Plant

Conclusion

The Simscape model is quite accurate for the transfer function matrices from $\bm{u}$ to $\bm{\tau}_m$ and from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ except at frequencies of the flexible modes of the top-plate. The Simscape model can therefore be used to develop the control strategies.

Integral Force Feedback

<<sec:test_nhexa_enc_plates_iff>>

Introduction   ignore

In this section, the Integral Force Feedback (IFF) control strategy is applied to the nano-hexapod in order to add damping to the suspension modes.

The control architecture is shown in Figure ref:fig:test_nhexa_control_architecture_iff:

• $\bm{\tau}_m$ is the measured voltage of the 6 force sensors
• $\bm{K}_{\text{IFF}}$ is the $6 \times 6$ diagonal controller
• $\bm{u}$ is the plant input (voltage generated by the 6 DACs)
• $\bm{u}^\prime$ is the new plant inputs with added damping

\begin{tikzpicture}
  % Blocs
  \node[block={3.0cm}{2.0cm}] (P) {Plant};
  \coordinate[] (inputF) at ($(P.south west)!0.5!(P.north west)$);
  \coordinate[] (outputF) at ($(P.south east)!0.7!(P.north east)$);
  \coordinate[] (outputL) at ($(P.south east)!0.3!(P.north east)$);

  \node[block, above=0.4 of P] (Kiff) {$\bm{K}_\text{IFF}$};
  \node[addb, left= of inputF] (addF) {};

  % Connections and labels
  \draw[->] (outputF) -- ++(1, 0) node[below left]{$\bm{\tau}_m$};
  \draw[->] (outputL) -- ++(1, 0) node[below left]{$d\bm{\mathcal{L}}_m$};

  \draw[->] ($(outputF) + (0.6, 0)$)node[branch]{} |- (Kiff.east);
  \draw[->] (Kiff.west) -| (addF.north);
  \draw[->] (addF.east) -- (inputF) node[above left]{$\bm{u}$};
  \draw[<-] (addF.west) -- ++(-1, 0) node[above right]{$\bm{u}^\prime$};
\end{tikzpicture}

Integral Force Feedback Strategy

• Section ref:sec:test_nhexa_enc_struts_effect_iff_plant

Effect of IFF on the plant - Simscape Model

<<sec:test_nhexa_enc_struts_effect_iff_plant>>

The nano-hexapod is initialized with 2DoF APA and the encoders fixed to the struts.

%% Initialize the Simscape model in closed loop
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
                                       'flex_top_type', '4dof', ...
                                       'motion_sensor_type', 'plates', ...
                                       'actuator_type', '2dof', ...
                                       'controller_type', 'iff');

support.type = 1; % On top of vibration table
payload.type = 0; % No Payload

The same controller as the one developed when the encoder were fixed to the struts is used.

%% Optimal IFF controller
load('Kiff_struts_no_payload.mat', 'Kiff');

The transfer function from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ is identified.

%% Identify the (damped) transfer function from u to dLm for different values of the IFF gain
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'],  1, 'openinput');  io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Plate Displacement (encoder)

%% Transfer function from u to dL (IFF)
G_dL = exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options);

It is first verified that the system is stable:

isstable(G_dL)

1

The identified dynamics is saved for further use.

save('data_frf/simscape_plants_enc_plates_iff.mat', 'G_dL');

The diagonal and off-diagonal terms of the $6 \times 6$ transfer function matrices identified are compared in Figure ref:fig:test_nhexa_enc_plates_iff_gains_effect_dvf_plant. It is shown, as was the case when the encoders were fixed to the struts, that the IFF control strategy is very effective in damping the suspension modes of the nano-hexapod.

Effect of the IFF control strategy on the transfer function from $\bm{\tau}$ to $d\bm{\mathcal{L}}_m$

Effect of IFF on the plant - FRF

The IFF control strategy is experimentally implemented. The (damped) transfer function from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ is experimentally identified.

The identification data are loaded:

%% Load Identification Data
meas_iff_plates = {};

for i = 1:6
    meas_iff_plates(i) = {load(sprintf('frf_exc_iff_strut_%i_enc_plates_noise.mat', i), 't', 'Va', 'Vs', 'de', 'u')};
end

And the parameters used for the transfer function estimation are defined below.

% Sampling Time [s]
Ts = (meas_iff_plates{1}.t(end) - (meas_iff_plates{1}.t(1)))/(length(meas_iff_plates{1}.t)-1);

% Hannning Windows
win = hanning(ceil(1/Ts));

% And we get the frequency vector
[~, f] = tfestimate(meas_iff_plates{1}.Va, meas_iff_plates{1}.de, win, [], [], 1/Ts);

The estimation is performed using the tfestimate command.

%% Estimation of the transfer function matrix from u to dL when IFF is applied
G_dL = zeros(length(f), 6, 6);

for i = 1:6
    G_dL(:,:,i) = tfestimate(meas_iff_plates{i}.Va, meas_iff_plates{i}.de, win, [], [], 1/Ts);
end

The experimentally identified plant is saved for further use.

save('matlab/data_frf/damped_plant_enc_plates.mat', 'f', 'Ts', 'G_dL')

save('data_frf/damped_plant_enc_plates.mat', 'f', 'Ts', 'G_dL')

The obtained diagonal and off-diagonal elements of the transfer function from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ are shown in Figure ref:fig:test_nhexa_enc_plant_plates_effect_iff both without and with IFF.

Effect of the IFF control strategy on the transfer function from $\bm{\tau}$ to $d\bm{\mathcal{L}}_m$

As was predicted with the Simscape model, the IFF control strategy is very effective in damping the suspension modes of the nano-hexapod. Little damping is also applied on the first flexible mode of the strut at 235Hz. However, no damping is applied on other modes, such as the flexible modes of the top plate.

Comparison of the measured FRF and the Simscape model

Let's now compare the obtained damped plants obtained experimentally with the one extracted from Simscape:

• Figure ref:fig:test_nhexa_enc_plates_opt_iff_comp_simscape_all: the individual transfer function from $u_1^\prime$ to the six encoders are comapred
• Figure ref:fig:test_nhexa_damped_iff_plates_plant_comp_diagonal: all the diagonal elements are compared
• Figure ref:fig:test_nhexa_damped_iff_plates_plant_comp_off_diagonal: all the off-diagonal elements are compared

FRF from one actuator to all the encoders when the plant is damped using IFF

Comparison of the diagonal elements of the transfer functions from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ with active damping (IFF) applied with an optimal gain $g = 400$

Comparison of the off-diagonal elements of the transfer functions from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ with active damping (IFF) applied with an optimal gain $g = 400$

From Figures ref:fig:test_nhexa_damped_iff_plates_plant_comp_diagonal and ref:fig:test_nhexa_damped_iff_plates_plant_comp_off_diagonal, it is clear that the Simscape model very well represents the dynamics of the nano-hexapod. This is true to around 400Hz, then the dynamics depends on the flexible modes of the top plate which are not modelled.

Effect of Payload mass on the Dynamics

<<sec:test_nhexa_added_mass>>

Introduction   ignore

In this section, the encoders are fixed to the plates, and we identify the dynamics for several payloads. The added payload are half cylinders, and three layers can be added for a total of around 40kg (Figure ref:fig:test_nhexa_picture_added_3_masses).

First the dynamics from $\bm{u}$ to $d\mathcal{L}_m$ and $\bm{\tau}_m$ is identified. Then, the Integral Force Feedback controller is developed and applied as shown in Figure ref:fig:test_nhexa_nano_hexapod_signals_iff. Finally, the dynamics from $\bm{u}^\prime$ to $d\mathcal{L}_m$ is identified and the added damping can be estimated.

\definecolor{instrumentation}{rgb}{0, 0.447, 0.741}
\definecolor{mechanics}{rgb}{0.8500, 0.325, 0.098}
\definecolor{control}{rgb}{0.4660, 0.6740, 0.1880}

\begin{tikzpicture}
  % Blocs
  \node[block={4.0cm}{3.0cm}, fill=mechanics!20!white] (nano_hexapod) {Mechanics};
  \coordinate[] (inputF)  at (nano_hexapod.west);
  \coordinate[] (outputL) at ($(nano_hexapod.south east)!0.8!(nano_hexapod.north east)$);
  \coordinate[] (outputF) at ($(nano_hexapod.south east)!0.2!(nano_hexapod.north east)$);

  \node[block, left= 0.8 of inputF,  fill=instrumentation!20!white, align=center] (F_stack) {\tiny Actuator \\ \tiny stacks};
  \node[block, left= 0.8 of F_stack, fill=instrumentation!20!white] (PD200)   {PD200};
  \node[DAC,   left= 0.8 of PD200,   fill=instrumentation!20!white] (F_DAC)   {DAC};
  \node[block, right=0.8 of outputF, fill=instrumentation!20!white, align=center] (Fm_stack){\tiny Sensor \\ \tiny stack};
  \node[ADC,   right=0.8 of Fm_stack,fill=instrumentation!20!white] (Fm_ADC)  {ADC};
  \node[block, right=0.8 of outputL, fill=instrumentation!20!white] (encoder) {\tiny Encoder};
  \node[addb,  left= 0.8 of F_DAC,   fill=control!20!white]         (add_iff) {};
  \node[block, below=0.8 of add_iff, fill=control!20!white]         (Kiff) {\tiny $K_{\text{IFF}}(s)$};

  % Connections and labels
  \draw[->] (add_iff.east) node[above right]{$\bm{u}$} node[below right]{$[V]$} -- node[sloped]{$/$} (F_DAC.west);
  \draw[->] (F_DAC.east)   -- node[midway, above]{$\tilde{\bm{u}}$}node[midway, below]{$[V]$} (PD200.west);
  \draw[->] (PD200.east)   -- node[midway, above]{$\bm{u}_a$}node[midway, below]{$[V]$} (F_stack.west);
  \draw[->] (F_stack.east) -- (inputF) node[above left]{$\bm{\tau}$}node[below left]{$[N]$};

  \draw[->] (outputF)       -- (Fm_stack.west) node[above left]{$\bm{\epsilon}$} node[below left]{$[m]$};
  \draw[->] (Fm_stack.east) -- node[midway, above]{$\tilde{\bm{\tau}}_m$}node[midway, below]{$[V]$} (Fm_ADC.west);
  \draw[->] (Fm_ADC.east)   -- node[sloped]{$/$} ++(0.8, 0)coordinate(end) node[above left]{$\bm{\tau}_m$}node[below left]{$[V]$};

  \draw[->] (outputL)      -- (encoder.west) node[above left]{$d\bm{\mathcal{L}}$} node[below left]{$[m]$};
  \draw[->] (encoder.east) -- node[sloped]{$/$} (encoder-|end) node[above left]{$d\bm{\mathcal{L}}_m$}node[below left]{$[m]$};

  \draw[->] ($(Fm_ADC.east)+(0.14,0)$) node[branch]{} -- node[sloped]{$/$} ++(0, -1.8) -| (Kiff.south);
  \draw[->] (Kiff.north) -- node[sloped]{$/$} (add_iff.south);
  \draw[->] ($(add_iff.west)+(-0.8,0)$) node[above right]{$\bm{u}^\prime$} node[below right]{$[V]$} -- node[sloped]{$/$} (add_iff.west);

  % Nano-Hexapod
  \begin{scope}[on background layer]
    \node[fit={(F_stack.west|-nano_hexapod.south) (Fm_stack.east|-nano_hexapod.north)}, fill=black!20!white, draw, inner sep=2pt] (system) {};
    \node[above] at (system.north) {Nano-Hexapod};
  \end{scope}
\end{tikzpicture}

Block Diagram of the experimental setup and model

Measured Frequency Response Functions

The following data are loaded:

• Va: the excitation voltage (corresponding to $u_i$)
• Vs: the generated voltage by the 6 force sensors (corresponding to $\bm{\tau}_m$)
• de: the measured motion by the 6 encoders (corresponding to $d\bm{\mathcal{L}}_m$)

%% Load Identification Data
meas_added_mass = {};

for i_mass = i_masses
    for i_strut = 1:6
        meas_added_mass(i_strut, i_mass+1) = {load(sprintf('frf_data_exc_strut_%i_realigned_vib_table_%im.mat', i_strut, i_mass), 't', 'Va', 'Vs', 'de')};
    end
end

The window win and the frequency vector f are defined.

% Sampling Time [s]
Ts = (meas_added_mass{1,1}.t(end) - (meas_added_mass{1,1}.t(1)))/(length(meas_added_mass{1,1}.t)-1);

% Hannning Windows
win = hanning(ceil(1/Ts));

% And we get the frequency vector
[~, f] = tfestimate(meas_added_mass{1,1}.Va, meas_added_mass{1,1}.de, win, [], [], 1/Ts);

Finally the $6 \times 6$ transfer function matrices from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ and from $\bm{u}$ to $\bm{\tau}_m$ are identified:

%% DVF Plant (transfer function from u to dLm)
G_dL = {};

for i_mass = i_masses
    G_dL(i_mass+1) = {zeros(length(f), 6, 6)};
    for i_strut = 1:6
        G_dL{i_mass+1}(:,:,i_strut) = tfestimate(meas_added_mass{i_strut, i_mass+1}.Va, meas_added_mass{i_strut, i_mass+1}.de, win, [], [], 1/Ts);
    end
end

%% IFF Plant (transfer function from u to taum)
G_tau = {};

for i_mass = i_masses
    G_tau(i_mass+1) = {zeros(length(f), 6, 6)};
    for i_strut = 1:6
        G_tau{i_mass+1}(:,:,i_strut) = tfestimate(meas_added_mass{i_strut, i_mass+1}.Va, meas_added_mass{i_strut, i_mass+1}.Vs, win, [], [], 1/Ts);
    end
end

The identified dynamics are then saved for further use.

save('data_frf/frf_vib_table_m.mat', 'f', 'Ts', 'G_tau', 'G_dL')

Rigidification of the added payloads

• figure

%% Load Identification Data
meas_added_mass = {};

for i_strut = 1:6
    meas_added_mass(i_strut) = {load(sprintf('frf_data_exc_strut_%i_spindle_1m_solid.mat', i_strut), 't', 'Va', 'Vs', 'de')};
end

The window win and the frequency vector f are defined.

% Sampling Time [s]
Ts = (meas_added_mass{1}.t(end) - (meas_added_mass{1}.t(1)))/(length(meas_added_mass{1}.t)-1);

% Hannning Windows
win = hanning(ceil(1/Ts));

% And we get the frequency vector
[~, f] = tfestimate(meas_added_mass{1}.Va, meas_added_mass{1}.de, win, [], [], 1/Ts);

Finally the $6 \times 6$ transfer function matrices from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ and from $\bm{u}$ to $\bm{\tau}_m$ are identified:

%% DVF Plant (transfer function from u to dLm)

G_dL = zeros(length(f), 6, 6);
for i_strut = 1:6
    G_dL(:,:,i_strut) = tfestimate(meas_added_mass{i_strut}.Va, meas_added_mass{i_strut}.de, win, [], [], 1/Ts);
end

%% IFF Plant (transfer function from u to taum)
G_tau = zeros(length(f), 6, 6);
for i_strut = 1:6
    G_tau(:,:,i_strut) = tfestimate(meas_added_mass{i_strut}.Va, meas_added_mass{i_strut}.Vs, win, [], [], 1/Ts);
end

Transfer function from Actuators to Encoders

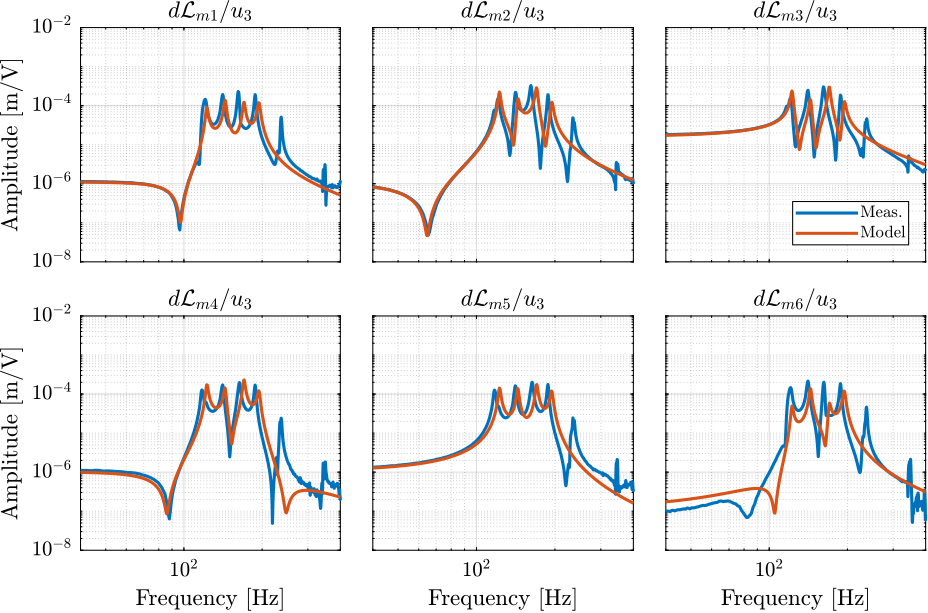
The transfer functions from $\bm{u}$ to $d\bm{\mathcal{L}}_{m}$ are shown in Figure ref:fig:test_nhexa_comp_plant_payloads_dvf.

Measured Frequency Response Functions from $u_i$ to $d\mathcal{L}_{m,i}$ for all 4 payload conditions. Diagonal terms are solid lines, and shaded lines are off-diagonal terms.

From Figure ref:fig:test_nhexa_comp_plant_payloads_dvf, we can observe few things:

• The obtained dynamics is changing a lot between the case without mass and when there is at least one added mass.
• Between 1, 2 and 3 added masses, the dynamics is not much different, and it would be easier to design a controller only for these cases.
• The flexible modes of the top plate is first decreased a lot when the first mass is added (from 700Hz to 400Hz). This is due to the fact that the added mass is composed of two half cylinders which are not fixed together. Therefore is adds a lot of mass to the top plate without adding a lot of rigidity in one direction. When more than 1 mass layer is added, the half cylinders are added with some angles such that rigidity are added in all directions (see Figure ref:fig:test_nhexa_picture_added_3_masses). In that case, the frequency of these flexible modes are increased. In practice, the payload should be one solid body, and we should not see a massive decrease of the frequency of this flexible mode.
• Flexible modes of the top plate are becoming less problematic as masses are added.
• First flexible mode of the strut at 230Hz is not much decreased when mass is added. However, its apparent amplitude is much decreased.

Transfer function from Actuators to Force Sensors

The transfer functions from $\bm{u}$ to $\bm{\tau}_{m}$ are shown in Figure ref:fig:test_nhexa_comp_plant_payloads_iff.

Measured Frequency Response Functions from $u_i$ to $\tau_{m,i}$ for all 4 payload conditions. Diagonal terms are solid lines, and shaded lines are off-diagonal terms.

From Figure ref:fig:test_nhexa_comp_plant_payloads_iff, we can see that for all added payloads, the transfer function from $\bm{u}$ to $\bm{\tau}_{m}$ always has alternating poles and zeros.

Coupling of the transfer function from Actuator to Encoders

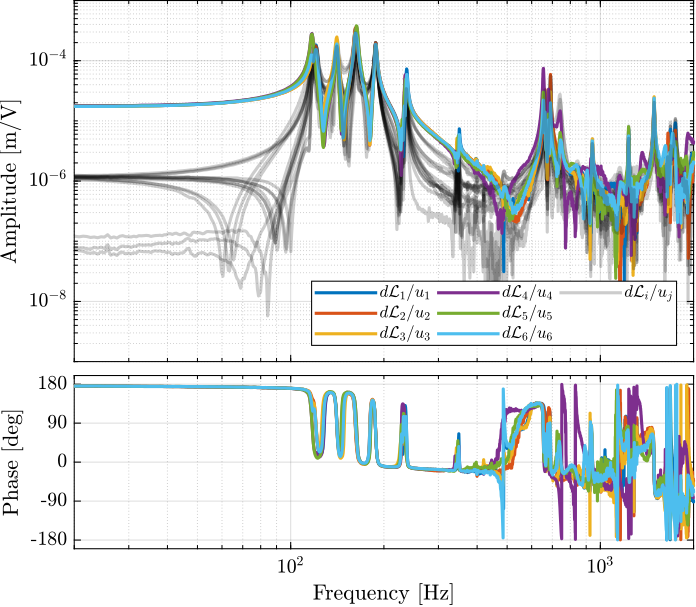
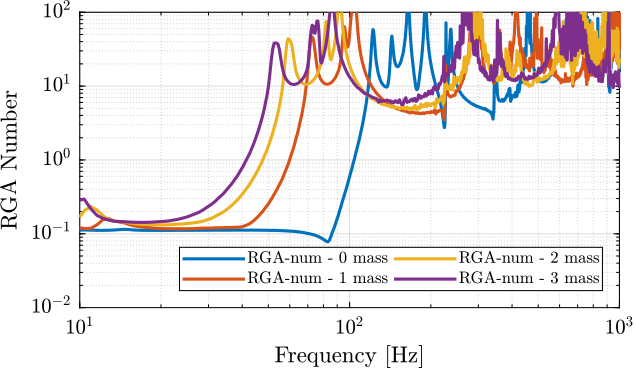
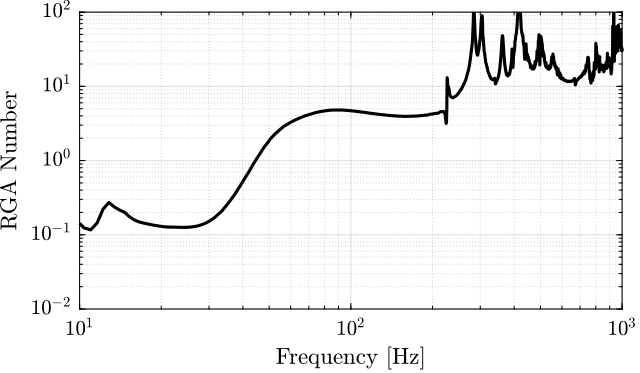
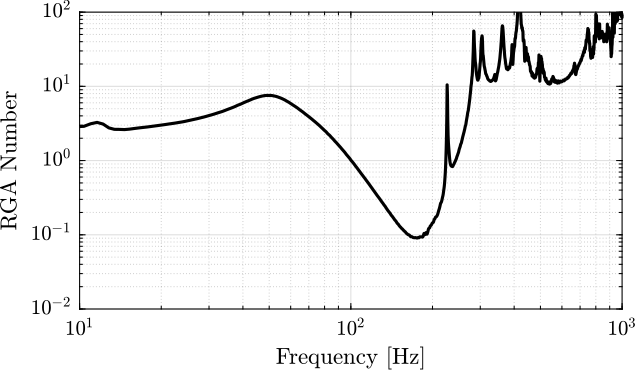
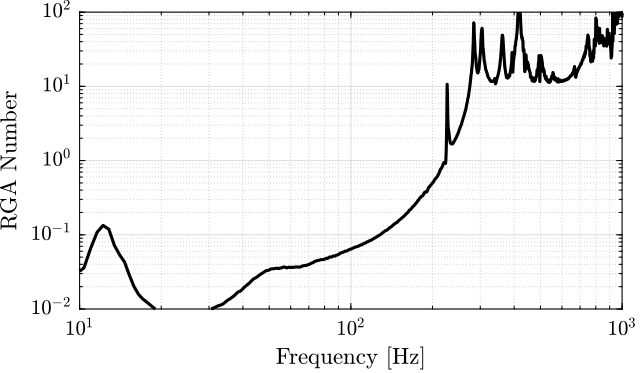
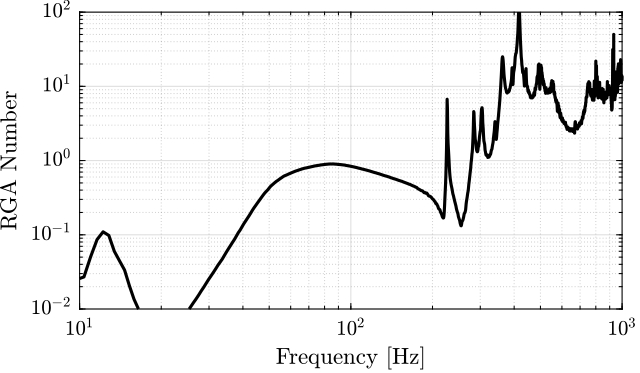
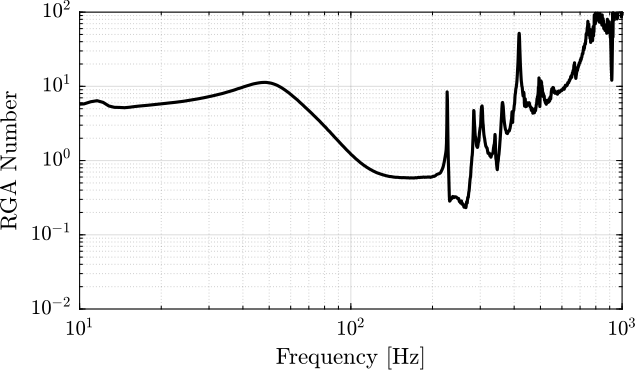
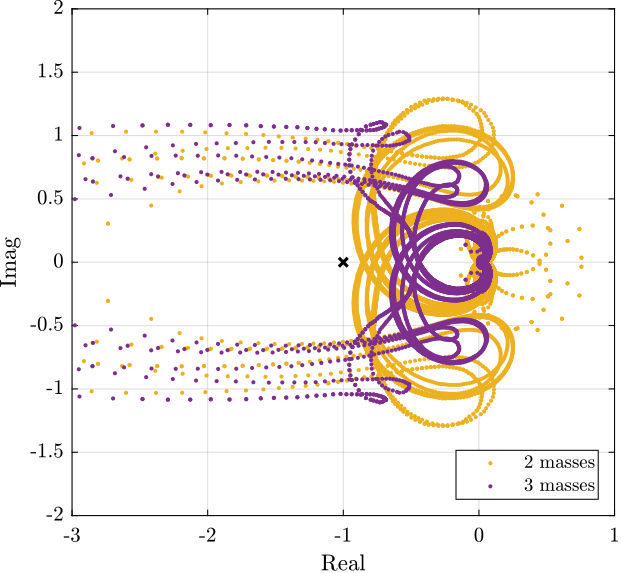
The RGA-number, which is a measure of the interaction in the system, is computed for the transfer function matrix from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ for all the payloads. The obtained numbers are compared in Figure ref:fig:test_nhexa_rga_num_ol_masses.

RGA-number for the open-loop transfer function from $\bm{u}$ to $d\bm{\mathcal{L}}_m$

From Figure ref:fig:test_nhexa_rga_num_ol_masses, it is clear that the coupling is quite large starting from the first suspension mode of the nano-hexapod. Therefore, is the payload's mass is increase, the coupling in the system start to become unacceptably large at lower frequencies.

Comparison with the Simscape model

<<sec:test_nhexa_added_mass_simscape>>

Introduction   ignore

Let's now compare the identified dynamics with the Simscape model. We wish to verify if the Simscape model is still accurate for all the tested payloads.

System Identification

Let's initialize the simscape model with the nano-hexapod fixed on top of the vibration table.

%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
                                       'flex_top_type', '4dof', ...
                                       'motion_sensor_type', 'plates', ...
                                       'actuator_type', '2dof');

support.type = 1; % On top of vibration table

First perform the identification for the transfer functions from $\bm{u}$ to $d\bm{\mathcal{L}}_m$:

%% Identify the DVF Plant (transfer function from u to dLm)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput');  io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Encoders

%% Identification for all the added payloads
G_dL = {};

for i = i_masses
    fprintf('i = %i\n', i)
    payload.type = i; % Change the payload on the nano-hexapod
    G_dL(i+1) = {exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options)};
end

%% Identify the IFF Plant (transfer function from u to taum)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput');  io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors

%% Identification for all the added payloads
G_tau = {};

for i = 0:3
    fprintf('i = %i\n', i)
    payload.type = i; % Change the payload on the nano-hexapod
    G_tau(i+1) = {exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options)};
end

The identified dynamics are then saved for further use.

save('data_frf/sim_vib_table_m.mat', 'G_tau', 'G_dL')

Transfer function from Actuators to Encoders

The measured FRF and the identified dynamics from $u_i$ to $d\mathcal{L}_{m,i}$ are compared in Figure ref:fig:test_nhexa_comp_masses_model_exp_dvf. A zoom near the "suspension" modes is shown in Figure ref:fig:test_nhexa_comp_masses_model_exp_dvf_zoom.

Comparison of the transfer functions from $u_i$ to $d\mathcal{L}_{m,i}$ - measured FRF and identification from the Simscape model

Comparison of the transfer functions from $u_i$ to $d\mathcal{L}_{m,i}$ - measured FRF and identification from the Simscape model (Zoom)

The Simscape model is very accurately representing the measured dynamics up. Only the flexible modes of the struts and of the top plate are not represented here as these elements are modelled as rigid bodies.

Transfer function from Actuators to Force Sensors

The measured FRF and the identified dynamics from $u_i$ to $\tau_{m,i}$ are compared in Figure ref:fig:test_nhexa_comp_masses_model_exp_iff. A zoom near the "suspension" modes is shown in Figure ref:fig:test_nhexa_comp_masses_model_exp_iff_zoom.

Comparison of the transfer functions from $u_i$ to $\tau_{m,i}$ - measured FRF and identification from the Simscape model

Comparison of the transfer functions from $u_i$ to $\tau_{m,i}$ - measured FRF and identification from the Simscape model (Zoom)

Integral Force Feedback Controller

<<sec:test_nhexa_robust_iff>>

Introduction   ignore

In this section, we wish to develop the Integral Force Feedback controller that is robust with respect to the added payload.

Robust IFF Controller

Based on the measured FRF from $\bm{u}$ to $\bm{\tau}_{m}$, the following IFF controller is developed:

%% IFF Controller
Kiff_g1 = -(1/(s + 2*pi*20))*... % LPF: provides integral action above 20[Hz]
           (s/(s + 2*pi*20))*... % HPF: limit low frequency gain
           (1/(1 + s/2/pi/400)); % LPF: more robust to high frequency resonances

Then, the Root Locus plot of Figure ref:fig:test_nhexa_iff_root_locus_masses is used to estimate the optimal gain. This Root Locus plot is computed from the Simscape model.

Root Locus for the IFF control strategy (for all payload conditions).

The found optimal IFF controller is:

%% Optimal controller
g_opt = 2e2;
Kiff = g_opt*Kiff_g1*eye(6);

It is saved for further use.

save('data_sim/Kiff_robust_opt.mat', 'Kiff')

The corresponding experimental loop gains are shown in Figure ref:fig:test_nhexa_iff_loop_gain_masses.

Loop gain for the Integral Force Feedback controller

Based on the above analysis:

• The same IFF controller can be used to damp the suspension modes for all payload conditions
• The IFF controller should be robust

Estimated Damped Plant from the Simscape model

Let's initialize the simscape model with the nano-hexapod fixed on top of the vibration table.

%% Initialize the Simscape model in closed loop
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
                                       'flex_top_type', '4dof', ...
                                       'motion_sensor_type', 'plates', ...
                                       'actuator_type', '2dof', ...
                                       'controller_type', 'iff');

support.type = 1; % On top of vibration table

And Load the IFF controller.

Finally, let's identify the damped plant from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ for all payloads.

%% Identify the (damped) transfer function from u to dLm
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput');  io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Plate Displacement (encoder)

%% Identify for all add masses
G_dL = {};

for i = i_masses
    payload.type = i;
    G_dL(i+1) = {exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options)};
end

The identified dynamics are then saved for further use.

save('data_frf/sim_iff_vib_table_m.mat', 'G_dL');

%% Load the identified dynamics
sim_iff = load('sim_iff_vib_table_m.mat', 'G_dL');

Transfer function from $u_i$ to $d\mathcal{L}_{m,i}$ (without active damping) and from $u^\prime_i$ to $d\mathcal{L}_{m,i}$ (with IFF)

Compute the identified FRF with IFF

Several experimental identifications are done in order to identify the dynamics from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ with the robust IFF controller implemented and with various payloads.

The following data are loaded:

• Va: the excitation voltage for the damped plant (corresponding to $u^\prime_i$)
• de: the measured motion by the 6 encoders (corresponding to $d\bm{\mathcal{L}}_m$)

%% Load Identification Data
meas_added_mass = {};

for i_mass = i_masses
    for i_strut = 1:6
        meas_iff_mass(i_strut, i_mass+1) = {load(sprintf('frf_data_exc_strut_%i_iff_vib_table_%im.mat', i_strut, i_mass), 't', 'Va', 'de')};
    end
end

The window win and the frequency vector f are defined.

% Sampling Time [s]
Ts = (meas_iff_mass{1,1}.t(end) - (meas_iff_mass{1,1}.t(1)))/(length(meas_iff_mass{1,1}.t)-1);

% Hannning Windows
win = hanning(ceil(1/Ts));

% And we get the frequency vector
[~, f] = tfestimate(meas_iff_mass{1,1}.Va, meas_iff_mass{1,1}.de, win, [], [], 1/Ts);

Finally the $6 \times 6$ transfer function matrix from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ is estimated:

%% DVF Plant (transfer function from u to dLm)
G_dL = {};

for i_mass = i_masses
    G_dL(i_mass+1) = {zeros(length(f), 6, 6)};
    for i_strut = 1:6
        G_dL{i_mass+1}(:,:,i_strut) = tfestimate(meas_iff_mass{i_strut, i_mass+1}.Va, meas_iff_mass{i_strut, i_mass+1}.de, win, [], [], 1/Ts);
    end
end

The identified dynamics are then saved for further use.

save('mat/frf_iff_vib_table_m.mat', 'f', 'Ts', 'G_dL');

Comparison of the measured FRF and the Simscape model

The following figures are computed:

• Figure ref:fig:test_nhexa_damped_iff_plant_meas_frf: the measured damped FRF are displayed
• Figure ref:fig:test_nhexa_comp_undamped_damped_plant_meas_frf: the open-loop and damped FRF are compared (diagonal elements)
• Figure ref:fig:test_nhexa_comp_iff_plant_frf_sim: the obtained damped FRF is compared with the identified damped from using the Simscape model

Diagonal and off-diagonal of the measured FRF matrix for the damped plant

Damped and Undamped measured FRF (diagonal elements)

Comparison of the measured FRF and the identified dynamics from the Simscape model

The IFF control strategy effectively damps all the suspensions modes of the nano-hexapod whatever the payload is. The obtained plant is easier to control (provided the flexible modes of the top platform are well damped).

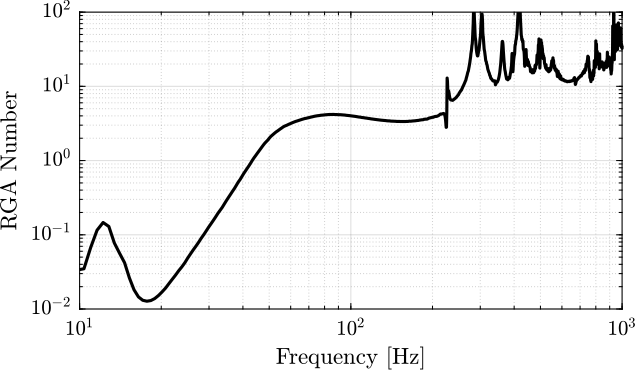
Change of coupling with IFF

Let's see how the Integral Force Feedback is changing the interaction in the system.

To study that, the RGA-number are computed both for the undamped plant and for the damped plant using IFF.

Both are compared in Figure ref:fig:test_nhexa_rga_num_ol_iff_masses.

Comparison of the RGA-Number (interaction estimate) without and without IFF

From Figure ref:fig:test_nhexa_picture_unbalanced_payload, it is clear that the interaction in the system is largest near the resonances. The Integral Force Feedback controller, by reducing the amplitude at the resonances, also reduces the coupling near these resonances. It however increases the coupling bellow the frequency of the suspension modes.

Un-Balanced mass

Introduction

In this section, we wish to see if a payload with a center of mass not aligned with the symmetry axis of the nano-hexapod could cause any issue.

To study that, the payload shown in Figure ref:fig:test_nhexa_picture_unbalanced_payload is used.

Compute the identified FRF with IFF

The following data are loaded:

• Va: the excitation voltage for the damped plant (corresponding to $u^\prime_i$)
• de: the measured motion by the 6 encoders (corresponding to $d\bm{\mathcal{L}}_m$)

%% Load Identification Data
meas_added_mass = {zeros(6,1)};

for i_strut = 1:6
    meas_iff_mass(i_strut) = {load(sprintf('frf_data_exc_strut_%i_iff_vib_table_1m_unbalanced.mat', i_strut), 't', 'Va', 'de')};
end

The window win and the frequency vector f are defined.

% Sampling Time [s]
Ts = (meas_iff_mass{1}.t(end) - (meas_iff_mass{1}.t(1)))/(length(meas_iff_mass{1}.t)-1);

% Hannning Windows
win = hanning(ceil(1/Ts));

% And we get the frequency vector
[~, f] = tfestimate(meas_iff_mass{1}.Va, meas_iff_mass{1}.de, win, [], [], 1/Ts);

Finally the $6 \times 6$ transfer function matrix from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ is estimated:

%% DVF Plant (transfer function from u to dLm)
G_dL = zeros(length(f), 6, 6);
for i_strut = 1:6
    G_dL(:,:,i_strut) = tfestimate(meas_iff_mass{i_strut}.Va, meas_iff_mass{i_strut}.de, win, [], [], 1/Ts);
end

The identified dynamics are then saved for further use.

save('data_frf/frf_iff_unbalanced_vib_table_m.mat', 'f', 'Ts', 'G_dL');

Effect of an unbalanced payload

The transfer functions from $u_i$ to $d\mathcal{L}_i$ are shown in Figure ref:fig:test_nhexa_frf_damp_unbalanced_mass. Due to the unbalanced payload, the system is not symmetrical anymore, and therefore each of the diagonal elements are not equal. This is due to the fact that each strut is not affected by the same inertia.

Transfer function from $u_i$ to $d\mathcal{L}_i$ for the nano-hexapod with an unbalanced payload

Conclusion

In this section, the dynamics of the nano-hexapod with the encoders fixed to the plates is studied.

It has been found that:

• The measured dynamics is in agreement with the dynamics of the simscape model, up to the flexible modes of the top plate. See figures ref:fig:test_nhexa_enc_plates_iff_comp_simscape and ref:fig:test_nhexa_enc_plates_iff_comp_offdiag_simscape for the transfer function to the force sensors and Figures ref:fig:test_nhexa_enc_plates_dvf_comp_simscape and ref:fig:test_nhexa_enc_plates_dvf_comp_offdiag_simscape for the transfer functions to the encoders
• The Integral Force Feedback strategy is very effective in damping the suspension modes of the nano-hexapod (Figure ref:fig:test_nhexa_enc_plant_plates_effect_iff).
• The transfer function from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ show nice dynamical properties and is a much better candidate for the high-authority-control than when the encoders were fixed to the struts. At least up to the flexible modes of the top plate, the diagonal elements of the transfer function matrix have alternating poles and zeros, and the phase is moving smoothly. Only the flexible modes of the top plates seems to be problematic for control.

Decentralized High Authority Control with Integral Force Feedback

<<sec:test_nhexa_decentralized_hac_iff>>

Introduction   ignore

In this section is studied the HAC-IFF architecture for the Nano-Hexapod. More precisely:

• The LAC control is a decentralized integral force feedback as studied in Section ref:sec:test_nhexa_enc_plates_iff
• The HAC control is a decentralized controller working in the frame of the struts

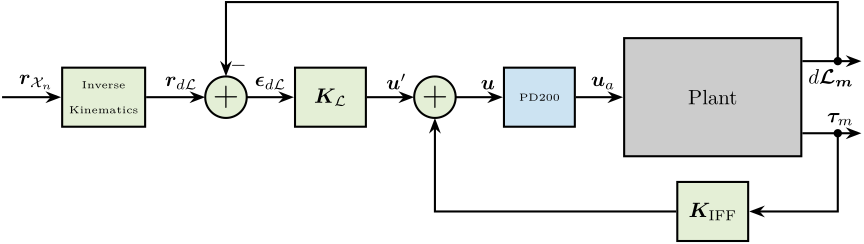
The corresponding control architecture is shown in Figure ref:fig:test_nhexa_control_architecture_hac_iff_struts with:

• $\bm{r}_{\mathcal{X}_n}$: the $6 \times 1$ reference signal in the cartesian frame
• $\bm{r}_{d\mathcal{L}}$: the $6 \times 1$ reference signal transformed in the frame of the struts thanks to the inverse kinematic
• $\bm{\epsilon}_{d\mathcal{L}}$: the $6 \times 1$ length error of the 6 struts
• $\bm{u}^\prime$: input of the damped plant
• $\bm{u}$: generated DAC voltages
• $\bm{\tau}_m$: measured force sensors
• $d\bm{\mathcal{L}}_m$: measured displacement of the struts by the encoders

\definecolor{instrumentation}{rgb}{0, 0.447, 0.741}
\definecolor{mechanics}{rgb}{0.8500, 0.325, 0.098}
\definecolor{control}{rgb}{0.4660, 0.6740, 0.1880}

\begin{tikzpicture}
  % Blocs
  \node[block={3.0cm}{2.0cm}, fill=black!20!white] (P) {Plant};
  \coordinate[] (inputF) at ($(P.south west)!0.5!(P.north west)$);
  \coordinate[] (outputF) at ($(P.south east)!0.2!(P.north east)$);
  \coordinate[] (outputL) at ($(P.south east)!0.8!(P.north east)$);

  \node[block, below=0.4 of P, fill=control!20!white] (Kiff) {$\bm{K}_\text{IFF}$};
  \node[block, left=0.8 of inputF, fill=instrumentation!20!white] (pd200) {\tiny PD200};
  \node[addb,  left=0.8 of pd200, fill=control!20!white] (addF) {};
  \node[block, left=0.8 of addF, fill=control!20!white] (K) {$\bm{K}_\mathcal{L}$};
  \node[addb={+}{}{-}{}{}, left=0.8 of K, fill=control!20!white] (subr) {};
  \node[block, align=center, left= of subr, fill=control!20!white] (J) {\tiny Inverse\\\tiny Kinematics};

  % Connections and labels
  \draw[->] (outputF) -- ++(1.0, 0) node[above left]{$\bm{\tau}_m$};
  \draw[->] ($(outputF) + (0.6, 0)$)node[branch]{} |- (Kiff.east);
  \draw[->] (Kiff.west) -| (addF.south);
  \draw[->] (addF.east) -- (pd200.west) node[above left]{$\bm{u}$};
  \draw[->] (pd200.east) -- (inputF) node[above left]{$\bm{u}_a$};

  \draw[->] (outputL) -- ++(1.0, 0) node[below left]{$d\bm{\mathcal{L}_m}$};
  \draw[->] ($(outputL) + (0.6, 0)$)node[branch]{} -- ++(0, 1) -| (subr.north);
  \draw[->] (subr.east) -- (K.west) node[above left]{$\bm{\epsilon}_{d\mathcal{L}}$};
  \draw[->] (K.east) -- (addF.west) node[above left]{$\bm{u}^\prime$};

  \draw[->] (J.east) -- (subr.west) node[above left]{$\bm{r}_{d\mathcal{L}}$};
  \draw[<-] (J.west)node[above left]{$\bm{r}_{\mathcal{X}_n}$} -- ++(-1, 0);
\end{tikzpicture}

HAC-LAC: IFF + Control in the frame of the legs

This part is structured as follow:

• Section ref:sec:test_nhexa_hac_iff_struts_ref_track: some reference tracking tests are performed
• Section ref:sec:test_nhexa_hac_iff_struts_controller: the decentralized high authority controller is tuned using the Simscape model and is implemented and tested experimentally
• Section ref:sec:test_nhexa_interaction_analysis: an interaction analysis is performed, from which the best decoupling strategy can be determined
• Section ref:sec:test_nhexa_robust_hac_design: Robust High Authority Controller are designed

Reference Tracking - Trajectories

<<sec:test_nhexa_hac_iff_struts_ref_track>>

Introduction   ignore

In this section, several trajectories representing the wanted pose (position and orientation) of the top platform with respect to the bottom platform are defined.

These trajectories will be used to test the HAC-LAC architecture.

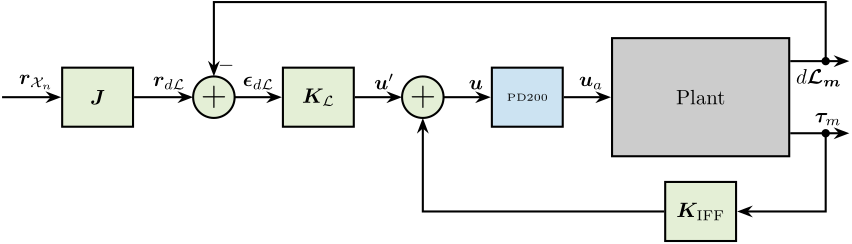
In order to transform the wanted pose to the wanted displacement of the 6 struts, the inverse kinematic is required. As a first approximation, the Jacobian matrix $\bm{J}$ can be used instead of using the full inverse kinematic equations.

Therefore, the control architecture with the input trajectory $\bm{r}_{\mathcal{X}_n}$ is shown in Figure ref:fig:test_nhexa_control_architecture_hac_iff_L.

\definecolor{instrumentation}{rgb}{0, 0.447, 0.741}
\definecolor{mechanics}{rgb}{0.8500, 0.325, 0.098}
\definecolor{control}{rgb}{0.4660, 0.6740, 0.1880}

\begin{tikzpicture}
  % Blocs
  \node[block={3.0cm}{2.0cm}, fill=black!20!white] (P) {Plant};
  \coordinate[] (inputF) at ($(P.south west)!0.5!(P.north west)$);
  \coordinate[] (outputF) at ($(P.south east)!0.2!(P.north east)$);
  \coordinate[] (outputL) at ($(P.south east)!0.8!(P.north east)$);

  \node[block, below=0.4 of P, fill=control!20!white] (Kiff) {$\bm{K}_\text{IFF}$};
  \node[block, left=0.8 of inputF, fill=instrumentation!20!white] (pd200) {\tiny PD200};
  \node[addb,  left=0.8 of pd200, fill=control!20!white] (addF) {};
  \node[block, left=0.8 of addF, fill=control!20!white] (K) {$\bm{K}_\mathcal{L}$};
  \node[addb={+}{}{-}{}{}, left=0.8 of K, fill=control!20!white] (subr) {};
  \node[block, align=center, left= of subr, fill=control!20!white] (J) {$\bm{J}$};

  % Connections and labels
  \draw[->] (outputF) -- ++(1.0, 0) node[above left]{$\bm{\tau}_m$};
  \draw[->] ($(outputF) + (0.6, 0)$)node[branch]{} |- (Kiff.east);
  \draw[->] (Kiff.west) -| (addF.south);
  \draw[->] (addF.east) -- (pd200.west) node[above left]{$\bm{u}$};
  \draw[->] (pd200.east) -- (inputF) node[above left]{$\bm{u}_a$};

  \draw[->] (outputL) -- ++(1.0, 0) node[below left]{$d\bm{\mathcal{L}_m}$};
  \draw[->] ($(outputL) + (0.6, 0)$)node[branch]{} -- ++(0, 1) -| (subr.north);
  \draw[->] (subr.east) -- (K.west) node[above left]{$\bm{\epsilon}_{d\mathcal{L}}$};
  \draw[->] (K.east) -- (addF.west) node[above left]{$\bm{u}^\prime$};

  \draw[->] (J.east) -- (subr.west) node[above left]{$\bm{r}_{d\mathcal{L}}$};
  \draw[<-] (J.west)node[above left]{$\bm{r}_{\mathcal{X}_n}$} -- ++(-1, 0);
\end{tikzpicture}

HAC-LAC: IFF + Control in the frame of the legs

In the following sections, several reference trajectories are defined:

• Section ref:sec:test_nhexa_yz_scans: simple scans in the Y-Z plane
• Section ref:sec:test_nhexa_tilt_scans: scans in tilt are performed
• Section ref:sec:test_nhexa_nass_scans: scans with X-Y-Z translations in order to draw the word "NASS"

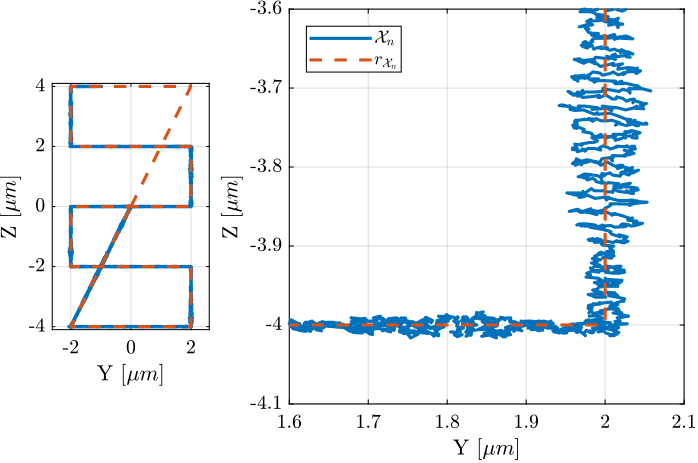
Y-Z Scans

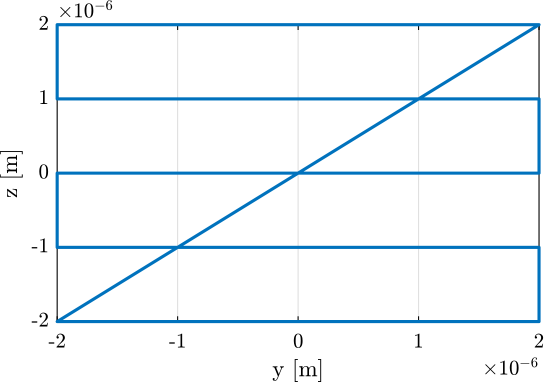
<<sec:test_nhexa_yz_scans>> A function generateYZScanTrajectory has been developed in order to easily generate scans in the Y-Z plane.

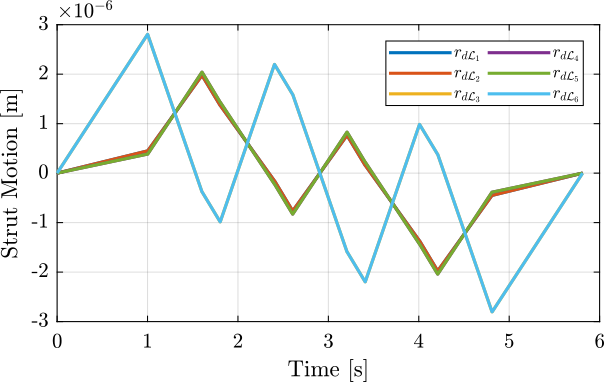
For instance, the following generated trajectory is represented in Figure ref:fig:test_nhexa_yz_scan_example_trajectory_yz_plane.

%% Generate the Y-Z trajectory scan
Rx_yz = generateYZScanTrajectory(...
    'y_tot', 4e-6, ... % Length of Y scans [m]
    'z_tot', 4e-6, ... % Total Z distance [m]
    'n', 5, ...     % Number of Y scans
    'Ts', 1e-3, ... % Sampling Time [s]
    'ti', 1, ...    % Time to go to initial position [s]
    'tw', 0, ...    % Waiting time between each points [s]
    'ty', 0.6, ...  % Time for a scan in Y [s]
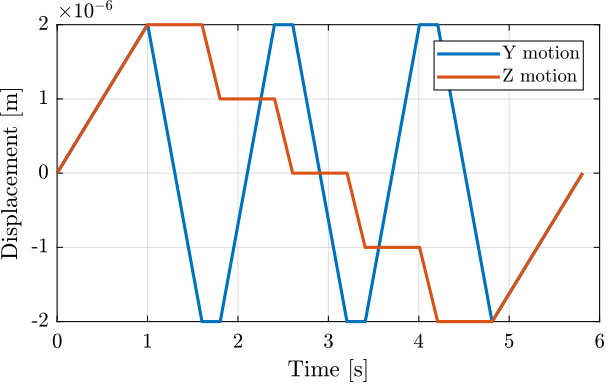
    'tz', 0.2);     % Time for a scan in Z [s]

Generated scan in the Y-Z plane

The Y and Z positions as a function of time are shown in Figure ref:fig:test_nhexa_yz_scan_example_trajectory.

Y and Z trajectories as a function of time

Using the Jacobian matrix, it is possible to compute the wanted struts lengths as a function of time:

\begin{equation} \bm{r}_{d\mathcal{L}} = \bm{J} \bm{r}_{\mathcal{X}_n} \end{equation}

%% Compute the reference in the frame of the legs
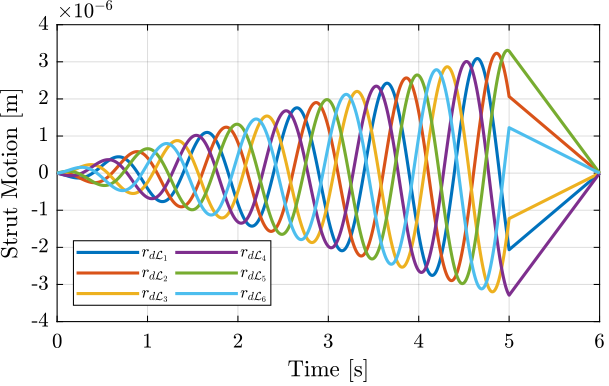
dL_ref = [J*Rx_yz(:, 2:7)']';

The reference signal for the strut length is shown in Figure ref:fig:test_nhexa_yz_scan_example_trajectory_struts.

Trajectories for the 6 individual struts

Tilt Scans

<<sec:test_nhexa_tilt_scans>>

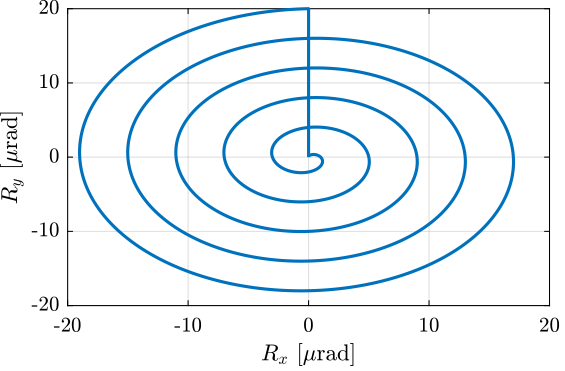
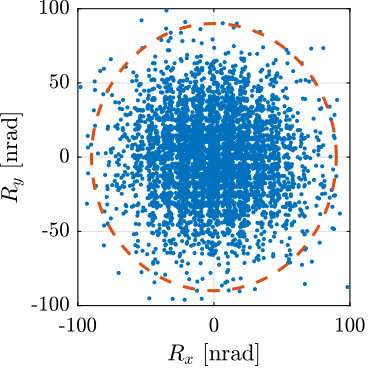
A function generalSpiralAngleTrajectory has been developed in order to easily generate $R_x,R_y$ tilt scans.

For instance, the following generated trajectory is represented in Figure ref:fig:test_nhexa_tilt_scan_example_trajectory.

%% Generate the "tilt-spiral" trajectory scan
R_tilt = generateSpiralAngleTrajectory(...
    'R_tot',  20e-6, ... % Total Tilt [ad]
    'n_turn', 5, ...     % Number of scans
    'Ts',     1e-3, ...  % Sampling Time [s]
    't_turn', 1, ...     % Turn time [s]
    't_end',  1);        % End time to go back to zero [s]

Generated "spiral" scan

The reference signal for the strut length is shown in Figure ref:fig:test_nhexa_tilt_scan_example_trajectory_struts.

Trajectories for the 6 individual struts - Tilt scan

"NASS" reference path

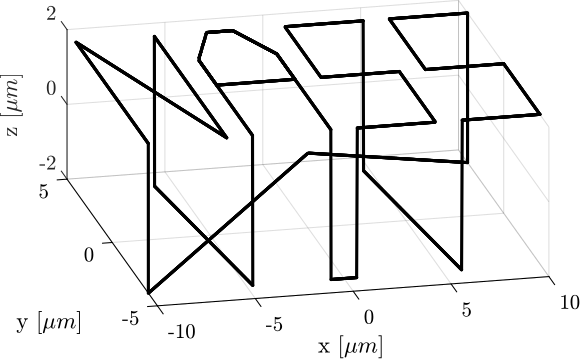
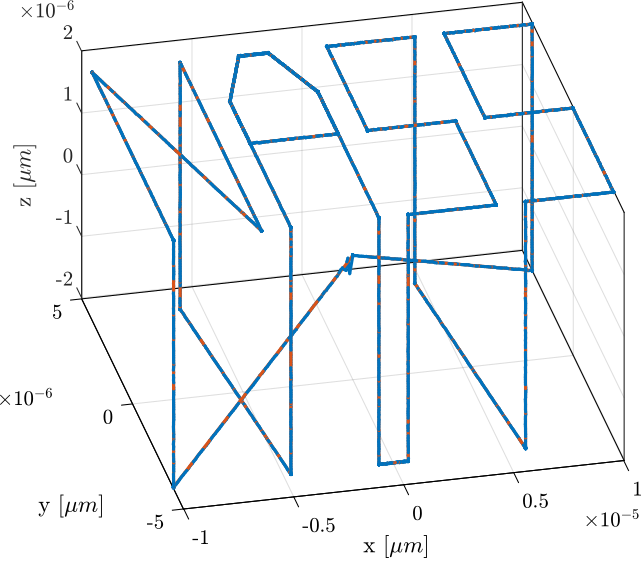
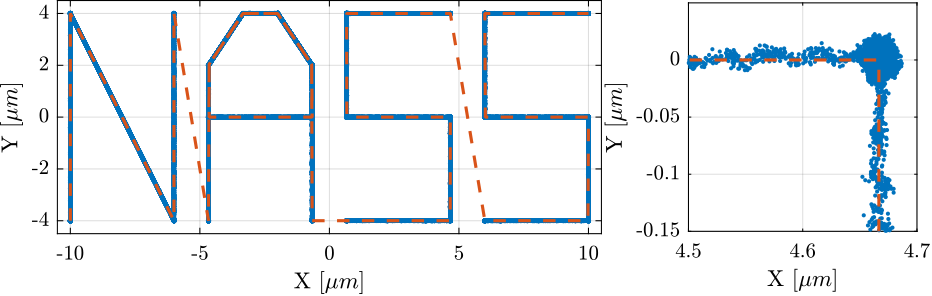
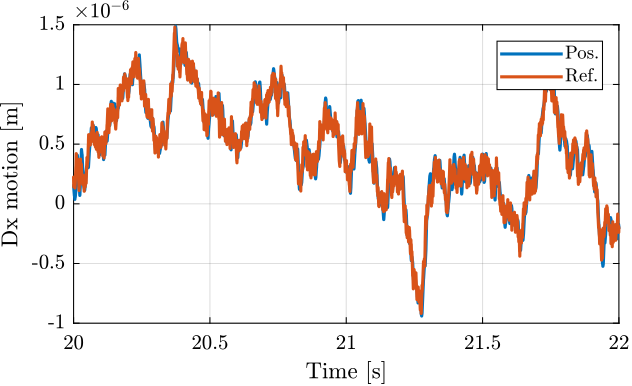
<<sec:test_nhexa_nass_scans>> In this section, a reference path that "draws" the work "NASS" is developed.

First, a series of points representing each letter are defined. Between each letter, a negative Z motion is performed.

%% List of points that draws "NASS"
ref_path = [ ...
    0, 0,0; % Initial Position
    0,0,1; 0,4,1; 3,0,1; 3,4,1; % N
    3,4,0; 4,0,0; % Transition
    4,0,1; 4,3,1; 5,4,1; 6,4,1; 7,3,1; 7,2,1; 4,2,1; 4,3,1; 5,4,1; 6,4,1; 7,3,1; 7,0,1; % A
    7,0,0; 8,0,0; % Transition
    8,0,1; 11,0,1; 11,2,1; 8,2,1; 8,4,1; 11,4,1; % S
    11,4,0; 12,0,0; % Transition
    12,0,1; 15,0,1; 15,2,1; 12,2,1; 12,4,1; 15,4,1; % S
    15,4,0;
           ];

%% Center the trajectory arround zero
ref_path = ref_path - (max(ref_path) - min(ref_path))/2;

%% Define the X-Y-Z cuboid dimensions containing the trajectory
X_max = 10e-6;
Y_max =  4e-6;
Z_max =  2e-6;

ref_path = ([X_max, Y_max, Z_max]./max(ref_path)).*ref_path; % [m]

Then, using the generateXYZTrajectory function, the $6 \times 1$ trajectory signal is computed.

%% Generating the trajectory
Rx_nass = generateXYZTrajectory('points', ref_path);

The trajectory in the X-Y plane is shown in Figure ref:fig:test_nhexa_ref_track_test_nass (the transitions between the letters are removed).

Reference path corresponding to the "NASS" acronym

It can also be better viewed in a 3D representation as in Figure ref:fig:test_nhexa_ref_track_test_nass_3d.

Reference path that draws "NASS" - 3D view

First Basic High Authority Controller

<<sec:test_nhexa_hac_iff_struts_controller>>

Introduction   ignore

In this section, a simple decentralized high authority controller $\bm{K}_{\mathcal{L}}$ is developed to work without any payload.

The diagonal controller is tuned using classical Loop Shaping in Section ref:sec:test_nhexa_hac_iff_no_payload_tuning. The stability is verified in Section ref:sec:test_nhexa_hac_iff_no_payload_stability using the Simscape model.

HAC Controller

<<sec:test_nhexa_hac_iff_no_payload_tuning>>

Let's first try to design a first decentralized controller with:

• a bandwidth of 100Hz
• sufficient phase margin
• simple and understandable components

After some very basic and manual loop shaping, A diagonal controller is developed. Each diagonal terms are identical and are composed of:

• A lead around 100Hz
• A first order low pass filter starting at 200Hz to add some robustness to high frequency modes
• A notch at 700Hz to cancel the flexible modes of the top plate
• A pure integrator

%% Lead to increase phase margin
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
wc = 2*pi*100; % Frequency with the maximum phase lead [rad/s]

H_lead = (1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));

%% Low Pass filter to increase robustness
H_lpf = 1/(1 + s/2/pi/200);

%% Notch at the top-plate resonance
gm = 0.02;
xi = 0.3;
wn = 2*pi*700;

H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

%% Decentralized HAC
Khac_iff_struts = -(1/(2.87e-5)) * ... % Gain
                  H_lead * ...       % Lead
                  H_notch * ...      % Notch
                  (2*pi*100/s) * ... % Integrator
                  eye(6);            % 6x6 Diagonal

This controller is saved for further use.

save('data_sim/Khac_iff_struts.mat', 'Khac_iff_struts')

The experimental loop gain is computed and shown in Figure ref:fig:test_nhexa_loop_gain_hac_iff_struts.

L_hac_iff_struts = pagemtimes(permute(frf_iff.G_dL{1}, [2 3 1]), squeeze(freqresp(Khac_iff_struts, frf_iff.f, 'Hz')));

Diagonal and off-diagonal elements of the Loop gain for "HAC-IFF-Struts"

Verification of the Stability using the Simscape model

<<sec:test_nhexa_hac_iff_no_payload_stability>>

The HAC-IFF control strategy is implemented using Simscape.

%% Initialize the Simscape model in closed loop
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
                                       'flex_top_type', '4dof', ...
                                       'motion_sensor_type', 'plates', ...
                                       'actuator_type', 'flexible', ...
                                       'controller_type', 'hac-iff-struts');

%% Identify the (damped) transfer function from u to dLm
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput');  io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Plate Displacement (encoder)

We identify the closed-loop system.

%% Identification
Gd_iff_hac_opt = linearize(mdl, io, 0.0, options);

And verify that it is indeed stable.

%% Verify the stability
isstable(Gd_iff_hac_opt)

1

Experimental Validation

Both the Integral Force Feedback controller (developed in Section ref:sec:test_nhexa_enc_plates_iff) and the high authority controller working in the frame of the struts (developed in Section ref:sec:test_nhexa_hac_iff_struts_controller) are implemented experimentally.

Two reference tracking experiments are performed to evaluate the stability and performances of the implemented control.

%% Load the experimental data
load('hac_iff_struts_yz_scans.mat', 't', 'de')

The position of the top-platform is estimated using the Jacobian matrix:

%% Pose of the top platform from the encoder values
load('jacobian.mat', 'J');
Xe = [inv(J)*de']';

%% Generate the Y-Z trajectory scan
Rx_yz = generateYZScanTrajectory(...
    'y_tot', 4e-6, ... % Length of Y scans [m]
    'z_tot', 8e-6, ... % Total Z distance [m]
    'n', 5, ...     % Number of Y scans
    'Ts', 1e-3, ... % Sampling Time [s]
    'ti', 1, ...    % Time to go to initial position [s]
    'tw', 0, ...    % Waiting time between each points [s]
    'ty', 0.6, ...  % Time for a scan in Y [s]
    'tz', 0.2);     % Time for a scan in Z [s]

The reference path as well as the measured position are partially shown in the Y-Z plane in Figure ref:fig:test_nhexa_yz_scans_exp_results_first_K.

Measured position $\bm{\mathcal{X}}_n$ and reference signal $\bm{r}_{\mathcal{X}_n}$ in the Y-Z plane - Zoom on a change of direction

It is clear from Figure ref:fig:test_nhexa_yz_scans_exp_results_first_K that the position of the nano-hexapod effectively tracks to reference signal. However, oscillations with amplitudes as large as 50nm can be observe.

It turns out that the frequency of these oscillations is 100Hz which is corresponding to the crossover frequency of the High Authority Control loop. This clearly indicates poor stability margins. In the next section, the controller is re-designed to improve the stability margins.

Controller with increased stability margins

The High Authority Controller is re-designed in order to improve the stability margins.

%% Lead
a  = 5;  % Amount of phase lead / width of the phase lead / high frequency gain
wc = 2*pi*110; % Frequency with the maximum phase lead [rad/s]

H_lead = (1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));

%% Low Pass Filter
H_lpf = 1/(1 + s/2/pi/300);

%% Notch
gm = 0.02;
xi = 0.5;
wn = 2*pi*700;

H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

%% HAC Controller
Khac_iff_struts = -2.2e4 * ... % Gain
            H_lead * ...       % Lead
            H_lpf * ...        % Lead
            H_notch * ...      % Notch
            (2*pi*100/s) * ... % Integrator
            eye(6);            % 6x6 Diagonal

The bode plot of the new loop gain is shown in Figure ref:fig:test_nhexa_hac_iff_plates_exp_loop_gain_redesigned_K.

Loop Gain for the updated decentralized HAC controller

This new controller is implemented experimentally and several tracking tests are performed.

%% Load Measurements
load('hac_iff_more_lead_nass_scan.mat', 't', 'de')

The pose of the top platform is estimated from the encoder position using the Jacobian matrix.

%% Compute the pose of the top platform
load('jacobian.mat', 'J');
Xe = [inv(J)*de']';

The measured motion as well as the trajectory are shown in Figure ref:fig:test_nhexa_nass_scans_first_test_exp.

Measured position $\bm{\mathcal{X}}_n$ and reference signal $\bm{r}_{\mathcal{X}_n}$ for the "NASS" trajectory

The trajectory and measured motion are also shown in the X-Y plane in Figure ref:fig:test_nhexa_ref_track_nass_exp_hac_iff_struts.

Reference path and measured motion in the X-Y plane

The orientation errors during all the scans are shown in Figure ref:fig:test_nhexa_nass_ref_rx_ry.

Orientation errors during the scan

Using the updated High Authority Controller, the nano-hexapod can follow trajectories with high accuracy (the position errors are in the order of 50nm peak to peak, and the orientation errors 300nrad peak to peak).

Interaction Analysis and Decoupling

<<sec:test_nhexa_interaction_analysis>>

Introduction   ignore

In this section, the interaction in the identified plant is estimated using the Relative Gain Array (RGA) Chap. 3.4.

Then, several decoupling strategies are compared for the nano-hexapod.

The RGA Matrix is defined as follow:

\begin{equation} \text{RGA}(G(f)) = G(f) \times (G(f)^{-1})^T \end{equation}

Then, the RGA number is defined:

\begin{equation} \text{RGA-num}(f) = \| \text{I - RGA(G(f))} \|_{\text{sum}} \end{equation}

In this section, the plant with 2 added mass is studied.

Parameters

wc = 100; % Wanted crossover frequency [Hz]
[~, i_wc] = min(abs(frf_iff.f - wc)); % Indice corresponding to wc

%% Plant to be decoupled
frf_coupled = frf_iff.G_dL{2};
G_coupled = sim_iff.G_dL{2};

No Decoupling (Decentralized)

<<sec:test_nhexa_interaction_decentralized>>

\begin{tikzpicture}
  \node[block] (G) {$\bm{G}$};

  % Connections and labels
  \draw[<-] (G.west) -- ++(-1.8, 0) node[above right]{$\bm{\tau}$};
  \draw[->] (G.east) -- ++( 1.8, 0) node[above left]{$d\bm{\mathcal{L}}$};

  \begin{scope}[on background layer]
    \node[fit={(G.south west) (G.north east)}, fill=black!10!white, draw, dashed, inner sep=16pt] (Gdec) {};
    \node[below right] at (Gdec.north west) {$\bm{G}_{\text{dec}}$};
  \end{scope}
\end{tikzpicture}

Block diagram representing the plant.

Bode Plot of the decentralized plant (diagonal and off-diagonal terms)

RGA number for the decentralized plant

Static Decoupling

<<sec:test_nhexa_interaction_static>>

\begin{tikzpicture}
  \node[block] (G) {$\bm{G}$};
  \node[block, left=0.8 of G] (Ginv) {$\bm{\hat{G}}(j0)^{-1}$};

  % Connections and labels
  \draw[<-] (Ginv.west) -- ++(-1.8, 0) node[above right]{$\bm{u}$};
  \draw[->] (Ginv.east) -- (G.west)    node[above left]{$\bm{\tau}$};
  \draw[->] (G.east) -- ++( 1.8, 0)    node[above left]{$d\bm{\mathcal{L}}$};

  \begin{scope}[on background layer]
    \node[fit={(Ginv.south west) (G.north east)}, fill=black!10!white, draw, dashed, inner sep=16pt] (Gx) {};
    \node[below right] at (Gx.north west) {$\bm{G}_{\text{static}}$};
  \end{scope}
\end{tikzpicture}

Decoupling using the inverse of the DC gain of the plant

The DC gain is evaluated from the model as be have bad low frequency identification.

-62011.5	3910.6	4299.3	660.7	-4016.5	-4373.6
3914.4	-61991.2	-4356.8	-4019.2	640.2	4281.6
-4020.0	-4370.5	-62004.5	3914.6	4295.8	653.8
660.9	4292.4	3903.3	-62012.2	-4366.5	-4008.9
4302.8	655.6	-4025.8	-4377.8	-62006.0	3919.7
-4377.9	-4013.2	668.6	4303.7	3906.8	-62019.3

Bode Plot of the static decoupled plant

RGA number for the statically decoupled plant

Decoupling at the Crossover

<<sec:test_nhexa_interaction_crossover>>

\begin{tikzpicture}
  \node[block] (G) {$\bm{G}$};
  \node[block, left=0.8 of G] (Ginv) {$\bm{\hat{G}}(j\omega_c)^{-1}$};

  % Connections and labels
  \draw[<-] (Ginv.west) -- ++(-1.8, 0) node[above right]{$\bm{u}$};
  \draw[->] (Ginv.east) -- (G.west)    node[above left]{$\bm{\tau}$};
  \draw[->] (G.east) -- ++( 1.8, 0)    node[above left]{$d\bm{\mathcal{L}}$};

  \begin{scope}[on background layer]
    \node[fit={(Ginv.south west) (G.north east)}, fill=black!10!white, draw, dashed, inner sep=16pt] (Gx) {};
    \node[below right] at (Gx.north west) {$\bm{G}_{\omega_c}$};
  \end{scope}
\end{tikzpicture}

Decoupling using the inverse of a dynamical model $\bm{\hat{G}}$ of the plant dynamics $\bm{G}$

67229.8	3769.3	-13704.6	-23084.8	-6318.2	23378.7
3486.2	67708.9	23220.0	-6314.5	-22699.8	-14060.6
-5731.7	22471.7	66701.4	3070.2	-13205.6	-21944.6
-23305.5	-14542.6	2743.2	70097.6	24846.8	-5295.0
-14882.9	-22957.8	-5344.4	25786.2	70484.6	2979.9
24353.3	-5195.2	-22449.0	-14459.2	2203.6	69484.2

Bode Plot of the plant decoupled at the crossover

%% Compute RGA Matrix
RGA_wc = zeros(size(frf_coupled));
for i = 1:length(frf_iff.f)
    RGA_wc(i,:,:) = squeeze(G_dL_wc(i,:,:)).*inv(squeeze(G_dL_wc(i,:,:))).';
end

%% Compute RGA-number
RGA_wc_sum = zeros(size(RGA_wc, 1), 1);
for i = 1:size(RGA_wc, 1)
    RGA_wc_sum(i) = sum(sum(abs(eye(6) - squeeze(RGA_wc(i,:,:)))));
end

RGA number for the plant decoupled at the crossover

SVD Decoupling

<<sec:test_nhexa_interaction_svd>>

\begin{tikzpicture}
  \node[block] (G) {$\bm{G}$};

  \node[block, left=0.8 of G.west] (V) {$V^{-T}$};
  \node[block, right=0.8 of G.east] (U) {$U^{-1}$};

  % Connections and labels
  \draw[<-] (V.west) -- ++(-1.0, 0) node[above right]{$u$};
  \draw[->] (V.east) -- (G.west) node[above left]{$\bm{\tau}$};
  \draw[->] (G.east) -- (U.west) node[above left]{$d\bm{\mathcal{L}}$};
  \draw[->] (U.east) -- ++( 1.0, 0) node[above left]{$y$};

  \begin{scope}[on background layer]
    \node[fit={(V.south west) (G.north-|U.east)}, fill=black!10!white, draw, dashed, inner sep=14pt] (Gsvd) {};
    \node[below right] at (Gsvd.north west) {$\bm{G}_{SVD}$};
  \end{scope}
\end{tikzpicture}

Decoupling using the Singular Value Decomposition

Bode Plot of the plant decoupled using the Singular Value Decomposition

%% Compute the RGA matrix for the SVD decoupled plant
RGA_svd = zeros(size(frf_coupled));
for i = 1:length(frf_iff.f)
    RGA_svd(i,:,:) = squeeze(G_dL_svd(i,:,:)).*inv(squeeze(G_dL_svd(i,:,:))).';
end

%% Compute the RGA-number
RGA_svd_sum = zeros(size(RGA_svd, 1), 1);
for i = 1:length(frf_iff.f)
    RGA_svd_sum(i) = sum(sum(abs(eye(6) - squeeze(RGA_svd(i,:,:)))));
end

%% RGA Number for the SVD decoupled plant
figure;
plot(frf_iff.f, RGA_svd_sum, 'k-');
set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log');
xlabel('Frequency [Hz]'); ylabel('RGA Number');
xlim([10, 1e3]); ylim([1e-2, 1e2]);

RGA number for the plant decoupled using the SVD

Dynamic decoupling

<<sec:test_nhexa_interaction_dynamic>>

\begin{tikzpicture}
  \node[block] (G) {$\bm{G}$};
  \node[block, left=0.8 of G] (Ginv) {$\bm{\hat{G}}^{-1}$};

  % Connections and labels
  \draw[<-] (Ginv.west) -- ++(-1.8, 0) node[above right]{$\bm{u}$};
  \draw[->] (Ginv.east) -- (G.west)    node[above left]{$\bm{\tau}$};
  \draw[->] (G.east) -- ++( 1.8, 0)    node[above left]{$d\bm{\mathcal{L}}$};

  \begin{scope}[on background layer]
    \node[fit={(Ginv.south west) (G.north east)}, fill=black!10!white, draw, dashed, inner sep=16pt] (Gx) {};
    \node[below right] at (Gx.north west) {$\bm{G}_{\text{inv}}$};
  \end{scope}
\end{tikzpicture}

Decoupling using the inverse of a dynamical model $\bm{\hat{G}}$ of the plant dynamics $\bm{G}$

Bode Plot of the dynamically decoupled plant

RGA number for the dynamically decoupled plant

Jacobian Decoupling - Center of Stiffness

<<sec:test_nhexa_interaction_jacobian_cok>>

\begin{tikzpicture}
  \node[block] (G) {$\bm{G}$};
  \node[block, left=0.8 of G] (Jt) {$J_{s,\{K\}}^{-T}$};
  \node[block, right=0.8 of G] (Ja) {$J_{a,\{K\}}^{-1}$};

  % Connections and labels
  \draw[<-] (Jt.west) -- ++(-1.8, 0) node[above right]{$\bm{\mathcal{F}}_{\{K\}}$};
  \draw[->] (Jt.east) -- (G.west)  node[above left]{$\bm{\tau}$};
  \draw[->] (G.east) -- (Ja.west)  node[above left]{$d\bm{\mathcal{L}}$};
  \draw[->] (Ja.east) -- ++( 1.8, 0)  node[above left]{$\bm{\mathcal{X}}_{\{K\}}$};

  \begin{scope}[on background layer]
    \node[fit={(Jt.south west) (Ja.north east)}, fill=black!10!white, draw, dashed, inner sep=16pt] (Gx) {};
    \node[below right] at (Gx.north west) {$\bm{G}_{\{K\}}$};
  \end{scope}
\end{tikzpicture}

Decoupling using Jacobian matrices evaluated at the Center of Stiffness

The obtained plant is shown in Figure ref:fig:test_nhexa_interaction_J_cok_plant_not_normalized. We can see that the stiffness in the $x$, $y$ and $z$ directions are equal, which is due to the cubic architecture of the Stewart platform.

Bode Plot of the plant decoupled using the Jacobian evaluated at the "center of stiffness"

Because the plant in translation and rotation has very different gains, we choose to normalize the plant inputs such that the gain of the diagonal term is equal to $1$ at 100Hz.

The results is shown in Figure ref:fig:test_nhexa_interaction_J_cok_plant.

Bode Plot of the plant decoupled using the Jacobian evaluated at the "center of stiffness"

RGA number for the plant decoupled using the Jacobian evaluted at the Center of Stiffness

Jacobian Decoupling - Center of Mass

<<sec:test_nhexa_interaction_jacobian_com>>

\begin{tikzpicture}
  \node[block] (G) {$\bm{G}$};
  \node[block, left=0.8 of G] (Jt) {$J_{s,\{M\}}^{-T}$};
  \node[block, right=0.8 of G] (Ja) {$J_{a,\{M\}}^{-1}$};

  % Connections and labels
  \draw[<-] (Jt.west) -- ++(-1.8, 0) node[above right]{$\bm{\mathcal{F}}_{\{M\}}$};
  \draw[->] (Jt.east) -- (G.west)  node[above left]{$\bm{\tau}$};
  \draw[->] (G.east) -- (Ja.west)  node[above left]{$d\bm{\mathcal{L}}$};
  \draw[->] (Ja.east) -- ++( 1.8, 0)  node[above left]{$\bm{\mathcal{X}}_{\{M\}}$};

  \begin{scope}[on background layer]
    \node[fit={(Jt.south west) (Ja.north east)}, fill=black!10!white, draw, dashed, inner sep=16pt] (Gx) {};
    \node[below right] at (Gx.north west) {$\bm{G}_{\{M\}}$};
  \end{scope}
\end{tikzpicture}

Decoupling using Jacobian matrices evaluated at the Center of Mass

Bode Plot of the plant decoupled using the Jacobian evaluated at the Center of Mass

RGA number for the plant decoupled using the Jacobian evaluted at the Center of Mass

Decoupling Comparison

<<sec:test_nhexa_interaction_comparison>>

Let's now compare all of the decoupling methods (Figure ref:fig:test_nhexa_interaction_compare_rga_numbers).

From Figure ref:fig:test_nhexa_interaction_compare_rga_numbers, the following remarks are made:

• Decentralized plant: well decoupled below suspension modes
• Static inversion: similar to the decentralized plant as the decentralized plant has already a good decoupling at low frequency
• Crossover inversion: the decoupling is improved around the crossover frequency as compared to the decentralized plant. However, the decoupling is increased at lower frequency.
• SVD decoupling: Very good decoupling up to 235Hz. Especially between 100Hz and 200Hz.
• Dynamic Inversion: the plant is very well decoupled at frequencies where the model is accurate (below 235Hz where flexible modes are not modelled).
• Jacobian - Stiffness: good decoupling at low frequency. The decoupling increases at the frequency of the suspension modes, but is acceptable up to the strut flexible modes (235Hz).
• Jacobian - Mass: bad decoupling at low frequency. Better decoupling above the frequency of the suspension modes, and acceptable decoupling up to the strut flexible modes (235Hz).

Comparison of the obtained RGA-numbers for all the decoupling methods

Decoupling Robustness

<<sec:test_nhexa_interaction_robustness>>

Let's now see how the decoupling is changing when changing the payload's mass.

frf_new = frf_iff.G_dL{3};

The obtained RGA-numbers are shown in Figure ref:fig:test_nhexa_interaction_compare_rga_numbers_rob.

From Figure ref:fig:test_nhexa_interaction_compare_rga_numbers_rob:

• The decoupling using the Jacobian evaluated at the "center of stiffness" seems to give the most robust results.

Change of the RGA-number with a change of the payload. Indication of the robustness of the inversion method.

Conclusion

Several decoupling methods can be used:

• SVD
• Inverse
• Jacobian (CoK)

Method	RGA	Diag Plant	Robustness
Decentralized	–	Equal	++
Static dec.	–	Equal	++
Crossover dec.	-	Equal	0
SVD	++	Diff	+
Dynamic dec.	++	Unity, equal	-
Jacobian - CoK	+	Diff	++
Jacobian - CoM	0	Diff	+

Robust High Authority Controller

<<sec:test_nhexa_robust_hac_design>>

Introduction   ignore

In this section we wish to develop a robust High Authority Controller (HAC) that is working for all payloads.

cite:indri20_mechat_robot

Using Jacobian evaluated at the center of stiffness

Decoupled Plant

G_nom = frf_iff.G_dL{2}; % Nominal Plant

Bode plot of the decoupled plant using the Jacobian evaluated at the Center of Stiffness

SISO Controller Design

As the diagonal elements of the plant are not equal, several SISO controllers are designed and then combined to form a diagonal controller. All the diagonal terms of the controller consists of:

• A double integrator to have high gain at low frequency
• A lead around the crossover frequency to increase stability margins
• Two second order low pass filters above the crossover frequency to increase the robustness to high frequency modes

Obtained Loop Gain

Bode plot of the Loop Gain when using the Jacobian evaluated at the Center of Stiffness to decouple the system

%% Controller to be implemented
Kd = inv(J_cok')*input_normalize*ss(Kd_diag)*inv(Js_cok);

Verification of the Stability

Now the stability of the feedback loop is verified using the generalized Nyquist criteria.

Loci of $L(j\omega)$ in the complex plane.

Save for further analysis

save('data_sim/Khac_iff_struts_jacobian_cok.mat', 'Kd')

Sensitivity transfer function from the model

The results are shown in Figure ref:fig:test_nhexa_sensitivity_hac_jacobian_cok_3m_comp_model.

Estimated sensitivity transfer functions for the HAC controller using the Jacobian estimated at the Center of Stiffness

Using Singular Value Decomposition

Decoupled Plant

G_nom = frf_iff.G_dL{2}; % Nominal Plant

Bode plot of the decoupled plant using the SVD

Controller Design

Loop Gain

Bode plot of Loop Gain when using the SVD

Stability Verification

%% Compute the Eigenvalues of the loop gain
Ldet = zeros(3, 6, length(frf_iff.f));

for i = 1:3
    Lmimo = pagemtimes(permute(frf_iff.G_dL{i}, [2,3,1]),squeeze(freqresp(Kd, frf_iff.f, 'Hz')));
    for i_f = 2:length(frf_iff.f)
        Ldet(i,:, i_f) = eig(squeeze(Lmimo(:,:,i_f)));
    end
end

Locis of $L(j\omega)$ in the complex plane.

Save for further analysis

save('data_sim/Khac_iff_struts_svd.mat', 'Kd')

Measured Sensitivity Transfer Function

The sensitivity transfer function is estimated by adding a reference signal $R_x$ consisting of a low pass filtered white noise, and measuring the position error $E_x$ at the same time.

The transfer function from $R_x$ to $E_x$ is the sensitivity transfer function.

In order to identify the sensitivity transfer function for all directions, six reference signals are used, one for each direction.

An example is shown in Figure ref:fig:test_nhexa_ref_track_hac_svd_3m where both the reference signal and the measured position are shown for translations in the $x$ direction.

Reference position and measured position

The sensitivity transfer functions estimated for all directions are shown in Figure ref:fig:test_nhexa_sensitivity_hac_svd_3m.

Measured diagonal elements of the sensitivity transfer function matrix.

From Figure ref:fig:test_nhexa_sensitivity_hac_svd_3m:

• The sensitivity transfer functions are similar for all directions
• The disturbance attenuation at 1Hz is almost a factor 1000 as wanted
• The sensitivity transfer functions for $R_x$ and $R_y$ have high peak values which indicate poor stability margins.

Sensitivity transfer function from the model

The sensitivity transfer function is now estimated using the model and compared with the one measured.

The results are shown in Figure ref:fig:test_nhexa_sensitivity_hac_svd_3m_comp_model. The model is quite effective in estimating the sensitivity transfer functions except around 60Hz were there is a peak for the measurement.

Comparison of the measured sensitivity transfer functions with the model

Bibliography   ignore