phd-test-bench-nano-hexapod/test-bench-nano-hexapod.org

Nano-Hexapod - Test Bench

• Introduction
• Mounting Procedure
  • Mounting Goals
  • Mounting Bench
  • Mounting Procedure
  • Nano-Hexapod Mounting
    • Introduction
    • Plates
    • Mounting Tool
    • Mounted Hexapod
• Suspended Table
  • Introduction
  • Experimental Setup
    • Introduction
    • CAD Model
    • Instrumentation
    • Suspended table
    • Inertial Sensors
  • Compute the 6DoF solid body motion from several inertial sensors
    • Introduction
    • Define accelerometers positions/orientations
    • Transformation matrix from motion of the solid body to accelerometer measurements
    • Compute the transformation matrix from accelerometer measurement to motion of the solid body
  • Simscape Model
    • Introduction
    • Simscape Sub-systems
      • Springs
      • Inertial Shaker (IS20)
      • 3D accelerometer (356B18)
    • Identification
      • Number of states
      • Resonance frequencies and mode shapes
    • Verify transformation
  • Nano-Hexapod
    • Introduction
    • Nano-Hexapod
    • Computation of the transmissibility from accelerometer data
      • Introduction
      • Jacobian matrices
      • Using linearize function
    • Comparison with "true" transmissibility
  • Identification of the table's dynamics
    • Mode Shapes
• Nano-Hexapod Dynamics
  • Introduction
  • Identification of the dynamics
    • Introduction
    • Data Loading and Spectral Analysis Setup
    • Transfer function from Actuator to Encoder
    • Transfer function from Actuator to Force Sensor
    • Save Identified Plants
  • Comparison with the Simscape Model
    • Introduction
    • Identification with the Simscape Model
    • Dynamics from Actuator to Force Sensors
    • Dynamics from Actuator to Encoder
    • Conclusion
  • Effect of Payload mass on the Dynamics
    • Introduction
    • Measured Frequency Response Functions
    • Rigidification of the added payloads
    • Transfer function from Actuators to Encoders
    • Transfer function from Actuators to Force Sensors
    • Coupling of the transfer function from Actuator to Encoders
  • Comparison with the Simscape model
    • Introduction
    • System Identification
    • Transfer function from Actuators to Encoders
    • Transfer function from Actuators to Force Sensors
  • Conclusion
• Bibliography
• Glossary
• Footnotes

---

This report is also available as a pdf.

---

Introduction   ignore

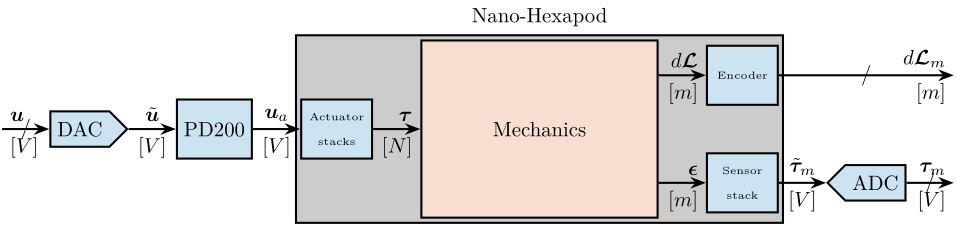
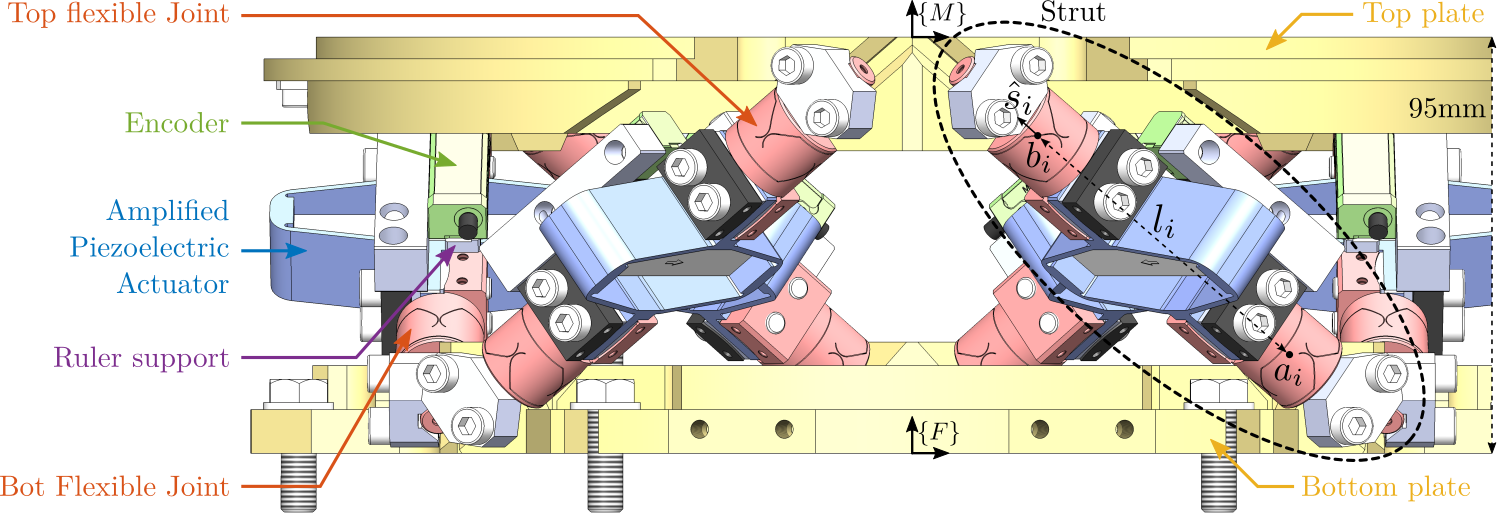
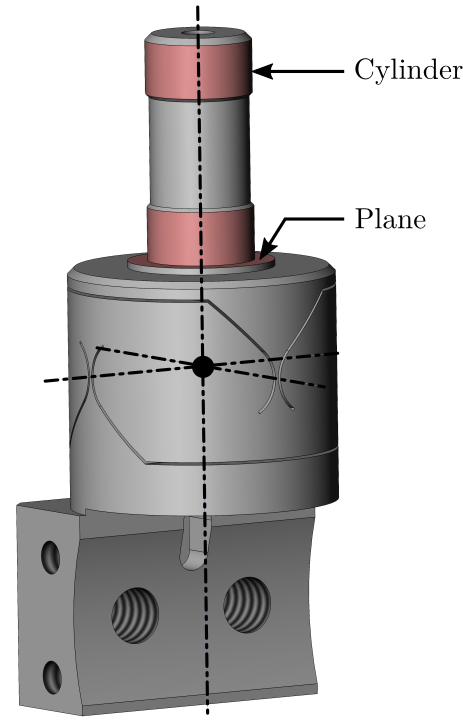
This document is dedicated to the experimental study of the nano-hexapod shown in Figure ref:fig:test_nhexa_picture_bench_granite_nano_hexapod.

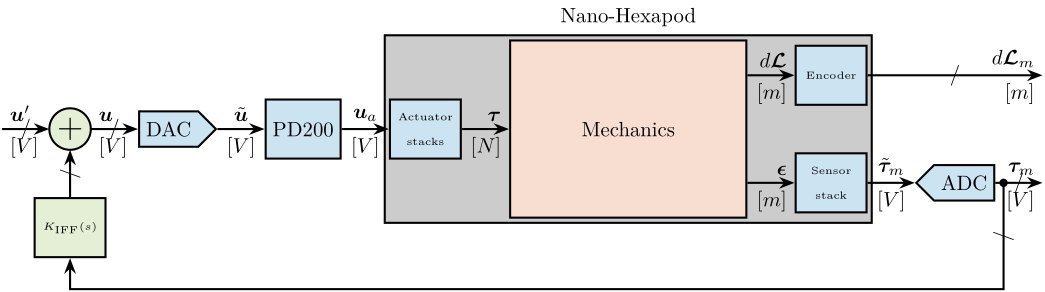
In Figure ref:fig:test_nhexa_nano_hexapod_signals is shown a block diagram of the experimental setup. When possible, the notations are consistent with this diagram and summarized in Table ref:tab:list_signals.

\definecolor{instrumentation}{rgb}{0, 0.447, 0.741}
\definecolor{mechanics}{rgb}{0.8500, 0.325, 0.098}

\begin{tikzpicture}
  % Blocs
  \node[block={4.0cm}{3.0cm}, fill=mechanics!20!white] (nano_hexapod) {Mechanics};
  \coordinate[] (inputF)  at (nano_hexapod.west);
  \coordinate[] (outputL) at ($(nano_hexapod.south east)!0.8!(nano_hexapod.north east)$);
  \coordinate[] (outputF) at ($(nano_hexapod.south east)!0.2!(nano_hexapod.north east)$);

  \node[block, left= 0.8 of inputF,  fill=instrumentation!20!white, align=center] (F_stack) {\tiny Actuator \\ \tiny stacks};
  \node[block, left= 0.8 of F_stack, fill=instrumentation!20!white] (PD200)   {PD200};
  \node[DAC,   left= 0.8 of PD200,   fill=instrumentation!20!white] (F_DAC)   {DAC};
  \node[block, right=0.8 of outputF, fill=instrumentation!20!white, align=center] (Fm_stack){\tiny Sensor \\ \tiny stack};
  \node[ADC,   right=0.8 of Fm_stack,fill=instrumentation!20!white] (Fm_ADC)  {ADC};
  \node[block, right=0.8 of outputL, fill=instrumentation!20!white] (encoder) {\tiny Encoder};

  % Connections and labels
  \draw[->] ($(F_DAC.west)+(-0.8,0)$) node[above right]{$\bm{u}$} node[below right]{$[V]$} -- node[sloped]{$/$} (F_DAC.west);
  \draw[->] (F_DAC.east)   -- node[midway, above]{$\tilde{\bm{u}}$}node[midway, below]{$[V]$} (PD200.west);
  \draw[->] (PD200.east)   -- node[midway, above]{$\bm{u}_a$}node[midway, below]{$[V]$} (F_stack.west);
  \draw[->] (F_stack.east) -- (inputF) node[above left]{$\bm{\tau}$}node[below left]{$[N]$};

  \draw[->] (outputF)       -- (Fm_stack.west) node[above left]{$\bm{\epsilon}$} node[below left]{$[m]$};
  \draw[->] (Fm_stack.east) -- node[midway, above]{$\tilde{\bm{\tau}}_m$}node[midway, below]{$[V]$} (Fm_ADC.west);
  \draw[->] (Fm_ADC.east)   -- node[sloped]{$/$} ++(0.8, 0)coordinate(end) node[above left]{$\bm{\tau}_m$}node[below left]{$[V]$};

  \draw[->] (outputL)      -- (encoder.west) node[above left]{$d\bm{\mathcal{L}}$} node[below left]{$[m]$};
  \draw[->] (encoder.east) -- node[sloped]{$/$} (encoder-|end) node[above left]{$d\bm{\mathcal{L}}_m$}node[below left]{$[m]$};

  % Nano-Hexapod
  \begin{scope}[on background layer]
    \node[fit={(F_stack.west|-nano_hexapod.south) (Fm_stack.east|-nano_hexapod.north)}, fill=black!20!white, draw, inner sep=2pt] (system) {};
    \node[above] at (system.north) {Nano-Hexapod};
  \end{scope}
\end{tikzpicture}

	Unit	Matlab	Vector	Elements
Control Input (wanted DAC voltage)	[V]	u	$\bm{u}$	$u_i$
DAC Output Voltage	[V]	u	$\tilde{\bm{u}}$	$\tilde{u}_i$
PD200 Output Voltage	[V]	ua	$\bm{u}_a$	$u_{a,i}$
Actuator applied force	[N]	tau	$\bm{\tau}$	$\tau_i$
Strut motion	[m]	dL	$d\bm{\mathcal{L}}$	$d\mathcal{L}_i$
Encoder measured displacement	[m]	dLm	$d\bm{\mathcal{L}}_m$	$d\mathcal{L}_{m,i}$
Force Sensor strain	[m]	epsilon	$\bm{\epsilon}$	$\epsilon_i$
Force Sensor Generated Voltage	[V]	taum	$\tilde{\bm{\tau}}_m$	$\tilde{\tau}_{m,i}$
Measured Generated Voltage	[V]	taum	$\bm{\tau}_m$	$\tau_{m,i}$
Motion of the top platform	[m,rad]	dX	$d\bm{\mathcal{X}}$	$d\mathcal{X}_i$
Metrology measured displacement	[m,rad]	dXm	$d\bm{\mathcal{X}}_m$	$d\mathcal{X}_{m,i}$

This document is divided in the following sections:

• Section ref:sec:test_nhexa_mounting: mounting of the nano-hexapod
• Section ref:sec:test_nhexa_encoders_plates: the same is done when the encoders are fixed to the plates.
• Section ref:sec:test_nhexa_decentralized_hac_iff: a decentralized HAC-LAC strategy is studied and implemented.

Mounting Procedure

<<sec:test_nhexa_mounting>>

Mounting Goals

Fixation of the flexible points to the nano-hexapod plates

#+caption:Reference surfaces of the flexible joint interface with the plates

Mounting Bench

Mounting Procedure

1. Fix the bottom plate with the cylindrical tool
2. Put the top plate on the granite
3. Put the cylindrical tool and bottom plate on top of the top plate (Figure ref:fig:test_nhexa_mounting_tool_hexapod_bot_view). This position the bottom plate with respect to the top plate in X, Y, Z, Rx, Ry
4. Put the pin to position/fix the Rz. Now the two plates should be position and clamped together
5. Fix the 6 struts
6. Remove the pin and the tool
7. Put the nano-hexapod in place

Nano-Hexapod Mounting

<<sec:nano_hexapod_mounting>>

Introduction   ignore

Plates

Mounting Tool

A mounting tool is used to position the top and bottom platforms. Then the struts can be mounted one by one. When all the struts are mounted, the "mounting tool" is disassembled and the nano-hexapod is considered to be mounted.

The main goal of this "mounting tool" is to position the "V" shapes of both plates such that they are coaxial.

The straightness is the diameter of the smallest cylinder containing all points of the axis.

Strut nb	Meas 1	Meas 2
1	7um	3um
2	11um	11um
3	15um	14um
4	6um	6um
5	7um	5um
6	6um	7um

Using the FARO arm, the coaxiality of the "V" shapes have been measured to better than $15\,\mu m$! This means that the two cylinders corresponding to the flexible joints are both within a perfect cylinder with a diameter of $15\,\mu m$. This is probably better than that, but we reached the limit of the FARO arm's precision.

Mounted Hexapod

Suspended Table

Introduction

This document is divided as follows:

• Section ref:sec:experimental_setup: the experimental setup and all the instrumentation are described
• Section ref:sec:meas_transformation: the mathematics used to compute the 6DoF motion of a solid body from several inertial sensor is derived
• Section ref:sec:simscape_model: a Simscape model of the vibration table is developed
• Section ref:sec:table_dynamics: the table dynamics is identified and compared with the Simscape model

Experimental Setup

<<sec:experimental_setup>>

Introduction   ignore

CAD Model

Instrumentation

Here are the documentation of the equipment used for this vibration table:

• Modal Shaker: Watson and Gearing
• Inertial Shaker: IS20
• Viscoelastic supports: 810002
• Spring supports: MV803-12CC
• Optical Table: B4545A
• Triaxial Accelerometer: 356B18
• OROS

Suspended table

Dimensions

450 mm x 450 mm x 60 mm

Mass

21.30 kg

If we include including the bottom interface plate:

• Total mass: 30.7 kg
• CoM: 42mm below Center of optical table
• Ix = 0.54, Iy = 0.54, Iz = 1.07 (with respect to CoM)

Inertial Sensors

Equipment
(2x) 1D accelerometer PCB 393B05
(4x) 3D accelerometer PCB 356B18

Compute the 6DoF solid body motion from several inertial sensors

<<sec:meas_transformation>>

Introduction   ignore

Let's consider a solid body with several accelerometers attached to it (Figure ref:fig:local_to_global_coordinates).

Schematic of the measured motions of a solid body

The goal of this section is to see how to compute the acceleration/angular acceleration of the solid body from the accelerations $\vec{a}_i$ measured by the accelerometers.

The acceleration/angular acceleration of the solid body is defined as the vector ${}^O\vec{x}$:

\begin{equation} {}^O\vec{x} = \begin{bmatrix} \dot{v}_x \\ \dot{v}_y \\ \dot{v}_z \\ \dot{\omega}_x \\ \dot{\omega}_y \\ \dot{\omega}_z \end{bmatrix} \end{equation}

As we want to measure 6dof, we suppose that we have 6 uniaxial acceleremoters (we could use more, but 6 is enough). The measurement of the individual vectors is defined as the vector $\vec{a}$:

\begin{equation} \vec{a} = \begin{bmatrix} a_1 \\ a_2 \\ a_3 \\ a_4 \\ a_5 \\ a_6 \end{bmatrix} \end{equation}

From the positions and orientations of the acceleremoters (defined in Section ref:sec:accelerometer_pos), it is quite straightforward to compute the accelerations measured by the sensors from the acceleration/angular acceleration of the solid body (Section sec:transformation_motion_to_acc). From this, we can easily build a transformation matrix $M$, such that:

\begin{equation} \vec{a} = M \cdot {}^O\vec{x} \end{equation}

If the matrix is invertible, we can just take the inverse in order to obtain the transformation matrix giving the 6dof acceleration of the solid body from the accelerometer measurements (Section ref:sec:transformation_acc_to_motion):

\begin{equation} {}^O\vec{x} = M^{-1} \cdot \vec{a} \end{equation}

If it is not invertible, then it means that it is not possible to compute all 6dof of the solid body from the measurements. The solution is then to change the location/orientation of some of the accelerometers.

Define accelerometers positions/orientations

<<sec:accelerometer_pos>> Let's first define the position and orientation of all measured accelerations with respect to a defined frame $\{O\}$.

Opm = [-0.1875, -0.1875, -0.245;
       -0.1875, -0.1875, -0.245;
        0.1875, -0.1875, -0.245;
        0.1875, -0.1875, -0.245;
        0.1875,  0.1875, -0.245;
        0.1875,  0.1875, -0.245]';

There are summarized in Table ref:tab:accelerometers_table_positions.

	$a_1$	$a_2$	$a_3$	$a_4$	$a_5$	$a_6$
x	-0.188	-0.188	0.188	0.188	0.188	0.188
y	-0.188	-0.188	-0.188	-0.188	0.188	0.188
z	-0.245	-0.245	-0.245	-0.245	-0.245	-0.245

We then define the direction of the measured accelerations (unit vectors):

Osm = [0, 1, 0;
       0, 0, 1;
       1, 0, 0;
       0, 0, 1;
       1, 0, 0;
       0, 1, 0]';

They are summarized in Table ref:tab:accelerometers_table_orientations.

	$\hat{s}_1$	$\hat{s}_2$	$\hat{s}_3$	$\hat{s}_4$	$\hat{s}_5$	$\hat{s}_6$
x	0	0	1	0	1	0
y	1	0	0	0	0	0
z	0	1	0	1	0	1

Transformation matrix from motion of the solid body to accelerometer measurements

<<sec:transformation_motion_to_acc>>

Let's try to estimate the x-y-z acceleration of any point of the solid body from the acceleration/angular acceleration of the solid body expressed in $\{O\}$. For any point $p_i$ of the solid body (corresponding to an accelerometer), we can write:

\begin{equation} \begin{bmatrix} a_{i,x} \\ a_{i,y} \\ a_{i,z} \end{bmatrix} = \begin{bmatrix} \dot{v}_x \\ \dot{v}_y \\ \dot{v}_z \end{bmatrix} + p_i \times \begin{bmatrix} \dot{\omega}_x \\ \dot{\omega}_y \\ \dot{\omega}_z \end{bmatrix} \end{equation}

We can write the cross product as a matrix product using the skew-symmetric transformation:

\begin{equation} \begin{bmatrix} a_{i,x} \\ a_{i,y} \\ a_{i,z} \end{bmatrix} = \begin{bmatrix} \dot{v}_x \\ \dot{v}_y \\ \dot{v}_z \end{bmatrix} + \underbrace{\begin{bmatrix} 0 & p_{i,z} & -p_{i,y} \\ -p_{i,z} & 0 & p_{i,x} \\ p_{i,y} & -p_{i,x} & 0 \end{bmatrix}}_{P_{i,[\times]}} \cdot \begin{bmatrix} \dot{\omega}_x \\ \dot{\omega}_y \\ \dot{\omega}_z \end{bmatrix} \end{equation}

If we now want to know the (scalar) acceleration $a_i$ of the point $p_i$ in the direction of the accelerometer direction $\hat{s}_i$, we can just project the 3d acceleration on $\hat{s}_i$:

\begin{equation} a_i = \hat{s}_i^T \cdot \begin{bmatrix} a_{i,x} \\ a_{i,y} \\ a_{i,z} \end{bmatrix} = \hat{s}_i^T \cdot \begin{bmatrix} \dot{v}_x \\ \dot{v}_y \\ \dot{v}_z \end{bmatrix} + \left( \hat{s}_i^T \cdot P_{i,[\times]} \right) \cdot \begin{bmatrix} \dot{\omega}_x \\ \dot{\omega}_y \\ \dot{\omega}_z \end{bmatrix} \end{equation}

Which is equivalent as a simple vector multiplication:

\begin{equation} a_i = \begin{bmatrix} \hat{s}_i^T & \hat{s}_i^T \cdot P_{i,[\times]} \end{bmatrix} \begin{bmatrix} \dot{v}_x \\ \dot{v}_y \\ \dot{v}_z \\ \dot{\omega}_x \\ \dot{\omega}_y \\ \dot{\omega}_z \end{bmatrix} = \begin{bmatrix} \hat{s}_i^T & \hat{s}_i^T \cdot P_{i,[\times]} \end{bmatrix} {}^O\vec{x} \end{equation}

And finally we can combine the 6 (line) vectors for the 6 accelerometers to write that in a matrix form. We obtain Eq. eqref:eq:M_matrix.

The transformation from solid body acceleration ${}^O\vec{x}$ from sensor measured acceleration $\vec{a}$ is: \begin{equation} \label{eq:M_matrix} \vec{a} = _brace{\begin{bmatrix} \hat{s}_1^T & \hat{s}_1^T \cdot P_{1,[\times]} \\ \vdots & \vdots \\ \hat{s}_6^T & \hat{s}_6^T \cdot P_{6,[\times]} \end{bmatrix}}_M {}^O\vec{x}

\end{equation}

with $\hat{s}_i$ the unit vector representing the measured direction of the i'th accelerometer expressed in frame $\{O\}$ and $P_{i,[\times]}$ the skew-symmetric matrix representing the cross product of the position of the i'th accelerometer expressed in frame $\{O\}$.

Let's define such matrix using matlab:

M = zeros(length(Opm), 6);

for i = 1:length(Opm)
    Ri = [0,         Opm(3,i), -Opm(2,i);
         -Opm(3,i),  0,         Opm(1,i);
          Opm(2,i), -Opm(1,i),  0];
    M(i, 1:3) = Osm(:,i)';
    M(i, 4:6) = Osm(:,i)'*Ri;
end

The obtained matrix is shown in Table ref:tab:effect_motion_on_meas.

	$\dot{x}_x$	$\dot{x}_y$	$\dot{x}_z$	$\dot{\omega}_x$	$\dot{\omega}_y$	$\dot{\omega}_z$
$a_1$	0.0	1.0	0.0	0.24	0.0	-0.19
$a_2$	0.0	0.0	1.0	-0.19	0.19	0.0
$a_3$	1.0	0.0	0.0	0.0	-0.24	0.19
$a_4$	0.0	0.0	1.0	-0.19	-0.19	0.0
$a_5$	1.0	0.0	0.0	0.0	-0.24	-0.19
$a_6$	0.0	0.0	1.0	0.19	-0.19	0.0

Compute the transformation matrix from accelerometer measurement to motion of the solid body

<<sec:transformation_acc_to_motion>>

In order to compute the motion of the solid body ${}^O\vec{x}$ with respect to frame $\{O\}$ from the accelerometer measurements $\vec{a}$, we have to inverse the transformation matrix $M$.

\begin{equation} {}^O\vec{x} = M^{-1} \vec{a} \end{equation}

We therefore need the determinant of $M$ to be non zero:

det(M)

The obtained inverse of the matrix is shown in Table ref:tab:compute_motion_from_meas.

	$a_1$	$a_2$	$a_3$	$a_4$	$a_5$	$a_6$
$\dot{x}_x$	0.0	0.7	0.5	-0.7	0.5	0.0
$\dot{x}_y$	1.0	0.0	0.5	0.7	-0.5	-0.7
$\dot{x}_z$	0.0	0.5	0.0	0.0	0.0	0.5
$\dot{\omega}_x$	0.0	0.0	0.0	-2.7	0.0	2.7
$\dot{\omega}_y$	0.0	2.7	0.0	-2.7	0.0	0.0
$\dot{\omega}_z$	0.0	0.0	2.7	0.0	-2.7	0.0

Simscape Model

<<sec:simscape_model>>

Introduction   ignore

In this section, the Simscape model of the vibration table is described.

Simscape Sub-systems

<<sec:simscape_parameters>>

Parameters for sub-components of the simscape model are defined below.

Springs

<<sec:simscape_springs>>

The 4 springs supporting the suspended optical table are modelled with "bushing joints" having stiffness and damping in the x-y-z directions:

spring.kx = 1e4; % X- Stiffness [N/m]
spring.cx = 1e1; % X- Damping [N/(m/s)]

spring.ky = 1e4; % Y- Stiffness [N/m]
spring.cy = 1e1; % Y- Damping [N/(m/s)]

spring.kz = 1e4; % Z- Stiffness [N/m]
spring.cz = 1e1; % Z- Damping [N/(m/s)]

spring.z0 = 32e-3; % Equilibrium z-length [m]

And we can increase the "equilibrium position" of the vertical springs to take into account the gravity forces and start closer to equilibrium:

spring.dl = (30.5918/4)*9.80665/spring.kz;

Inertial Shaker (IS20)

<<sec:simscape_inertial_shaker>>

The inertial shaker is defined as two solid bodies:

• the "housing" that is fixed to the element that we want to excite
• the "inertial mass" that is suspended inside the housing

The inertial mass is guided inside the housing and an actuator (coil and magnet) can be used to apply a force between the inertial mass and the support. The "reacting" force on the support is then used as an excitation.

Characteristic	Value
Output Force	20 N
Frequency Range	10-3000 Hz
Moving Mass	0.1 kg
Total Mass	0.3 kg

From the datasheet in Table ref:tab:is20_characteristics, we can estimate the parameters of the physical shaker.

These parameters are defined below

shaker.w0 = 2*pi*10; % Resonance frequency of moving mass [rad/s]
shaker.m = 0.1; % Moving mass [m]
shaker.m_tot = 0.3; % Total mass [m]
shaker.k = shaker.m*shaker.w0^2; % Spring constant [N/m]
shaker.c = 0.2*sqrt(shaker.k*shaker.m); % Damping [N/(m/s)]

3D accelerometer (356B18)

<<sec:simscape_accelerometers>>

An accelerometer consists of 2 solids:

• a "housing" rigidly fixed to the measured body
• an "inertial mass" suspended inside the housing by springs and guided in the measured direction

The relative motion between the housing and the inertial mass gives a measurement of the acceleration of the measured body (up to the suspension mode of the inertial mass).

Characteristic	Value
Sensitivity	0.102 V/(m/s2)
Frequency Range	0.5 to 3000 Hz
Resonance Frequency	> 20 kHz
Resolution	0.0005 m/s2 rms
Weight	0.025 kg
Size	20.3x26.1x20.3 [mm]

Here are defined the parameters for the triaxial accelerometer:

acc_3d.m = 0.005; % Inertial mass [kg]
acc_3d.m_tot = 0.025; % Total mass [m]

acc_3d.w0 = 2*pi*20e3; % Resonance frequency [rad/s]

acc_3d.kx = acc_3d.m*acc_3d.w0^2; % Spring constant [N/m]
acc_3d.ky = acc_3d.m*acc_3d.w0^2; % Spring constant [N/m]
acc_3d.kz = acc_3d.m*acc_3d.w0^2; % Spring constant [N/m]

acc_3d.cx = 1e2; % Damping [N/(m/s)]
acc_3d.cy = 1e2; % Damping [N/(m/s)]
acc_3d.cz = 1e2; % Damping [N/(m/s)]

DC gain between support acceleration and inertial mass displacement is $-m/k$:

acc_3d.g_x = 1/(-acc_3d.m/acc_3d.kx); % [m/s^2/m]
acc_3d.g_y = 1/(-acc_3d.m/acc_3d.ky); % [m/s^2/m]
acc_3d.g_z = 1/(-acc_3d.m/acc_3d.kz); % [m/s^2/m]

We also define the sensitivity in order to have the outputs in volts.

acc_3d.gV_x = 0.102; % [V/(m/s^2)]
acc_3d.gV_y = 0.102; % [V/(m/s^2)]
acc_3d.gV_z = 0.102; % [V/(m/s^2)]

The problem with using such model for accelerometers is that this adds states to the identified models (2x3 states for each triaxial accelerometer). These states represents the dynamics of the suspended inertial mass. In the frequency band of interest (few Hz up to ~1 kHz), the dynamics of the inertial mass can be ignore (its resonance is way above 1kHz). Therefore, we might as well use idealized "transform sensors" blocks as they will give the same result up to ~20kHz while allowing to reduce the number of identified states.

The accelerometer model can be chosen by setting the type property:

acc_3d.type = 2; % 1: inertial mass, 2: perfect

Identification

<<sec:simscape_parameters>>

Number of states

Let's first use perfect 3d accelerometers:

acc_3d.type = 2; % 1: inertial mass, 2: perfect

And identify the dynamics from the shaker force to the measured accelerations:

%% Name of the Simulink File
mdl = 'vibration_table';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'],  1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/acc'],  1, 'openoutput'); io_i = io_i + 1;

%% Run the linearization
Gp = linearize(mdl, io);
Gp.InputName  = {'F'};
Gp.OutputName  = {'a1', 'a2', 'a3', 'a4', 'a5', 'a6'};

size(Gp)
State-space model with 6 outputs, 1 inputs, and 12 states.

We indeed have the 12 states corresponding to the 6 DoF of the suspended optical table.

Let's now consider the inertial masses for the triaxial accelerometers:

acc_3d.type = 1; % 1: inertial mass, 2: perfect

%% Name of the Simulink File
mdl = 'vibration_table';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'],  1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/acc'],  1, 'openoutput'); io_i = io_i + 1;

%% Run the linearization
Ga = linearize(mdl, io);
Ga.InputName  = {'F'};
Ga.OutputName  = {'a1', 'a2', 'a3', 'a4', 'a5', 'a6'};

size(Ga)
State-space model with 6 outputs, 1 inputs, and 30 states.

And we can see that 18 states have been added. This corresponds to 6 states for each triaxial accelerometers.

Resonance frequencies and mode shapes

Let's now identify the resonance frequency and mode shapes associated with the suspension modes of the optical table.

acc_3d.type = 2; % 1: inertial mass, 2: perfect

%% Name of the Simulink File
mdl = 'vibration_table';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'],      1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/a1,a2'],  1, 'openoutput'); io_i = io_i + 1;

%% Run the linearization
G = linearize(mdl, io);
G.InputName  = {'F'};
G.OutputName  = {'ax'};

Compute the resonance frequencies

ws = eig(G.A);
ws = ws(imag(ws) > 0);

And the associated response of the optical table

x_mod = zeros(6, 6);

for i = 1:length(ws)
    xi = evalfr(G, ws(i));
    x_mod(:,i) = xi./norm(xi);
end

The results are shown in Table ref:tab:mode_shapes. The motion associated to the mode shapes are just indicative.

$\omega_0$ [Hz]	5.6	5.6	5.7	8.2	8.2	8.2
x	0.1	0.7	0.0	0.0	0.2	0.0
y	0.7	0.1	0.0	0.0	0.0	0.2
z	0.0	0.0	1.0	0.0	0.0	0.0
Rx	0.7	0.1	0.0	0.0	0.1	1.0
Ry	0.1	0.7	0.0	0.0	1.0	0.1
Rz	0.0	0.0	0.0	1.0	0.0	0.0

Verify transformation

%% Options for Linearized
options = linearizeOptions;
options.SampleTime = 0;

%% Name of the Simulink File
mdl = 'vibration_table';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'],  1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/acc'],  1, 'openoutput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/acc_O'],  1, 'openoutput'); io_i = io_i + 1;

%% Run the linearization
G = linearize(mdl, io, 0.0, options);
G.InputName  = {'F'};
G.OutputName = {'a1', 'a2', 'a3', 'a4', 'a5', 'a6', ...
                'Dx', 'Dy', 'Dz', 'Rx', 'Ry', 'Rz'};

G_acc = inv(M)*G(1:6, 1);
G_id = G(7:12, 1);

bodeFig({G_acc(1), G_id(1)})
bodeFig({G_acc(2), G_id(2)})
bodeFig({G_acc(3), G_id(3)})
bodeFig({G_acc(4), G_id(4)})
bodeFig({G_acc(5), G_id(5)})
bodeFig({G_acc(6), G_id(6)})

Nano-Hexapod

<<sec:nano_hexapod>>

Introduction   ignore

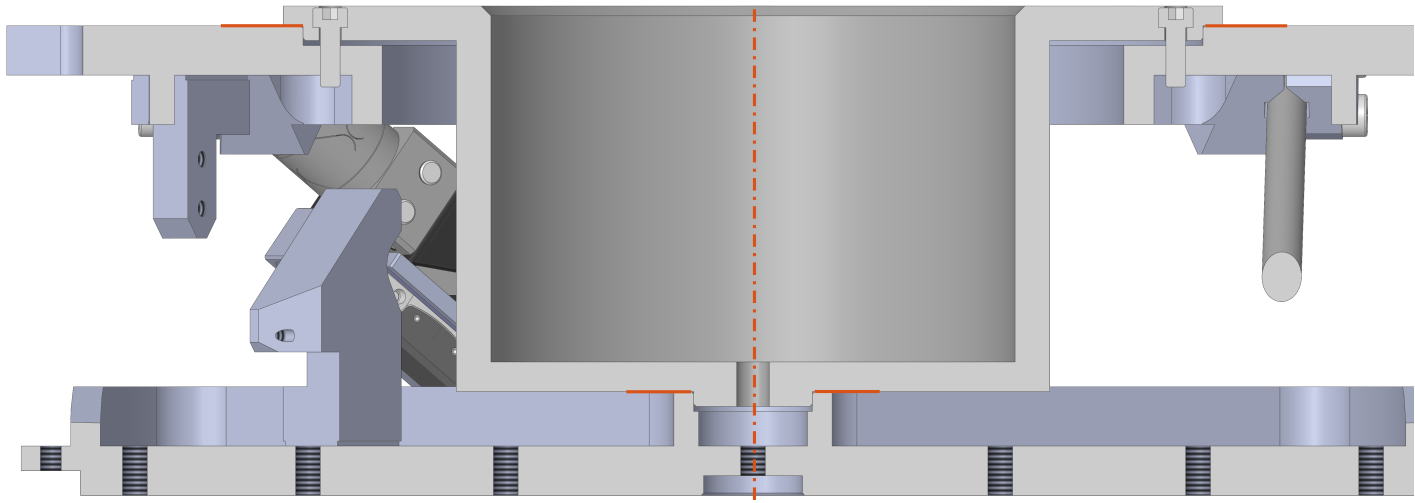
A configuration is added to be able to put the nano-hexapod on top of the vibration table as shown in Figure ref:fig:simscape_vibration_table.

The nano-hexapod's simscape model is taken from another git repository.

Nano-Hexapod

n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
                                       'flex_top_type', '4dof', ...
                                       'motion_sensor_type', 'plates', ...
                                       'actuator_type', 'flexible');

Computation of the transmissibility from accelerometer data

Introduction   ignore

The goal is to compute the $6 \times 6$ transfer function matrix corresponding to the transmissibility of the Nano-Hexapod.

To do so, several accelerometers are located both on the vibration table and on the top of the nano-hexapod.

The vibration table is then excited using a Shaker and all the accelerometers signals are recorded.

Using transformation (jacobian) matrices, it is then possible to compute both the motion of the top and bottom platform of the nano-hexapod.

Finally, it is possible to compute the $6 \times 6$ transmissibility matrix.

Such procedure is explained in cite:marneffe04_stewar_platf_activ_vibrat_isolat.

Jacobian matrices

How to compute the Jacobian matrices is explained in Section ref:sec:meas_transformation.

%% Bottom Accelerometers
Opb = [-0.1875, -0.1875, -0.245;
       -0.1875, -0.1875, -0.245;
        0.1875, -0.1875, -0.245;
        0.1875, -0.1875, -0.245;
        0.1875,  0.1875, -0.245;
        0.1875,  0.1875, -0.245]';

Osb = [0, 1, 0;
       0, 0, 1;
       1, 0, 0;
       0, 0, 1;
       1, 0, 0;
       0, 0, 1;]';

Jb = zeros(length(Opb), 6);

for i = 1:length(Opb)
    Ri = [0,         Opb(3,i), -Opb(2,i);
         -Opb(3,i),  0,         Opb(1,i);
          Opb(2,i), -Opb(1,i),  0];
    Jb(i, 1:3) = Osb(:,i)';
    Jb(i, 4:6) = Osb(:,i)'*Ri;
end

Jbinv = inv(Jb);

	$a_1$	$a_2$	$a_3$	$a_4$	$a_5$	$a_6$
$\dot{x}_x$	0.0	0.7	0.5	-0.7	0.5	0.0
$\dot{x}_y$	1.0	0.0	0.5	0.7	-0.5	-0.7
$\dot{x}_z$	0.0	0.5	0.0	0.0	0.0	0.5
$\dot{\omega}_x$	0.0	0.0	0.0	-2.7	0.0	2.7
$\dot{\omega}_y$	0.0	2.7	0.0	-2.7	0.0	0.0
$\dot{\omega}_z$	0.0	0.0	2.7	0.0	-2.7	0.0

%% Top Accelerometers
Opt = [-0.1,   0,     -0.150;
       -0.1,   0,     -0.150;
        0.05,  0.075, -0.150;
        0.05,  0.075, -0.150;
        0.05, -0.075, -0.150;
        0.05, -0.075, -0.150]';

Ost = [0, 1, 0;
       0, 0, 1;
       1, 0, 0;
       0, 0, 1;
       1, 0, 0;
       0, 0, 1;]';

Jt = zeros(length(Opt), 6);

for i = 1:length(Opt)
    Ri = [0,         Opt(3,i), -Opt(2,i);
         -Opt(3,i),  0,         Opt(1,i);
          Opt(2,i), -Opt(1,i),  0];
    Jt(i, 1:3) = Ost(:,i)';
    Jt(i, 4:6) = Ost(:,i)'*Ri;
end

Jtinv = inv(Jt);

	$b_1$	$b_2$	$b_3$	$b_4$	$b_5$	$b_6$
$\dot{x}_x$	0.0	1.0	0.5	-0.5	0.5	-0.5
$\dot{x}_y$	1.0	0.0	-0.7	-1.0	0.7	1.0
$\dot{x}_z$	0.0	0.3	0.0	0.3	0.0	0.3
$\dot{\omega}_x$	0.0	0.0	0.0	6.7	0.0	-6.7
$\dot{\omega}_y$	0.0	6.7	0.0	-3.3	0.0	-3.3
$\dot{\omega}_z$	0.0	0.0	-6.7	0.0	6.7	0.0

Using linearize function

acc_3d.type = 2; % 1: inertial mass, 2: perfect

%% Name of the Simulink File
mdl = 'vibration_table';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F_shaker'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/acc'],      1, 'openoutput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/acc_top'],  1, 'openoutput'); io_i = io_i + 1;

%% Run the linearization
G = linearize(mdl, io);
G.InputName  = {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};
G.OutputName  = {'a1', 'a2', 'a3', 'a4', 'a5', 'a6', ...
                 'b1', 'b2', 'b3', 'b4', 'b5', 'b6'};

Gb = Jbinv*G({'a1', 'a2', 'a3', 'a4', 'a5', 'a6'}, :);
Gt = Jtinv*G({'b1', 'b2', 'b3', 'b4', 'b5', 'b6'}, :);

T = inv(Gb)*Gt;
T = minreal(T);
T = prescale(T, {2*pi*0.1, 2*pi*1e3});

Comparison with "true" transmissibility

%% Name of the Simulink File
mdl = 'test_transmissibility';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/d'],   1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/acc'], 1, 'openoutput'); io_i = io_i + 1;

%% Run the linearization
G = linearize(mdl, io);
G.InputName  = {'Dx', 'Dy', 'Dz', 'Rx', 'Ry', 'Rz'};
G.OutputName  = {'Ax', 'Ay', 'Az', 'Bx', 'By', 'Bz'};

Tp = G/s^2;

Identification of the table's dynamics

<<sec:table_dynamics>>

Mode Shapes

	Freq. [Hz]	Description
1	1.3	X-translation
2	1.3	Y-translation
3	1.95	Z-rotation
4	6.85	Z-translation
5	8.9	Tilt
6	8.9	Tilt
7	700	Flexible Mode

Nano-Hexapod Dynamics

<<sec:test_nhexa_encoders_plates>>

Introduction   ignore

In this section, the encoders are fixed to the plates rather than to the struts as shown in Figure ref:fig:test_nhexa_enc_fixed_to_struts.

It is structured as follow:

• Section ref:sec:test_nhexa_enc_plates_plant_id: The dynamics of the nano-hexapod is identified.
• Section ref:sec:test_nhexa_enc_plates_comp_simscape: The identified dynamics is compared with the Simscape model.
• Section ref:sec:test_nhexa_enc_plates_iff: The Integral Force Feedback (IFF) control strategy is applied and the dynamics of the damped nano-hexapod is identified and compare with the Simscape model.

Identification of the dynamics

<<sec:test_nhexa_enc_plates_plant_id>>

Introduction   ignore

In this section, the dynamics of the nano-hexapod with the encoders fixed to the plates is identified.

First, the measurement data are loaded in Section ref:sec:test_nhexa_enc_plates_plant_id_setup, then the transfer function matrix from the actuators to the encoders are estimated in Section ref:sec:test_nhexa_enc_plates_plant_id_dvf. Finally, the transfer function matrix from the actuators to the force sensors is estimated in Section ref:sec:test_nhexa_enc_plates_plant_id_iff.

Data Loading and Spectral Analysis Setup

<<sec:test_nhexa_enc_plates_plant_id_setup>>

The actuators are excited one by one using a low pass filtered white noise. For each excitation, the 6 force sensors and 6 encoders are measured and saved.

%% Load Identification Data
meas_data = {};

for i = 1:6
    meas_data(i) = {load(sprintf('frf_exc_strut_%i_enc_plates_noise.mat', i), 't', 'Va', 'Vs', 'de')};
end

Transfer function from Actuator to Encoder

<<sec:test_nhexa_enc_plates_plant_id_dvf>>

The 6x6 transfer function matrix from the excitation voltage $\bm{u}$ and the displacement $d\bm{\mathcal{L}}_m$ as measured by the encoders is estimated.

%% Transfer function from u to dLm
G_dL = zeros(length(f), 6, 6);

for i = 1:6
    G_dL(:,:,i) = tfestimate(meas_data{i}.Va, meas_data{i}.de, win, Noverlap, Nfft, 1/Ts);
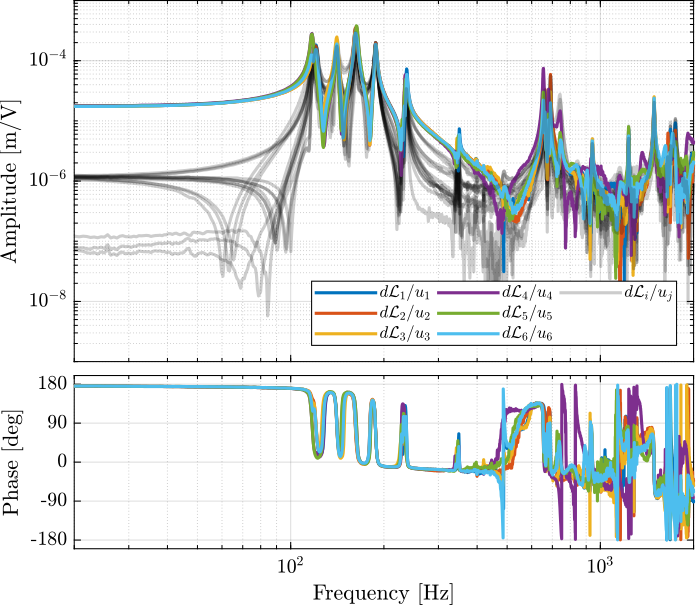
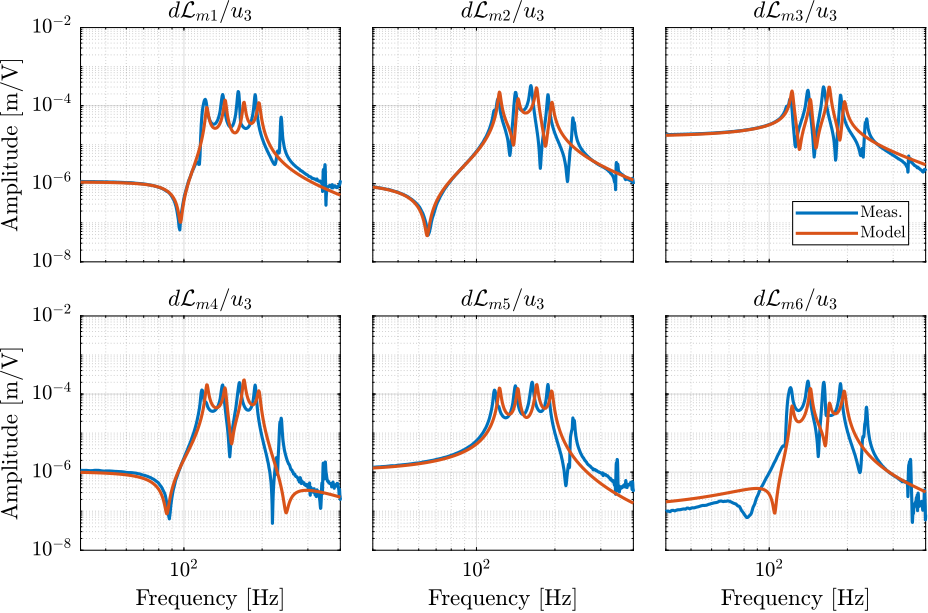
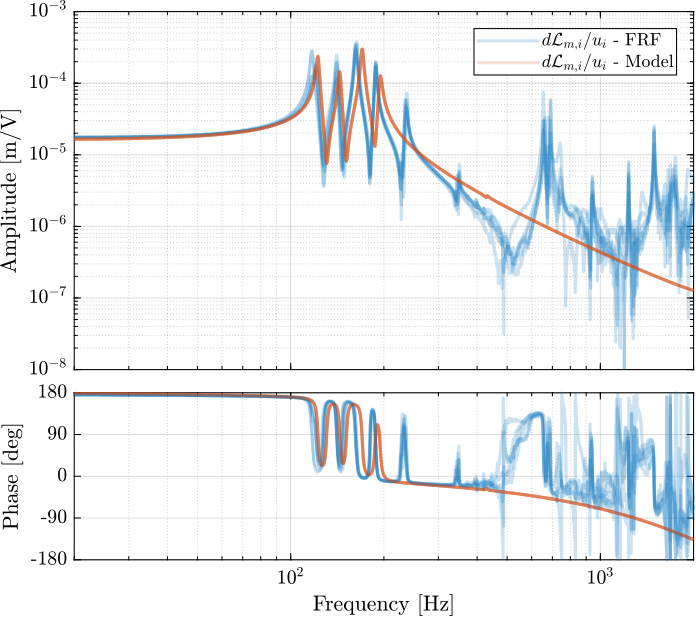
end

The diagonal and off-diagonal terms of this transfer function matrix are shown in Figure ref:fig:test_nhexa_enc_plates_dvf_frf.

Measured FRF for the transfer function from $\bm{u}$ to $d\bm{\mathcal{L}}_m$

From Figure ref:fig:test_nhexa_enc_plates_dvf_frf, we can draw few conclusions on the transfer functions from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ when the encoders are fixed to the plates:

• the decoupling is rather good at low frequency (below the first suspension mode). The low frequency gain is constant for the off diagonal terms, whereas when the encoders where fixed to the struts, the low frequency gain of the off-diagonal terms were going to zero (Figure ref:fig:test_nhexa_enc_struts_dvf_frf).
• the flexible modes of the struts at 226Hz and 337Hz are indeed shown in the transfer functions, but their amplitudes are rather low.
• the diagonal terms have alternating poles and zeros up to at least 600Hz: the flexible modes of the struts are not affecting the alternating pole/zero pattern. This what not the case when the encoders were fixed to the struts (Figure ref:fig:test_nhexa_enc_struts_dvf_frf).

Transfer function from Actuator to Force Sensor

<<sec:test_nhexa_enc_plates_plant_id_iff>> Then the 6x6 transfer function matrix from the excitation voltage $\bm{u}$ and the voltage $\bm{\tau}_m$ generated by the Force senors is estimated.

%% IFF Plant
G_tau = zeros(length(f), 6, 6);

for i = 1:6
    G_tau(:,:,i) = tfestimate(meas_data{i}.Va, meas_data{i}.Vs, win, Noverlap, Nfft, 1/Ts);
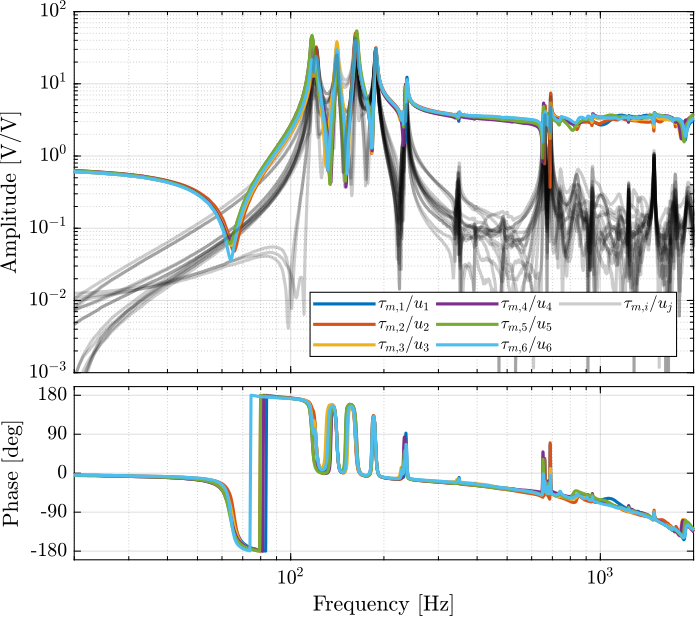
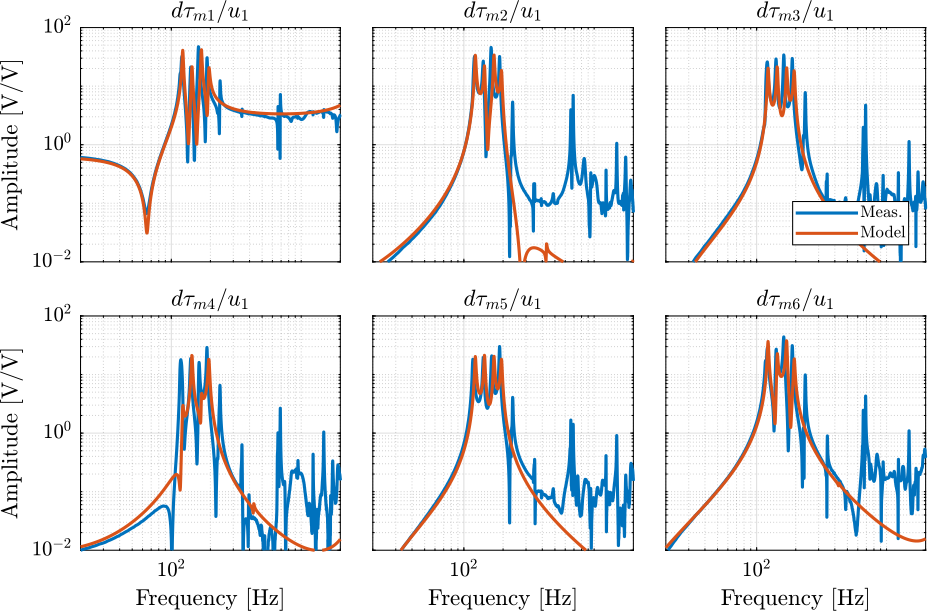
end

The bode plot of the diagonal and off-diagonal terms are shown in Figure ref:fig:test_nhexa_enc_plates_iff_frf.

Measured FRF for the IFF plant

It is shown in Figure ref:fig:test_nhexa_enc_plates_iff_comp_simscape_all that:

• The IFF plant has alternating poles and zeros
• The first flexible mode of the struts as 235Hz is appearing, and therefore is should be possible to add some damping to this mode using IFF
• The decoupling is quite good at low frequency (below the first model) as well as high frequency (above the last suspension mode, except near the flexible modes of the top plate)

Save Identified Plants

The identified dynamics is saved for further use.

save('data_frf/identified_plants_enc_plates.mat', 'f', 'Ts', 'G_tau', 'G_dL')

Comparison with the Simscape Model

<<sec:test_nhexa_enc_plates_comp_simscape>>

Introduction   ignore

In this section, the measured dynamics done in Section ref:sec:test_nhexa_enc_plates_plant_id is compared with the dynamics estimated from the Simscape model.

Identification with the Simscape Model

The nano-hexapod is initialized with the APA taken as 2dof models.

%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
                                       'flex_top_type', '4dof', ...
                                       'motion_sensor_type', 'plates', ...
                                       'actuator_type', '2dof');

support.type = 1; % On top of vibration table
payload.type = 0; % No Payload

Then the transfer function from $\bm{u}$ to $\bm{\tau}_m$ is identified using the Simscape model.

%% Identify the transfer function from u to taum
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput');   io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors

G_tau = exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options);

Now, the dynamics from the DAC voltage $\bm{u}$ to the encoders $d\bm{\mathcal{L}}_m$ is estimated using the Simscape model.

%% Identify the DVtransfer function from u to dLm
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'],  1, 'openinput');  io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Encoders

G_dL = exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options);

The identified dynamics is saved for further use.

save('data_frf/simscape_plants_enc_plates.mat', 'G_tau', 'G_dL');

Dynamics from Actuator to Force Sensors

The identified dynamics is compared with the measured FRF:

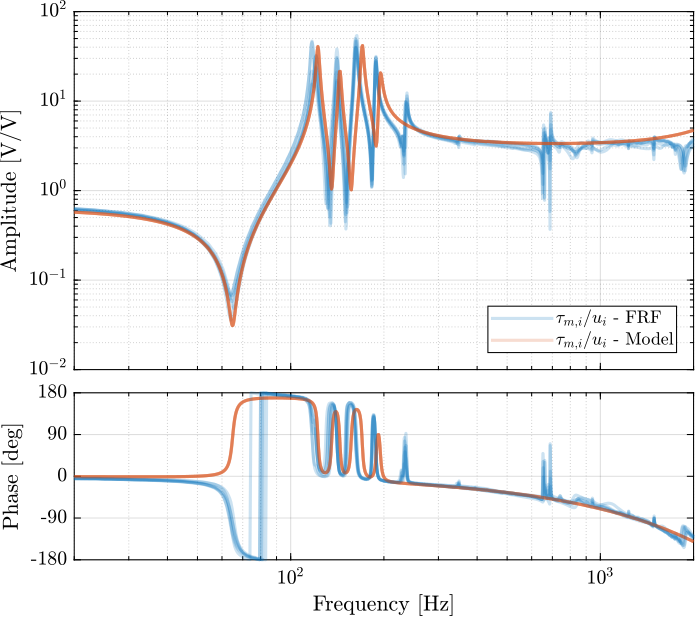
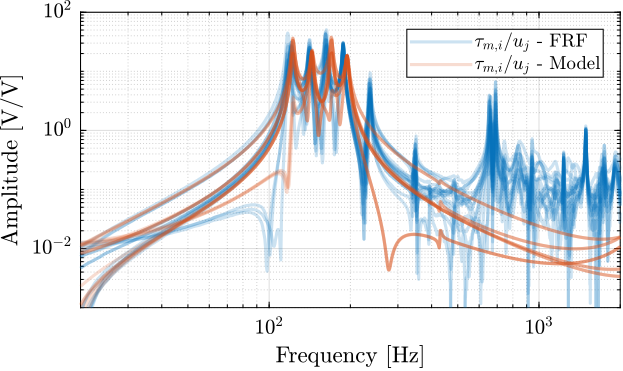
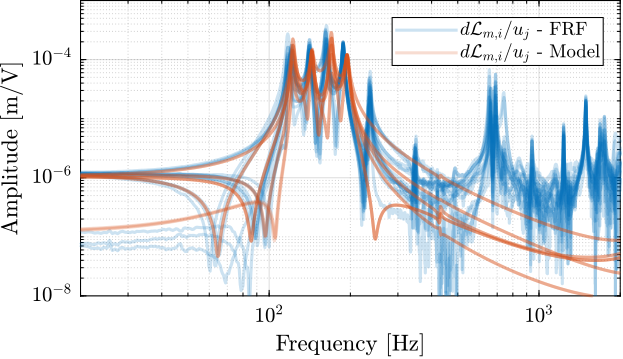
• Figure ref:fig:test_nhexa_enc_plates_iff_comp_simscape_all: the individual transfer function from $u_1$ (the DAC voltage for the first actuator) to the force sensors of all 6 struts are compared
• Figure ref:fig:test_nhexa_enc_plates_iff_comp_simscape: all the diagonal elements are compared
• Figure ref:fig:test_nhexa_enc_plates_iff_comp_offdiag_simscape: all the off-diagonal elements are compared

IFF Plant for the first actuator input and all the force senosrs

Diagonal elements of the IFF Plant

Off diagonal elements of the IFF Plant

Dynamics from Actuator to Encoder

The identified dynamics is compared with the measured FRF:

• Figure ref:fig:test_nhexa_enc_plates_dvf_comp_simscape_all: the individual transfer function from $u_3$ (the DAC voltage for the actuator number 3) to the six encoders
• Figure ref:fig:test_nhexa_enc_plates_dvf_comp_simscape: all the diagonal elements are compared
• Figure ref:fig:test_nhexa_enc_plates_dvf_comp_offdiag_simscape: all the off-diagonal elements are compared

DVF Plant for the first actuator input and all the encoders

Diagonal elements of the DVF Plant

Off diagonal elements of the DVF Plant

Conclusion

The Simscape model is quite accurate for the transfer function matrices from $\bm{u}$ to $\bm{\tau}_m$ and from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ except at frequencies of the flexible modes of the top-plate. The Simscape model can therefore be used to develop the control strategies.

Effect of Payload mass on the Dynamics

<<sec:test_nhexa_added_mass>>

Introduction   ignore

In this section, the encoders are fixed to the plates, and we identify the dynamics for several payloads. The added payload are half cylinders, and three layers can be added for a total of around 40kg (Figure ref:fig:test_nhexa_picture_added_3_masses).

First the dynamics from $\bm{u}$ to $d\mathcal{L}_m$ and $\bm{\tau}_m$ is identified. Then, the Integral Force Feedback controller is developed and applied as shown in Figure ref:fig:test_nhexa_nano_hexapod_signals_iff. Finally, the dynamics from $\bm{u}^\prime$ to $d\mathcal{L}_m$ is identified and the added damping can be estimated.

\definecolor{instrumentation}{rgb}{0, 0.447, 0.741}
\definecolor{mechanics}{rgb}{0.8500, 0.325, 0.098}
\definecolor{control}{rgb}{0.4660, 0.6740, 0.1880}

\begin{tikzpicture}
  % Blocs
  \node[block={4.0cm}{3.0cm}, fill=mechanics!20!white] (nano_hexapod) {Mechanics};
  \coordinate[] (inputF)  at (nano_hexapod.west);
  \coordinate[] (outputL) at ($(nano_hexapod.south east)!0.8!(nano_hexapod.north east)$);
  \coordinate[] (outputF) at ($(nano_hexapod.south east)!0.2!(nano_hexapod.north east)$);

  \node[block, left= 0.8 of inputF,  fill=instrumentation!20!white, align=center] (F_stack) {\tiny Actuator \\ \tiny stacks};
  \node[block, left= 0.8 of F_stack, fill=instrumentation!20!white] (PD200)   {PD200};
  \node[DAC,   left= 0.8 of PD200,   fill=instrumentation!20!white] (F_DAC)   {DAC};
  \node[block, right=0.8 of outputF, fill=instrumentation!20!white, align=center] (Fm_stack){\tiny Sensor \\ \tiny stack};
  \node[ADC,   right=0.8 of Fm_stack,fill=instrumentation!20!white] (Fm_ADC)  {ADC};
  \node[block, right=0.8 of outputL, fill=instrumentation!20!white] (encoder) {\tiny Encoder};
  \node[addb,  left= 0.8 of F_DAC,   fill=control!20!white]         (add_iff) {};
  \node[block, below=0.8 of add_iff, fill=control!20!white]         (Kiff) {\tiny $K_{\text{IFF}}(s)$};

  % Connections and labels
  \draw[->] (add_iff.east) node[above right]{$\bm{u}$} node[below right]{$[V]$} -- node[sloped]{$/$} (F_DAC.west);
  \draw[->] (F_DAC.east)   -- node[midway, above]{$\tilde{\bm{u}}$}node[midway, below]{$[V]$} (PD200.west);
  \draw[->] (PD200.east)   -- node[midway, above]{$\bm{u}_a$}node[midway, below]{$[V]$} (F_stack.west);
  \draw[->] (F_stack.east) -- (inputF) node[above left]{$\bm{\tau}$}node[below left]{$[N]$};

  \draw[->] (outputF)       -- (Fm_stack.west) node[above left]{$\bm{\epsilon}$} node[below left]{$[m]$};
  \draw[->] (Fm_stack.east) -- node[midway, above]{$\tilde{\bm{\tau}}_m$}node[midway, below]{$[V]$} (Fm_ADC.west);
  \draw[->] (Fm_ADC.east)   -- node[sloped]{$/$} ++(0.8, 0)coordinate(end) node[above left]{$\bm{\tau}_m$}node[below left]{$[V]$};

  \draw[->] (outputL)      -- (encoder.west) node[above left]{$d\bm{\mathcal{L}}$} node[below left]{$[m]$};
  \draw[->] (encoder.east) -- node[sloped]{$/$} (encoder-|end) node[above left]{$d\bm{\mathcal{L}}_m$}node[below left]{$[m]$};

  \draw[->] ($(Fm_ADC.east)+(0.14,0)$) node[branch]{} -- node[sloped]{$/$} ++(0, -1.8) -| (Kiff.south);
  \draw[->] (Kiff.north) -- node[sloped]{$/$} (add_iff.south);
  \draw[->] ($(add_iff.west)+(-0.8,0)$) node[above right]{$\bm{u}^\prime$} node[below right]{$[V]$} -- node[sloped]{$/$} (add_iff.west);

  % Nano-Hexapod
  \begin{scope}[on background layer]
    \node[fit={(F_stack.west|-nano_hexapod.south) (Fm_stack.east|-nano_hexapod.north)}, fill=black!20!white, draw, inner sep=2pt] (system) {};
    \node[above] at (system.north) {Nano-Hexapod};
  \end{scope}
\end{tikzpicture}

Block Diagram of the experimental setup and model

Measured Frequency Response Functions

The following data are loaded:

• Va: the excitation voltage (corresponding to $u_i$)
• Vs: the generated voltage by the 6 force sensors (corresponding to $\bm{\tau}_m$)
• de: the measured motion by the 6 encoders (corresponding to $d\bm{\mathcal{L}}_m$)

%% Load Identification Data
meas_added_mass = {};

for i_mass = i_masses
    for i_strut = 1:6
        meas_added_mass(i_strut, i_mass+1) = {load(sprintf('frf_data_exc_strut_%i_realigned_vib_table_%im.mat', i_strut, i_mass), 't', 'Va', 'Vs', 'de')};
    end
end

The window win and the frequency vector f are defined.

% Sampling Time [s]
Ts = (meas_added_mass{1,1}.t(end) - (meas_added_mass{1,1}.t(1)))/(length(meas_added_mass{1,1}.t)-1);

% Hannning Windows
win = hanning(ceil(1/Ts));

% And we get the frequency vector
[~, f] = tfestimate(meas_added_mass{1,1}.Va, meas_added_mass{1,1}.de, win, Noverlap, Nfft, 1/Ts);

Finally the $6 \times 6$ transfer function matrices from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ and from $\bm{u}$ to $\bm{\tau}_m$ are identified:

%% DVF Plant (transfer function from u to dLm)
G_dL = {};

for i_mass = i_masses
    G_dL(i_mass+1) = {zeros(length(f), 6, 6)};
    for i_strut = 1:6
        G_dL{i_mass+1}(:,:,i_strut) = tfestimate(meas_added_mass{i_strut, i_mass+1}.Va, meas_added_mass{i_strut, i_mass+1}.de, win, Noverlap, Nfft, 1/Ts);
    end
end

%% IFF Plant (transfer function from u to taum)
G_tau = {};

for i_mass = i_masses
    G_tau(i_mass+1) = {zeros(length(f), 6, 6)};
    for i_strut = 1:6
        G_tau{i_mass+1}(:,:,i_strut) = tfestimate(meas_added_mass{i_strut, i_mass+1}.Va, meas_added_mass{i_strut, i_mass+1}.Vs, win, Noverlap, Nfft, 1/Ts);
    end
end

The identified dynamics are then saved for further use.

save('data_frf/frf_vib_table_m.mat', 'f', 'Ts', 'G_tau', 'G_dL')

Rigidification of the added payloads

• figure

%% Load Identification Data
meas_added_mass = {};

for i_strut = 1:6
    meas_added_mass(i_strut) = {load(sprintf('frf_data_exc_strut_%i_spindle_1m_solid.mat', i_strut), 't', 'Va', 'Vs', 'de')};
end

The window win and the frequency vector f are defined.

% Sampling Time [s]
Ts = (meas_added_mass{1}.t(end) - (meas_added_mass{1}.t(1)))/(length(meas_added_mass{1}.t)-1);

% Hannning Windows
win = hanning(ceil(1/Ts));

% And we get the frequency vector
[~, f] = tfestimate(meas_added_mass{1}.Va, meas_added_mass{1}.de, win, Noverlap, Nfft, 1/Ts);

Finally the $6 \times 6$ transfer function matrices from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ and from $\bm{u}$ to $\bm{\tau}_m$ are identified:

%% DVF Plant (transfer function from u to dLm)

G_dL = zeros(length(f), 6, 6);
for i_strut = 1:6
    G_dL(:,:,i_strut) = tfestimate(meas_added_mass{i_strut}.Va, meas_added_mass{i_strut}.de, win, Noverlap, Nfft, 1/Ts);
end

%% IFF Plant (transfer function from u to taum)
G_tau = zeros(length(f), 6, 6);
for i_strut = 1:6
    G_tau(:,:,i_strut) = tfestimate(meas_added_mass{i_strut}.Va, meas_added_mass{i_strut}.Vs, win, Noverlap, Nfft, 1/Ts);
end

Transfer function from Actuators to Encoders

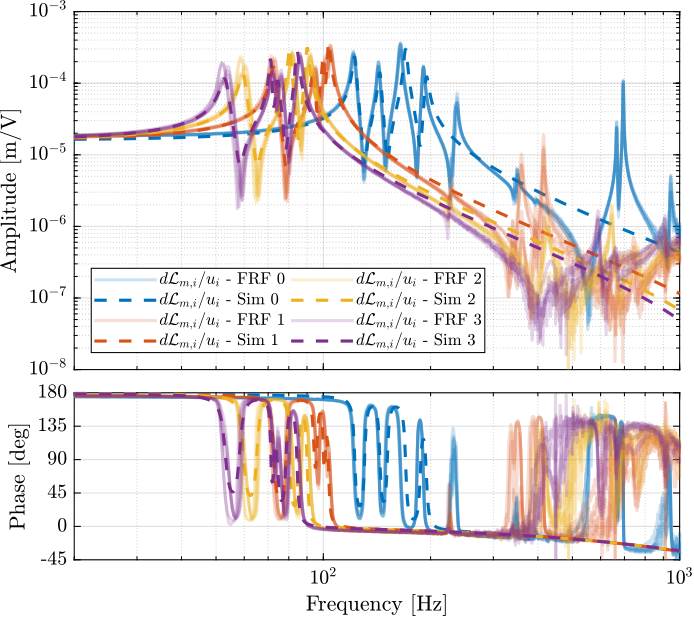
The transfer functions from $\bm{u}$ to $d\bm{\mathcal{L}}_{m}$ are shown in Figure ref:fig:test_nhexa_comp_plant_payloads_dvf.

Measured Frequency Response Functions from $u_i$ to $d\mathcal{L}_{m,i}$ for all 4 payload conditions. Diagonal terms are solid lines, and shaded lines are off-diagonal terms.

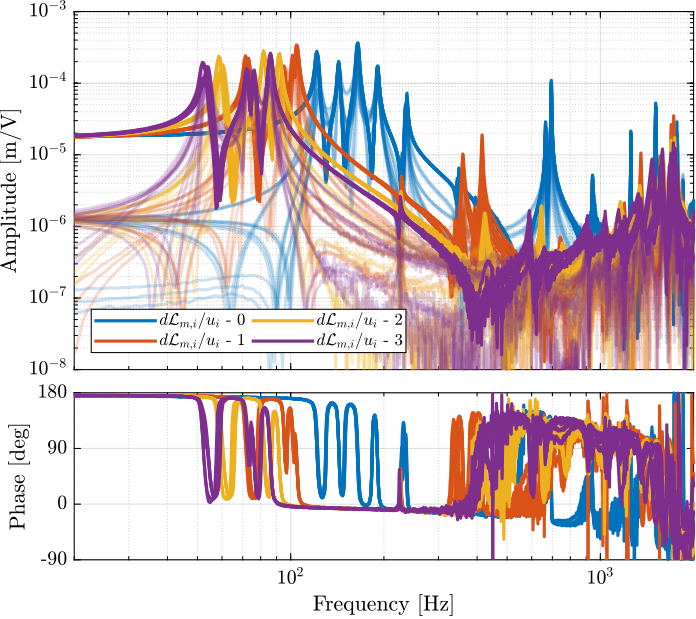
From Figure ref:fig:test_nhexa_comp_plant_payloads_dvf, we can observe few things:

• The obtained dynamics is changing a lot between the case without mass and when there is at least one added mass.
• Between 1, 2 and 3 added masses, the dynamics is not much different, and it would be easier to design a controller only for these cases.
• The flexible modes of the top plate is first decreased a lot when the first mass is added (from 700Hz to 400Hz). This is due to the fact that the added mass is composed of two half cylinders which are not fixed together. Therefore is adds a lot of mass to the top plate without adding a lot of rigidity in one direction. When more than 1 mass layer is added, the half cylinders are added with some angles such that rigidity are added in all directions (see Figure ref:fig:test_nhexa_picture_added_3_masses). In that case, the frequency of these flexible modes are increased. In practice, the payload should be one solid body, and we should not see a massive decrease of the frequency of this flexible mode.
• Flexible modes of the top plate are becoming less problematic as masses are added.
• First flexible mode of the strut at 230Hz is not much decreased when mass is added. However, its apparent amplitude is much decreased.

Transfer function from Actuators to Force Sensors

The transfer functions from $\bm{u}$ to $\bm{\tau}_{m}$ are shown in Figure ref:fig:test_nhexa_comp_plant_payloads_iff.

Measured Frequency Response Functions from $u_i$ to $\tau_{m,i}$ for all 4 payload conditions. Diagonal terms are solid lines, and shaded lines are off-diagonal terms.

From Figure ref:fig:test_nhexa_comp_plant_payloads_iff, we can see that for all added payloads, the transfer function from $\bm{u}$ to $\bm{\tau}_{m}$ always has alternating poles and zeros.

Coupling of the transfer function from Actuator to Encoders

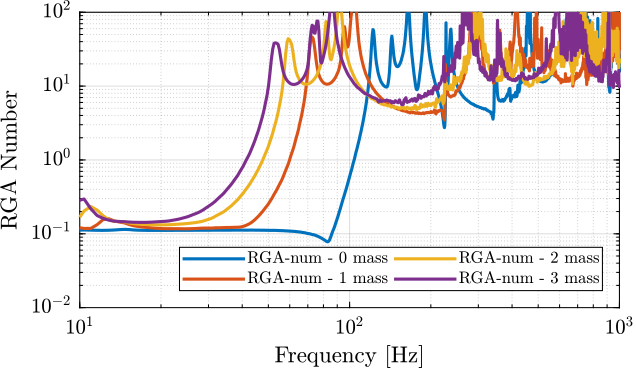
The RGA-number, which is a measure of the interaction in the system, is computed for the transfer function matrix from $\bm{u}$ to $d\bm{\mathcal{L}}_m$ for all the payloads. The obtained numbers are compared in Figure ref:fig:test_nhexa_rga_num_ol_masses.

RGA-number for the open-loop transfer function from $\bm{u}$ to $d\bm{\mathcal{L}}_m$

From Figure ref:fig:test_nhexa_rga_num_ol_masses, it is clear that the coupling is quite large starting from the first suspension mode of the nano-hexapod. Therefore, is the payload's mass is increase, the coupling in the system start to become unacceptably large at lower frequencies.

Comparison with the Simscape model

<<sec:test_nhexa_added_mass_simscape>>

Introduction   ignore

Let's now compare the identified dynamics with the Simscape model. We wish to verify if the Simscape model is still accurate for all the tested payloads.

System Identification

Let's initialize the simscape model with the nano-hexapod fixed on top of the vibration table.

%% Initialize Nano-Hexapod
n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ...
                                       'flex_top_type', '4dof', ...
                                       'motion_sensor_type', 'plates', ...
                                       'actuator_type', '2dof');

support.type = 1; % On top of vibration table

First perform the identification for the transfer functions from $\bm{u}$ to $d\bm{\mathcal{L}}_m$:

%% Identify the DVF Plant (transfer function from u to dLm)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput');  io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Encoders

%% Identification for all the added payloads
G_dL = {};

for i = i_masses
    fprintf('i = %i\n', i)
    payload.type = i; % Change the payload on the nano-hexapod
    G_dL(i+1) = {exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options)};
end

%% Identify the IFF Plant (transfer function from u to taum)
clear io; io_i = 1;
io(io_i) = linio([mdl, '/du'], 1, 'openinput');  io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors

%% Identification for all the added payloads
G_tau = {};

for i = 0:3
    fprintf('i = %i\n', i)
    payload.type = i; % Change the payload on the nano-hexapod
    G_tau(i+1) = {exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options)};
end

The identified dynamics are then saved for further use.

save('data_frf/sim_vib_table_m.mat', 'G_tau', 'G_dL')

Transfer function from Actuators to Encoders

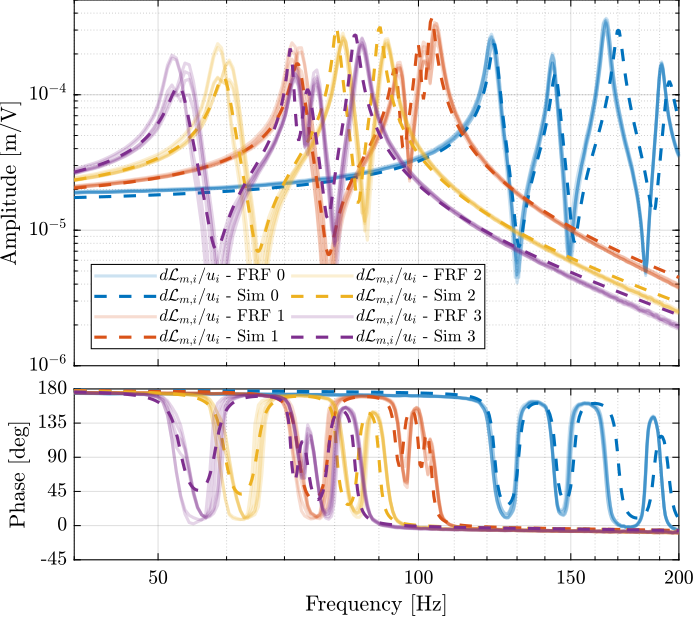
The measured FRF and the identified dynamics from $u_i$ to $d\mathcal{L}_{m,i}$ are compared in Figure ref:fig:test_nhexa_comp_masses_model_exp_dvf. A zoom near the "suspension" modes is shown in Figure ref:fig:test_nhexa_comp_masses_model_exp_dvf_zoom.

Comparison of the transfer functions from $u_i$ to $d\mathcal{L}_{m,i}$ - measured FRF and identification from the Simscape model

Comparison of the transfer functions from $u_i$ to $d\mathcal{L}_{m,i}$ - measured FRF and identification from the Simscape model (Zoom)

The Simscape model is very accurately representing the measured dynamics up. Only the flexible modes of the struts and of the top plate are not represented here as these elements are modelled as rigid bodies.

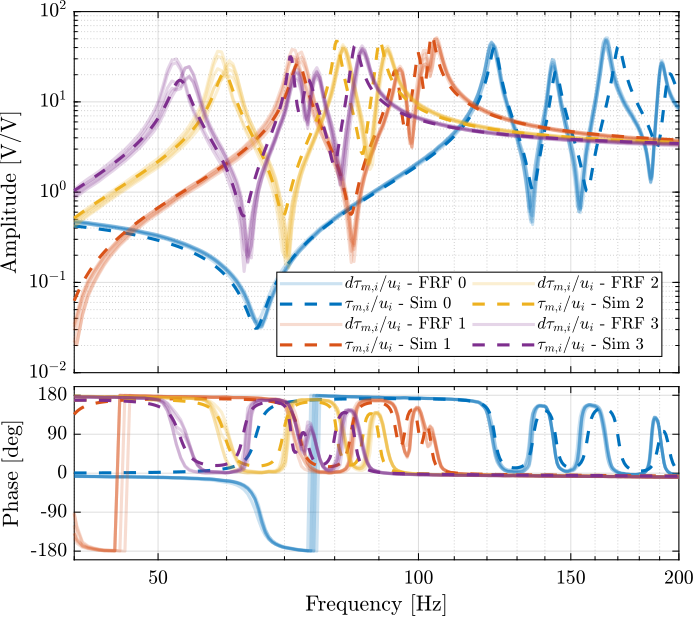
Transfer function from Actuators to Force Sensors

The measured FRF and the identified dynamics from $u_i$ to $\tau_{m,i}$ are compared in Figure ref:fig:test_nhexa_comp_masses_model_exp_iff. A zoom near the "suspension" modes is shown in Figure ref:fig:test_nhexa_comp_masses_model_exp_iff_zoom.

Comparison of the transfer functions from $u_i$ to $\tau_{m,i}$ - measured FRF and identification from the Simscape model

Comparison of the transfer functions from $u_i$ to $\tau_{m,i}$ - measured FRF and identification from the Simscape model (Zoom)

Conclusion

In this section, the dynamics of the nano-hexapod with the encoders fixed to the plates is studied.

It has been found that:

• The measured dynamics is in agreement with the dynamics of the simscape model, up to the flexible modes of the top plate. See figures ref:fig:test_nhexa_enc_plates_iff_comp_simscape and ref:fig:test_nhexa_enc_plates_iff_comp_offdiag_simscape for the transfer function to the force sensors and Figures ref:fig:test_nhexa_enc_plates_dvf_comp_simscape and ref:fig:test_nhexa_enc_plates_dvf_comp_offdiag_simscape for the transfer functions to the encoders
• The Integral Force Feedback strategy is very effective in damping the suspension modes of the nano-hexapod (Figure ref:fig:test_nhexa_enc_plant_plates_effect_iff).
• The transfer function from $\bm{u}^\prime$ to $d\bm{\mathcal{L}}_m$ show nice dynamical properties and is a much better candidate for the high-authority-control than when the encoders were fixed to the struts. At least up to the flexible modes of the top plate, the diagonal elements of the transfer function matrix have alternating poles and zeros, and the phase is moving smoothly. Only the flexible modes of the top plates seems to be problematic for control.

Bibliography   ignore

Glossary   ignore

printglossaries:

Footnotes