phd-test-bench-id31/test-bench-id31.org

Nano-Hexapod on the micro-station

• Introduction
• Short Stroke Metrology System
  • Introduction
  • Kinematics
  • Rough alignment of spheres using comparators
  • Alignment of spheres using interferometers
    • Angular alignment
    • Eccentricity alignment
  • Residual error after alignment
  • Metrology acceptance
• Simscape Model
  • Introduction
  • Init model
  • Identify Transfer functions
  • IFF Plant
  • Encoder plant
  • HAC Undamped plant
• Identified Open Loop Plant
  • Introduction
  • IFF Plant
  • Encoder plant
  • HAC Undamped plant
  • Decoupling improvement thanks to better Rz alignment
    • Alignment procedure
    • m0
    • m3
  • Conclusion
• Noise Budget
  • Introduction
  • Open-Loop Noise Budget
  • Effect of LAC
  • Effect of rotation
  • Effect of HAC
  • Noise coming from force sensor
• Integral Force Feedback
  • Introduction
  • IFF Plants
    • Introduction
    • 6x6 Plant
    • Effect of Rotation
    • Effect of Mass
    • Compare with the model
  • IFF Controller
    • Controller Design
    • Verify Stability
    • Save Controller
  • Estimated Damped Plant
• High Authority Control
  • Introduction
  • Identify Spurious modes
  • HAC Plants
    • Introduction
    • 6x6 Plant
    • Effect of Mass
    • Compare with the model
    • Comparison with Undamped plant
  • Robust HAC
    • Controller design
    • Verify Stability
    • Estimated performances
    • Save Controller
  • High Performance HAC
    • Introduction
    • Mass 0
      • Load Plant
      • Plant
      • Controller design
      • Verify Stability
      • Estimated performances
      • Save Controller
      • Experimental Validation
      • Closed-Loop identification
    • Mass 1
      • Load Plant
      • Plant
      • Plant Inverse
      • Controller design
      • Verify Stability
      • Estimated performances
      • Save Controller
  • Tomography - Performances
    • First scan with closed-loop at middle
    • Slow Rotation - 6RPM
    • Rapid Rotation - 30RPM
• 6DoF Control in Cartesian plane (rotating with the nano-hexapod)
  • Introduction
  • 5x5 plant in Cartesian plane
  • Controller Design
  • Check Stability
  • Save controllers
  • Performances
• 3DoF Control in Cartesian plane (fixed)
  • Introduction
  • 3x3 plant in Cartesian plane
  • Controller Design
    • Dy
    • Dz
    • Ry
    • 3x3 controller
  • Check Stability
  • Save controllers
    • Save Controller
  • Controller Design (normalized)
  • Verify Stability
  • Control Performances
• Complementary Filter Control
  • m0
    • 3x3 plant in Cartesian plane
    • Plant Invert
    • Save Plant Inverse
    • Control Performances
      • 5Hz
      • 20Hz
      • Different bandwidth for different directions
      • Dz 25Hz
    • Better plant invert
      • Dy
      • Dz
      • Ry
      • Compare Invert plants
      • Save plant inverse
      • Compare Digital Invert plants
    • Control Performances
      • Better plant invert
    • Scans with good controller
      • 1rpm
      • 30rpm
  • m1
    • 3x3 plant in Cartesian plane
    • Better plant invert
      • Dy
      • Dz
      • Ry
      • Compare Invert plants
      • Save plant inverse
      • Compare Digital Invert plants
    • Control Performances
      • Better plant invert
    • Scans with good controller
      • 1rpm
      • 30rpm
  • m2
    • 3x3 plant in Cartesian plane
    • Better plant invert
      • Dy
      • Dz
      • Ry
      • Compare Invert plants
      • Save plant inverse
      • Compare Digital Invert plants
    • Control Performances
      • Better plant invert
    • Scans with good controller
      • 1rpm
      • 30rpm
  • m3
    • 3x3 plant in Cartesian plane
    • Better plant invert
      • Dy
      • Dz
      • Ry
      • Compare Invert plants
      • Save plant inverse
      • Compare Digital Invert plants
    • Control Performances
      • Better plant invert
    • Scans with good controller
      • 1rpm
      • 30rpm
• Scans
  • Introduction
  • $R_z$ scans: Tomography
    • Introduction
    • Robust Control - 1rpm
    • Robust Control - 6rpm
    • Robust Control - 30rpm
  • $D_z$ scans: Dirty Layer Scans
    • Step by Step $D_z$ motion
    • Continuous $D_z$ motion: Dirty Layer Scans
  • $R_y$ scans: Reflectivity
  • $D_y$ Scans
    • Introduction
    • Open Loop
    • Closed Loop
    • Faster Scan
  • Combined $R_z$ and $D_y$: Diffraction Tomography
  • Summary of experiments
• Bibliography

---

This report is also available as a pdf.

---

Introduction   ignore

Short Stroke Metrology System

<<sec:id31_short_stroke_metrology>>

Introduction   ignore

The control of the nano-hexapod requires an external metrology system measuring the relative position of the nano-hexapod top platform with respect to the granite. As the long-stroke ($\approx 1\,cm^3$) metrology system is not developed yet, a stroke stroke ($> 100\,\mu m^3$) can be used instead to validate the nano-hexapod control.

This short stroke metrology system consists of 5 interferometers pointing at 2 spheres fixed on top of the nano-hexapod (Figure ref:fig:LION_picture_close).

This short stroke metrology system is fixed to the main granite using a gantry made of granite blocs to have good vibration and thermal stability (see Figure ref:fig:short_stroke_metrology_overview).

As the metrology system as limited stroke (estimated to be in the order of hundreds of micro-meters in x-y-z), it has to be well aligned in the rest position.

The alignment procedure is as follows:

1. The granite is aligned to be perpendicular to gravity (using inclinometer and adjusting airlocks)
2. The height of micro-hexapod is tuned to be able to position the short stroke metrology without additional shim
3. It is verified that the spindle axis is well perpendicular to the granite using the laser tracker
4. The micro hexapod is then used to align the two spheres with the spindle axis.

Kinematics

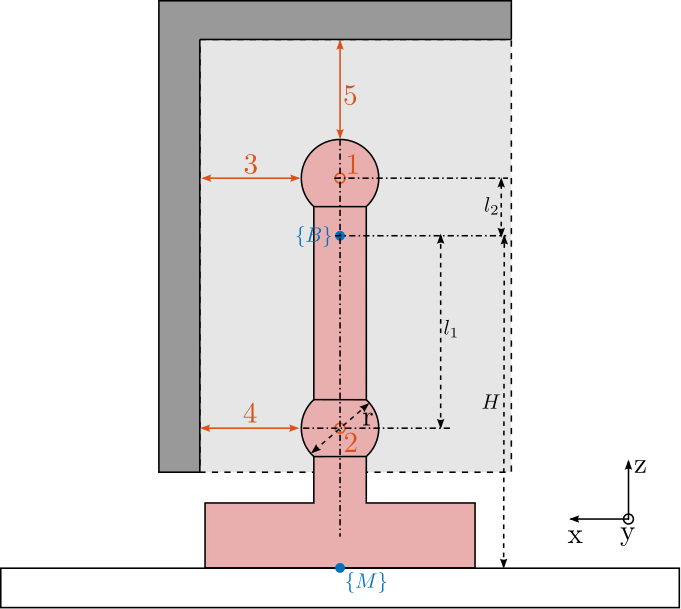
We have the following set of equations:

\begin{align} d_1 &= +D_y - l_2 R_x \\ d_2 &= +D_y + l_1 R_x \\ d_3 &= -D_x - l_2 R_y \\ d_4 &= -D_x + l_1 R_y \\ d_5 &= -D_z \end{align}

That can be written as a linear transformation:

\begin{equation} \begin{bmatrix} d_1 \\ d_2 \\ d_3 \\ d_4 \\ d_5 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & -l_2 & 0 \\ 0 & 1 & 0 & l_1 & 0 \\ -1 & 0 & 0 & 0 & -l_2 \\ -1 & 0 & 0 & 0 & l_1 \\ 0 & 0 & -1 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} D_x \\ D_y \\ D_z \\ R_x \\ R_y \end{bmatrix} \end{equation}

By inverting the matrix, we obtain the Jacobian relation:

\begin{equation} \begin{bmatrix} D_x \\ D_y \\ D_z \\ R_x \\ R_y \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & -l_2 & 0 \\ 0 & 1 & 0 & l_1 & 0 \\ -1 & 0 & 0 & 0 & -l_2 \\ -1 & 0 & 0 & 0 & l_1 \\ 0 & 0 & -1 & 0 & 0 \end{bmatrix}^{-1} \cdot \begin{bmatrix} d_1 \\ d_2 \\ d_3 \\ d_4 \\ d_5 \end{bmatrix} \end{equation}

%% Parameters
H = 150e-3;
l1 = (150-48-42)*1e-3;
l2 = (76.2+48+42-150)*1e-3;

%% Transformation matrix
Hm = [ 0  1  0 -l2  0;
       0  1  0  l1  0;
      -1  0  0  0  -l2;
      -1  0  0  0   l1;
       0  0 -1  0   0];

	d1	d2	d3	d4	d5
Dx	0.0	0.0	-0.79	-0.21	0.0
Dy	0.79	0.21	0.0	0.0	0.0
Dz	0.0	0.0	0.0	0.0	-1.0
Rx	-13.12	13.12	-0.0	0.0	0.0
Ry	-0.0	-0.0	-13.12	13.12	0.0

Rough alignment of spheres using comparators

Bottom Sphere, then top sphere.

Alignment better than 10um. But the coaxiality between the cylinder and the sphere might not be good.

Two mechanical comparators used to align the top sphere with the rotation axis of the spindle

Alignment of spheres using interferometers

Angular alignment

%% Load Data
data_it0 = h5scan(data_dir, 'alignment', 'h1rx_h1ry', 1);
data_it1 = h5scan(data_dir, 'alignment', 'h1rx_h1ry_0002', 3);
data_it2 = h5scan(data_dir, 'alignment', 'h1rx_h1ry_0002', 5);

%% Offset wrong points
i_it0 = find(abs(data_it0.Rx_int_filtered(2:end)-data_it0.Rx_int_filtered(1:end-1))>1e-5);
data_it0.Rx_int_filtered(i_it0+1:end) = data_it0.Rx_int_filtered(i_it0+1:end) + data_it0.Rx_int_filtered(i_it0) - data_it0.Rx_int_filtered(i_it0+1);
i_it1 = find(abs(data_it1.Rx_int_filtered(2:end)-data_it1.Rx_int_filtered(1:end-1))>1e-5);
data_it1.Rx_int_filtered(i_it1+1:end) = data_it1.Rx_int_filtered(i_it1+1:end) + data_it1.Rx_int_filtered(i_it1) - data_it1.Rx_int_filtered(i_it1+1);
i_it2 = find(abs(data_it2.Rx_int_filtered(2:end)-data_it2.Rx_int_filtered(1:end-1))>1e-5);
data_it2.Rx_int_filtered(i_it2+1:end) = data_it2.Rx_int_filtered(i_it2+1:end) + data_it2.Rx_int_filtered(i_it2) - data_it2.Rx_int_filtered(i_it2+1);

%% Compute circle fit and get radius
[~, ~, R_it0, ~] = circlefit(1e6*data_it0.Rx_int_filtered, 1e6*data_it0.Ry_int_filtered);
[~, ~, R_it1, ~] = circlefit(1e6*data_it1.Rx_int_filtered, 1e6*data_it1.Ry_int_filtered);
[~, ~, R_it2, ~] = circlefit(1e6*data_it2.Rx_int_filtered, 1e6*data_it2.Ry_int_filtered);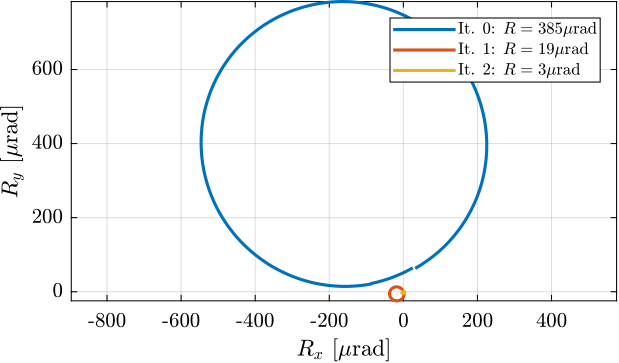

Rx/Ry alignment of the spheres using the micro-station

Eccentricity alignment

%% Load Data
data_it0 = h5scan(data_dir, 'alignment', 'h1rx_h1ry_0002', 5);
data_it1 = h5scan(data_dir, 'alignment', 'h1dx_h1dy', 1);

%% Offset wrong points
i_it0 = find(abs(data_it0.Dy_int_filtered(2:end)-data_it0.Dy_int_filtered(1:end-1))>1e-5);
data_it0.Dy_int_filtered(i_it0+1:end) = data_it0.Dy_int_filtered(i_it0+1:end) + data_it0.Dy_int_filtered(i_it0) - data_it0.Dy_int_filtered(i_it0+1);

%% Compute circle fit and get radius
[~, ~, R_it0, ~] = circlefit(1e6*data_it0.Dx_int_filtered, 1e6*data_it0.Dy_int_filtered);
[~, ~, R_it1, ~] = circlefit(1e6*data_it1.Dx_int_filtered, 1e6*data_it1.Dy_int_filtered);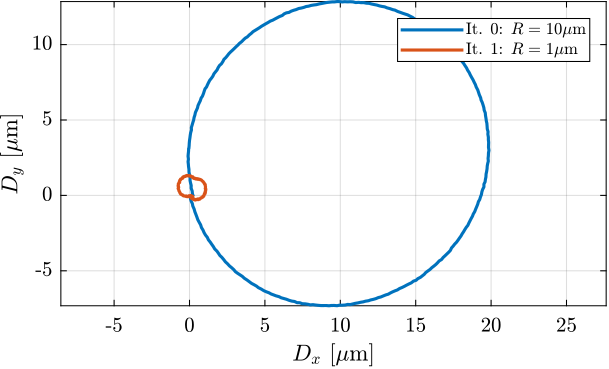

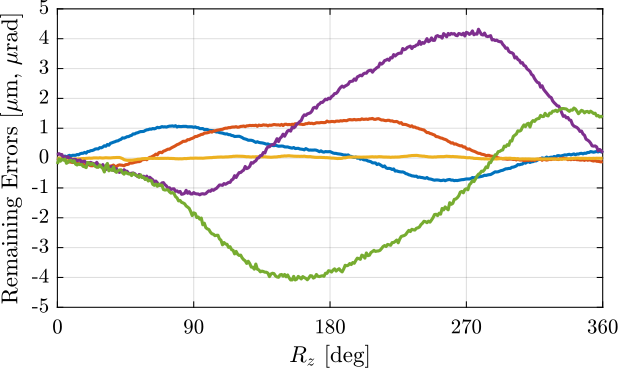
Dx/Dy alignment of the spheres using the micro-station

Residual error after alignment

%% Load Data
data = h5scan(data_dir, 'alignment', 'h1dx_h1dy', 1);

• Dx and Dy are less than 1um.
• Dz less than 0.1um.
• Rx and Ry less than 4urad.

Remaining errors after aligning the metrology using the interferometers

Metrology acceptance

Because the interferometers are pointing to spheres and not flat surfaces, the lateral acceptance is limited.

data = h5scan(data_dir, 'metrology_acceptance', 'after_int_align_meshXY', 1);

x = 1e3*detrend(data.h1tx, 0); % [um]
y = 1e3*detrend(data.h1ty, 0); % [um]
z = 1e6*data.Dz_int_filtered - max(data.Dz_int_filtered); % [um]

mdl = scatteredInterpolant(x, y, z);
[xg, yg] = meshgrid(unique(x), unique(y));
zg = mdl(xg, yg);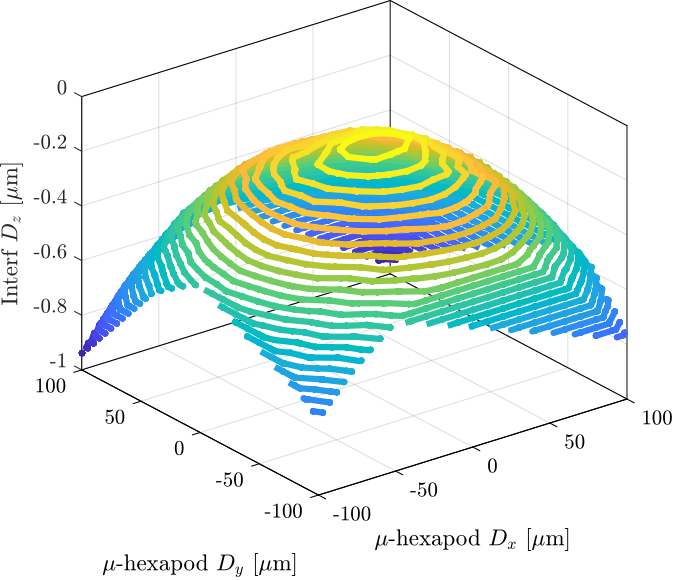

XY mapping of the Z measurement by the interferometer

Simscape Model

<<sec:id31_simscape_model>>

Introduction   ignore

Init model

%% Add directories to path for Simscape Model
addpath('mat')
addpath('matlab/subsystems')
addpath('STEPS/nano_hexapod')
addpath('STEPS/metrology')
addpath('STEPS/png')

%% Options for Linearized
options = linearizeOptions;
options.SampleTime = 0;

%% Name of the Simulink File
mdl = 'nass_model_id31';

open(mdl)

load('mat/conf_simulink.mat');

%% Initialize each Simscape model elements
initializeGround();
initializeGranite();
initializeTy();
initializeRy();
initializeRz();
initializeMicroHexapod();

initializeSimscapeConfiguration();
initializeDisturbances('enable', false);
initializeLoggingConfiguration('log', 'none');

initializeController('type', 'open-loop');

initializeNanoHexapod('flex_bot_type', '2dof', ...
                      'flex_top_type', '3dof', ...
                      'motion_sensor_type', 'plates', ...
                      'actuator_type', '2dof');

initializeSample('type', '0');

initializePosError();

initializeReferences();

initializeRzEstimate('type', 'encoders');

initializeLion();

Identify Transfer functions

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Controller'],     1, 'openinput');               io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/Micro-Station'],  3, 'openoutput', [], 'Fnlm');  io_i = io_i + 1; % Force Sensors
io(io_i) = linio([mdl, '/Micro-Station'],  3, 'openoutput', [], 'Dnlm');  io_i = io_i + 1; % Encoders
io(io_i) = linio([mdl, '/Tracking Error'], 1, 'openoutput', [], 'EdL');   io_i = io_i + 1; % Position Errors
io(io_i) = linio([mdl, '/Micro-Station/metrology_5dof/Lion_Metrology'], 1, 'output');   io_i = io_i + 1; % Interferometers

IFF Plant

IFF transfer function - Simscape model

Encoder plant

ENC transfer function - Simscape model

HAC Undamped plant

INT transfer function - Simscape model

Identified Open Loop Plant

<<sec:id31_open_loop_plant>>

Introduction   ignore

IFF Plant

Measured transfer function from generated voltages to measured voltage on the force sensors

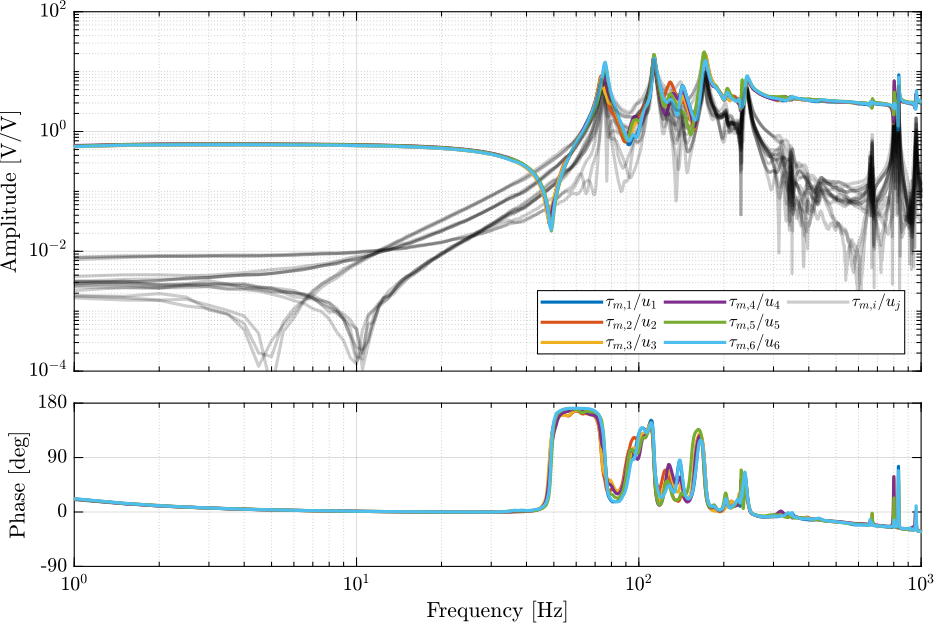
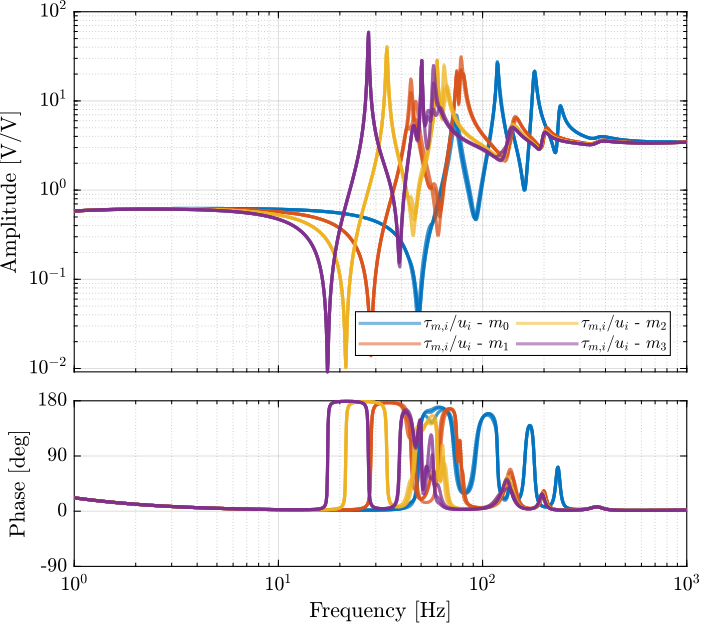
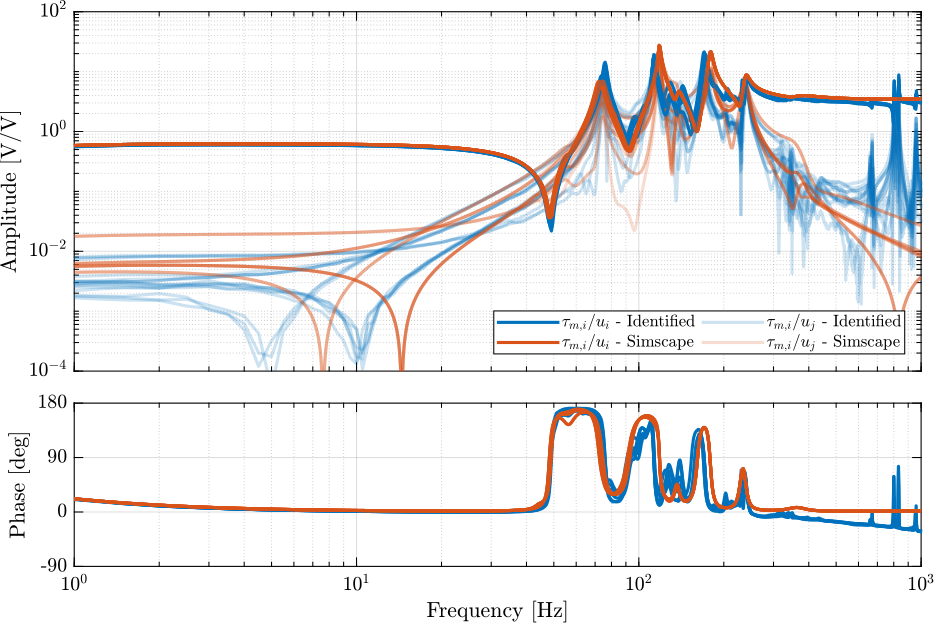
The measured frequency response functions from DAC voltages $u_i$ to measured voltages on the force sensors $\tau_{m,i}$ are compared with the simscape model in Figure ref:fig:id31_comp_simscape_frf_ol_iff.

Comparison of the Simscape model and identified IFF plant

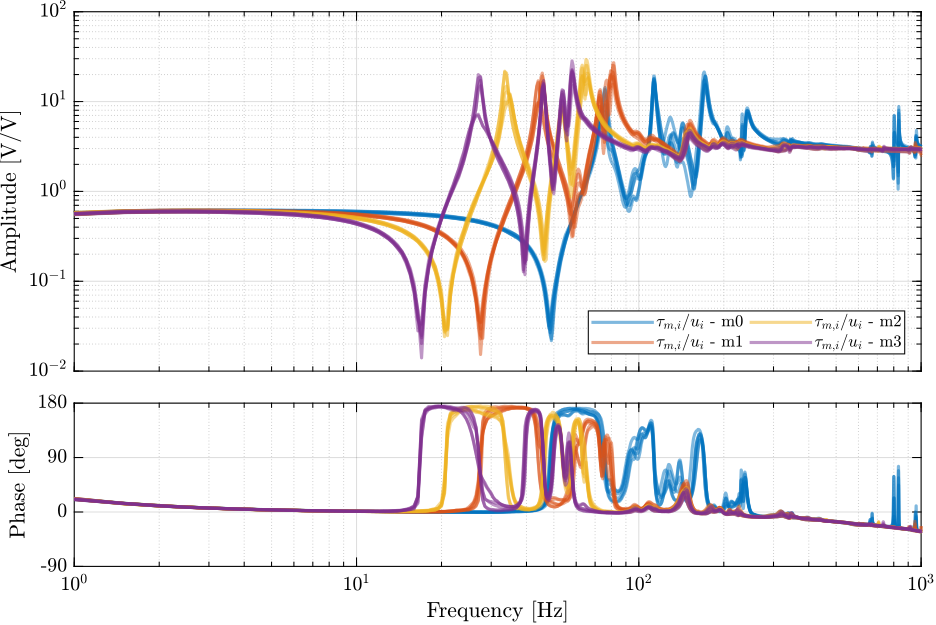
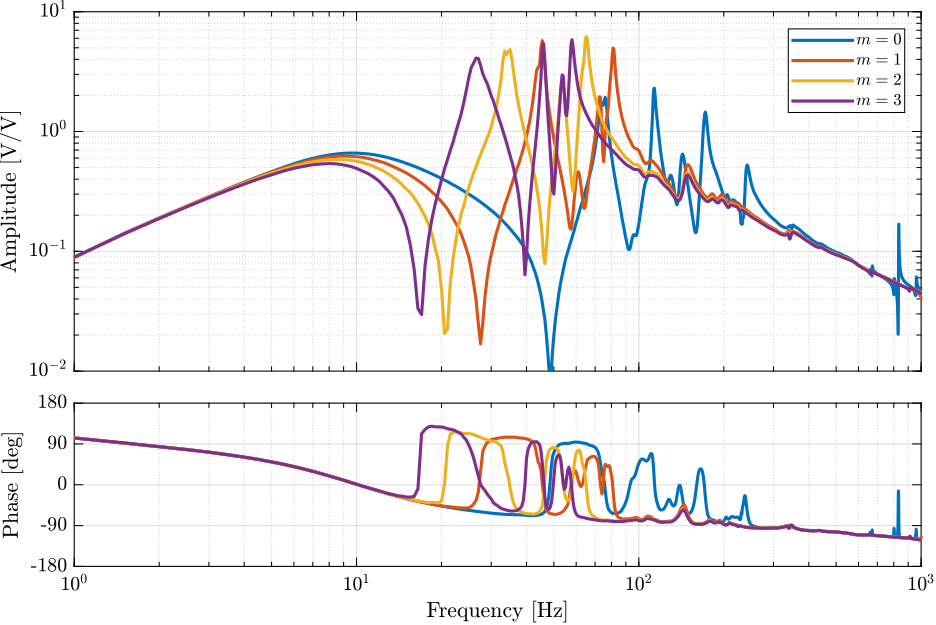
The effect of the payload mass on the diagonal elements are shown in Figure ref:fig:id31_effect_mass_frf_ol_iff.

Effect of the payload mass on the IFF plant

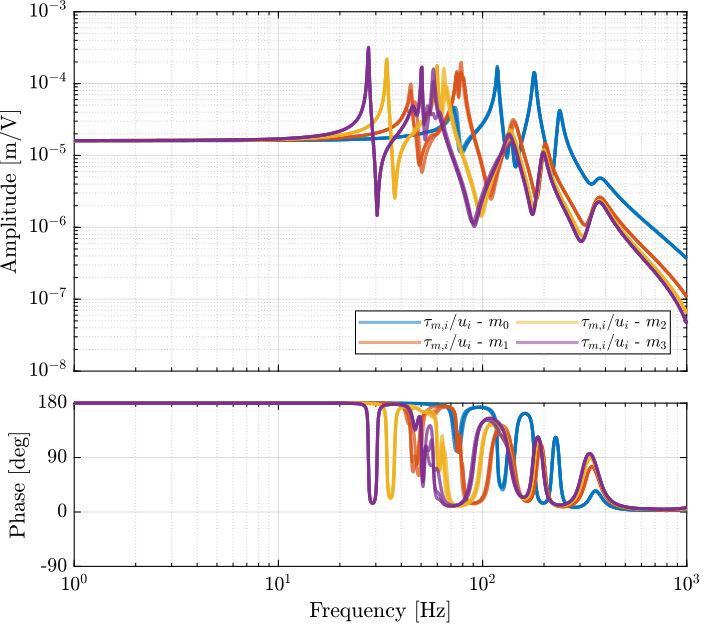
Encoder plant

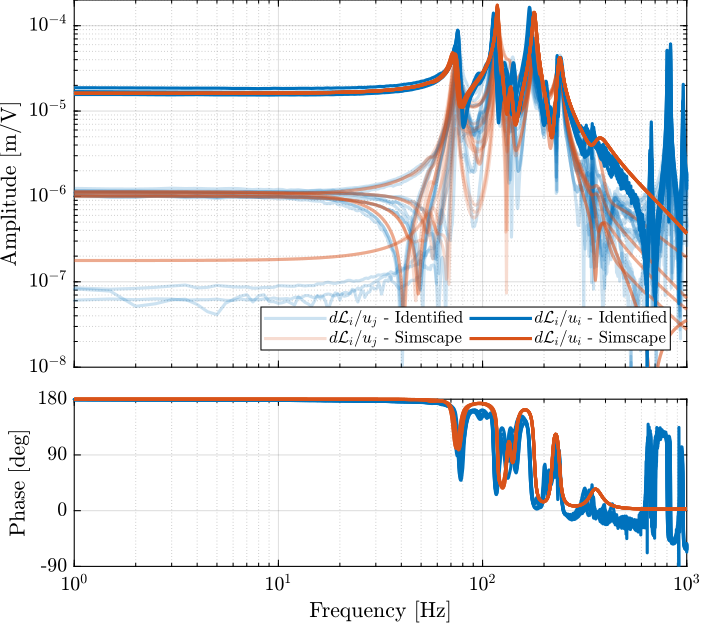
The identified frequency response functions from general voltages $u_i$ to measured displacement of the struts by the encoders $d\mathcal{L}_i$ are compared with the simscape model in Figure ref:fig:id31_comp_simscape_frf_ol_enc.

Comparison of the Simscape model and identified plant - Transfer functions from voltages to encoders

Effect of the payload mass on the transfer function from actuator voltage to encoder displacement

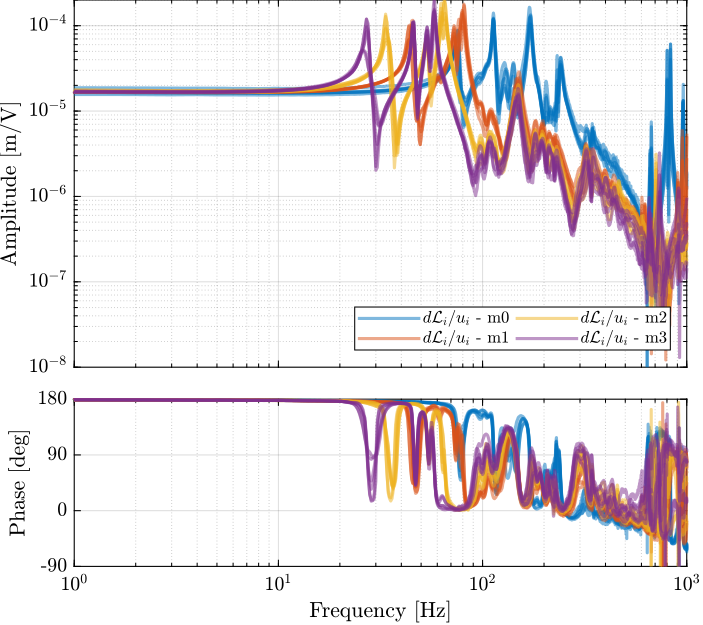
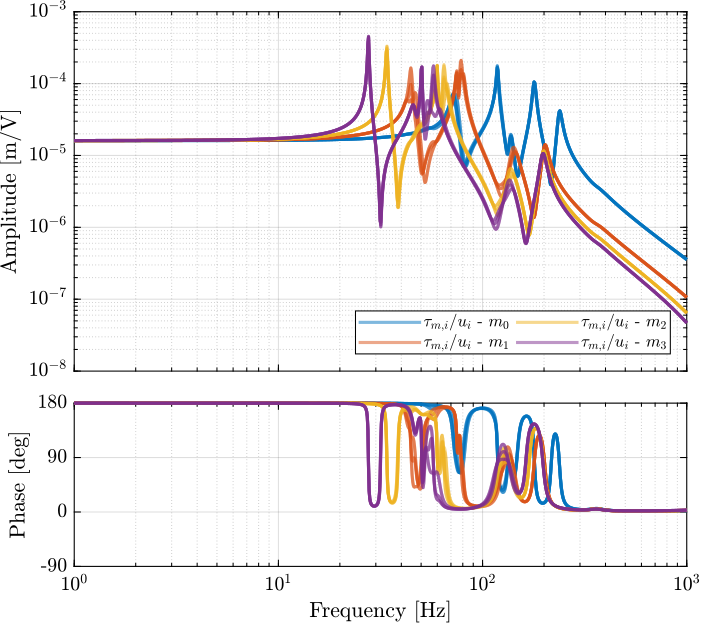
HAC Undamped plant

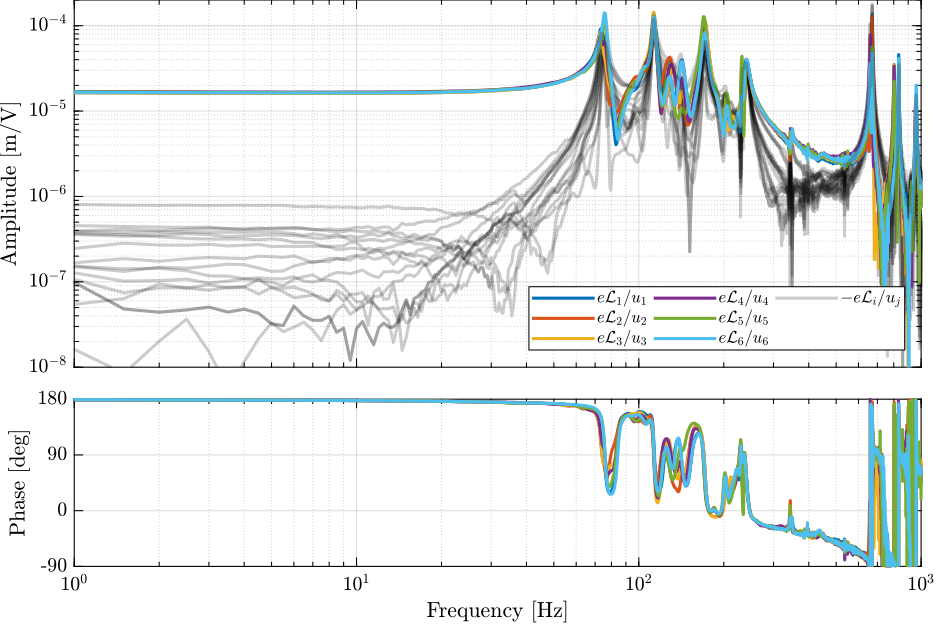
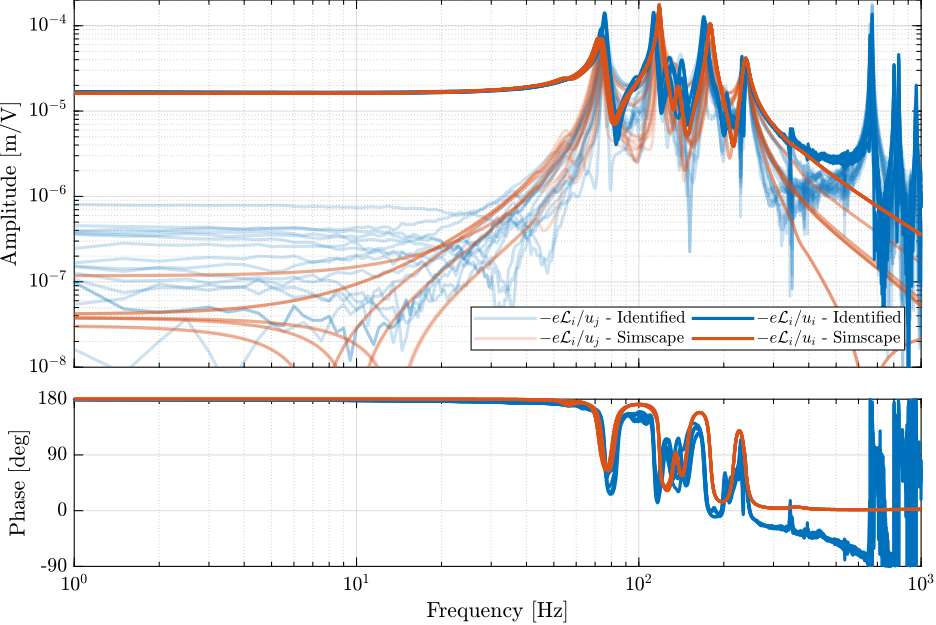
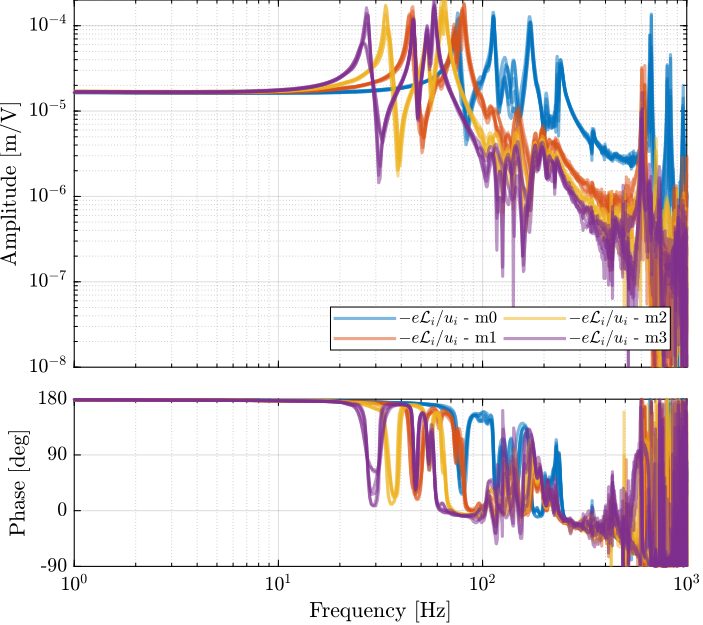
The identified frequency response functions from actuator voltages $u_i$ to measured strut motion from the external metrology (i.e. the interferometers) are compare with the simscape model in Figure ref:fig:id31_comp_simscape_frf_ol_int.

Measured transfer function from generated voltages to measured voltage on the force sensors

Comparison of the Simscape model and identified plant - Transfer functions from voltages to estimated strut motion from interferometers

Effect of the payload mass on the transfer functions from actuator voltage to measured strut motion by the external metrology

Decoupling improvement thanks to better Rz alignment

Alignment procedure

• Control based on encoders
• Slow moving in X and Y
• Compare with X and Y from interf

%% Load Data
data_1_dx = h5scan(data_dir, 'align_int_enc_Rz', 'tx_first_scan', 2);
data_1_dy = h5scan(data_dir, 'align_int_enc_Rz', 'tx_first_scan', 3);
data_2_dx = h5scan(data_dir, 'align_int_enc_Rz', 'verif-after-correct-offset', 1);
data_2_dy = h5scan(data_dir, 'align_int_enc_Rz', 'verif-after-correct-offset', 2);

figure;
hold on;
plot(1e6*data_1_dx.Dx_int_filtered, 1e6*data_1_dx.Dy_int_filtered, 'color', colors(1,:), 'DisplayName', 'Measurement')
plot(1e6*data_1_dy.Dx_int_filtered, 1e6*data_1_dy.Dy_int_filtered, 'color', colors(1,:), 'HandleVisibility', 'off')
plot(1e6*[-10:10]*cos(2.7*pi/180), -1e6*[-10:10]*sin(2.7*pi/180), '--', 'color', colors(2,:), 'DisplayName', '$R_z = 2.7$ deg')
plot(1e6*[-10:10]*sin(2.7*pi/180), 1e6*[-10:10]*cos(2.7*pi/180), '--', 'color', colors(2,:), 'HandleVisibility', 'off')
hold off;
xlabel('Interf $D_x$ [$\mu$m]');
ylabel('Interf $D_y$ [$\mu$m]');
legend('location', 'northeast', 'FontSize', 8, 'NumColumns', 1);
axis equal
xlim([-10, 10]); ylim([-10, 10]);
xticks([-10:5:10]); yticks([-10:5:10]);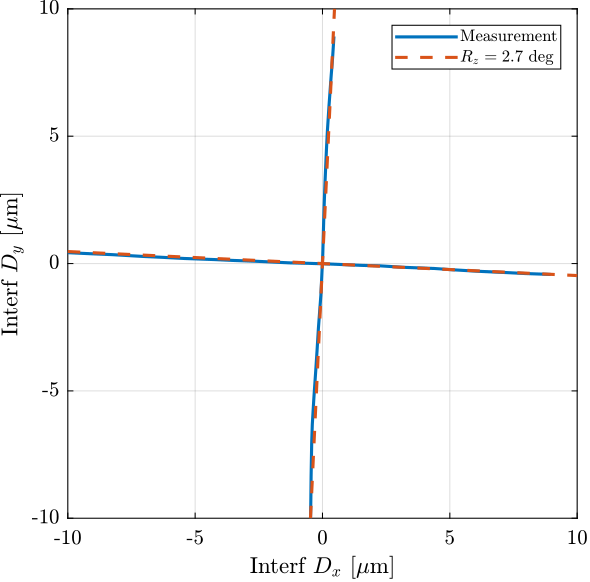

description

figure;
hold on;
plot(1e6*data_1_dx.Dx_int_filtered, 1e6*data_1_dx.Dy_int_filtered, 'color', colors(1,:), 'DisplayName', 'Initial')
plot(1e6*data_1_dy.Dx_int_filtered, 1e6*data_1_dy.Dy_int_filtered, 'color', colors(1,:), 'HandleVisibility', 'off')
plot(1e6*data_2_dx.Dx_int_filtered, 1e6*data_2_dx.Dy_int_filtered, 'color', colors(2,:), 'DisplayName', 'After $R_z$ calib')
plot(1e6*data_2_dy.Dx_int_filtered, 1e6*data_2_dy.Dy_int_filtered, 'color', colors(2,:), 'HandleVisibility', 'off')
hold off;
xlabel('Interf $D_x$ [$\mu$m]');
ylabel('Interf $D_y$ [$\mu$m]');
legend('location', 'northeast', 'FontSize', 8, 'NumColumns', 1);
axis equal
xlim([-10, 10]); ylim([-10, 10]);
xticks([-10:5:10]); yticks([-10:5:10]);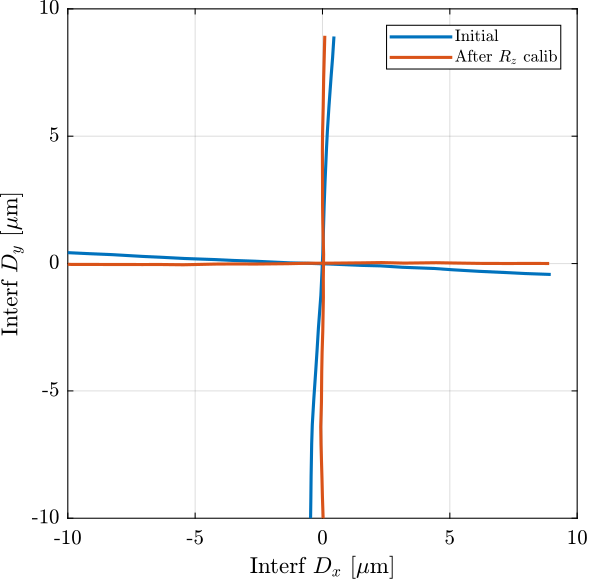

description

m0

data = load(sprintf('%s/dynamics/2023-08-08_16-17_ol_plant_m0_Wz0.mat', mat_dir));
data_align = load(sprintf('%s/dynamics/2023-08-17_17-37_ol_plant_m0_Wz0_new_Rz_align.mat', mat_dir));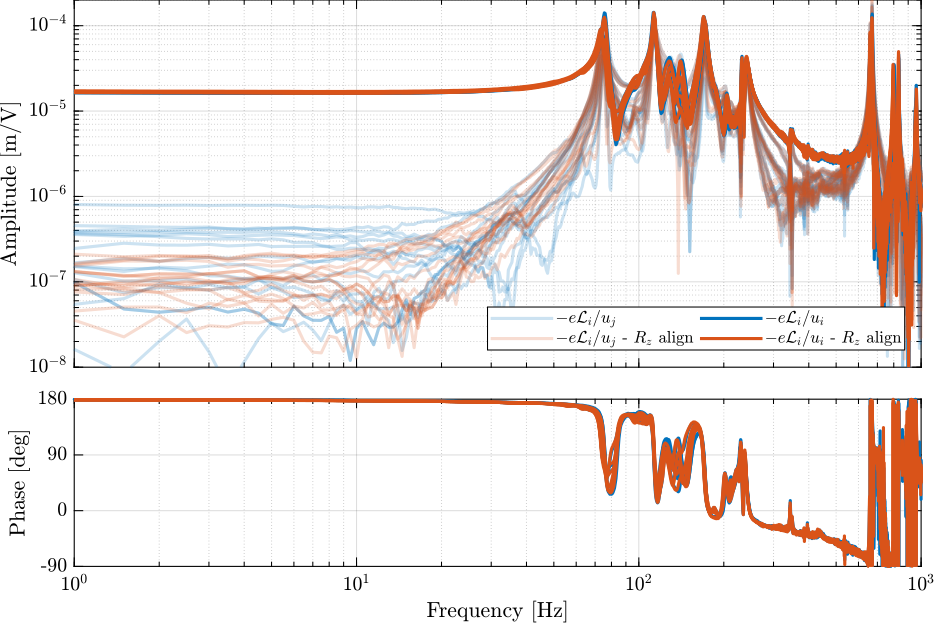

Decrease of the coupling with better Rz alignment

m3

data = load(sprintf('%s/dynamics/2023-08-10_18-16_damp_plant_m3_Wz0.mat', mat_dir));
data_align = load(sprintf('%s/dynamics/2023-08-21_15-52_damp_plant_m3_new_Rz.mat', mat_dir));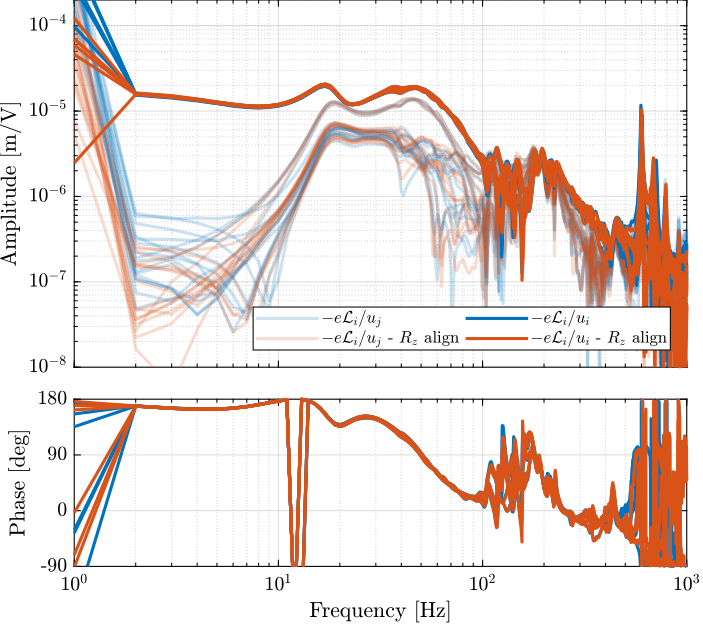

Decrease of the coupling with better Rz alignment

Conclusion

• Good match between the model and experiment

TODO Noise Budget

<<sec:id31_noise_budget>>

Introduction   ignore

In this section, the noise budget is performed. The vibrations of the sample is measured in different conditions using the external metrology.

Open-Loop Noise Budget

First, the noise is measured while no motion is performed.

%% Load measured noise
data_m0 = load(sprintf('%s/freq_analysis/2023-08-11_16-51_m0_lac_off.mat', mat_dir));

Noise budget in the cartesian frame

Data in the time domain

Measured vibration with the interferometers

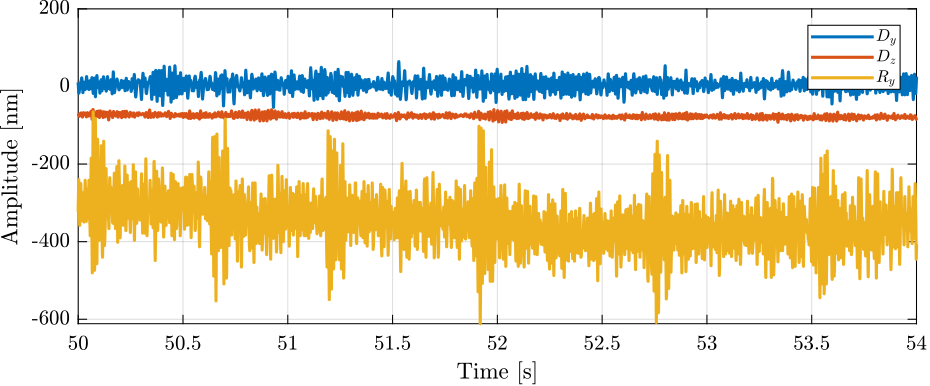
In the frequency domain

Measured vibration with the interferometers

Measured vibration with the interferometers

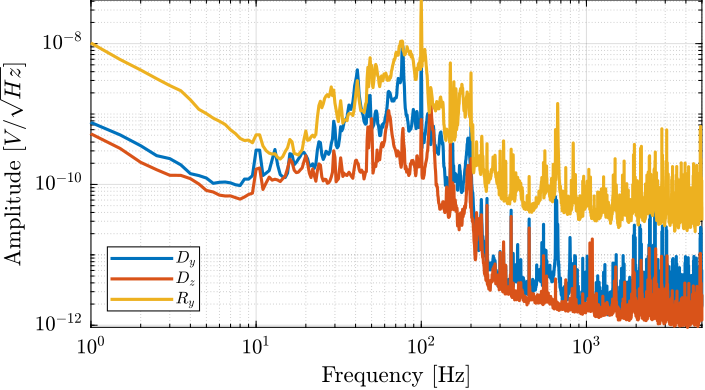
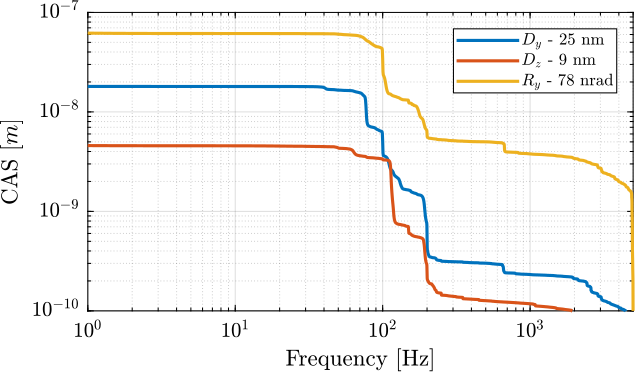
Effect of LAC

%% Load measured noise
data_ol = load(sprintf('%s/freq_analysis/2023-08-11_16-51_m0_lac_off.mat', mat_dir));
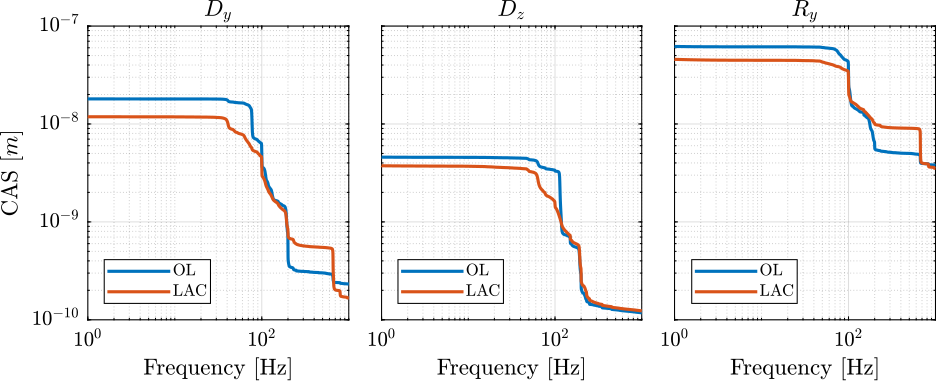
data_lac = load(sprintf('%s/freq_analysis/2023-08-11_16-46_m0_lac_on.mat', mat_dir));

Effect of LAC (Figure ref:fig:id31_noise_budget_effect_lac_m0):

• reduce amplitude around 80Hz
• Inject some noise between 200 and 700Hz?

Measured vibration with the interferometers

Measured vibration with the interferometers

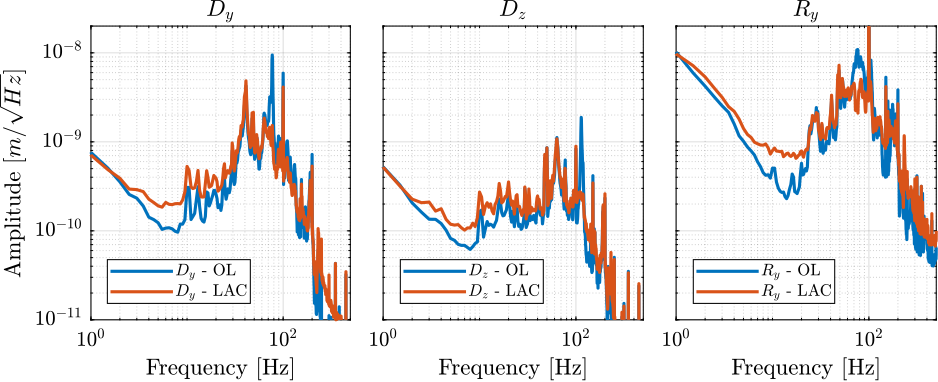
Effect of rotation

data_Wz0 = load(sprintf('%s/freq_analysis/2023-08-11_16-51_m0_lac_off.mat',       mat_dir));
data_Wz1 = load(sprintf('%s/freq_analysis/2023-08-11_17-18_m0_lac_off_1rpm.mat',  mat_dir));
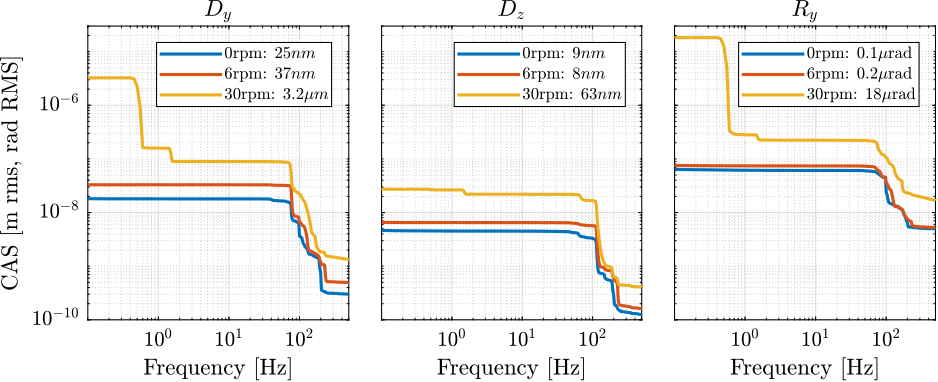
data_Wz2 = load(sprintf('%s/freq_analysis/2023-08-11_17-39_m0_lac_off_30rpm.mat', mat_dir));

Rotation induces lots of vibrations, especially at high velocity.

Cumulative Amplitude Spectrum for the three important directions ($D_y$, $D_z$ and $R_y$). Three rotating velocities are shown. Integrated RMS values are shown in the legend.

Effect of HAC

%% Load measured noise
data_ol  = load(sprintf('%s/freq_analysis/2023-08-11_16-51_m0_lac_off.mat', mat_dir));
data_lac = load(sprintf('%s/freq_analysis/2023-08-11_16-46_m0_lac_on.mat' , mat_dir));
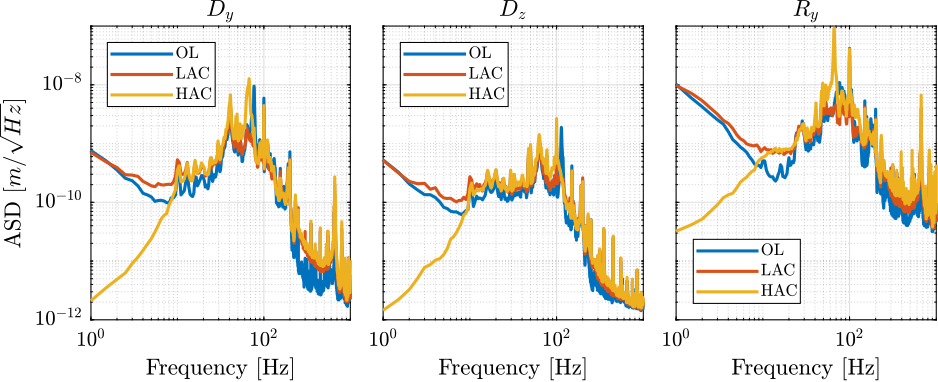
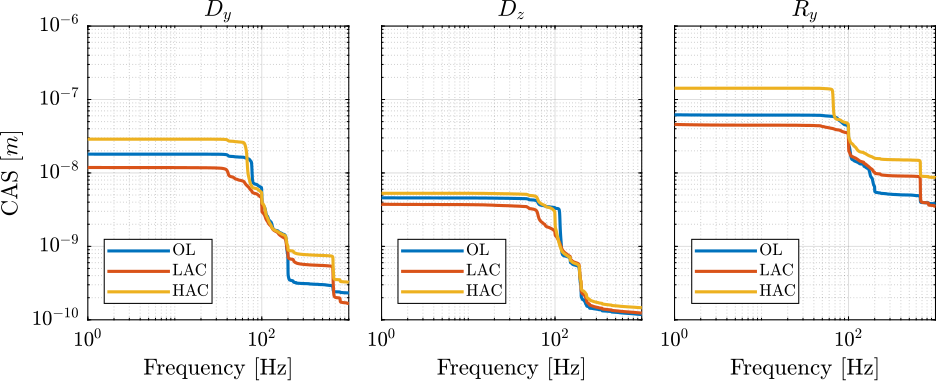
data_hac = load(sprintf('%s/freq_analysis/2023-08-11_16-49_m0_hac_on.mat' , mat_dir));

Bandwidth is approximately 10Hz.

Measured vibration with the interferometers

Measured vibration with the interferometers

TODO Noise coming from force sensor

Integral Force Feedback

<<sec:id31_iff>>

Introduction   ignore

IFF Plants

Introduction   ignore

6x6 Plant

%% Load identification data
data = load(sprintf('%s/dynamics/2023-08-08_16-17_ol_plant_m0_Wz0.mat', mat_dir));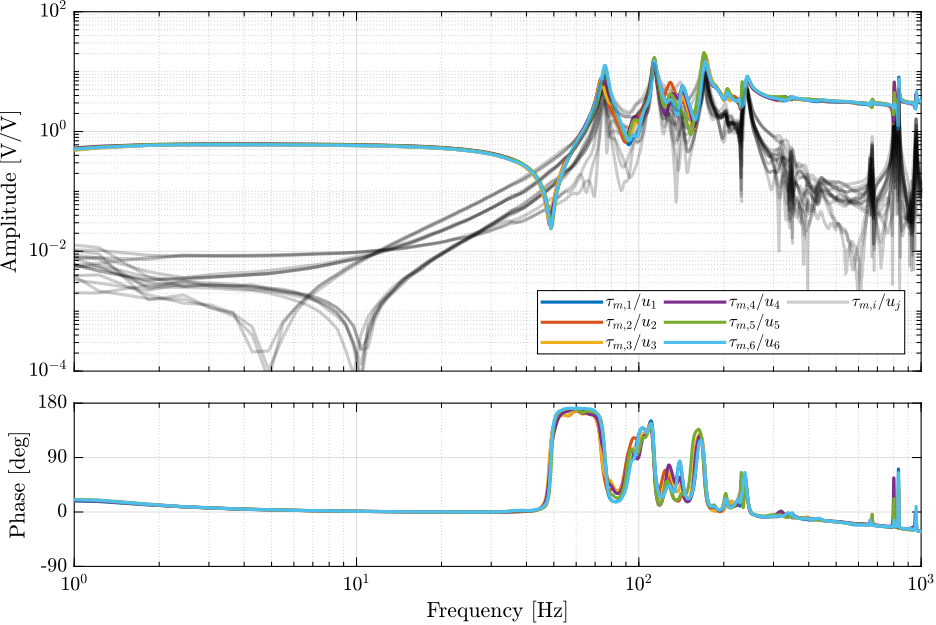

Obtained transfer function from generated voltages to measured voltages on the piezoelectric force sensor

Compare with Model:

load('Gm_iff.mat');

Effect of Rotation

%% Load identification data
data_Wz0 = load(sprintf('%s/dynamics/2023-08-08_16-17_ol_plant_m0_Wz0.mat', mat_dir));
data_Wz1 = load(sprintf('%s/dynamics/2023-08-08_16-28_ol_plant_m0_Wz36.mat', mat_dir));
data_Wz2 = load(sprintf('%s/dynamics/2023-08-08_16-45_ol_plant_m0_Wz180.mat', mat_dir));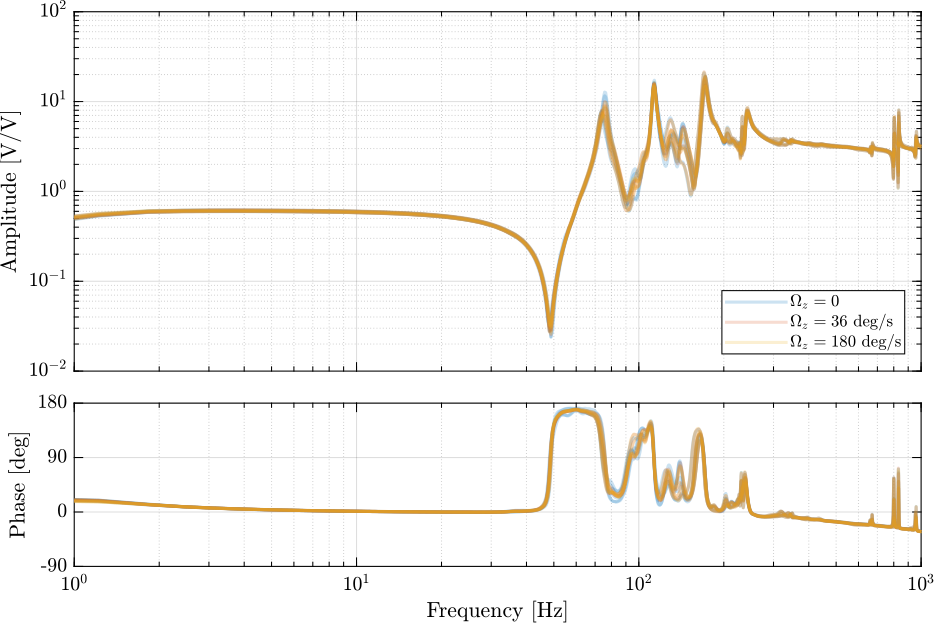

Obtained transfer function from generated voltages to measured voltages on the piezoelectric force sensor

Effect of Mass

load('G_ol.mat', 'G_iff_m0', 'G_iff_m1', 'G_iff_m2', 'G_iff_m3', 'f');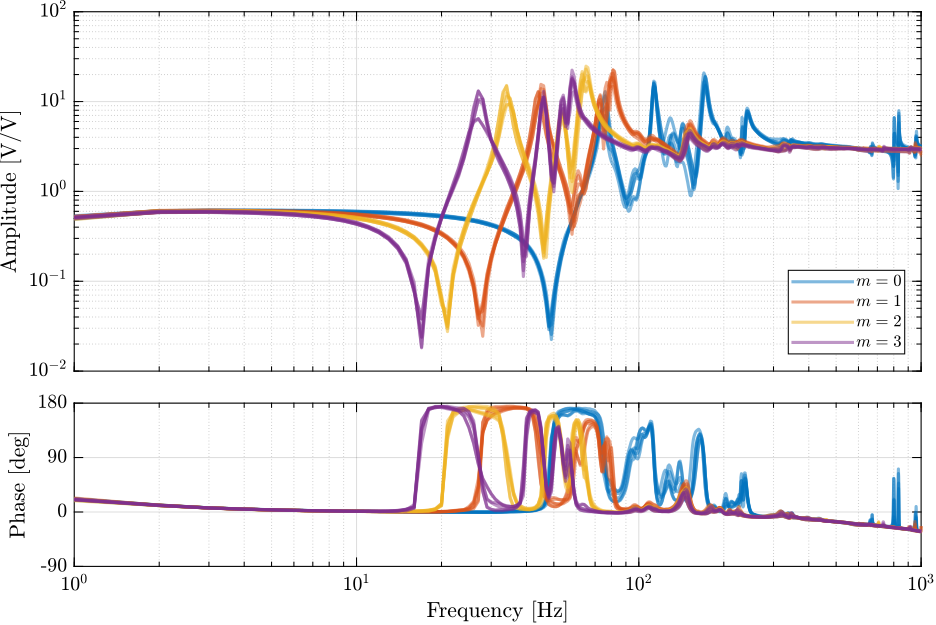

Obtained transfer function from generated voltages to measured voltages on the piezoelectric force sensor

Compare with the model

load('Gm.mat')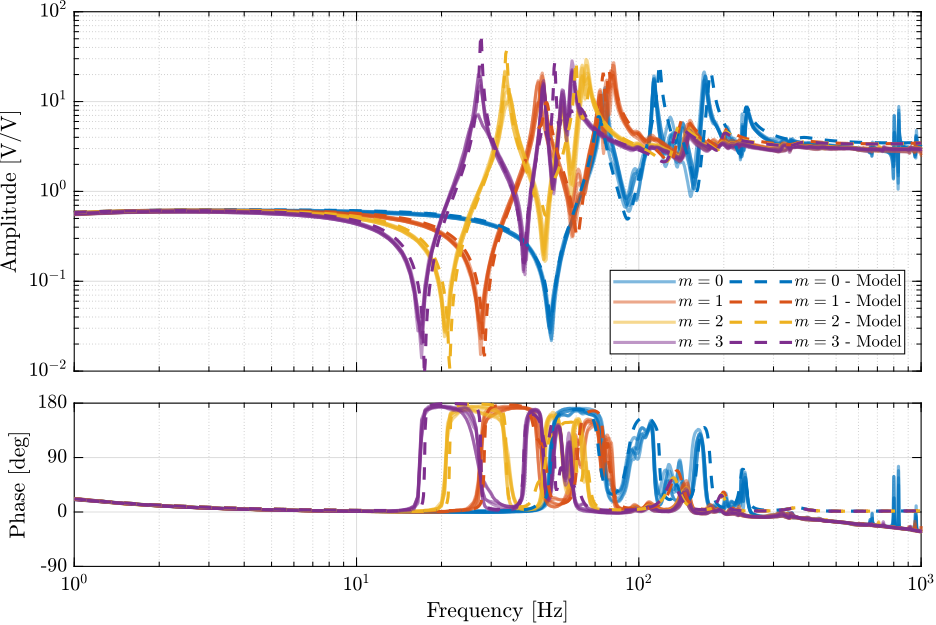

Comparison of the identified IFF plant and the IFF plant extracted from the simscape model

IFF Controller

Controller Design

Test second order high pass filter:

wz = 2*pi*10;
xiz = 0.7;
Ghpf = (s^2/wz^2)/(s^2/wz^2 + 2*xiz*s/wz + 1)
       % s/(2*pi*1)/(1 + s/(2*pi*1)) * ... % HPF: reduce gain at low frequency

We want integral action between 20Hz and 200Hz.

%% IFF Controller
Kiff = -1e2 * ...                           % Gain
       1/(0.01*2*pi + s) * ...               % LPF: provides integral action
       Ghpf * ...
       eye(6);                             % Diagonal 6x6 controller
Kiff.InputName = {'Fn1', 'Fn2', 'Fn3', 'Fn4', 'Fn5', 'Fn6'};
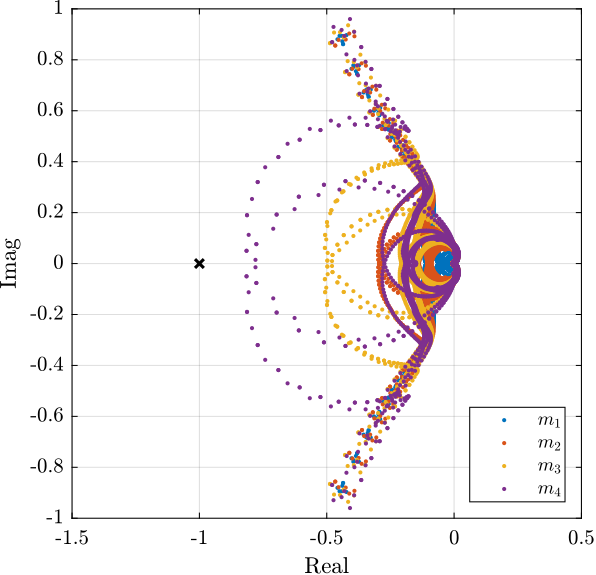
Kiff.OutputName = {'u1', 'u2', 'u3', 'u4', 'u5', 'u6'};

Loop Gain:

IFF Loop gain of the diagonal terms

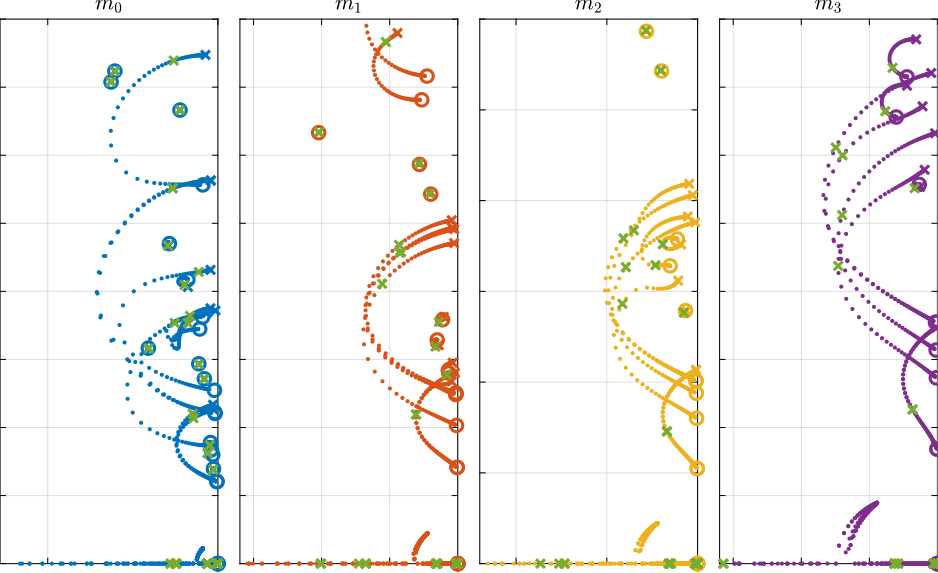
Root Locus to obtain optimal gain.

Root Locus for IFF. Green crosses are closed-loop poles for the same choosen IFF gain.

TODO Verify Stability

Verify Stability with Nyquist plot:

• Why bad stability margins?

Save Controller

save('./matlab/mat/K_iff.mat', 'Kiff')

Estimated Damped Plant

%% Damped plant from Simscape model
Gm_hac_m0 = -feedback(Gm_m0, Kiff, 'name', +1);
Gm_hac_m1 = -feedback(Gm_m1, Kiff, 'name', +1);
Gm_hac_m2 = -feedback(Gm_m2, Kiff, 'name', +1);
Gm_hac_m3 = -feedback(Gm_m3, Kiff, 'name', +1);

%% Verify Stability
isstable(Gm_hac_m0)
isstable(Gm_hac_m1)
isstable(Gm_hac_m2)
isstable(Gm_hac_m3)

%% Save Damped Plants
save('./matlab/mat/Gm.mat', 'Gm_hac_m0', 'Gm_hac_m1', 'Gm_hac_m2', 'Gm_hac_m3', '-append');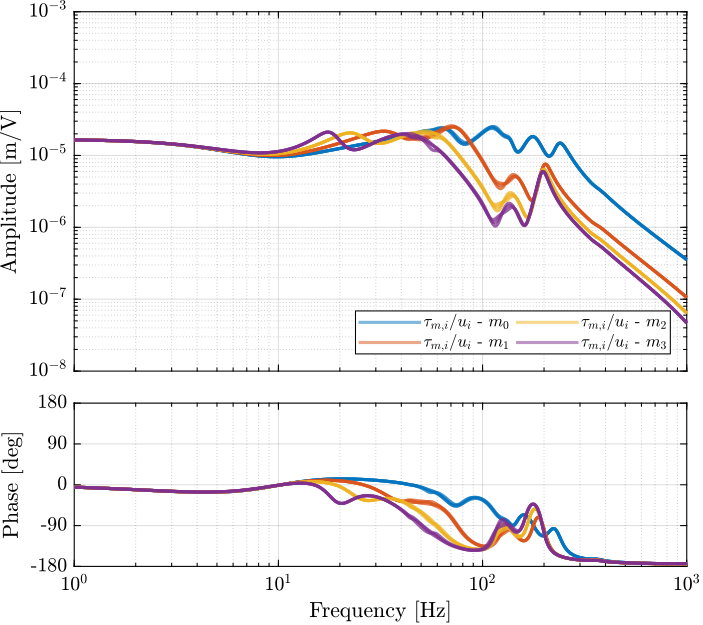

description

High Authority Control

<<sec:id31_iff_hac>>

Introduction   ignore

Identify Spurious modes

%% Load identification data
data = load(sprintf('%s/dynamics/2023-08-10_18-32_identify_spurious_modes.mat', mat_dir));

HAC Plants

Introduction   ignore

6x6 Plant

%% Load identification data
data = load(sprintf('%s/dynamics/2023-08-17_17-53_damp_plant_m0_Wz0.mat', mat_dir));

Compare with Model:

load('Gm.mat');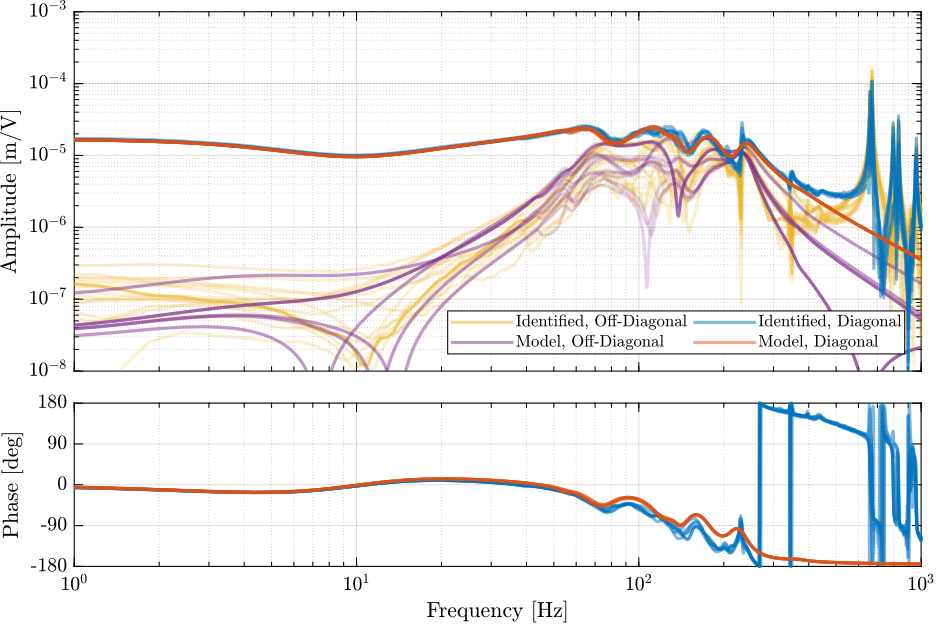

6x6 plant from generated voltages to displacement of the struts as measured by the external metrology

Effect of Mass

%% Load identification data
data_m0 = load(sprintf('%s/dynamics/2023-08-17_17-53_damp_plant_m0_Wz0.mat', mat_dir));
data_m1 = load(sprintf('%s/dynamics/2023-08-10_16-01_damp_plant_m1_Wz0.mat', mat_dir));
data_m2 = load(sprintf('%s/dynamics/2023-08-10_17-28_damp_plant_m2_Wz0.mat', mat_dir));
data_m3 = load(sprintf('%s/dynamics/2023-08-10_18-16_damp_plant_m3_Wz0.mat', mat_dir));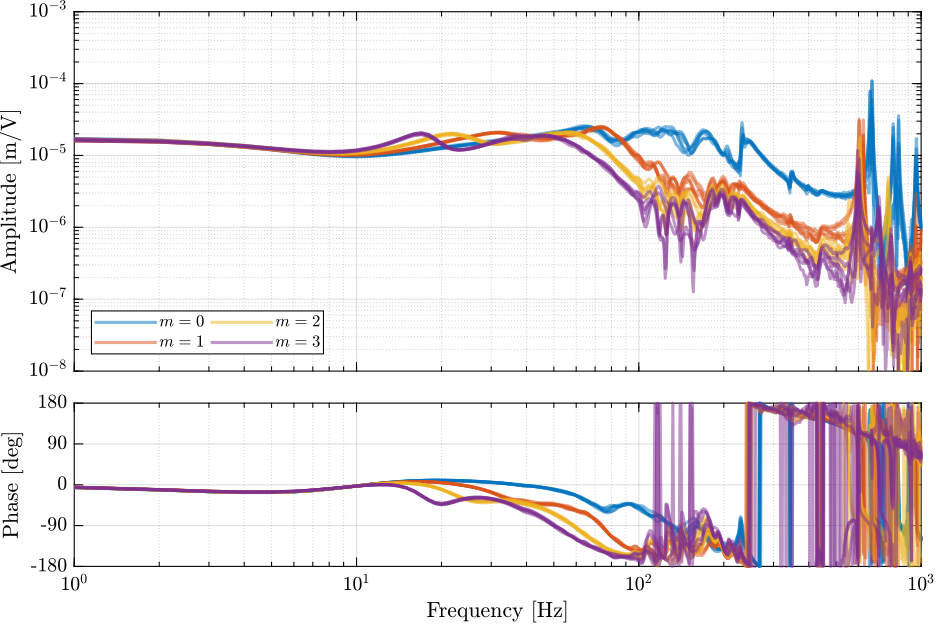

Obtained transfer function from generated voltages to measured voltages on the piezoelectric force sensor

Compare with the model

load('G_hac.mat')
load('Gm.mat')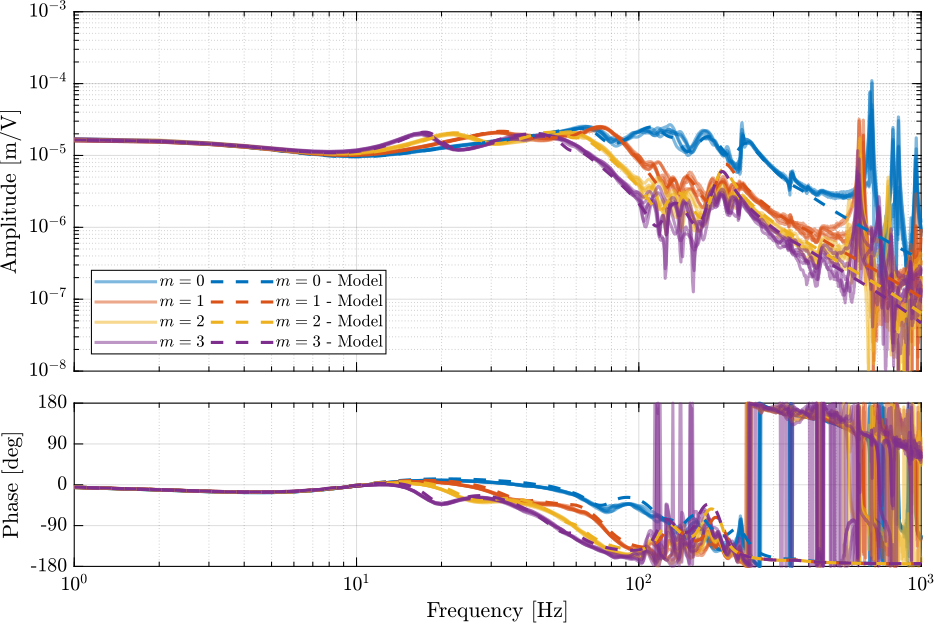

Comparison of the identified HAC plant and the HAC plant extracted from the simscape model

Comparison with Undamped plant

load('G_ol.mat');
load('G_hac.mat');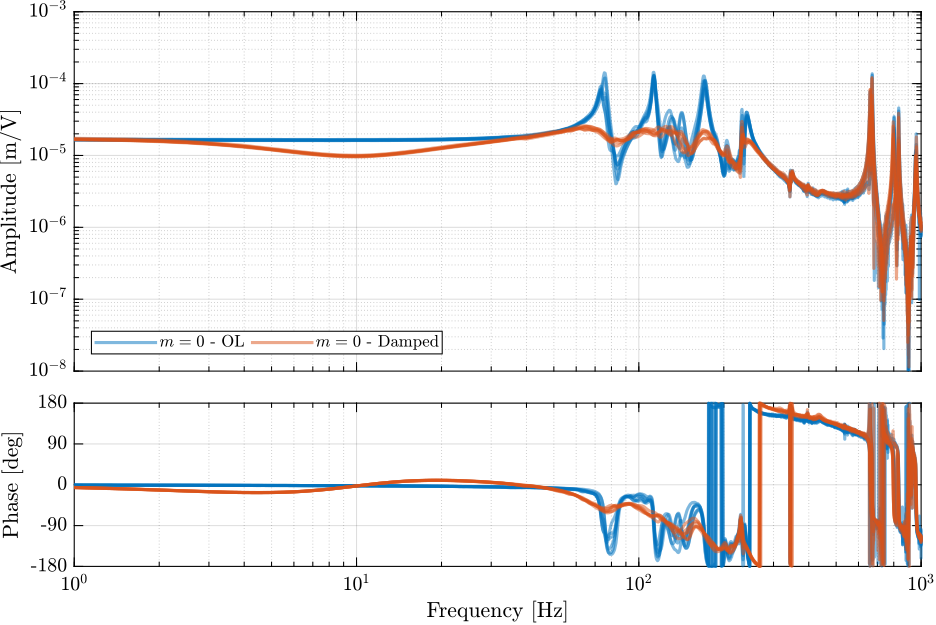

description

Robust HAC

load('G_hac.mat')
load('Gm.mat')

Controller design

%% Wanted crossover
wc = 2*pi*5;

%% Double Integrator
% H_int = (wc^2)/(s + 1e-1*2*pi)^2;
H_int = wc/s;

%% Lead to increase phase margin
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain

H_lead = 1/sqrt(a)*(1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));

%% Low Pass filter to increase robustness
H_lpf = 1/(1 + s/2/pi/30);

%% Notch at the top-plate resonance
% gm = 0.02;
% xi = 0.3;
% wn = 2*pi*665;

% H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

%% Gain to have unitary crossover at 30Hz
[~, i_f] = min(abs(f - wc/2/pi));
H_gain = 1./abs(G_hac_m0(i_f, 1, 1));

%% Decentralized HAC
Khac = H_gain  * ... % Gain
       H_int   * ... % Integrator
       H_lpf   * ... % Integrator
       eye(6);            % 6x6 Diagonal

Loop gain

description

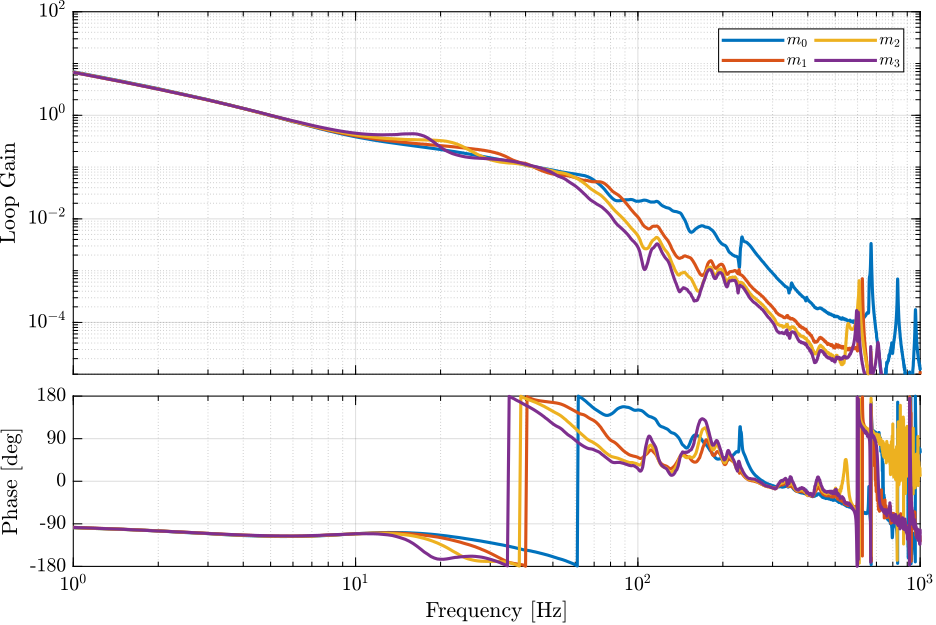
Verify Stability

description

Estimated performances

Save Controller

save('./matlab/mat/K_hac.mat', 'Khac')

High Performance HAC

Introduction   ignore

The goal is to make a controller specific for one mass in order to have high bandwidth.

Mass 0

Load Plant

load('G_hac.mat')
load('Gm.mat')

Plant

Controller design

%% Wanted crossover
wc = 2*pi*50;

%% Double Integrator
H_int = 1/(s + 0.1*2*pi) * ...
        1/(0.1*2*pi + s);
H_int = H_int/abs(evalfr(H_int, 1j*wc));
% H_int = wc/s;

%% Lead to increase phase margin
a  = 3;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = 1/sqrt(a)*(1 + s/(1.5*wc/sqrt(a)))/(1 + s/(1.5*wc*sqrt(a)));
a  = 3;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = H_lead/sqrt(a)*(1 + s/(2.5*wc/sqrt(a)))/(1 + s/(2.5*wc*sqrt(a)));

%% Low Pass filter to increase robustness
H_lpf = 1/(1 + s/2/pi/500);

%% Notch at the top-plate resonance
% gm = 0.02;
% xi = 0.3;
% wn = 2*pi*665;

% H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

%% Gain to have unitary crossover at 30Hz
[~, i_f] = min(abs(f - wc/2/pi));
H_gain = 1./abs(G_hac_m0(i_f, 1, 1));

%% Decentralized HAC
Khac = H_gain  * ... % Gain
       H_int   * ... % Integrator
       H_lpf   * ... % Low Pass Filter
       H_lead  * ... % Integrator
       eye(6);            % 6x6 Diagonal

Khac.InputName = {'eL1', 'eL2', 'eL3', 'eL4', 'eL5', 'eL6'};
Khac.OutputName = {'u1', 'u2', 'u3', 'u4', 'u5', 'u6'};

Loop gain

Loop gain for the High Authority Control

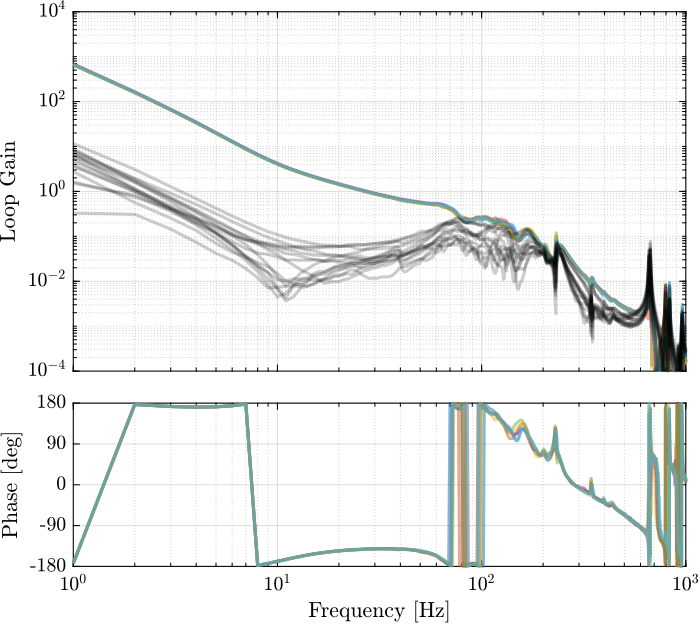
Verify Stability

Nyquist plot for the High Authority Control

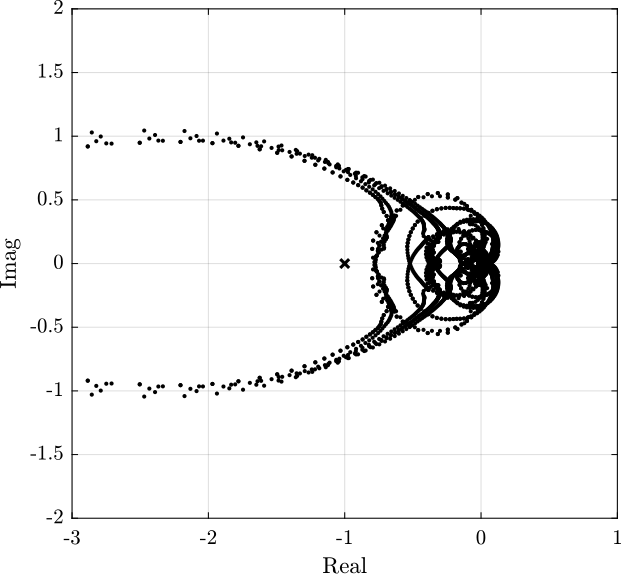
Estimated performances

Loop gain with model

Gm_cl_m0 = feedback(Gm_hac_m0, 0.8*Khac, 'name', -1);

isstable(Gm_cl_m0)

Save Controller

Experimental Validation

data_1rpm = load(sprintf('%s/scans/2023-08-18_10-43_m0_1rpm.mat', mat_dir));
data_30rpm = load(sprintf('%s/scans/2023-08-18_10-45_m0_30rpm.mat', mat_dir));

	Dy [nm]	Dz [nm]	Ry [urad]
1rpm	55.3	5.9	0.1
30rpm	85.2	12.5	0.3

Closed-Loop identification

data_cl = load(sprintf('%s/dynamics/2023-08-18_11-03_m0_perf_hac.mat', mat_dir));

Mass 1

Load Plant

load('G_hac.mat')
load('Gm.mat')

Plant

Plant Inverse

Gm_hac_red_m1 = flipRphZeros(-balred(Gm_hac_m1('eL1', 'u1'), 6, ...
                                    balredOptions('StateProjection', 'MatchDC', ...
                                                  'FreqIntervals', [0, 80])));

%% Plant Inverse
Gm_hac_inv_m1 = inv(Gm_hac_red_m1);

Controller design

%% Wanted crossover
wc = 2*pi*30;

%% Double Integrator
H_int = 1/(s + 0.1*2*pi) * ...
        (50*2*pi + s)/(0.01*2*pi + s);
H_int = H_int/abs(evalfr(H_int, 1j*wc));
% H_int = wc/s;

%% Lead to increase phase margin
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = 1/sqrt(a)*(1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = H_lead*1/sqrt(a)*(1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));

%% Low Pass filter to increase robustness
H_lpf = 1/(1 + s/2/pi/200);

%% Notch at the top-plate resonance
% gm = 0.02;
% xi = 0.3;
% wn = 2*pi*665;

% H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

%% Gain to have unitary crossover at 30Hz
[~, i_f] = min(abs(f - wc/2/pi));
H_gain = 1./abs(G_hac_m0(i_f, 1, 1));

%% Decentralized HAC
Khac = 0.8*H_gain  * ... % Gain
       H_int   * ... % Integrator
       H_lpf   * ... % Low Pass Filter
       H_lead  * ... % Integrator
       eye(6);            % 6x6 Diagonal

Khac.InputName = {'eL1', 'eL2', 'eL3', 'eL4', 'eL5', 'eL6'};
Khac.OutputName = {'u1', 'u2', 'u3', 'u4', 'u5', 'u6'};

Loop gain

Verify Stability

Estimated performances

Loop gain with model

Gm_cl_m0 = feedback(Gm_hac_m0, Khac, 'name', +1);

isstable(Gm_hac_m0)

Save Controller

Tomography - Performances

First scan with closed-loop at middle

data = load(sprintf('%s/scans/2023-08-17_15-22_tomography_30rpm_m0_robust.mat', mat_dir));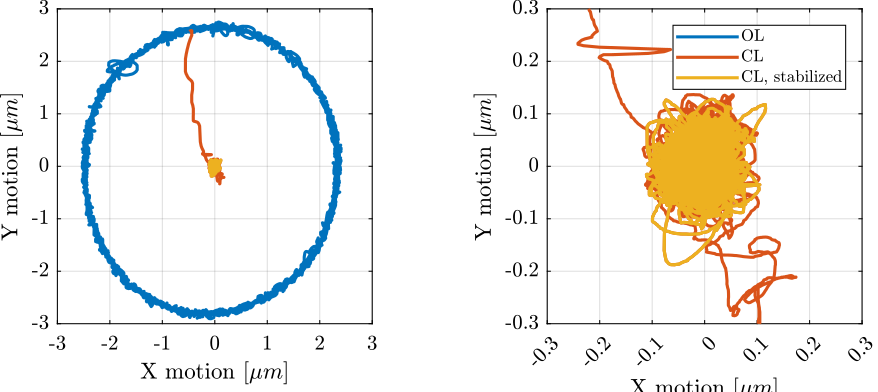

description

Slow Rotation - 6RPM

%% Load measured noise
data_ol  = load(sprintf('%s/freq_analysis/2023-08-11_17-18_m0_lac_off_1rpm.mat', mat_dir));
data_lac = load(sprintf('%s/freq_analysis/2023-08-11_17-16_m0_lac_on_1rpm.mat', mat_dir));
data_hac = load(sprintf('%s/freq_analysis/2023-08-11_17-14_m0_hac_on_1rpm.mat', mat_dir));

%% Coordinate transform
J_int_to_X = [ 0                 0                -0.787401574803149 -0.212598425196851  0;
               0.78740157480315  0.21259842519685  0                  0                  0;
               0                 0                 0                  0                 -1;
             -13.1233595800525  13.1233595800525   0                  0                  0;
               0                 0               -13.1233595800525   13.1233595800525    0];

a = J_int_to_X*[data_ol.d1; data_ol.d2; data_ol.d3; data_ol.d4; data_ol.d5];
data_ol.Dx_int = a(1,:);
data_ol.Dy_int = a(2,:);
data_ol.Dz_int = a(3,:);
data_ol.Rx_int = a(4,:);
data_ol.Ry_int = a(5,:);

a = J_int_to_X*[data_lac.d1; data_lac.d2; data_lac.d3; data_lac.d4; data_lac.d5];
data_lac.Dx_int = a(1,:);
data_lac.Dy_int = a(2,:);
data_lac.Dz_int = a(3,:);
data_lac.Rx_int = a(4,:);
data_lac.Ry_int = a(5,:);

a = J_int_to_X*[data_hac.d1; data_hac.d2; data_hac.d3; data_hac.d4; data_hac.d5];
data_hac.Dx_int = a(1,:);
data_hac.Dy_int = a(2,:);
data_hac.Dz_int = a(3,:);
data_hac.Rx_int = a(4,:);
data_hac.Ry_int = a(5,:);

Rapid Rotation - 30RPM

%% Load measured noise
data_ol  = load(sprintf('%s/freq_analysis/2023-08-11_17-39_m0_lac_off_30rpm.mat', mat_dir));
data_lac = load(sprintf('%s/freq_analysis/2023-08-11_17-36_m0_lac_on_30rpm.mat', mat_dir));
data_hac = load(sprintf('%s/freq_analysis/2023-08-11_17-34_m0_hac_on_30rpm.mat', mat_dir));

%% Coordinate transform
J_int_to_X = [ 0                 0                -0.787401574803149 -0.212598425196851  0;
               0.78740157480315  0.21259842519685  0                  0                  0;
               0                 0                 0                  0                 -1;
             -13.1233595800525  13.1233595800525   0                  0                  0;
               0                 0               -13.1233595800525   13.1233595800525    0];

a = J_int_to_X*[data_ol.d1; data_ol.d2; data_ol.d3; data_ol.d4; data_ol.d5];
data_ol.Dx_int = a(1,:);
data_ol.Dy_int = a(2,:);
data_ol.Dz_int = a(3,:);
data_ol.Rx_int = a(4,:);
data_ol.Ry_int = a(5,:);

a = J_int_to_X*[data_lac.d1; data_lac.d2; data_lac.d3; data_lac.d4; data_lac.d5];
data_lac.Dx_int = a(1,:);
data_lac.Dy_int = a(2,:);
data_lac.Dz_int = a(3,:);
data_lac.Rx_int = a(4,:);
data_lac.Ry_int = a(5,:);

a = J_int_to_X*[data_hac.d1; data_hac.d2; data_hac.d3; data_hac.d4; data_hac.d5];
data_hac.Dx_int = a(1,:);
data_hac.Dy_int = a(2,:);
data_hac.Dz_int = a(3,:);
data_hac.Rx_int = a(4,:);
data_hac.Ry_int = a(5,:);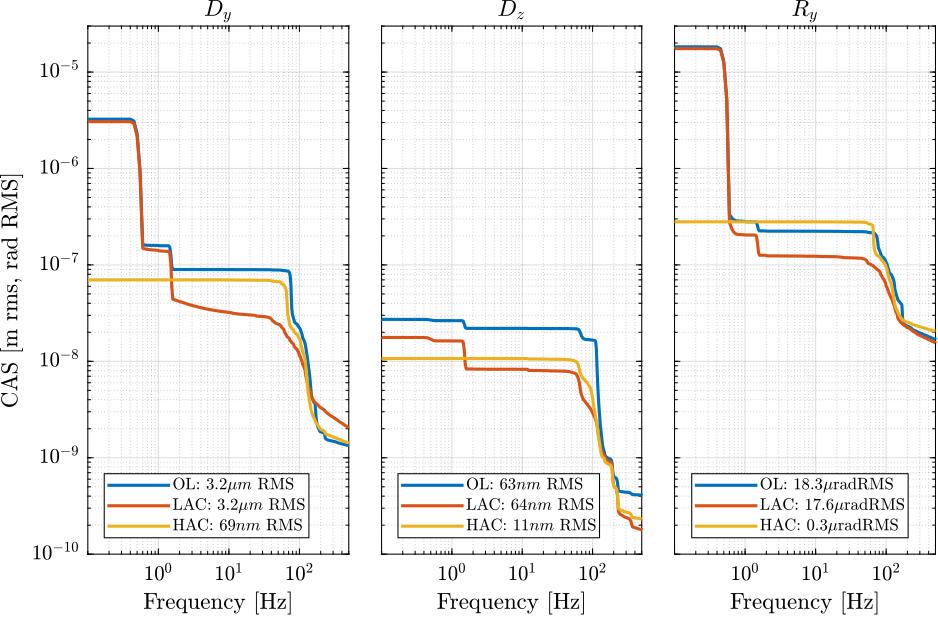

Cumulative Amplitude Spectrum of the errors in $D_y$, $D_z$ and $R_y$ during a tomography scan at 30RPM. Three control configuration are compared: Open-Loop, Low Authority Control, and High Authority Control

6DoF Control in Cartesian plane (rotating with the nano-hexapod)

<<sec:id31_cart_hac_rot>>

Introduction   ignore

As only Dy, Dz and Ry directions are important, we could only control them. This lead to a 3x3 plant that may be more decoupled than the 6x6 plant.

5x5 plant in Cartesian plane

%% Jacobian for 3x3 plant
n_hexapod = initializeNanoHexapod('flex_bot_type', '2dof', ...
                                  'flex_top_type', '3dof', ...
                                  'motion_sensor_type', 'plates', ...
                                  'actuator_type', '2dof');

Jt_inv = pinv(n_hexapod.geometry.J');
Jt_inv = Jt_inv(:,[1,2,3,4,5]);

J_int_to_X = [ 0                 0                -0.787401574803149 -0.212598425196851  0;
               0.78740157480315  0.21259842519685  0                  0                  0;
               0                 0                 0                  0                 -1;
             -13.1233595800525  13.1233595800525   0                  0                  0;
               0                 0               -13.1233595800525   13.1233595800525    0];

Compute identified plant in the Cartesian plane:

%% Load Data
% data_m0 = load(sprintf('%s/dynamics/2023-08-17_10-44_lac_plant_m0_Wz0_interf.mat', mat_dir));
%% New data after calibrating the Rz-offset
data_m0 = load(sprintf('%s/dynamics/2023-08-17_16-23_lac_plant_m0_Wz0_interf_Rz_align.mat', mat_dir));

Compute plant model in the Cartesian plane:

Gm_cart = J_int_to_X*Gm_hac_m0({'d1', 'd2', 'd3', 'd4', 'd5'}, {'u1', 'u2', 'u3', 'u4', 'u5', 'u6'})*Jt_inv;
Gm_cart.InputName = {'Fx', 'Fy', 'Fz', 'Mx', 'My'};
Gm_cart.OutputName = {'Dx', 'Dy', 'Dz', 'Rx', 'Ry'};

Controller Design

%% Wanted crossover
wc = 2*pi*30;

%% Double Integrator
H_int = 1/(s + 1*2*pi) * ...
        1/(s + 0.01*2*pi);
H_int = H_int/abs(evalfr(H_int, 1j*wc));

%% Lead to increase phase margin
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = 1/sqrt(a)*(1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = H_lead*1/sqrt(a)*(1 + s/(1.5*wc/sqrt(a)))/(1 + s/(1.5*wc*sqrt(a)));

%% Low Pass filter to increase robustness
H_lpf = 1/(1 + s/2/pi/300);

%% Notch at the top-plate resonance
% gm = 0.02;
% xi = 0.3;
% wn = 2*pi*665;

% H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

%% Gain to have unitary crossover at 30Hz
[~, i_f] = min(abs(f - wc/2/pi));
H_gain = -1./abs(G_cart(i_f,1,1));

%% Decentralized HAC
Khac_Dx = H_gain  * ... % Gain
          H_int   * ... % Integrator
          H_lpf   * ... % Low Pass Filter
          H_lead;       % Integrator

%% Wanted crossover
wc = 2*pi*30;

%% Double Integrator
H_int = 1/(s + 1*2*pi) * ...
        1/(s + 0.01*2*pi);
H_int = H_int/abs(evalfr(H_int, 1j*wc));

%% Lead to increase phase margin
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = 1/sqrt(a)*(1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = H_lead*1/sqrt(a)*(1 + s/(1.5*wc/sqrt(a)))/(1 + s/(1.5*wc*sqrt(a)));

%% Low Pass filter to increase robustness
H_lpf = 1/(1 + s/2/pi/300);

%% Notch at the top-plate resonance
% gm = 0.02;
% xi = 0.3;
% wn = 2*pi*665;

% H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

%% Gain to have unitary crossover at 30Hz
[~, i_f] = min(abs(f - wc/2/pi));
H_gain = -1./abs(G_cart(i_f,2,2));

%% Decentralized HAC
Khac_Dy = H_gain  * ... % Gain
          H_int   * ... % Integrator
          H_lpf   * ... % Low Pass Filter
          H_lead;       % Integrator

%% Wanted crossover
wc = 2*pi*40;

%% Double Integrator
H_int = 1/(s + 2*2*pi) * ...
        1/(s + 0.01*2*pi);
H_int = H_int/abs(evalfr(H_int, 1j*wc));

%% Lead to increase phase margin
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = 1/sqrt(a)*(1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = H_lead*1/sqrt(a)*(1 + s/(1.5*wc/sqrt(a)))/(1 + s/(1.5*wc*sqrt(a)));

%% Low Pass filter to increase robustness
H_lpf = 1/(1 + s/2/pi/300);

%% Notch at the top-plate resonance
% gm = 0.02;
% xi = 0.3;
% wn = 2*pi*665;

% H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

%% Gain to have unitary crossover at 30Hz
[~, i_f] = min(abs(f - wc/2/pi));
H_gain = -1./abs(G_cart(i_f,3,3));

%% Decentralized HAC
Khac_Dz = H_gain  * ... % Gain
          H_int   * ... % Integrator
          H_lpf   * ... % Low Pass Filter
          H_lead;       % Integrator

%% Wanted crossover
wc = 2*pi*10;

%% Double Integrator
H_int = 1/(s + 1.5*2*pi) * ...
        1/(s + 0.01*2*pi);
H_int = H_int/abs(evalfr(H_int, 1j*wc));

%% Lead to increase phase margin
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = 1/sqrt(a)*(1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));

%% Low Pass filter to increase robustness
H_lpf = 1/(1 + s/2/pi/300);

%% Notch at the top-plate resonance
% gm = 0.02;
% xi = 0.3;
% wn = 2*pi*665;

% H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

%% Gain to have unitary crossover at 30Hz
[~, i_f] = min(abs(f - wc/2/pi));
H_gain = -1./abs(G_cart(i_f,4,4));

%% Decentralized HAC
Khac_Rx = H_gain  * ... % Gain
          H_int   * ... % Integrator
          H_lpf   * ... % Low Pass Filter
          H_lead;       % Integrator

%% Wanted crossover
wc = 2*pi*10;

%% Double Integrator
H_int = 1/(s + 1.5*2*pi) * ...
        1/(s + 0.01*2*pi);
H_int = H_int/abs(evalfr(H_int, 1j*wc));

%% Lead to increase phase margin
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = 1/sqrt(a)*(1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));

%% Low Pass filter to increase robustness
H_lpf = 1/(1 + s/2/pi/300);

%% Notch at the top-plate resonance
% gm = 0.02;
% xi = 0.3;
% wn = 2*pi*665;

% H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

%% Gain to have unitary crossover at 30Hz
[~, i_f] = min(abs(f - wc/2/pi));
H_gain = -1./abs(G_cart(i_f,5,5));

%% Decentralized HAC
Khac_Ry = H_gain  * ... % Gain
          H_int   * ... % Integrator
          H_lpf   * ... % Low Pass Filter
          H_lead;       % Integrator

Khac = blkdiag(Khac_Dx, Khac_Dy, Khac_Dz, Khac_Rx, Khac_Ry);

Check Stability

Save controllers

Performances

2023-08-18_18-33_m0_1rpm_K_cart.mat

3DoF Control in Cartesian plane (fixed)

<<sec:id31_cart_hac_fix>>

Introduction   ignore

As only Dy, Dz and Ry directions are important, we could only control them. This lead to a 3x3 plant that may be more decoupled than the 6x6 plant.

3x3 plant in Cartesian plane

%% Jacobian for 3x3 plant
n_hexapod = initializeNanoHexapod('flex_bot_type', '2dof', ...
                                  'flex_top_type', '3dof', ...
                                  'motion_sensor_type', 'plates', ...
                                  'actuator_type', '2dof');

Jt_inv = pinv(n_hexapod.geometry.J');

J_int_to_X = [0.78740157480315  0.21259842519685  0                  0                  0;
              0                 0                 0                  0                 -1;
              0                 0               -13.1233595800525   13.1233595800525    0];

Compute identified plant in the Cartesian plane:

%% Load Data
% data_m0 = load(sprintf('%s/dynamics/2023-08-17_10-44_lac_plant_m0_Wz0_interf.mat', mat_dir));
%% New data after calibrating the Rz-offset
data_m0 = load(sprintf('%s/dynamics/2023-08-17_16-23_lac_plant_m0_Wz0_interf_Rz_align.mat', mat_dir));

Compute plant model in the Cartesian plane:

Gm_cart = J_int_to_X*Gm_hac_m0({'d1', 'd2', 'd3', 'd4', 'd5'}, {'u1', 'u2', 'u3', 'u4', 'u5', 'u6'})*Jt_inv(:,[2,3,5]);
Gm_cart.InputName = {'Fy', 'Fz', 'My'};
Gm_cart.OutputName = {'Dy', 'Dz', 'Ry'};

Diagonal elements are matching quite well, but off-diagonal elements are very different.

Why so much more coupling than from the model?

• Is it due to the metrology? The spheres could induce coupling as for instance X motion will also be seen as Z motion. This is especially true if not well centered with the sphere (as seemed to be the case for the lateral interferometers).

3x3 cartesian plant

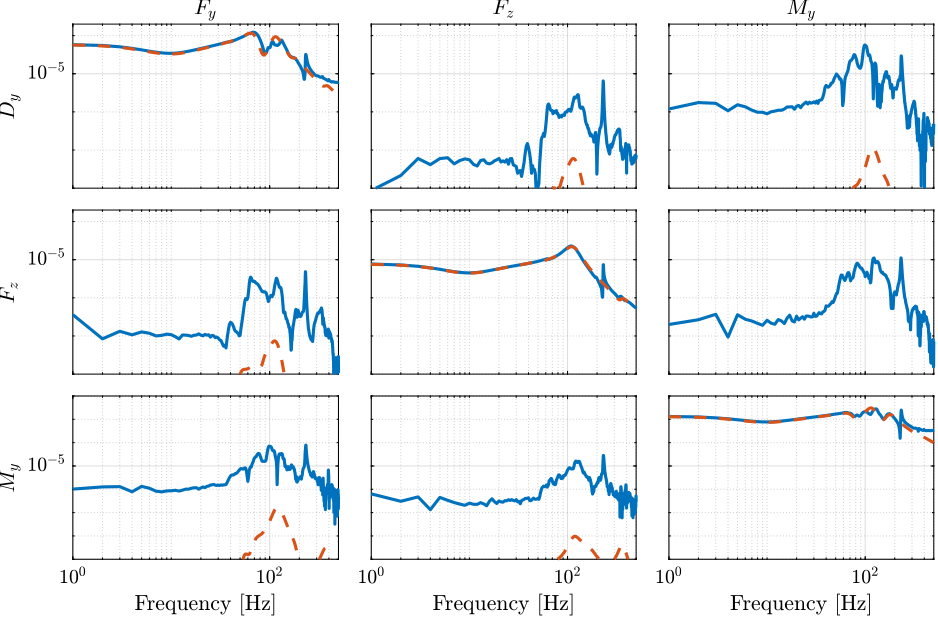
Normalization of outputs:

Gm_cart_normalized = -diag(1./diag(dcgain(Gm_cart)))*Gm_cart;
Gm_cart_normalized.InputName = {'Fy', 'Fz', 'My'};
Gm_cart_normalized.OutputName = {'Dy', 'Dz', 'Ry'};

G_cart_normalized = permute(pagemtimes(-diag(1./diag(dcgain(Gm_cart))), permute(G_cart, [2,3,1])), [3,1,2]);

Controller Design

Dy

%% Wanted crossover
wc = 2*pi*30;

%% Double Integrator
H_int = 1/(s + 0.1*2*pi) * ...
        1/(s + 0.01*2*pi);
H_int = H_int/abs(evalfr(H_int, 1j*wc));

%% Lead to increase phase margin
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = 1/sqrt(a)*(1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = H_lead*1/sqrt(a)*(1 + s/(1.5*wc/sqrt(a)))/(1 + s/(1.5*wc*sqrt(a)));

%% Low Pass filter to increase robustness
H_lpf = 1/(1 + s/2/pi/300);

%% Notch at the top-plate resonance
% gm = 0.02;
% xi = 0.3;
% wn = 2*pi*665;

% H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

%% Gain to have unitary crossover at 30Hz
[~, i_f] = min(abs(f - wc/2/pi));
H_gain = -1./abs(G_cart(i_f,1,1));

%% Decentralized HAC
Khac_Dy = H_gain  * ... % Gain
          H_int   * ... % Integrator
          H_lpf   * ... % Low Pass Filter
          H_lead;       % Integrator

Dz

%% Wanted crossover
wc = 2*pi*50;

%% Double Integrator
H_int = 1/(s + 0.1*2*pi) * ...
        1/(s + 0.01*2*pi);
H_int = H_int/abs(evalfr(H_int, 1j*wc));

%% Lead to increase phase margin
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = 1/sqrt(a)*(1 + s/(1.5*wc/sqrt(a)))/(1 + s/(1.5*wc*sqrt(a)));
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = H_lead*1/sqrt(a)*(1 + s/(1.5*wc/sqrt(a)))/(1 + s/(1.5*wc*sqrt(a)));

%% Low Pass filter to increase robustness
H_lpf = 1/(1 + s/2/pi/300);

%% Notch at the top-plate resonance
% gm = 0.02;
% xi = 0.3;
% wn = 2*pi*665;

% H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

%% Gain to have unitary crossover at 30Hz
[~, i_f] = min(abs(f - wc/2/pi));
H_gain = -1./abs(G_cart(i_f,2,2));

%% Decentralized HAC
Khac_Dz = H_gain  * ... % Gain
          H_int   * ... % Integrator
          H_lpf   * ... % Low Pass Filter
          H_lead;       % Integrator

Ry

%% Wanted crossover
wc = 2*pi*30;

%% Double Integrator
H_int = 1/(s + 0.1*2*pi) * ...
        1/(s + 0.01*2*pi);
H_int = H_int/abs(evalfr(H_int, 1j*wc));

%% Lead to increase phase margin
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = 1/sqrt(a)*(1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = H_lead*1/sqrt(a)*(1 + s/(1.5*wc/sqrt(a)))/(1 + s/(1.5*wc*sqrt(a)));

%% Low Pass filter to increase robustness
H_lpf = 1/(1 + s/2/pi/300);

%% Notch at the top-plate resonance
% gm = 0.02;
% xi = 0.3;
% wn = 2*pi*665;

% H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

%% Gain to have unitary crossover at 30Hz
[~, i_f] = min(abs(f - wc/2/pi));
H_gain = -1./abs(G_cart(i_f,3,3));

%% Decentralized HAC
Khac_Ry = H_gain  * ... % Gain
          H_int   * ... % Integrator
          H_lpf   * ... % Low Pass Filter
          H_lead;       % Integrator

3x3 controller

Khac = blkdiag(Khac_Dy, Khac_Dz, Khac_Ry);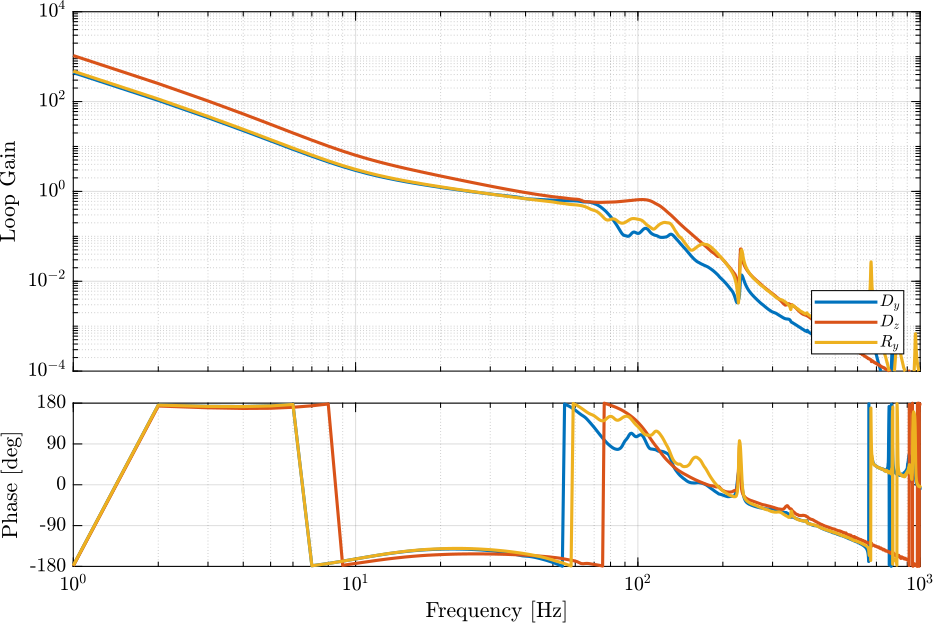

description

Check Stability

description

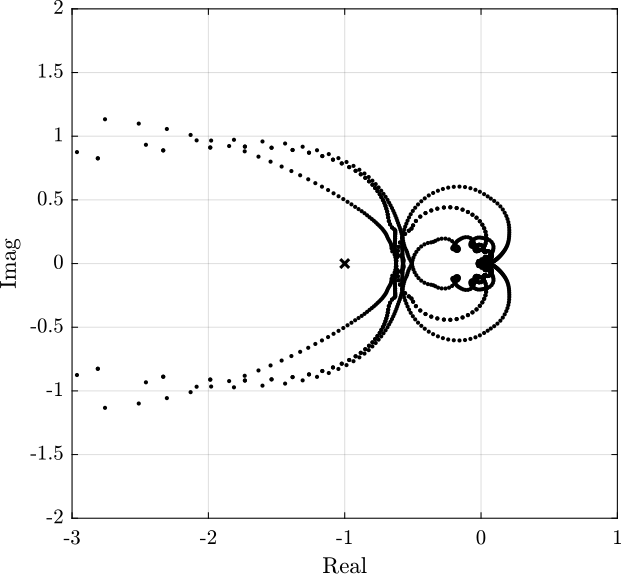
Save controllers

Save Controller

Controller Design (normalized)

%% Wanted crossover
wc = 2*pi*30;

%% Double Integrator
H_int = 1/(s + 0.1*2*pi) * ...
        (50*2*pi + s)/(0.01*2*pi + s);
H_int = H_int/abs(evalfr(H_int, 1j*wc));
% H_int = wc/s;

%% Lead to increase phase margin
a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = 1/sqrt(a)*(1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));
% a  = 2;  % Amount of phase lead / width of the phase lead / high frequency gain
% H_lead = H_lead*1/sqrt(a)*(1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a)));

%% Low Pass filter to increase robustness
H_lpf = 1/(1 + s/2/pi/200);

%% Notch at the top-plate resonance
% gm = 0.02;
% xi = 0.3;
% wn = 2*pi*665;

% H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

%% Gain to have unitary crossover at 30Hz
[~, i_f] = min(abs(f - wc/2/pi));
H_gain = 1./abs(G_cart_normalized(i_f, 1, 1));

%% Decentralized HAC
Khac = H_gain  * ... % Gain
       H_int   * ... % Integrator
       H_lpf   * ... % Low Pass Filter
       H_lead  * ... % Integrator
       eye(3);            % 6x6 Diagonal

% Khac.InputName = {'eL1', 'eL2', 'eL3', 'eL4', 'eL5', 'eL6'};
% Khac.OutputName = {'u1', 'u2', 'u3', 'u4', 'u5', 'u6'};

Verify Stability

Control Performances

data_cl = load(sprintf('%s/dynamics/2023-08-21_10-36_m0_cart_fixed.mat', mat_dir));

• Compare with estimated performances

Complementary Filter Control

<<sec:id31_cart_hac_complementary_filter>>

m0

3x3 plant in Cartesian plane

%% Jacobian for 3x3 plant
n_hexapod = initializeNanoHexapod('flex_bot_type', '2dof', ...
                                  'flex_top_type', '3dof', ...
                                  'motion_sensor_type', 'plates', ...
                                  'actuator_type', '2dof');

Jt_inv = pinv(n_hexapod.geometry.J');

J_int_to_X = [0.78740157480315  0.21259842519685  0                  0                  0;
              0                 0                 0                  0                 -1;
              0                 0               -13.1233595800525   13.1233595800525    0];

Compute identified plant in the Cartesian plane:

%% New data after calibrating the Rz-offset
data_m0 = load(sprintf('%s/dynamics/2023-08-21_13-32_damp_plant_m0.mat', mat_dir));

Compute plant model in the Cartesian plane:

Gm_cart = J_int_to_X*Gm_hac_m0({'d1', 'd2', 'd3', 'd4', 'd5'}, {'u1', 'u2', 'u3', 'u4', 'u5', 'u6'})*Jt_inv(:,[2,3,5]);
Gm_cart.InputName = {'Fy', 'Fz', 'My'};
Gm_cart.OutputName = {'Dy', 'Dz', 'Ry'};

Plant Invert

Reduce model size

Gm_cart_dy = flipRphZeros(balred(-Gm_cart('Dy', 'Fy'), 10));
Gm_cart_dz = flipRphZeros(balred(-Gm_cart('Dz', 'Fz'), 10));
Gm_cart_ry = flipRphZeros(balred(-Gm_cart('Ry', 'My'), 10));

Add first resonance

% gm = 200;
% xi = 0.003;
% wn = 2*pi*670;

% Gm_cart_dy = Gm_cart_dy*(s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

% gm = 200;
% xi = 0.003;
% wn = 2*pi*1086;

% Gm_cart_dz = Gm_cart_dz*(s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

% gm = 200;
% xi = 0.003;
% wn = 2*pi*670;

% Gm_cart_ry = Gm_cart_ry*(s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);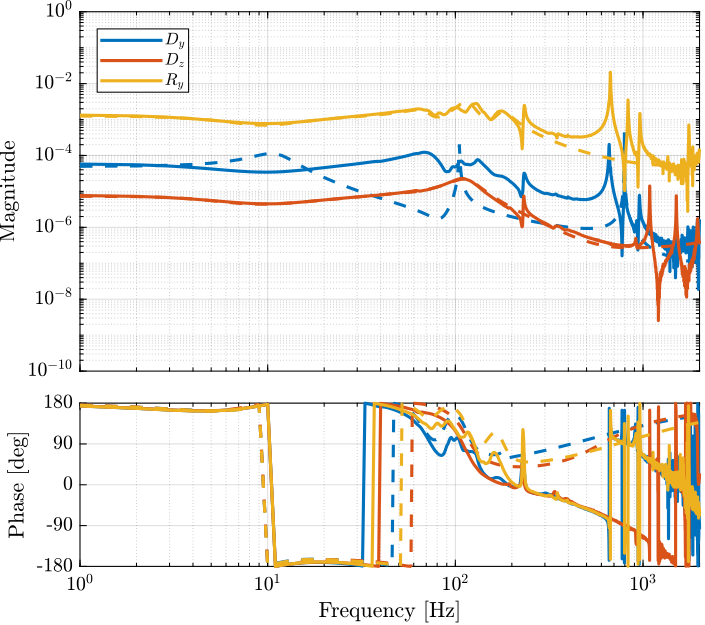

Comparaison of the measured direct terms and the reduced order models

Invert and make realizable

Gm_cart_dy_inv = inv(Gm_cart_dy);
Gm_cart_dz_inv = inv(Gm_cart_dz);
Gm_cart_ry_inv = inv(Gm_cart_ry);

isstable(Gm_cart_dy_inv)
isstable(Gm_cart_dz_inv)
isstable(Gm_cart_ry_inv)

Save Plant Inverse

Control Performances

5Hz

data_cl = load(sprintf('%s/dynamics/2023-08-21_10-59_m0_cf_5Hz.mat', mat_dir));

• Compare with estimated performances

20Hz

data_cl = load(sprintf('%s/dynamics/2023-08-21_11-04_m0_cf_20Hz.mat', mat_dir));

• Compare with estimated performances

Different bandwidth for different directions

data_cl = load(sprintf('%s/dynamics/2023-08-21_11-16_m0_cf_different.mat', mat_dir));

• Compare with estimated performances

Dz 25Hz

data_cl = load(sprintf('%s/dynamics/', mat_dir));

• Compare with estimated performances

Better plant invert

Dy

%% Estimate resonance frequency and damping
for iter =1:Niter
    [G_est, poles, ~, frf_est] = vectfit3(G_cart(f>2&f<800,1,1).', 1i*2*pi*f(f>2&f<800)', poles, 1./(f(f>2&f<800))', opts);
end

Gfit_dy = ss(G_est.A, G_est.B, G_est.C, G_est.D);

Stable Inverse

Ginv_dy = inv(-flipRphZeros(Gfit_dy))/(1 + s/2/pi/1e3);
isstable(Ginv_dy)

Dz

%% Estimate resonance frequency and damping
for iter =1:Niter
    [G_est, poles, ~, frf_est] = vectfit3(G_cart(f>2&f<1500,2,2).', 1i*2*pi*f(f>2&f<1500)', poles, 1./(f(f>2&f<1500))', opts);
end

Gfit_dz = ss(G_est.A, G_est.B, G_est.C, G_est.D);

Stable Inverse

Ginv_dz = inv(-flipRphZeros(Gfit_dz))/(1 + s/2/pi/1e3);
isstable(Ginv_dz)

Ry

%% Estimate resonance frequency and damping
for iter =1:Niter
    [G_est, poles, ~, frf_est] = vectfit3(G_cart(f>2&f<800,3,3).', 1i*2*pi*f(f>2&f<800)', poles, 1./(f(f>2&f<800))', opts);
end

Gfit_ry = ss(G_est.A, G_est.B, G_est.C, G_est.D);

Stable Inverse

Ginv_ry = inv(flipRphZeros(Gfit_ry))/(1 + s/2/pi/1e3);
isstable(Ginv_ry)

Compare Invert plants

Save plant inverse

Compare Digital Invert plants

Control Performances

Better plant invert

data_cl = load(sprintf('%s/dynamics/2023-08-21_13-36_m0_cf_inv_fit.mat', mat_dir));

Scans with good controller

1rpm

1RPM scans are performed for all the masses with the same controller.

data_m0 = load(sprintf("%s/scans/2023-08-21_14-28_m0_1rpm_K_cf.mat", mat_dir));
data_m0.time = Ts*[0:length(data_m0.Rz)-1];

%% Compute RMS values while in closed-loop
data_m0.Dx_rms_cl = rms(detrend(data_m0.Dx_int, 0));
data_m0.Dy_rms_cl = rms(detrend(data_m0.Dy_int, 0));
data_m0.Dz_rms_cl = rms(detrend(data_m0.Dz_int, 0));
data_m0.Rx_rms_cl = rms(detrend(data_m0.Rx_int, 0));
data_m0.Ry_rms_cl = rms(detrend(data_m0.Ry_int, 0));

	Dx [nm]	Dy [nm]	Dz [nm]	Rx [nrad]	Ry [nrad]
m0	796	20	8	8209	73

30rpm

1RPM scans are performed for all the masses with the same controller.

data_m0 = load(sprintf("%s/scans/2023-08-21_14-33_m0_30rpm_cf_control.mat", mat_dir));
data_m0.time = Ts*[0:length(data_m0.Rz)-1];

%% Compute RMS values while in closed-loop
data_m0.Dx_rms_cl = rms(detrend(data_m0.Dx_int, 0));
data_m0.Dy_rms_cl = rms(detrend(data_m0.Dy_int, 0));
data_m0.Dz_rms_cl = rms(detrend(data_m0.Dz_int, 0));
data_m0.Rx_rms_cl = rms(detrend(data_m0.Rx_int, 0));
data_m0.Ry_rms_cl = rms(detrend(data_m0.Ry_int, 0));

	Dx [nm]	Dy [nm]	Dz [nm]	Rx [nrad]	Ry [nrad]
m0	820	39	13	7790	156

m1

3x3 plant in Cartesian plane

%% Jacobian for 3x3 plant
n_hexapod = initializeNanoHexapod('flex_bot_type', '2dof', ...
                                  'flex_top_type', '3dof', ...
                                  'motion_sensor_type', 'plates', ...
                                  'actuator_type', '2dof');

Jt_inv = pinv(n_hexapod.geometry.J');

J_int_to_X = [0.78740157480315  0.21259842519685  0                  0                  0;
              0                 0                 0                  0                 -1;
              0                 0               -13.1233595800525   13.1233595800525    0];

Compute identified plant in the Cartesian plane:

%% New data after calibrating the Rz-offset
data_m1 = load(sprintf('%s/dynamics/2023-08-21_19-05_damp_plant_m1_new_Rz.mat', mat_dir));

Compute plant model in the Cartesian plane:

Gm_cart_m1 = J_int_to_X*Gm_hac_m1({'d1', 'd2', 'd3', 'd4', 'd5'}, {'u1', 'u2', 'u3', 'u4', 'u5', 'u6'})*Jt_inv(:,[2,3,5]);
Gm_cart_m1.InputName = {'Fy', 'Fz', 'My'};
Gm_cart_m1.OutputName = {'Dy', 'Dz', 'Ry'};

Normalization of outputs:

Gm_cart_m1_normalized = -diag(1./diag(dcgain(Gm_cart_m1)))*Gm_cart_m1;
Gm_cart_m1_normalized.InputName = {'Fy', 'Fz', 'My'};
Gm_cart_m1_normalized.OutputName = {'Dy', 'Dz', 'Ry'};

G_cart_m1_normalized = permute(pagemtimes(-diag(1./diag(dcgain(Gm_cart_m1))), permute(G_cart_m1, [2,3,1])), [3,1,2]);

Better plant invert

N = 9; %Order of approximation

Dy

%% Estimate resonance frequency and damping
for iter =1:Niter
    [G_est, poles, ~, frf_est] = vectfit3(G_cart_m1(f>1&f<1500,1,1).', 1i*2*pi*f(f>1&f<1500)', poles, 1./sqrt(f(f>1&f<1500))', opts);
end

Gfit_dy = ss(G_est.A, G_est.B, G_est.C, G_est.D);

Stable Inverse

Ginv_dy = inv(flipRphZeros(Gfit_dy))/(1 + s/2/pi/1e3);
isstable(Ginv_dy)

Dz

%% Estimate resonance frequency and damping
for iter =1:Niter
    [G_est, poles, ~, frf_est] = vectfit3(G_cart_m1(f>2&f<1500,2,2).', 1i*2*pi*f(f>2&f<1500)', poles, 1./sqrt(f(f>2&f<1500))', opts);
end

Gfit_dz = ss(G_est.A, G_est.B, G_est.C, G_est.D);

Stable Inverse

Ginv_dz = inv(-flipRphZeros(Gfit_dz))/(1 + s/2/pi/1e3);
isstable(Ginv_dz)

Ry

%% Estimate resonance frequency and damping
for iter =1:Niter
    [G_est, poles, ~, frf_est] = vectfit3(G_cart_m1(f>2&f<800,3,3).', 1i*2*pi*f(f>2&f<800)', poles, 1./(f(f>2&f<800))', opts);
end

Gfit_ry = ss(G_est.A, G_est.B, G_est.C, G_est.D);

Stable Inverse

Ginv_ry = inv(flipRphZeros(Gfit_ry))/(1 + s/2/pi/1e3);
isstable(Ginv_ry)

Compare Invert plants

Save plant inverse

Compare Digital Invert plants

TODO Control Performances

Better plant invert

data_cl = load(sprintf('%s/dynamics/2023-08-21_13-36_m0_cf_inv_fit.mat', mat_dir));

TODO Scans with good controller

1rpm

1RPM scans are performed for all the masses with the same controller.

data_m0 = load(sprintf("%s/scans/2023-08-21_14-28_m0_1rpm_K_cf.mat", mat_dir));
data_m0.time = Ts*[0:length(data_m0.Rz)-1];

%% Compute RMS values while in closed-loop
data_m0.Dx_rms_cl = rms(detrend(data_m0.Dx_int, 0));
data_m0.Dy_rms_cl = rms(detrend(data_m0.Dy_int, 0));
data_m0.Dz_rms_cl = rms(detrend(data_m0.Dz_int, 0));
data_m0.Rx_rms_cl = rms(detrend(data_m0.Rx_int, 0));
data_m0.Ry_rms_cl = rms(detrend(data_m0.Ry_int, 0));

	Dx [nm]	Dy [nm]	Dz [nm]	Rx [nrad]	Ry [nrad]
m0	796	20	8	8209	73

30rpm

1RPM scans are performed for all the masses with the same controller.

data_m0 = load(sprintf("%s/scans/2023-08-21_14-33_m0_30rpm_cf_control.mat", mat_dir));
data_m0.time = Ts*[0:length(data_m0.Rz)-1];

%% Compute RMS values while in closed-loop
data_m0.Dx_rms_cl = rms(detrend(data_m0.Dx_int, 0));
data_m0.Dy_rms_cl = rms(detrend(data_m0.Dy_int, 0));
data_m0.Dz_rms_cl = rms(detrend(data_m0.Dz_int, 0));
data_m0.Rx_rms_cl = rms(detrend(data_m0.Rx_int, 0));
data_m0.Ry_rms_cl = rms(detrend(data_m0.Ry_int, 0));

	Dx [nm]	Dy [nm]	Dz [nm]	Rx [nrad]	Ry [nrad]
m0	820	39	13	7790	156

m2

3x3 plant in Cartesian plane

%% Jacobian for 3x3 plant
n_hexapod = initializeNanoHexapod('flex_bot_type', '2dof', ...
                                  'flex_top_type', '3dof', ...
                                  'motion_sensor_type', 'plates', ...
                                  'actuator_type', '2dof');

Jt_inv = pinv(n_hexapod.geometry.J');

J_int_to_X = [0.78740157480315  0.21259842519685  0                  0                  0;
              0                 0                 0                  0                 -1;
              0                 0               -13.1233595800525   13.1233595800525    0];

Compute identified plant in the Cartesian plane:

%% New data after calibrating the Rz-offset
data_m2 = load(sprintf('%s/dynamics/2023-08-21_17-32_damp_plant_m2_new_Rz.mat', mat_dir));

Compute plant model in the Cartesian plane:

Gm_cart_m2 = J_int_to_X*Gm_hac_m2({'d1', 'd2', 'd3', 'd4', 'd5'}, {'u1', 'u2', 'u3', 'u4', 'u5', 'u6'})*Jt_inv(:,[2,3,5]);
Gm_cart_m2.InputName = {'Fy', 'Fz', 'My'};
Gm_cart_m2.OutputName = {'Dy', 'Dz', 'Ry'};

Normalization of outputs:

Gm_cart_m2_normalized = -diag(1./diag(dcgain(Gm_cart_m2)))*Gm_cart_m2;
Gm_cart_m2_normalized.InputName = {'Fy', 'Fz', 'My'};
Gm_cart_m2_normalized.OutputName = {'Dy', 'Dz', 'Ry'};

G_cart_m2_normalized = permute(pagemtimes(-diag(1./diag(dcgain(Gm_cart_m2))), permute(G_cart_m2, [2,3,1])), [3,1,2]);

Better plant invert

N = 9; %Order of approximation

Dy

%% Estimate resonance frequency and damping
for iter =1:Niter
    [G_est, poles, ~, frf_est] = vectfit3(G_cart_m2(f>1&f<1500,1,1).', 1i*2*pi*f(f>1&f<1500)', poles, 1./sqrt(f(f>1&f<1500))', opts);
end

Gfit_dy = ss(G_est.A, G_est.B, G_est.C, G_est.D);

Stable Inverse

Ginv_dy = inv(-flipRphZeros(Gfit_dy))/(1 + s/2/pi/1e3);
isstable(Ginv_dy)

Dz

%% Estimate resonance frequency and damping
for iter =1:Niter
    [G_est, poles, ~, frf_est] = vectfit3(G_cart_m2(f>2&f<1500,2,2).', 1i*2*pi*f(f>2&f<1500)', poles, 1./(f(f>2&f<1500))', opts);
end

Gfit_dz = ss(G_est.A, G_est.B, G_est.C, G_est.D);

Stable Inverse

Ginv_dz = inv(-flipRphZeros(Gfit_dz))/(1 + s/2/pi/1e3);
isstable(Ginv_dz)

Ry

%% Estimate resonance frequency and damping
for iter =1:Niter
    [G_est, poles, ~, frf_est] = vectfit3(G_cart_m2(f>2&f<800,3,3).', 1i*2*pi*f(f>2&f<800)', poles, 1./(f(f>2&f<800))', opts);
end

Gfit_ry = ss(G_est.A, G_est.B, G_est.C, G_est.D);

Stable Inverse

Ginv_ry = inv(-flipRphZeros(Gfit_ry))/(1 + s/2/pi/1e3);
isstable(Ginv_ry)

Compare Invert plants

Save plant inverse

Compare Digital Invert plants

TODO Control Performances

Better plant invert

data_cl = load(sprintf('%s/dynamics/2023-08-21_13-36_m0_cf_inv_fit.mat', mat_dir));

TODO Scans with good controller

1rpm

1RPM scans are performed for all the masses with the same controller.

data_m0 = load(sprintf("%s/scans/2023-08-21_14-28_m0_1rpm_K_cf.mat", mat_dir));
data_m0.time = Ts*[0:length(data_m0.Rz)-1];

%% Compute RMS values while in closed-loop
data_m0.Dx_rms_cl = rms(detrend(data_m0.Dx_int, 0));
data_m0.Dy_rms_cl = rms(detrend(data_m0.Dy_int, 0));
data_m0.Dz_rms_cl = rms(detrend(data_m0.Dz_int, 0));
data_m0.Rx_rms_cl = rms(detrend(data_m0.Rx_int, 0));
data_m0.Ry_rms_cl = rms(detrend(data_m0.Ry_int, 0));

	Dx [nm]	Dy [nm]	Dz [nm]	Rx [nrad]	Ry [nrad]
m0	796	20	8	8209	73

30rpm

1RPM scans are performed for all the masses with the same controller.

data_m0 = load(sprintf("%s/scans/2023-08-21_14-33_m0_30rpm_cf_control.mat", mat_dir));
data_m0.time = Ts*[0:length(data_m0.Rz)-1];

%% Compute RMS values while in closed-loop
data_m0.Dx_rms_cl = rms(detrend(data_m0.Dx_int, 0));
data_m0.Dy_rms_cl = rms(detrend(data_m0.Dy_int, 0));
data_m0.Dz_rms_cl = rms(detrend(data_m0.Dz_int, 0));
data_m0.Rx_rms_cl = rms(detrend(data_m0.Rx_int, 0));
data_m0.Ry_rms_cl = rms(detrend(data_m0.Ry_int, 0));

	Dx [nm]	Dy [nm]	Dz [nm]	Rx [nrad]	Ry [nrad]
m0	820	39	13	7790	156

m3

3x3 plant in Cartesian plane

%% Jacobian for 3x3 plant
n_hexapod = initializeNanoHexapod('flex_bot_type', '2dof', ...
                                  'flex_top_type', '3dof', ...
                                  'motion_sensor_type', 'plates', ...
                                  'actuator_type', '2dof');

Jt_inv = pinv(n_hexapod.geometry.J');

J_int_to_X = [0.78740157480315  0.21259842519685  0                  0                  0;
              0                 0                 0                  0                 -1;
              0                 0               -13.1233595800525   13.1233595800525    0];

Compute identified plant in the Cartesian plane:

%% New data after calibrating the Rz-offset
data_m3 = load(sprintf('%s/dynamics/2023-08-21_16-33_damp_plant_m3_new_Rz_fast.mat', mat_dir));

Compute plant model in the Cartesian plane:

Gm_cart_m3 = J_int_to_X*Gm_hac_m3({'d1', 'd2', 'd3', 'd4', 'd5'}, {'u1', 'u2', 'u3', 'u4', 'u5', 'u6'})*Jt_inv(:,[2,3,5]);
Gm_cart_m3.InputName = {'Fy', 'Fz', 'My'};
Gm_cart_m3.OutputName = {'Dy', 'Dz', 'Ry'};

Normalization of outputs:

Gm_cart_m3_normalized = -diag(1./diag(dcgain(Gm_cart_m3)))*Gm_cart_m3;
Gm_cart_m3_normalized.InputName = {'Fy', 'Fz', 'My'};
Gm_cart_m3_normalized.OutputName = {'Dy', 'Dz', 'Ry'};

G_cart_m3_normalized = permute(pagemtimes(-diag(1./diag(dcgain(Gm_cart_m3))), permute(G_cart_m3, [2,3,1])), [3,1,2]);

Better plant invert

N = 9; %Order of approximation

Dy

%% Estimate resonance frequency and damping
for iter =1:Niter
    [G_est, poles, ~, frf_est] = vectfit3(G_cart_m3(f>2&f<800,1,1).', 1i*2*pi*f(f>2&f<800)', poles, 1./(f(f>2&f<800))', opts);
end

Gfit_dy = ss(G_est.A, G_est.B, G_est.C, G_est.D);

Stable Inverse

Ginv_dy = inv(flipRphZeros(Gfit_dy))/(1 + s/2/pi/1e3);
isstable(Ginv_dy)

Dz

%% Estimate resonance frequency and damping
for iter =1:Niter
    [G_est, poles, ~, frf_est] = vectfit3(G_cart_m3(f>2&f<1500,2,2).', 1i*2*pi*f(f>2&f<1500)', poles, 1./(f(f>2&f<1500))', opts);
end

Gfit_dz = ss(G_est.A, G_est.B, G_est.C, G_est.D);

Stable Inverse

Ginv_dz = inv(-flipRphZeros(Gfit_dz))/(1 + s/2/pi/1e3);
isstable(Ginv_dz)

Ry

%% Estimate resonance frequency and damping
for iter =1:Niter
    [G_est, poles, ~, frf_est] = vectfit3(G_cart_m3(f>2&f<800,3,3).', 1i*2*pi*f(f>2&f<800)', poles, 1./(f(f>2&f<800))', opts);
end

Gfit_ry = ss(G_est.A, G_est.B, G_est.C, G_est.D);

Stable Inverse

Ginv_ry = inv(-flipRphZeros(Gfit_ry))/(1 + s/2/pi/1e3);
isstable(Ginv_ry)

Compare Invert plants

Save plant inverse

Compare Digital Invert plants

TODO Control Performances

Better plant invert

data_cl = load(sprintf('%s/dynamics/2023-08-21_13-36_m0_cf_inv_fit.mat', mat_dir));

TODO Scans with good controller

1rpm

1RPM scans are performed for all the masses with the same controller.

data_m0 = load(sprintf("%s/scans/2023-08-21_14-28_m0_1rpm_K_cf.mat", mat_dir));
data_m0.time = Ts*[0:length(data_m0.Rz)-1];

%% Compute RMS values while in closed-loop
data_m0.Dx_rms_cl = rms(detrend(data_m0.Dx_int, 0));
data_m0.Dy_rms_cl = rms(detrend(data_m0.Dy_int, 0));
data_m0.Dz_rms_cl = rms(detrend(data_m0.Dz_int, 0));
data_m0.Rx_rms_cl = rms(detrend(data_m0.Rx_int, 0));
data_m0.Ry_rms_cl = rms(detrend(data_m0.Ry_int, 0));

	Dx [nm]	Dy [nm]	Dz [nm]	Rx [nrad]	Ry [nrad]
m0	796	20	8	8209	73

30rpm

1RPM scans are performed for all the masses with the same controller.

data_m0 = load(sprintf("%s/scans/2023-08-21_14-33_m0_30rpm_cf_control.mat", mat_dir));
data_m0.time = Ts*[0:length(data_m0.Rz)-1];

%% Compute RMS values while in closed-loop
data_m0.Dx_rms_cl = rms(detrend(data_m0.Dx_int, 0));
data_m0.Dy_rms_cl = rms(detrend(data_m0.Dy_int, 0));
data_m0.Dz_rms_cl = rms(detrend(data_m0.Dz_int, 0));
data_m0.Rx_rms_cl = rms(detrend(data_m0.Rx_int, 0));
data_m0.Ry_rms_cl = rms(detrend(data_m0.Ry_int, 0));

	Dx [nm]	Dy [nm]	Dz [nm]	Rx [nrad]	Ry [nrad]
m0	820	39	13	7790	156

Scans

<<sec:id31_scans>>

Introduction   ignore

• Section ref:sec:id31_scans_tomography
• Section ref:sec:id31_scans_dz
• Section ref:sec:id31_scans_reflectivity
• Section ref:sec:id31_scans_dy
• Section ref:sec:id31_scans_diffraction_tomo

$R_z$ scans: Tomography

<<sec:id31_scans_tomography>>

Introduction   ignore

m0: 30rpm, 6rpm, 1rpm m1: 6rpm, 1rpm m2: 6rpm, 1rpm m3: 1rpm

Robust Control - 1rpm

1RPM scans are performed for all the masses with the same robust controller.

%% Load Tomography scans with robust controller
data_tomo_1rpm_m0 = load(sprintf("%s/scans/2023-08-11_11-37_tomography_1rpm_m0.mat", mat_dir));
data_tomo_1rpm_m0.time = Ts*[0:length(data_tomo_1rpm_m0.Rz)-1];

data_tomo_1rpm_m1 = load(sprintf("%s/scans/2023-08-11_11-15_tomography_1rpm_m1.mat", mat_dir));
data_tomo_1rpm_m1.time = Ts*[0:length(data_tomo_1rpm_m1.Rz)-1];

data_tomo_1rpm_m2 = load(sprintf("%s/scans/2023-08-11_10-59_tomography_1rpm_m2.mat", mat_dir));
data_tomo_1rpm_m2.time = Ts*[0:length(data_tomo_1rpm_m2.Rz)-1];

data_tomo_1rpm_m3 = load(sprintf("%s/scans/2023-08-11_10-24_tomography_1rpm_m3.mat", mat_dir));
data_tomo_1rpm_m3.time = Ts*[0:length(data_tomo_1rpm_m3.Rz)-1];

The problem for these scans is that the position initialization was not make properly, so the open-loop errors are quite large (see Figure ref:fig:id31_tomo_1rpm_robust_m0).

$D_x$, $D_y$ and $D_z$ motion during a slow (1RPM) tomography experiment. Open Loop data is shown in blue and closed-loop data in red

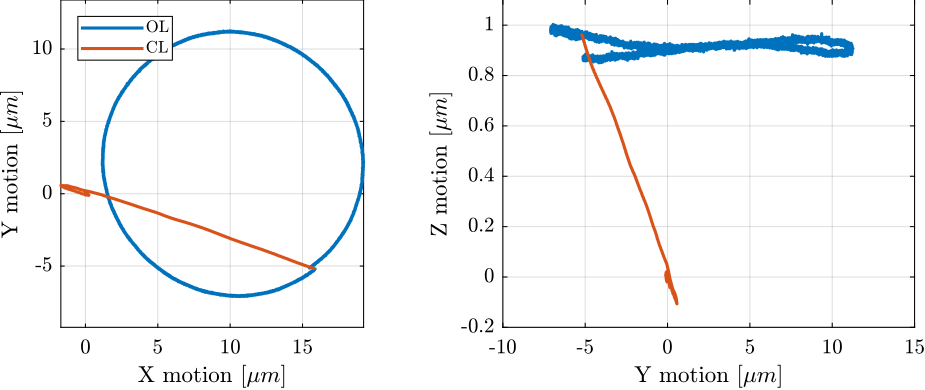
yztomographymovie('movies/tomography_1rpm_m0', data_tomo_1rpm_m0, 'xlim_ax1', [-10, 15], 'ylim_ax1', [-0.2, 1.2], 'xlim_ax2', [-300, 300], 'ylim_ax2', [-100, 100])
yztomographymovie('movies/tomography_1rpm_m0_di_5000', data_tomo_1rpm_m0, 'xlim_ax1', [-10, 15], 'ylim_ax1', [-0.2, 1.2], 'xlim_ax2', [-300, 300], 'ylim_ax2', [-100, 100], 'di', 5000)

The obtained open-loop and closed-loop errors are shown in tables ref:tab:id31_tomo_1rpm_robust_ol_errors and ref:tab:id31_tomo_1rpm_robust_cl_errors respectively.

%% Compute RMS values while in closed-loop and open-loop
[~, i_m0] = find(data_tomo_1rpm_m0.hac_status == 1);
data_tomo_1rpm_m0.Dx_rms_cl = rms(detrend(data_tomo_1rpm_m0.Dx_int(i_m0+50000:end), 0));
data_tomo_1rpm_m0.Dy_rms_cl = rms(detrend(data_tomo_1rpm_m0.Dy_int(i_m0+50000:end), 0));
data_tomo_1rpm_m0.Dz_rms_cl = rms(detrend(data_tomo_1rpm_m0.Dz_int(i_m0+50000:end), 0));
data_tomo_1rpm_m0.Rx_rms_cl = rms(detrend(data_tomo_1rpm_m0.Rx_int(i_m0+50000:end), 0));
data_tomo_1rpm_m0.Ry_rms_cl = rms(detrend(data_tomo_1rpm_m0.Ry_int(i_m0+50000:end), 0));

data_tomo_1rpm_m0.Dx_rms_ol = rms(detrend(data_tomo_1rpm_m0.Dx_int(1:i_m0), 0));
data_tomo_1rpm_m0.Dy_rms_ol = rms(detrend(data_tomo_1rpm_m0.Dy_int(1:i_m0), 0));
data_tomo_1rpm_m0.Dz_rms_ol = rms(detrend(data_tomo_1rpm_m0.Dz_int(1:i_m0), 0));
data_tomo_1rpm_m0.Rx_rms_ol = rms(detrend(data_tomo_1rpm_m0.Rx_int(1:i_m0), 0));
data_tomo_1rpm_m0.Ry_rms_ol = rms(detrend(data_tomo_1rpm_m0.Ry_int(1:i_m0), 0));

%% Compute RMS values while in closed-loop and open-loop
[~, i_m1] = find(data_tomo_1rpm_m1.hac_status == 1);
data_tomo_1rpm_m1.Dx_rms_cl = rms(detrend(data_tomo_1rpm_m1.Dx_int(i_m1+50000:end), 0));
data_tomo_1rpm_m1.Dy_rms_cl = rms(detrend(data_tomo_1rpm_m1.Dy_int(i_m1+50000:end), 0));
data_tomo_1rpm_m1.Dz_rms_cl = rms(detrend(data_tomo_1rpm_m1.Dz_int(i_m1+50000:end), 0));
data_tomo_1rpm_m1.Rx_rms_cl = rms(detrend(data_tomo_1rpm_m1.Rx_int(i_m1+50000:end), 0));
data_tomo_1rpm_m1.Ry_rms_cl = rms(detrend(data_tomo_1rpm_m1.Ry_int(i_m1+50000:end), 0));

data_tomo_1rpm_m1.Dx_rms_ol = rms(detrend(data_tomo_1rpm_m1.Dx_int(1:i_m1), 0));
data_tomo_1rpm_m1.Dy_rms_ol = rms(detrend(data_tomo_1rpm_m1.Dy_int(1:i_m1), 0));
data_tomo_1rpm_m1.Dz_rms_ol = rms(detrend(data_tomo_1rpm_m1.Dz_int(1:i_m1), 0));
data_tomo_1rpm_m1.Rx_rms_ol = rms(detrend(data_tomo_1rpm_m1.Rx_int(1:i_m1), 0));
data_tomo_1rpm_m1.Ry_rms_ol = rms(detrend(data_tomo_1rpm_m1.Ry_int(1:i_m1), 0));

%% Compute RMS values while in closed-loop and open-loop
[~, i_m2] = find(data_tomo_1rpm_m2.hac_status == 1);
data_tomo_1rpm_m2.Dx_rms_cl = rms(detrend(data_tomo_1rpm_m2.Dx_int(i_m2+50000:end), 0));
data_tomo_1rpm_m2.Dy_rms_cl = rms(detrend(data_tomo_1rpm_m2.Dy_int(i_m2+50000:end), 0));
data_tomo_1rpm_m2.Dz_rms_cl = rms(detrend(data_tomo_1rpm_m2.Dz_int(i_m2+50000:end), 0));
data_tomo_1rpm_m2.Rx_rms_cl = rms(detrend(data_tomo_1rpm_m2.Rx_int(i_m2+50000:end), 0));
data_tomo_1rpm_m2.Ry_rms_cl = rms(detrend(data_tomo_1rpm_m2.Ry_int(i_m2+50000:end), 0));

data_tomo_1rpm_m2.Dx_rms_ol = rms(detrend(data_tomo_1rpm_m2.Dx_int(1:i_m2), 0));
data_tomo_1rpm_m2.Dy_rms_ol = rms(detrend(data_tomo_1rpm_m2.Dy_int(1:i_m2), 0));
data_tomo_1rpm_m2.Dz_rms_ol = rms(detrend(data_tomo_1rpm_m2.Dz_int(1:i_m2), 0));
data_tomo_1rpm_m2.Rx_rms_ol = rms(detrend(data_tomo_1rpm_m2.Rx_int(1:i_m2), 0));
data_tomo_1rpm_m2.Ry_rms_ol = rms(detrend(data_tomo_1rpm_m2.Ry_int(1:i_m2), 0));

%% Compute RMS values while in closed-loop and open-loop
[~, i_m3] = find(data_tomo_1rpm_m3.hac_status == 1);
data_tomo_1rpm_m3.Dx_rms_cl = rms(detrend(data_tomo_1rpm_m3.Dx_int(i_m3+50000:end), 0));
data_tomo_1rpm_m3.Dy_rms_cl = rms(detrend(data_tomo_1rpm_m3.Dy_int(i_m3+50000:end), 0));
data_tomo_1rpm_m3.Dz_rms_cl = rms(detrend(data_tomo_1rpm_m3.Dz_int(i_m3+50000:end), 0));
data_tomo_1rpm_m3.Rx_rms_cl = rms(detrend(data_tomo_1rpm_m3.Rx_int(i_m3+50000:end), 0));
data_tomo_1rpm_m3.Ry_rms_cl = rms(detrend(data_tomo_1rpm_m3.Ry_int(i_m3+50000:end), 0));

data_tomo_1rpm_m3.Dx_rms_ol = rms(detrend(data_tomo_1rpm_m3.Dx_int(1:i_m3), 0));
data_tomo_1rpm_m3.Dy_rms_ol = rms(detrend(data_tomo_1rpm_m3.Dy_int(1:i_m3), 0));
data_tomo_1rpm_m3.Dz_rms_ol = rms(detrend(data_tomo_1rpm_m3.Dz_int(1:i_m3), 0));
data_tomo_1rpm_m3.Rx_rms_ol = rms(detrend(data_tomo_1rpm_m3.Rx_int(1:i_m3), 0));
data_tomo_1rpm_m3.Ry_rms_ol = rms(detrend(data_tomo_1rpm_m3.Ry_int(1:i_m3), 0));

	$D_x$ [$\mu m$]	$D_y$ [$\mu m$]	$D_z$ [$nm$]	$R_x$ [$\mu\text{rad}$]	$R_y$ [$\mu\text{rad}$]
$m_0$	6	6	32	34	34
$m_1$	6	7	26	51	55
$m_2$	36	38	36	259	253
$m_3$	31	33	38	214	203

	$D_x$ [nm]	$D_y$ [nm]	$D_z$ [nm]	$R_x$ [nrad]	$R_y$ [nrad]
$m_0$	13	15	5	57	55
$m_1$	16	25	6	102	55
$m_2$	25	25	7	120	103
$m_3$	40	53	9	225	169

Robust Control - 6rpm

data_tomo_6rpm_m0 = load(sprintf("%s/scans/2023-08-11_11-31_tomography_6rpm_m0.mat", mat_dir));
data_tomo_6rpm_m0.time = Ts*[0:length(data_tomo_6rpm_m0.Rz)-1];

data_tomo_6rpm_m1 = load(sprintf("%s/scans/2023-08-11_11-23_tomography_6rpm_m1.mat", mat_dir));
data_tomo_6rpm_m1.time = Ts*[0:length(data_tomo_6rpm_m1.Rz)-1];

%% Compute RMS values while in closed-loop
[~, i_m0] = find(data_tomo_6rpm_m0.hac_status == 1);
data_tomo_6rpm_m0.Dx_rms_cl = rms(detrend(data_tomo_6rpm_m0.Dx_int(i_m0+50000:end), 0));
data_tomo_6rpm_m0.Dy_rms_cl = rms(detrend(data_tomo_6rpm_m0.Dy_int(i_m0+50000:end), 0));
data_tomo_6rpm_m0.Dz_rms_cl = rms(detrend(data_tomo_6rpm_m0.Dz_int(i_m0+50000:end), 0));
data_tomo_6rpm_m0.Rx_rms_cl = rms(detrend(data_tomo_6rpm_m0.Rx_int(i_m0+50000:end), 0));
data_tomo_6rpm_m0.Ry_rms_cl = rms(detrend(data_tomo_6rpm_m0.Ry_int(i_m0+50000:end), 0));

data_tomo_6rpm_m0.Dx_rms_ol = rms(detrend(data_tomo_6rpm_m0.Dx_int(1:i_m0), 0));
data_tomo_6rpm_m0.Dy_rms_ol = rms(detrend(data_tomo_6rpm_m0.Dy_int(1:i_m0), 0));
data_tomo_6rpm_m0.Dz_rms_ol = rms(detrend(data_tomo_6rpm_m0.Dz_int(1:i_m0), 0));
data_tomo_6rpm_m0.Rx_rms_ol = rms(detrend(data_tomo_6rpm_m0.Rx_int(1:i_m0), 0));
data_tomo_6rpm_m0.Ry_rms_ol = rms(detrend(data_tomo_6rpm_m0.Ry_int(1:i_m0), 0));

%% Compute RMS values while in closed-loop
[~, i_m1] = find(data_tomo_6rpm_m1.hac_status == 1);
data_tomo_6rpm_m1.Dx_rms_cl = rms(detrend(data_tomo_6rpm_m1.Dx_int(i_m1+50000:end), 0));
data_tomo_6rpm_m1.Dy_rms_cl = rms(detrend(data_tomo_6rpm_m1.Dy_int(i_m1+50000:end), 0));
data_tomo_6rpm_m1.Dz_rms_cl = rms(detrend(data_tomo_6rpm_m1.Dz_int(i_m1+50000:end), 0));
data_tomo_6rpm_m1.Rx_rms_cl = rms(detrend(data_tomo_6rpm_m1.Rx_int(i_m1+50000:end), 0));
data_tomo_6rpm_m1.Ry_rms_cl = rms(detrend(data_tomo_6rpm_m1.Ry_int(i_m1+50000:end), 0));

data_tomo_6rpm_m1.Dx_rms_ol = rms(detrend(data_tomo_6rpm_m1.Dx_int(1:i_m1), 0));
data_tomo_6rpm_m1.Dy_rms_ol = rms(detrend(data_tomo_6rpm_m1.Dy_int(1:i_m1), 0));
data_tomo_6rpm_m1.Dz_rms_ol = rms(detrend(data_tomo_6rpm_m1.Dz_int(1:i_m1), 0));
data_tomo_6rpm_m1.Rx_rms_ol = rms(detrend(data_tomo_6rpm_m1.Rx_int(1:i_m1), 0));
data_tomo_6rpm_m1.Ry_rms_ol = rms(detrend(data_tomo_6rpm_m1.Ry_int(1:i_m1), 0));

	$D_x$ [$\mu m$]	$D_y$ [$\mu m$]	$D_z$ [$nm$]	$R_x$ [$\mu\text{rad}$]	$R_y$ [$\mu\text{rad}$]
$m_0$	8	7	20	41	41
$m_1$	4	4	21	39	39

	$D_x$ [nm]	$D_y$ [nm]	$D_z$ [nm]	$R_x$ [nrad]	$R_y$ [nrad]
$m_0$	17	19	5	70	73
$m_1$	20	26	7	110	77

Robust Control - 30rpm

%% Load Data
data_tomo_30rpm_m0 = load(sprintf("%s/scans/2023-08-17_15-26_tomography_30rpm_m0_robust.mat", mat_dir));
data_tomo_30rpm_m0.time = Ts*[0:length(data_tomo_30rpm_m0.Rz)-1];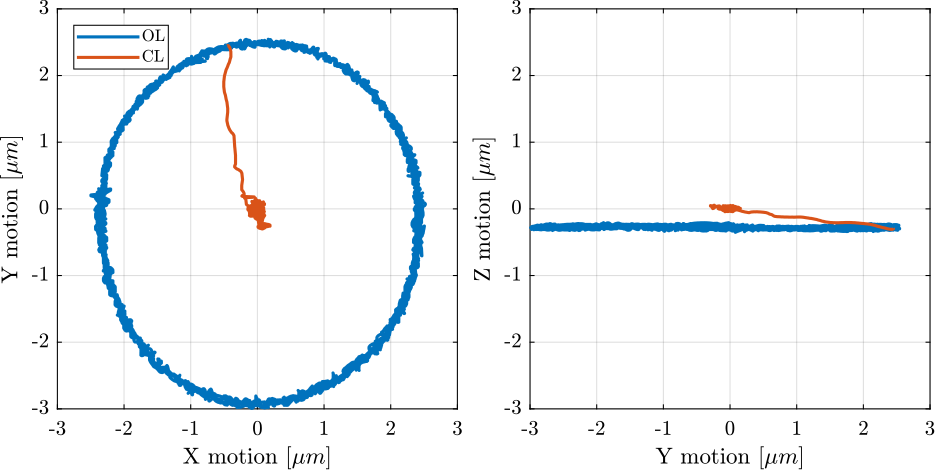

Measured motion during tomography scan at 30RPM with a robust controller

%% Compute RMS values while in closed-loop
[~, i_m0] = find(data_tomo_30rpm_m0.hac_status == 1);
data_tomo_30rpm_m0.Dx_rms_cl = rms(detrend(data_tomo_30rpm_m0.Dx_int(i_m0+50000:end), 0));
data_tomo_30rpm_m0.Dy_rms_cl = rms(detrend(data_tomo_30rpm_m0.Dy_int(i_m0+50000:end), 0));
data_tomo_30rpm_m0.Dz_rms_cl = rms(detrend(data_tomo_30rpm_m0.Dz_int(i_m0+50000:end), 0));
data_tomo_30rpm_m0.Rx_rms_cl = rms(detrend(data_tomo_30rpm_m0.Rx_int(i_m0+50000:end), 0));
data_tomo_30rpm_m0.Ry_rms_cl = rms(detrend(data_tomo_30rpm_m0.Ry_int(i_m0+50000:end), 0));

data_tomo_30rpm_m0.Dx_rms_ol = rms(detrend(data_tomo_30rpm_m0.Dx_int(1:i_m0), 0));
data_tomo_30rpm_m0.Dy_rms_ol = rms(detrend(data_tomo_30rpm_m0.Dy_int(1:i_m0), 0));
data_tomo_30rpm_m0.Dz_rms_ol = rms(detrend(data_tomo_30rpm_m0.Dz_int(1:i_m0), 0));
data_tomo_30rpm_m0.Rx_rms_ol = rms(detrend(data_tomo_30rpm_m0.Rx_int(1:i_m0), 0));
data_tomo_30rpm_m0.Ry_rms_ol = rms(detrend(data_tomo_30rpm_m0.Ry_int(1:i_m0), 0));

	$D_x$ [$\mu m$]	$D_y$ [$\mu m$]	$D_z$ [$nm$]	$R_x$ [$\mu\text{rad}$]	$R_y$ [$\mu\text{rad}$]
$m_0$	2	2	24	10	10

	$D_x$ [nm]	$D_y$ [nm]	$D_z$ [nm]	$R_x$ [nrad]	$R_y$ [nrad]
$m_0$	34	38	10	127	129

$D_z$ scans: Dirty Layer Scans

<<sec:id31_scans_dz>>

Step by Step $D_z$ motion

%% Load Dz MIM data
data_dz_steps_3nm = load(sprintf("%s/scans/2023-08-18_14-57_dz_mim_3_nm.mat", mat_dir));
data_dz_steps_3nm.time = Ts*[0:length(data_dz_steps_3nm.Dz_int)-1];

data_dz_steps_10nm = load(sprintf("%s/scans/2023-08-18_14-57_dz_mim_10_nm.mat", mat_dir));
data_dz_steps_10nm.time = Ts*[0:length(data_dz_steps_10nm.Dz_int)-1];

data_dz_steps_100nm = load(sprintf("%s/scans/2023-08-18_14-57_dz_mim_100_nm.mat", mat_dir));
data_dz_steps_100nm.time = Ts*[0:length(data_dz_steps_100nm.Dz_int)-1];

data_dz_steps_1000nm = load(sprintf("%s/scans/2023-08-18_14-57_dz_mim_1000_nm.mat", mat_dir));
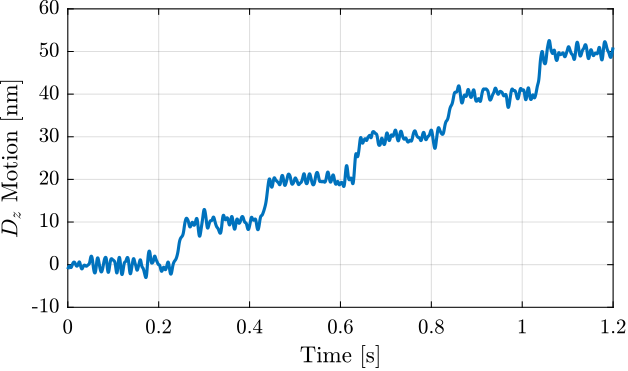
data_dz_steps_1000nm.time = Ts*[0:length(data_dz_steps_1000nm.Dz_int)-1];

Three step sizes are tested:

• $10\,nm$ steps (Figure ref:fig:id31_dz_mim_10nm_steps)
• $100\,nm$ steps (Figure ref:fig:id31_dz_mim_100nm_steps)
• $1\,\mu m$ steps (Figure ref:fig:id31_dz_steps_response)

Dz MIM test with 10nm steps (low pass filter with cut-off frequency of 10Hz is applied)

Dz MIM test with 100nm steps

$D_z$ step response - Stabilization time is around 70ms

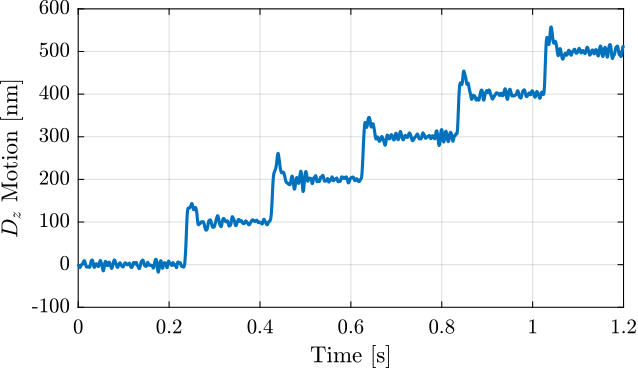
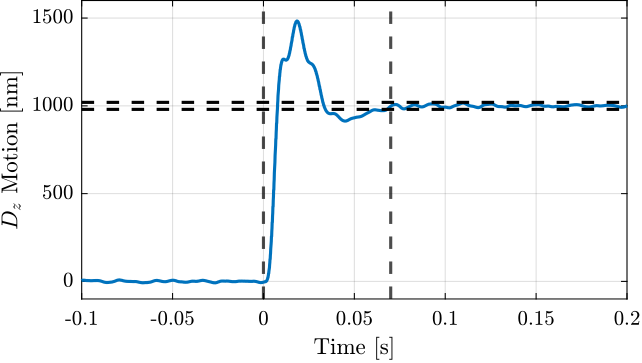
Continuous $D_z$ motion: Dirty Layer Scans

data_dz_10ums = load(sprintf("%s/scans/2023-08-18_15-33_dirty_layer_m0_small.mat", mat_dir));
data_dz_10ums.time = Ts*[0:length(data_dz_10ums.Dz_int)-1];

data_dz_100ums = load(sprintf("%s/scans/2023-08-18_15-32_dirty_layer_m0.mat", mat_dir));
data_dz_100ums.time = Ts*[0:length(data_dz_100ums.Dz_int)-1];

Two $D_z$ scans are performed:

• at $10\,\mu m/s$ in Figure ref:fig:id31_dirty_layer_scan_m0
• at $100\,\mu m/s$ in Figure ref:fig:id31_dirty_layer_scan_m0_large

Dirty layer scan: $D_z$ motion at $10\,\mu m/s$

Dirty layer scan: $D_z$ motion at $100\,\mu m/s$

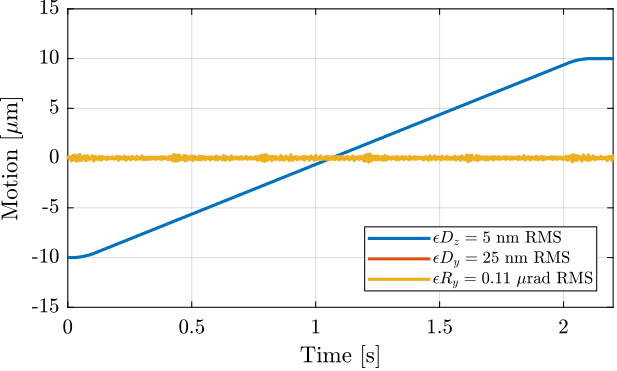
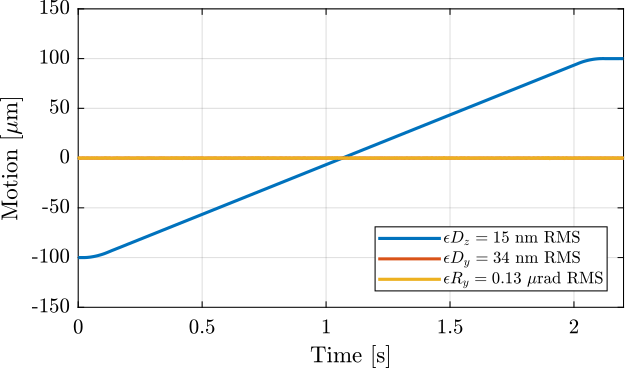
%% Not so good results with the CF controller
data_cf = load(sprintf("%s/scans/2023-08-21_19-20_dirty_layer_m1_cf.mat", mat_dir));
data_cf.time = Ts*[0:length(data_cf.Dz_int)-1];

$R_y$ scans: Reflectivity

<<sec:id31_scans_reflectivity>>

%% Load data for the reflectivity scan
data_ry = load(sprintf("%s/scans/2023-08-18_15-24_first_reflectivity_m0.mat", mat_dir));
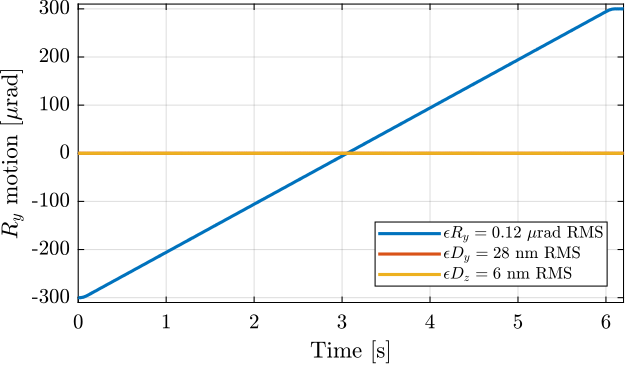
data_ry.time = Ts*[0:length(data_ry.Ry_int)-1];

An $R_y$ scan is performed at $100\,\mu rad/s$ velocity (Figure ref:fig:id31_reflectivity_scan_Ry_100urads). During the $R_y$ scan, the errors in $D_y$ are $D_z$ are kept small.

$R_y$ reflecitivity scan at $100\,\mu\text{rad}/s$ velocity

$D_y$ Scans

<<sec:id31_scans_dy>>

Introduction   ignore

The steps generated by the IcePAP for the $T_y$ stage are send to the Speedgoat. Then, we can know in real time what is the wanted position in $D_y$ during $T_y$ scans.

Open Loop

%% Slow Ty scan (10um/s)
data_ty_ol_slow = load(sprintf("%s/scans/2023-08-21_20-05_ty_scan_m1_open_loop_slow.mat", mat_dir));
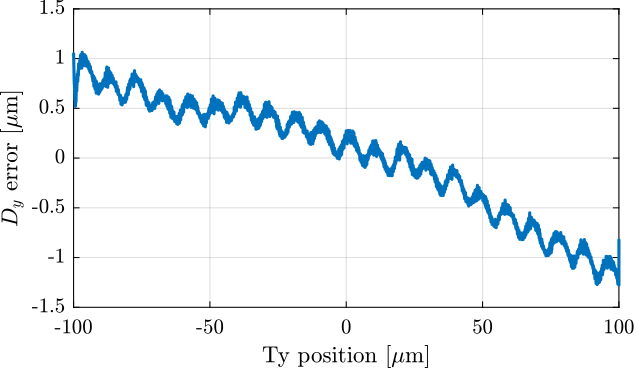
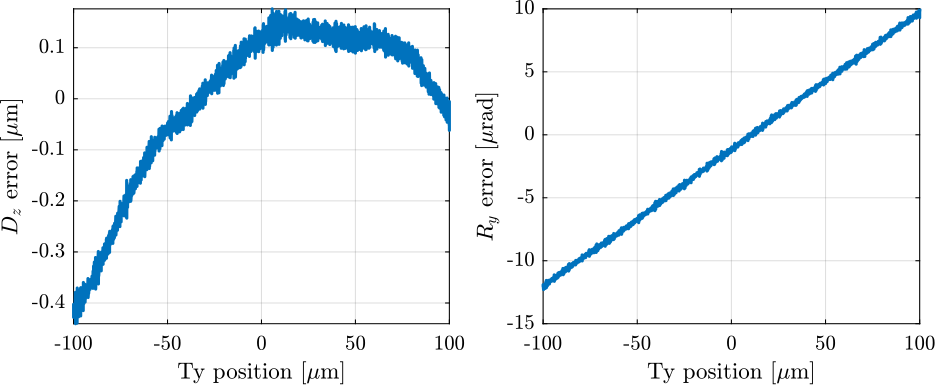
data_ty_ol_slow.time = Ts*[0:length(data_ty_ol_slow.Dy_int)-1];

We can clearly see micro-stepping errors of the stepper motor used for the $T_y$ stage. The errors have a period of $10\,\mu m$ with an amplitude of $\pm 100\,nm$.

$T_y$ scan (at $10\,\mu m/s$) - $D_y$ errors. The micro-stepping errors can clearly be seen with a period of $10\,\mu m$ and an amplitude of $\pm 100\,nm$

$T_y$ scan (at $10\,\mu m/s$) - $D_z$ and $R_y$ errors. The $D_z$ error is most likely due to having the top interferometer pointing to a sphere. The large $R_y$ errors might also be due to the metrology system

Closed Loop

%% Slow Ty scan (10um/s) - CL
data_ty_cl_slow = load(sprintf("%s/scans/2023-08-21_20-07_ty_scan_m1_cf_closed_loop_slow.mat", mat_dir));
data_ty_cl_slow.time = Ts*[0:length(data_ty_cl_slow.Dy_int)-1];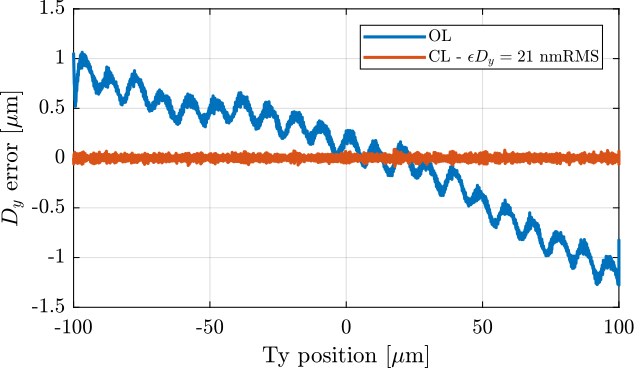

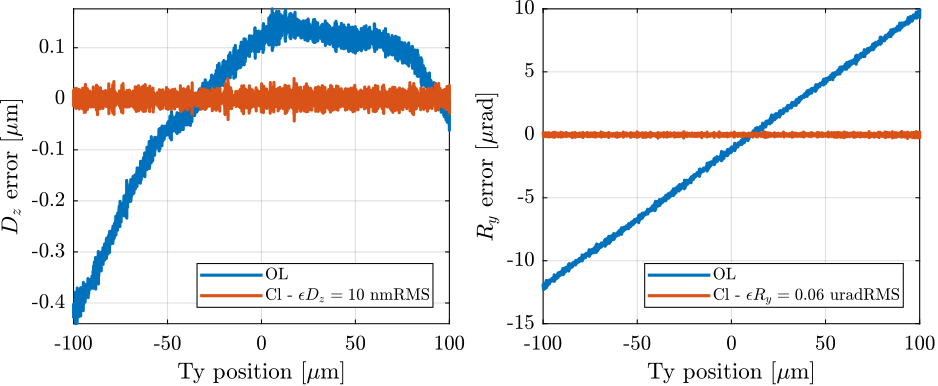
$T_y$ scan (at $10\,\mu m/s$) - $D_y$ errors. Open-loop and Closed-loop scans

$T_y$ scan (at $10\,\mu m/s$) - $D_z$ and $R_y$ errors. Open-loop and Closed-loop scans

Faster Scan

%% Fast Ty scan (100um/s) - OL
data_ty_ol_fast = load(sprintf("%s/scans/2023-08-21_20-05_ty_scan_m1_open_loop.mat", mat_dir));
data_ty_ol_fast.time = Ts*[0:length(data_ty_ol_fast.Dy_int)-1];

%% Fast Ty scan (10um/s) - CL
data_ty_cl_fast = load(sprintf("%s/scans/2023-08-21_20-07_ty_scan_m1_cf_closed_loop.mat", mat_dir));
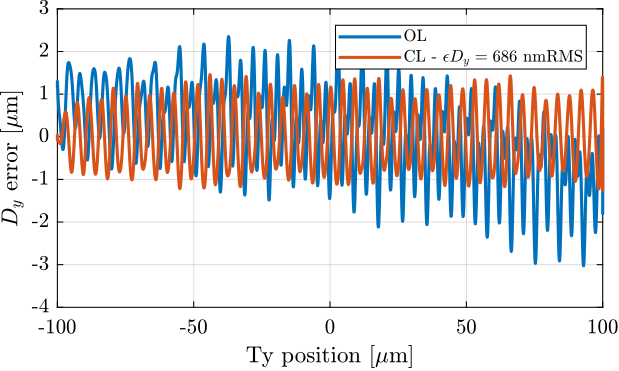
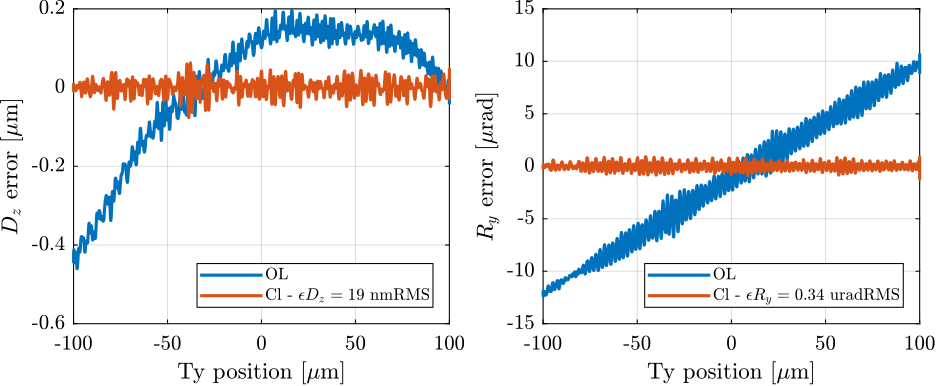
data_ty_cl_fast.time = Ts*[0:length(data_ty_cl_fast.Dy_int)-1];

Because of micro-stepping errors of the Ty stepper motor, when scanning at high velocity this induce high frequency vibration that are outside the bandwidth of the feedback controller.

At $100\,\mu m/s$, the micro-stepping errors with a period of $10\,\mu m$ (see Figure ref:fig:id31_ty_scan_10ums_ol_dy_errors) are at 10Hz. These errors are them amplified by some resonances in the system.

This could be easily solved by changing the stepper motor for a torque motor for instance.

$T_y$ scan (at $100\,\mu m/s$) - $D_y$ errors. Open-loop and Closed-loop scans

$T_y$ scan (at $100\,\mu m/s$) - $D_z$ and $R_y$ errors. Open-loop and Closed-loop scans

Combined $R_z$ and $D_y$: Diffraction Tomography

<<sec:id31_scans_diffraction_tomo>> Instead of doing a fast $R_z$ motion a slow $D_y$, the idea is to perform slow $R_z$ (here 1rpm) and fast $D_y$ scans with the nano-hexapod.

%% 100um/s - Robust controller
data_dt_100ums = load(sprintf("%s/scans/2023-08-18_17-12_diffraction_tomo_m0.mat", mat_dir));
data_dt_100ums.time = Ts*[0:length(data_dt_100ums.Dy_int)-1];

%% 500um/s - Robust controller (Not used)
% data_dt_500ums = load(sprintf("%s/scans/2023-08-18_17-19_diffraction_tomo_m0_fast.mat", mat_dir));
% data_dt_500ums.time = Ts*[0:length(data_dt_500ums.Dy_int)-1];

%% 500um/s - Complementary filters
data_dt_500ums = load(sprintf("%s/scans/2023-08-21_15-15_diffraction_tomo_m0_fast_cf.mat", mat_dir));
data_dt_500ums.time = Ts*[0:length(data_dt_500ums.Dy_int)-1];

%% 1mm/s - Complementary filters
data_dt_1000ums = load(sprintf("%s/scans/2023-08-21_15-16_diffraction_tomo_m0_fast_cf.mat", mat_dir));
data_dt_1000ums.time = Ts*[0:length(data_dt_1000ums.Dy_int)-1];

%% 5mm/s - Complementary filters
% data_dt_5000ums = load(sprintf("%s/scans/2023-08-21_18-03_diffraction_tomo_m2_fast_cf.mat", mat_dir));
% data_dt_5000ums.time = Ts*[0:length(data_dt_5000ums.Dy_int)-1];

%% 10mm/s - Complementary filters
data_dt_10000ums = load(sprintf("%s/scans/2023-08-21_15-17_diffraction_tomo_m0_fast_cf.mat", mat_dir));
data_dt_10000ums.time = Ts*[0:length(data_dt_10000ums.Dy_int)-1];

Here, the $D_y$ scans are performed only with the nano-hexapod (the Ty stage is not moving), so we are limited to $\pm 100\,\mu m$.

Several $D_y$ velocities are tested: $0.1\,mm/s$, $0.5\,mm/s$, $1\,mm/s$ and $10\,mm/s$ (see Figure ref:fig:id31_diffraction_tomo_velocities).

Dy motion for several configured velocities

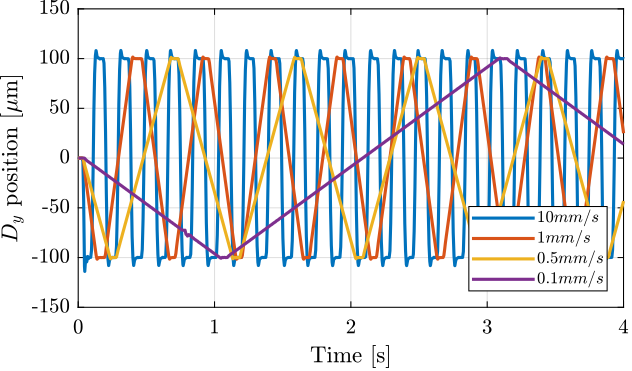
The corresponding "repetition rate" and $D_y$ scan per spindle turn are shown in Table ref:tab:diffraction_tomo_velocities.

The main issue here is the "waiting" time between two scans that is in the order of 50ms. By removing this waiting time (fairly easily), we can double the repetition rate at 10mm/s.

$D_y$ Velocity	Repetition rate	Scans per turn (at 1RPM)
0.1 mm/s	4 s	15
0.5 mm/s	0.9 s	65
1 mm/s	0.5 s	120
10 mm/s	0.18 s	330

The scan results for a velocity of 1mm/s is shown in Figure ref:fig:id31_diffraction_tomo_1mms. The $D_z$ and $R_y$ errors are quite small during the scan.

The $D_y$ errors are quite large as the velocity is increased. This type of scan can probably be massively improved by using feed-forward and optimizing the trajectory. Also, if the detectors are triggered in position (the Speedgoat could generate an encoder signal for instance), we don't care about the $D_y$ errors.

Diffraction tomography with Dy velocity of 1mm/s and Rz velocity of 1RPM

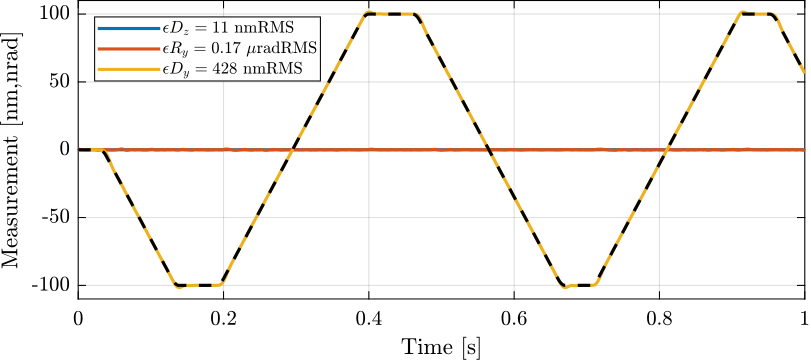
Velocity	$D_y$ [nmRMS]	$D_z$ [nmRMS]	$R_y$ [$\mu\text{radRMS}$]
0.1 mm/s	75.5	9.1	0.1
0.5 mm/s	190.5	10.0	0.1
1 mm/s	428.0	11.2	0.2
10 mm/s	4639.9	55.9	1.4

Summary of experiments

For each conducted experiments, the $D_y$, $D_z$ and $R_y$ errors are computed and summarized in Table ref:tab:id31_experiments_results_summary.

%% Summary of results
data_results = [...
    1e9*data_tomo_1rpm_m0.Dy_rms_cl,                                      1e9*data_tomo_1rpm_m0.Dz_rms_cl,            1e9*data_tomo_1rpm_m0.Ry_rms_cl           ; ... % Tomo 1rpm
    1e9*data_tomo_6rpm_m0.Dy_rms_cl,                                      1e9*data_tomo_6rpm_m0.Dz_rms_cl,            1e9*data_tomo_6rpm_m0.Ry_rms_cl           ; ... % Tomo 6rpm
    1e9*data_tomo_30rpm_m0.Dy_rms_cl,                                     1e9*data_tomo_30rpm_m0.Dz_rms_cl,           1e9*data_tomo_30rpm_m0.Ry_rms_cl          ; ... % Tomo 30rpm
    1e9*rms(detrend(data_dz_10ums.e_dy, 0)),                              1e9*rms(detrend(data_dz_10ums.e_dz, 0)),    1e9*rms(detrend(data_dz_10ums.e_ry, 0))   ; ... % Dz 10um/s
    1e9*rms(detrend(data_dz_100ums.e_dy,0)),                              1e9*rms(detrend(data_dz_100ums.e_dz,0)),    1e9*rms(detrend(data_dz_100ums.e_ry,0))   ; ... % Dz 100um/s
    1e9*rms(detrend(data_ry.e_dy,0)),                                     1e9*rms(detrend(data_ry.e_dz,0)),           1e9*rms(detrend(data_ry.e_ry,0))          ; ... % Ry 100urad/s
    1e9*rms(detrend(data_ty_cl_slow.e_dy, 0)),                            1e9*rms(detrend(data_ty_cl_slow.e_dz, 0)),  1e9*rms(detrend(data_ty_cl_slow.e_rz, 0)) ; ... % Dy 10 um/s
    1e9*rms(detrend(data_dt_100ums.Dy_int-data_dt_100ums.m_hexa_dy,  0)), 1e9*rms(detrend(data_dt_100ums.Dz_int, 0)), 1e9*rms(detrend(data_dt_100ums.Ry_int, 0)); ... % Diffraction tomo 0.1mm/s
    1e9*rms(detrend(data_dt_1000ums.Dy_int-data_dt_1000ums.m_hexa_dy,0)), 1e9*rms(detrend(data_dt_1000ums.Dz_int,0)), 1e9*rms(detrend(data_dt_1000ums.Ry_int,0))  ... % Diffraction tomo 1mm/s
];

	$D_y$ [nmRMS]	$D_z$ [nmRMS]	$R_y$ [nradRMS]
Tomography ($R_z$ 1rpm)	15	5	55
Tomography ($R_z$ 6rpm)	19	5	73
Tomography ($R_z$ 30rpm)	38	10	129
Dirty Layer ($D_z$ $10\,\mu m/s$)	25	5	114
Dirty Layer ($D_z$ $100\,\mu m/s$)	34	15	130
Reflectivity ($R_y$ $100\,\mu\text{rad}/s$)	28	6	118
Lateral Scan ($D_y$ $10\,\mu m/s$)	21	10	37
Diffraction Tomography ($R_z$ 1rpm, $D_y$ 0.1mm/s)	75	9	118
Diffraction Tomography ($R_z$ 1rpm, $D_y$ 1mm/s)	428	11	169

Bibliography   ignore