137 KiB
Test Bench - Amplified Piezoelectric Actuator
- Introduction
- Model of the Amplified Piezoelectric Actuator
- First Basic Measurements
- Dynamical measurements - APA
- Test Bench APA300ML - Simscape Model
- Conclusion
- Bibliography
This report is also available as a pdf.
Introduction ignore
The first goal is to characterize the APA300ML in terms of:
- The, geometric features, electrical capacitance, stroke, hysteresis, spurious resonances. This is performed in Section ref:sec:first_measurements.
- The dynamics from the generated DAC voltage (going to the voltage amplifiers and then applied on the actuator stacks) to the induced displacement, and to the measured voltage by the force sensor stack. Also the "actuator constant" and "sensor constant" are identified. This is done in Section ref:sec:dynamical_meas_apa.
- Compare the measurements with the Simscape models (2DoF, Super-Element) in order to tuned/validate the models. This is explained in Section ref:sec:simscape_bench_apa.
| Sections | Matlab File |
|---|---|
| Section ref:sec:test_bench_apa_ | test_bench_apa_1_.m |
Model of the Amplified Piezoelectric Actuator
<<sec:model_apa>>
Introduction ignore
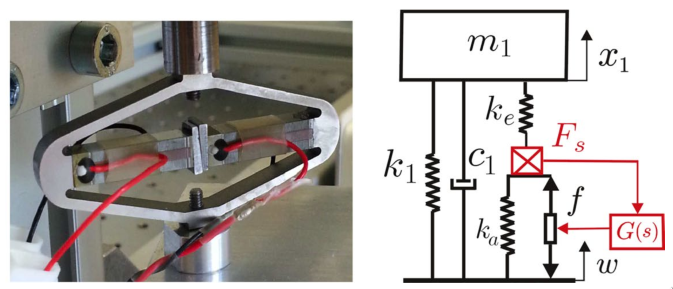
The Amplified Piezoelectric Actuator (APA) used is the APA300ML from Cedrat technologies (Figure fig:apa300ML).
Two simscape models of the APA300ML are developed:
- Section ref:sec:apa_2dof_model: a simple 2 degrees of freedom (DoF) model
- Section ref:sec:apa_flexible_model: a "flexible" model using a "super-element" extracted from a Finite Element Model of the APA
For both models, an "actuator constant" and a "sensor constant" are used. These constants are used to link the electrical domain and the mechanical domain. They are described in Section ref:sec:apa_constants.
Two Degrees of Freedom Model
<<sec:apa_2dof_model>>
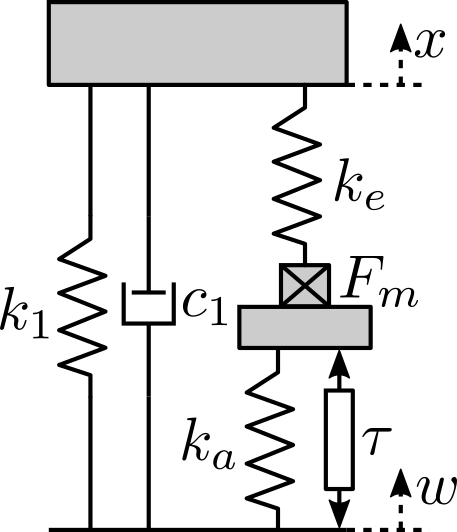
The presented model is based on cite:souleille18_concep_activ_mount_space_applic and represented in Figure ref:fig:souleille18_model_piezo.
The parameters are described in Table ref:tab:souleille18_model_params.
| Meaning | |
|---|---|
| $k_e$ | Stiffness used to adjust the pole of the isolator |
| $k_1$ | Stiffness of the metallic suspension when the stack is removed |
| $k_a$ | Stiffness of the actuator |
| $c_1$ | Added viscous damping |
The model is shown again in Figure ref:fig:2dof_apa_model. As will be shown in the next section, such model can be quite accurate in modelling the axial behavior of the APA. However, it does not model the flexibility of the APA in the other directions.
Therefore this model can be useful for quick simulations as it contains a very limited number of states, but when more complex dynamics of the APA is to be modelled, a flexible model will be used.
Flexible Model
<<sec:apa_flexible_model>>
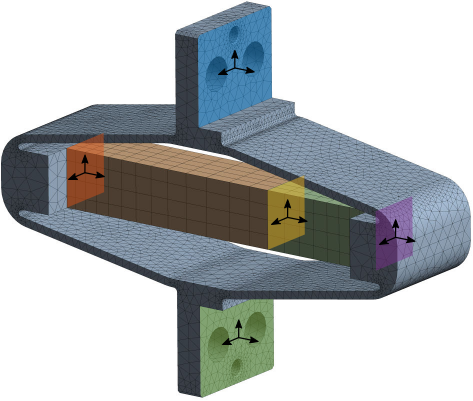
In order to model with high accuracy the behavior of the APA, a flexible model can be used.
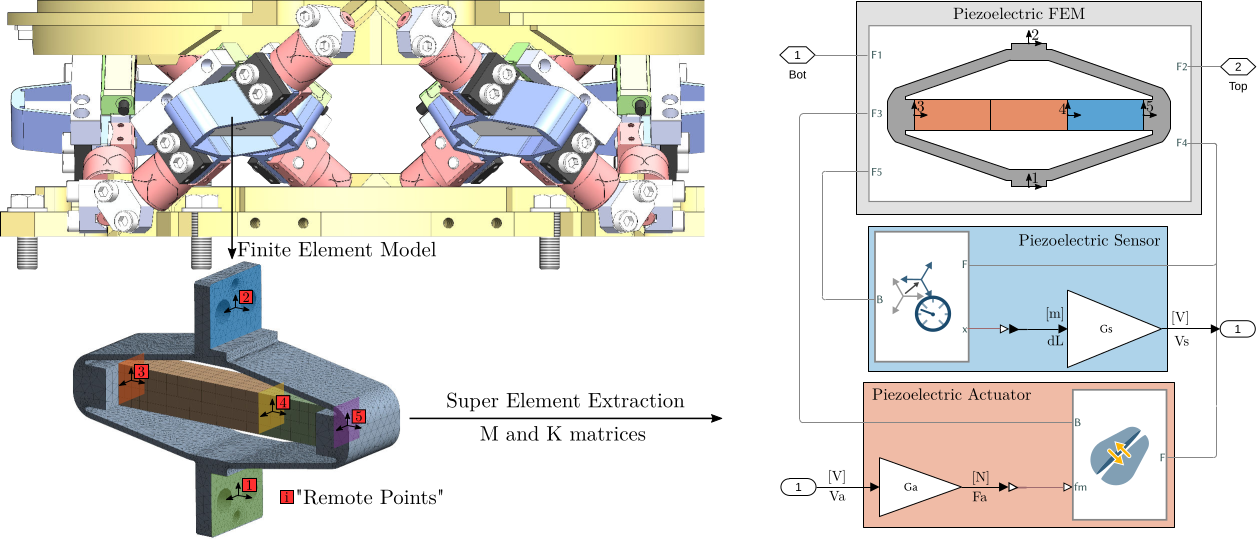
The idea is to do a Finite element model of the structure, and to defined "remote points" as shown in Figure ref:fig:apa300ml_ansys. Then, on the finite element software, a "super-element" can be extracted which consists of a mass matrix, a stiffness matrix, and the coordinates of the remote points.
This "super-element" can then be included in the Simscape model as shown in Figure ref:fig:figure_name. The remotes points are defined as "frames" in Simscape, and the "super-element" can be connected with other Simscape elements (mechanical joints, masses, force actuators, etc..).
Actuator and Sensor constants
<<sec:apa_constants>>
On Simscape, we want to model both the actuator stacks and the sensors stack. We therefore need to link the electrical domain (voltages, charges) with the mechanical domain (forces, strain). To do so, we use the "actuator constant" and the "sensor constant".
Consider a schematic of the Amplified Piezoelectric Actuator in Figure ref:fig:apa_model_schematic.
A voltage $V_a$ applied to the actuator stacks will induce an actuator force $F_a$:
\begin{equation} \boxed{F_a = g_a \cdot V_a} \end{equation}A change of length $dl$ of the sensor stack will induce a voltage $V_s$:
\begin{equation} \boxed{V_s = g_s \cdot dl} \end{equation}The block-diagram model of the piezoelectric actuator is then as shown in Figure fig:apa-model-simscape-schematic.
\begin{tikzpicture}
\node[block={2.0cm}{2.0cm}, align=center] (model) at (0,0){Simscape\\Model};
\node[block, left=1.0 of model] (ga){$g_a(s)$};
\node[block, right=1.0 of model] (gs){$g_s(s)$};
\draw[<-] (ga.west) -- node[midway, above]{$V_a$} node[midway, below]{$[V]$} ++(-1.0, 0);
\draw[->] (ga.east) --node[midway, above]{$F_a$} node[midway, below]{$[N]$} (model.west);
\draw[->] (model.east) --node[midway, above]{$dl$} node[midway, below]{$[m]$} (gs.west);
\draw[->] (gs.east) -- node[midway, above]{$V_s$} node[midway, below]{$[V]$} ++(1.0, 0);
\end{tikzpicture}The constants $g_a$ and $g_s$ will be experimentally estimated.
First Basic Measurements
<<sec:first_measurements>>
Introduction ignore
Before using the measurement bench to characterize the APA300ML, first simple measurements are performed:
- Section ref:sec:geometrical_measurements: the geometric tolerances of the interface planes are checked
- Section ref:sec:electrical_measurements: the capacitance of the stacks are measured
- Section ref:sec:stroke_measurements: the stroke of the APA are measured
- Section ref:sec:spurious_resonances: the "spurious" resonances of the APA are investigated
- Section ref:sec:spurious_resonances_struts: the "spurious" resonances of the struts are measured and compared with the FEM
Geometrical Measurements
<<sec:geometrical_measurements>>
Measurement Setup
Measurement Results
The height (Z) measurements at the 8 locations (4 points by plane) are defined below.
%% Measured height for all the APA at the 8 locations
apa1 = 1e-6*[0, -0.5 , 3.5 , 3.5 , 42 , 45.5, 52.5 , 46];
apa2 = 1e-6*[0, -2.5 , -3 , 0 , -1.5 , 1 , -2 , -4];
apa3 = 1e-6*[0, -1.5 , 15 , 17.5 , 6.5 , 6.5 , 21 , 23];
apa4 = 1e-6*[0, 6.5 , 14.5 , 9 , 16 , 22 , 29.5 , 21];
apa5 = 1e-6*[0, -12.5, 16.5 , 28.5 , -43 , -52 , -22.5, -13.5];
apa6 = 1e-6*[0, -8 , -2 , 5 , -57.5, -62 , -55.5, -52.5];
apa7 = 1e-6*[0, 19.5 , -8 , -29.5, 75 , 97.5, 70 , 48];
apa7b = 1e-6*[0, 9 , -18.5, -30 , 31 , 46.5, 16.5 , 7.5];
apa = {apa1, apa2, apa3, apa4, apa5, apa6, apa7b};The X/Y Positions of the 8 measurement points are defined below.
%% X-Y positions of the measurements points
W = 20e-3; % Width [m]
L = 61e-3; % Length [m]
d = 1e-3; % Distance from border [m]
l = 15.5e-3; % [m]
pos = [[-L/2 + d; W/2 - d],
[-L/2 + l - d; W/2 - d],
[-L/2 + l - d; -W/2 + d],
[-L/2 + d; -W/2 + d],
[L/2 - l + d; W/2 - d],
[L/2 - d; W/2 - d],
[L/2 - d; -W/2 + d],
[L/2 - l + d; -W/2 + d]];
Finally, the flatness is estimated by fitting a plane through the 8 points using the fminsearch command.
%% Using fminsearch to find the best fitting plane
apa_d = zeros(1, 7);
for i = 1:7
fun = @(x)max(abs(([pos; apa{i}]-[0;0;x(1)])'*([x(2:3);1]/norm([x(2:3);1]))));
x0 = [0;0;0];
[x, min_d] = fminsearch(fun,x0);
apa_d(i) = min_d;
endThe obtained flatness are shown in Table ref:tab:flatness_meas.
| Flatness $[\mu m]$ | |
|---|---|
| APA 1 | 8.9 |
| APA 2 | 3.1 |
| APA 3 | 9.1 |
| APA 4 | 3.0 |
| APA 5 | 1.9 |
| APA 6 | 7.1 |
| APA 7 | 18.7 |
The measured flatness of the APA300ML interface planes are within the specifications.
Electrical Measurements
<<sec:electrical_measurements>>
Measurement Setup
The capacitance of the stacks is measure with the LCR-800 Meter (doc) shown in Figure fig:LCR_meter. The excitation frequency is set to be 1kHz.
Measured Capacitance
From the documentation of the APA300ML, the total capacitance of the three stacks should be between $18\mu F$ and $26\mu F$ with a nominal capacitance of $20\mu F$. However, from the documentation of the stack themselves, it can be seen that the capacitance of a single stack should be $4.4\mu F$. Clearly, the total capacitance of the APA300ML if more than just three times the capacitance of one stack.
Could it be possible that the capacitance of the stacks increase that much when they are pre-stressed?
The measured capacitance of the stacks are summarized in Table ref:tab:apa300ml_capacitance.
| Sensor Stack | Actuator Stacks | |
|---|---|---|
| APA 1 | 5.10 | 10.03 |
| APA 2 | 4.99 | 9.85 |
| APA 3 | 1.72 | 5.18 |
| APA 4 | 4.94 | 9.82 |
| APA 5 | 4.90 | 9.66 |
| APA 6 | 4.99 | 9.91 |
| APA 7 | 4.85 | 9.85 |
From the measurements (Table ref:tab:apa300ml_capacitance), the capacitance of one stack is found to be $\approx 5 \mu F$.
There is clearly a problem with APA300ML number 3 The APA number 3 has ben sent back to Cedrat, and a new APA300ML has been shipped back.
Stroke measurement
<<sec:stroke_measurements>>
Introduction ignore
We here wish to estimate the stroke of the APA.
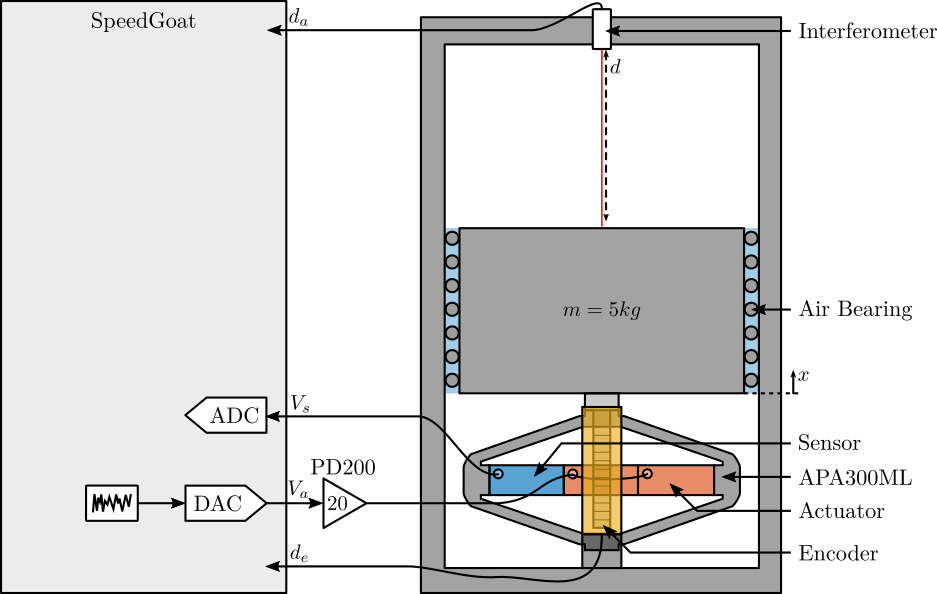
To do so, one side of the APA is fixed, and a displacement probe is located on the other side as shown in Figure ref:fig:stroke_test_bench.
Then, a voltage is applied on either one or two stacks using a DAC and a voltage amplifier.
Here are the documentation of the equipment used for this test bench:
- Voltage Amplifier: PD200 with a gain of 20
- 16bits DAC: IO313 Speedgoat card
- Displacement Probe: Millimar C1216 electronics and Millimar 1318 probe
From the documentation, the nominal stroke of the APA300ML is $304\,\mu m$.
Voltage applied on one stack
Let's first look at the relation between the voltage applied to one stack to the displacement of the APA as measured by the displacement probe.
The applied voltage is shown in Figure ref:fig:apa_stroke_voltage_time.
The obtained displacements for all the APA are shown in Figure ref:fig:apa_stroke_time_1s. The displacement is set to zero at initial time when the voltage applied is -20V.
Finally, the displacement is shown as a function of the applied voltage in Figure fig:apa_d_vs_V_1s. We can clearly see that there is a problem with the APA 3. Also, there is a large hysteresis.
We can clearly confirm from Figure fig:apa_d_vs_V_1s that there is a problem with the APA number 3.
Voltage applied on two stacks
Now look at the relation between the voltage applied to the two other stacks to the displacement of the APA as measured by the displacement probe.
The obtained displacement is shown in Figure ref:fig:apa_stroke_time_2s. The displacement is set to zero at initial time when the voltage applied is -20V.
Finally, the displacement is shown as a function of the applied voltage in Figure fig:apa_d_vs_V_2s.
Voltage applied on all three stacks
Finally, we can combine the two measurements to estimate the relation between the displacement and the voltage applied to the three stacks (Figure fig:apa_d_vs_V_3s).
The obtained maximum stroke for all the APA are summarized in Table ref:tab:apa_measured_stroke.
| Stroke $[\mu m]$ | |
|---|---|
| APA 1 | 373.2 |
| APA 2 | 365.5 |
| APA 3 | 181.7 |
| APA 4 | 359.7 |
| APA 5 | 361.5 |
| APA 6 | 363.9 |
| APA 7 | 358.4 |
Conclusion
The except from APA 3 that has a problem, all the APA are similar when it comes to stroke and hysteresis. Also, the obtained stroke is more than specified in the documentation. Therefore, only two stacks can be used as an actuator.
Spurious resonances - APA
<<sec:spurious_resonances>>
Introduction
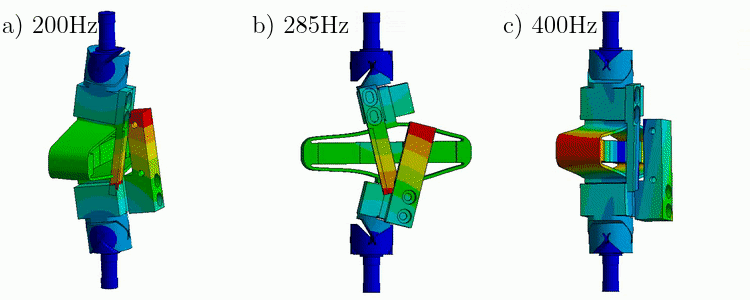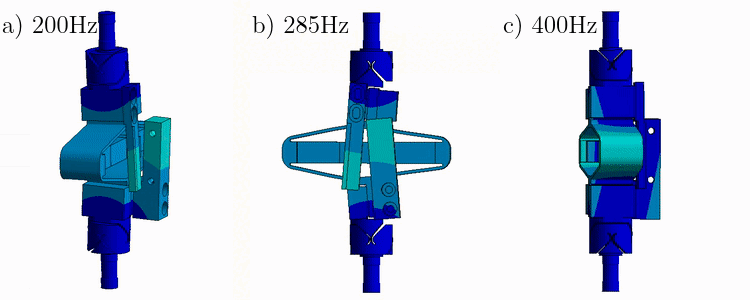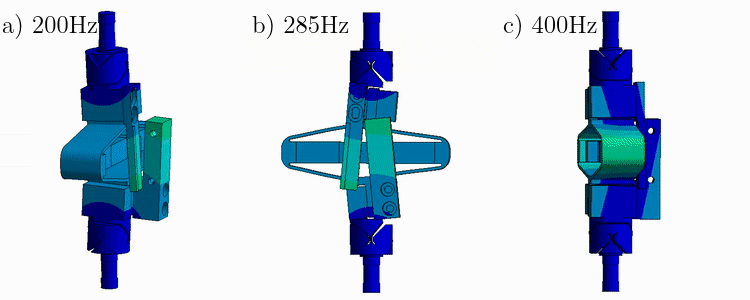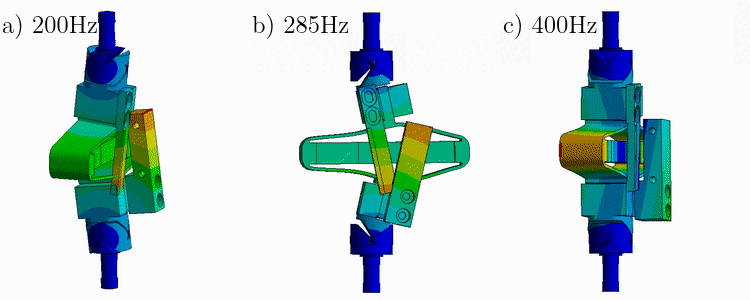
From a Finite Element Model of the struts, it have been found that three main resonances are foreseen to be problematic for the control of the APA300ML (Figure ref:fig:apa_mode_shapes_ter):
- Mode in X-bending at 189Hz
- Mode in Y-bending at 285Hz
- Mode in Z-torsion at 400Hz
These modes are present when flexible joints are fixed to the ends of the APA300ML.
In this section, we try to find the resonance frequency of these modes when one end of the APA is fixed and the other is free.
In the section ref:sec:spurious_resonances_struts, a similar measurement will be performed directly on the struts.
Measurement Setup
The measurement setup is shown in Figure ref:fig:measurement_setup_torsion. A Laser vibrometer is measuring the difference of motion between two points. The APA is excited with an instrumented hammer and the transfer function from the hammer to the measured rotation is computed.
The instrumentation used are:
- Laser Doppler Vibrometer Polytec OFV512
- Instrumented hammer
X-Bending Mode
The vibrometer is setup to measure the X-bending motion is shown in Figure fig:measurement_setup_X_bending. The APA is excited with an instrumented hammer having a solid metallic tip. The impact point is on the back-side of the APA aligned with the top measurement point.
The data is loaded.
%% Load Data
bending_X = load('apa300ml_bending_X_top.mat');
The configuration (Sampling time and windows) for tfestimate is done:
%% Spectral Analysis setup
Ts = bending_X.Track1_X_Resolution; % Sampling Time [s]
win = hann(ceil(1/Ts));The transfer function from the input force to the output "rotation" (difference between the two measured distances).
%% Compute the transfer function from applied force to measured rotation
[G_bending_X, f] = tfestimate(bending_X.Track1, bending_X.Track2, win, [], [], 1/Ts);The result is shown in Figure ref:fig:apa300ml_meas_freq_bending_x.
The can clearly observe a nice peak at 280Hz, and then peaks at the odd "harmonics" (third "harmonic" at 840Hz, and fifth "harmonic" at 1400Hz).
Then the APA is in the "free-free" condition, this bending mode is foreseen to be at 200Hz (Figure ref:fig:apa_mode_shapes_ter). We are here in the "fixed-free" condition. If we consider that we therefore double the stiffness associated with this mode, we should obtain a resonance a factor $\sqrt{2}$ higher than 200Hz which is indeed 280Hz. Not sure this reasoning is correct though.
Y-Bending Mode
The setup to measure the Y-bending is shown in Figure fig:measurement_setup_Y_bending.
The impact point of the instrumented hammer is located on the back surface of the top interface (on the back of the 2 measurements points).
The data is loaded, and the transfer function from the force to the measured rotation is computed.
%% Load Data
bending_Y = load('apa300ml_bending_Y_top.mat');
%% Compute the transfer function
[G_bending_Y, ~] = tfestimate(bending_Y.Track1, bending_Y.Track2, win, [], [], 1/Ts);The results are shown in Figure ref:fig:apa300ml_meas_freq_bending_y. The main resonance is at 412Hz, and we also see the third "harmonic" at 1220Hz.
We can apply the same reasoning as in the previous section and estimate the mode to be a factor $\sqrt{2}$ higher than the mode estimated in the "free-free" condition. We would obtain a mode at 403Hz which is very close to the one estimated here.
Z-Torsion Mode
Finally, we measure the Z-torsion resonance as shown in Figure ref:fig:measurement_setup_torsion_bis.
The excitation is shown on the other side of the APA, on the side to excite the torsion motion.
The data is loaded, and the transfer function computed.
%% Load Data
torsion = load('apa300ml_torsion_left.mat');
%% Compute transfer function
[G_torsion, ~] = tfestimate(torsion.Track1, torsion.Track2, win, [], [], 1/Ts);The results are shown in Figure ref:fig:apa300ml_meas_freq_torsion_z. We observe a first peak at 267Hz, which corresponds to the X-bending mode that was measured at 280Hz. And then a second peak at 415Hz, which corresponds to the X-bending mode that was measured at 412Hz. A third mode at 800Hz could correspond to this torsion mode.
In order to verify that, the APA is excited on the top part such that the torsion mode should not be excited.
%% Load data
torsion = load('apa300ml_torsion_top.mat');
%% Compute transfer function
[G_torsion_top, ~] = tfestimate(torsion.Track1, torsion.Track2, win, [], [], 1/Ts);The two FRF are compared in Figure ref:fig:apa300ml_meas_freq_torsion_z_comp. It is clear that the first two modes does not correspond to the torsional mode. Maybe the resonance at 800Hz, or even higher resonances. It is difficult to conclude here.
Compare
Conclusion
When two flexible joints are fixed at each ends of the APA, the APA is mostly in a free/free condition in terms of bending/torsion (the bending/torsional stiffness of the joints being very small).
In the current tests, the APA are in a fixed/free condition. Therefore, it is quite obvious that we measured higher resonance frequencies than what is foreseen for the struts. It is however quite interesting that there is a factor $\approx \sqrt{2}$ between the two (increased of the stiffness by a factor 2?).
| Mode | FEM - Strut mode | Measured Frequency |
|---|---|---|
| X-Bending | 189Hz | 280Hz |
| Y-Bending | 285Hz | 410Hz |
| Z-Torsion | 400Hz | 800Hz? |
Dynamical measurements - APA
<<sec:dynamical_meas_apa>>
Introduction ignore
In this section, a measurement test bench is used to extract all the important parameters of the Amplified Piezoelectric Actuator APA300ML.
This include:
- Stroke
- Stiffness
- Hysteresis
- "Actuator constant": Gain from the applied voltage $V_a$ to the generated Force $F_a$
- "Sensor constant": Gain from the sensor stack strain $\delta L$ to the generated voltage $V_s$
- Dynamical behavior from the actuator to the force sensor and to the motion of the APA
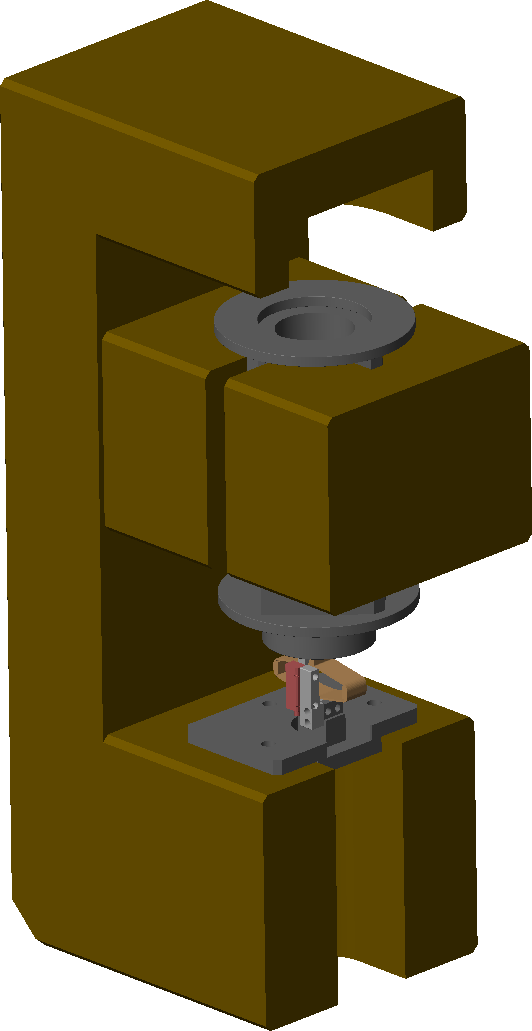
The bench is shown in Figure ref:fig:picture_apa_bench, and a zoom picture on the APA and encoder is shown in Figure ref:fig:picture_apa_bench_encoder.
The bench is schematically shown in Figure ref:fig:test_bench_apa_alone and the signal used are summarized in Table ref:tab:test_bench_apa_variables.
| Variable | Description | Unit | Hardware |
|---|---|---|---|
Va |
Output DAC voltage | [V] | DAC - Ch. 1 - PD200 - APA |
Vs |
Measured stack voltage (ADC) | [V] | APA - ADC - Ch. 1 |
de |
Encoder Measurement | [m] | PEPU Ch. 1 - IO318(1) Ch. 1 |
da |
Attocube Measurement | [m] | PEPU Ch. 2 - IO318(1) Ch. 2 |
t |
Time | [s] |
This section is structured as follows:
- Section ref:sec:meas_one_apa: the measurements are first performed on one APA.
- Section ref:sec:meas_all_apa: the same measurements are performed on all the APA and are compared.
Measurements on APA 1
<<sec:meas_one_apa>>
Introduction ignore
Measurements are first performed on only one APA. Once the measurement procedure is validated, it is performed on all the other APA.
Excitation Signals
Different excitation signals are used to perform FRF estimations.
Typically, this is done in three steps:
- A low pass filtered white noise is used with rather small amplitudes (Figure ref:fig:exc_signal_1_noise). This first excitation is used to estimate the main resonance of the system.
- A sweep-sine from 10Hz to 400Hz is used (Figure ref:fig:exc_signal_2_sweep). The sweep-sine is is notched around the estimated resonance of the system.
- A band-limited white noise from 300Hz to 2kHz is used to estimate the high frequency behavior (Figure ref:fig:exc_signal_3_hf_noise).
For all the excitation signals, before the excitation starts, the mean voltage is slowly increased halfway between the minimum voltage (-20V) and the maximum (150V).
The first measurement is only used to have a first estimation of the dynamics and verify that everything is setup correctly. The second excitation is done to estimate the dynamics from 10Hz to 350Hz and the third excitation from 350Hz to 2kHz. The second and third measurements are therefore combined in the frequency domain to form one good estimation of the dynamics from 10Hz up to 2kHz.
First Measurement
For this first measurement for the first APA, a basic logarithmic sweep is used between 10Hz and 2kHz.
The data are loaded.
%% Load data
apa_sweep = load(sprintf('mat/frf_data_%i_sweep.mat', 1), 't', 'Va', 'Vs', 'da', 'de');The initial time is set to zero.
%% Time vector
t = apa_sweep.t - apa_sweep.t(1) ; % Time vector [s]The excitation signal is shown in Figure ref:fig:apa_bench_exc_sweep. It is a sweep sine from 10Hz up to 2kHz filtered with a notch centered with the main resonance of the system and a low pass filter.
FRF - Setup
Let's define the sampling time/frequency.
%% Sampling Frequency / Time
Ts = (t(end) - t(1))/(length(t)-1); % Sampling Time [s]
Fs = 1/Ts; % Sampling Frequency [Hz]Then we defined a "Hanning" windows that will be used for the spectral analysis:
win = hanning(ceil(1*Fs)); % Hannning WindowsWe get the frequency vector that will be the same for all the frequency domain analysis.
% Only used to have the frequency vector "f"
[~, f] = tfestimate(apa_sweep.Va, apa_sweep.de, win, [], [], 1/Ts);FRF - Encoder and Interferometer
In this section, the transfer function from the excitation voltage $V_a$ to the encoder measured displacement $d_e$ and interferometer measurement $d_a$.
The coherence from $V_a$ to $d_e$ and from $V_a$ to $d_a$ are computed and shown in Figure ref:fig:apa_1_coh_dvf. They are quite good from 10Hz up to 500Hz.
%% Compute the coherence
[enc_coh, ~] = mscohere(apa_sweep.Va, apa_sweep.de, win, [], [], 1/Ts);
[int_coh, ~] = mscohere(apa_sweep.Va, apa_sweep.da, win, [], [], 1/Ts);The transfer functions are then estimated and shown in Figure ref:fig:apa_1_frf_dvf.
%% TF - Encoder and interferometer
[frf_enc, ~] = tfestimate(apa_sweep.Va, apa_sweep.de, win, [], [], 1/Ts);
[frf_int, ~] = tfestimate(apa_sweep.Va, apa_sweep.da, win, [], [], 1/Ts);It is shown than both the encoder and interferometers are measuring the same dynamics up to $\approx 700\,Hz$. Above that, it is possible that there is some flexible elements apart from the APA that is adding resonances into one or the other FRF.
The transfer functions obtained in Figure ref:fig:apa_1_frf_dvf are very close to what was expected:
- constant gain at low frequency
- resonance at around 100Hz which corresponds to the APA axial mode
- no further resonance up until high frequency ($\approx 700\,Hz$) at which points several elements of the test bench can induces resonances in the measured FRF
However, it was not expected to observe a "double resonance" at around 95Hz (instead of only one resonance).
FRF - Force Sensor
Now the dynamics from excitation voltage $V_a$ to the force sensor stack voltage $V_s$ is identified.
The coherence is computed and shown in Figure ref:fig:apa_1_coh_iff and found very good from 10Hz up to 2kHz.
%% Compute the coherence from Va to Vs
[iff_coh, ~] = mscohere(apa_sweep.Va, apa_sweep.Vs, win, [], [], 1/Ts);The transfer function is estimated and shown in Figure ref:fig:apa_1_frf_iff.
%% Compute the TF from Va to Vs
[iff_sweep, ~] = tfestimate(apa_sweep.Va, apa_sweep.Vs, win, [], [], 1/Ts);The obtained dynamics from the excitation voltage $V_a$ to the measured sensor stack voltage $V_s$ is corresponding to what was expected:
- constant gain at low frequency
- complex conjugate zero and then complex conjugate pole
- constant gain at high frequency
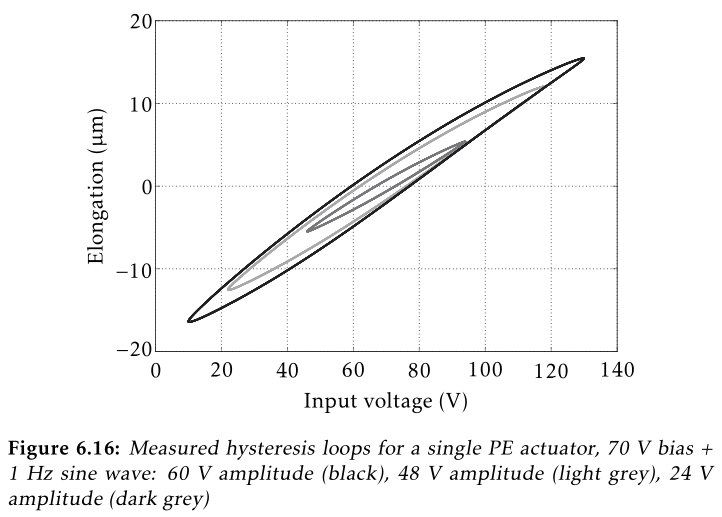
Hysteresis
We here wish to visually see the amount of hysteresis present in the APA.
To do so, a quasi static sinusoidal excitation $V_a$ at different voltages is used.
The offset is 65V (halfway between -20V and 150V), and the sin amplitude is ranging from 1V up to 80V (full range).
For each excitation amplitude, the vertical displacement $d$ of the mass is measured.
Then, $d$ is plotted as a function of $V_a$ for all the amplitudes.
We expect to obtained something like the hysteresis shown in Figure ref:fig:expected_hysteresis.
The data is loaded.
%% Load measured data - hysteresis
apa_hyst = load('frf_data_1_hysteresis.mat', 't', 'Va', 'de');
% Initial time set to zero
apa_hyst.t = apa_hyst.t - apa_hyst.t(1);The excitation voltage amplitudes are:
ampls = [0.1, 0.2, 0.4, 1, 2, 4]; % Excitation voltage amplitudesThe excitation voltage and the measured displacement are shown in Figure ref:fig:hyst_exc_signal_time.
For each amplitude, we only take the last sinus in order to reduce possible transients. Also, the motion is centered on zero.
The measured displacement at a function of the output voltage are shown in Figure ref:fig:hyst_results_multi_ampl.
From Figure ref:fig:hyst_results_multi_ampl, it is quite clear that hysteresis is increasing with the excitation amplitude. For small excitation amplitudes ($V_a < 0.4\,V$) the hysteresis stays reasonably small.
Also, it is quite interesting to see that no hysteresis is found on the sensor stack voltage when using the same excitation signal.
Estimation of the APA axial stiffness
In order to estimate the stiffness of the APA, a weight with known mass $m_a$ is added on top of the suspended granite and the deflection $d_e$ is measured using the encoder.
The APA stiffness can then be estimated to be:
\begin{equation} k_{\text{apa}} = \frac{m_a g}{d} \end{equation}The data is loaded, and the measured displacement is shown in Figure ref:fig:apa_1_meas_stiffness.
%% Load data for stiffness measurement
apa_mass = load(sprintf('frf_data_%i_add_mass_closed_circuit.mat', 1), 't', 'de');
apa_mass.de = apa_mass.de - mean(apa_mass.de(apa_mass.t<11));From Figure ref:fig:apa_1_meas_stiffness, it can be seen that there are some drifts that are probably due to some creep. This will induce some uncertainties in the measured stiffness.
Here, a mass of 6.4 kg was used:
added_mass = 6.4; % Added mass [kg]The stiffness is then computed as follows:
k = 9.8 * added_mass / (mean(apa_mass.de(apa_mass.t > 12 & apa_mass.t < 12.5)) - mean(apa_mass.de(apa_mass.t > 20 & apa_mass.t < 20.5)));And the stiffness obtained is very close to the one specified in the documentation ($k = 1.794\,[N/\mu m]$).
k = 1.68 [N/um]
The stiffness could also be estimated based on the main vertical resonance of the system at $\omega_z = 2\pi \cdot 94 \,[rad/s]$. The suspended mass is $m_{\text{sus}} = 5\,kg$. And therefore, the axial stiffness of the APA can be estimated to be:
\begin{equation} k_{\text{APA}} = m_{\text{sus}} \omega_z^2 \end{equation}wz = 2*pi*94; % [rad/s]
msus = 5.7; % [kg]
k = msus * wz^2;k = 1.99 [N/um]
The two values are found relatively close to each other. Anyway, the stiffness of the model will be tuned to match the measured FRF.
Stiffness change due to electrical connections
Changes in the electrical impedance connected to the piezoelectric actuator causes changes in the mechanical compliance (or stiffness) of the piezoelectric actuator.
In this section is measured the stiffness of the APA whether the piezoelectric actuator is connected to an open circuit or a short circuit (e.g. the output of a voltage amplifier).
Note here that the resistor in parallel to the sensor stack is present in both cases.
First, the data are loaded.
%% Load Data
add_mass_oc = load(sprintf('frf_data_%i_add_mass_open_circuit.mat', 1), 't', 'de');
add_mass_cc = load(sprintf('frf_data_%i_add_mass_closed_circuit.mat', 1), 't', 'de');And the initial displacement is set to zero.
%% Zero displacement at initial time
add_mass_oc.de = add_mass_oc.de - mean(add_mass_oc.de(add_mass_oc.t<11));
add_mass_cc.de = add_mass_cc.de - mean(add_mass_cc.de(add_mass_cc.t<11));The measured displacements are shown in Figure ref:fig:apa_meas_k_time_oc_cc.
And the stiffness is estimated in both case. The results are shown in Table tab:APA_measured_k_oc_cc.
apa_k_oc = 9.8 * added_mass / (mean(add_mass_oc.de(add_mass_oc.t > 12 & add_mass_oc.t < 12.5)) - mean(add_mass_oc.de(add_mass_oc.t > 20 & add_mass_oc.t < 20.5)));
apa_k_cc = 9.8 * added_mass / (mean(add_mass_cc.de(add_mass_cc.t > 12 & add_mass_cc.t < 12.5)) - mean(add_mass_cc.de(add_mass_cc.t > 20 & add_mass_cc.t < 20.5)));| $k [N/\mu m]$ | |
|---|---|
| Not connected | 2.3 |
| Connected | 1.7 |
Clearly, connecting the actuator stacks to the amplified (basically equivalent as to short circuiting them) lowers its stiffness.
Effect of the resistor on the IFF Plant
A resistor $R \approx 80.6\,k\Omega$ is added in parallel with the sensor stack. This has the effect to form a high pass filter with the capacitance of the stack.
This is done for two reasons (explained in details this document):
- Limit the voltage offset due to the input bias current of the ADC
- Limit the low frequency gain
The (low frequency) transfer function from $V_a$ to $V_s$ with and without this resistor have been measured.
%% Load the data
wi_k = load('frf_data_1_sweep_lf_with_R.mat', 't', 'Vs', 'Va'); % With the resistor
wo_k = load('frf_data_1_sweep_lf.mat', 't', 'Vs', 'Va'); % Without the resistorWe use a very long "Hanning" window for the spectral analysis in order to estimate the low frequency behavior.
win = hanning(ceil(50*Fs)); % Hannning WindowsAnd we estimate the transfer function from $V_a$ to $V_s$ in both cases:
%% Compute the transfer functions from Va to Vs
[frf_wo_k, f] = tfestimate(wo_k.Va, wo_k.Vs, win, [], [], 1/Ts);
[frf_wi_k, ~] = tfestimate(wi_k.Va, wi_k.Vs, win, [], [], 1/Ts);With the following values of the resistor and capacitance, we obtain a first order high pass filter with a crossover frequency equal to:
%% Model for the high pass filter
C = 5.1e-6; % Sensor Stack capacitance [F]
R = 80.6e3; % Parallel Resistor [Ohm]
f0 = 1/(2*pi*R*C); % Crossover frequency of RC HPF [Hz]f0 = 0.39 [Hz]
The transfer function of the corresponding high pass filter is:
G_hpf = 0.6*(s/2*pi*f0)/(1 + s/2*pi*f0);Let's compare the transfer function from actuator stack to sensor stack with and without the added resistor in Figure fig:frf_iff_effect_R.
The added resistor has indeed the expected effect of forming an high pass filter.
Comparison of all the APA
<<sec:meas_all_apa>>
Introduction ignore
The same measurements that was performed in Section ref:sec:meas_one_apa are now performed on all the APA and then compared.
Axial Stiffnesses - Comparison
Let's first compare the APA axial stiffnesses.
The added mass is:
added_mass = 6.4; % Added mass [kg]Here are the numbers of the APA that have been measured:
apa_nums = [1 2 4 5 6 7 8];The data are loaded.
%% Load Data
apa_mass = {};
for i = 1:length(apa_nums)
apa_mass(i) = {load(sprintf('frf_data_%i_add_mass_closed_circuit.mat', apa_nums(i)), 't', 'de')};
% The initial displacement is set to zero
apa_mass{i}.de = apa_mass{i}.de - mean(apa_mass{i}.de(apa_mass{i}.t<11));
endThe raw measurements are shown in Figure ref:fig:apa_meas_k_time. All the APA seems to have similar stiffness except the APA 7 which show strange behavior.
It is however strange that the displacement $d_e$ when the mass is removed is higher for the APA 7 than for the other APA.
It turns out the PD200 amplifier was connected to only one stack, the other stack was open circuited. Therefore, the total axial stiffness of the APA was increased.
The stiffnesses are computed for all the APA and are summarized in Table tab:APA_measured_k.
| APA Num | $k [N/\mu m]$ |
|---|---|
| 1 | 1.68 |
| 2 | 1.69 |
| 4 | 1.7 |
| 5 | 1.7 |
| 6 | 1.7 |
| 7 | 1.93 |
| 8 | 1.73 |
The APA300ML manual specifies the nominal stiffness to be $1.8\,[N/\mu m]$ which is very close to what have been measured. Only the APA number 7 is a little bit higher, due to the fact that one of the stack was open-circuited instead of short circuited.
FRF - Setup
As the APA7 was not correctly wired, it is ignored:
apa_nums = [1 2 4 5 6 8];The identification is performed in three steps:
- White noise excitation with small amplitude. This is used to determine the main resonance of the system.
- Sweep sine excitation with the amplitude lowered around the resonance. The sweep sine is from 10Hz to 400Hz.
- High frequency noise. The noise is band-passed between 300Hz and 2kHz.
Then, the result of the second identification is used between 10Hz and 350Hz and the result of the third identification if used between 350Hz and 2kHz.
The data are loaded for both the second and third identification:
%% Second identification
apa_sweep = {};
for i = 1:length(apa_nums)
apa_sweep(i) = {load(sprintf('frf_data_%i_sweep.mat', apa_nums(i)), 't', 'Va', 'Vs', 'de', 'da')};
end
%% Third identification
apa_noise_hf = {};
for i = 1:length(apa_nums)
apa_noise_hf(i) = {load(sprintf('frf_data_%i_noise_hf.mat', apa_nums(i)), 't', 'Va', 'Vs', 'de', 'da')};
endThe time is the same for all measurements.
%% Time vector
t = apa_sweep{1}.t - apa_sweep{1}.t(1) ; % Time vector [s]
%% Sampling
Ts = (t(end) - t(1))/(length(t)-1); % Sampling Time [s]
Fs = 1/Ts; % Sampling Frequency [Hz]Then we defined a "Hanning" windows that will be used for the spectral analysis:
win = hanning(ceil(0.5*Fs)); % Hannning WindowsWe get the frequency vector that will be the same for all the frequency domain analysis.
% Only used to have the frequency vector "f"
[~, f] = tfestimate(apa_sweep{1}.Va, apa_sweep{1}.de, win, [], [], 1/Ts);
i_lf = f <= 350;
i_hf = f > 350;FRF - Encoder and Interferometer
In this section, the dynamics from excitation voltage $V_a$ to encoder measured displacement $d_e$ is identified.
We compute the coherence for 2nd and 3rd identification:
%% Coherence computation
coh_enc = zeros(length(f), length(apa_nums));
for i = 1:length(apa_nums)
[coh_lf, ~] = mscohere(apa_sweep{i}.Va, apa_sweep{i}.de, win, [], [], 1/Ts);
[coh_hf, ~] = mscohere(apa_noise_hf{i}.Va, apa_noise_hf{i}.de, win, [], [], 1/Ts);
coh_enc(:, i) = [coh_lf(i_lf); coh_hf(i_hf)];
endThe coherence is shown in Figure ref:fig:apa_frf_dvf_plant_coh, and it is found that the coherence is good from low frequency up to 700Hz.
Then, the transfer function from the DAC output voltage $V_a$ to the measured displacement by the encoders is computed:
%% Transfer function estimation
enc_frf = zeros(length(f), length(apa_nums));
for i = 1:length(apa_nums)
[frf_lf, ~] = tfestimate(apa_sweep{i}.Va, apa_sweep{i}.de, win, [], [], 1/Ts);
[frf_hf, ~] = tfestimate(apa_noise_hf{i}.Va, apa_noise_hf{i}.de, win, [], [], 1/Ts);
enc_frf(:, i) = [frf_lf(i_lf); frf_hf(i_hf)];
endThe obtained transfer functions are shown in Figure ref:fig:apa_frf_dvf_plant_tf. They are all superimposed.
A zoom on the main resonance is shown in Figure ref:fig:apa_frf_dvf_zoom_res_plant_tf. It is clear that the responses around the resonances are well matching for all the APA.
It is also clear that there is not a single resonance but two resonances, a first one at 95Hz and a second one at 105Hz.
Why is there a double resonance at around 94Hz?
FRF - Force Sensor
In this section, the dynamics from $V_a$ to $V_s$ is identified.
First the coherence is computed and shown in Figure ref:fig:apa_frf_iff_plant_coh. The coherence is very nice from 10Hz to 2kHz. It is only dropping near a zeros at 40Hz, and near the resonance at 95Hz (the excitation amplitude being lowered).
%% Compute the Coherence
coh_iff = zeros(length(f), length(apa_nums));
for i = 1:length(apa_nums)
[coh_lf, ~] = mscohere(apa_sweep{i}.Va, apa_sweep{i}.Vs, win, [], [], 1/Ts);
[coh_hf, ~] = mscohere(apa_noise_hf{i}.Va, apa_noise_hf{i}.Vs, win, [], [], 1/Ts);
coh_iff(:, i) = [coh_lf(i_lf); coh_hf(i_hf)];
endThen the FRF are estimated and shown in Figure ref:fig:apa_frf_iff_plant_tf
%% FRF estimation of the transfer function from Va to Vs
iff_frf = zeros(length(f), length(apa_nums));
for i = 1:length(apa_nums)
[frf_lf, ~] = tfestimate(apa_sweep{i}.Va, apa_sweep{i}.Vs, win, [], [], 1/Ts);
[frf_hf, ~] = tfestimate(apa_noise_hf{i}.Va, apa_noise_hf{i}.Vs, win, [], [], 1/Ts);
iff_frf(:, i) = [frf_lf(i_lf); frf_hf(i_hf)];
end#+caption:Identified IFF Plant
Conclusion
So far, all the measured FRF are showing the dynamical behavior that was expected.
%% Save the measured FRF
save('mat/meas_apa_frf.mat', 'f', 'Ts', 'enc_frf', 'iff_frf', 'apa_nums');Test Bench APA300ML - Simscape Model
<<sec:simscape_bench_apa>>
Introduction ignore
In this section, a simscape model (Figure ref:fig:model_bench_apa) of the measurement bench is used to compare the model of the APA with the measured FRF.
After the transfer functions are extracted from the model (Section ref:sec:simscape_bench_apa_first_id), the comparison of the obtained dynamics with the measured FRF will permit to:
- Estimate the "actuator constant" and "sensor constant" (Section ref:sec:simscape_bench_apa_id_constants)
- Tune the model of the APA to match the measured dynamics (Section ref:sec:simscape_bench_apa_tune_2dof_model)
First Identification
<<sec:simscape_bench_apa_first_id>>
The APA is first initialized with default parameters:
%% Initialize the structure with default values
n_hexapod = struct();
n_hexapod.actuator = initializeAPA(...
'type', '2dof', ...
'Ga', 1, ... % Actuator constant [N/V]
'Gs', 1); % Sensor constant [V/m]The transfer function from excitation voltage $V_a$ (before the amplification of $20$ due to the PD200 amplifier) to:
- the sensor stack voltage $V_s$
- the measured displacement by the encoder $d_e$
- the measured displacement by the interferometer $d_a$
%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Va'], 1, 'openinput'); io_i = io_i + 1; % DAC Voltage
io(io_i) = linio([mdl, '/Vs'], 1, 'openoutput'); io_i = io_i + 1; % Sensor Voltage
io(io_i) = linio([mdl, '/de'], 1, 'openoutput'); io_i = io_i + 1; % Encoder
io(io_i) = linio([mdl, '/da'], 1, 'openoutput'); io_i = io_i + 1; % Interferometer
%% Run the linearization
Ga = linearize(mdl, io, 0.0, options);
Ga.InputName = {'Va'};
Ga.OutputName = {'Vs', 'de', 'da'};The obtain dynamics are shown in Figure ref:fig:apa_model_bench_bode_vs and ref:fig:apa_model_bench_bode_dl_z. It can be seen that:
- the shape of these bode plots are very similar to the one measured in Section ref:sec:dynamical_meas_apa expect from a change in gain and exact location of poles and zeros
- there is a sign error for the transfer function from $V_a$ to $V_s$. This will be corrected by taking a negative "sensor gain".
- the low frequency zero of the transfer function from $V_a$ to $V_s$ is minimum phase as expected. The measured FRF are showing non-minimum phase zero, but it is most likely due to measurements artifacts.
Identify Sensor/Actuator constants and compare with measured FRF
<<sec:simscape_bench_apa_id_constants>>
How to identify these constants?
Piezoelectric Actuator Constant
Using the measurement test-bench, it is rather easy the determine the static gain between the applied voltage $V_a$ to the induced displacement $d$.
\begin{equation} d = g_{d/V_a} \cdot V_a \end{equation}Using the Simscape model of the APA, it is possible to determine the static gain between the actuator force $F_a$ to the induced displacement $d$:
\begin{equation} d = g_{d/F_a} \cdot F_a \end{equation}From the two gains, it is then easy to determine $g_a$: \begin{equation} \label{eq:actuator_constant_formula} \boxed{g_a = \frac{F_a}{V_a} = \frac{F_a}{d} ⋅ \frac{d}{V_a} = \frac{gd/V_a}{gd/F_a}}
\end{equation}
Piezoelectric Sensor Constant
Similarly, it is easy to determine the gain from the excitation voltage $V_a$ to the voltage generated by the sensor stack $V_s$:
\begin{equation} V_s = g_{V_s/V_a} V_a \end{equation}Note here that there is an high pass filter formed by the piezoelectric capacitor and parallel resistor.
The gain can be computed from the dynamical identification and taking the gain at the wanted frequency (above the first resonance).
Using the simscape model, compute the gain at the same frequency from the actuator force $F_a$ to the strain of the sensor stack $dl$:
\begin{equation} dl = g_{dl/F_a} F_a \end{equation}Then, the "sensor" constant is: \begin{equation} \label{eq:sensor_constant_formula} \boxed{g_s = \frac{V_s}{dl} = \frac{V_s}{V_a} ⋅ \frac{V_a}{F_a} ⋅ \frac{F_a}{dl} = \frac{gV_s/V_a}{g_a ⋅ gdl/F_a}}
\end{equation}
Identification Data
Let's load the measured FRF from the DAC voltage to the measured encoder and to the sensor stack voltage.
%% Load Data
load('meas_apa_frf.mat', 'f', 'Ts', 'enc_frf', 'iff_frf', 'apa_nums');2DoF APA
2DoF APA
Let's initialize the APA as a 2DoF model with unity sensor and actuator gains.
%% Initialize a 2DoF APA with Ga=Gs=1
n_hexapod.actuator = initializeAPA(...
'type', '2dof', ...
'ga', 1, ...
'gs', 1);Identification without actuator or sensor constants
The transfer function from $V_a$ to $V_s$, $d_e$ and $d_a$ is identified.
%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Va'], 1, 'openinput'); io_i = io_i + 1; % Actuator Voltage
io(io_i) = linio([mdl, '/Vs'], 1, 'openoutput'); io_i = io_i + 1; % Sensor Voltage
io(io_i) = linio([mdl, '/de'], 1, 'openoutput'); io_i = io_i + 1; % Encoder
io(io_i) = linio([mdl, '/da'], 1, 'openoutput'); io_i = io_i + 1; % Attocube
%% Identification
Gs = linearize(mdl, io, 0.0, options);
Gs.InputName = {'Va'};
Gs.OutputName = {'Vs', 'de', 'da'};Actuator Constant
Then, the actuator constant can be computed as shown in Eq. eqref:eq:actuator_constant_formula by dividing the measured DC gain of the transfer function from $V_a$ to $d_e$ by the estimated DC gain of the transfer function from $V_a$ (in truth the actuator force called $F_a$) to $d_e$ using the Simscape model.
%% Estimated Actuator Constant
ga = -mean(abs(enc_frf(f>10 & f<20)))./dcgain(Gs('de', 'Va')); % [N/V]ga = -32.2 [N/V]
Sensor Constant
Similarly, the sensor constant can be estimated using Eq. eqref:eq:sensor_constant_formula.
%% Estimated Sensor Constant
gs = -mean(abs(iff_frf(f>400 & f<500)))./(ga*abs(squeeze(freqresp(Gs('Vs', 'Va'), 1e3, 'Hz')))); % [V/m]gs = 0.088 [V/m]
Comparison
Let's now initialize the APA with identified sensor and actuator constant:
%% Set the identified constants
n_hexapod.actuator = initializeAPA(...
'type', '2dof', ...
'ga', ga, ... % Actuator gain [N/V]
'gs', gs); % Sensor gain [V/m]And identify the dynamics with included constants.
%% Identify again the dynamics with correct Ga,Gs
Gs = linearize(mdl, io, 0.0, options);
Gs = Gs*exp(-Ts*s);
Gs.InputName = {'Va'};
Gs.OutputName = {'Vs', 'de', 'da'};The transfer functions from $V_a$ to $d_e$ are compared in Figure ref:fig:apa_act_constant_comp and the one from $V_a$ to $V_s$ are compared in Figure ref:fig:apa_sens_constant_comp.
The "actuator constant" and "sensor constant" can indeed be identified using this test bench. After identifying these constants, the 2DoF model shows good agreement with the measured dynamics.
Flexible APA
Introduction ignore
In this section, the sensor and actuator "constants" are also estimated for the flexible model of the APA.
Flexible APA
The Simscape APA model is initialized as a flexible one with unity "constants".
%% Initialize the APA as a flexible body
n_hexapod.actuator = initializeAPA(...
'type', 'flexible', ...
'ga', 1, ...
'gs', 1);Identification without actuator or sensor constants
The dynamics from $V_a$ to $V_s$, $d_e$ and $d_a$ is identified.
%% Identify the dynamics
Gs = linearize(mdl, io, 0.0, options);
Gs.InputName = {'Va'};
Gs.OutputName = {'Vs', 'de', 'da'};Actuator Constant
Then, the actuator constant can be computed as shown in Eq. eqref:eq:actuator_constant_formula:
%% Actuator Constant
ga = -mean(abs(enc_frf(f>10 & f<20)))./dcgain(Gs('de', 'Va')); % [N/V]ga = 23.5 [N/V]
Sensor Constant
%% Sensor Constant
gs = -mean(abs(iff_frf(f>400 & f<500)))./(ga*abs(squeeze(freqresp(Gs('Vs', 'Va'), 1e3, 'Hz')))); % [V/m]gs = -4839841.756 [V/m]
Comparison
Let's now initialize the flexible APA with identified sensor and actuator constant:
%% Set the identified constants
n_hexapod.actuator = initializeAPA(...
'type', 'flexible', ...
'ga', ga, ... % Actuator gain [N/V]
'gs', gs); % Sensor gain [V/m]And identify the dynamics with included constants.
%% Identify with updated constants
Gs = linearize(mdl, io, 0.0, options);
Gs = Gs*exp(-Ts*s);
Gs.InputName = {'Va'};
Gs.OutputName = {'Vs', 'de', 'da'};The obtained dynamics is compared with the measured one in Figures ref:fig:apa_act_constant_comp_flex and ref:fig:apa_sens_constant_comp_flex.
The flexible model is a bit "soft" as compared with the experimental results.
Optimize 2-DoF model to fit the experimental Data
<<sec:simscape_bench_apa_tune_2dof_model>> The parameters of the 2DoF model presented in Section ref:sec:apa_2dof_model are now optimize such that the model best matches the measured FRF.
After optimization, the following parameters are used:
%% Optimized parameters
n_hexapod.actuator = initializeAPA('type', '2dof', ...
'Ga', -32.2, ...
'Gs', 0.088, ...
'k', ones(6,1)*0.38e6, ...
'ke', ones(6,1)*1.75e6, ...
'ka', ones(6,1)*3e7, ...
'c', ones(6,1)*1.3e2, ...
'ce', ones(6,1)*1e1, ...
'ca', ones(6,1)*1e1 ...
);The dynamics is identified using the Simscape model and compared with the measured FRF in Figure ref:fig:comp_apa_plant_after_opt.
The tuned 2DoF is very well representing the (axial) dynamics of the APA.
Conclusion
<<sec:test_bench_apa_conclusion>>