phd-simscape-nano-hexapod/simscape-nano-hexapod.org

Simscape Model - Nano Hexapod

• Introduction
• Active Vibration Platforms
  • Introduction
  • Active vibration control of sample stages
  • Serial and Parallel Manipulators
• The Stewart platform
  • Introduction
  • Mechanical Architecture
  • Kinematic Analysis
    • Introduction
    • Loop Closure
    • Inverse Kinematics
    • Forward Kinematics
  • The Jacobian Matrix
    • Introduction
    • Jacobian Computation - Velocity Loop Closure
    • Approximate solution of the Forward and Inverse Kinematic problems
    • Range validity of the approximate inverse kinematics
    • Static Forces
    • Singularities
  • Static Analysis
  • Dynamic Analysis
  • Conclusion
• Multi-Body Model
  • Introduction
  • Model Definition
  • Nano Hexapod
  • Model Dynamics
  • Conclusion
• Control of Stewart Platforms
  • Introduction
  • Centralized and Decentralized Control
  • Choice of the control space
  • Active Damping with Decentralized IFF
  • MIMO High-Authority Control - Low-Authority Control
  • Conclusion
• Conclusion
• Bibliography
• Footnotes

Introduction   ignore

Now that the multi-body model of the micro-station has been developed and validated using dynamical measurements, a model of the active vibration platform can be integrated.

First, the mechanical architecture of the active platform needs to be carefully chosen. In Section ref:sec:nhexa_platform_review, a quick review of active vibration platforms is performed.

The chosen architecture is the Stewart platform, which is presented in Section ref:sec:nhexa_stewart_platform. It is a parallel manipulator that require the use of specific tools to study its kinematics.

However, to study the dynamics of the Stewart platform, the use of analytical equations is very complex. Instead, a multi-body model of the Stewart platform is developed (Section ref:sec:nhexa_model), that can then be easily integrated on top of the micro-station's model.

From a control point of view, the Stewart platform is a MIMO system with complex dynamics. To control such system, it requires several tools to study interaction (Section ref:sec:nhexa_control).

Active Vibration Platforms

<<sec:nhexa_platform_review>>

Introduction   ignore

Goals:

• Quick review of active vibration platforms (5 or 6DoF) similar to NASS
• Explain why Stewart platform architecture is chosen
• Wanted controlled DOF: Y, Z, Ry
• But because of continuous rotation (key specificity): X,Y,Z,Rx,Ry in the frame of the active platform

• Literature review? (maybe more suited for chapter 2)

  • file:~/Cloud/work-projects/ID31-NASS/matlab/stewart-simscape/org/bibliography.org
  • Talk about flexible joint? Maybe not so much as it should be topic of second chapter. Just say that we must of flexible joints that can be defined as 3 to 6DoF joints, and it will be optimize in chapter 2.
• cite:&taghirad13_paral
• For some systems, just XYZ control (stack stages), example: holler
• For other systems, Stewart platform (ID16a), piezo based
• Examples of Stewart platforms for general vibration control, some with Piezo, other with Voice coil. IFF, … Show different geometry configuration
• DCM: tripod?

Active vibration control of sample stages

Review of stages with online metrology for Synchrotrons

• Talk about external metrology? Maybe not the topic here.
• Talk about control architecture?
• Comparison with the micro-station / NASS

Serial and Parallel Manipulators

Goal:

• Explain why a parallel manipulator is here preferred
• Compact, 6DoF, higher control bandwidth, linear, simpler
• Show some example of serial and parallel manipulators
• A review of Stewart platform will be given in Chapter related to the detailed design of the Nano-Hexapod

	Serial Robots	Parallel Robots
Advantages	Large Workspace	High Stiffness
Disadvantages	Low Stiffness	Small Workspace
Kinematic Struture	Open	Closed-loop

The Stewart platform

<<sec:nhexa_stewart_platform>>

Introduction   ignore

• Some history about Stewart platforms
• What is so special and why it is so used in different fields: give examples Explain advantages compared to serial architecture
• Little review (very quick: two extreme sizes, piezo + voice coil) Complete review of Stewart platforms will be made in Chapter 2
• Presentation of tools used to analyze the properties of the Stewart platform => useful for design and control

The Stewart Platform is very adapted for the NASS application for the following reasons:

• it is a fully parallel manipulator, thus all the motions errors can be compensated
• it is very compact compared to a serial manipulator
• it has high stiffness and good dynamic performances

The main disadvantage of Stewart platforms is the small workspace when compare the serial manipulators which is not a problem here.

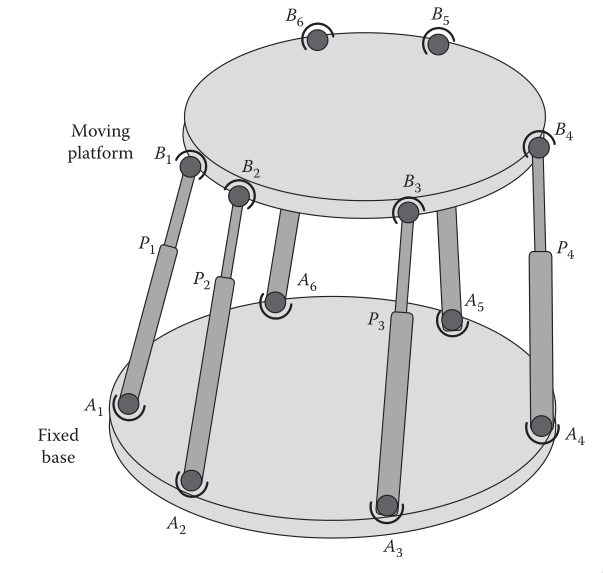
Mechanical Architecture

<<ssec:nhexa_stewart_platform_architecture>>

• Use this file as a reference: file:~/Cloud/work-projects/ID31-NASS/matlab/stewart-simscape/org/stewart-architecture.org

Presentation of the typical architecture

• Explain the different frames, etc…

• explain key elements:

  • two plates
  • joints
  • actuators

The Stewart Platform:

• Has 6 degrees-of-freedom
• Is a Fully parallel manipulator as the number of actuators is equal to the number of dof
• Is a Symmetrical parallel manipulator as all the struts are the same

	Base Joint	Actuator Joint	Top Joint
6-SPS	Spherical	Prismatic	Spherical
6-UPS	Universal	Prismatic	Spherical

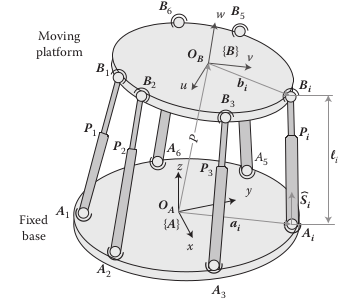
Make well defined notations.

• {F}, {M}
• si, li, ai, bi, etc.
• Make figure with defined frames, joints, etc…

These frames are used to describe the relative motion of the two platforms through the position vector ${}^A\bm{P}_B$ of $\{B\}$ expressed in $\{A\}$ and the rotation matrix ${}^A\bm{R}_B$ expressing the orientation of $\{B\}$ with respect to $\{A\}$. For the nano-hexapod, these frames are chosen to be located at the theoretical focus point of the X-ray light (xxx mm above the top platform).

Stewart platforms are generated in multiple steps.

We define 4 important frames:

• $\{F\}$: Frame fixed to the Fixed base and located at the center of its bottom surface. This is used to fix the Stewart platform to some support.
• $\{M\}$: Frame fixed to the Moving platform and located at the center of its top surface. This is used to place things on top of the Stewart platform.
• $\{A\}$: Frame fixed to the fixed base. It defined the center of rotation of the moving platform.
• $\{B\}$: Frame fixed to the moving platform. The motion of the moving platforms and forces applied to it are defined with respect to this frame $\{B\}$.

Then, we define the location of the spherical joints:

• $\bm{a}_{i}$ are the position of the spherical joints fixed to the fixed base
• $\bm{b}_{i}$ are the position of the spherical joints fixed to the moving platform

We define the rest position of the Stewart platform:

• For simplicity, we suppose that the fixed base and the moving platform are parallel and aligned with the vertical axis at their rest position.
• Thus, to define the rest position of the Stewart platform, we just have to defined its total height $H$. $H$ corresponds to the distance from the bottom of the fixed base to the top of the moving platform.

From $\bm{a}_{i}$ and $\bm{b}_{i}$, we can determine the length and orientation of each strut:

• $l_{i}$ is the length of the strut
• ${}^{A}\hat{\bm{s}}_{i}$ is the unit vector align with the strut

Kinematic Analysis

<<ssec:nhexa_stewart_platform_kinematics>>

Introduction   ignore

Kinematic analysis refers to the study of the geometry of motion of a robot, without considering the forces that cause the motion.

The relation between the geometry of the manipulator with the final motion of the moving platform is derived and analyzed.

Definition of the geometry of the Stewart Platform:

• $\bm{a}_i$: position of the attachment points on the fixed base
• $\bm{b}_i$: position of moving attachment points
• $l_i$: length of each limb
• $\hat{\bm{s}}_i$: unit vector representing the direction of each limb

Loop Closure

At the displacement level, the closure of each kinematic loop can be express in the vector form as \[ \vec{AB} = \vec{AA_i} + \vec{A_iB_i} - \vec{BB_i} \quad \text{for } i = 1,2,\dots,n \] in which $\vec{AA_i}$ and $\vec{BB_i}$ can be easily obtained from the geometry of the attachment points in the base and in the moving platform.

The loop closure can be written as the unknown pose variables ${}^A\bm{P}$ and ${}^A\bm{R}_B$, the position vectors describing the known geometry of the base and of the moving platform, $\bm{a}_i$ and $\bm{b}_i$, and the limb vector $l_i {}^A\hat{\bm{s}}_i$:

\begin{equation*} {}^A\bm{P} = {}^A\bm{a}_i + l_i{}^A\hat{\bm{s}}_i - {}^A\bm{R}_B {}^B\bm{b}_i \quad \text{for } i=1,2,\dots,n \end{equation*}

Inverse Kinematics

For inverse kinematic analysis, it is assumed that the position ${}^A\bm{P}$ and orientation of the moving platform ${}^A\bm{R}_B$ are given and the problem is to obtain the joint variables $\bm{\mathcal{L}} = \left[ l_1, l_2, l_3, l_4, l_5, l_6 \right]^T$.

This problem can be easily solved using the loop closures.

The obtain joint variables are:

\begin{equation*} \begin{aligned} l_i = &\Big[ {}^A\bm{P}^T {}^A\bm{P} + {}^B\bm{b}_i^T {}^B\bm{b}_i + {}^A\bm{a}_i^T {}^A\bm{a}_i - 2 {}^A\bm{P}^T {}^A\bm{a}_i + \dots\\ &2 {}^A\bm{P}^T \left[{}^A\bm{R}_B {}^B\bm{b}_i\right] - 2 \left[{}^A\bm{R}_B {}^B\bm{b}_i\right]^T {}^A\bm{a}_i \Big]^{1/2} \end{aligned} \end{equation*}

If the position and orientation of the platform lie in the feasible workspace, the solution is unique. Otherwise, the solution gives complex numbers.

Forward Kinematics

In forward kinematic analysis, it is assumed that the vector of limb lengths $\bm{L}$ is given and the problem is to find the position ${}^A\bm{P}$ and the orientation ${}^A\bm{R}_B$.

This is a difficult problem that requires to solve nonlinear equations.

In a next section, an approximate solution of the forward kinematics problem is proposed for small displacements.

The Jacobian Matrix

Introduction   ignore

In vector calculus, the Jacobian matrix of a vector-valued function in several variables is the matrix of all its first-order partial derivatives.

Suppose $\bm{f}: \mathbb{R}^n \rightarrow \mathbb{R}^m$ is a function such that each of its first-order partial derivatives exist on $\mathbb{R}^n$. This function takes a point $\bm{x} \in \mathbb{R}^n$ as input and produces the vector $\bm{f}(\bm{x}) \in \mathbb{R}^m$ as output.

Then the Jacobian matrix $\bm{J}$ of $\bm{f}$ is defined to be an $n \times m$ matrix, whose its (i,j)'th entry is $J_{ij} = \frac{\partial f_i}{\partial x_j}$.

The Jacobian matrix is the linear transformation that best approximates $\bm{f}$ for points close to $\bm{x}$.

Summary: Linear approximation of a function with several inputs and outputs around a working point.

Jacobian Computation - Velocity Loop Closure

Let's note:

• $\bm{\mathcal{L}} = \left[ l_1, l_2, \ldots, l_6 \right]^T$: vector of actuated joint coordinates
• $\bm{\mathcal{X}} = \left[ {}^A\bm{P}, \bm{}^A\hat{\bm{s}} \right]^T$: vector of platform motion variables

$\bm{\mathcal{L}}$ and $\bm{\mathcal{X}}$ are related through a system of nonlinear algebraic equations representing the kinematic constraints imposed by the struts, which can be generally written as $f(\bm{\mathcal{L}}, \bm{\mathcal{X}}) = 0$.

We can differentiate this equation with respect to time and obtain:

\begin{equation*} \bm{J}_x \dot{\bm{\mathcal{X}}} = \bm{J}_l \dot{\bm{\mathcal{L}}} \quad \text{where} \quad \bm{J}_x = \frac{\partial f}{\partial \bm{\mathcal{X}}} \quad \text{and} \quad \bm{J}_l = -\frac{\partial f}{\partial \bm{\mathcal{L}}} \end{equation*}

With:

• $\dot{\bm{\mathcal{L}}} = [ \dot{l}_1, \dot{l}_2, \dot{l}_3, \dot{l}_4, \dot{l}_5, \dot{l}_6 ]^T$
• $\dot{\bm{X}} = [^A\bm{v}_p, {}^A\bm{\omega}]^T$:

The general Jacobian matrix is defined as:

\begin{equation*} \dot{\bm{\mathcal{L}}} = \bm{J} \dot{\bm{\mathcal{X}}} \quad \text{with} \quad \bm{J} = {\bm{J}_l}^{-1} \bm{J}_x \end{equation*}

The velocity loop closures are used for obtaining the Jacobian matrices in a straightforward manner:

\begin{align*} {}^A\bm{P} + {}^A\bm{R}_B {}^B\bm{b}_i = l_i {}^A\hat{\bm{s}}_i + {}^A\bm{a}_i & \underset{\frac{\partial}{\partial t}}{\rightarrow} {}^A\bm{v}_p + {}^A \dot{\bm{R}}_B {}^B\bm{b}_i = \dot{l}_i {}^A\hat{\bm{s}}_i + l_i {}^A\dot{\hat{\bm{s}}}_i \\ & \Leftrightarrow\hat{\bm{s}}_i {}^A\bm{v}_p + ({}^A\bm{b}_i \times \hat{\bm{s}}_i) {}^A\bm{\omega} = \dot{l}_i \end{align*}

We can rearrange the equations in a matrix form: \[ \dot{\bm{\mathcal{L}}} = \bm{J} \dot{\bm{\mathcal{X}}} \quad \text{with} \ \dot{\bm{\mathcal{L}}} = [ \dot{l}_1 \ \dots \ \dot{l}_6 ]^T \ \text{and} \ \dot{\bm{\mathcal{X}}} = [{}^A\bm{v}_p ,\ {}^A\bm{\omega}]^T \]

\begin{equation} \bm{J} = \begin{bmatrix} {\hat{\bm{s}}_1}^T & (\bm{b}_1 \times \hat{\bm{s}}_1)^T \\ {\hat{\bm{s}}_2}^T & (\bm{b}_2 \times \hat{\bm{s}}_2)^T \\ {\hat{\bm{s}}_3}^T & (\bm{b}_3 \times \hat{\bm{s}}_3)^T \\ {\hat{\bm{s}}_4}^T & (\bm{b}_4 \times \hat{\bm{s}}_4)^T \\ {\hat{\bm{s}}_5}^T & (\bm{b}_5 \times \hat{\bm{s}}_5)^T \\ {\hat{\bm{s}}_6}^T & (\bm{b}_6 \times \hat{\bm{s}}_6)^T \end{bmatrix} \end{equation}

$\bm{J}$ then depends only on:

• $\hat{\bm{s}}_i$ the orientation of the limbs expressed in $\{A\}$
• $\bm{b}_i$ the position of the joints with respect to $O_B$ and express in $\{A\}$

Approximate solution of the Forward and Inverse Kinematic problems

For small displacements mobile platform displacement $\delta \bm{\mathcal{X}} = [\delta x, \delta y, \delta z, \delta \theta_x, \delta \theta_y, \delta \theta_z ]^T$ around $\bm{\mathcal{X}}_0$, the associated joint displacement can be computed using the Jacobian (approximate solution of the inverse kinematic problem):

\begin{equation*} \delta\bm{\mathcal{L}} = \bm{J} \delta\bm{\mathcal{X}} \end{equation*}

Similarly, for small joint displacements $\delta\bm{\mathcal{L}} = [ \delta l_1,\ \dots,\ \delta l_6 ]^T$ around $\bm{\mathcal{L}}_0$, it is possible to find the induced small displacement of the mobile platform (approximate solution of the forward kinematic problem):

\begin{equation*} \delta\bm{\mathcal{X}} = \bm{J}^{-1} \delta\bm{\mathcal{L}} \end{equation*}

These two relations solve the forward and inverse kinematic problems for small displacement in a approximate way. As the inverse kinematic can be easily solved exactly this is not much useful, however, as the forward kinematic problem is difficult to solve, this approximation can be very useful for small displacements.

Range validity of the approximate inverse kinematics

• Estimation of the range validity of the approximate inverse kinematics

Static Forces

The principle of virtual work states that the total virtual work, $\delta W$, done by all actuators and external forces is equal to zero:

\begin{align*} \delta W &= \bm{\tau}^T \delta \bm{\mathcal{L}} - \bm{\mathcal{F}}^T \delta \bm{\mathcal{X}}\\ & = 0 \end{align*}

If we note:

• $\bm{\tau} = [\tau_1, \tau_2, \cdots, \tau_6]^T$: vector of actuator forces applied in each strut
• $\bm{\mathcal{F}} = [\bm{f}, \bm{n}]^T$: external force/torque action on the mobile platform at $\bm{O}_B$

From the definition of the Jacobian ($\delta \bm{\mathcal{L}} = \bm{J} \cdot \delta \bm{\mathcal{X}}$), we have $\left( \bm{\tau}^T \bm{J} - \bm{\mathcal{F}}^T \right) \delta \bm{\mathcal{X}} = 0$ that holds for any $\delta \bm{\mathcal{X}}$, hence:

\[ \bm{\tau}^T \bm{J} - \bm{\mathcal{F}}^T = 0 \quad \Rightarrow \quad \tcmbox{\bm{\mathcal{F}} = \bm{J}^T \bm{\tau}} \quad \text{and} \quad \tcmbox{\bm{\tau} = \bm{J}^{-T} \bm{\mathcal{F}}} \]

Singularities

• Briefly mention singularities, and say that for small stroke, it is not an issue, the Jacobian matrix may be considered constant

Static Analysis

<<ssec:nhexa_stewart_platform_static>>

How stiffness varies with orientation of struts. Same with stroke? Or maybe in the detailed chapter?

The stiffness of the actuator $k_i$ links the applied actuator force $\delta \tau_i$ and the corresponding small deflection $\delta l_i$:

\begin{equation*} \tau_i = k_i \delta l_i, \quad i = 1,\ \dots,\ 6 \end{equation*}

If we combine these 6 relations:

\begin{equation*} \bm{\tau} = \mathcal{K} \delta \bm{\mathcal{L}} \quad \mathcal{K} = \text{diag}\left[ k_1,\ \dots,\ k_6 \right] \end{equation*}

Substituting $\bm{\tau} = \bm{J}^{-T} \bm{\mathcal{F}}$ and $\delta \bm{\mathcal{L}} = \bm{J} \cdot \delta \bm{\mathcal{X}}$ gives

\begin{equation*} \bm{\mathcal{F}} = \bm{J}^T \mathcal{K} \bm{J} \cdot \delta \bm{\mathcal{X}} \end{equation*}

And then we identify the stiffness matrix $\bm{K}$:

\begin{equation*} \bm{K} = \bm{J}^T \mathcal{K} \bm{J} \end{equation*}

If the stiffness matrix $\bm{K}$ is inversible, the compliance matrix of the manipulator is defined as

\begin{equation*} \bm{C} = \bm{K}^{-1} = (\bm{J}^T \mathcal{K} \bm{J})^{-1} \end{equation*}

The compliance matrix of a manipulator shows the mapping of the moving platform wrench applied at $\bm{O}_B$ to its small deflection by

\begin{equation*} \delta \bm{\mathcal{X}} = \bm{C} \cdot \bm{\mathcal{F}} \end{equation*}

Dynamic Analysis

<<ssec:nhexa_stewart_platform_dynamics>>

Very complex => multi-body model For instance, compute the plant for massless struts and perfect joints (will be compared with Simscape model). But say that if we want to model more complex cases, it becomes impractical (cite papers).

Conclusion

Dynamic analysis of parallel manipulators presents an inherent complexity due to their closed-loop structure and kinematic constraints.

All depends on the geometry. Reasonable choice of geometry is made in chapter 1. Optimization of the geometry will be made in chapter 2.

Multi-Body Model

<<sec:nhexa_model>>

Introduction   ignore

Goal:

• Study the dynamics of Stewart platform
• Instead of working with complex analytical models: a multi-body model is used. Complex because has to model the inertia of the struts. Cite papers that tries to model the stewart platform analytically Advantage: it will be easily included in the model of the NASS
• Mention the Toolbox (maybe make a DOI for that)

• Have a table somewhere that summarizes the main characteristics of the nano-hexapod model

  • location of joints
  • size / mass of platforms, etc…

Model Definition

<<ssec:nhexa_model_def>>

• Make a schematic of the definition process (for instance knowing the ai, bi points + {A} and {B} allows to compute Jacobian, etc…)

• What is important for the model:

  • Inertia of plates and struts
  • Positions of joints / Orientation of struts
  • Definition of frames (for Jacobian, stiffness analysis, etc…)

Then, several things can be computed:

• Kinematics, stiffness, platform mobility, dynamics, etc…

• Joints: can be 2dof to 6dof
• Actuators: can be modelled as wanted

Nano Hexapod

<<ssec:nhexa_model_nano_hexapod>>

Start simple:

• Perfect joints, massless actuators

Joints: perfect 2dof/3dof (+ mass-less) Actuators: APA + Encoder (mass-less)

• k = 1N/um
• Force sensor

Definition of each part + Plant with defined inputs/outputs (force sensor, relative displacement sensor, etc…)

Model Dynamics

<<ssec:nhexa_model_dynamics>>

• If all is perfect (mass-less struts, perfect joints, etc…), maybe compare analytical model with simscape model?
• Say something about the model order Model order is 12, and that we can compute modes from matrices M and K, compare with the Simscape model
• Compare with analytical formulas (see number of states)

Conclusion

• Validation of multi-body model in a simple case

• Possible to increase the model complexity when required

  • If considered 6dof joint stiffness, model order increases
  • Can have an effect on IFF performances: cite:&preumont07_six_axis_singl_stage_activ
  • Conclusion: during the conceptual design, we consider a perfect, but will be taken into account later
  • Optimization of the Flexible joint will be performed in Chapter 2.2
• MIMO system: how to control? => next section

Control of Stewart Platforms

<<sec:nhexa_control>>

Introduction   ignore

MIMO control: much more complex than SISO control because of interaction. Possible to ignore interaction when good decoupling is achieved. Important to have tools to study interaction Different ways to try to decouple a MIMO plant.

Reference book: cite:&skogestad07_multiv_feedb_contr

Centralized and Decentralized Control

<<ssec:nhexa_control_centralized_decentralized>>

• Explain what is centralized and decentralized:

  • linked to the sensor position relative to the actuators
  • linked to the fact that sensors and actuators pairs are "independent" or each other (related to the control architecture, not because there is no coupling)
• When can decentralized control be used and when centralized control is necessary? Study of interaction: RGA

Choice of the control space

<<ssec:nhexa_control_space>>

• file:~/Cloud/research/matlab/decoupling-strategies/svd-control.org
• Jacobian matrices, CoK, CoM, control in the frame of the struts, SVD, Modal, …
• Combined CoM and CoK => Discussion of cubic architecture ? (quick, as it is going to be in detailed in chapter 2)
• Explain also the link with the setpoint: it is interesting to have the controller in the frame of the performance variables Also speak about disturbances? (and how disturbances can be mixed to different outputs due to control and interaction)
• Table that summarizes the trade-off for each strategy
• Say that in this study, we will do the control in the frame of the struts for simplicity (even though control in the cartesian frame was also tested)

Active Damping with Decentralized IFF

<<ssec:nhexa_control_iff>>

Guaranteed stability: cite:&preumont08_trans_zeros_struc_contr_with

• I think there is another paper about that

For decentralized control: "MIMO root locus" can be used to estimate the damping / optimal gain Poles and converging towards transmission zeros

How to optimize the added damping to all modes?

• Add some papers citations

Compute:

• Plant dynamics
• Root Locus

MIMO High-Authority Control - Low-Authority Control

<<ssec:nhexa_control_hac_lac>>

Compute:

• compare open-loop and damped plant (outputs are the encoders)
• Implement decentralized control?

• Check stability:

  • Characteristic Loci: Eigenvalues of $G(j\omega)$ plotted in the complex plane
  • Generalized Nyquist Criterion: If $G(s)$ has $p_0$ unstable poles, then the closed-loop system with return ratio $kG(s)$ is stable if and only if the characteristic loci of $kG(s)$, taken together, encircle the point $-1$, $p_0$ times anti-clockwise, assuming there are no hidden modes
• Show some performance metric? For instance compliance?

Conclusion

Conclusion

<<sec:nhexa_conclusion>>

• Configurable Stewart platform model
• Will be included in the multi-body model of the micro-station => nass multi body model
• Control: complex problem, try to use simplest architecture

Bibliography   ignore

Footnotes

¹Different architecture exists, typically referred as "6-SPS" (Spherical, Prismatic, Spherical) or "6-UPS" (Universal, Prismatic, Spherical)

---