269 KiB
Nano Active Stabilization System - Uniaxial Model
- Introduction
- Micro Station Model
- Nano-Hexapod Model
- Disturbance Identification
- Open-Loop Dynamic Noise Budgeting
- Active Damping
- Position Feedback Controller
- Effect of limited micro-station compliance
- Effect of Payload Dynamics
- Conclusion
- Bibliography
This report is also available as a pdf.
Introduction ignore
In this report, a uniaxial model of the Nano Active Stabilization System (NASS) is developed and used to have a first idea of the challenges involved in this complex system. Note that in this document, only the vertical direction is considered (which is the most stiff), but other directions were considered as well and yields similar conclusions. The model is schematically shown in Figure ref:fig:uniaxial_overview_model_sections where the colors are representing the studied parts in different sections.
In order to have a relevant model, the micro-station dynamics is first identified and its model is tuned to match the measurements (Section ref:sec:micro_station_model). Then, a model of the nano-hexapod is added on top of the micro-station. With added sample and sensors, this gives a uniaxial dynamical model of the NASS that will be used for further analysis (Section ref:sec:nano_station_model).
The disturbances affecting the position stability are identified experimentally (Section ref:sec:uniaxial_disturbances) and included in the model for dynamical noise budgeting (Section ref:sec:uniaxial_noise_budgeting). In all the following analysis, there nano-hexapod stiffnesses are considered to better understand the trade-offs and to find the most adequate nano-hexapod design. Three sample masses are also considered to verify the robustness of the applied control strategies to a change of sample.
Three active damping techniques are then applied on the nano-hexapod. This helps to reduce the effect of disturbances as well as render the system easier to control afterwards (Section ref:sec:uniaxial_active_damping).
Once the system is well damped, a feedback position controller is applied, and the obtained performance are compared (Section ref:sec:uniaxial_position_control).
Two key effects that may limit that positioning performances are then considered: the limited micro-station compliance (Section ref:sec:uniaxial_support_compliance) and the presence of dynamics between the nano-hexapod and the sample's point of interest (Section ref:sec:uniaxial_payload_dynamics).
Conclusion remarks are given in Section ref:sec:uniaxial_conclusion.
| Sections | Matlab File |
|---|---|
| Section ref:sec:micro_station_model | uniaxial_1_micro_station_model.m |
| Section ref:sec:nano_station_model | uniaxial_2_nano_hexapod_model.m |
| Section ref:sec:uniaxial_disturbances | uniaxial_3_disturbances.m |
| Section ref:sec:uniaxial_noise_budgeting | uniaxial_4_dynamic_noise_budget.m |
| Section ref:sec:uniaxial_active_damping | uniaxial_5_active_damping.m |
| Section ref:sec:uniaxial_position_control | uniaxial_6_hac_lac.m |
| Section ref:sec:uniaxial_support_compliance | uniaxial_7_support_compliance |
| Section ref:sec:uniaxial_payload_dynamics | uniaxial_8_payload_dynamics |
\begin{tikzpicture}
% ====================
% Parameters
% ====================
\def\massw{2.2} % Width of the masses
\def\massh{0.8} % Height of the masses
\def\spaceh{1.2} % Height of the springs/dampers
\def\dispw{0.4} % Width of the dashed line for the displacement
\def\disph{0.3} % Height of the arrow for the displacements
\def\bracs{0.05} % Brace spacing vertically
\def\brach{-12pt} % Brace shift horizontaly
\def\fsensh{0.2} % Height of the force sensor
\def\velsize{0.2} % Size of the velocity sensor
% ====================
% IFF
% ====================
% Ground
% ====================
\draw[draw=colorblue] (-0.5*\massw, 0) -- (0.5*\massw, 0);
\draw[dashed,draw=coloryellow] (0.5*\massw, 0) -- ++(\dispw, 0);
\draw[->, color=coloryellow] (0.5*\massw+0.5*\dispw, 0) -- ++(0, 2*\disph) node[right, color=coloryellow]{$x_{f}$};
% ====================
% ====================
% Granite
\begin{scope}[shift={(0, 0)}]
% Mass
\draw[draw=colorblue,fill=colorblue!10!white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5,color=colorblue]{$m_{g}$};
% Spring, Damper, and Actuator
\draw[spring,draw=colorblue] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1, color=colorblue]{$k_{g}$};
\draw[damper={colorblue}{}{}] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2, color=colorblue]{$c_{g}$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{Granite};
% Displacements
\draw[dashed, draw=colorpurple] (0.5*\massw, \spaceh+\massh) -- ++(7.5*\dispw, 0) coordinate(xg);
\end{scope}
% ====================
% ====================
% Stages
\begin{scope}[shift={(0, \spaceh+\massh)}]
% Mass
\draw[draw=colorblue,fill=colorblue!10!white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5,color=colorblue]{$m_{t}$};
% Spring, Damper, and Actuator
\draw[spring,draw=colorblue] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1,color=colorblue]{$k_{t}$};
\draw[damper={colorblue}{}{}] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2,color=colorblue]{$c_{t}$};
% Disturbance
\draw[actuator={0.45}{0.2}{coloryellow}] ( 0.3*\massw, 0) -- (0.3*\massw, \spaceh) node[midway, right=0.1, color=coloryellow](ft){$f_{t}$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$T_y$/$R_y$/$R_z$};
\end{scope}
% ====================
% ====================
% Hexapod
\begin{scope}[shift={(0, 2*(\spaceh+\massh))}]
% Mass
\draw[draw=colorblue,fill=colorblue!10!white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5,color=colorblue]{$m_h$};
% Spring, Damper, and Actuator
\draw[spring,draw=colorblue] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1,color=colorblue]{$k_h$};
\draw[damper={colorblue}{}{}] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2,color=colorblue]{$c_h$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$\mu\text{-hexa}$};
\end{scope}
% ====================
% ====================
% NASS
\begin{scope}[shift={(0, 3*(\spaceh+\massh))}]
% Mass
\draw[draw=colorred,fill=colorred!10!white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5,color=colorred]{$m_{n}$};
% Force Sensor
\node[forcesensor={\massw}{\fsensh}{colorgreen}] (fsensn) at (0, \spaceh-\fsensh){};
\node[right, color=colorgreen] (fn) at (fsensn.east) {$f_n$};
% Spring, Damper, and Actuator
\draw[spring,draw=colorred] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh-\fsensh) node[midway, left=0.1,color=colorred]{$k_{n}$};
\draw[damper={colorred}{}{}] (0, 0) -- ( 0, \spaceh-\fsensh) node[midway, left=0.2,color=colorred]{$c_{n}$};
\draw[actuator={0.4}{0.2}{colorred}] ( 0.3*\massw, 0) -- (0.3*\massw, \spaceh-\fsensh) node[midway, right=0.1,color=colorred](f){$f$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$\nu\text{-hexa}$};
% Displacements
\draw[dashed,draw=colorpurple] (0.5*\massw, \spaceh+\massh) -- ++(7.5*\dispw, 0) coordinate(xnpos);
\end{scope}
% ====================
% ====================
% sample
\begin{scope}[shift={(0, 4*(\spaceh+\massh))}]
% Mass
\draw[draw=colorcyan,fill=colorcyan!10!white] (-0.3*\massw, \spaceh) rectangle (0.3*\massw, \spaceh+\massh) node[pos=0.5, color=colorcyan]{$m_{s}$};
% Spring, Damper, and Actuator
\draw[spring,draw=colorcyan] (-0.2*\massw, 0) -- (-0.2*\massw, \spaceh) node[midway, left=0.1, color=colorcyan]{$k_{s}$};
\draw[damper={colorcyan}{}{}] ( 0.2*\massw, 0) -- ( 0.2*\massw, \spaceh) node[midway, left=0.2, color=colorcyan]{$c_{s}$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) %
node[midway,rotate=90,anchor=south,yshift=10pt,align=center]{Sample};
% External Force
\draw[->, color=coloryellow] (0, \spaceh+\massh) node[]{$\bullet$} -- ++(0, 0.5*\massh) node[right, color=coloryellow]{$f_s$};
\end{scope}
% ====================
% Measured displacement
\draw[<->, dashed, draw=colorpurple] ($(xg)+(-0.1, 0)$) -- node[left, color=colorpurple](d){$d$} ($(xnpos)+(-0.1, 0)$);
% ====================
% IFF Control
\node[block={2em}{2em}, right=1.0 of fn, color=colorgreen, fill=colorgreen!10!white] (iff) {$K_{\textsc{IFF}}$};
\node[addb, draw=colorgreen, fill=colorgreen!10!white, right=0.5 of f.east] (ctrladd) {};
\node[block={2em}{2em}, color=colorpurple, fill=colorpurple!10!white] (Khac) at (ctrladd|-d) {$K_{\textsc{HAC}}$};
\draw[->, draw=colorgreen] (fn.east) -- (iff.west);
\draw[->, draw=colorgreen] (iff.south) |- (ctrladd.east);
\draw[->, draw=colorgreen] (ctrladd.west) -- (f.east);
\draw[->, draw=colorpurple] (d.west) -- (Khac.east);
\draw[->, draw=colorpurple] (Khac.north) -- (ctrladd.south) node[below right, color=colorpurple]{$f^{\prime}$};
% ====================
\end{tikzpicture}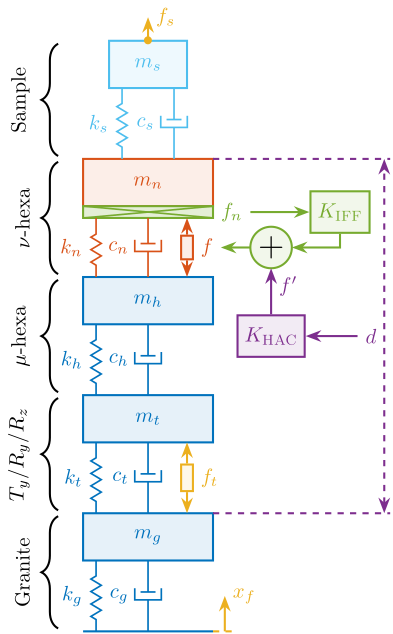
Micro Station Model
<<sec:micro_station_model>>
Introduction ignore
In this section, a uni-axial model of the micro-station is tuned in order to match measurements made on the micro-station The measurement setup is shown in Figure ref:fig:uniaxial_ustation_first_meas_dynamics where several geophones are fixed to the micro-station and an instrumented hammer is used to inject forces on different stages of the micro-station.
From the measured frequency response functions (FRF), the model can be tuned to approximate the uniaxial dynamics of the micro-station.

Measured dynamics
The measurement setup is schematically shown in Figure ref:fig:uniaxial_ustation_meas_dynamics_schematic where:
- Two hammer hits are performed, one on the Granite (force $F_g$), and one on the micro-hexapod's top platform (force $F_h$)
- The inertial motion of the granite $x_g$ and the micro-hexapod's top platform $x_h$ are measured using geophones.
From the forces applied by the instrumented hammer and the responses of the geophones, the following frequency response functions can be computed:
- from $F_h$ to $d_h$ (i.e. the compliance of the micro-station)
- from $F_g$ to $d_h$ (or from $F_h$ to $d_g$)
- from $F_g$ to $d_g$
\begin{tikzpicture}
% Parameters
\def\blockw{6.0cm}
\def\blockh{1.2cm}
\def\tiltdeg{0}
\coordinate[] (rotationpoint) at (0, 4.5*\blockh);
\begin{scope}[rotate around={\tiltdeg:(rotationpoint)}]
% Tilt
\path[] ([shift=(-120:4*\blockh)]rotationpoint) coordinate(beginarc) arc (-120:-110:4*\blockh) %
-- ([shift=(-70:4*\blockh)]rotationpoint) arc (-70:-60:4*\blockh)%
|- ++(-0.15*\blockw, 0.6*\blockh) coordinate (spindlene)%
|- ($(beginarc) + (0.15*\blockw, 0.2*\blockh)$) coordinate (spindlesw) -- ++(0, 0.4*\blockh) coordinate(tiltte) -| cycle;
% Spindle
\coordinate[] (spindlese) at (spindlesw-|spindlene);
\draw[fill=black!30] ($(spindlese)+(-0.1,0.1)+(-0.1*\blockw, 0)$) -| ($(spindlene)+(-0.1, 0)$) -| coordinate[pos=0.25](spindletop) ($(spindlesw)+(0.1,0.1)$) -| ++(0.1*\blockw, -\blockh) -| coordinate[pos=0.25](spindlebot) cycle;
% \draw[dashed, color=black!60] ($(spindletop)+(0, 0.2)$) -- ($(spindlebot)+(0,-0.2)$);
% Tilt
\draw[fill=black!60] ([shift=(-120:4*\blockh)]rotationpoint) coordinate(beginarc) arc (-120:-110:4*\blockh) %
-- ([shift=(-70:4*\blockh)]rotationpoint) arc (-70:-60:4*\blockh)%
|- coordinate (tiltne) ++(-0.15*\blockw, 0.6*\blockh) coordinate (spindlene)%
|- ($(beginarc) + (0.15*\blockw, 0.2*\blockh)$) coordinate (spindlesw) -- ++(0, 0.4*\blockh) -| cycle;
% Micro-Hexapod
\begin{scope}[shift={(spindletop)}]
% Parameters definitions
\def\baseh{0.22*\blockh} % Height of the base
\def\naceh{0.18*\blockh} % Height of the nacelle
\def\baser{0.22*\blockw} % Radius of the base
\def\nacer{0.18*\blockw} % Radius of the nacelle
\def\armr{0.2*\blockh} % Radius of the arms
\def\basearmborder{0.2}
\def\nacearmborder{0.2}
\def\xnace{0} \def\ynace{\blockh-\naceh} \def\anace{0}
\def\xbase{0} \def\ybase{0} \def\abase{0}
% Hexapod1
\begin{scope}[shift={(\xbase, \ybase)}, rotate=\abase]
% Base
\draw[fill=white] (-\baser, 0) coordinate[](uhexabot) rectangle (\baser, \baseh);
\coordinate[] (armbasel) at (-\baser+\basearmborder+\armr, \baseh);
\coordinate[] (armbasec) at (0, \baseh);
\coordinate[] (armbaser) at (\baser-\basearmborder-\armr, \baseh);
\begin{scope}[shift={(\xnace, \ynace)}, rotate=\anace]
\draw[fill=white] (-\nacer, 0) rectangle (\nacer, \naceh);
\coordinate[] (uhexatop) at (0, \naceh);
\coordinate[] (armnacel) at (-\nacer+\nacearmborder+\armr, 0);
\coordinate[] (armnacec) at (0, 0);
\coordinate[] (armnacer) at (\nacer-\nacearmborder-\armr, 0);
\end{scope}
\draw[] (armbasec) -- (armnacer);
\draw[] (armbasec) -- (armnacel);
\draw[] (armbasel) -- coordinate(mhexaw) (armnacel);
\draw[] (armbasel) -- (armnacec);
\draw[] (armbaser) -- (armnacec);
\draw[] (armbaser) -- coordinate(mhexae) (armnacer);
\end{scope}
\end{scope}
\begin{scope}[shift={(uhexatop)}] % Geophone - Hexapod
\draw[draw=colorgreen, fill=colorgreen!10!white] (-0.3, 0) rectangle node[midway, color=colorgreen, rotate=90]{\tiny geophone} (0.3, 1.2);
\draw[rounded corners=0.1, draw=colorgreen, fill=colorgreen!10!white] (-0.1, 1.2) -- ++(0, 0.1) -- ++(0.1, 0.1) -- ++(0.1, -0.1) -- ++(0, -0.1) --cycle;
\node[fill,shape=circle,minimum size=3pt,inner sep=0pt, color=colorgreen] at (0, 1.4){};
\draw[out=90, in=180, draw=colorgreen] (0, 1.4) to ++(0.4, 0.2) node[right, color=colorgreen]{$x_h$};
\end{scope}
\begin{scope}[shift={(uhexatop)}] % Instrumented Hammer - Hexapod
\begin{scope}[shift={(-1.5, 0)}]
\draw[fill=white, rounded corners=0.2, draw=colorblue, fill=colorblue!10!white] (-0.5, 0.42) rectangle (0.5, 0.58);
\draw[fill=white, rounded corners=0.2, draw=colorblue, fill=colorblue!10!white] (0.5, 0.15) rectangle (0.7, 0.8);
\draw[fill=white, rounded corners=0.2, color=colorblue] (0.55, 0.15) rectangle (0.65, 0);
\draw[out=180, in=0, draw=colorblue] (-0.5, 0.5) to ++(-0.6, -0.1) node[above, color=colorblue]{$F_h$};
\node[fill,shape=circle,minimum size=3pt,inner sep=0pt, color=colorblue] at (-0.5, 0.5){};
\end{scope}
\end{scope}
\end{scope}
\begin{scope}[shift={(0, -0.3*\blockh)}]
% Translation Stage - fixed part
\draw[fill=black!40] (-0.5*\blockw, 0) coordinate[](tyb) rectangle (0.5*\blockw, 0.15*\blockh);
\coordinate[] (measposbot) at (0.5*\blockw, 0);
% Translation Stage - mobile part
\draw[fill=black!10, fill opacity=0.5] (-0.5*\blockw, 0.2*\blockh) -- (-0.5*\blockw, 1.5*\blockh) coordinate[](tyt) -- (0.5*\blockw, 1.5*\blockh) -- (0.5*\blockw, 0.2*\blockh) -- (0.35*\blockw, 0.2*\blockh) -- (0.35*\blockw, 0.8*\blockh) -- (-0.35*\blockw, 0.8*\blockh) -- (-0.35*\blockw, 0.2*\blockh) -- cycle;
% Translation Guidance
\draw[dashed, color=black!60] ($(-0.5*\blockw, 0)+( 0.075*\blockw,0.5*\blockh)$) circle (0.2*\blockh);
\draw[dashed, color=black!60] ($( 0.5*\blockw, 0)+(-0.075*\blockw,0.5*\blockh)$) circle (0.2*\blockh);
% \draw[fill, color=black] ($( 0.5*\blockw, 0)+(-0.075*\blockw,0.5*\blockh)$) circle (0.04);
% \node[draw, circle, inner sep=0pt, minimum size=0.3cm, label=above:$T_y$] at ($( 0.5*\blockw, 0)+(-0.075*\blockw,0.5*\blockh)$){};
% Tilt Guidance
\draw[dashed, color=black!60] ([shift=(-107:4.1*\blockh)]rotationpoint) arc (-107:-120:4.1*\blockh);
\draw[dashed, color=black!60] ([shift=( -73:4.1*\blockh)]rotationpoint) arc (-73:-60:4.1*\blockh);
\begin{scope}[shift={(4.0, 0)}] % Geophone - Granite
\draw[draw=colorgreen, fill=colorgreen!10!white] (-0.3, 0) rectangle node[midway, color=colorgreen, rotate=90]{\tiny geophone} (0.3, 1.2);
\draw[rounded corners=0.1, draw=colorgreen, fill=colorgreen!10!white] (-0.1, 1.2) -- ++(0, 0.1) -- ++(0.1, 0.1) -- ++(0.1, -0.1) -- ++(0, -0.1) --cycle;
\node[fill,shape=circle,minimum size=3pt,inner sep=0pt, color=colorgreen] at (0, 1.4){};
\draw[out=90, in=180, draw=colorgreen] (0, 1.4) to ++(0.4, 0.2) node[right, color=colorgreen]{$x_g$};
\end{scope}
\begin{scope}[shift={(-4.0, 0)}] % Instrumented Hammer - Granite
\draw[fill=white, rounded corners=0.2, draw=colorblue, fill=colorblue!10!white] (-0.5, 0.42) rectangle (0.5, 0.58);
\draw[fill=white, rounded corners=0.2, draw=colorblue, fill=colorblue!10!white] (0.5, 0.15) rectangle (0.7, 0.8);
\draw[fill=white, rounded corners=0.2, color=colorblue] (0.55, 0.15) rectangle (0.65, 0);
\draw[out=180, in=0, draw=colorblue] (-0.5, 0.5) to ++(-0.6, -0.1) node[above, color=colorblue]{$F_g$};
\node[fill,shape=circle,minimum size=3pt,inner sep=0pt, color=colorblue] at (-0.5, 0.5){};
\end{scope}
\end{scope}
% Granite
\draw[fill=black!40] (-0.8*\blockw, -0.3*\blockh) rectangle node[midway]{Granite} (0.8*\blockw, -1.5*\blockh);
% Vertical line
% \draw[dashed, color=black] (spindlebot) -- ++(0, 2*\blockh);
% \node[] at ($(spindlebot)+(0, 1.1*\blockh)$) {\AxisRotator[rotate=-90]};
% \node[right, shift={(0.3,0)}] at ($(spindlebot)+(0, 1.1*\blockh)$) {$\theta_z$};
% Axis
\begin{scope}[shift={(-0.6*\blockw, 2.5*\blockh)}]
\def\axissize{0.8cm}
\draw[->] (0, 0) -- ++(0, \axissize) node[right]{$z$};
\draw[->] (0, 0) -- ++(-\axissize, 0) node[above]{$x$};
\draw[fill, color=black] (0, 0) circle (0.05*\axissize);
\node[draw, circle, inner sep=0pt, minimum size=0.4*\axissize, label=right:$y$] (yaxis) at (0, 0){};
\end{scope}
\end{tikzpicture}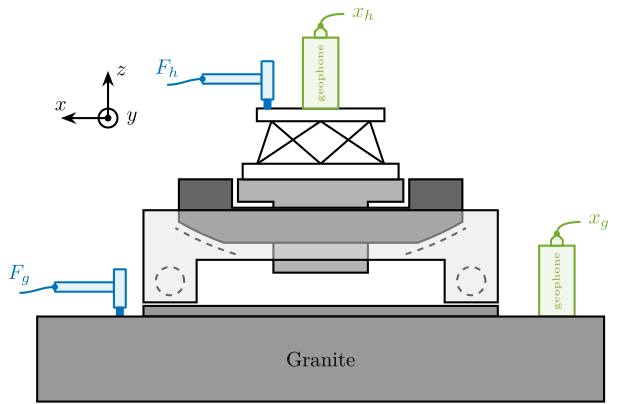
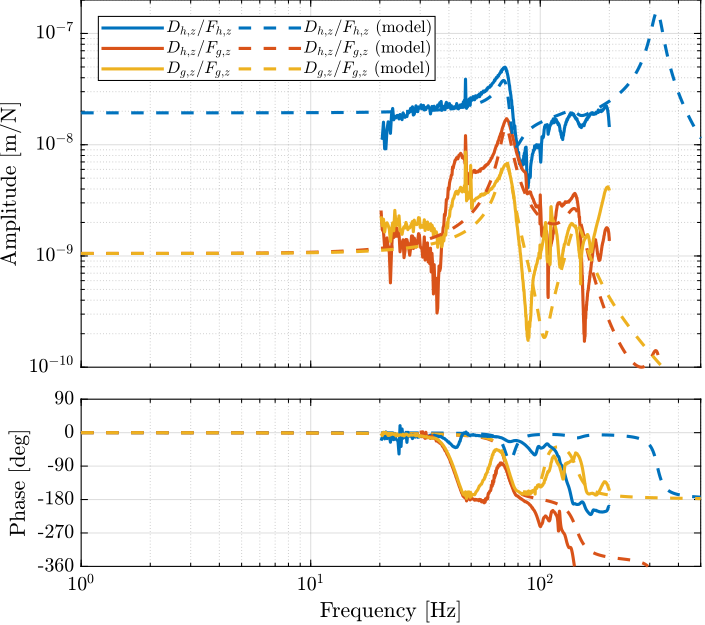
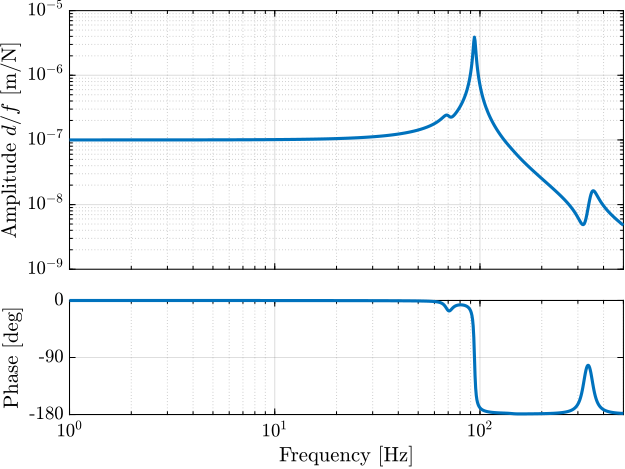
Due to the bad coherence at low frequency, the frequency response functions will only be shown between 20 and 200Hz (solid lines in Figure ref:fig:uniaxial_comp_frf_meas_model).
%% Load measured FRF
load('meas_microstation_frf.mat');Uniaxial Model
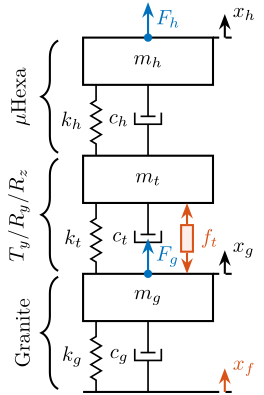
The uni-axial model of the micro-station is shown in Figure ref:fig:uniaxial_model_micro_station, with:
-
Disturbances:
- $x_f$: Floor motion
- $f_t$: Stage vibrations
- Hammer impacts: $F_h$ and $F_g$.
- Geophones: $x_h$ and $x_g$
\begin{tikzpicture}
% ====================
% Parameters
% ====================
\def\massw{2.2} % Width of the masses
\def\massh{0.8} % Height of the masses
\def\spaceh{1.2} % Height of the springs/dampers
\def\dispw{0.4} % Width of the dashed line for the displacement
\def\disph{0.4} % Height of the arrow for the displacements
\def\bracs{0.05} % Brace spacing vertically
\def\brach{-12pt} % Brace shift horizontaly
\def\fsensh{0.2} % Height of the force sensor
\def\velsize{0.2} % Size of the velocity sensor
% ====================
% ====================
% Floor
% ====================
\draw (-0.5*\massw, 0) -- (0.5*\massw, 0);
\draw[dashed] (0.5*\massw, 0) -- ++(\dispw, 0);
\draw[->, draw=colorred] (0.5*\massw+0.5*\dispw, 0) -- ++(0, \disph) node[right, color=colorred]{$x_{f}$};
% ====================
% ====================
% Granite
\begin{scope}[shift={(0, 0)}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{g}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{g}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{g}$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{Granite};
% Displacement
\draw[dashed] (0.5*\massw, \spaceh+\massh) -- ++(\dispw, 0);
\draw[->] (0.5*\massw+0.5*\dispw, \spaceh+\massh) -- ++(0, \disph) node[right]{$x_{g}$};
\end{scope}
% ====================
% ====================
% Stages
\begin{scope}[shift={(0, \spaceh+\massh)}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{t}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{t}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{t}$};
% Disturbance
\draw[actuator={0.45}{0.2}{colorred}] ( 0.3*\massw, 0) -- (0.3*\massw, \spaceh) node[midway, right=0.1, color=colorred](ft){$f_t$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$T_y$/$R_y$/$R_z$};
% External Force
\draw[->, color=colorblue] (0, 0)node[branch] -- ++(0, 1.5*\dispw) node[below right]{$F_g$};
% % Displacement
% \draw[dashed] (0.5*\massw, \spaceh+\massh) -- ++(\dispw, 0);
% \draw[->] (0.5*\massw+0.5*\dispw, \spaceh+\massh) -- ++(0, \disph) node[right]{$x_{t}$};
\end{scope}
% ====================
% ====================
% Hexapod
\begin{scope}[shift={(0, 2*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{h}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{h}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{h}$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$\mu\text{Hexa}$};
% Displacement
\draw[dashed] (0.5*\massw, \spaceh+\massh) -- ++(\dispw, 0);
\draw[->] (0.5*\massw+0.5*\dispw, \spaceh+\massh) -- ++(0, \disph) node[right]{$x_{h}$};
% External Force
\draw[->, color=colorblue] (0, \spaceh+\massh)node[branch] -- ++(0, 1.5*\dispw) node[below right]{$F_h$};
\end{scope}
% ====================
\end{tikzpicture}Masses are estimated from the CAD.
%% Parameters - Mass
mh = 15; % Micro Hexapod [kg]
mt = 1200; % Ty + Ry + Rz [kg]
mg = 2500; % Granite [kg]And stiffnesses from the data-sheet of stage manufacturers.
%% Parameters - Stiffnesses
kh = 6.11e+07; % [N/m]
kt = 5.19e+08; % [N/m]
kg = 9.50e+08; % [N/m]The damping coefficients are tuned to match the identified damping from the measurements.
%% Parameters - damping
ch = 2*0.05*sqrt(kh*mh); % [N/(m/s)]
ct = 2*0.05*sqrt(kt*mt); % [N/(m/s)]
cg = 2*0.08*sqrt(kg*mg); % [N/(m/s)]Comparison of the model and measurements
The comparison between the measurements and the model is shown in Figure ref:fig:uniaxial_comp_frf_meas_model.
Only three modes are modelled with frequencies at 70Hz, 140Hz and 320Hz.
As the model is simplistic, the goal is not to match exactly the measurement but to have a first approximation. More accurate models will be used later on.
Nano-Hexapod Model
<<sec:nano_station_model>>
Introduction ignore
A model of the nano-hexapod and sample is now added on top of the uni-axial model of the micro-station (Figure ref:fig:uniaxial_model_micro_station-nass).
Disturbances (shown in red) are:
- $f_s$: direct forces applied to the sample (for instance cable forces)
- $f_t$: disturbances coming from the imperfect stage scanning performance
- $x_f$: floor motion
The control signal is the force applied by the nano-hexapod $f$ and the measurement is the relative motion between the sample and the granite $d$.
The sample is here considered as a rigid body and rigidly fixed to the nano-hexapod. The effect of having resonances between the sample's point of interest and the nano-hexapod actuator will be considered in further analysis.
\begin{tikzpicture}
% ====================
% Parameters
% ====================
\def\massw{2.2} % Width of the masses
\def\massh{0.8} % Height of the masses
\def\spaceh{1.2} % Height of the springs/dampers
\def\dispw{0.4} % Width of the dashed line for the displacement
\def\disph{0.3} % Height of the arrow for the displacements
\def\bracs{0.05} % Brace spacing vertically
\def\brach{-12pt} % Brace shift horizontaly
\def\fsensh{0.2} % Height of the force sensor
\def\velsize{0.2} % Size of the velocity sensor
% ====================
% ====================
% Ground
% ====================
\draw (-0.5*\massw, 0) -- (0.5*\massw, 0);
\draw[dashed] (0.5*\massw, 0) -- ++(\dispw, 0);
\draw[->, color=colorred] (0.5*\massw+0.5*\dispw, 0) -- ++(0, 2*\disph) node[right, color=colorred]{$x_{f}$};
% ====================
% ====================
% Marble
\begin{scope}[shift={(0, 0)}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{g}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{g}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{g}$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{Granite};
% Displacements
\draw[dashed] (0.5*\massw, \spaceh+\massh) -- ++(2*\dispw, 0) coordinate(xm) -- ++(\dispw, 0) coordinate(dbot);
\end{scope}
% ====================
% ====================
% Stages
\begin{scope}[shift={(0, \spaceh+\massh)}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{t}$};
% % Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{t}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{t}$};
\draw[actuator={0.45}{0.2}{colorred}] ( 0.3*\massw, 0) -- (0.3*\massw, \spaceh) node[midway, right=0.1, color=colorred](ft){$f_{t}$};
Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$T_y$/$R_y$/$R_z$};
\end{scope}
% ====================
% ====================
% Hexapod
\begin{scope}[shift={(0, 2*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{h}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{h}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{h}$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$\mu\text{-hexa}$};
\end{scope}
% ====================
% ====================
% NASS
\begin{scope}[shift={(0, 3*(\spaceh+\massh))}]
% Mass
\draw[fill=colorblue!10!white, draw=colorblue] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5,color=colorblue]{$m_{n}$};
% Spring, Damper, and Actuator
\draw[spring, draw=colorblue] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1, color=colorblue]{$k_{n}$};
\draw[damper={colorblue}{}{}] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2, color=colorblue]{$c_{n}$};
\draw[actuator={0.4}{0.2}{colorblue}] ( 0.3*\massw, 0) -- (0.3*\massw, \spaceh) node[midway, right=0.1, color=colorblue](F){$f$};
% Displacements
\draw[dashed] (0.5*\massw, \spaceh+\massh) -- ++(2*\dispw, 0) coordinate(xn) -- ++(\dispw, 0) coordinate(drtop);
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$\nu\text{-hexa}$};
\end{scope}
% ====================
% ====================
% sample
\begin{scope}[shift={(0, 4*(\spaceh+\massh))}]
% Mass
\draw[fill=colorgreen!10!white, draw=colorgreen] (-0.3*\massw, 0) rectangle (0.3*\massw, \massh) node[pos=0.5,color=colorgreen]{$m_{s}$};
% External Force
\draw[->, color=colorred] (0, \massh) node[]{$\bullet$} -- ++(0, 0.5*\massh) node[right, color=colorred]{$f_s$};
\end{scope}
% ====================
% ====================
% Measured Displacement
\draw[<->, dashed] (xm) -- node[midway, right]{$d$} (xn);
% ====================
\end{tikzpicture}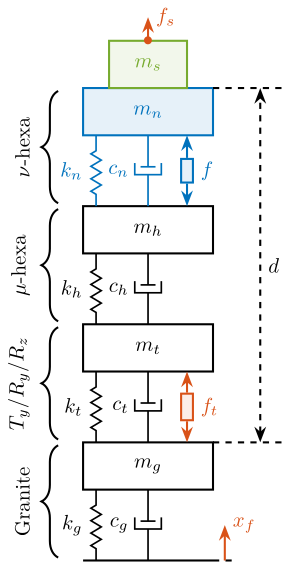
Nano-Hexapod Parameters
The parameters for the nano-hexapod and sample are:
- $m_s$ the sample mass that can vary from 1kg up to 50kg
- $m_n$ the nano-hexapod mass which is set to 15kg
- $k_n$ the nano-hexapod stiffness, which can vary depending on the chosen architecture/technology
As a first example, let's choose a nano-hexapod stiffness of $10\,N/\mu m$ and a sample mass of 10kg.
%% Nano-Hexapod Parameters
mn = 15; % [kg]
kn = 1e7; % [N/m]
cn = 2*0.01*sqrt(mn*kn); % [N/(m/s)]
%% Sample Mass
ms = 10; % [kg]Obtained Dynamic Response
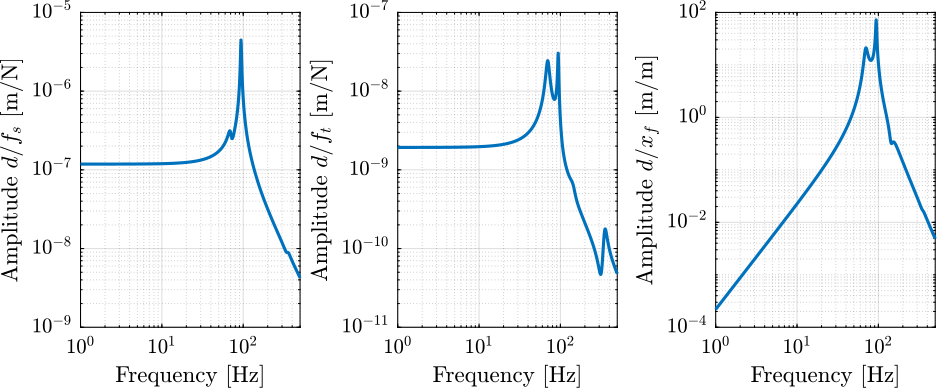
The sensitivity to disturbances (i.e. $x_f$, $f_t$ and $f_s$) are shown in Figure ref:fig:uniaxial_sensitivity_dist_first_params. The plant (i.e. the transfer function from actuator force $f$ to measured displacement $d$) is shown in Figure ref:fig:uniaxial_plant_first_params.
For further analysis, 9 configurations are considered: three nano-hexapod stiffnesses ($k_n = 0.01\,N/\mu m$, $k_n = 1\,N/\mu m$ and $k_n = 100\,N/\mu m$) combined with three sample's masses ($m_s = 1\,kg$, $m_s = 25\,kg$ and $m_s = 50\,kg$).
Disturbance Identification
<<sec:uniaxial_disturbances>>
Introduction ignore
In order to measure disturbances, two geophones are used, on located on the floor and on on the micro-hexapod's top platform (see Figure ref:fig:uniaxial_ustation_meas_disturbances).
The geophone on the floor is used to measured the floor motion $x_f$ while the geophone on the micro-hexapod is used to measure vibrations introduced by scanning of the $T_y$ stage and $R_z$ stage.
\begin{tikzpicture}
% Parameters
\def\blockw{6.0cm}
\def\blockh{1.2cm}
\def\tiltdeg{0}
\coordinate[] (rotationpoint) at (0, 4.5*\blockh);
\begin{scope}[rotate around={\tiltdeg:(rotationpoint)}]
% Tilt
\path[] ([shift=(-120:4*\blockh)]rotationpoint) coordinate(beginarc) arc (-120:-110:4*\blockh) %
-- ([shift=(-70:4*\blockh)]rotationpoint) arc (-70:-60:4*\blockh)%
|- ++(-0.15*\blockw, 0.6*\blockh) coordinate (spindlene)%
|- ($(beginarc) + (0.15*\blockw, 0.2*\blockh)$) coordinate (spindlesw) -- ++(0, 0.4*\blockh) coordinate(tiltte) -| cycle;
% Spindle
\coordinate[] (spindlese) at (spindlesw-|spindlene);
\draw[fill=black!30] ($(spindlese)+(-0.1,0.1)+(-0.1*\blockw, 0)$) -| ($(spindlene)+(-0.1, 0)$) -| coordinate[pos=0.25](spindletop) ($(spindlesw)+(0.1,0.1)$) -| ++(0.1*\blockw, -\blockh) -| coordinate[pos=0.25](spindlebot) cycle;
% \draw[dashed, color=black!60] ($(spindletop)+(0, 0.2)$) -- ($(spindlebot)+(0,-0.2)$);
% Tilt
\draw[fill=black!60] ([shift=(-120:4*\blockh)]rotationpoint) coordinate(beginarc) arc (-120:-110:4*\blockh) %
-- ([shift=(-70:4*\blockh)]rotationpoint) arc (-70:-60:4*\blockh)%
|- coordinate (tiltne) ++(-0.15*\blockw, 0.6*\blockh) coordinate (spindlene)%
|- ($(beginarc) + (0.15*\blockw, 0.2*\blockh)$) coordinate (spindlesw) -- ++(0, 0.4*\blockh) -| cycle;
% Micro-Hexapod
\begin{scope}[shift={(spindletop)}]
% Parameters definitions
\def\baseh{0.22*\blockh} % Height of the base
\def\naceh{0.18*\blockh} % Height of the nacelle
\def\baser{0.22*\blockw} % Radius of the base
\def\nacer{0.18*\blockw} % Radius of the nacelle
\def\armr{0.2*\blockh} % Radius of the arms
\def\basearmborder{0.2}
\def\nacearmborder{0.2}
\def\xnace{0} \def\ynace{\blockh-\naceh} \def\anace{0}
\def\xbase{0} \def\ybase{0} \def\abase{0}
% Hexapod
\begin{scope}[shift={(\xbase, \ybase)}, rotate=\abase]
% Base
\draw[fill=white] (-\baser, 0) coordinate[](uhexabot) rectangle (\baser, \baseh);
\coordinate[] (armbasel) at (-\baser+\basearmborder+\armr, \baseh);
\coordinate[] (armbasec) at (0, \baseh);
\coordinate[] (armbaser) at (\baser-\basearmborder-\armr, \baseh);
\begin{scope}[shift={(\xnace, \ynace)}, rotate=\anace]
\draw[fill=white] (-\nacer, 0) rectangle (\nacer, \naceh);
\coordinate[] (uhexatop) at (0, \naceh);
\coordinate[] (armnacel) at (-\nacer+\nacearmborder+\armr, 0);
\coordinate[] (armnacec) at (0, 0);
\coordinate[] (armnacer) at (\nacer-\nacearmborder-\armr, 0);
\end{scope}
\draw[] (armbasec) -- (armnacer);
\draw[] (armbasec) -- (armnacel);
\draw[] (armbasel) -- coordinate(mhexaw) (armnacel);
\draw[] (armbasel) -- (armnacec);
\draw[] (armbaser) -- (armnacec);
\draw[] (armbaser) -- coordinate(mhexae) (armnacer);
\end{scope}
\end{scope}
\begin{scope}[shift={(uhexatop)}] % Geophone - Hexapod
\draw[rounded corners=0.1, draw=colorred, fill=colorred!10!white] (-0.5, 0.2) -- ++(0, -0.1) -- ++(0.1, -0.1) -- ++(0.1, 0.1) -- ++(0, 0.1) --cycle;
\draw[rounded corners=0.1, draw=colorred, fill=colorred!10!white] ( 0.3, 0.2) -- ++(0, -0.1) -- ++(0.1, -0.1) -- ++(0.1, 0.1) -- ++(0, 0.1) --cycle;
\draw[draw=colorred, fill=colorred!10!white] (0.6, 0.4) rectangle ++(0.2, 0.2);
\node[shape=circle,minimum size=3pt,inner sep=0pt, draw=colorred, fill=colorred] at (0.8, 0.5){};
\draw[out=0, in=180, draw=colorred] (0.8, 0.5) to ++(0.6, -0.1) node[above, color=colorred]{$x_h$};
\draw[draw=colorred, fill=colorred!10!white] (-0.6, 0.2) rectangle node[midway, color=colorred]{\tiny geophone} (0.6, 0.8);
\end{scope}
\end{scope}
\begin{scope}[shift={(0, -0.3*\blockh)}]
% Translation Stage - fixed part
\draw[fill=black!40] (-0.5*\blockw, 0) coordinate[](tyb) rectangle (0.5*\blockw, 0.15*\blockh);
\coordinate[] (measposbot) at (0.5*\blockw, 0);
% Translation Stage - mobile part
\draw[fill=black!10, fill opacity=0.5] (-0.5*\blockw, 0.2*\blockh) -- (-0.5*\blockw, 1.5*\blockh) coordinate[](tyt) -- (0.5*\blockw, 1.5*\blockh) -- (0.5*\blockw, 0.2*\blockh) -- (0.35*\blockw, 0.2*\blockh) -- (0.35*\blockw, 0.8*\blockh) -- (-0.35*\blockw, 0.8*\blockh) -- (-0.35*\blockw, 0.2*\blockh) -- cycle;
% Translation Guidance
\draw[dashed, color=black!60] ($(-0.5*\blockw, 0)+( 0.075*\blockw,0.5*\blockh)$) circle (0.2*\blockh);
\draw[dashed, color=black!60] ($( 0.5*\blockw, 0)+(-0.075*\blockw,0.5*\blockh)$) circle (0.2*\blockh);
\draw[fill, color=black] ($( 0.5*\blockw, 0)+(-0.075*\blockw,0.5*\blockh)$) circle (0.04);
\node[draw, circle, inner sep=0pt, minimum size=0.3cm, label=above:$T_y$] at ($( 0.5*\blockw, 0)+(-0.075*\blockw,0.5*\blockh)$){};
% Tilt Guidance
\draw[dashed, color=black!60] ([shift=(-107:4.1*\blockh)]rotationpoint) arc (-107:-120:4.1*\blockh);
\draw[dashed, color=black!60] ([shift=( -73:4.1*\blockh)]rotationpoint) arc (-73:-60:4.1*\blockh);
\begin{scope}[shift={(4.0, 0)}] % Geophone - Granite
\draw[rounded corners=0.1, draw=colorred, fill=colorred!10!white] (-0.5, 0.2) -- ++(0, -0.1) -- ++(0.1, -0.1) -- ++(0.1, 0.1) -- ++(0, 0.1) --cycle;
\draw[rounded corners=0.1, draw=colorred, fill=colorred!10!white] ( 0.3, 0.2) -- ++(0, -0.1) -- ++(0.1, -0.1) -- ++(0.1, 0.1) -- ++(0, 0.1) --cycle;
\draw[draw=colorred, fill=colorred!10!white] (0.6, 0.4) rectangle ++(0.2, 0.2);
\node[shape=circle,minimum size=3pt,inner sep=0pt, draw=colorred, fill=colorred] at (0.8, 0.5){};
\draw[out=0, in=180, draw=colorred] (0.8, 0.5) to ++(0.6, -0.1) node[above, color=colorred]{$x_g$};
\draw[draw=colorred, fill=colorred!10!white] (-0.6, 0.2) rectangle node[midway, color=colorred]{\tiny geophone} (0.6, 0.8);
\end{scope}
\end{scope}
% Granite
\draw[fill=black!40] (-0.8*\blockw, -0.3*\blockh) rectangle node[midway]{Granite} (0.8*\blockw, -1.5*\blockh);
\begin{scope}[shift={(4.0, -1.5*\blockh)}] % Geophone - Floor
\draw[rounded corners=0.1, draw=colorred, fill=colorred!10!white] (-0.5, 0.2) -- ++(0, -0.1) -- ++(0.1, -0.1) -- ++(0.1, 0.1) -- ++(0, 0.1) --cycle;
\draw[rounded corners=0.1, draw=colorred, fill=colorred!10!white] ( 0.3, 0.2) -- ++(0, -0.1) -- ++(0.1, -0.1) -- ++(0.1, 0.1) -- ++(0, 0.1) --cycle;
\draw[draw=colorred, fill=colorred!10!white] (0.6, 0.4) rectangle ++(0.2, 0.2);
\node[shape=circle,minimum size=3pt,inner sep=0pt, draw=colorred, fill=colorred] at (0.8, 0.5){};
\draw[out=0, in=180, draw=colorred] (0.8, 0.5) to ++(0.6, -0.1) node[above, color=colorred]{$x_f$};
\draw[draw=colorred, fill=colorred!10!white] (-0.6, 0.2) rectangle node[midway, color=colorred]{\tiny geophone} (0.6, 0.8);
\end{scope}
% Vertical line
\draw[dashed, color=black] (spindlebot) -- ++(0, 2*\blockh);
\node[] at ($(spindlebot)+(0, 1.1*\blockh)$) {\AxisRotator[rotate=-90]};
\node[right, shift={(0.3,0)}] at ($(spindlebot)+(0, 1.1*\blockh)$) {$\theta_z$};
% Axis
\begin{scope}[shift={(-0.6*\blockw, 2.5*\blockh)}]
\def\axissize{0.8cm}
\draw[->] (0, 0) -- ++(0, \axissize) node[right]{$z$};
\draw[->] (0, 0) -- ++(-\axissize, 0) node[above]{$x$};
\draw[fill, color=black] (0, 0) circle (0.05*\axissize);
\node[draw, circle, inner sep=0pt, minimum size=0.4*\axissize, label=right:$y$] (yaxis) at (0, 0){};
\end{scope}
\end{tikzpicture}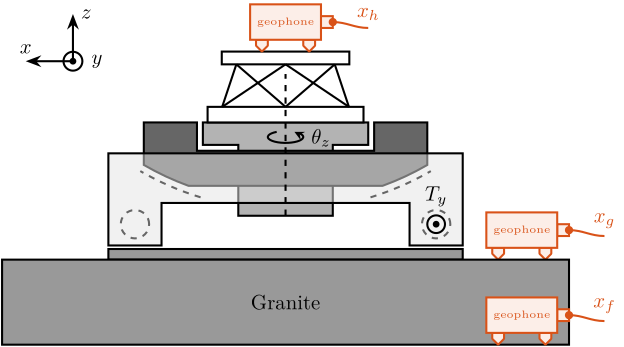

Ground Motion
The geophone fixed to the floor to measure the floor motion.
%% Load floor motion data
% t: time in [s]
% V: measured voltage genrated by the geophone and amplified by a 60dB gain voltage amplifier [V]
load('ground_motion_measurement.mat', 't', 'V');The voltage generated by each geophone is amplified using a voltage amplifier (gain of 60dB) before going to the ADC. The sensitivity of the geophone as well as the gain of the voltage amplifier are then taken into account to reconstruct the floor displacement.
%% Sensitivity of the geophone
S0 = 88; % Sensitivity [V/(m/s)]
f0 = 2; % Cut-off frequency [Hz]
S = S0*(s/2/pi/f0)/(1+s/2/pi/f0); % Geophone's transfer function [V/(m/s)]
%% Gain of the voltage amplifier
G0_db = 60; % [dB]
G0 = 10^(G0_db/20); % [abs]
%% Transfer function from measured voltage to displacement
G_geo = 1/S/G0/s; % [m/V]The PSD $S_{V_f}$ of the measured voltage $V_f$ is computed.
%% Compute measured voltage PSD
Fs = 1/(t(2)-t(1)); % Sampling Frequency [Hz]
win = hanning(ceil(2*Fs)); % Hanning window
[psd_V, f] = pwelch(V, win, [], [], Fs); % [V^2/Hz]The PSD of the corresponding displacement can be computed as follows:
\begin{equation} S_{x_f}(\omega) = \frac{S_{V_f}(\omega)}{|S_{\text{geo}}(j\omega)| \cdot G_{\text{amp}} \cdot \omega} \end{equation}with:
- $S_{\text{geo}}$ the sensitivity of the Geophone in $[Vs/m]$
- $G_{\text{amp}}$ the gain of the voltage amplifier
- $\omega$ is here to integrate and have the displacement instead of the velocity
%% Ground Motion ASD
psd_xf = psd_V.*abs(squeeze(freqresp(G_geo, f, 'Hz'))).^2; % [m^2/Hz]The amplitude spectral density $\Gamma_{x_f}$ of the measured displacement $x_f$ is shown in Figure ref:fig:uniaxial_asd_floor_motion_id31.
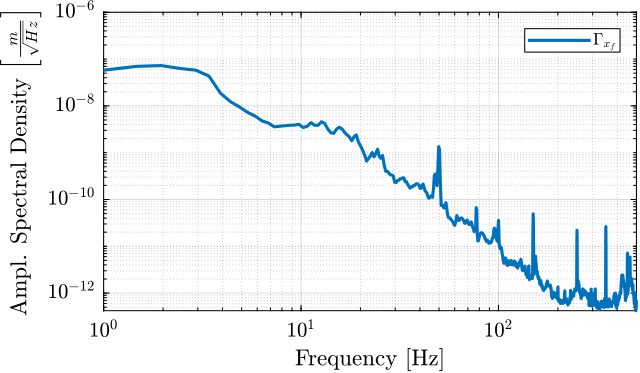
Stage Vibration
During Spindle rotation (here at 6rpm), the granite velocity and micro-hexapod's top platform velocity are measured with the geophones.
%% Measured velocity of granite and hexapod during spindle rotation
% t: time in [s]
% vg: measured granite velocity [m/s]
% vg: measured micro-hexapod's top platform velocity [m/s]
load('meas_spindle_on.mat', 't', 'vg', 'vh');
spindle_off = load('meas_spindle_off.mat', 't', 'vg', 'vh'); % No RotationThe Power Spectral Density of the relative velocity between the hexapod and the granite is computed.
%% Compute Power Spectral Density of the relative velocity between granite and hexapod during spindle rotation
Fs = 1/(t(2)-t(1)); % Sampling Frequency [Hz]
win = hanning(ceil(2*Fs)); % Hanning window
[psd_vft, f] = pwelch(vh-vg, win, [], [], Fs); % [(m/s)^2/Hz]
[psd_off, ~] = pwelch(spindle_off.vh-spindle_off.vg, win, [], [], Fs); % [(m/s)^2/Hz]It is then integrated to obtain the Amplitude Spectral Density of the relative motion which is compared with a non-rotating case (Figure ref:fig:uniaxial_asd_vibration_spindle_rotation). It is shown that the spindle rotation induces vibrations in a wide frequency spectrum.
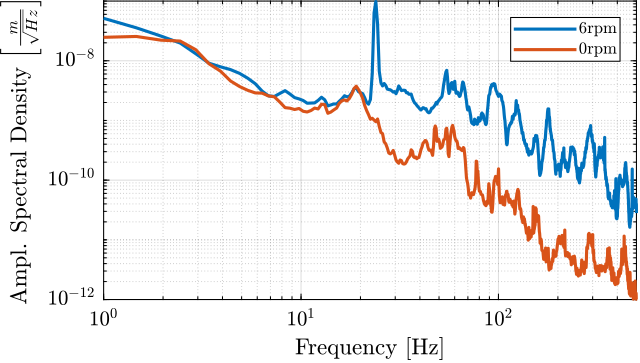
In order to compute the equivalent disturbance force $f_t$ that induces such motion, the transfer function from $f_t$ to the relative motion of the hexapod's top platform and the granite is extracted from the model.
The power spectral density $\Gamma_{f_{t}}$ of the disturbance force can be computed as follows:
\begin{equation} \Gamma_{f_{t}}(\omega) = \frac{\Gamma_{v_{t}}(\omega)}{|G_{\text{model}}(j\omega)|^2} \end{equation}with:
- $\Gamma_{v_{t}}$ the measured power spectral density of the relative motion between the micro-hexapod's top platform and the granite during the spindle's rotation
- $G_{\text{model}}$ the transfer function (extracted from the uniaxial model) from $f_t$ to the relative motion between the micro-hexapod's top platform and the granite
The obtained amplitude spectral density of the disturbance force $f_t$ is shown in Figure ref:fig:uniaxial_asd_disturbance_force.
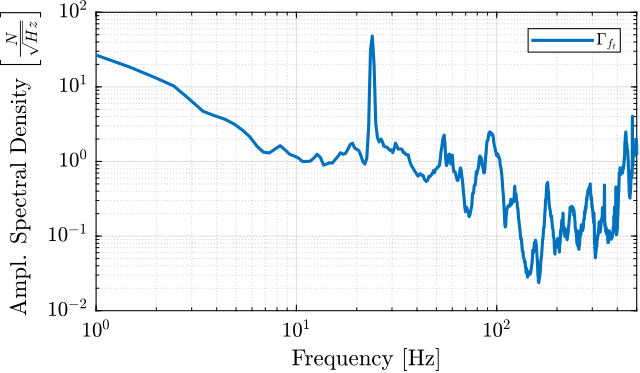
The vibrations induced by the $T_y$ stage are not considered here because:
- the induced vibrations have less amplitude than the vibrations induced by the $R_z$ stage
- it can be scanned at lower velocities if the induced vibrations are an issue
Open-Loop Dynamic Noise Budgeting
<<sec:uniaxial_noise_budgeting>>
Introduction ignore
Now that we have a model of the NASS and an estimation of the power spectral density of the disturbances, it is possible to perform an open-loop dynamic noise budgeting.
Sensitivity to disturbances
From the Uni-axial model, the transfer function from the disturbances ($f_s$, $x_f$ and $f_t$) to the displacement $d$ are computed.
This is done for two extreme sample masses $m_s = 1\,\text{kg}$ and $m_s = 50\,\text{kg}$ and three nano-hexapod stiffnesses:
- $k_n = 0.01\,N/\mu m$ that could represent a voice coil actuator with soft flexible guiding
- $k_n = 1\,N/\mu m$ that could represent a voice coil actuator with a stiff flexible guiding or a mechanically amplified piezoelectric actuator
- $k_n = 100\,N/\mu m$ that could represent a stiff piezoelectric stack actuator
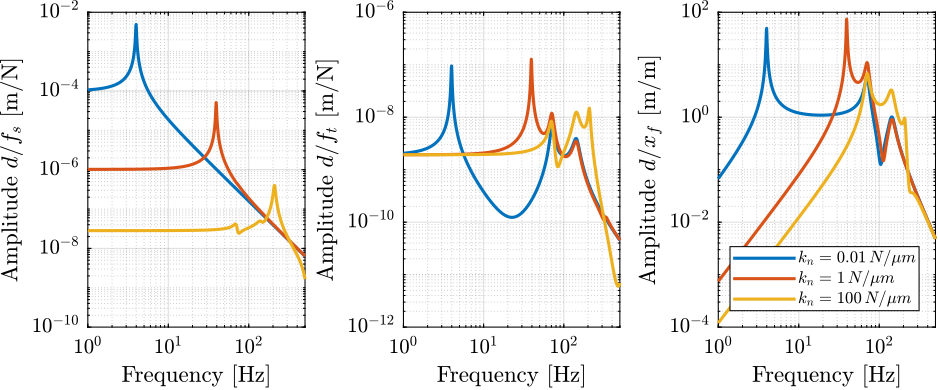
The obtained sensitivity to disturbances for the three nano-hexapod stiffnesses are shown in Figure ref:fig:uniaxial_sensitivity_disturbances_nano_hexapod_stiffnesses for the light sample (same conclusions can be drawn with the heavy one).
From Figure ref:fig:uniaxial_sensitivity_disturbances_nano_hexapod_stiffnesses, the following can be concluded for the soft nano-hexapod:
- It is more sensitive to forces applied on the sample (cable forces for instance), which is expected due to the lower stiffness
- Between the suspension mode of the nano-hexapod (here at 5Hz) and the first mode of the micro-station (here at 70Hz), the disturbances induced by the stage vibrations are filtered out.
- Above the suspension mode of the nano-hexapod, the sample's motion is unaffected by the floor motion, and therefore the sensitivity to floor motion is close to $1$.
Open-Loop Dynamic Noise Budgeting
Now, the power spectral density of the disturbances is taken into account to estimate the residual motion $d$ in each case.
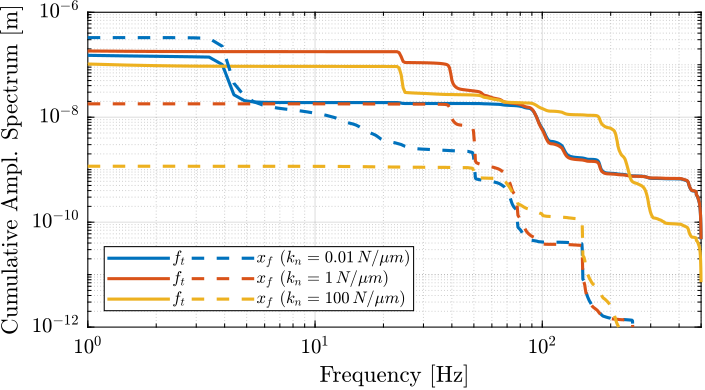
The Cumulative Amplitude Spectrum of the relative motion $d$ due to both the floor motion $x_f$ and the stage vibrations $f_t$ are shown in Figure ref:fig:uniaxial_cas_d_disturbances_stiffnesses for the three nano-hexapod stiffnesses.
It is shown that the effect of the floor motion is much less than the stage vibrations, except for the soft nano-hexapod below 5Hz.
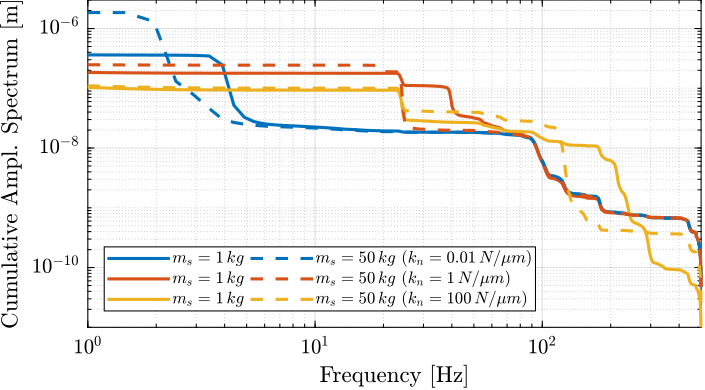
The total cumulative amplitude spectrum for the three nano-hexapod stiffnesses and for the two sample's masses are shown in Figure ref:fig:uniaxial_cas_d_disturbances_payload_masses. The conclusion is that the sample's mass has little effect on the cumulative amplitude spectrum of the relative motion $d$.
Conclusion
In order to have a closed-loop residual vibration $d \approx 20\,nm\text{ rms}$, if a simple feedback controller is used, the required closed-loop bandwidth would be:
- $\approx 10\,\text{Hz}$ for the soft nano-hexapod ($k_n = 0.01\,N/\mu m$)
- $\approx 50\,\text{Hz}$ for the relatively stiff nano-hexapod ($k_n = 1\,N/\mu m$)
- $\approx 100\,\text{Hz}$ for the stiff nano-hexapod ($k_n = 100\,N/\mu m$)
This can be explained by the fact that for frequencies larger than the suspension mode of the nano-hexapod, the stage vibrations are filtered out (see Figure ref:fig:uniaxial_sensitivity_disturbances_nano_hexapod_stiffnesses).
This gives a first advantage to having a soft nano-hexapod.
Active Damping
<<sec:uniaxial_active_damping>>
Introduction ignore
In this section, three active damping are applied on the nano-hexapod (see Figure ref:fig:uniaxial_active_damping_strategies): Integral Force Feedback (IFF) cite:preumont91_activ, Relative Damping Control (RDC) cite:&preumont18_vibrat_contr_activ_struc_fourt_edition Chapter 7.2 and Direct Velocity Feedback (DVF) cite:karnopp74_vibrat_contr_using_semi_activ_force_gener,serrand00_multic_feedb_contr_isolat_base_excit_vibrat,preumont02_force_feedb_versus_accel_feedb.
These damping strategies will be described in Section ref:ssec:uniaxial_active_damping_strategies.
These active damping techniques are compared in terms of:
- Achievable damping of the nano-hexapod mode (Section ref:ssec:uniaxial_active_damping_achievable_damping)
- Reduction of the effect of disturbances (i.e. $x_f$, $f_t$ and $f_s$) on the displacement $d$ (Sections ref:ssec:uniaxial_active_damping_sensitivity_disturbances and ref:ssec:uniaxial_active_damping_noise_budget)
- Robustness to a change of sample's mass (Section ref:ssec:uniaxial_active_damping_robustness)
\begin{tikzpicture}
% ====================
% Parameters
% ====================
\def\massw{2.2} % Width of the masses
\def\massh{0.8} % Height of the masses
\def\spaceh{1.2} % Height of the springs/dampers
\def\dispw{0.4} % Width of the dashed line for the displacement
\def\disph{0.3} % Height of the arrow for the displacements
\def\bracs{0.05} % Brace spacing vertically
\def\brach{-12pt} % Brace shift horizontaly
\def\fsensh{0.2} % Height of the force sensor
\def\velsize{0.2} % Size of the velocity sensor
% ====================
% IFF
\begin{scope}
% ====================
% Ground
% ====================
\draw (-0.5*\massw, 0) -- (0.5*\massw, 0);
\draw[dashed] (0.5*\massw, 0) -- ++(\dispw, 0);
\draw[->, color=colorpurple] (0.5*\massw+0.5*\dispw, 0) -- ++(0, 2*\disph) node[right, color=colorpurple]{$x_{f}$};
% ====================
% ====================
% Granite
\begin{scope}[shift={(0, 0)}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{g}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{g}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{g}$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{Granite};
\end{scope}
% ====================
% ====================
% Stages
\begin{scope}[shift={(0, \spaceh+\massh)}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{t}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{t}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{t}$};
\draw[actuator={0.45}{0.2}{colorpurple}] ( 0.3*\massw, 0) -- (0.3*\massw, \spaceh) node[midway, right=0.1, color=colorpurple](ft){$f_{t}$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$T_y$/$R_y$/$R_z$};
\end{scope}
% ====================
% ====================
% Hexapod
\begin{scope}[shift={(0, 2*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_h$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_h$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_h$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$\mu\text{-hexa}$};
\end{scope}
% ====================
% ====================
% NASS
\begin{scope}[shift={(0, 3*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{n}$};
% Force Sensor
\node[forcesensor={\massw}{\fsensh}{colorblue}] (fsensn) at (0, \spaceh-\fsensh){};
\node[right, color=colorblue] (fn) at (fsensn.east) {$f_n$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh-\fsensh) node[midway, left=0.1]{$k_{n}$};
\draw[damper] (0, 0) -- ( 0, \spaceh-\fsensh) node[midway, left=0.2]{$c_{n}$};
\draw[actuator={0.4}{0.2}{black}] ( 0.3*\massw, 0) -- ( 0.3*\massw, \spaceh-\fsensh) node[midway, right=0.1](f){$f$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$\nu\text{-hexa}$};
\end{scope}
% ====================
% ====================
% sample
\begin{scope}[shift={(0, 4*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.3*\massw, 0) rectangle (0.3*\massw, \massh) node[pos=0.5]{$m_{s}$};
% External Force
\draw[->, color=colorpurple] (0, \massh) node[]{$\bullet$} -- ++(0, 0.5*\massh) node[right, color=colorpurple]{$f_s$};
\end{scope}
% ====================
% ====================
% IFF Control
\node[block={2em}{2em}, right=0.3 of fn, color=colorblue, fill=colorblue!10!white] (iff) {$K_{\text{IFF}}$};
\draw[->, draw=colorblue] (fn.east) -- (iff.west);
\draw[->, draw=colorblue] (iff.south) |- (f.east);
% ====================
\end{scope}
\begin{scope}[shift={(5,0)}]
% ====================
% Ground
% ====================
\draw (-0.5*\massw, 0) -- (0.5*\massw, 0);
\draw[dashed] (0.5*\massw, 0) -- ++(\dispw, 0);
\draw[->, color=colorpurple] (0.5*\massw+0.5*\dispw, 0) -- ++(0, 2*\disph) node[right, color=colorpurple]{$x_{f}$};
% ====================
% ====================
% Granite
\begin{scope}[shift={(0, 0)}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{g}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{g}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{g}$};
\end{scope}
% ====================
% ====================
% Stages
\begin{scope}[shift={(0, \spaceh+\massh)}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{t}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{t}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{t}$};
\draw[actuator={0.45}{0.2}{colorpurple}] ( 0.3*\massw, 0) -- (0.3*\massw, \spaceh) node[midway, right=0.1, color=colorpurple](ft){$f_{t}$};
\end{scope}
% ====================
% ====================
% Hexapod
\begin{scope}[shift={(0, 2*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_h$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_h$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_h$};
\draw[dashed] (0.5*\massw, \spaceh+\massh) -- ++(2*\dispw, 0) coordinate(drbot);
\end{scope}
% ====================
% ====================
% NASS
\begin{scope}[shift={(0, 3*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{n}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{n}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{n}$};
\draw[actuator={0.4}{0.2}{black}] ( 0.3*\massw, 0) -- (0.3*\massw, \spaceh) node[midway, right=0.1](f){$f$};
\draw[dashed, draw=colorred] (0.5*\massw, \spaceh+\massh) -- ++(2*\dispw, 0) coordinate(drtop);
\end{scope}
% ====================
% ====================
% sample
\begin{scope}[shift={(0, 4*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.3*\massw, 0) rectangle (0.3*\massw, \massh) node[pos=0.5]{$m_{s}$};
% External Force
\draw[->, color=colorpurple] (0, \massh) node[]{$\bullet$} -- ++(0, 0.5*\massh) node[right, color=colorpurple]{$f_s$};
\end{scope}
% ====================
\draw[<->, dashed, draw=colorred] ($(drbot)+(-0.1, 0)$) -- ($(drtop)+(-0.1, 0)$) node[right, color=colorred](dr){$d\mathcal{L}$};
% ====================
% RDC Control
\node[block={2em}{2em}, below right=0.2 and -0.2 of dr, color=colorred, fill=colorred!10!white] (rdc) {$K_{\text{RDC}}$};
\draw[->, draw=colorred] (dr.east) -| (rdc.north);
\draw[->, draw=colorred] (rdc.south) |- (f.east);
% ====================
\end{scope}
\begin{scope}[shift={(10,0)}]
% ====================
% Ground
% ====================
\draw (-0.5*\massw, 0) -- (0.5*\massw, 0);
\draw[dashed] (0.5*\massw, 0) -- ++(\dispw, 0);
\draw[->, color=colorpurple] (0.5*\massw+0.5*\dispw, 0) -- ++(0, 2*\disph) node[right, color=colorpurple]{$x_{f}$};
% ====================
% ====================
% Marble
\begin{scope}[shift={(0, 0)}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{g}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{g}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{g}$};
\end{scope}
% ====================
% ====================
% Stages
\begin{scope}[shift={(0, \spaceh+\massh)}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{t}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{t}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{t}$};
\draw[actuator={0.45}{0.2}{colorpurple}] ( 0.3*\massw, 0) -- (0.3*\massw, \spaceh) node[midway, right=0.1, color=colorpurple](ft){$f_{t}$};
\end{scope}
% ====================
% ====================
% Hexapod
\begin{scope}[shift={(0, 2*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{h}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{h}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{h}$};
\end{scope}
% ====================
% ====================
% NASS
\begin{scope}[shift={(0, 3*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{n}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{n}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{n}$};
\draw[actuator={0.4}{0.2}{black}] ( 0.3*\massw, 0) -- (0.3*\massw, \spaceh) node[midway, right=0.1](f){$f$};
% Velocity Sensor
\node[inertialsensor={\velsize}{coloryellow}] (veln) at (0.5*\massw, \spaceh+\massh) {};
\node[right, color=coloryellow] (xn) at (veln.north east) {$v_n$};
\end{scope}
% ====================
% ====================
% sample
\begin{scope}[shift={(0, 4*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.3*\massw, 0) rectangle (0.3*\massw, \massh) node[pos=0.5]{$m_{s}$};
% External Force
\draw[->, color=colorpurple] (0, \massh) node[]{$\bullet$} -- ++(0, 0.5*\massh) node[right, color=colorpurple]{$f_s$};
\end{scope}
% ====================
% ====================
% DVF Control
\node[block={2em}{2em}, below right=0.4 and 0.1 of xn, color=coloryellow, fill=coloryellow!10!white] (ppf) {$K_{\text{DVF}}$};
\draw[->, draw=coloryellow] (xn.east) -| (ppf.north);
\draw[->, draw=coloryellow] (ppf.south) |- (f.east);
% ====================
\end{scope}
\end{tikzpicture}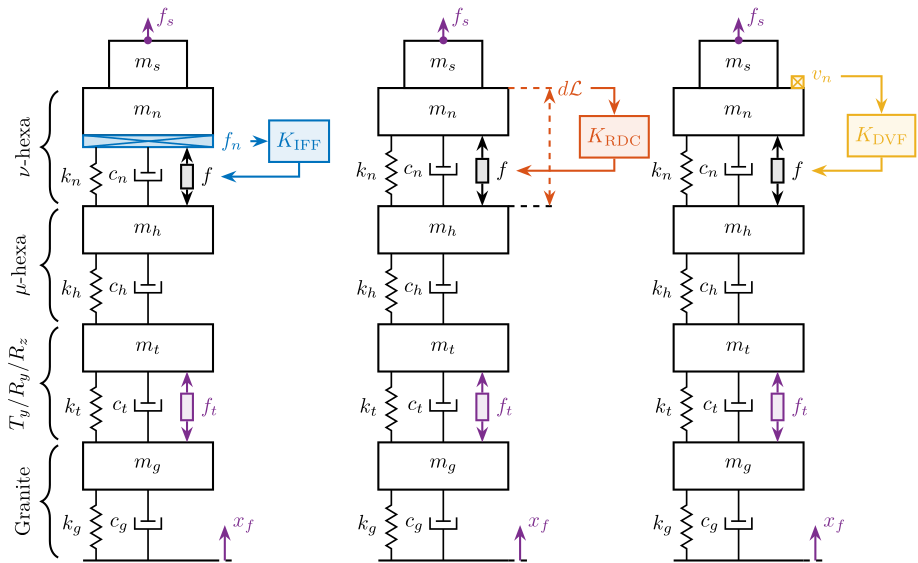
Active Damping Strategies
<<ssec:uniaxial_active_damping_strategies>>
Integral Force Feedback (IFF)
The Integral Force Feedback strategy consists of using a force sensor in series with the actuator (see Figure ref:fig:uniaxial_active_damping_iff_equiv, left).
The control strategy consists of integrating the measured force and feeding it back to the actuator:
\begin{equation} \boxed{K_{\text{IFF}}(s) = \frac{g}{s}} \end{equation}The mechanical equivalent of this strategy is to add a dashpot in series with the actuator stiffness with a damping coefficient equal to the stiffness of the actuator divided by the controller gain $k/g$ (see Figure ref:fig:uniaxial_active_damping_iff_equiv, right).
\begin{tikzpicture}
% ====================
% Parameters
% ====================
\def\massw{2.2} % Width of the masses
\def\massh{0.8} % Height of the masses
\def\spaceh{1.2} % Height of the springs/dampers
\def\dispw{0.4} % Width of the dashed line for the displacement
\def\disph{0.3} % Height of the arrow for the displacements
\def\bracs{0.05} % Brace spacing vertically
\def\brach{-12pt} % Brace shift horizontaly
\def\fsensh{0.2} % Height of the force sensor
\def\velsize{0.2} % Size of the velocity sensor
% ====================
\begin{scope}
% ====================
% Stage Below
\begin{scope}
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh);
\draw[spring] (-0.25*\massw, 0) -- (-0.25*\massw, \spaceh);
\draw[damper] ( 0.25*\massw, 0) -- ( 0.25*\massw, \spaceh);
\draw[decorate,decoration={zigzag,segment length=6pt},draw=black!50!white,very thick] (-0.5*\massw, 0) -- (0.5*\massw, 0);
\draw[draw=black!50!white,very thick, dashed] (-0.5*\massw, 0) -- ++(-0.5, 0);
\draw[draw=black!50!white,very thick, dashed] ( 0.5*\massw, 0) -- ++( 0.5, 0);
\end{scope}
% ====================
% ====================
% NASS
\begin{scope}[shift={(0, \spaceh+\massh)}]
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m$};
\node[forcesensor={\massw}{\fsensh}{colorblue}] (fsensn) at (0, \spaceh-\fsensh){};
\node[right, color=colorblue] (fn) at (fsensn.east) {$f_m$};
\draw[spring] (-0.25*\massw, 0) -- (-0.25*\massw, \spaceh-\fsensh) node[midway, left=0.1]{$k$};
\draw[actuator={0.4}{0.2}{black}] ( 0.25*\massw, 0) -- (0.25*\massw, \spaceh-\fsensh) coordinate[midway, shift={(0.1,0)}](f);
\end{scope}
% ====================
% ====================
% Stage Above
\begin{scope}[shift={(0, 2*(\spaceh+\massh))}]
\draw[spring] (-0.25*\massw, 0) -- (-0.25*\massw, \spaceh);
\draw[damper] ( 0.25*\massw, 0) -- ( 0.25*\massw, \spaceh);
\draw[decorate,decoration={zigzag,segment length=6pt},draw=black!50!white,very thick] (-0.5*\massw, \spaceh) -- (0.5*\massw, \spaceh);
\draw[draw=black!50!white,very thick, dashed] (-0.5*\massw, \spaceh) -- ++(-0.5, 0);
\draw[draw=black!50!white,very thick, dashed] ( 0.5*\massw, \spaceh) -- ++( 0.5, 0);
\end{scope}
% ====================
% ====================
% IFF Control
\node[block={2em}{2em}, right=1.0 of f, color=colorblue, fill=colorblue!10!white] (iff) {$g/s$};
\draw[->, draw=colorblue] (fn.east) -- ++(1.0, 0) |- (iff.east);
\draw[->, draw=colorblue] (iff.west) -- (f.east) node[above right, color=colorblue]{$f$};
% ====================
\end{scope}
\begin{scope}[shift={(6, 0)}]
% ====================
% Stage Below
\begin{scope}
\draw[fill=white] (-0.5*\massw, 0.8*\spaceh) rectangle (0.5*\massw, 0.8*\spaceh+\massh);
\draw[spring] (-0.25*\massw, 0) -- (-0.25*\massw, 0.8*\spaceh);
\draw[damper] ( 0.25*\massw, 0) -- ( 0.25*\massw, 0.8*\spaceh);
\draw[decorate,decoration={zigzag,segment length=6pt},draw=black!50!white,very thick] (-0.5*\massw, 0) -- (0.5*\massw, 0);
\draw[draw=black!50!white,very thick, dashed] (-0.5*\massw, 0) -- ++(-0.5, 0);
\draw[draw=black!50!white,very thick, dashed] ( 0.5*\massw, 0) -- ++( 0.5, 0);
\end{scope}
% ====================
% ====================
% NASS
\begin{scope}[shift={(0, 0.8*\spaceh+\massh)}]
\draw[fill=white] (-0.5*\massw, 1.4*\spaceh) rectangle (0.5*\massw, 1.4*\spaceh+\massh) node[pos=0.5]{$m$};
\draw[spring] (0, 0) -- node[midway, left=0.1]{$k$} (0, 0.8*\spaceh);
\draw[damper={colorblue}{}{}] (0, 0.8*\spaceh) node[branch]{} -- (0, 1.4*\spaceh) node[midway, left=0.2, color=colorblue]{$k/g$};
\end{scope}
% ====================
% ====================
% Stage Above
\begin{scope}[shift={(0, 0.8*\spaceh+\massh+1.4*\spaceh+\massh)}]
\draw[spring] (-0.25*\massw, 0) -- (-0.25*\massw, 0.8*\spaceh);
\draw[damper] ( 0.25*\massw, 0) -- ( 0.25*\massw, 0.8*\spaceh);
\draw[decorate,decoration={zigzag,segment length=6pt},draw=black!50!white,very thick] (-0.5*\massw, 0.8*\spaceh) -- (0.5*\massw, 0.8*\spaceh);
\draw[draw=black!50!white,very thick, dashed] (-0.5*\massw, 0.8*\spaceh) -- ++(-0.5, 0);
\draw[draw=black!50!white,very thick, dashed] ( 0.5*\massw, 0.8*\spaceh) -- ++( 0.5, 0);
\end{scope}
% ====================
\end{scope}
% Equiv
\draw[double, <->, draw=colorblue, double distance=1.5] (3.0, 1.5*\spaceh+\massh) -- ++(1.5,0);
\end{tikzpicture}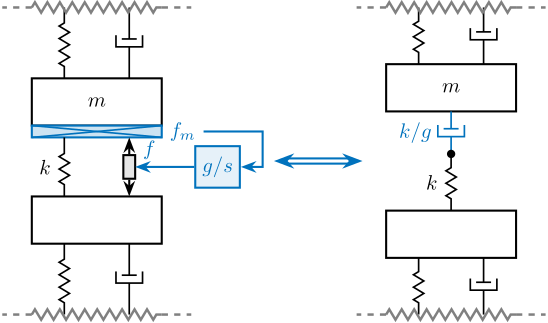
Relative Damping Control (RDC)
For the Relative Damping Control strategy, a relative motion sensor that measures the motion of the actuator is used (see Figure ref:fig:uniaxial_active_damping_rdc_equiv, left).
The derivative of this relative motion is used for the feedback signal:
\begin{equation} \boxed{K_{\text{RDC}}(s) = - g \cdot s} \end{equation}The mechanical equivalent is to add a dashpot in parallel with the actuator with a damping coefficient equal to the controller gain $g$ (see Figure ref:fig:uniaxial_active_damping_rdc_equiv, right).
\begin{tikzpicture}
% ====================
% Parameters
% ====================
\def\massw{2.2} % Width of the masses
\def\massh{0.8} % Height of the masses
\def\spaceh{1.2} % Height of the springs/dampers
\def\dispw{0.4} % Width of the dashed line for the displacement
\def\disph{0.3} % Height of the arrow for the displacements
\def\bracs{0.05} % Brace spacing vertically
\def\brach{-12pt} % Brace shift horizontaly
\def\fsensh{0.2} % Height of the force sensor
\def\velsize{0.2} % Size of the velocity sensor
% ====================
\begin{scope}
% ====================
% Stage Below
\begin{scope}
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh);
\draw[spring] (-0.25*\massw, 0) -- (-0.25*\massw, \spaceh);
\draw[damper] ( 0.25*\massw, 0) -- ( 0.25*\massw, \spaceh);
\draw[dashed, draw=colorred] (0.5*\massw, \spaceh+\massh) -- ++(1*\dispw, 0) coordinate(drbot);
\draw[decorate,decoration={zigzag,segment length=6pt},draw=black!50!white,very thick] (-0.5*\massw, 0) -- (0.5*\massw, 0);
\draw[draw=black!50!white,very thick, dashed] (-0.5*\massw, 0) -- ++(-0.5, 0);
\draw[draw=black!50!white,very thick, dashed] ( 0.5*\massw, 0) -- ++( 0.5, 0);
\end{scope}
% ====================
% ====================
% NASS
\begin{scope}[shift={(0, \spaceh+\massh)}]
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m$};
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c$};
\draw[actuator={0.4}{0.2}{black}] ( 0.3*\massw, 0) -- (0.3*\massw, \spaceh) coordinate[midway, shift={(0.1,0)}](f);
\draw[dashed, draw=colorred] (0.5*\massw, \spaceh+\massh) -- ++(1*\dispw, 0) coordinate(drtop);
\end{scope}
% ====================
% ====================
% Stage Above
\begin{scope}[shift={(0, 2*(\spaceh+\massh))}]
\draw[spring] (-0.25*\massw, 0) -- (-0.25*\massw, \spaceh);
\draw[damper] ( 0.25*\massw, 0) -- ( 0.25*\massw, \spaceh);
\draw[decorate,decoration={zigzag,segment length=6pt},draw=black!50!white,very thick] (-0.5*\massw, \spaceh) -- (0.5*\massw, \spaceh);
\draw[draw=black!50!white,very thick, dashed] (-0.5*\massw, \spaceh) -- ++(-0.5, 0);
\draw[draw=black!50!white,very thick, dashed] ( 0.5*\massw, \spaceh) -- ++( 0.5, 0);
\end{scope}
% ====================
\draw[<->, dashed, draw=colorred] ($(drbot)+(-0.1, 0)$) -- ($(drtop)+(-0.1, 0)$) node[right, color=colorred](dr){$d\mathcal{L}$};
% ====================
% RDC Control
\node[block={2em}{2em}, below right=0.2 and -0.3 of dr, color=colorred, fill=colorred!10!white] (rdc) {$-g \cdot s$};
\draw[->, draw=colorred] (dr.east) -| (rdc.north);
\draw[->, draw=colorred] (rdc.south) |- (f.east) node[above right, color=colorred]{$f$};
% ====================
\end{scope}
\begin{scope}[shift={(6, 0)}]
% ====================
% Stage Below
\begin{scope}
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh);
\draw[spring] (-0.25*\massw, 0) -- (-0.25*\massw, \spaceh);
\draw[damper] ( 0.25*\massw, 0) -- ( 0.25*\massw, \spaceh);
\draw[decorate,decoration={zigzag,segment length=6pt},draw=black!50!white,very thick] (-0.5*\massw, 0) -- (0.5*\massw, 0);
\draw[draw=black!50!white,very thick, dashed] (-0.5*\massw, 0) -- ++(-0.5, 0);
\draw[draw=black!50!white,very thick, dashed] ( 0.5*\massw, 0) -- ++( 0.5, 0);
\end{scope}
% ====================
% ====================
% NASS
\begin{scope}[shift={(0, \spaceh+\massh)}]
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m$};
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c$};
\draw[damper={colorred}{}{}] ( 0.4*\massw, 0) -- ( 0.4*\massw, \spaceh) node[midway, left=0.15, color=colorred]{$g$};
\end{scope}
% ====================
% ====================
% Stage Above
\begin{scope}[shift={(0, 2*(\spaceh+\massh))}]
\draw[spring] (-0.25*\massw, 0) -- (-0.25*\massw, \spaceh);
\draw[damper] ( 0.25*\massw, 0) -- ( 0.25*\massw, \spaceh);
\draw[decorate,decoration={zigzag,segment length=6pt},draw=black!50!white,very thick] (-0.5*\massw, \spaceh) -- (0.5*\massw, \spaceh);
\draw[draw=black!50!white,very thick, dashed] (-0.5*\massw, \spaceh) -- ++(-0.5, 0);
\draw[draw=black!50!white,very thick, dashed] ( 0.5*\massw, \spaceh) -- ++( 0.5, 0);
\end{scope}
% ====================
\end{scope}
% Equiv
\draw[double, <->, draw=colorred, double distance=1.5] (3.0, 1.5*\spaceh+\massh) -- ++(1.5,0);
\end{tikzpicture}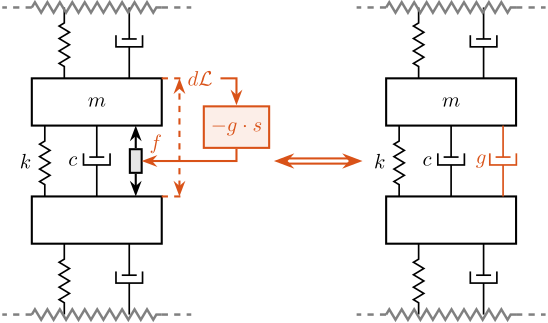
Direct Velocity Feedback (DVF)
Finally, the Direct Velocity Feedback strategy consists of using an inertial sensor (usually a geophone), that measured the "absolute" velocity of the body fixed on top of the actuator (se Figure ref:fig:uniaxial_active_damping_dvf_equiv, left).
The measured velocity is then fed back to the actuator:
\begin{equation} \boxed{K_{\text{DVF}}(s) = - g} \end{equation}This is equivalent as to fix a dashpot (with a damping coefficient equal to the controller gain $g$) between the body (one which the inertial sensor is fixed) and an inertial reference frame (see Figure ref:fig:uniaxial_active_damping_dvf_equiv, right). This is usually refers to as "sky hook damper".
\begin{tikzpicture}
% ====================
% Parameters
% ====================
\def\massw{2.2} % Width of the masses
\def\massh{0.8} % Height of the masses
\def\spaceh{1.2} % Height of the springs/dampers
\def\dispw{0.4} % Width of the dashed line for the displacement
\def\disph{0.3} % Height of the arrow for the displacements
\def\bracs{0.05} % Brace spacing vertically
\def\brach{-12pt} % Brace shift horizontaly
\def\fsensh{0.2} % Height of the force sensor
\def\velsize{0.2} % Size of the velocity sensor
% ====================
\begin{scope}
% ====================
% Stage Below
\begin{scope}
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh);
\draw[spring] (-0.25*\massw, 0) -- (-0.25*\massw, \spaceh);
\draw[damper] ( 0.25*\massw, 0) -- ( 0.25*\massw, \spaceh);
\draw[decorate,decoration={zigzag,segment length=6pt},draw=black!50!white,very thick] (-0.5*\massw, 0) -- (0.5*\massw, 0);
\draw[draw=black!50!white,very thick, dashed] (-0.5*\massw, 0) -- ++(-0.5, 0);
\draw[draw=black!50!white,very thick, dashed] ( 0.5*\massw, 0) -- ++( 0.5, 0);
\end{scope}
% ====================
% ====================
% NASS
\begin{scope}[shift={(0, \spaceh+\massh)}]
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m$};
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c$};
\draw[actuator={0.4}{0.2}{black}] ( 0.3*\massw, 0) -- (0.3*\massw, \spaceh) coordinate[midway, shift={(0.1,0)}](f);
% Velocity Sensor
\node[inertialsensor={\velsize}{coloryellow}] (veln) at (0.5*\massw, \spaceh+\massh) {};
\end{scope}
% ====================
% ====================
% Stage Above
\begin{scope}[shift={(0, 2*(\spaceh+\massh))}]
\draw[spring] (-0.25*\massw, 0) -- (-0.25*\massw, \spaceh);
\draw[damper] ( 0.25*\massw, 0) -- ( 0.25*\massw, \spaceh);
\draw[decorate,decoration={zigzag,segment length=6pt},draw=black!50!white,very thick] (-0.5*\massw, \spaceh) -- (0.5*\massw, \spaceh);
\draw[draw=black!50!white,very thick, dashed] (-0.5*\massw, \spaceh) -- ++(-0.5, 0);
\draw[draw=black!50!white,very thick, dashed] ( 0.5*\massw, \spaceh) -- ++( 0.5, 0);
\end{scope}
% ====================
% ====================
% DVF Control
\node[block={2em}{2em}, below right=0.3 and 0.4 of veln, color=coloryellow, fill=coloryellow!10!white] (ppf) {$-g$};
\draw[->, draw=coloryellow] (veln.east) node[above right, color=coloryellow]{$v$} -| (ppf.north);
\draw[->, draw=coloryellow] (ppf.south) |- (f.east) node[above right, color=coloryellow]{$f$};
% ====================
\end{scope}
\begin{scope}[shift={(6, 0)}]
% ====================
% Stage Below
\begin{scope}
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh);
\draw[spring] (-0.25*\massw, 0) -- (-0.25*\massw, \spaceh);
\draw[damper] ( 0.25*\massw, 0) -- ( 0.25*\massw, \spaceh);
\draw[decorate,decoration={zigzag,segment length=6pt},draw=black!50!white,very thick] (-0.5*\massw, 0) -- (0.5*\massw, 0);
\draw[draw=black!50!white,very thick, dashed] (-0.5*\massw, 0) -- ++(-0.5, 0);
\draw[draw=black!50!white,very thick, dashed] ( 0.5*\massw, 0) -- ++( 0.5, 0);
\end{scope}
% ====================
% ====================
% NASS
\begin{scope}[shift={(0, \spaceh+\massh)}]
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m$};
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c$};
\draw[damper={coloryellow}{}{}] ( 0.8*\massw, \massh) -- ( 0.8*\massw, \massh+\spaceh)node[midway, left=0.2, color=coloryellow]{$g$};
\draw[draw=coloryellow] (0.5*\massw, \massh+\spaceh) -- ( 0.8*\massw, \massh+\spaceh);
\node[mground={0.5}{0.3}{coloryellow}] at (0.8*\massw, \massh);
\end{scope}
% ====================
% ====================
% Stage Above
\begin{scope}[shift={(0, 2*(\spaceh+\massh))}]
\draw[spring] (-0.25*\massw, 0) -- (-0.25*\massw, \spaceh);
\draw[damper] ( 0.25*\massw, 0) -- ( 0.25*\massw, \spaceh);
\draw[decorate,decoration={zigzag,segment length=6pt},draw=black!50!white,very thick] (-0.5*\massw, \spaceh) -- (0.5*\massw, \spaceh);
\draw[draw=black!50!white,very thick, dashed] (-0.5*\massw, \spaceh) -- ++(-0.5, 0);
\draw[draw=black!50!white,very thick, dashed] ( 0.5*\massw, \spaceh) -- ++( 0.5, 0);
\end{scope}
% ====================
\end{scope}
% Equiv
\draw[double, <->, draw=coloryellow, double distance=1.5] (2.5, 1.5*\spaceh+\massh) -- ++(1.5,0);
\end{tikzpicture}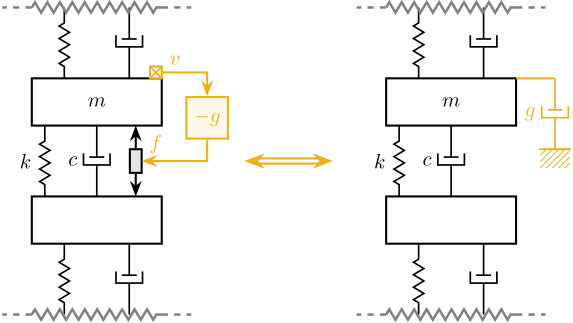
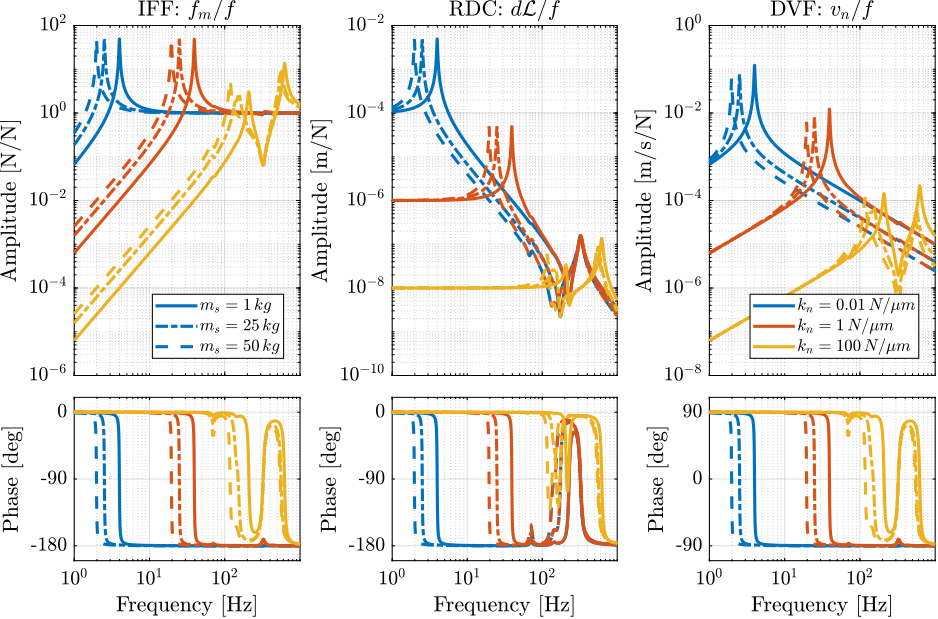
Plant Dynamics for Active Damping
The plant dynamics for all three active damping techniques are shown in Figure ref:fig:uniaxial_plant_active_damping_techniques. All have alternating poles and zeros meaning that the phase do not vary by more than $\pm 90\,\text{deg}$ which makes the design of a robust controller very easy. The reason all three plants in Figure ref:fig:uniaxial_plant_active_damping_techniques have alternating poles and zeros is because the three sensors are all collocated with the actuator cite:&preumont18_vibrat_contr_activ_struc_fourt_edition Chapter 7.
When the nano-hexapod's suspension modes are at lower frequencies than the resonances of the micro-station (blue and red curves in Figure ref:fig:uniaxial_plant_active_damping_techniques), the resonances of the micro-stations have little impact on the IFF and DVF transfer functions.
For the stiff nano-hexapod (yellow curves), the micro-station dynamics can be seen on the transfer functions in Figure ref:fig:uniaxial_plant_active_damping_techniques. Therefore, it is expected that the micro-station dynamics might impact the achievable damping if a stiff nano-hexapod is used.
Achievable Damping - Root Locus
<<ssec:uniaxial_active_damping_achievable_damping>> The Root Locus are computed for the three nano-hexapod stiffnesses and for the three active damping techniques. They are shown in Figure ref:fig:uniaxial_root_locus_damping_techniques.
All three active damping approach can lead to critical damping of the nano-hexapod suspension mode.
There is even some damping authority on micro-station modes in the following cases:
- IFF with a stiff nano-hexapod (Figure ref:fig:uniaxial_root_locus_damping_techniques, right)
- This can be understood from the mechanical equivalent of IFF shown in Figure ref:fig:uniaxial_active_damping_iff_equiv (right) considering an high stiffness $k$. The micro-station top platform is connected to an inertial mass (the nano-hexapod) through a damper, which damps the micro-station suspension suspension mode.
- DVF with a stiff nano-hexapod (Figure ref:fig:uniaxial_root_locus_damping_techniques, right)
- In that case, the "sky hook damper" (see mechanical equivalent of IFF in Figure ref:fig:uniaxial_active_damping_dvf_equiv, right) is connected to the micro-station top platform through the stiff nano-hexapod.
- RDC with a soft nano-hexapod (Figure ref:fig:uniaxial_root_locus_damping_techniques_micro_station_mode)
- At the frequency of the micro-station mode, the nano-hexapod top mass is behaving as an inertial reference as the suspension mode of the soft nano-hexapod is at much lower frequency. The micro-station and the nano-hexapod masses are connected through a large damper induced by RDC (see mechanical equivalent in Figure ref:fig:uniaxial_active_damping_rdc_equiv, right) which allows some damping of the micro-station.
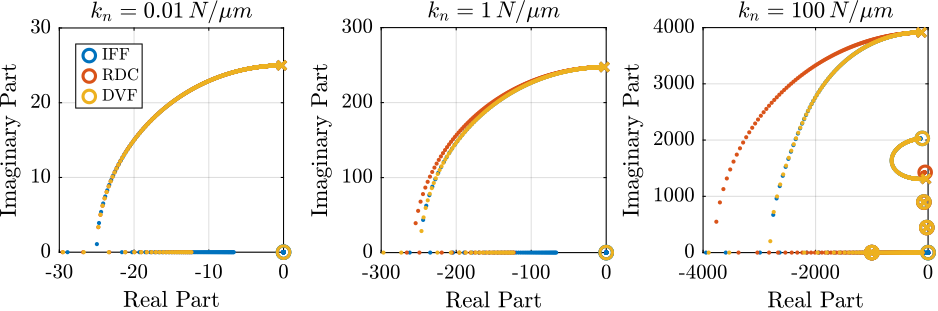
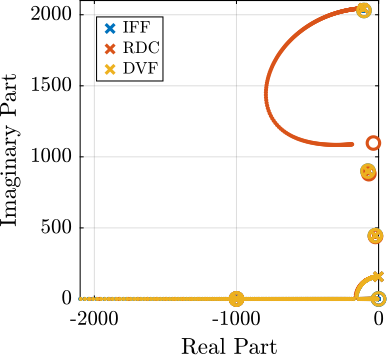
Change of sensitivity to disturbances
<<ssec:uniaxial_active_damping_sensitivity_disturbances>>
The sensitivity to disturbances (direct forces $f_s$, stage vibrations $f_t$ and floor motion $x_f$) for all three active damping techniques are compared in Figure ref:fig:uniaxial_sensitivity_dist_active_damping. The comparison is done with the nano-hexapod having a stiffness $k_n = 1\,N/\mu m$.
Conclusions from Figure ref:fig:uniaxial_sensitivity_dist_active_damping are:
- IFF degrades the sensitivity to direct forces on the sample (i.e. the compliance) below the resonance of the nano-hexapod
- RDC degrades the sensitivity to stage vibrations around the nano-hexapod's resonance as compared to the other two methods
- both IFF and DVF degrades the sensitivity to floor motion below the resonance of the nano-hexapod
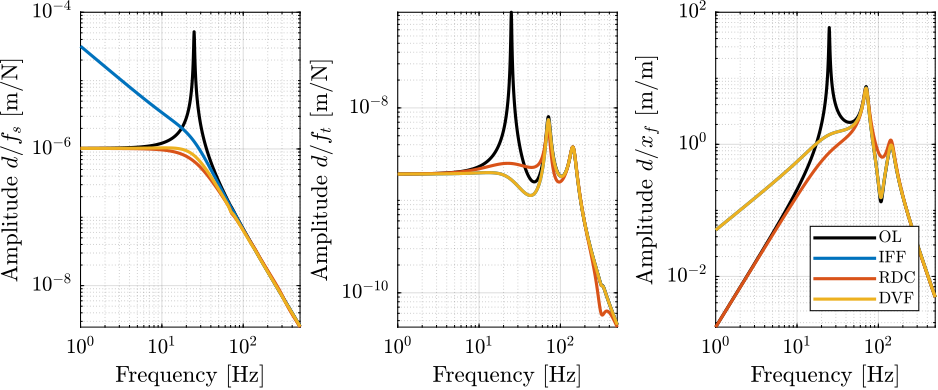
Noise Budgeting after Active Damping
<<ssec:uniaxial_active_damping_noise_budget>> Cumulative Amplitude Spectrum of the distance $d$ with all three active damping techniques are compared in Figure ref:fig:uniaxial_cas_active_damping. All three active damping methods are giving similar results (except the RDC which is a little bit worse for the stiff nano-hexapod).
Compared to the open-loop case, the active damping helps to lower the vibrations induced by the nano-hexapod resonance.
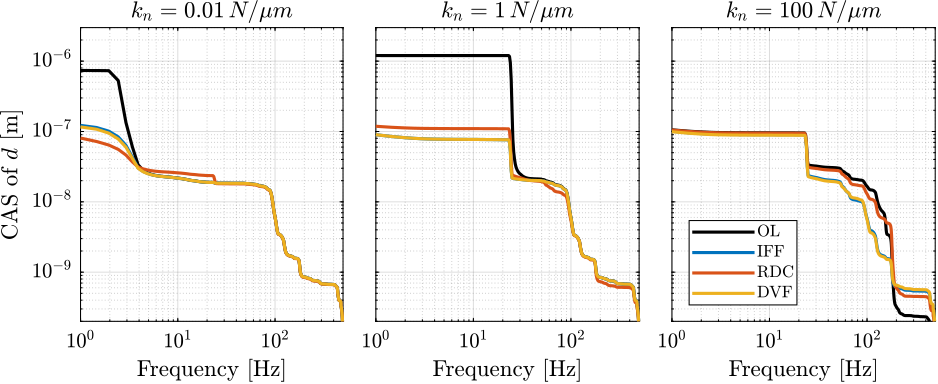
Obtained Closed Loop Response
The transfer functions from the plant input $f$ to the relative displacement $d$ while the active damping is implemented are shown in Figure ref:fig:uniaxial_damped_plant_three_active_damping_techniques. All three active damping techniques yield similar damped plants.
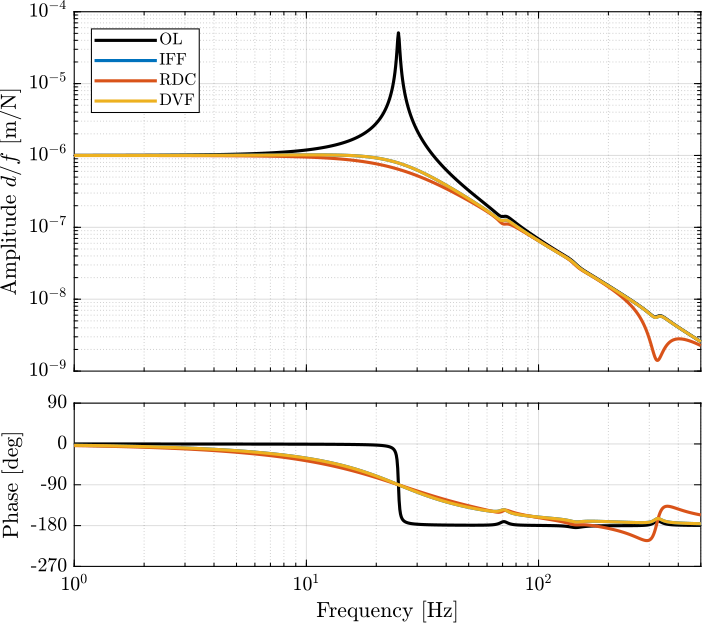
The damped plants are shown in Figure ref:fig:uniaxial_damped_plant_change_sample_mass for all three techniques, with the three considered nano-hexapod stiffnesses and sample's masses.
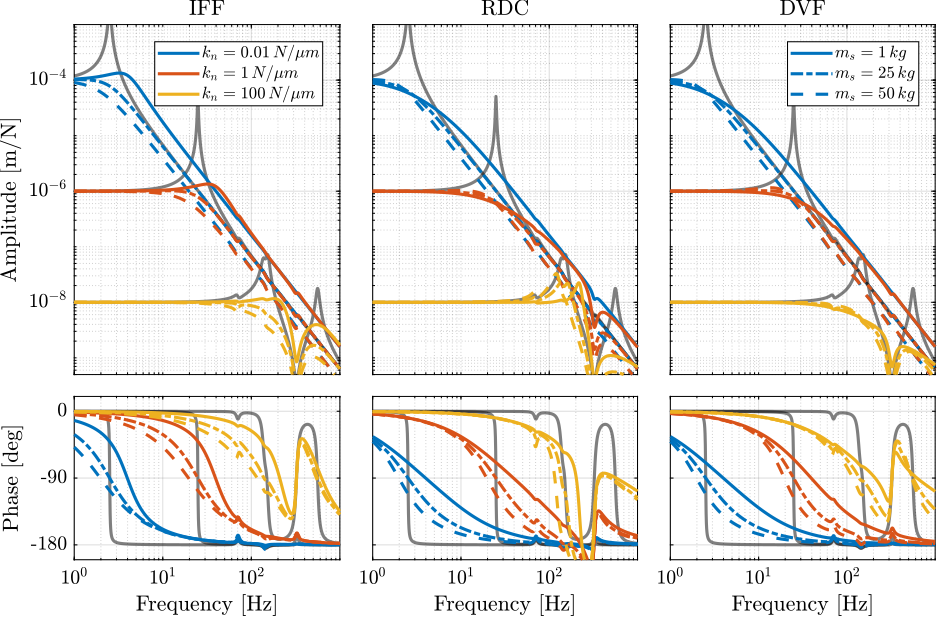
Robustness to change of payload's mass
<<ssec:uniaxial_active_damping_robustness>>
The Root Locus for the three damping techniques are shown in Figure ref:fig:uniaxial_active_damping_robustness_mass_root_locus for three sample's mass (1kg, 25kg and 50kg). The closed-loop poles are shown by the squares for a specific gain.
We can see that having heavier samples yields larger damping for IFF and smaller damping for RDC and DVF.
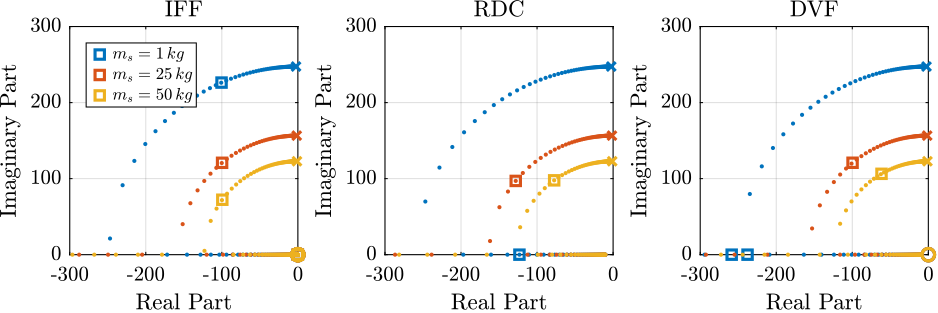
Conclusion
Conclusions for Active Damping:
- All three active damping techniques yields good damping (Figure ref:fig:uniaxial_root_locus_damping_techniques) and similar remaining vibrations (Figure ref:fig:uniaxial_cas_active_damping)
- The obtained damped plants (Figure ref:fig:uniaxial_damped_plant_change_sample_mass) are equivalent for the three active damping techniques
- Which one to be used will be determined with the use of more accurate models and will depend on which is the easiest to implement in practice
| IFF | RDC | DVF | |
|---|---|---|---|
| Sensor | Force sensor | Relative motion sensor | Inertial sensor |
| Damping | Up to critical | Up to critical | Up to Critical |
| Robustness | Requires collocation | Requires collocation | Impacted by geophone resonances |
| $f_s$ Disturbance | $\nearrow$ at low frequency | $\searrow$ near resonance | $\searrow$ near resonance |
| $f_t$ Disturbance | $\searrow$ near resonance | $\nearrow$ near resonance | $\searrow$ near resonance |
| $x_f$ Disturbance | $\nearrow$ at low frequency | $\searrow$ near resonance | $\nearrow$ at low frequency |
Position Feedback Controller
<<sec:uniaxial_position_control>>
Introduction ignore
The High Authority Control - Low Authority Control (HAC-LAC) architecture is shown in Figure ref:fig:uniaxial_hac_lac_architecture. It corresponds to a two step control strategy:
- First, an active damping controller $\bm{K}_{\textsc{LAC}}$ is implemented (see Section ref:sec:uniaxial_active_damping). It allows to reduce the vibration level, and it also makes the damped plant (transfer function from $u^{\prime}$ to $y$) easier to control than the undamped plant (transfer function from $u$ to $y$).
- Then, a position controller $\bm{K}_{\textsc{HAC}}$ is implemented which is used to control the position $d$.
\begin{tikzpicture}
% Blocs
\node[block={3.0cm}{3.0cm}] (P) {Plant};
\coordinate[] (input) at ($(P.south west)!0.5!(P.north west)$);
\coordinate[] (outputH) at ($(P.south east)!0.2!(P.north east)$);
\coordinate[] (outputL) at ($(P.south east)!0.8!(P.north east)$);
\node[block, above=0.4 of P] (Klac) {$\bm{K}_{\textsc{LAC}}$};
\node[addb, left=0.6 of input] (addF) {};
\node[block, left=1.0 of addF] (Khac) {$\bm{K}_{\textsc{HAC}}$};
\node[addb={+}{}{}{}{-}, left=0.6 of Khac] (subr) {};
% Connections and labels
\draw[->] (outputL) -- ++(0.6, 0) coordinate(eastlac) |- (Klac.east);
\node[above right] at (outputL){$y^{\prime}$};
\draw[->] (Klac.west) -| (addF.north);
\draw[->] (addF.east) -- (input) node[above left]{$u$};
\draw[<-] (subr.west) --node[midway, above]{$r$} ++(-0.8, 0);
\draw[->] (outputH) -- ++(1.6, 0);
\draw[->] ($(outputH) + (1.2, 0)$)node[branch]{} node[above]{$y$} -- ++(0, -1.2) -| (subr.south);
\draw[->] (subr.east) -- (Khac.west) node[above left]{$\epsilon$};
\draw[->] (Khac.east) -- (addF.west) node[above left=0 and 0.2]{$u^{\prime}$};
\begin{scope}[on background layer]
\node[fit={(Klac.north-|eastlac) (addF.west|-P.south)}, fill=black!20!white, draw, dashed, inner sep=6pt] (Pi) {};
\node[anchor={north west}] at (Pi.north west){\small Damped Plant};
\end{scope}
\end{tikzpicture}When applied on the uniaxial model with IFF used as the Low Authority Control, the schematic shown in Figure ref:fig:uniaxial_hac_lac_model is obtained.
\begin{tikzpicture}
% ====================
% Parameters
% ====================
\def\massw{2.2} % Width of the masses
\def\massh{0.8} % Height of the masses
\def\spaceh{1.2} % Height of the springs/dampers
\def\dispw{0.4} % Width of the dashed line for the displacement
\def\disph{0.3} % Height of the arrow for the displacements
\def\bracs{0.05} % Brace spacing vertically
\def\brach{-12pt} % Brace shift horizontaly
\def\fsensh{0.2} % Height of the force sensor
\def\velsize{0.2} % Size of the velocity sensor
% ====================
% IFF
% ====================
% Ground
% ====================
\draw (-0.5*\massw, 0) -- (0.5*\massw, 0);
\draw[dashed] (0.5*\massw, 0) -- ++(\dispw, 0);
\draw[->, color=colorpurple] (0.5*\massw+0.5*\dispw, 0) -- ++(0, 2*\disph) node[right, color=colorpurple]{$x_{f}$};
% ====================
% ====================
% Granite
\begin{scope}[shift={(0, 0)}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{g}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{g}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{g}$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{Granite};
% Displacements
\draw[dashed] (0.5*\massw, \spaceh+\massh) -- ++(7.5*\dispw, 0) coordinate(xg);
\end{scope}
% ====================
% ====================
% Stages
\begin{scope}[shift={(0, \spaceh+\massh)}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{t}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{t}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{t}$};
\draw[actuator={0.45}{0.2}{colorpurple}] ( 0.3*\massw, 0) -- (0.3*\massw, \spaceh) node[midway, right=0.1, color=colorpurple](ft){$f_{t}$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$T_y$/$R_y$/$R_z$};
\end{scope}
% ====================
% ====================
% Hexapod
\begin{scope}[shift={(0, 2*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_h$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_h$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_h$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$\mu\text{-hexa}$};
\end{scope}
% ====================
% ====================
% NASS
\begin{scope}[shift={(0, 3*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{n}$};
% Force Sensor
\node[forcesensor={\massw}{\fsensh}{colorblue}] (fsensn) at (0, \spaceh-\fsensh){};
\node[right, color=colorblue] (fn) at (fsensn.east) {$f_n$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh-\fsensh) node[midway, left=0.1]{$k_{n}$};
\draw[damper] (0, 0) -- ( 0, \spaceh-\fsensh) node[midway, left=0.2]{$c_{n}$};
\draw[actuator={0.4}{0.2}{black}] ( 0.3*\massw, 0) -- ( 0.3*\massw, \spaceh-\fsensh) node[midway, right=0.1](f){$f$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$\nu\text{-hexa}$};
% Displacements
\draw[dashed] (0.5*\massw, \spaceh+\massh) -- ++(7.5*\dispw, 0) coordinate(xnpos);
\end{scope}
% ====================
% ====================
% sample
\begin{scope}[shift={(0, 4*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.3*\massw, 0) rectangle (0.3*\massw, \massh) node[pos=0.5]{$m_{s}$};
% External Force
\draw[->, color=colorpurple] (0, \massh) node[]{$\bullet$} -- ++(0, 0.5*\massh) node[right, color=colorpurple]{$f_s$};
\end{scope}
% ====================
% Measured displacement
\draw[<->, dashed, draw=colorred] ($(xg)+(-0.1, 0)$) -- node[left, color=colorred](d){$d$} ($(xnpos)+(-0.1, 0)$);
% ====================
% IFF Control
\node[block={2em}{2em}, right=1.0 of fn, color=colorblue, fill=colorblue!10!white] (iff) {$K_{\textsc{IFF}}$};
\node[addb, right=0.5 of f.east] (ctrladd) {};
\node[block={2em}{2em}, color=colorred, fill=colorred!10!white] (Khac) at (ctrladd|-d) {$K_{\textsc{HAC}}$};
\draw[->, draw=colorblue] (fn.east) -- (iff.west);
\draw[->, draw=colorblue] (iff.south) |- (ctrladd.east);
\draw[->] (ctrladd.west) -- (f.east);
\draw[->, draw=colorred] (d.west) -- (Khac.east);
\draw[->, draw=colorred] (Khac.north) -- (ctrladd.south) node[below right, color=colorred]{$f^{\prime}$};
% ====================
\end{tikzpicture}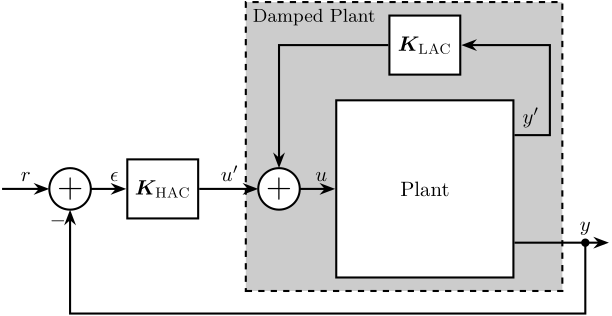
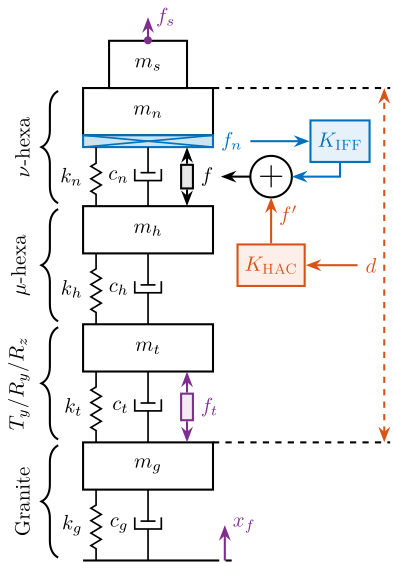
Damped Plant Dynamics
<<ssec:uniaxial_position_control_damped_dynamics>>
As was shown in Section ref:sec:uniaxial_active_damping, all three proposed active damping techniques yield similar damping plants. Therefore, Integral Force Feedback will be used in this section to study the HAC-LAC performance.
The obtained damped plants for the three nano-hexapod stiffnesses are shown in Figure ref:fig:uniaxial_hac_iff_damped_plants_masses. For $k_n = 0.01\,N/\mu m$ and $k_n = 1\,N/\mu m$, except from the nano-hexapod mode, the dynamics is quite simple and can be well approximated by a second order plant. However, this is not the case for the stiff nano-hexapod ($k_n = 100\,N/\mu m$) where two modes can be seen (Figure ref:fig:uniaxial_hac_iff_damped_plants_masses, right).
This is due to the interaction between the micro-station (modelled modes at 70Hz, 140Hz and 320Hz) and the nano-hexapod. Such effect will be explained in Section ref:sec:uniaxial_support_compliance.
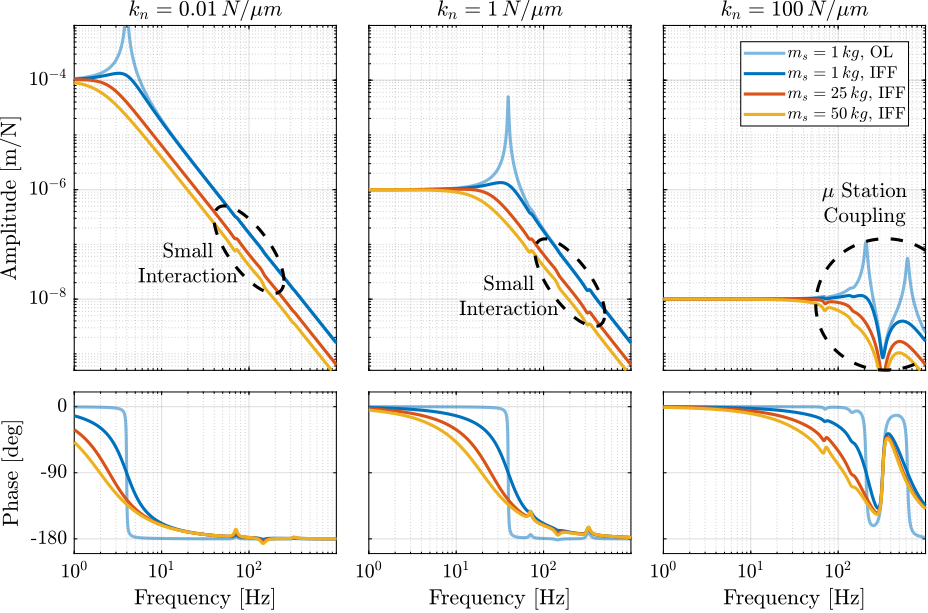
Position Feedback Controller
<<ssec:uniaxial_position_control_design>>
The objective now is to design a position feedback controller for each of the three nano-hexapods that are robust to the change of sample's mass.
The required feedback bandwidth was approximately determined in Section ref:sec:uniaxial_noise_budgeting:
- $\approx 10\,\text{Hz}$ for the soft nano-hexapod ($k_n = 0.01\,N/\mu m$). Near this frequency, the plants are equivalent to a mass line. The gain of the mass line can vary up to a fact $\approx 5$ (suspended mass from $16\,kg$ up to $65\,kg$). This means that the designed controller will need to have large gain margins to be robust to the change of sample's mass.
- $\approx 50\,\text{Hz}$ for the relatively stiff nano-hexapod ($k_n = 1\,N/\mu m$). Similarly to the soft nano-hexapod, the plants near the crossover frequency are equivalent to a mass line. It will be probably easier to have a little bit more bandwidth in this configuration to be further away from the nano-hexapod suspension mode.
- $\approx 100\,\text{Hz}$ for the stiff nano-hexapod ($k_n = 100\,N/\mu m$). Contrary to the two first nano-hexapod stiffnesses, here the plants have more complex dynamics near the wanted crossover frequency. The micro-station is not stiff enough to have a clear stiffness line at this frequency. Therefore, there are both a change of phase and gain depending on the sample's mass. This makes the robust design of the controller a little bit more complicated.
Position feedback controllers are designed for each nano-hexapod such that it is stable for all considered sample masses with similar stability margins (see Nyquist plots in Figure ref:fig:uniaxial_nyquist_hac). These high authority controllers are generally composed of a lag at low frequency for disturbance rejection, a lead to increase the phase margin near the crossover frequency and a low pass filter to increase the robustness to high frequency dynamics. The controllers used for the three nano-hexapod are shown in Equation eqref:eq:uniaxial_hac_formulas, and the parameters are summarized in Table ref:tab:uniaxial_feedback_controller_parameters.
\begin{subequations} \label{eq:uniaxial_hac_formulas}
\begin{align} K_{\text{soft}}(s) &= g \cdot \underbrace{\frac{s + \omega_0}{s + \omega_i}}_{\text{lag}} \cdot \underbrace{\frac{1 + \frac{s}{\omega_c/\sqrt{a}}}{1 + \frac{s}{\omega_c \sqrt{a}}}}_{\text{lead}} \cdot \underbrace{\frac{1}{1 + \frac{s}{\omega_l}}}_{\text{LPF}} \\ K_{\text{mid}}(s) &= g \cdot \underbrace{\left(\frac{s + \omega_0}{s + \omega_i}\right)^2}_{\text{2 lags}} \cdot \underbrace{\frac{1 + \frac{s}{\omega_c/\sqrt{a}}}{1 + \frac{s}{\omega_c \sqrt{a}}}}_{\text{lead}} \cdot \underbrace{\frac{1}{1 + \frac{s}{\omega_l}}}_{\text{LPF}} \\ K_{\text{stiff}}(s) &= g \cdot \underbrace{\left(\frac{1}{s + \omega_i}\right)^2}_{\text{2 lags}} \cdot \underbrace{\left(\frac{1 + \frac{s}{\omega_c/\sqrt{a}}}{1 + \frac{s}{\omega_c \sqrt{a}}}\right)^2}_{\text{2 leads}} \cdot \underbrace{\frac{1}{1 + \frac{s}{\omega_l}}}_{\text{LPF}} \end{align}\end{subequations}
| Soft | Moderately stiff | Stiff | |
|---|---|---|---|
| Gain | $g = 4 \cdot 10^5$ | $g = 3 \cdot 10^6$ | $g = 6 \cdot 10^12$ |
| Lead | $a = 5$, $\omega_c = 20\,Hz$ | $a = 4$, $\omega_c = 70\,Hz$ | $a = 5$, $\omega_c = 100\,Hz$ |
| Lag | $\omega_0 = 5\,Hz$, $\omega_i = 0.01\,Hz$ | $\omega_0 = 20\,Hz$, $\omega_i = 0.01\,Hz$ | $\omega_i = 0.01\,Hz$ |
| LPF | $\omega_l = 200\,Hz$ | $\omega_l = 300\,Hz$ | $\omega_l = 500\,Hz$ |
The loop gains for the three nano-hexapod are shown in Figure ref:fig:uniaxial_loop_gain_hac. We can see that:
- for the soft and moderately stiff nano-hexapod, the crossover frequency varies a lot with the sample mass. This is due to the fact that the crossover frequency corresponds to the mass line of the plant.
- for the stiff nano-hexapod, the obtained crossover frequency is not at high as what was estimated necessary. The crossover frequency in that case is close to the stiffness line of the plant, which makes the robust design of the controller easier.
Note that these controllers were quickly tuned by hand and not designed using any optimization methods. The goal is just to have a first estimation of the attainable performance.
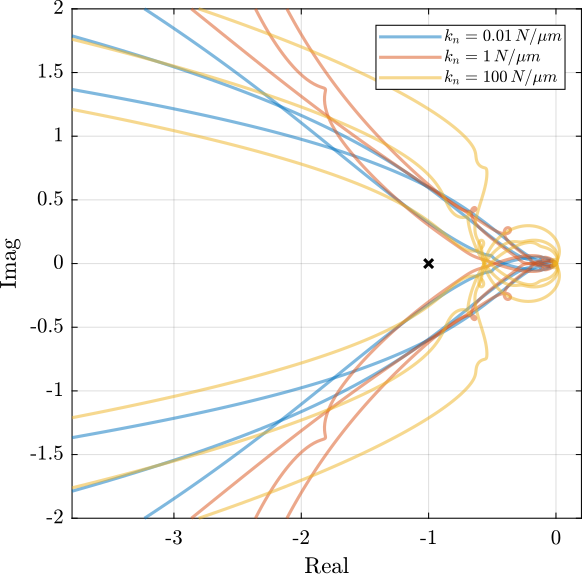
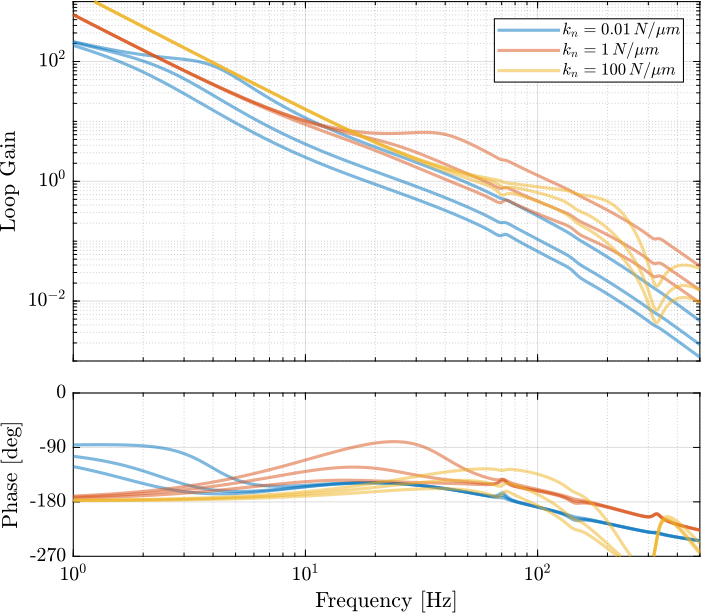
Closed-Loop Noise Budgeting
<<ssec:uniaxial_position_control_cl_noise_budget>>
The high authority position feedback controllers are then implemented and the closed-loop sensitivity to disturbances are computed. These are compared with the open-loop and damped plants cases in Figure ref:fig:uniaxial_sensitivity_dist_hac_lac for just one configuration (moderately stiff nano-hexapod with 25kg sample's mass). As expected, the sensitivity to disturbances is decreased in the controller bandwidth and slightly increase outside this bandwidth.
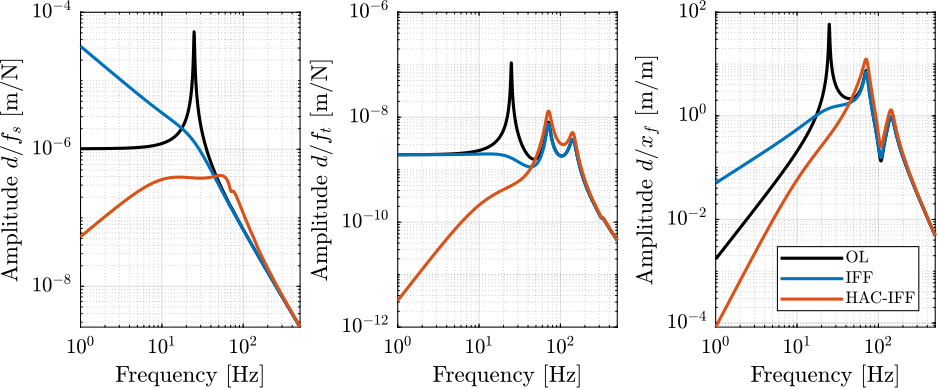
The cumulative amplitude spectrum of the motion $d$ is computed for all nano-hexapod configurations, all sample masses and in the open-loop (OL), damped (IFF) and position controlled (HAC-IFF) cases. The results are shown in Figure ref:fig:uniaxial_cas_hac_lac. Obtained root mean square values of the distance $d$ are better for the soft nano-hexapod ($\approx 25\,nm$ to $\approx 35\,nm$ depending on the sample's mass) than for the stiffer nano-hexapod (from $\approx 30\,nm$ to $\approx 70\,nm$).
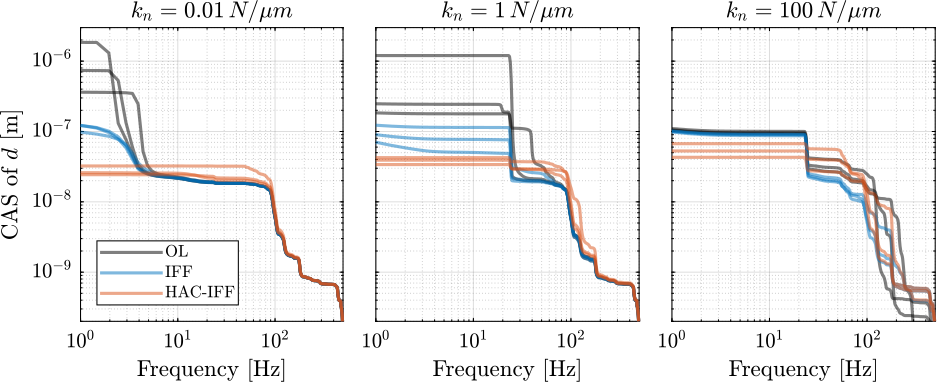
Conclusion
Based on the open-loop noise budgeting made in Section ref:sec:uniaxial_noise_budgeting, the closed-loop bandwidth required to obtain acceptable vibration levels was estimated. In order to obtain such bandwidth, the HAC-LAC strategy was followed which consists of applying an active damping controller and then a high authority position feedback controller.
In this section, feedback controllers were design in such a way that the required closed-loop bandwidth was reached while being robust to a change of payload mass. The attainable vibration control performances were estimated for the three nano-hexapod stiffnesses and were found to be close to the required values. A slight advantage can be given to the soft nano-hexapod as it requires less feedback bandwidth while giving better stability results.
Effect of limited micro-station compliance
<<sec:uniaxial_support_compliance>>
Introduction ignore
In this section, the impact of the compliance of the support (i.e. the micro-station) on the dynamics of the plant to control will be studied.
This is a critical point as the dynamics of the micro-station is complex, depends on the considered direction (see measurements in Figure ref:fig:uniaxial_comp_frf_meas_model) and may vary with position and time. It would be much better to have a plant dynamics which is not impacted by the micro-station.
Therefore, the objective in this section is to obtain some guidance for the design of a nano-hexapod that will not by impacted by the complex micro-station dynamics.
In order to study this, two models are used (Figure ref:fig:uniaxial_support_compliance_models) with:
- the nano-hexapod directly fixed on top of the granite, therefore neglecting any support compliance (Figure ref:fig:uniaxial_support_compliance_nano_hexapod_only)
- the nano-hexapod fixed on top of the micro-station having some limited compliance (Figure ref:fig:uniaxial_support_compliance_test_system)
\begin{tikzpicture}
% Parameters
\def\massw{2.2} % Width of the masses
\def\massh{0.8} % Height of the masses
\def\spaceh{1.2} % Height of the springs/dampers
\def\dispw{0.3} % Width of the dashed line for the displacement
\def\disph{0.5} % Height of the arrow for the displacements
\def\bracs{0.05} % Brace spacing vertically
\def\brach{-10pt} % Brace shift horizontaly
% Granite
\draw[fill=white!70!black] (-1*\massw, -\massh) rectangle (\massw, 0) node[pos=0.5]{Granite};
\coordinate(origin) at (0,0);
% Nano Hexapod
\begin{scope}[shift={(0, 0)}]
% Mass
\draw[draw=colorred,fill=colorred!10!white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5, color=colorred]{$m_{n}$};
% Spring, Damper, and Actuator
\draw[spring,draw=colorred] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1, color=colorred]{$k_{n}$};
\draw[damper={colorred}{}{}] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2, color=colorred]{$c_{n}$};
\draw[actuator={0.4}{0.2}{colorred}] ( 0.4*\massw, 0) -- (0.4*\massw, \spaceh) node[midway, left=0.1, color=colorred](F){$f$};
% Displacements
\draw[dashed] (0.5*\massw, \spaceh) -- coordinate[near end](dhigh) ++(1.2, 0);
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) %
node[midway,rotate=90,anchor=south,yshift=10pt,align=center]{$\nu$-hexapod};
\end{scope}
\draw[<->, dashed, colorblue] (dhigh) --node[midway, right]{$L^\prime$} (origin-|dhigh);
\end{tikzpicture}\begin{tikzpicture}
% Parameters
\def\massw{2.2} % Width of the masses
\def\massh{0.8} % Height of the masses
\def\spaceh{1.2} % Height of the springs/dampers
\def\dispw{0.3} % Width of the dashed line for the displacement
\def\disph{0.5} % Height of the arrow for the displacements
\def\bracs{0.05} % Brace spacing vertically
\def\brach{-10pt} % Brace shift horizontaly
% Granite
\draw[fill=white!70!black] (-1*\massw, -\massh) rectangle (\massw, 0) node[pos=0.5]{Granite};
\coordinate(origin) at (0,0);
% Micro Station
\begin{scope}[shift={(0, 0)}]
% Mass
\draw[draw=colorblue,fill=colorblue!10!white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5, color=colorblue]{$m_{\mu}$};
% Spring, Damper, and Actuator
\draw[spring,draw=colorblue] (-0.3*\massw, 0) -- (-0.3*\massw, \spaceh) node[midway, left=0.1, color=colorblue]{$k_{\mu}$};
\draw[damper={colorblue}{}{}] ( 0.3*\massw, 0) -- ( 0.3*\massw, \spaceh) node[midway, left=0.2, color=colorblue]{$c_{\mu}$};
% Displacements
\draw[dashed] (0.5*\massw, \spaceh+\massh) -- coordinate[near end](dmid) ++(0.3, 0);
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) %
node[midway,rotate=90,anchor=south,yshift=10pt]{$\mu$-station};
\end{scope}
% Nano Station
\begin{scope}[shift={(0, \spaceh+\massh)}]
% Mass
\draw[draw=colorred,fill=colorred!10!white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5, color=colorred]{$m_{n}$};
% Spring, Damper, and Actuator
\draw[spring,draw=colorred] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1, color=colorred]{$k_{n}$};
\draw[damper={colorred}{}{}] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2, color=colorred]{$c_{n}$};
\draw[actuator={0.4}{0.2}{colorred}] ( 0.4*\massw, 0) -- (0.4*\massw, \spaceh) node[midway, left=0.1, color=colorred](F){$f$};
% Displacements
\draw[dashed] (0.5*\massw, \spaceh) -- coordinate[near end](dhigh) ++(1.2, 0);
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) %
node[midway,rotate=90,anchor=south,yshift=10pt,align=center]{$\nu$-hexapod};
\end{scope}
\draw[<->, dashed, coloryellow] (dhigh) --node[midway, right]{$d$} (origin-|dhigh);
\draw[<->, dashed, colorred] (dmid) --node[midway, right]{$L$} (dhigh-|dmid);
\end{tikzpicture}
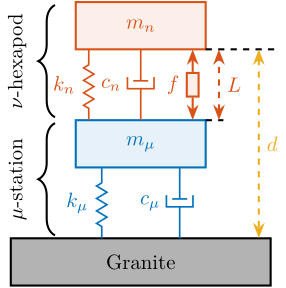
Neglected support compliance
Let's first neglect the limited compliance of the micro-station and use the uniaxial model show in Figure ref:fig:uniaxial_support_compliance_nano_hexapod_only. Let's choose a nano-hexapod mass (including the payload) of $20\,\text{kg}$ and three hexapod stiffnesses such that their resonance frequencies are at $\omega_{\nu} = 10\,\text{Hz}$, $\omega_{\nu} = 70\,\text{Hz}$ and $\omega_{\nu} = 400\,\text{Hz}$.
The obtained transfer functions from $F$ to $L^\prime$ are shown in Figure ref:fig:uniaxial_effect_support_compliance_neglected. When neglecting the support compliance, large feedback bandwidth can be achieve for all three Nano-Hexapod.
Effect of support compliance on $L/F$
Let's now add some support compliance and use the model shown in Figure ref:fig:uniaxial_support_compliance_test_system. The parameters of the support (i.e. $m^{\prime}$, $c^{\prime}$ and $k^{\prime}$) are chosen in such a way that the main vertical mode at $\omega_\mu = 70\,\text{Hz}$ seen on the micro-station is matched (Figure ref:fig:uniaxial_comp_frf_meas_model, yellow curve).
%% Parameters of the support compliance
w0h = 2*pi*70; % [rad/s]
xih = 0.1; % [-]
mh = 20; % [kg]
kh = mh*w0h^2;
ch = xih*2*sqrt(kh*mh);The transfer functions from $F$ to $L$ (i.e. control of the relative motion of the nano-hexapod) and from $L$ to $d$ (i.e. control of the position between the nano-hexapod and the fixed granite) can then be computed.
When the relative displacement of the nano-hexapod $L$ is to be controlled (dynamics shown in Figure ref:fig:uniaxial_effect_support_compliance_dynamics), having a stiff nano-hexapod (i.e. with a suspension mode at higher frequency than the mode of the support) makes the dynamics less affected by the limited support compliance (Figure ref:fig:uniaxial_effect_support_compliance_dynamics, right).
This is why it is very common to have stiff piezoelectric stages fixed at the very top of positioning stages. In such case, the control of the piezoelectric stage using its integrated metrology (typically capacitive sensors) is quite simple as the plant is not much affected by the dynamics of the support on which is it fixed.
If a soft nano-hexapod is used, the support dynamics appears in the dynamics between $F$ and $L$ (see Figure ref:fig:uniaxial_effect_support_compliance_dynamics, left) which will impact the control robustness and performance.
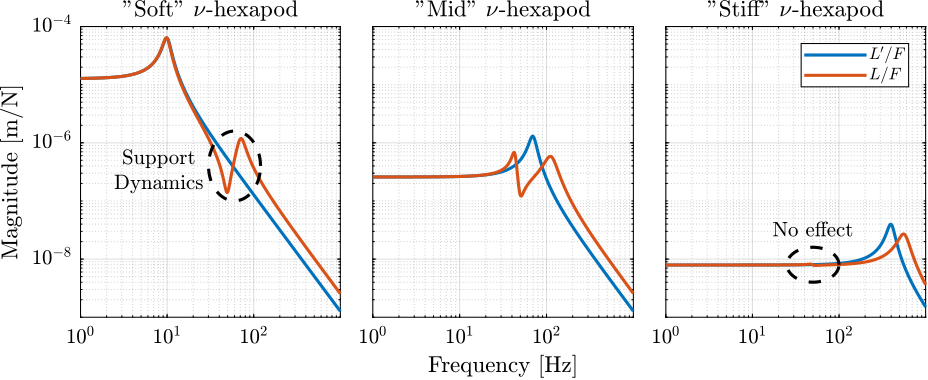
Effect of support compliance on $d/F$
When the motion to be controlled is the relative displacement $d$ between the granite and the nano-hexapod's top platform, the effect of the support compliance on the plant dynamics is opposite than what was previously observed. Indeed, using a "soft" nano-hexapod (i.e. with a suspension mode at lower frequency than the mode of the support) makes the dynamics less affected by the support dynamics (Figure ref:fig:uniaxial_effect_support_compliance_dynamics_d, left). On the contrary, if a "stiff" nano-hexapod is used, the support dynamics appears in the plant dynamics (Figure ref:fig:uniaxial_effect_support_compliance_dynamics_d, right).
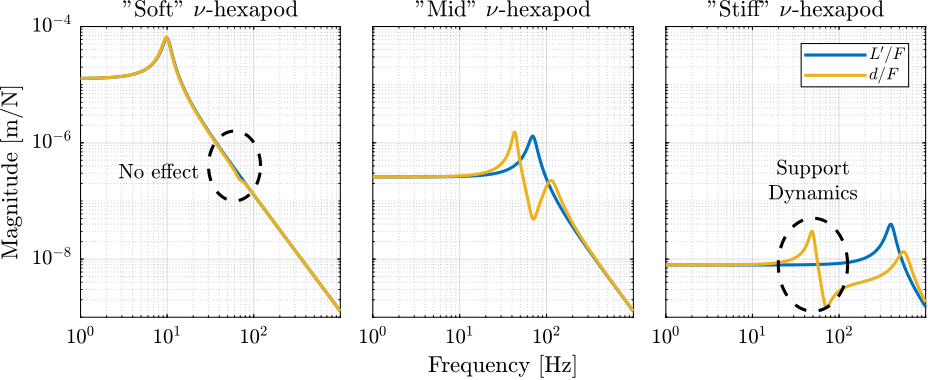
Conclusion
In order to study the impact of the support compliance on the plant dynamics, simple models shown in Figure ref:fig:uniaxial_support_compliance_models were used.
Depending on the quantity to be controlled ($L$ or $d$ in Figure ref:fig:uniaxial_support_compliance_test_system) and on the relative location of $\omega_\nu$ (suspension mode of the nano-hexapod) and $\omega_\mu$ (modes of the support), the interaction between the support and the nano-hexapod dynamics can change drastically (observations made are summarized in Table ref:tab:uniaxial_effect_compliance).
For the NASS, having the suspension mode of the nano-hexapod at lower frequencies than the suspension modes of the micro-station would make the plant less dependent on the micro-station dynamics, and therefore easier to control.
Note that observations made in this section are also affected by the ratio between the support mass $m^{\prime}$ and the nano-hexapod mass $m$ (the effect is more pronounced when the ratio $m/m^{\prime}$ increases).
| $\omega_{\nu} \ll \omega_{\mu}$ | $\omega_{\nu} \approx \omega_{\mu}$ | $\omega_{\nu} \gg \omega_{\mu}$ | |
|---|---|---|---|
| $d/F$: | small | large | large |
| $L/F$: | large | large | small |
Effect of Payload Dynamics
<<sec:uniaxial_payload_dynamics>>
Introduction ignore
Up to this section, the sample was modelled as a mass rigidly fixed to the nano-hexapod (as shown in Figure ref:fig:uniaxial_paylaod_dynamics_rigid_schematic). However, such sample may present internal dynamics and its fixation to the nano-hexapod may have limited stiffness.
To study the effect of the sample dynamics, models shown in Figure ref:fig:uniaxial_paylaod_dynamics_schematic are used is this Section.
\begin{tikzpicture}
% Parameters
\def\massw{2.2} % Width of the masses
\def\massh{0.8} % Height of the masses
\def\spaceh{1.2} % Height of the springs/dampers
\def\dispw{0.3} % Width of the dashed line for the displacement
\def\disph{0.5} % Height of the arrow for the displacements
\def\bracs{0.05} % Brace spacing vertically
\def\brach{-10pt} % Brace shift horizontaly
% Granite
\draw[fill=white!70!black] (-1*\massw, -\massh) rectangle (\massw, 0) node[pos=0.5]{Granite};
\coordinate(origin) at (0,0);
% Nano Station
\begin{scope}[shift={(0, 0)}]
% Mass
\draw[draw=colorred,fill=colorred!10!white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5, color=colorred]{$m_{n}$};
% Spring, Damper, and Actuator
\draw[spring,draw=colorred] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1, color=colorred]{$k_{n}$};
\draw[damper={colorred}{}{}] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2, color=colorred]{$c_{n}$};
\draw[actuator={0.4}{0.2}{colorred}] ( 0.4*\massw, 0) -- (0.4*\massw, \spaceh) node[midway, left=0.1, color=colorred](F){$f$};
% Displacements
\draw[dashed] (0.5*\massw, \spaceh) -- coordinate[near end](dhigh) ++(1.2, 0);
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) %
node[midway,rotate=90,anchor=south,yshift=10pt,align=center]{$\nu$-hexapod};
\end{scope}
% Sample
\begin{scope}[shift={(0, \spaceh+\massh)}]
% Mass
\draw[draw=colorblue,fill=colorblue!10!white] (-0.3*\massw, 0) rectangle (0.3*\massw, \massh) node[pos=0.5, color=colorblue]{$m_{s}$};
\end{scope}
\draw[<->, dashed] (dhigh) --node[midway, right]{$L$} (origin-|dhigh);
\end{tikzpicture}\begin{tikzpicture}
% Parameters
\def\massw{2.2} % Width of the masses
\def\massh{0.8} % Height of the masses
\def\spaceh{1.2} % Height of the springs/dampers
\def\dispw{0.3} % Width of the dashed line for the displacement
\def\disph{0.5} % Height of the arrow for the displacements
\def\bracs{0.05} % Brace spacing vertically
\def\brach{-10pt} % Brace shift horizontaly
% Granite
\draw[fill=white!70!black] (-1*\massw, -\massh) rectangle (\massw, 0) node[pos=0.5]{Granite};
\coordinate(origin) at (0,0);
% Nano Station
\begin{scope}[shift={(0, 0)}]
% Mass
\draw[draw=colorred,fill=colorred!10!white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5, color=colorred]{$m_{n}$};
% Spring, Damper, and Actuator
\draw[spring,draw=colorred] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1, color=colorred]{$k_{n}$};
\draw[damper={colorred}{}{}] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2, color=colorred]{$c_{n}$};
\draw[actuator={0.4}{0.2}{colorred}] ( 0.4*\massw, 0) -- (0.4*\massw, \spaceh) node[midway, left=0.1, color=colorred](F){$f$};
% Displacements
\draw[dashed] (0.5*\massw, \spaceh) -- coordinate[near end](dhigh) ++(1.2, 0);
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) %
node[midway,rotate=90,anchor=south,yshift=10pt,align=center]{$\nu$-hexapod};
\end{scope}
% Sample
\begin{scope}[shift={(0, \spaceh+\massh)}]
% Mass
\draw[draw=colorblue,fill=colorblue!10!white] (-0.3*\massw, \spaceh) rectangle (0.3*\massw, \spaceh+\massh) node[pos=0.5, color=colorblue]{$m_{s}$};
% Spring, Damper, and Actuator
\draw[spring,draw=colorblue] (-0.2*\massw, 0) -- (-0.2*\massw, \spaceh) node[midway, left=0.1, color=colorblue]{$k_{s}$};
\draw[damper={colorblue}{}{}] ( 0.2*\massw, 0) -- ( 0.2*\massw, \spaceh) node[midway, left=0.2, color=colorblue]{$c_{s}$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) %
node[midway,rotate=90,anchor=south,yshift=10pt,align=center]{Payload};
\end{scope}
\draw[<->, dashed] (dhigh) --node[midway, right]{$L^\prime$} (origin-|dhigh);
\end{tikzpicture}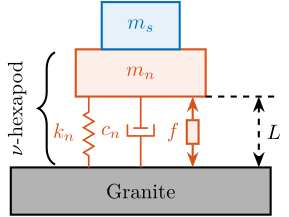
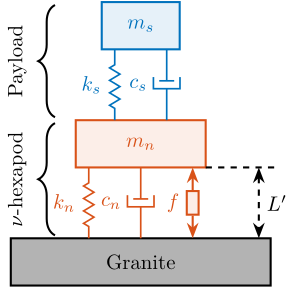
Impact on the plant dynamics
<<ssec:uniaxial_payload_dynamics_effect_dynamics>>
To study the impact of sample dynamics, the following sample configurations are considered:
- rigid sample, corresponding to Figure ref:fig:uniaxial_paylaod_dynamics_rigid_schematic
- two flexible samples with a resonance at $\omega_s = 200\,\text{Hz}$ and at $\omega_s = 20\,\text{Hz}$ respectively, corresponding to Figure ref:fig:uniaxial_paylaod_dynamics_schematic
- for all cases, two sample masses are considered: $m_s = 1\,\text{kg}$ and $m_s = 50\,\text{kg}$
The transfer functions from the nano-hexapod force to the motion of the nano-hexapod top platform are computed for all the above configurations and are compared for a soft Nano-Hexapod $k_n = 0.01\,N/\mu m$ in Figure ref:fig:uniaxial_payload_dynamics_soft_nano_hexapod.
It can be seen that the mode of the sample adds an anti-resonance followed by a resonance (zero/pole pattern). The frequency of the anti-resonance corresponds to the "free" resonance of the sample $\omega_s = \sqrt{k_s/m_s}$. The flexibility of the sample also changes the high frequency gain (the mass line is shifted from $\frac{1}{(m_n + m_s)s^2}$ to $\frac{1}{m_ns^2}$).
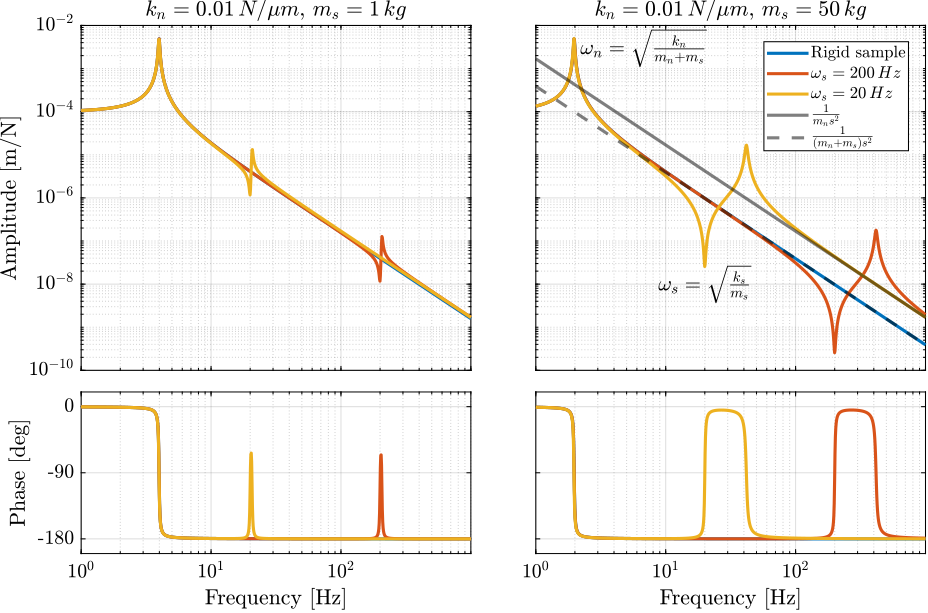
The same transfer functions are now compared when using a stiff nano-hexapod ($k_n = 100\,N/\mu m$) in Figure ref:fig:uniaxial_payload_dynamics_stiff_nano_hexapod. In that case, the sample's resonance $\omega_n$ is smaller than the nano-hexapod resonance $\omega_n$. This changes the zero/pole pattern to a pole/zero pattern (the frequency of the zero still being equal to $\omega_s$). Even tough the added sample's flexibility still changes the high frequency mass line from $\frac{1}{(m_n + m_s)s^2}$ to $\frac{1}{m_ns^2}$, the overall dynamics is much less impacted, even if the sample mass is high (see yellow curve in Figure ref:fig:uniaxial_payload_dynamics_stiff_nano_hexapod, right).
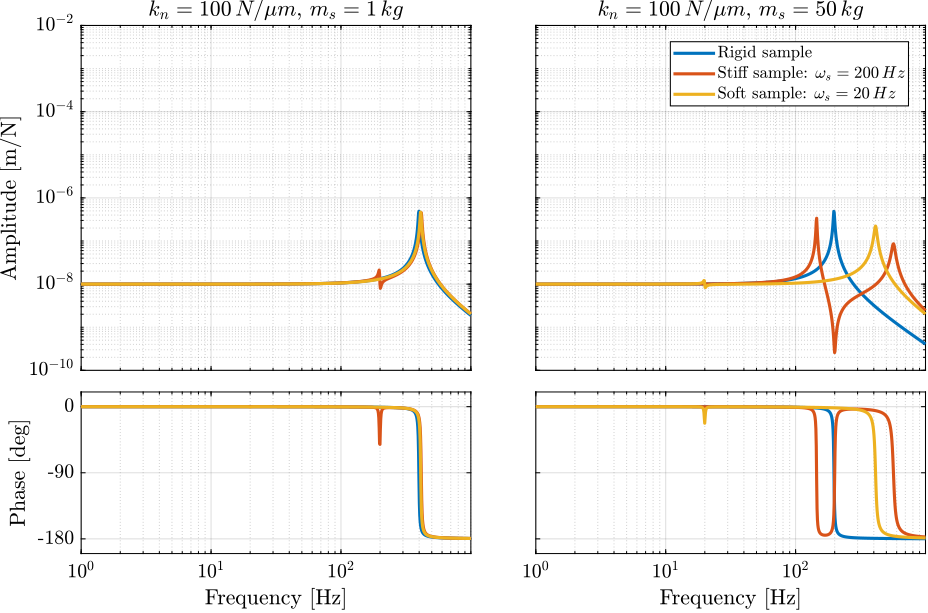
The impact of the sample dynamics on the plant varies with the sample mass and the relative resonance frequency of the sample $\omega_s$ and of the nano-hexapod $\omega_n$. The larger the sample mass, the larger the effect (i.e. change of high frequency gain, appearance of additional resonances and anti-resonances). A zero/pole pattern is observed if $\omega_s > \omega_n$ and a pole/zero pattern if $\omega_s > \omega_n$. Such additional dynamics can induce stability issues depending on their position relative to the wanted feedback bandwidth as explained in cite:&rankers98_machin Section 4.2.
The general conclusion is that the stiffer the nano-hexapod, the less it is impacted by the payload's dynamics, which would make the feedback controller more robust to a change of payload.
This is why high-bandwidth soft positioning stages are usually restricted to constant and calibrated payloads (CD-player, lithography machines, isolation system for gravitational wave detectors, …), while stiff positioning systems can more easily accept various payloads.
Impact on the positioning stability
<<ssec:uniaxial_payload_dynamics_effect_stability>>
Having a flexibility between the measured position (i.e. the top platform of the nano-hexapod) and the point-of-interest to be positioned relative to the x-ray can also impact the positioning stability. This is due to the fact that the measured (and therefore controlled) distance is no longer equal to the important distance for the experiment.
In order to estimate if the sample flexibility is critical for the position stability of the point of interest, the model shown in Figure ref:fig:uniaxial_sample_flexibility_control is used. This is the same model that was used in Section ref:sec:uniaxial_position_control but with an added flexibility between the nano-hexapod and the sample (considered sample modes are at $\omega_s = 20\,\text{Hz}$ and $\omega_n = 200\,\text{Hz}$).
\begin{tikzpicture}
% Parameters
\def\massw{2.2} % Width of the masses
\def\massh{0.8} % Height of the masses
\def\spaceh{1.2} % Height of the springs/dampers
\def\dispw{0.4} % Width of the dashed line for the displacement
\def\disph{0.3} % Height of the arrow for the displacements
\def\bracs{0.05} % Brace spacing vertically
\def\brach{-12pt} % Brace shift horizontaly
\def\fsensh{0.2} % Height of the force sensor
\def\velsize{0.2} % Size of the velocity sensor
% Ground
\draw (-0.5*\massw, 0) -- (0.5*\massw, 0);
\draw[dashed] (0.5*\massw, 0) -- ++(\dispw, 0);
\draw[->, color=colorpurple] (0.5*\massw+0.5*\dispw, 0) -- ++(0, 2*\disph) node[right, color=colorpurple]{$x_{f}$};
% ====================
% Granite
\begin{scope}[shift={(0, 0)}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{g}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{g}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{g}$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{Granite};
% Displacements
\draw[dashed] (0.5*\massw, \spaceh+\massh) -- ++(9.0*\dispw, 0) coordinate(xg);
\end{scope}
% ====================
% ====================
% Stages
\begin{scope}[shift={(0, \spaceh+\massh)}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{t}$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_{t}$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_{t}$};
\draw[actuator={0.45}{0.2}{colorpurple}] ( 0.3*\massw, 0) -- (0.3*\massw, \spaceh) node[midway, right=0.1, color=colorpurple](ft){$f_{t}$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$T_y$/$R_y$/$R_z$};
\end{scope}
% ====================
% ====================
% Hexapod
\begin{scope}[shift={(0, 2*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_h$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh) node[midway, left=0.1]{$k_h$};
\draw[damper] (0, 0) -- ( 0, \spaceh) node[midway, left=0.2]{$c_h$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$\mu\text{-hexa}$};
\end{scope}
% ====================
% ====================
% NASS
\begin{scope}[shift={(0, 3*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.5*\massw, \spaceh) rectangle (0.5*\massw, \spaceh+\massh) node[pos=0.5]{$m_{n}$};
% Force Sensor
\node[forcesensor={\massw}{\fsensh}{colorblue}] (fsensn) at (0, \spaceh-\fsensh){};
\node[right, color=colorblue] (fn) at (fsensn.east) {$f_n$};
% Spring, Damper, and Actuator
\draw[spring] (-0.4*\massw, 0) -- (-0.4*\massw, \spaceh-\fsensh) node[midway, left=0.1]{$k_{n}$};
\draw[damper] (0, 0) -- ( 0, \spaceh-\fsensh) node[midway, left=0.2]{$c_{n}$};
\draw[actuator={0.4}{0.2}{black}] ( 0.3*\massw, 0) -- (0.3*\massw, \spaceh-\fsensh) node[midway, right=0.1](f){$f$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) node[midway,rotate=90,anchor=south,yshift=10pt]{$\nu\text{-hexa}$};
% Displacements
\draw[dashed] (0.5*\massw, \spaceh+\massh) -- ++(7.5*\dispw, 0) coordinate(xnpos);
\end{scope}
% ====================
% ====================
% sample
\begin{scope}[shift={(0, 4*(\spaceh+\massh))}]
% Mass
\draw[fill=white] (-0.3*\massw, \spaceh) rectangle (0.3*\massw, \spaceh+\massh) coordinate[pos=0.5](poi);
% Spring, Damper, and Actuator
\draw[spring] (-0.2*\massw, 0) -- (-0.2*\massw, \spaceh) node[midway, left=0.1]{$k_{s}$};
\draw[damper] ( 0.2*\massw, 0) -- ( 0.2*\massw, \spaceh) node[midway, left=0.2]{$c_{s}$};
% Legend
\draw[decorate, decoration={brace, amplitude=8pt}, xshift=\brach] %
(-0.5*\massw, \bracs) -- (-0.5*\massw, \spaceh+\massh-\bracs) %
node[midway,rotate=90,anchor=south,yshift=10pt,align=center]{Sample};
% X-ray
\draw[dashed, draw=red, -<-=.5] (poi)node[branch, color=red]{} -- node[near end, above]{x-ray} ++(2.5, 0);
% Displacements
\draw[dashed] (0.2*\massw, \spaceh)coordinate(a) -- (xg|-a) coordinate(xspos);
\end{scope}
% ====================
% Measured displacement
\draw[<->, dashed, draw=colorred] ($(xnpos)+(-0.1, 0)$)coordinate(a) -- node[left, color=colorred](d){$d$} (xg-|a);
\draw[<->, dashed] ($(xg)+(-0.1, 0)$) -- node[left]{$y$} ($(xspos)+(-0.1, 0)$);
% ====================
% IFF Control
\node[block={2em}{2em}, right=1.0 of fn, color=colorblue, fill=colorblue!10!white] (iff) {$K_{\textsc{IFF}}$};
\node[addb, right=0.5 of f.east] (ctrladd) {};
\node[block={2em}{2em}, color=colorred, fill=colorred!10!white] (Khac) at (ctrladd|-d) {$K_{\textsc{HAC}}$};
\draw[->, draw=colorblue] (fn.east) -- (iff.west);
\draw[->, draw=colorblue] (iff.south) |- (ctrladd.east);
\draw[->] (ctrladd.west) -- (f.east);
\draw[->, draw=colorred] (d.west) -- (Khac.east);
\draw[->, draw=colorred] (Khac.north) -- (ctrladd.south) node[below right, color=colorred]{$f^{\prime}$};
% ====================
\end{tikzpicture}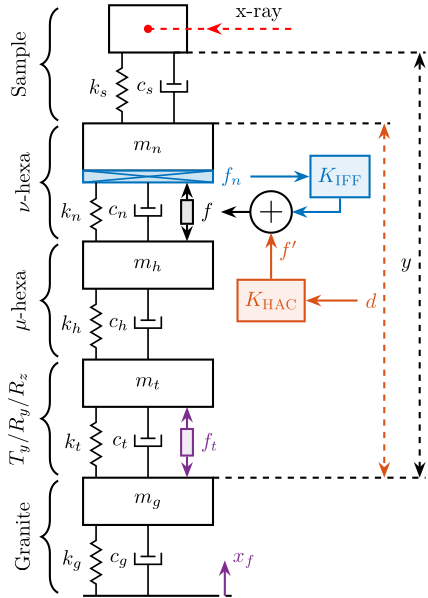
After the system dynamics extracted from the model, IFF is applied using the same gains as the ones used in Section ref:sec:uniaxial_active_damping. Thanks to the collocation between the nano-hexapod and the force sensor used for IFF, the damped plants are still stable and similar damping values are obtained than when considering a rigid sample.
The High Authority Controllers used in Section ref:sec:uniaxial_position_control are then implemented on the damped plants. The obtained closed-loop systems are stable, indicating good robustness.
Finally, closed-loop noise budgeting is computed for the obtained the closed-loop system and the cumulative amplitude spectrum of $d$ and $y$ are shown in Figure ref:fig:uniaxial_sample_flexibility_noise_budget_y. The cumulative amplitude spectrum of the measured distance $d$ (Figure ref:fig:uniaxial_sample_flexibility_noise_budget_d) shows that the added flexibility at the sample location have very little effect on the control performance. However, the cumulative amplitude spectrum of the distance $y$ (Figure ref:fig:uniaxial_sample_flexibility_noise_budget_y) shows that the stability of $y$ is degraded when the sample flexibility is considered and is degraded as $\omega_s$ is lowered.
What happens is that above $\omega_s$, even though the motion $d$ can be controlled perfectly, the sample's mass is "isolated" from the motion of the nano-hexapod and the control on $y$ is not effective.
%% Apply IFF and verify stability
% Soft Nano-Hexapod
G_iff_vc_light_rigid = feedback(G_vc_light_rigid, K_iff_vc, 'name', +1);
G_iff_vc_light_soft = feedback(G_vc_light_soft , K_iff_vc, 'name', +1);
G_iff_vc_light_stiff = feedback(G_vc_light_stiff, K_iff_vc, 'name', +1);
isstable(G_iff_vc_light_rigid)
isstable(G_iff_vc_light_soft)
isstable(G_iff_vc_light_stiff)
% Stiff Nano-Hexapod
G_iff_pz_light_rigid = feedback(G_pz_light_rigid, K_iff_pz, 'name', +1);
G_iff_pz_light_soft = feedback(G_pz_light_soft , K_iff_pz, 'name', +1);
G_iff_pz_light_stiff = feedback(G_pz_light_stiff, K_iff_pz, 'name', +1);
isstable(G_iff_pz_light_rigid)
isstable(G_iff_pz_light_soft)
isstable(G_iff_pz_light_stiff)%% Compute closed-loop plants and verify stability
% Soft Nano-Hexapod
G_hac_iff_vc_light_rigid = feedback(G_iff_vc_light_rigid, K_hac_vc, 'name', -1);
G_hac_iff_vc_light_soft = feedback(G_iff_vc_light_soft , K_hac_vc, 'name', -1);
G_hac_iff_vc_light_stiff = feedback(G_iff_vc_light_stiff, K_hac_vc, 'name', -1);
isstable(G_hac_iff_vc_light_rigid)
isstable(G_hac_iff_vc_light_soft)
isstable(G_hac_iff_vc_light_stiff)
% Stiff Nano-Hexapod
G_hac_iff_pz_light_rigid = feedback(G_iff_pz_light_rigid, K_hac_pz, 'name', -1);
G_hac_iff_pz_light_soft = feedback(G_iff_pz_light_soft , K_hac_pz, 'name', -1);
G_hac_iff_pz_light_stiff = feedback(G_iff_pz_light_stiff, K_hac_pz, 'name', -1);
isstable(G_hac_iff_pz_light_rigid)
isstable(G_hac_iff_pz_light_soft)
isstable(G_hac_iff_pz_light_stiff)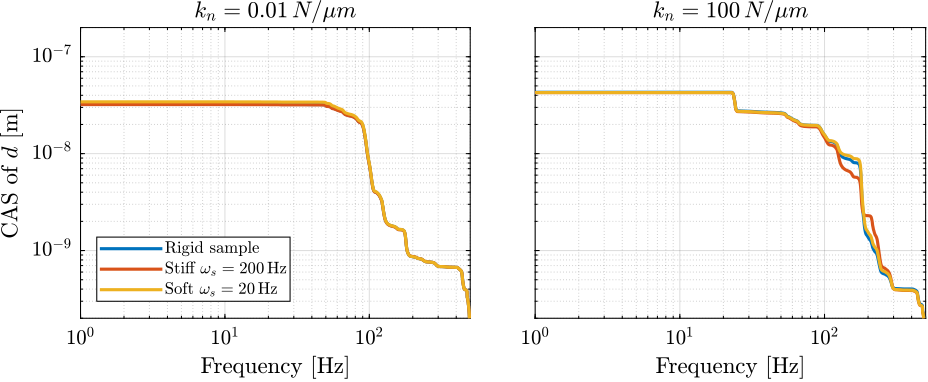
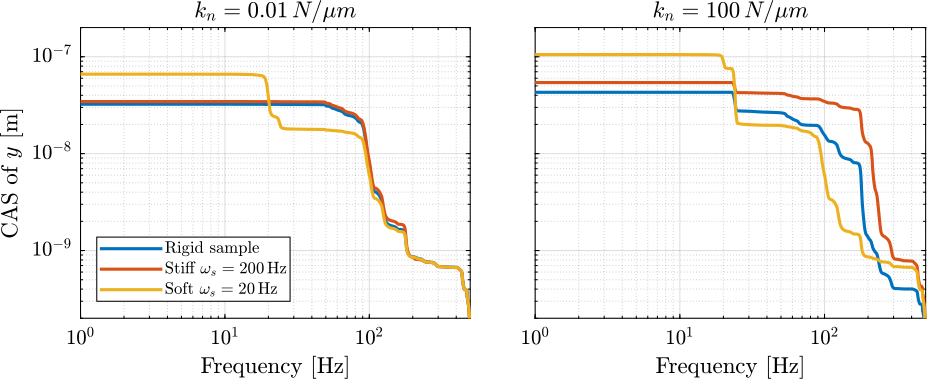
Conclusion
Payload dynamics is usually a major concern when designing a positioning system. For the NASS, the sample may present internal dynamics and limited fixation stiffness to the nano-hexapod platform. On top of that, its mass can vary from 1kg up to 50kg which is a first challenge.
This sample dynamics can add pole/zero or zero/pole pattern in the plant as shown in Section ref:ssec:uniaxial_payload_dynamics_effect_dynamics which may impact the stability and makes the design of the controller more complex. However, it was shown that this issue is less critical if a stiff nano-hexapod is used.
Having some flexibility between the measurement point and the point of interest (i.e. the sample point to be position on the x-ray) also degrades the position stability as shown in Section ref:ssec:uniaxial_payload_dynamics_effect_stability.
It will be therefore important to take special care when designing sampling environments, especially is a soft nano-hexapod is used.
Conclusion
<<sec:uniaxial_conclusion>>
In this study, a uniaxial model of the nano-active-stabilization-system has been tuned both from dynamical measurements (Section ref:sec:micro_station_model) and from disturbances measurements (Section ref:sec:uniaxial_disturbances).
It has been shown that three active damping techniques can be used to critically damp the nano-hexapod resonances (Section ref:sec:uniaxial_active_damping). However, this model does not allows to determine which one is most suited to this application.
Position feedback controllers have been developed for three considered nano-hexapod stiffnesses (Section ref:sec:uniaxial_position_control). These controllers were shown to be robust to the change of sample's masses, and to provide good rejection of disturbances. It has been found that having a soft nano-hexapod makes the plant dynamics easier to control (because decoupled from the micro-station dynamics, see Section ref:sec:uniaxial_support_compliance) and requires less position feedback bandwidth to fulfill the requirements. The moderately stiff nano-hexapod ($k_n = 1\,N/\mu m$) is requiring a bit more position feedback bandwidth, but it still seems to give acceptable results. However, the stiff nano-hexapod is the most complex to control and gives the worst positioning performance.