62 KiB
Nano Active Stabilization System - Introduction
- Context of this thesis
- Challenge definition
- Literature Review
- Original Contributions
- Introduction
- Active Damping of rotating mechanical systems using Integral Force Feedback
- Design of complementary filters using $\mathcal{H}_\infty$ Synthesis and sensor fusion
- Multi-body simulations with reduced order flexible bodies obtained by FEA
- Robustness by design
- Mechatronics design
- 6DoF vibration control of a rotating platform
- Experimental validation of the Nano Active Stabilization System
- Thesis Outline - Mechatronics Design Approach
- Bibliography
- Footnotes
Context of this thesis
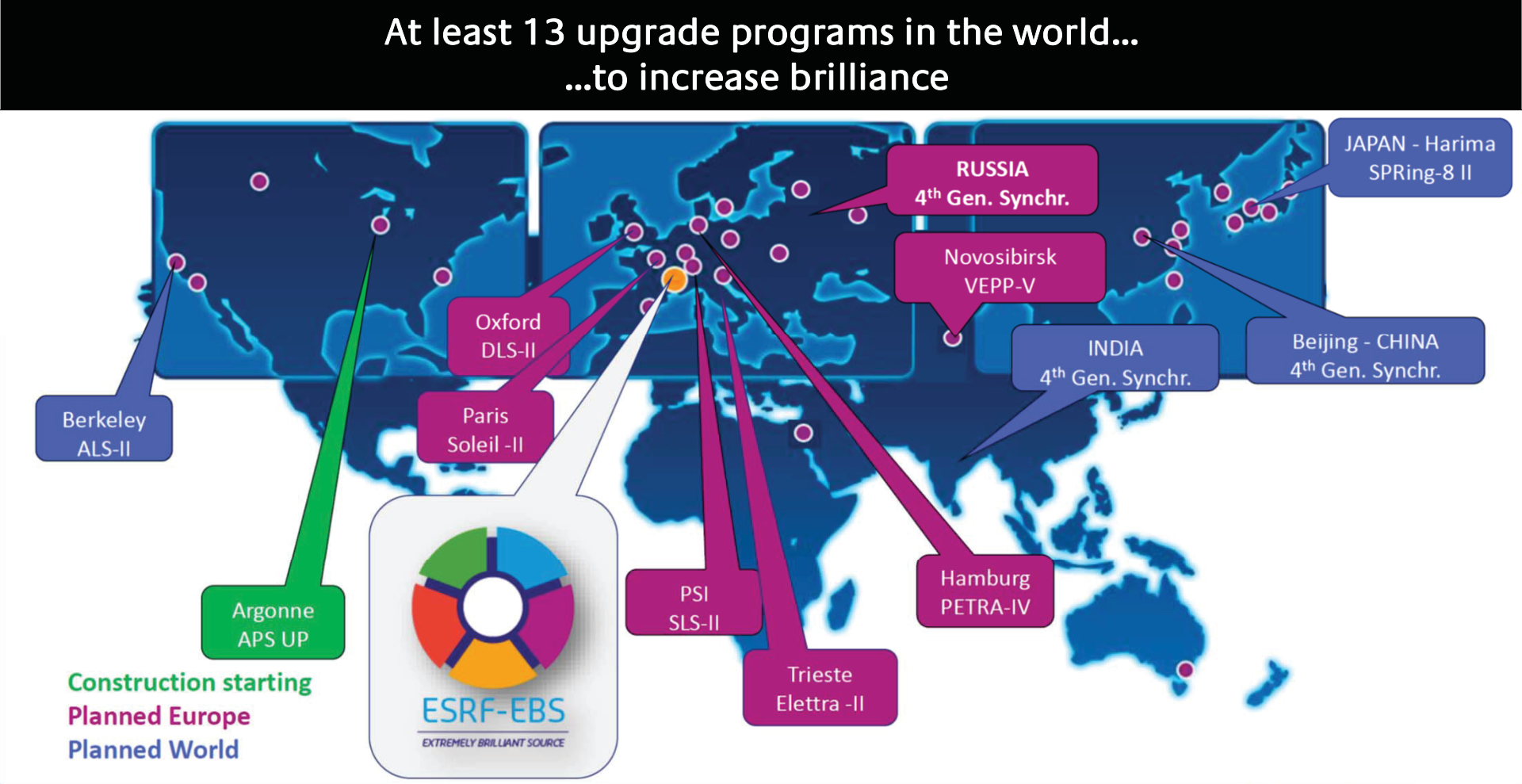
Synchrotron Radiation Facilities
Accelerating electrons to produce intense X-ray
- Explain what is a Synchrotron: light source
- Say how many there are in the world (~50)
- Electron part: LINAC, Booster, Storage Ring ref:fig:introduction_esrf_schematic
- Synchrotron radiation: Insertion device / Bending magnet
- Many beamlines (large diversity in terms of instrumentation and science)
-
Science that can be performed:
- structural biology, structure of materials, matter at extreme, …
3rd and 4th generation Synchrotrons
Brilliance: figure of merit for synchrotron
-
4th generation light sources
- cite:&raimondi21_commis_hybrid_multib_achrom_lattic
- Picture of 3rd generation "beam source" vs 4th generation?
- Picture showing Synchrotron "moore's law"
figs/introduction_moore_law.pdf
The ID31 ESRF Beamline
Beamline Layout
- Beamline layout (OH, EH)
- ID31 and Micro Station (Figure ref:fig:introduction_id31_microstation_picture) Check https://www.esrf.fr/UsersAndScience/Experiments/StructMaterials/ID31 https://www.wayforlight.eu/beamline/23244
- X-ray beam + detectors + sample stage (Figure ref:fig:introduction_id31_beamline_schematic)
- Focusing optics
- Optical schematic with: source, lens, sample and detector. Explain that what is the most important is the relative position between the sample and the lens.
-
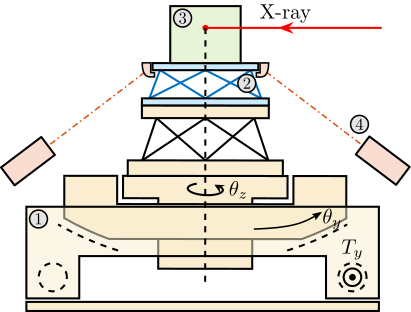
Explain the XYZ frame for all the thesis (ESRF convention: X: x-ray, Z gravity up)
- Add XYZ on figure ref:fig:introduction_id31_cad
\begin{tikzpicture}
\node[inner sep=0pt, anchor=south west] (photo) at (0,0)
{\includegraphics[width=0.39\textwidth]{/home/thomas/Cloud/documents/reports/phd-thesis/figs/exp_setup_photo.png}};
\coordinate[] (aheight) at (photo.north west);
\coordinate[] (awidth) at (photo.south east);
\coordinate[] (granite) at ($0.1*(aheight)+0.1*(awidth)$);
\coordinate[] (trans) at ($0.5*(aheight)+0.4*(awidth)$);
\coordinate[] (tilt) at ($0.65*(aheight)+0.75*(awidth)$);
\coordinate[] (hexapod) at ($0.7*(aheight)+0.5*(awidth)$);
\coordinate[] (sample) at ($0.9*(aheight)+0.55*(awidth)$);
% Granite
\node[labelc] at (granite) {1};
% Translation stage
\node[labelc] at (trans) {2};
% Tilt Stage
\node[labelc] at (tilt) {3};
% Micro-Hexapod
\node[labelc] at (hexapod) {4};
% Sample
\node[labelc] at (sample) {5};
% Axis
\begin{scope}[shift={($0.07*(aheight)+0.87*(awidth)$)}]
\draw[->] (0, 0) -- ++(55:0.7) node[above] {$y$};
\draw[->] (0, 0) -- ++(90:0.9) node[left] {$z$};
\draw[->] (0, 0) -- ++(-20:0.7) node[above] {$x$};
\end{scope}
\end{tikzpicture}Positioning End Station: The Micro-Station
Micro-Station:
- DoF with strokes: Ty, Ry, Rz, Hexapod
- Experiments: tomography, reflectivity, truncation rod, … Make a table to explain the different "experiments"
- Explain how it is used (positioning, scans), what it does. But not about the performances
- Different sample environments
\begin{tikzpicture}
% Parameters
\def\blockw{6.0cm}
\def\blockh{1.2cm}
\def\tiltdeg{3}
\coordinate[] (rotationpoint) at (0, 4.5*\blockh);
\begin{scope}[rotate around={\tiltdeg:(rotationpoint)}]
% Tilt
\path[] ([shift=(-120:4*\blockh)]rotationpoint) coordinate(beginarc) arc (-120:-110:4*\blockh) %
-- ([shift=(-70:4*\blockh)]rotationpoint) arc (-70:-60:4*\blockh)%
|- ++(-0.15*\blockw, 0.6*\blockh) coordinate (spindlene)%
|- ($(beginarc) + (0.15*\blockw, 0.2*\blockh)$) coordinate (spindlesw) -- ++(0, 0.4*\blockh) coordinate(tiltte) -| cycle;
% Spindle
\coordinate[] (spindlese) at (spindlesw-|spindlene);
\draw[fill=black!30] ($(spindlese)+(-0.1,0.1)+(-0.1*\blockw, 0)$) -| ($(spindlene)+(-0.1, 0)$) -| coordinate[pos=0.25](spindletop) ($(spindlesw)+(0.1,0.1)$) -| ++(0.1*\blockw, -\blockh) -| coordinate[pos=0.25](spindlebot) cycle;
% \draw[dashed, color=black!60] ($(spindletop)+(0, 0.2)$) -- ($(spindlebot)+(0,-0.2)$);
% Tilt
\draw[fill=black!60] ([shift=(-120:4*\blockh)]rotationpoint) coordinate(beginarc) arc (-120:-110:4*\blockh) %
-- ([shift=(-70:4*\blockh)]rotationpoint) arc (-70:-60:4*\blockh)%
|- coordinate (tiltne) ++(-0.15*\blockw, 0.6*\blockh) coordinate (spindlene)%
|- ($(beginarc) + (0.15*\blockw, 0.2*\blockh)$) coordinate (spindlesw) -- ++(0, 0.4*\blockh) -| cycle;
% Micro-Hexapod
\begin{scope}[shift={(spindletop)}]
% Parameters definitions
\def\baseh{0.22*\blockh} % Height of the base
\def\naceh{0.18*\blockh} % Height of the nacelle
\def\baser{0.22*\blockw} % Radius of the base
\def\nacer{0.18*\blockw} % Radius of the nacelle
\def\armr{0.2*\blockh} % Radius of the arms
\def\basearmborder{0.2}
\def\nacearmborder{0.2}
\def\xnace{0} \def\ynace{\blockh-\naceh} \def\anace{0}
\def\xbase{0} \def\ybase{0} \def\abase{0}
% Hexapod1
\begin{scope}[shift={(\xbase, \ybase)}, rotate=\abase]
% Base
\draw[fill=white] (-\baser, 0) coordinate[](uhexabot) rectangle (\baser, \baseh);
\coordinate[] (armbasel) at (-\baser+\basearmborder+\armr, \baseh);
\coordinate[] (armbasec) at (0, \baseh);
\coordinate[] (armbaser) at (\baser-\basearmborder-\armr, \baseh);
\begin{scope}[shift={(\xnace, \ynace)}, rotate=\anace]
\draw[fill=white] (-\nacer, 0) rectangle (\nacer, \naceh);
\coordinate[] (uhexatop) at (0, \naceh);
\coordinate[] (armnacel) at (-\nacer+\nacearmborder+\armr, 0);
\coordinate[] (armnacec) at (0, 0);
\coordinate[] (armnacer) at (\nacer-\nacearmborder-\armr, 0);
\end{scope}
\draw[] (armbasec) -- (armnacer);
\draw[] (armbasec) -- (armnacel);
\draw[] (armbasel) -- coordinate(mhexaw) (armnacel);
\draw[] (armbasel) -- (armnacec);
\draw[] (armbaser) -- (armnacec);
\draw[] (armbaser) -- coordinate(mhexae) (armnacer);
\end{scope}
\end{scope}
% Sample
\begin{scope}[shift={(uhexatop)}]
\draw[fill=white] (-0.1*\blockw, 0) coordinate[](samplebot) rectangle coordinate[pos=0.5](samplecenter) node[pos=0.5, above]{Sample} (0.1*\blockw, \blockh) coordinate[](samplene);
\coordinate[](samplenw) at (-0.1*\blockw, \blockh);
\end{scope}
\end{scope}
\begin{scope}[shift={(0, -0.3*\blockh)}]
% Translation Stage - fixed part
\draw[fill=black!40] (-0.5*\blockw, 0) coordinate[](tyb) rectangle (0.5*\blockw, 0.15*\blockh);
\coordinate[] (measposbot) at (0.5*\blockw, 0);
% Translation Stage - mobile part
\draw[fill=black!10, fill opacity=0.5] (-0.5*\blockw, 0.2*\blockh) -- (-0.5*\blockw, 1.5*\blockh) coordinate[](tyt) -- (0.5*\blockw, 1.5*\blockh) -- (0.5*\blockw, 0.2*\blockh) -- (0.35*\blockw, 0.2*\blockh) -- (0.35*\blockw, 0.8*\blockh) -- (-0.35*\blockw, 0.8*\blockh) -- (-0.35*\blockw, 0.2*\blockh) -- cycle;
% Translation Guidance
\draw[dashed, color=black!60] ($(-0.5*\blockw, 0)+( 0.075*\blockw,0.5*\blockh)$) circle (0.2*\blockh);
\draw[dashed, color=black!60] ($( 0.5*\blockw, 0)+(-0.075*\blockw,0.5*\blockh)$) circle (0.2*\blockh);
% Tilt Guidance
\draw[dashed, color=black!60] ([shift=(-107:4.1*\blockh)]rotationpoint) arc (-107:-120:4.1*\blockh);
\draw[dashed, color=black!60] ([shift=( -73:4.1*\blockh)]rotationpoint) arc (-73:-60:4.1*\blockh);
\end{scope}
% % Vertical line
% \draw[dashed, color=black] (samplecenter) -- ++(0, -4*\blockh);
% \begin{scope}[rotate around={\tiltdeg:(samplecenter)}]
% \draw[dashed, color=black] (samplecenter) -- ++(0, -4*\blockh);
% \node[] at ($(samplecenter)+(0, -2.3*\blockh)$) {\AxisRotator[rotate=-90]};
% \node[right, shift={(0.3,0)}] at ($(samplecenter)+(0, -2.3*\blockh)$) {$\theta_z$};
% \end{scope}
% \draw[->] ([shift=(-90:3.6*\blockh)]samplecenter) arc (-90:-87:3.6*\blockh) node[right]{$\theta_y$};
% Laser
\begin{scope}[shift={(samplecenter)}]
\draw[color=red, -<-=0.3] (samplecenter) node[circle, fill=red, inner sep=0pt, minimum size=3pt]{} -- node[pos=0.3, above, color=black]{X-ray} ($(samplecenter)+(1.2*\blockw,0)$);
\end{scope}
% Axis
\begin{scope}[shift={(-0.35*\blockw, 3*\blockh)}]
\def\axissize{0.8cm}
\draw[->] (0, 0) -- ++(0, \axissize) node[right]{$z$};
\draw[->] (0, 0) -- ++(-\axissize, 0) node[above]{$x$};
\draw[fill, color=black] (0, 0) circle (0.05*\axissize);
\node[draw, circle, inner sep=0pt, minimum size=0.4*\axissize, label=right:$y$] (yaxis) at (0, 0){};
% \node[draw, circle, inner sep=0pt, cross, minimum size=0.4*\axissize, label=left:$y$] (yaxis) at (0, 0){};
\end{scope}
\node[fit={($(-0.6*\blockw, -0.5*\blockh)$) ($(0.6*\blockw, 4*\blockh)$)}, inner sep=0pt, draw, dashed, color=gray, label={Positioning Station}] (possystem) {};
\draw[fill=black!30] ($(tyb)+(-5, -1)$) coordinate[](granitesw) rectangle node[pos=0.5]{Granite Frame} ($(measposbot)+(5, 0)$) coordinate[](granitene);
% Focusing Optics
\draw[fill=black!20] ($(granitene)+(-1.5, 3)$) rectangle ++(-1, 2);
\draw[spring] ($(granitene)+(-2, 0)$) -- ++(0, 3);
\node[fit={($(granitene)+(-2.8, -0.2)$) ($(granitene)+(-1.2, 5.2)$)}, inner sep=0pt, draw, dashed, color=gray, label={Focusing Optics}] () {};
% Measurement Optics
\draw[fill=black!20] ($(granitesw)+(1.5, 4)$) rectangle ++(1, 2);
\draw[spring] ($(granitesw)+(2, 1)$) -- ++(0, 3);
\node[fit={($(granitesw)+(2.8, 0.8)$) ($(granitesw)+(1.2, 6.2)$)}, inner sep=0pt, draw, dashed, color=gray, label={Imagery System}] () {};
\end{tikzpicture}- Alternative:
id31_microstation_cad_view.png(CAD view)
Science performed on ID31
- Few words about science made on ID31 and why nano-meter accuracy is required
-
Typical experiments (tomography, …), various samples (up to 50kg), sample environments (high temp, cryo, etc..)
- Alignment of the sample, then
- Reflectivity
- Tomography
- Diffraction tomography: most critical
- Example of picture obtained (Figure ref:fig:introduction_id31_tomography_result) with resolution
introduction_exp_scanning and introduction_exp_scanning_image
Need of accurate positioning end stations with high dynamics
A push towards brighter and smaller beams…
Improvement of both the light source and the instrumentation:
- EBS: smaller source + higher flux ref:fig:introduction_beam_ebs

- Better focusing optic (add some links): beam size in the order of 10 to 20nm FWHM (reference) ref:fig:introduction_moore_law_focus crossed silicon compound refractive lenses, KB mirrors [17], zone plates [18], or multilayer Laue lenses [19] cite:&barrett16_reflec_optic_hard_x_ray

Higher flux density (+high energy of the ID31 beamline) => Radiation damage: needs to scan the sample quite fast with respect to the focused beam
- Allowed by better detectors: higher sampling rates and lower noise => possible to scan fast cite:&hatsui15_x_ray_imagin_detec_synch_xfel_sourc
…Requires the use of dynamical positioning
"from traditional step by step scans to fly-scan"
Fast scans + needs of high accuracy and stability => need mechatronics system with:
- accurate metrology
- multi degree of freedom positioning systems
- fast feedback loops
Shift from step by step scan to fly-scan cite:huang15_fly_scan_ptych
- Much lower pixel size + large image => takes of lot of time if captured step by step. Explain what is step by step scanning: move motors from point A to point B, stops, start detector acquisition, open shutter , close the shutter, move to point C, …
In traditional step scan mode, each exposure position requires the system to stop prior to data acquisition, which may become a limiting factor when fast data collection is required. Fly-scanning is chosen as a preferred solution that helps overcome such speed limitations [5, 6]. In fly-scan mode, the sample keeps moving and a triggering system generates trigger signals based on the position of the sample or the time elapsed. The trigger signals are used to control detector exposure.
-
Make picture representing a typical experiment (maybe YZ scan?) with: Probably already shown earlier
introduction_exp_scanning- nano focusing optics (see the beam focused)
- positioning stage with displayed YZ motion (pixel by pixel in the YZ plane)
- detector
Subject of this thesis: design of high performance positioning station with high dynamics and nanometer accuracy
Challenge definition
Multi DoF, Highly accurate, and Long stroke positioning end station?
Performance limitation of "stacked stages" end-stations
Typical positioning end station:
- stacked stages
- ballscrew, linear guides, rotary motor
Explain the limitation of performances:
- Backlash, play, thermal expansion, guiding imperfections, …
- Give some numbers: straightness of the Ty stage for instance, change of $0.1^oC$ with steel gives x nm of motion
- Vibrations
- Explain that this micro-station can only have ~10um of accuracy due to physical limitation
- Possibility to have linear/rotary encoders that correct the motion in the considered DoF, but does not change anything to the other 5DoF
Talk about flexure based positioning stations? Advantages: no backlash, etc… But: limited to short stroke Picture of schematic of one positioning station based on flexure
The ID31 Micro-Station
Presentation of the Micro-Station in details ref:fig:introduction_id31_microstation_cad:
- Goal of each stage (e.g. micro-hexapod: static positioning, Ty and Rz: scans, …)
- Stroke
- Initial design objectives: as stiff as possible, smallest errors as possible
New positioning requirements
- To benefits from nano-focusing optics, new source, etc… new positioning requirements
-
Positioning requirements on ID31:
- Maybe make a table with the requirements and the associated performances of the micro-station
- Make tables with the wanted motion, stroke, accuracy in different DoF, etc..
- Sample masses
The goal in this thesis is to increase the positioning accuracy of the micro-station to fulfil the initial positioning requirements.
Goal: Improve accuracy of 6DoF long stroke position platform
The Nano Active Stabilization System
NASS Concept
Briefly describe the NASS concept. 4 parts:
- Micro Station
- multi-DoF positioning system with good dynamics
- 5DoF metrology system
- Control system and associated instrumentation
6DoF vibration control platform on top of a complex positioning platform that correct positioning errors based on an external metrology
- Add the control system in the schematic
Metrology system
Requirements:
- 5 DoF
- long stroke
- nano-meter accurate
- high bandwidth
The accuracy of the NASS will only depend on the accuracy of the metrology system.
Concept:
- Fiber interferometers
- Spherical reflector with flat bottom
- Tracking system
Complex mechatronics system on its own.
This metrology system is not further discussed in this thesis as it is still under active development.
In the following of this thesis, it is supposed that the metrology system is accurate, etc..
- Say that there are several high precision sensors, but only interferometers for long stroke / high accuracy?
Multi-DoF Positioning stage for error compensation
- 5 DoF
- High dynamics
- nano-meter capable (no backlash,)
- Accept payloads up to 50kg
MIMO robust control strategies
Explain the robustness need?
- 24 7/7 …
- That is why most of end-stations are based on well-proven design (stepper motors, linear guides, ball bearing, …)
- Plant uncertainty: many different samples, use cases, rotating velocities, etc…
Trade-off between robustness and performance in the design of feedback system.
Predictive Design
-
The performances of the system will depend on many factors:
- sensors
- actuators
- mechanical design
- achievable bandwidth
- …
- Need to evaluate the different concepts, and predict the performances to guide the design
- The goal is to design, built and test this system such that it work as expected the first time. Very costly system, so much be correct.
Control Challenge
High bandwidth, 6 DoF system for vibration control, fixed on top of a complex multi DoF positioning station, robust, …
- Many different configurations (tomography, Ty scans, slow fast, …)
- Complex MIMO system. Dynamics of the system could be coupled to the complex dynamics of the micro station
- Rotation aspect, gyroscopic effects, actuators are rotating with respect to the sensors
- Robustness to payload change: very critical. Say that high performance systems (lithography machines, etc…) works with calibrated payloads. Being robust to change of payload inertia means large stability margins and therefore less performance.
Literature Review
Nano Positioning end-stations
End Station with Stacked Stages
Stacked stages:
- errors are combined
To have acceptable performances / stability:
- limited number of stages
- high performances stages (air bearing etc…)
Examples:
- ID16b cite:&martinez-criado16_id16b
- ID13 cite:&riekel10_progr_micro_nano_diffr_at
- ID11 cite:wright20_new_oppor_at_mater_scien
- ID01 cite:&leake19_nanod_beaml_id01
- Maybe make a table to compare stations
Explain limitations => Thermal drifts, run-out errors of spindles (improved by using air bearing), straightness of translation stages, …
Online Metrology and Active Control of Positioning Errors
The idea of having an external metrology to correct for errors is not new.
- To have even better performances: online metrology are required.
-
Several strategies:
- only used for measurements (post processing)
- for calibration
- for triggering detectors
- for real time positioning control
- HXN cite:&xu23_high_nsls_ii Laser interferometers on reference ring (on top of rotary stage). Used to trigger the detectors (ptychography, microscope) Similar to cite:&wang12_autom_marker_full_field_hard
| Architecture | Sensors and measured DoFs | Actuators and controlled DoFs | Institute, BL | OL/CL (bandwidth) | Stroke, DoF | Samples | Ref |
|---|---|---|---|---|---|---|---|
| XYZ, Spherical retroreflector, Sample | 3 interferometers1, Y,Z | YZ piezo stages | PETRA III, P06 | OL | 100um | light | cite:&schroer17_ptynam;&schropp20_ptynam |
| Spindle / Metrology Ring / XYZ Stage / Sample | 3 Capacitive, Y,Z,Rx | NSLS, X8C | OL, post processing | micron scale | cite:&wang12_autom_marker_full_field_hard | ||
| Hexapod / Spindle / Metrology Ring / Sample | 12 Capacitive2, X,Y,Z,Rx,Ry | Piezo (Hexapod) | ESRF, ID16a | CL, 10Hz bandwidth | 50um, 500urad | light | cite:&villar18_nanop_esrf_id16a_nano_imagin_beaml |
| XYZ, Rz, XY, Cylindrical reference | 5 interferometers3, X,Y,Z,Rx,Ry | XYZ linear motors | Soleil | CL | light | cite:&engblom18_nanop_resul;&stankevic17_inter_charac_rotat_stages_x_ray_nanot | |
| XYZ, Rz, XYZ Spherical reference | 3 Interferometers4, Y,Z,Rx | XYZ parallel piezo stage | PSI, OMNY | CL | 400um | light | cite:&holler18_omny_tomog_nano_cryo_stage;&holler17_omny_pin_versat_sampl_holder |
| XYZ, mirrors/sample | 3 interferometers3, XYZ | XYZ piezo stage | APS | CL, 3 PID | 3mm | light | cite:&nazaretski15_pushin_limit |
| Rz, Parallel XYZ stage | 3 interferometers1 | 3xVCM parallel stage | LNLS, CARNAUBA | CL, 100Hz bandwidth | YZ: 3mm, Rz: +-110deg | light | cite:&geraldes23_sapot_carnaub_sirius_lnls |
| Parallel XYZ stage | 3 interferometers4, XYZ | 3xVCM parallel stage | Diamond, I14 | CL, 100Hz bandwidth | XYZ: 3mm | up to 350g | cite:&kelly22_delta_robot_long_travel_nano |
- Figure with different stages
- Compared to the existing stages (see table), what are the challenges here? Rotation, large stroke, light to heavy payloads, lots of DoF (5 to be controlled)
- Comparison with NASS?
| Architecture | Sensors | Actuators | Institute, BL | OL/CL (bandwidth) | Stroke, DoF | Samples | Ref |
|---|---|---|---|---|---|---|---|
| Ty,Ry,Rz,Hexapod,Sample | 6+ Interferometers | ESRF, ID31 | CL | Ty, Ry, Rz, Hexa | up to 50kg |
Long Stroke - Short Stroke architecture
Speak about two stage control?
- Long stroke + short stroke
- Usually applied to 1dof, 3dof (show some examples: disk drive, wafer scanner)
- Any application in 6DoF? Maybe new!
- In the table, say which ones are long stroke / short stroke. Some new stages are just long stroke (voice coil)
Multi-DoF dynamical positioning stations
Serial and Parallel Kinematics
Example of several dynamical stations:
- XYZ piezo stages
- Delta robot? Octoglide?
- Stewart platform
Serial vs parallel kinematics (table?)
Mechatronics approach
Predicting performances using models
-
cite:&monkhorst04_dynam_error_budget
high costs of the design process: the designed system must be first time right. When the system is finally build, its performance level should satisfy the specifications. No significant changes are allowed in the post design phase. Because of this, the designer wants to be able to predict the performance of the system a-priori and gain insight in the performance limiting factors of the system.
Can use several models:
- Lumped mass-spring-damper models cite:rankers98_machin
- Multi-Body Models
- Finite element models Sub structuring?
Closed-Loop Simulations
cite:&schmidt20_desig_high_perfor_mechat_third_revis_edition
Say what can limit the performances for a complex mechatronics systems as this one:
- disturbances
- measurement noise
- DAC / amplifier noise (actuator)
- feedback system / bandwidth
Simulations can help evaluate the behavior of the system.
Dynamic Error Budgeting
-
cite:&monkhorst04_dynam_error_budget
high costs of the design process: the designed system must be first time right. When the system is finally build, its performance level should satisfy the specifications. No significant changes are allowed in the post design phase. Because of this, the designer wants to be able to predict the performance of the system a-priori and gain insight in the performance limiting factors of the system.
- cite:jabben07_mechat
-
cite:&okyay16_mechat_desig_dynam_contr_metrol
Error budgets [23] are frequently used in the design of precision machines, in order to assess the contributions of different factors such as parasitic motions, thermal expansion, and servo accuracy, on the positioning accuracy of a machine. Dynamic Error Budgeting (DEB) or ‘Spectral Analysis’ extends this concept to the realm of feedback control. Recognizing that the controller can provide only a finite attenuation of disturbance signals interfering with the servo, DEB provides a methodology for predicting the cumulative effect of such signals on the control error as a function of their spectral (frequency) content. The method can be used to predict the control accuracy of a system implemented using a set of certain devices under certain conditions before it is realized. Furthermore, as it is formulated in the frequency domain, it can be used to optimize the controller design as well, typically leading to an H2 - optimal control framework. In DEB, the disturbance signals are modeled with their power spectral density (PSD), assuming that they are stationary stochastic processes which are not correlated with each other. Then, these PSD’s are transmitted to the performance goal, most often the positioning error, using linear time invariant (LTI) system theory. The transmitted PSD’s are summed up into the variance of the performance goal, which constitutes a comparative measure of performance. Most importantly, the influence of different dynamic factors and disturbance sources, which have the greatest impact on the achievable performance (e.g., accuracy) can be easily spotted and improved, through this kind of analysis. An approach similar to DEB was followed to decompose the contribution of different noise sources on the hard disk position error in [1], [2], [45]. DEB has been used to assess the performance of a geophone and a vibration isolation system in [75]. Jabben [49] has used DEB in the mechatronic design of a magnetically suspended rotating platform. Aguirre et al. [3] have analyzed the performance of active aerostatic thrust bearings using DEB.
TODO Control architecture
Maybe make a simple review of control strategies for Stewart platform control.
Original Contributions
Introduction ignore
This thesis proposes several contributions in the fields of Control, Mechatronics Design and Experimental validation.
Active Damping of rotating mechanical systems using Integral Force Feedback
cite:&dehaeze20_activ_dampin_rotat_platf_integ_force_feedb;&dehaeze21_activ_dampin_rotat_platf_using
This paper investigates the use of Integral Force Feedback (IFF) for the active damping of rotating mechanical systems. Guaranteed stability, typical benefit of IFF, is lost as soon as the system is rotating due to gyroscopic effects. To overcome this issue, two modifications of the classical IFF control scheme are proposed. The first consists of slightly modifying the control law while the second consists of adding springs in parallel with the force sensors. Conditions for stability and optimal parameters are derived. The results reveal that, despite their different implementations, both modified IFF control scheme have almost identical damping authority on the suspension modes.
Design of complementary filters using $\mathcal{H}_\infty$ Synthesis and sensor fusion
cite:&dehaeze19_compl_filter_shapin_using_synth cite:&verma20_virtual_sensor_fusion_high_precis_contr cite:&tsang22_optim_sensor_fusion_method_activ
- Several uses (link to some papers).
- For the NASS, they could be use to further improve the robustness of the system.
Multi-body simulations with reduced order flexible bodies obtained by FEA
cite:&brumund21_multib_simul_reduc_order_flexib_bodies_fea
Combined multi-body / FEA techniques and experimental validation on a Stewart platform containing amplified piezoelectric actuators Super-element of amplified piezoelectric actuator / combined multibody-FEA technique, experimental validation on an amplified piezoelectric actuator and further validated on a complete stewart platform
We considered sub-components in the multi-body model as reduced order flexible bodies representing the component’s modal behaviour with reduced mass and stiffness matrices obtained from finite element analysis (FEA) models. These matrices were created from FEA models via modal reduction techniques, more specifically the component mode synthesis (CMS). This makes this design approach a combined multibody-FEA technique. We validated the technique with a test bench that confirmed the good modelling capabilities using reduced order flexible body models obtained from FEA for an amplified piezoelectric actuator (APA).
Robustness by design
- Design of a Stewart platform and associated control architecture that is robust to large plant uncertainties due to large variety of payload and experimental conditions.
- Instead of relying on complex controller synthesis (such as $\mathcal{H}_\infty$ synthesis or $\mu\text{-synthesis}$) to guarantee the robustness and performance.
- The approach here is to choose an adequate architecture (mechanics, sensors, actuators) such that controllers are robust by nature.
- Example: collocated actuator/sensor pair => controller can easily be made robust
- This is done by using models and using HAC-LAC architecture
Mechatronics design
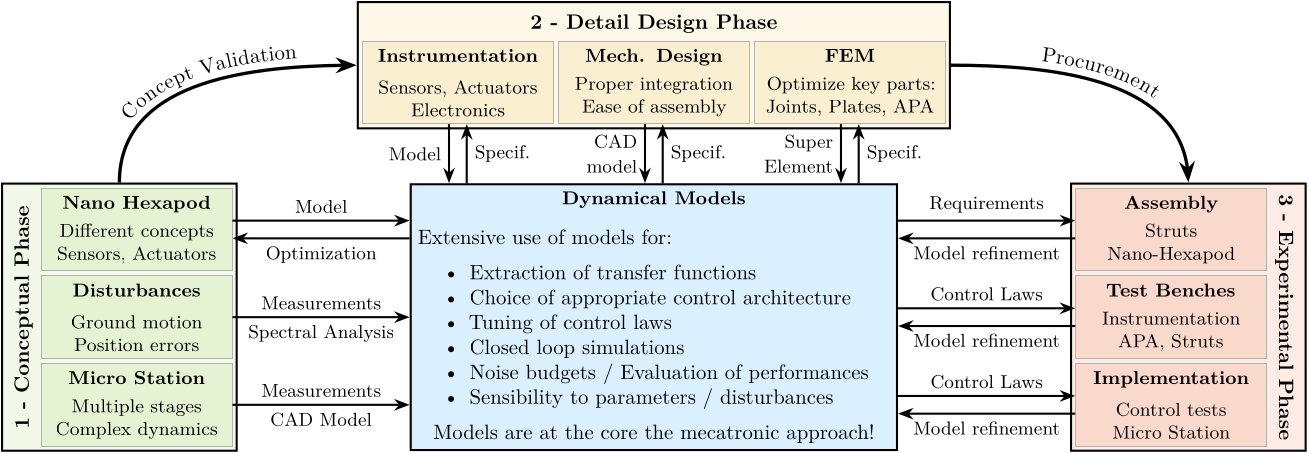
Conduct a rigorous mechatronics design approach for a nano active stabilization system cite:&dehaeze18_sampl_stabil_for_tomog_exper;&dehaeze21_mechat_approac_devel_nano_activ_stabil_system
Approach from start to finish:
- From first concepts using basic models, to concept validation
- Detailed design phase
- Experimental phase
Complete design with clear choices based on models. Such approach, while not new, is here applied This can be used for the design of future end-stations.
% \graphicspath{ {/home/thomas/Cloud/thesis/papers/dehaeze21_mechatronics_approach_nass/tikz/figs-tikz} }
\begin{tikzpicture}
% Styles
\tikzset{myblock/.style= {draw, thin, color=white!70!black, fill=white, text width=3cm, align=center, minimum height=1.4cm}};
\tikzset{mylabel/.style= {anchor=north, below, font=\bfseries\small, color=black, text width=3cm, align=center}};
\tikzset{mymodel/.style= {anchor=south, above, font=\small, color=black, text width=3cm, align=center}};
\tikzset{mystep/.style= {->, ultra thick}};
% Blocks
\node[draw, fill=lightblue, align=center, label={[mylabel, text width=8.0cm] Dynamical Models}, minimum height = 4.5cm, text width = 8.0cm] (model) at (0, 0) {};
\node[myblock, fill=lightgreen, label={[mylabel] Disturbances}, left = 3 of model.west] (dist) {};
\node[myblock, fill=lightgreen, label={[mylabel] Micro Station}, below = 2pt of dist] (mustation) {};
\node[myblock, fill=lightgreen, label={[mylabel] Nano Hexapod}, above = 2pt of dist] (nanohexapod) {};
\node[myblock, fill=lightyellow, label={[mylabel] Mech. Design}, above = 1 of model.north] (mechanical) {};
\node[myblock, fill=lightyellow, label={[mylabel] Instrumentation}, left = 2pt of mechanical] (instrumentation) {};
\node[myblock, fill=lightyellow, label={[mylabel] FEM}, right = 2pt of mechanical] (fem) {};
\node[myblock, fill=lightred, label={[mylabel] Test Benches}, right = 3 of model.east] (testbenches) {};
\node[myblock, fill=lightred, label={[mylabel] Assembly}, above = 2pt of testbenches] (mounting) {};
\node[myblock, fill=lightred, label={[mylabel] Implementation}, below = 2pt of testbenches] (implementation) {};
% Text
\node[anchor=south, above, text width=8cm, align=left] at (model.south) {Extensive use of models for:\begin{itemize}[noitemsep,topsep=5pt]\item Extraction of transfer functions \\ \item Choice of appropriate control architecture \\ \item Tuning of control laws \\ \item Closed loop simulations \\ \item Noise budgets / Evaluation of performances \\ \item Sensibility to parameters / disturbances\end{itemize}\centerline{Models are at the core the mecatronic approach!}};
\node[mymodel] at (mustation.south) {Multiple stages \\ Complex dynamics};
\node[mymodel] at (dist.south) {Ground motion \\ Position errors};
\node[mymodel] at (nanohexapod.south) {Different concepts \\ Sensors, Actuators};
\node[mymodel] at (instrumentation.south) {Sensors, Actuators \\ Electronics};
\node[mymodel] at (mechanical.south) {Proper integration \\ Ease of assembly};
\node[mymodel] at (fem.south) {Optimize key parts: \\ Joints, Plates, APA};
\node[mymodel] at (mounting.south) {Struts \\ Nano-Hexapod};
\node[mymodel] at (testbenches.south) {Instrumentation \\ APA, Struts};
\node[mymodel] at (implementation.south) {Control tests \\ Micro Station};
% Links
\draw[->] (dist.east) -- node[above, midway]{{\small Measurements}} node[below,midway]{{\small Spectral Analysis}} (dist.east-|model.west);
\draw[->] (mustation.east) -- node[above, midway]{{\small Measurements}} node[below, midway]{{\small CAD Model}} (mustation.east-|model.west);
\draw[->] ($(nanohexapod.east-|model.west)-(0, 0.15)$) -- node[below, midway]{{\small Optimization}} ($(nanohexapod.east)-(0, 0.15)$);
\draw[<-] ($(nanohexapod.east-|model.west)+(0, 0.15)$) -- node[above, midway]{{\small Model}} ($(nanohexapod.east)+(0, 0.15)$);
\draw[->] ($(fem.south|-model.north)+(0.15, 0)$) -- node[right, midway]{{\small Specif.}} ($(fem.south)+(0.15,0)$);
\draw[<-] ($(fem.south|-model.north)-(0.15, 0)$) -- node[left, midway,align=right]{{\small Super}\\{\small Element}} ($(fem.south)-(0.15,0)$);
\draw[->] ($(mechanical.south|-model.north)+(0.15, 0)$) -- node[right, midway]{{\small Specif.}} ($(mechanical.south)+(0.15,0)$);
\draw[<-] ($(mechanical.south|-model.north)-(0.15, 0)$) -- node[left, midway,align=right]{{\small CAD}\\{\small model}} ($(mechanical.south)-(0.15,0)$);
\draw[->] ($(instrumentation.south|-model.north)+(0.15, 0)$) -- node[right, midway]{{\small Specif.}} ($(instrumentation.south)+(0.15,0)$);
\draw[<-] ($(instrumentation.south|-model.north)-(0.15, 0)$) -- node[left, midway]{{\small Model}} ($(instrumentation.south)-(0.15,0)$);
\draw[->] ($(mounting.west-|model.east)+(0, 0.15)$) -- node[above, midway]{{\small Requirements}} ($(mounting.west)+(0, 0.15)$);
\draw[<-] ($(mounting.west-|model.east)-(0, 0.15)$) -- node[below, midway]{{\small Model refinement}} ($(mounting.west)-(0, 0.15)$);
\draw[->] ($(testbenches.west-|model.east)+(0, 0.15)$) -- node[above, midway]{{\small Control Laws}} ($(testbenches.west)+(0, 0.15)$);
\draw[<-] ($(testbenches.west-|model.east)-(0, 0.15)$) -- node[below, midway]{{\small Model refinement}} ($(testbenches.west)-(0, 0.15)$);
\draw[->] ($(implementation.west-|model.east)+(0, 0.15)$) -- node[above, midway]{{\small Control Laws}} ($(implementation.west)+(0, 0.15)$);
\draw[<-] ($(implementation.west-|model.east)-(0, 0.15)$) -- node[below, midway]{{\small Model refinement}} ($(implementation.west)-(0, 0.15)$);
% Main steps
\node[font=\bfseries, rotate=90, anchor=south, above] (conceptual_phase_node) at (dist.west) {1 - Conceptual Phase};
\node[font=\bfseries, above] (detailed_phase_node) at (mechanical.north) {2 - Detail Design Phase};
\node[font=\bfseries, rotate=-90, anchor=south, above] (implementation_phase_node) at (testbenches.east) {3 - Experimental Phase};
\begin{scope}[on background layer]
\node[fit={(conceptual_phase_node.north|-nanohexapod.north) (mustation.south east)}, fill=lightgreen!50!white, draw, inner sep=2pt] (conceptual_phase) {};
\node[fit={(detailed_phase_node.north-|instrumentation.west) (fem.south east)}, fill=lightyellow!50!white, draw, inner sep=2pt] (detailed_phase) {};
\node[fit={(implementation_phase_node.north|-mounting.north) (implementation.south west)}, fill=lightred!50!white, draw, inner sep=2pt] (implementation_phase) {};
% \node[above left] at (dob.south east) {DOB};
\end{scope}
% Between main steps
\draw[mystep, postaction={decorate,decoration={raise=1ex,text along path,text align=center,text={Concept Validation}}}] (conceptual_phase.north) to[out=90, in=180] (detailed_phase.west);
\draw[mystep, postaction={decorate,decoration={raise=1ex,text along path,text align=center,text={Procurement}}}] (detailed_phase.east) to[out=0, in=90] (implementation_phase.north);
% % Inside Model
% \node[inner sep=1pt, outer sep=6pt, anchor=north west, draw, fill=white, thin] (multibodymodel) at ($(model.north west) - (0, 0.5)$)
% {\includegraphics[width=5.6cm]{simscape_nano_hexapod.png}};
% \node[inner sep=1pt, outer sep=6pt, anchor=south west, draw, fill=white, thin] (simscape) at (model.south west)
% {\includegraphics[width=5.6cm]{simscape_picture.jpg}};
% % Feedback Model
% \node[inner sep=3pt, outer sep=6pt, anchor=north east, draw, fill=white, thin] (simscape_sim) at ($(model.north east) - (0, 0.5)$)
% {\includegraphics[width=3.6cm]{simscape_simulations.pdf}};
% % FeedBack
% \node[inner sep=3pt, outer sep=6pt, anchor=south east, draw, fill=white, thin] (feedback) at (model.south east)
% {\includegraphics[width=3.6cm]{classical_feedback_small.pdf}};
\end{tikzpicture}6DoF vibration control of a rotating platform
Vibration control in 5DoF of a rotating stage To the author's knowledge, the use of a continuously rotating stewart platform for vibration control has not been proved in the literature.
Experimental validation of the Nano Active Stabilization System
Demonstration of the improvement of the the positioning accuracy of a complex multi DoF (the micro-station) by several orders of magnitude (Section …) using …
Thesis Outline - Mechatronics Design Approach
Introduction ignore
Conceptual design development
- Start with simple models for witch trade offs can be easily understood (uniaxial)
- Increase the model complexity if important physical phenomenon are to be modelled (cf the rotating model)
- Only when better understanding of the physical effects in play, and only if required, go for higher model complexity (here multi-body model)
- The system concept and main characteristics should be extracted from the different models and validated with closed-loop simulations with the most accurate model
- Once the concept is validated, the chosen concept can be design in mode details
Detailed design
- During this detailed design phase, models are refined from the obtained CAD and using FEM
- The models are used to assists the design and to optimize each element based on dynamical analysis and closed-loop simulations
- The requirements for all the associated instrumentation can be determined from a dynamical noise budgeting
- After converging to a detailed design that give acceptable performance based on the models, the different parts can be ordered and the experimental phase begins
Experimental validation
- It is advised that the important characteristics of the different elements are evaluated individually Systematic validation/refinement of models with experimental measurements
- The obtained characteristics can be used to refine the models
- Then, an accurate model of the system is obtained which can be used during experimental tests (for control synthesis for instance)