98 KiB
Nano Active Stabilization System - Instrumentation
- Introduction
- Dynamic Error Budgeting
- Choice of Instrumentation
- Characterization of Instrumentation
- Conclusion
- Bibliography
- Footnotes
Introduction ignore
The goal is to show that each element in the system has been properly chosen based on certain requirements.
In order to determine the maximum noise of each instrumentation, a dynamic error budgeting is performed in Section ref:sec:instrumentation_dynamic_error_budgeting.
The required instrumentation are then selected based on obtained noise specifications and other requirements summarized in Section ref:sec:detail_instrumentation_choice.
The received instrumentation are characterized in Section ref:sec:detail_instrumentation_characterization.
- Say the the real time controller is a Speedgoat machine, as it is the standard real time controller used at the ESRF
\begin{tikzpicture}
% Blocs
\node[block={2.0cm}{2.0cm}, align=center] (plant) {NASS};
\coordinate[] (inputVa) at ($(plant.south west)!0.5!(plant.north west)$);
\coordinate[] (outputVs) at ($(plant.south east)!0.7!(plant.north east)$);
\coordinate[] (outputde) at ($(plant.south east)!0.3!(plant.north east)$);
\node[addb={+}{}{}{}{}, left=0.8 of inputVa] (ampl_noise) {};
\node[block={1.0cm}{1.0cm}, left=0.4 of ampl_noise] (ampl_tf) {$G_{\text{ampl}}$};
\node[addb={+}{}{}{}{}, left=0.8 of ampl_tf] (dac_noise) {};
\node[DAC, left=0.4 of dac_noise] (dac_tf) {};
\node[addb={+}{}{}{}{}, left=1.0 of dac_tf] (iff_sum) {};
\node[block={1.0cm}{1.0cm}, above=0.4 of iff_sum] (Kiff) {$\bm{K}_{\text{IFF}}$};
\node[block={1.0cm}{1.0cm}, left=0.4 of iff_sum] (Khac) {$\bm{K}_{\text{HAC}}$};
\node[addb={+}{}{}{}{}, right=0.8 of outputVs] (adc_noise) {};
\node[ADC, right=0.4 of adc_noise] (adc_tf) {};
\draw[->] (iff_sum.east) --node[midway, above]{$\bm{u}$} node[near start, sloped]{$/$} (dac_tf.west);
\draw[->] (dac_tf.east) -- (dac_noise.west);
\draw[->] (dac_noise.east) -- (ampl_tf.west);
\draw[->] (ampl_tf.east) -- (ampl_noise.west);
\draw[->] (ampl_noise.east) -- (inputVa)node[above left]{$\bm{V}_a$};
\draw[->] (outputVs)node[above right]{$\bm{V}_s$} -- (adc_noise.west);
\draw[->] (adc_noise.east) -- (adc_tf.west);
\draw[->] (adc_tf.east) -| ++(0.4, 1.8) -| node[near start, sloped]{$/$} (Kiff.north);
\draw[->] (Kiff.south) -- node[sloped]{$/$} (iff_sum.north);
\draw[->] (outputde)node[above right]{$\bm{\epsilon}_{\mathcal{L}}$} -| ++(0.6, -1.0) -| node[near start, sloped]{$/$} ($(Khac.west)+(-0.6, 0)$) -- (Khac.west);
\draw[->] (Khac.east) -- node[sloped]{$/$} (iff_sum.west);
\draw[<-] (dac_noise.north) -- ++(0, 0.8)coordinate(dac_noise_input) node[below left]{$n_{\text{da}}$};
\draw[<-] (ampl_noise.north) -- ++(0, 0.8)coordinate(ampl_noise_input) node[below left]{$n_{\text{amp}}$};
\draw[<-] (adc_noise.north) -- ++(0, 0.8)coordinate(adc_noise_input) node[below right]{$n_{\text{ad}}$};
\begin{scope}[on background layer]
\node[fit={(dac_tf.south west) (dac_noise.east|-dac_noise_input)}, fill=colorblue!20!white, draw, dashed, inner sep=4pt] (dac_system) {};
\node[anchor={north}] at (dac_system.south){$\text{DAC}$};
\end{scope}
\begin{scope}[on background layer]
\node[fit={(ampl_tf.south west) (ampl_noise.east|-ampl_noise_input)}, fill=colorred!20!white, draw, dashed, inner sep=4pt] (ampl_system) {};
\node[anchor={north}] at (ampl_system.south){$\text{Amplifier}$};
\end{scope}
\begin{scope}[on background layer]
\node[fit={(adc_noise.south -| adc_noise.west) (adc_tf.east|-adc_noise_input)}, fill=coloryellow!20!white, draw, dashed, inner sep=4pt] (adc_system) {};
\node[anchor={north}] at (adc_system.south){$\text{ADC}$};
\end{scope}
\begin{scope}[on background layer]
\node[fit={(Khac.south west) (Kiff.north east)}, fill=black!20!white, draw, dashed, inner sep=4pt] (control_system) {};
\node[anchor={north}] at (control_system.south){$\text{RT Controller}$};
\end{scope}
\end{tikzpicture}Dynamic Error Budgeting
<<sec:detail_instrumentation_dynamic_error_budgeting>>
Introduction ignore
Goal:
- Write specifications regarding the maximum noise of instrumentation (ADC, DAC and voltage amplifier) such that it induces acceptable vibrations levels
Procedure:
- Get closed-loop transfer functions from disturbance sources (noise of ADC, DAC and amplifier noise) to positioning error This is done using the multi-body model, with 2DoF APA model (having voltage input and outputs)
- Focus is made on the vertical direction, as it is the direction with the most stringent requirements. If horizontal directions are considered, requirements are just less stringent than for the vertical direction.
- Deduce the maximum acceptable ASD of the noise sources
As the voltage amplifier gain will impact how the DAC noise will be amplified, some assumption are made:
- we want to apply -20 to 150V to the stacks
- Typical ADC are +/-10V
- Assumption of voltage amplifier with gain 20
Closed-Loop Sensitivity to Instrumentation Disturbances
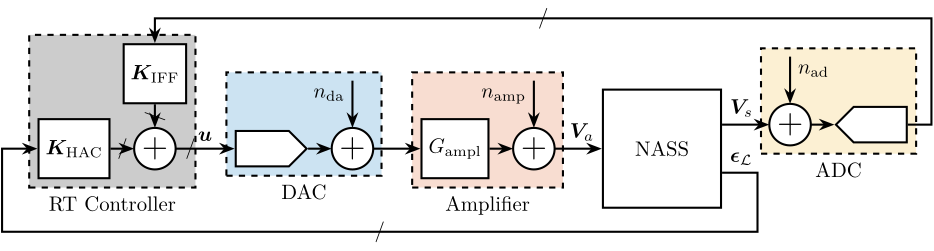
The following noise sources are considered (Figure ref:fig:detail_instrumentation_plant):
- $n_{da}$: output voltage noise of the DAC
- $n_{amp}$: output voltage noise of the voltage amplifier
- $n_{ad}$: voltage noise of the ADC measuring the force sensor stacks
Encoder noise, only used to estimate $R_z$ is found to have little impact on the vertical sample error and is therefore ommited from this analysis for clarity.
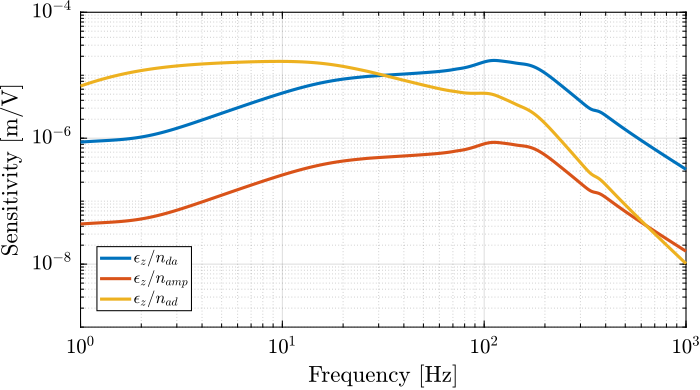
The transfer function from these three noise sources (for one strut) to the vertical error of the sample are estimated from the multi-body model, including the APA300ML and the designed flexible joints (Figure ref:fig:detail_instrumentation_noise_sensitivities).
The lateral error was also considered, but the specifications are less stringent than vertical error and the sensitivity to disturbances is smaller.
%% Identify the transfer functions from disturbance sources to vertical position error
% Let's initialize all the stages with default parameters.
initializeGround();
initializeGranite();
initializeTy();
initializeRy();
initializeRz();
initializeMicroHexapod();
initializeSample('m', 1);
initializeSimplifiedNanoHexapod();
initializeSimscapeConfiguration();
initializeDisturbances('enable', false);
initializeLoggingConfiguration('log', 'none');
initializeController('type', 'hac-iff');
initializeReferences();
% Decentralized IFF controller
wz = 2*pi*2;
xiz = 0.7;
Ghpf = (s^2/wz^2)/(s^2/wz^2 + 2*xiz*s/wz + 1);
Kiff = -200 * ... % Gain
1/(0.01*2*pi + s) * ... % LPF: provides integral action
Ghpf * ... % 2nd order HPF (limit low frequency gain)
eye(6); % Diagonal 6x6 controller (i.e. decentralized)
% Centralized HAC
wc = 2*pi*10; % Wanted crossover [rad/s]
H_int = wc/s; % Integrator
a = 2; % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = 1/sqrt(a)*(1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a))); % Lead to increase phase margin
H_lpf = 1/(1 + s/2/pi/80); % Low Pass filter to increase robustness
Khac = -5e4 * ... % Gain
H_int * ... % Integrator
H_lead * ... % Low Pass filter
H_lpf * ... % Low Pass filter
eye(6); % 6x6 Diagonal
% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/dac_noise'], 1, 'input'); io_i = io_i + 1; % DAC noise [V]
io(io_i) = linio([mdl, '/amp_noise'], 1, 'input'); io_i = io_i + 1; % Voltage Amplifier noise [V]
io(io_i) = linio([mdl, '/NASS/adc_noise'], 1, 'input'); io_i = io_i + 1; % ADC noise [V]
io(io_i) = linio([mdl, '/NASS/enc_noise'], 1, 'input'); io_i = io_i + 1; % Encoder noise [m]
io(io_i) = linio([mdl, '/NASS'], 2, 'output', [], 'z'); io_i = io_i + 1; % Vertical error [m]
io(io_i) = linio([mdl, '/NASS'], 2, 'output', [], 'y'); io_i = io_i + 1; % Lateral error [m]
Gd = linearize(mdl, io);
Gd.InputName = {...
'nda1', 'nda2', 'nda3', 'nda4', 'nda5', 'nda6', ... % DAC and Voltage amplifier noise
'namp1', 'namp2', 'namp3', 'namp4', 'namp5', 'namp6', ... % DAC and Voltage amplifier noise
'nad1', 'nad2', 'nad3', 'nad4', 'nad5', 'nad6', ... % ADC noise
'ddL1', 'ddL2', 'ddL3', 'ddL4', 'ddL5', 'ddL6' ... % Encoder noise
};
Gd.OutputName = {'y', 'z'}; % Vertical error of the sampleEstimation of maximum instrumentation noise
From previous analysis, we know how the noise of the instrumentation will affect the vertical error of the sample. Now, we want to determine specifications for each instrumentation such that the effect on the vertical error of the sample is within specifications.
Most stringent requirement:
- vertical vibrations less than the smallest expected beam size of 100nm
- This corresponds to a maximum allowed vibration of 15nm RMS
Assumption on the noise:
- uncorrelated, which is reasonable. This means that the PSD of the different noise sources adds up.
Use of system symmetry to simplify the analysis:
- the effect of all the struts on the vertical errors are identical (verify from the extracted sensitivity curves). Therefore only one strut can be considered for this analysis, and the total effect of the six struts is just six times the effect of one strut (in terms of power, but in terms of RMS value it's only sqrt(6)=2.5)
In order to have specifications for the noise of the instrumentation, assumptions:
- flat noise, which is quite typical
The noise specification is computed such that if all the instrumentation have this maximum noise, the specification in terms of vertical error is still respected. This is a pessimistic choice, but it gives a rough idea of the specifications.
% Maximum wanted effect of each noise source on the vertical error
% Specifications: 15nm RMS
% divide by sqrt(6) because 6 struts
% divide by sqrt(3) because 3 considered noise sources
max_asd_z = 15e-9 / sqrt(6) / sqrt(3); % [m/sqrt(Hz)]
% Suppose unitary flat noise ASD => compute the effect on vertical noise
unit_asd = ones(1, length(freqs));
rms_unit_asd_dac = sqrt(sum((unit_asd.*abs(squeeze(freqresp(Gd('z', 'nda1' ), freqs, 'Hz'))).').^2));
rms_unit_asd_amp = sqrt(sum((unit_asd.*abs(squeeze(freqresp(Gd('z', 'namp1'), freqs, 'Hz'))).').^2));
rms_unit_asd_adc = sqrt(sum((unit_asd.*abs(squeeze(freqresp(Gd('z', 'nad1' ), freqs, 'Hz'))).').^2));
% Obtained maximum ASD for different instruments
max_dac_asd = max_asd_z./rms_unit_asd_dac; % [V/sqrt(Hz)]
max_amp_asd = max_asd_z./rms_unit_asd_amp; % [V/sqrt(Hz)]
max_adc_asd = max_asd_z./rms_unit_asd_adc; % [V/sqrt(Hz)]
% Estimation of the equivalent RMS noise
max_dac_rms = 1e3*max_dac_asd*sqrt(5e3) % [mV RMS]
max_amp_rms = 1e3*max_amp_asd*sqrt(5e3) % [mV RMS]
max_adc_rms = 1e3*max_adc_asd*sqrt(5e3) % [mV RMS]Obtained maximum noise are:
- DAC maximum output noise ASD $14\,\mu V/\sqrt{Hz}$.
- Voltage amplifier maximum output voltage noise ASD $280\,\mu V/\sqrt{Hz}$
- ADC maximum measurement noise ASD $11\,\mu V/\sqrt{Hz}$.
In terms of RMS noise,
- DAC: <1 mV RMS
- Voltage amplifier: < 20 mV RMS
- ADC: < 0.8 mV RMS
| ADC | DAC | Amplifier | |
|---|---|---|---|
| Maximum ASD | $11\,\mu V/\sqrt{Hz}$ | $14\,\mu V/\sqrt{Hz}$ | $280\,\mu V/\sqrt{Hz}$ |
| RMS Noise | $0.8\,mV\,\text{RMS}$ | $1\,mV\,\text{RMS}$ | $20\,mV\,\text{RMS}$ |
If the Amplitude Spectral Density of the noise of the ADC, DAC and voltage amplifiers are all below the specified maximum noises, then the induced vertical error will be below 15nmRMS.
Choice of Instrumentation
<<sec:detail_instrumentation_choice>>
Introduction ignore
In previous section: noise characteristics. In this section, other characteristics (range, bandwidth, etc…)
ADC, DAC, Voltage amplifier, Encoder
Model of each instrument (transfer function + noise source).
In this section, also tell which instrumentation has been bought, and different options.
- block diagram of the model of the amplifier
Piezoelectric Voltage Amplifier
Introduction ignore
There are several characteristics of the piezoelectric voltage amplifiers that should be considered. To be able to use the full stroke of the piezoelectric actuator, the voltage output should be between -20 and 150V. It should accept an analog input voltage, preferably between -10 and 10V.
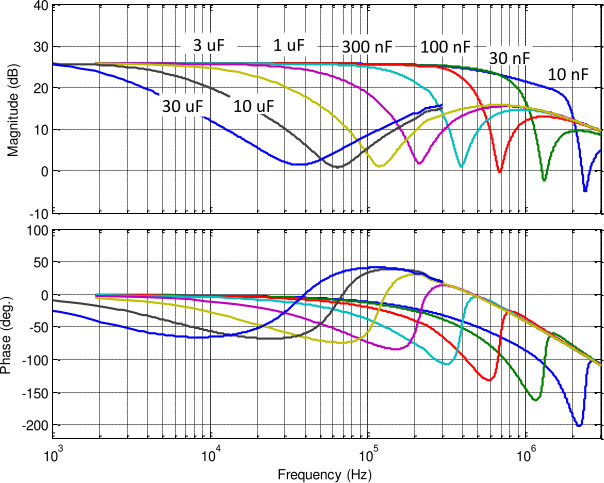
Small signal Bandwidth and Output Impedance
There are two bandwidth that should be considered for a piezoelectric voltage amplifier: large signal bandwidth and small signal bandwidth. Large signal bandwidth are linked to the output current capacities of the amplifier and will be discussed next.
Small signal bandwidth of the voltage amplifier is very important for feedback applications as it can limit the bandwidth of the complete feedback system.
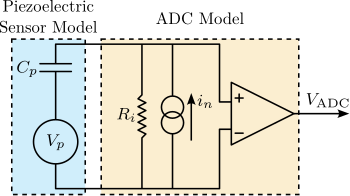
A simplified electrical model of a voltage amplifier connected to a piezoelectric stack is shown in Figure ref:fig:detail_instrumentation_amp_output_impedance. This model is only valid for small signals, but it well models the small signal bandwidth limitation cite:&fleming14_desig_model_contr_nanop_system, chap. 14. $R_o$ corresponds to the output impedance of the amplifier. With the piezoelectric load that corresponds to a capacitance $C_p$, it forms a first order low pass filter eqref:eq:detail_instrumentation_amp_output_impedance.
\begin{equation}\label{eq:detail_instrumentation_amp_output_impedance} \frac{V_a}{V_i}(s) = \frac{1}{1 + \frac{s}{ω_0}}, \quad ω_0 = \frac{1}{R_o C_p}
\end{equation}
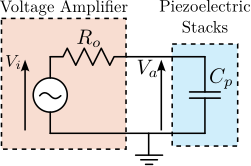
Therefore, the small signal bandwidth is load dependent. As the capacitance load of the two piezoelectric stacks correspond to a capacitance $C_p = 8.8\,\mu F$. If a small signal bandwidth of $f_0 = \frac{\omega_0}{2\pi} = 5\,kHz$ is wanted, it corresponds to a maximum output impedance of $R_0 = 3.6\,\Omega$.
Cp = 8.8e-6; % Capacitive load of the two piezoelectric actuators
f0 = 5e3; % Wanted low signal bandwidth [Hz]
Ro_max = 1/(2*pi*f0 * Cp); % Maximum wanted output impedance [Ohm]Large signal Bandwidth
Large signal bandwidth are linked to the maximum output capabilities of the amplifiers in terms of amplitude as a function of frequency cite:&spengen16_high_voltag_amplif.
As the primary objective of the NASS is to stabilize the position and not to perform scans, this specification is not as important as the small signal bandwidth.
However, let's take into account scanning capabilities. In the worst case: constant velocity scan (i.e. triangular reference signal) with a repetition rate of $f_r = 100\,\text{Hz}$ and using full voltage capabilities of the piezoelectric actuator $V_{pp} = 170\,V$.
There are two things to consider:
- Slew rate that should be above $2 \cdot V_{pp} \cdot f_r = 34\,V/ms$ This specification is easily achieved
- Current output capabilities: as the capacitance impedance decreases the the inverse of the frequency, it can reach very low values at high frequency In order to reach high voltage at high frequency, the required current that the voltage amplifier needs to provide may reach very large values. $I_{\text{max}} = 2 \cdot V_{pp} \cdot f \cdot C_p = 0.3\,A$
%% Slew-rate specifications - Triangular scan
Vpp = 170; % Full voltage scan [V]
f0 = 100; % Repetition rate of the triangular scan [Hz]
slew_rate = 1e-3*2*Vpp*f0 % Required slew rate [V/ms]
%% Maximum Output Current - Triangular scan
max_current = 2*Vpp*f0*Cp % [A]Output voltage noise
As discussed in Section ref:sec:detail_instrumentation_dynamic_error_budgeting, the output noise of the voltage amplifier should be smaller than $20\,mV\,\text{RMS}$.
As explained in cite:&spengen20_high_voltag_amplif, the load capacitance of the piezoelectric stack filters the output noise of the amplifier (low pass filter of Figure ref:fig:detail_instrumentation_amp_output_impedance). Therefore, when comparing noise of different voltage amplifiers, it should be noted what capacitance of the load is considered (i.e. the low signal bandwidth considered).
Here, the output noise should be smaller than 20mVRMS for a load of 8.8uF.
Choice of voltage amplifier
The specifications as well as the amplifier characteristics as shown in the datasheet are summarized in Table ref:tab:pd200_characteristics.
The most important characteristics are the (small signal) bandwidth > 5 [kHz] and the output voltage noise (< 20 [mV RMS]).
- Issue for the selection: manufacturers are not specifying the output noise as a function of frequency (i.e. the ASD of the noise), but only the RMS value (i.e. the integrated value over all frequency). It does not take into account the frequency dependency of the noise, that is very important to perform error budgets Also, the load the estimate the bandwidth and noise is often not mentioned (or no load for the bandwidth, and high capacitive load for the noise).
-
Explain why the PD200 was selected:
- fulfill the specification
- clear documentation, especially about noise and bandwidth (Figure ref:fig:detail_instrumentation_pd200_specs)
| Specification | PD200 | WMA-200 | LA75B | E-505 |
|---|---|---|---|---|
| Input Voltage Range: $\pm 10\,V$ | $\pm 10\,V$ | $\pm8.75\,V$ | $-1/7.5\,V$ | |
| Output Voltage Range: $-20/150\,V$ | $-50/150\,V$ | $\pm 175\,V$ | $-20/150\,V$ | -30/130 |
| Gain | 20 | 20 | 20 | 10 |
| Output Current $> 50\,mA$ | $900\,mA$ | $150\,mA$ | $360\,mA$ | $215\,mA$ |
| Slew Rate $> 34\,V/ms$ | $150\,V/\mu s$ | $80\,V/\mu s$ | n/a | n/a |
| Output noise (10uF load) $< 20\,mV\ \text{RMS}$ | $0.7\,mV\,\text{RMS}$ ($10\,\mu F$ load) | $0.05\,mV$ ($10\,\mu F$ load) | $3.4\,mV$ | $0.6\,mV$ |
| Small Signal Bandwidth ($10\,\mu F$ load): $> 5\,kHz$ | $6.4\,kHz$ ($10\,\mu F$ load) | $300\,Hz$1 | $30\,kHz$ (unloaded) | n/a |
| Output Impedance: $< 3.6\,\Omega$ | n/a | $50\,\Omega$1 | n/a | n/a |
ADC and DAC
Synchronicity and Jitter
For control systems, it is very important that the inputs and outputs are sampled synchronously with the controller and with low jitter cite:&abramovitch22_pract_method_real_world_contr_system;&abramovitch23_tutor_real_time_comput_issues_contr_system.
Therefore, the ADC and DAC:
- Needs to be well interfaced with the Speedgoat
- Sampling frequency of 10kHz
- Synchronous with the Speedgoat
Sampling Frequency, Bandwidth and delays
Several requirements that may appear the same but are different:
- Sampling frequency: defines the interval between two sampled points, also determines the Nyquist frequency
- Bandwidth: defines the maximum frequency of a measured signal (typically specified as the -3dB point), usually limited by implemented anti-aliasing filters
- Delay/latency: delay between the analog signal at the input of the ADC to the digital information transferred to the control system
Sigma-Delta ADC can have extremely good noise characteristics, high bandwidth and sampling frequency but very poor latency. Typically, the latency can reach 20 times the sampling period cite:&schmidt20_desig_high_perfor_mechat_third_revis_edition, chapt. 8.4.
Therefore, Sigma-Delta ADC are very well used for signal acquisition, but has limited use for real-time control where latency is critical. Therefore, for real time control applications, SAR-ADC (Successive approximation ADCs) is still the mostly applied type because of its single sample latency.
ADC Noise
From the dynamical error budget in Section ref:sec:detail_instrumentation_dynamic_error_budgeting Measurement noise ASD should be bellow 11uV/sqrt(Hz), 0.8mV RMS
Linearity is not a concerned as it is not used for positioning but only for active damping So the accuracy of the measurement is not a concern
ADC are affected by various noise sources One of them is quantization noise, and is linked to the fact that input/output values can only take a finite number of values. Let's first find the number of bits such that the quantization noise is fulfilling the requirements.
Let's first suppose that the ADC is ideal and the only noise comes from the quantization error. Interestingly, the noise amplitude is uniformly distributed.
Let's note:
- $q = \frac{\Delta V}{2^n}$ the quantization in [V], which is the corresponding value in [V] of the least significant bit
- $\Delta V$ is the full range of the ADC in [V]
- $n$ is the number of ADC's bits
- $f_s$ is the sample frequency in [Hz]
The quantization noise can take a value between $\pm q/2$, and the probability density function is constant in this range (i.e., it’s a uniform distribution). Since the integral of the probability density function is equal to one, its value will be $1/q$ for $-q/2 < e < q/2$ (Fig. ref:fig:detail_instrumentation_adc_quantization).
\begin{tikzpicture}
\path[fill=black!20!white] (-1, 0) |- (1, 1) |- (-1, 0);
\draw[->] (-2, 0) -- (2, 0) node[above left]{$e$};
\draw[->] (0, -0.5) -- (0, 2) node[below right]{$p(e)$};
\draw[dashed] (-2, 0) -- (-1, 0) |- (1, 1) |- (2, 0);
\node[below] at (1, 0){$\frac{q}{2}$};
\node[below] at (-1, 0){$-\frac{q}{2}$};
\node[right] at (1, 1){$\frac{1}{q}$};
\end{tikzpicture}Now, we can calculate the time average power of the quantization noise as
\begin{equation} P_q = \int_{-q/2}^{q/2} e^2 p(e) de = \frac{q^2}{12} \end{equation}The other important parameter of a noise source is the power spectral density (PSD), which indicates how the noise power spreads in different frequency bands. To find the power spectral density, we need to calculate the Fourier transform of the autocorrelation function of the noise.
Assuming that the noise samples are not correlated with one another, we can approximate the autocorrelation function with a delta function in the time domain. Since the Fourier transform of a delta function is equal to one, the power spectral density will be frequency independent (i.e. white noise). Therefore, the quantization noise is white noise with total power equal to $P_q = \frac{q^2}{12}$.
Thus, the two-sided PSD (from $\frac{-f_s}{2}$ to $\frac{f_s}{2}$), we should divide the noise power $P_q$ by $f_s$:
\begin{equation} \int_{-f_s/2}^{f_s/2} \Gamma(f) d f = f_s \Gamma = \frac{q^2}{12} \end{equation}Finally, the Power Spectral Density of the quantization noise of an ADC is equal to:
\begin{equation} \begin{aligned} \Gamma &= \frac{q^2}{12 f_s} \\ &= \frac{\left(\frac{\Delta V}{2^n}\right)^2}{12 f_s} \quad \text{in} \quad \left[ \frac{V^2}{Hz} \right] \end{aligned} \end{equation}The minimum number of bits so that the quantization noise is above some define values can be computed using:
\begin{equation} n_{\text{min}} = \text{log}_2 \left( \frac{\Delta V}{\sqrt{12 Fs} \Phi_{\text{max}}} \right) \end{equation}With a sampling frequency $F_s = 10\,kHz$, a full range of $\Delta V = 20\,V$ and a maximum allowed ASD $\Phi_{\text{max}} = 11\,\mu V/\sqrt{Hz}$, the minimum number of bits is $n_{\text{min}} = 12.4$, which is easily satisfied.
delta_V = 20; % +/-10 V
Fs = 10e3; % Sampling Frequency [Hz]
max_adc_asd = 11e-6; % V/sqrt(Hz)
min_n = log2(delta_V/(sqrt(12*Fs)*max_adc_asd))%% Estimate quantization noise of the ADC
delta_V = 20; % +/-10 V
n = 16; % number of bits
Fs = 10e3; % [Hz]
q = delta_V/2^n; % Quantization in [V]
q_psd = q^2/12/Fs; % Quantization noise Power Spectral Density [V^2/Hz]
q_asd = sqrt(q_psd) % Quantization noise Amplitude Spectral Density [V/sqrt(Hz)]DAC Output voltage noise
Similarly, the DAC output voltage noise ASD should be below $14\,\mu V/\sqrt{Hz}$, 1mV RMS. This corresponds to a 13bits +/-10V DAC.
Choice of the ADC and DAC Board
Based on the above analysis, the choice of ADC and DAC is quite simple.
Integrated in Speedgoat for best synchronicity. Chosen model: IO131:
-
16 analog inputs, based on the AD7609
- 16 bits, +/- 10V
- Maximum sampling rate of 200kSPS
- Simultaneous sampling
- Differential inputs: can use shielded twisted pairs for high noise immunity
-
8 analog outputs, based on the AD5754R
- 16 bits, +/- 10V
- Conversion time 10us
- Simultaneous update
Noise is not specified, but as it has 16 bits resolution, it should be well below the requirements. It will be experimentally measured in Section ref:sec:detail_instrumentation_characterization.
Relative Displacement Sensors
Specifications:
- used for relative positioning
- Small enough to be integrated in each strut
- vertical errors of 15nmRMS => 6nmRMS for each strut => maximum 6nmRMS sensor noise
- Stroke > 100um
There are many different sensors that can fulfil the requirements cite:&fleming13_review_nanom_resol_posit_sensor:
- Encoders
- Capacitive Sensors
- Eddy current sensors
The implementation:
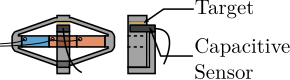
- slight advantage to capacitive or eddy current sensors as they can measure in line with the APA (Figure ref:fig:detail_instrumentation_capacitive_implementation)
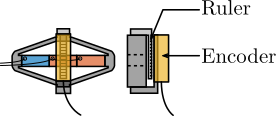
- for the encoder, the measurement has to be "offset" from the strut "action line", and therefore relative rotations between the two ends of the APA induces measurement errors (Figure ref:fig:detail_instrumentation_encoder_implementation).
One major issue is the fact that the sensor signals have to pass through an electrical slip-ring (because of the continuous spindle rotation). Some measurements were performed on the slip-ring integrated in the micro-station, and the cross-talk between different slip-ring channels were found to be quite high. It was preferred to use a sensor that transmit the measured displacement digitally, such that it is much less sensitive to noise and cross-talk. For that reason, an optical encoder with digital output was preferred (i.e. the interpolation is performed directly in the head).
The specifications are summarized in Table ref:tab:detail_instrumentation_sensor_specs.
| Specification | Renishaw Vionic | LION CPL190 | Cedrat ECP500 |
|---|---|---|---|
| Bandwidth $> 5\,\text{kHz}$ | > 500 kHz | 10kHz | 20kHz |
| Noise $< 6\,nm\,\text{RMS}$ | 1.6 nm rms | 4 nm rms | 15 nm rms |
| Range $> 100\,\mu m$ | Ruler length | 250 um | 500um |
| In line measurement | $\times$ | $\checkmark$ | |
| Digital Output | $\times$ |
Characterization of Instrumentation
<<sec:detail_instrumentation_characterization>>
Introduction ignore
All the instrumentation was then procured and tested individually to verify whether is fulfils the specifications or not.
-
Code couleur:
Yellow ADC Rouge PD200 Vert Femto blue DAC - Make sure that at some point I talk about twisted pairs etc.. Maybe use the nice schematic?
Analog to Digital Converters
Introduction ignore
Internally uses the AD7609 ADC from Analog Devices. 200kSPS, 16 bits, +/-10V
Measured Noise
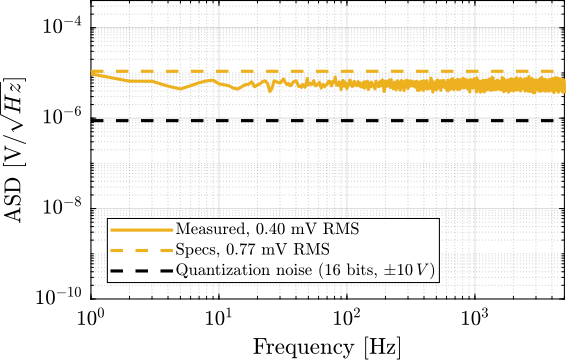
The ADC noise of the IO131 was simply measured by short-circuiting its input with a 50 Ohm resistor. Results are shown in Figure ref:fig:detail_instrumentation_adc_noise_measured. The ADC noise is a white noise with an amplitude spectral density of $5.6\,\mu V/\sqrt{Hz}$.
%% ADC noise
adc = load("2023-08-23_15-42_io131_adc_noise.mat");
% Spectral Analysis parameters
Ts = 1e-4;
Nfft = floor(1/Ts);
win = hanning(Nfft);
Noverlap = floor(Nfft/2);
% Identification of the transfer function from Va to di
[pxx, f] = pwelch(detrend(adc.adc_1, 0), win, Noverlap, Nfft, 1/Ts);
adc.pxx = pxx;
adc.f = f;
% estimated mean ASD
sprintf('Mean ASD of the ADC: %.1f uV/sqrt(Hz)', 1e6*sqrt(mean(adc.pxx)))
% Estimate quantization noise of the IO318 ADC
delta_V = 20; % +/-10 V
n = 16; % number of bits
Fs = 10e3; % [Hz]
adc.q = delta_V/2^n; % Quantization in [V]
adc.q_psd = adc.q^2/12/Fs; % Quantization noise Power Spectral Density [V^2/Hz]
adc.q_asd = sqrt(adc.q_psd); % Quantization noise Amplitude Spectral Density [V/sqrt(Hz)]If required, it is possible to apply some oversampling to lower the obtained noise cite:lab13_improv_adc.
To have additional $w$ bits of resolution, the oversampling frequency $f_{os}$ should be:
\begin{equation} f_{os} = 4^w \cdot f_s \end{equation}As the ADC can work at 200kSPS, and we only need 10kSPS, we can have an oversampling factor of 16 and have two more bits of resolution (i.e. reducing the noise by a factor 4). This works because the noise can be approximated by a white noise and the amplitude is larger than 1 LSB (0.3 mV) cite:hauser91_princ_overs_conver.
Reading of piezoelectric force sensor
There are few other things to consider when measuring the voltage generated by a piezoelectric stack.
The setup is shown in Figure ref:fig:detail_instrumentation_force_sensor_adc_setup where two stacks are used as actuator (in parallel) and one stack is used as sensor. The voltage amplifier used has a gain of 20 [V/V].
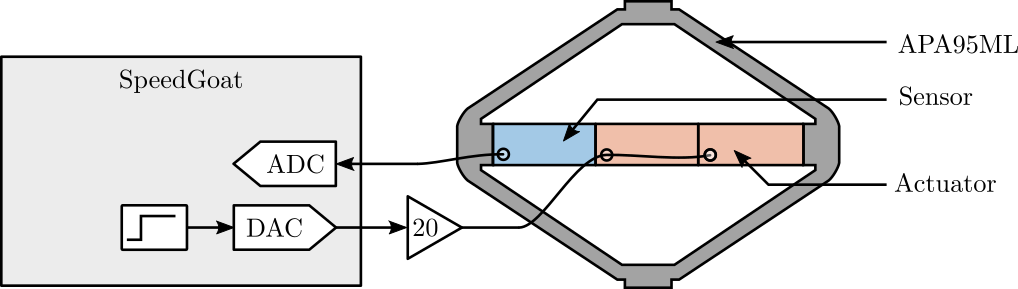
%% Read force sensor voltage with the ADC
load('force_sensor_steps.mat', 't', 'encoder', 'u', 'v');
% Exponential fit to compute the time constant
% Fit function
f_exp = @(b,x) b(1).*exp(-b(2).*x) + b(3);
% Three steps are performed at the following time intervals:
t_s = [ 2.5, 23;
23.8, 35;
35.8, 50];
tau = zeros(size(t_s, 1),1); % Time constant [s]
V0 = zeros(size(t_s, 1),1); % Offset voltage [V]
a = zeros(size(t_s, 1),1); %
for t_i = 1:size(t_s, 1)
t_cur = t(t_s(t_i, 1) < t & t < t_s(t_i, 2));
t_cur = t_cur - t_cur(1);
y_cur = v(t_s(t_i, 1) < t & t < t_s(t_i, 2));
nrmrsd = @(b) norm(y_cur - f_exp(b,t_cur)); % Residual Norm Cost Function
B0 = [0.5, 0.15, 2.2]; % Choose Appropriate Initial Estimates
[B,rnrm] = fminsearch(nrmrsd, B0); % Estimate Parameters ‘B’
a(t_i) = B(1);
tau(t_i) = 1/B(2);
V0(t_i) = B(3);
end
% Data to show the exponential fit
t_fit_1 = linspace(t_s(1,1), t_s(1,2), 100);
y_fit_1 = f_exp([a(1),1/tau(1),V0(1)], t_fit_1-t_s(1,1));
t_fit_2 = linspace(t_s(2,1), t_s(2,2), 100);
y_fit_2 = f_exp([a(2),1/tau(2),V0(2)], t_fit_2-t_s(2,1));
t_fit_3 = linspace(t_s(3,1), t_s(3,2), 100);
y_fit_3 = f_exp([a(3),1/tau(3),V0(3)], t_fit_3-t_s(3,1));
% Speedgoat ADC input impedance
Cp = 4.4e-6; % [F]
Rin = abs(mean(tau))/Cp; % [Ohm]
% Estimated input bias current
in = mean(V0)/Rin; % [A]
% Resistor added in parallel to the force sensor
fc = 3; % Wanted corner frequency [Hz]
Ra = Rin/(fc*Cp*Rin - 1); % [Ohm]
% New ADC offset voltage
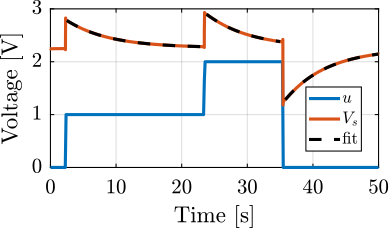
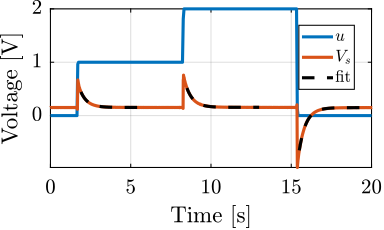
V_offset = Ra*Rin/(Ra + Rin) * in; % [V]The excitation signal (steps) and measured voltage across the sensor stack are shown in Figure ref:fig:detail_instrumentation_step_response_force_sensor. The measured voltage shows an exponential decay which indicates that the charge across the capacitor formed by the stack is discharging into a resistor. This corresponds to an RC circuit with a time constant $\tau = R_i C_p$. Therefore, first order high filter, with corner frequency $1/\tau$.
The exponential curves are fitted and a value of $\tau = 6.5\,s$ and an offset voltage of $2.26\,V$ are found.
With the capacitance being $C_p = 4.4 \mu F$, the internal impedance of the Speedgoat ADC can be computed as follows $R_i = \frac{\tau}{C_p} = 1.5\,M\Omega$.
It is close to the specified value of $1\,M\Omega$ found in the datasheet
\hfill
As shown in Figure ref:fig:detail_instrumentation_step_response_force_sensor, the voltage across the Piezoelectric sensor stack shows a constant voltage offset. This can be explained by looking at the electrical model shown in Figure ref:fig:detail_instrumentation_force_sensor_adc (taken from cite:reza06_piezoel_trans_vibrat_contr_dampin).
The differential amplifier in the Speedgoat has some input bias current $i_n$ that induces a voltage offset $V_{\text{off}}$ across its own internal resistance $R_i$. Note that the impedance of the piezoelectric stack is much larger that that at DC.
Therefore, the input bias current $i_n$ is estimated from $i_n = V_{\text{off}}/R_i = 1.5\,\mu A$.
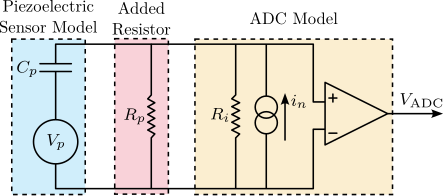
In order to reduce the input voltage offset and to increase the corner frequency of the high pass filter, a resistor is added in parallel to the force sensor.
- Reduction of input voltage offset: \[ V_{off} = \frac{R_a R_{in}}{R_a + R_{in}} i_n \]
- Increase the high pass corner frequency $f_c$ \[ C_p \frac{R_{in}R_a}{R_{in} + R_a} = \tau_c = \frac{1}{f_c} \] \[ R_a = \frac{R_i}{f_c C_p R_i - 1} \]
The resistor is chosen such that the high pass corner frequency is equal to 3Hz. This corresponds to a resistor of $R_p = 80\,k\Omega$.
With this parallel resistance value, the voltage offset would be $V_{\text{off}} = 0.11\,V$, which is much more acceptable.
To validate this, a resistor $R_p \approx 82\,k\Omega$ is then added in parallel with the force sensor as shown in Figure ref:fig:detail_instrumentation_force_sensor_adc_R. After the resistor is added, the same steps response is performed. And indeed, we obtain a much smaller offset voltage ($V_{\text{off}} = 0.15\,V$) and a much faster time constant ($\tau = 0.45\,s$). This validates the model of the ADC and the effectiveness of the added resistor.
%% Read force sensor voltage with the ADC with added 82.7kOhm resistor
load('force_sensor_steps_R_82k7.mat', 't', 'encoder', 'u', 'v');
% Step times
t_s = [1.9, 6;
8.5, 13;
15.5, 21;
22.6, 26;
30.0, 36;
37.5, 41;
46.2, 49.5]; % [s]
tau = zeros(size(t_s, 1),1); % Time constant [s]
V0 = zeros(size(t_s, 1),1); % Offset voltage [V]
a = zeros(size(t_s, 1),1); %
for t_i = 1:size(t_s, 1)
t_cur = t(t_s(t_i, 1) < t & t < t_s(t_i, 2));
t_cur = t_cur - t_cur(1);
y_cur = v(t_s(t_i, 1) < t & t < t_s(t_i, 2));
nrmrsd = @(b) norm(y_cur - f_exp(b,t_cur)); % Residual Norm Cost Function
B0 = [0.5, 0.1, 2.2]; % Choose Appropriate Initial Estimates
[B,rnrm] = fminsearch(nrmrsd, B0); % Estimate Parameters ‘B’
a(t_i) = B(1);
tau(t_i) = 1/B(2);
V0(t_i) = B(3);
end
% Data to show the exponential fit
t_fit_1 = linspace(t_s(1,1), t_s(1,2), 100);
y_fit_1 = f_exp([a(1),1/tau(1),V0(1)], t_fit_1-t_s(1,1));
t_fit_2 = linspace(t_s(2,1), t_s(2,2), 100);
y_fit_2 = f_exp([a(2),1/tau(2),V0(2)], t_fit_2-t_s(2,1));
t_fit_3 = linspace(t_s(3,1), t_s(3,2), 100);
y_fit_3 = f_exp([a(3),1/tau(3),V0(3)], t_fit_3-t_s(3,1));\hfill
Instrumentation Amplifier
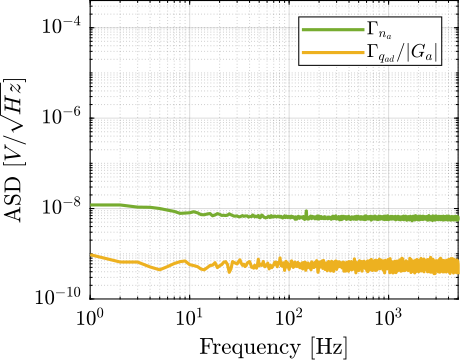
Because the ADC noise may be too large to measure noise of other instruments (anything below $5.6\,\mu V/\sqrt{Hz}$ cannot be distinguish from the noise of the ADC itself), a low noise instrumentation amplifier can be used.
Different instrumentation amplifiers were used:
- EG&G 5113, 4nV/sqrt(Hz), gain up to 100000 (100dB)
- Femto DLPVA-101-B-S 2nV/sqrt(Hz), gain from 20 to 80dB
- Koheron AMP200, 2.4nV/sqrt(Hz), gain up to 100
Here, the Femto amplifier is used.
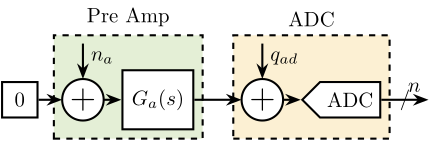
But first, the input noise of the amplifier is characterized.
- Footnote: for variable gain amplifiers, it is more convenient to refer to the input noise rather than the output noise.
Its input is short circuited, and the output voltage is measured by the ADC. The maximum amplifier gain of 80dB (i.e. 10000) is used.
The measured voltage is then divided by 10000 to obtain the equivalent noise at the input of the voltage amplifier. In that case, the noise of the ADC is negligible, thanks to the high gain used.
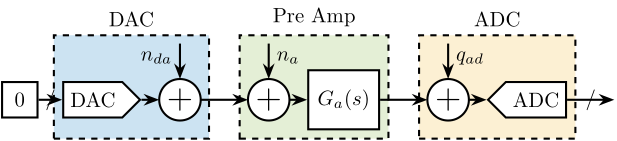
\begin{tikzpicture}
\node[block={0.6cm}{0.6cm}] (const) {$0$};
% Pre Amp
\node[addb, right=0.4 of const] (addna) {};
\node[block, right=0.3 of addna] (Ga) {$G_a(s)$};
% ADC
\node[addb, right=0.8 of Ga] (addqad){};
\node[ADC, right=0.3 of addqad] (ADC) {ADC};
\draw[->] (const.east) -- (addna.west);
\draw[->] (addna.east) -- (Ga.west);
\draw[->] (Ga.east) -- (addqad.west);
\draw[->] (addqad.east) -- (ADC.west);
\draw[->] (ADC.east) -- node[sloped]{$/$} ++(0.8, 0) node[above left]{$n$};
\draw[<-] (addna.north) -- ++(0, 0.6) node[below right](na){$n_{a}$};
\draw[<-] (addqad.north) -- ++(0, 0.6) node[below right](qad){$q_{ad}$};
\coordinate[] (top) at (na.north);
\coordinate[] (bot) at (Ga.south);
% 5113
\begin{scope}[on background layer]
\node[fit={(addna.west|-bot) (Ga.east|-top)}, inner sep=4pt, draw, dashed, fill=colorgreen!20!white] (P) {};
\node[above] at (P.north) {Pre Amp};
\end{scope}
% ADC
\begin{scope}[on background layer]
\node[fit={(addqad.west|-bot) (ADC.east|-top)}, inner sep=4pt, draw, dashed, fill=coloryellow!20!white] (P) {};
\node[above] at (P.north) {ADC};
\end{scope}
\end{tikzpicture}\hfill
Digital to Analog Converters
Noise Measurement
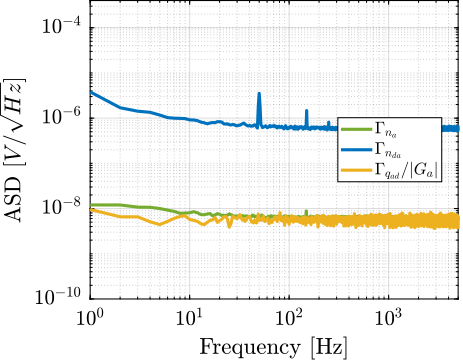
In order not to have any quantization noise and only measure the output voltage noise of the DAC, we "ask" the DAC to output a zero voltage.
The measurement setup is schematically represented in Figure ref:fig:detail_instrumentation_dac_setup. The gain of the pre-amplifier is adjusted such that the measured amplified noise is much larger than the quantization noise of the ADC.
The Amplitude Spectral Density $\Gamma_n(\omega)$ of the measured signal is computed. The Amplitude Spectral Density of the DAC output voltage noise $n_{da}$ can be computed taking into account the gain of the pre-amplifier:
\begin{equation} \Gamma_{n_{da}}(\omega) = \frac{\Gamma_m(\omega)}{|G_a(\omega)|} \end{equation}And it is verified that the Amplitude Spectral Density of $n_{da}$ is much larger than the one of $n_a$:
\begin{equation} \Gamma_{n_{da}} \gg \Gamma_{n_a} \end{equation}\begin{tikzpicture}
\node[block={0.6cm}{0.6cm}] (const) {$0$};
% DAC
\node[DAC, right=0.4 of const] (DAC) {DAC};
\node[addb, right=0.3 of DAC] (addnda){};
% Pre Amp
\node[addb, right=0.8 of addnda] (addna) {};
\node[block, right=0.3 of addna] (Ga) {$G_a(s)$};
% ADC
\node[addb, right=0.8 of Ga] (addqad){};
\node[ADC, right=0.3 of addqad] (ADC) {ADC};
\draw[->] (const.east) -- node[sloped]{$/$} (DAC.west);
\draw[->] (DAC.east) -- (addnda.west);
\draw[->] (addnda.east) -- (addna.west);
\draw[->] (addna.east) -- (Ga.west);
\draw[->] (Ga.east) -- (addqad.west);
\draw[->] (addqad.east) -- (ADC.west);
\draw[->] (ADC.east) -- node[sloped]{$/$} ++(0.8, 0);
\draw[<-] (addnda.north) -- ++(0, 0.6) node[below left](nda){$n_{da}$};
\draw[<-] (addna.north) -- ++(0, 0.6) node[below right](na){$n_{a}$};
\draw[<-] (addqad.north) -- ++(0, 0.6) node[below right](qad){$q_{ad}$};
\coordinate[] (top) at (na.north);
\coordinate[] (bot) at (Ga.south);
% DAC
\begin{scope}[on background layer]
\node[fit={(DAC.west|-bot) (addnda.east|-top)}, inner sep=4pt, draw, dashed, fill=colorblue!20!white] (P) {};
\node[above] at (P.north) {DAC};
\end{scope}
% 5113
\begin{scope}[on background layer]
\node[fit={(addna.west|-bot) (Ga.east|-top)}, inner sep=4pt, draw, dashed, fill=colorgreen!20!white] (P) {};
\node[above] at (P.north) {Pre Amp};
\end{scope}
% ADC
\begin{scope}[on background layer]
\node[fit={(addqad.west|-bot) (ADC.east|-top)}, inner sep=4pt, draw, dashed, fill=coloryellow!20!white] (P) {};
\node[above] at (P.north) {ADC};
\end{scope}
\end{tikzpicture}The obtained Amplitude Spectral Density of the DAC's output voltage is shown in Figure ref:fig:detail_instrumentation_dac_output_noise. It is almost white noise with an ASD of 0.6uV/sqrt(Hz). There is a little bit of 50Hz, and some low frequency noise (thermal noise?) which are not foreseen to be an issue as it will be inside the bandwidth.
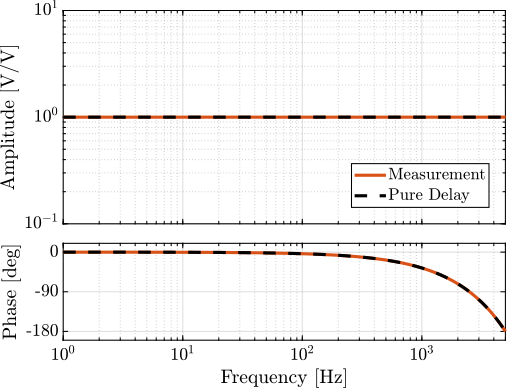
DAC is directly wired to the ADC. The transfer function from DAC to ADC is computed. It corresponds to 1 sample delay (Figure ref:fig:detail_instrumentation_dac_adc_tf).
%% Measure transfer function from DAC to ADC
data_dac_adc = load("2023-08-22_15-52_io131_dac_to_adc.mat");
% Frequency analysis parameters
Ts = 1e-4; % Sampling Time [s]
Nfft = floor(1.0/Ts);
win = hanning(Nfft);
Noverlap = floor(Nfft/2);
[G_dac_adc, f] = tfestimate(data_dac_adc.dac_1, data_dac_adc.adc_1, win, Noverlap, Nfft, 1/Ts);
%
G_delay = exp(-Ts*s);Piezoelectric Voltage Amplifier
Output Voltage Noise
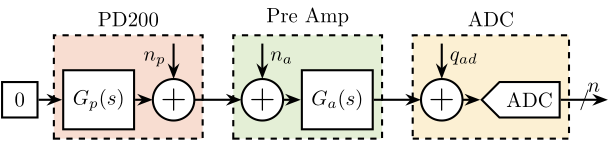
The measurement setup is shown in Figure ref:fig:detail_instrumentation_pd200_setup. The input of the PD200 amplifier is shunted with a 50 Ohm resistor such that there in no voltage input expected the PD200 input voltage noise. The gain of the pre-amplifier is increased in order to measure a signal much larger than the quantization noise of the ADC.
Two piezoelectric stacks of the APA95ML are connected to the PD200 output to have appropriate load.
\begin{tikzpicture}
\node[block={0.6cm}{0.6cm}] (const) {$0$};
% PD200
\node[block, right=0.4 of const] (Gp){$G_p(s)$};
\node[addb, right=0.3 of Gp] (addnp){};
% Pre Amp
\node[addb, right=0.8 of addnp] (addna) {};
\node[block, right=0.3 of addna] (Ga) {$G_a(s)$};
% ADC
\node[addb, right=0.8 of Ga] (addqad){};
\node[ADC, right=0.3 of addqad] (ADC) {ADC};
\draw[->] (const.east) -- (Gp.west);
\draw[->] (Gp.east) -- (addnp.west);
\draw[->] (addnp.east) -- (addna.west);
\draw[->] (addna.east) -- (Ga.west);
\draw[->] (Ga.east) -- (addqad.west);
\draw[->] (addqad.east) -- (ADC.west);
\draw[->] (ADC.east) -- node[sloped]{$/$} ++(0.8, 0) node[above left]{$n$};
\draw[<-] (addnp.north) -- ++(0, 0.6) node[below left](np){$n_{p}$};
\draw[<-] (addna.north) -- ++(0, 0.6) node[below right](na){$n_{a}$};
\draw[<-] (addqad.north) -- ++(0, 0.6) node[below right](qad){$q_{ad}$};
\coordinate[] (top) at (na.north);
\coordinate[] (bot) at (Ga.south);
% PD200
\begin{scope}[on background layer]
\node[fit={(addnp.east|-bot) (Gp.west|-top)}, inner sep=4pt, draw, dashed, fill=colorred!20!white] (P) {};
\node[above] at (P.north) {PD200};
\end{scope}
% 5113
\begin{scope}[on background layer]
\node[fit={(addna.west|-bot) (Ga.east|-top)}, inner sep=4pt, draw, dashed, fill=colorgreen!20!white] (P) {};
\node[above] at (P.north) {Pre Amp};
\end{scope}
% ADC
\begin{scope}[on background layer]
\node[fit={(addqad.west|-bot) (ADC.east|-top)}, inner sep=4pt, draw, dashed, fill=coloryellow!20!white] (P) {};
\node[above] at (P.north) {ADC};
\end{scope}
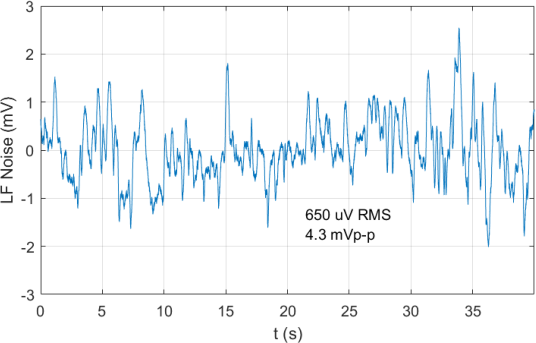
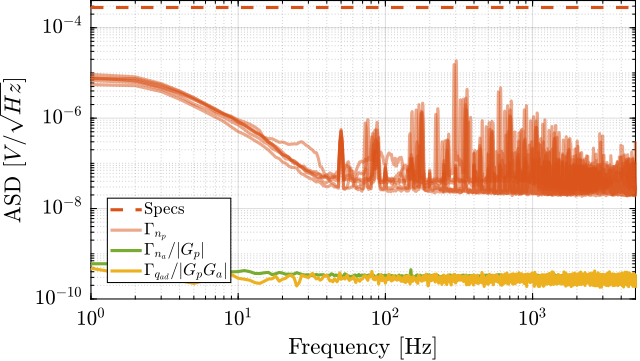
\end{tikzpicture}The measured low frequency (<20Hz) output noise of one of the PD200 amplifiers is shown in Figure ref:fig:pd200_noise_time_lpf. It is very similar to the one specified in the datasheet in Figure ref:fig:pd200_expected_noise.
The obtained RMS and peak to peak values of the measured output noise are shown in Table ref:tab:rms_pkp_noise and found to be very similar to the specified ones.
| RMS [$\mu V$] | Peak to Peak [$mV$] | |
|---|---|---|
| Specification [$10\,\mu F$] | 714.0 | 4.3 |
| PD200 1 | 565.1 | 3.7 |
| PD200 2 | 767.6 | 3.5 |
| PD200 3 | 479.9 | 3.0 |
| PD200 4 | 615.7 | 3.5 |
| PD200 5 | 651.0 | 2.4 |
| PD200 6 | 473.2 | 2.7 |
| PD200 7 | 423.1 | 2.3 |
The Amplitude Spectral Density $\Gamma_n(\omega)$ of the measured signal by the ADC is computed. The Amplitude Spectral Density of the input voltage noise of the PD200 amplifier $n_p$ is then computed taking into account the gain of the pre-amplifier and the gain of the PD200 amplifier:
\begin{equation} \Gamma_{n_p}(\omega) = \frac{\Gamma_n(\omega)}{|G_p(j\omega) G_a(j\omega)|} \end{equation}And we verify that we are indeed measuring the noise of the PD200 and not the noise of the pre-amplifier by checking that:
\begin{equation} \Gamma_{n_p}(\omega) |G_p(j\omega)| \ll \Gamma_{n_a} \end{equation}The Amplitude Spectral Density of the measured input noise is computed and shown in Figure ref:fig:asd_noise_pd200_10uF.
It is verified that the contribution of the PD200 noise is much larger than the contribution of the pre-amplifier noise of the quantization noise.
The Amplitude Spectral Density of the input noise of the PD200 amplifiers present sharp peaks. It is not clear yet what causes such peaks and if these peaks have high influence on the total RMS noise of the amplifiers.
Small Signal Bandwidth
Here the small signal dynamics of all the PD200 amplifiers are identified.
A (logarithmic) sweep sine excitation voltage is generated by the Speedgoat DAC with an amplitude of 0.1V and a frequency going from 1Hz up to 5kHz.
The output voltage of the PD200 amplifier is measured thanks to the monitor voltage of the PD200 amplifier. The input voltage of the PD200 amplifier (the generated voltage by the DAC) is measured with another ADC of the Speedgoat. This way, the time delay related to the ADC will not be apparent in the results.
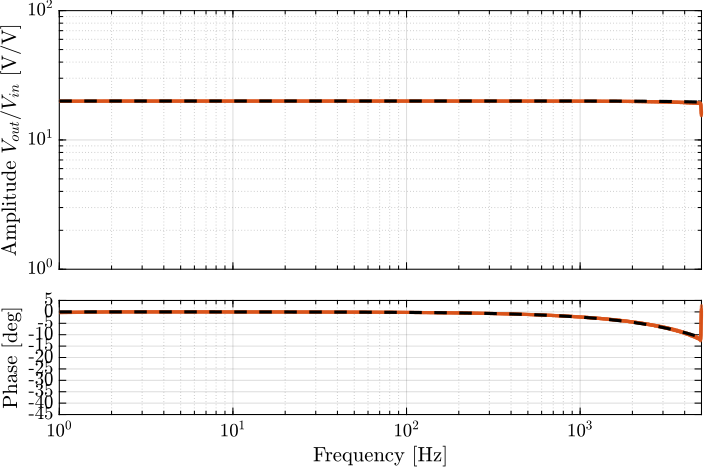
The obtained transfer functions from $V_{in}$ to $V_{out}$ are shown in Figure ref:fig:pd200_small_signal_tf.
We can see the very well matching between all the 7 amplifiers. The amplitude is constant over a wide frequency band and the phase drop is limited to less than 1 degree up to 500Hz.
The identified dynamics in Figure ref:fig:pd200_small_signal_tf can very well be modeled this dynamics with a first order low pass filter (even a constant could work fine).
Output Impedance
The goal of this experimental setup is to estimate the output impedance $R_\text{out}$ of the PD200 voltage amplifiers. A DAC with a constant output voltage (here 0.1V) is connected to the input of the PD200 amplifier.
Then, the output voltage of the PD200 amplifier is measured in two conditions:
- $V$ when the output is not connected to any load
- $V_p$ when a load $R_{\text{load}} = 10\,\Omega$ is connected at the output of the amplifier
The load and the output impedance form a voltage divider, and thus: \[ V^\prime = \frac{R}{R + R_\text{out}} V \]
From the two values of voltage, the output impedance of the amplifier can be estimated:
\begin{equation} R_{\text{out}} = R_{\text{load}} \frac{V - V_p}{V} \end{equation}From this measurement, all the PD200 amplifiers are found to have an output impedance $R_{\text{out}} \approx 1\,\Omega$.
With the capacitive load $C_p = 8.8\,\mu F$, the output resistor of the amplifier forms a low pass filter with a corner frequency equal to $f_0 = \frac{1}{R_{\text{out}} C_p}$. We get a corner frequency around $10\,\text{kHz}$ which is not far from the specified $7.4\,\text{kHz}$.
% Estimate output impedance of PD200 amplifiers
R_load = 10; % Load [Ohm]
% V Vp
meas = [1.988, 1.794; % PD200 - 1
1.990, 1.789; % PD200 - 2
1.982, 1.795; % PD200 - 3
1.984, 1.789; % PD200 - 4
1.998, 1.810; % PD200 - 5
1.984, 1.799];% PD200 - 6
R_out = R_load * (meas(:,1) - meas(:,2))./meas(:,2); % Output impedance [Ohm]
% Estimate corner frequency of the high pass filter
Cp = 8.8e-6; % Capacitive load of the two piezoelectric actuators
f0 = 1./(R_out*Cp)Conclusion
| Characteristics | Measurement | Manual | Specification |
|---|---|---|---|
| Input Voltage Range | - | +/- 10 [V] | +/- 10 [V] |
| Output Voltage Range | - | -50/150 [V] | -20/150 [V] |
| Gain | 20 [V/V] | - | |
| Maximum RMS current | 0.9 [A] | > 50 [mA] | |
| Maximum Pulse current | 10 [A] | - | |
| Slew Rate | 150 [V/us] | - | |
| Noise (10uF load) | 0.7 [mV RMS] | < 2 [mV rms] | |
| Small Signal Bandwidth (10uF load) | 7.4 [kHz] | > 5 [kHz] | |
| Large Signal Bandwidth (150V, 10uF) | 300 [Hz] | - |
Linear Encoders
To measure the noise $n$ of the encoder, one can rigidly fix the head and the ruler together such that no motion should be measured. Then, the measured signal $y_m$ corresponds to the noise $n$.
The measurement bench is shown in Figures ref:fig:meas_bench_top_view and ref:fig:meas_bench_side_view. Note that the bench is then covered with a "plastic bubble sheet" in order to keep disturbances as small as possible.
Then, and for all the 7 encoders, we record the measured motion during 100s with a sampling frequency of 20kHz.
External Metrology
Different options:
- Attocube: issue of non-linearity estimated from the encoders
- Smaract
- QuDIS
For the final tests, QuDIS were used.
Conclusion
f = dac.f;
length(dac.pxx)
length(adc.pxx)
length(pd200{1}.pxx)
length(enc{1}.pxx)
psd_z_dac = 6*(abs(squeeze(freqresp(Gd('z', 'nda1' ), f, 'Hz'))).^2).*dac.pxx;
psd_z_adc = 6*(abs(squeeze(freqresp(Gd('z', 'nad1' ), f, 'Hz'))).^2).*adc.pxx;
psd_z_amp = 6*(abs(squeeze(freqresp(Gd('z', 'namp1'), f, 'Hz'))).^2).*pd200{1}.pxx;
psd_z_enc = 6*(abs(squeeze(freqresp(Gd('z', 'ddL1' ), f, 'Hz'))).^2).*enc{1}.pxx;
psd_z_tot = psd_z_dac + psd_z_adc + psd_z_amp + psd_z_enc;
rms_z_tot = sqrt(trapz(f, psd_z_tot));- Compare with measurement noise? or effect of measurement noise => higher so it's OK?
- Or compare with specifications?
From all the measured noises, compute the obtained PSD error in Y and Z (show PSD of individual + Sum + Cumulative?)
Conclusion
<<sec:detail_instrumentation_conclusion>>
Bibliography ignore
Footnotes
The manufacturer proposed to remove the $50\,\Omega$ output resistor to improve to small signal bandwidth above $10\,kHz$