96 KiB
Nano Active Stabilization System - Instrumentation
- Introduction
- Dynamic Error Budgeting
- Choice of Instrumentation
- Characterization of Instrumentation
- Conclusion
- Bibliography
Introduction ignore
The goal is to show that each element in the system has been properly chosen based on certain requirements.
In order to determine the maximum noise of each instrumentation, a dynamic error budgeting is performed in Section ref:sec:instrumentation_dynamic_error_budgeting.
The required instrumentation are then selected based on obtained noise specifications and other requirements summarized in Section ref:sec:detail_instrumentation_choice.
The received instrumentation are characterized in Section ref:sec:detail_instrumentation_characterization.
- Say the the real time controller is a Speedgoat machine, as it is the standard real time controller used at the ESRF
\begin{tikzpicture}
% Blocs
\node[block={2.0cm}{2.0cm}, align=center] (plant) {NASS};
\coordinate[] (inputVa) at ($(plant.south west)!0.5!(plant.north west)$);
\coordinate[] (outputVs) at ($(plant.south east)!0.7!(plant.north east)$);
\coordinate[] (outputde) at ($(plant.south east)!0.3!(plant.north east)$);
\node[block={1.0cm}{1.0cm}, left=0.8 of inputVa] (ampl_tf) {$G_{\text{ampl}}$};
\node[addb={+}{}{}{}{}, left=0.4 of ampl_tf] (ampl_noise) {};
\node[addb={+}{}{}{}{}, left=0.8 of ampl_noise] (dac_noise) {};
\node[DAC, left=0.4 of dac_noise] (dac_tf) {};
\node[addb={+}{}{}{}{}, left=1.0 of dac_tf] (iff_sum) {};
\node[block={1.0cm}{1.0cm}, above=0.4 of iff_sum] (Kiff) {$\bm{K}_{\text{IFF}}$};
\node[block={1.0cm}{1.0cm}, left=0.4 of iff_sum] (Khac) {$\bm{K}_{\text{HAC}}$};
% \node[block={1.0cm}{1.0cm}, above=0.4 of plant] (Kiff) {$\bm{K}_{\text{IFF}}$};
% \node[block={1.0cm}{1.0cm}, below=0.4 of plant] (Khac) {$\bm{K}_{\text{HAC}}$};
\node[addb={+}{}{}{}{}, right=0.8 of outputVs] (adc_noise) {};
\node[ADC, right=0.4 of adc_noise] (adc_tf) {};
\draw[->] (iff_sum.east) --node[midway, above]{$\bm{u}$} node[near start, sloped]{$/$} (dac_tf.west);
\draw[->] (dac_tf.east) -- (dac_noise.west);
\draw[->] (dac_noise.east) -- (ampl_noise.west);
\draw[->] (ampl_noise.east) -- (ampl_tf.west);
\draw[->] (ampl_tf.east) -- (inputVa)node[above left]{$\bm{V}_a$};
\draw[->] (outputVs)node[above right]{$\bm{V}_s$} -- (adc_noise.west);
\draw[->] (adc_noise.east) -- (adc_tf.west);
\draw[->] (adc_tf.east) -| ++(0.4, 1.8) -| node[near start, sloped]{$/$} (Kiff.north);
\draw[->] (Kiff.south) -- node[sloped]{$/$} (iff_sum.north);
\draw[->] (outputde)node[above right]{$\bm{\epsilon}_{\mathcal{L}}$} -| ++(0.6, -1.0) -| node[near start, sloped]{$/$} ($(Khac.west)+(-0.6, 0)$) -- (Khac.west);
\draw[->] (Khac.east) -- node[sloped]{$/$} (iff_sum.west);
\draw[<-] (dac_noise.north) -- ++(0, 0.8)coordinate(dac_noise_input) node[below left]{$n_{\text{ad}}$};
\draw[<-] (ampl_noise.north) -- ++(0, 0.8)coordinate(ampl_noise_input) node[below right]{$n_{\text{ampl}}$};
\draw[<-] (adc_noise.north) -- ++(0, 0.8)coordinate(adc_noise_input) node[below right]{$n_{\text{da}}$};
\begin{scope}[on background layer]
\node[fit={(dac_tf.south west) (dac_noise.east|-dac_noise_input)}, fill=colorblue!20!white, draw, dashed, inner sep=4pt] (dac_system) {};
\node[anchor={north}] at (dac_system.south){$\text{DAC}$};
\end{scope}
\begin{scope}[on background layer]
\node[fit={(ampl_noise.west|-ampl_tf.south) (ampl_tf.east|-ampl_noise_input)}, fill=colorred!20!white, draw, dashed, inner sep=4pt] (ampl_system) {};
\node[anchor={north}] at (ampl_system.south){$\text{Amplifier}$};
\end{scope}
\begin{scope}[on background layer]
\node[fit={(adc_noise.south -| adc_noise.west) (adc_tf.east|-adc_noise_input)}, fill=coloryellow!20!white, draw, dashed, inner sep=4pt] (adc_system) {};
\node[anchor={north}] at (adc_system.south){$\text{ADC}$};
\end{scope}
\begin{scope}[on background layer]
\node[fit={(Khac.south west) (Kiff.north east)}, fill=black!20!white, draw, dashed, inner sep=4pt] (control_system) {};
\node[anchor={north}] at (control_system.south){$\text{RT Controller}$};
\end{scope}
\end{tikzpicture}Dynamic Error Budgeting
<<sec:detail_instrumentation_dynamic_error_budgeting>>
Introduction ignore
Goal:
- Write specifications regarding the maximum noise of instrumentation (ADC, DAC and voltage amplifier) such that it induces acceptable vibrations levels
Procedure:
- Get closed-loop transfer functions from disturbance sources (noise of ADC, DAC and amplifier noise) to positioning error This is done using the multi-body model, with 2DoF APA model (having voltage input and outputs)
- Focus is made on the vertical direction, as it is the direction with the most stringent requirements.
- Deduce the maximum ASD of the noise sources
As the voltage amplifier gain will impact how the DAC noise will be amplified, some assumption are made:
- we want to apply -20 to 150V to the stacks
- Typical ADC are +/-10V
- Assumption of voltage amplifier with gain 20
Closed-Loop Sensitivity to Instrumentation Disturbances
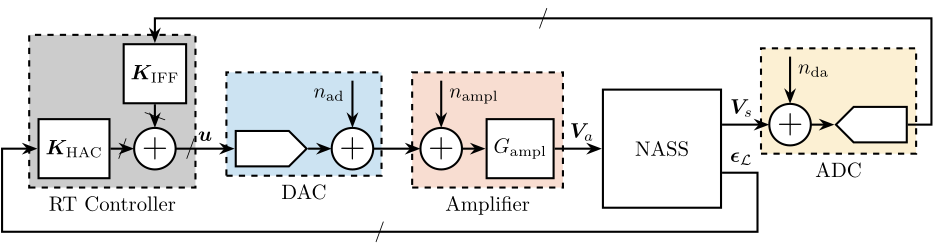
The following noise sources are considered (Figure ref:fig:detail_instrumentation_plant):
- $n_{da}$: output voltage noise of the DAC
- $n_{amp}$: (input referred) voltage noise of the voltage amplifier
- $n_{ad}$: voltage noise of the ADC measuring the force sensor stacks
Encoder noise, only used to estimate $R_z$ is found to have little impact on the vertical sample error and is therefore ommited from this analysis for clarity.
The transfer function from these three noise sources (for one strut) to the vertical error of the sample are estimated from the multi-body model, including the APA300ML and the designed flexible joints.
The latteral error was also considered, but the specifications are less stringent than vertical error and the sensitivity to disturbances is smaller.
%% Identify the transfer functions from disturbance sources to vertical position error
% Let's initialize all the stages with default parameters.
initializeGround();
initializeGranite();
initializeTy();
initializeRy();
initializeRz();
initializeMicroHexapod();
initializeSample('m', 1);
initializeSimplifiedNanoHexapod();
initializeSimscapeConfiguration();
initializeDisturbances('enable', false);
initializeLoggingConfiguration('log', 'none');
initializeController('type', 'hac-iff');
initializeReferences();
% Decentralized IFF controller
wz = 2*pi*2;
xiz = 0.7;
Ghpf = (s^2/wz^2)/(s^2/wz^2 + 2*xiz*s/wz + 1);
Kiff = -200 * ... % Gain
1/(0.01*2*pi + s) * ... % LPF: provides integral action
Ghpf * ... % 2nd order HPF (limit low frequency gain)
eye(6); % Diagonal 6x6 controller (i.e. decentralized)
% Centralized HAC
wc = 2*pi*10; % Wanted crossover [rad/s]
H_int = wc/s; % Integrator
a = 2; % Amount of phase lead / width of the phase lead / high frequency gain
H_lead = 1/sqrt(a)*(1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a))); % Lead to increase phase margin
H_lpf = 1/(1 + s/2/pi/80); % Low Pass filter to increase robustness
Khac = -5e4 * ... % Gain
H_int * ... % Integrator
H_lead * ... % Low Pass filter
H_lpf * ... % Low Pass filter
eye(6); % 6x6 Diagonal
% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/dac_noise'], 1, 'input'); io_i = io_i + 1; % DAC noise [V]
io(io_i) = linio([mdl, '/NASS/adc_noise'], 1, 'input'); io_i = io_i + 1; % ADC noise [V]
io(io_i) = linio([mdl, '/NASS/enc_noise'], 1, 'input'); io_i = io_i + 1; % Encoder noise [m]
io(io_i) = linio([mdl, '/NASS'], 2, 'output', [], 'z'); io_i = io_i + 1; % Vertical error [m]
io(io_i) = linio([mdl, '/NASS'], 2, 'output', [], 'y'); io_i = io_i + 1; % Lateral error [m]
Gd = linearize(mdl, io);
Gd.InputName = {...
'du1', 'du2', 'du3', 'du4', 'du5', 'du6', ... % DAC and Voltage amplifier noise
'dVs1', 'dVs2', 'dVs3', 'dVs4', 'dVs5', 'dVs6', ... % ADC noise
'ddL1', 'ddL2', 'ddL3', 'ddL4', 'ddL5', 'ddL6' ... % Encoder noise
};
Gd.OutputName = {'y', 'z'}; % Vertical error of the sampleSensitivity to disturbances.
Estimation of maximum instrumentation noise
From previous analysis, we know how the noise of the instrumentation will affect the vertical error of the sample. Now, we want to determine specifications for each instrumentation such that the effect on the vertical error of the sample is within specifications.
Most stringent requirement:
- vertical vibrations less than the smallest expected beam size of 100nm
- This corresponds to a maximum allowed vibration of 15nm RMS
Assumption on the noise:
- uncorrelated, which is reasonable. This means that the PSD of the different noise sources adds up.
Use of system symmetry to simplify the analysis:
- the effect of all the struts on the vertical errors are identical (verify from the extracted sensitivity curves). Therefore only one strut can be considered for this analysis, and the total effect of the six struts is just six times the effect of one strut (in terms of power, but in terms of RMS value it's only sqrt(6)=2.5)
In order to have specifications for the noise of the instrumentations, assumptions:
- flat noise, which is quite typical
The noise specification is computed such that if all the instrumentation have this maximum noise, the specification in terms of vertical error is still respected. This is a pessimistic choice, but it gives a rough idea of the specifications.
% Maximum wanted effect of each noise source on the vertical error
% Specifications: 15nm RMS
% divide by sqrt(6) because 6 struts
% divide by sqrt(3) because 3 considered noise sources
max_asd_z = 15e-9 / sqrt(6) / sqrt(3); % [m/sqrt(Hz)]
% Suppose unitary flat noise ASD => compute the effect on vertical noise
unit_asd = ones(1, length(freqs));
rms_unit_asd_dac = sqrt(sum((unit_asd.*abs(squeeze(freqresp(Gd('z', 'du1' ), freqs, 'Hz'))).').^2));
rms_unit_asd_amp = sqrt(sum((unit_asd.*abs(squeeze(freqresp(Gd('z', 'du1' ), freqs, 'Hz'))).').^2));
rms_unit_asd_adc = sqrt(sum((unit_asd.*abs(squeeze(freqresp(Gd('z', 'dVs1'), freqs, 'Hz'))).').^2));
rms_unit_asd_enc = sqrt(sum((unit_asd.*abs(squeeze(freqresp(Gd('z', 'ddL1'), freqs, 'Hz'))).').^2));
% Obtained maximum ASD for different instruments
max_dac_asd = max_asd_z./rms_unit_asd_dac;
max_amp_asd = max_asd_z./rms_unit_asd_amp;
max_adc_asd = max_asd_z./rms_unit_asd_adc;
max_enc_asd = max_asd_z./rms_unit_asd_enc;
% Estimation of the equivalent RMS noise
max_dac_rms = max_dac_asd*sqrt(5e3)
max_amp_rms = max_amp_asd*sqrt(5e3)
max_adc_rms = max_adc_asd*sqrt(5e3)
max_enc_rms = max_enc_asd*sqrt(5e3)Obtained maximum noise are:
- DAC maximum output noise ASD $32\,\mu V/\sqrt{Hz}$.
- Voltage amplifier maximum noise (referred to input) ASD $32\,\mu V/\sqrt{Hz}$
- ADC maximum measurement noise ASD $22\,\mu V/\sqrt{Hz}$.
In terms of RMS noise,
- DAC and voltage amplifier: <1 mV RMS
- ADC: < 0.8 mV RMS
- Maybe make a table to summarize the specifications
If the Amplitude Spectral Density of the noise of the ADC, DAC and voltage amplifiers are all below the specified maximum noises, then the induced vertical error will be below 15nmRMS.
Choice of Instrumentation
<<sec:detail_instrumentation_choice>>
Introduction ignore
In previous section: noise characteristics. In this section, other characteristics (range, bandwidth, etc…)
ADC, DAC, Voltage amplifier, Encoder
Model of each instrument (transfer function + noise source).
In this section, also tell which instrumentation has been bought, and different options.
- block diagram of the model of the amplifier
Piezoelectric Voltage Amplifier
Low pass Filter
- Capacitance of the piezoelectric actuator
- Output impedance of the voltage amplifier
Noise: cite:&spengen20_high_voltag_amplif
Bandwidth: cite:&spengen16_high_voltag_amplif
A picture of the PD200 amplifier is shown in Figure ref:fig:amplifier_PD200.
The specifications as well as the amplifier characteristics as shown in the datasheet are summarized in Table ref:tab:pd200_characteristics.
| Characteristics | Manual | Specification |
|---|---|---|
| Input Voltage Range | +/- 10 [V] | +/- 10 [V] |
| Output Voltage Range | -50/150 [V] | -20/150 [V] |
| Gain | 20 [V/V] | |
| Maximum RMS current | 0.9 [A] | > 50 [mA] |
| Maximum Pulse current | 10 [A] | |
| Slew Rate | 150 [V/us] | |
| Noise (10uF load) | 0.7 [mV RMS] | < 2 [mV rms] |
| Small Signal Bandwidth (10uF load) | 7.4 [kHz] | > 5 [kHz] |
| Large Signal Bandwidth (150V, 10uF) | 300 [Hz] | > 1 [Hz] |
The most important characteristics are the large (small signal) bandwidth > 5 [kHz] and the small noise (< 2 [mV RMS]).
For a load capacitance of $10\,\mu F$, the expected $-3\,dB$ bandwidth is $6.4\,kHz$ (Figure ref:fig:pd200_expected_small_signal_bandwidth) and the low frequency noise is $650\,\mu V\,\text{rms}$ (Figure ref:fig:pd200_expected_noise).
These two characteristics are respectively measured in Section ref:sec:tf_meas and Section ref:sec:noise_meas.
#+caption:Expected small signal bandwidth
ADC
Talk about input impedance, … Add resistor, reading of the force sensor: ADC + test-bench-force-sensor
DAC
ADC and DAC need to be sample synchronously with the control system, with low jitter. cite:&abramovitch22_pract_method_real_world_contr_system cite:&abramovitch23_tutor_real_time_comput_issues_contr_system
Relative Displacement Sensors
- Encoders
- Capacitive Sensors
- Eddy current sensors
- Speak about slip-ring issue
Specifications:
- used for relative positioning
- vertical errors of 15nmRMS => 6nmRMS for each strut
- Stroke > 100um
The Vionic encoder is shown in Figure ref:fig:encoder_vionic.
From the Renishaw website:
The VIONiC encoder features the third generation of Renishaw's unique filtering optics that average the contributions from many scale periods and effectively filter out non-periodic features such as dirt. The nominally square-wave scale pattern is also filtered to leave a pure sinusoidal fringe field at the detector. Here, a multiple finger structure is employed, fine enough to produce photocurrents in the form of four symmetrically phased signals. These are combined to remove DC components and produce sine and cosine signal outputs with high spectral purity and low offset while maintaining bandwidth to beyond 500 kHz.
Fully integrated advanced dynamic signal conditioning, Auto Gain , Auto Balance and Auto Offset Controls combine to ensure ultra-low Sub-Divisional Error (SDE) of typically $<\pm 15\, nm$.
This evolution of filtering optics, combined with carefully-selected electronics, provide incremental signals with wide bandwidth achieving a maximum speed of 12 m/s with the lowest positional jitter (noise) of any encoder in its class. Interpolation is within the readhead, with fine resolution versions being further augmented by additional noise-reducing electronics to achieve jitter of just 1.6 nm RMS.
The expected interpolation errors (non-linearity) is shown in Figure ref:fig:vionic_expected_noise.

The characteristics as advertise in the manual as well as our specifications are shown in Table ref:tab:vionic_characteristics.
| Characteristics | Specification | Manual |
|---|---|---|
| Time Delay | < 0.5 ms | < 10 ns |
| Bandwidth | > 5 kHz | > 500 kHz |
| Noise | < 50 nm rms | < 1.6 nm rms |
| Linearity | < +/- 15 nm | |
| Range | > 200 um | Ruler length |
Characterization of Instrumentation
<<sec:detail_instrumentation_characterization>>
Introduction ignore
For each element, make a table with the specifications, and the measured performances for comparison.
Analog to Digital Converters
Quantization Noise
Let's note:
- $q = \frac{\Delta V}{2^n}$ the quantization in [V], which is the corresponding value in [V] of the least significant bit
- $\Delta V$ is the full range of the ADC in [V]
- $n$ is the number of ADC's bits
- $f_s$ is the sample frequency in [Hz]
%% Estimate quantization noise of the ADC
delta_V = 20; % +/-10 V
n = 16; % number of bits
Fs = 10e3; % [Hz]
q = delta_V/2^n; % Quantization in [V]
q_psd = q^2/12/Fs; % Quantization noise Power Spectral Density [V^2/Hz]
q_asd = sqrt(q_psd); % Quantization noise Amplitude Spectral Density [V/sqrt(Hz)]Let's suppose that the ADC is ideal and the only noise comes from the quantization error. Interestingly, the noise amplitude is uniformly distributed.
The quantization noise can take a value between $\pm q/2$, and the probability density function is constant in this range (i.e., it’s a uniform distribution). Since the integral of the probability density function is equal to one, its value will be $1/q$ for $-q/2 < e < q/2$ (Fig. ref:fig:probability_density_function_adc).
\begin{tikzpicture}
\path[fill=black!20!white] (-1, 0) |- (1, 1) |- (-1, 0);
\draw[->] (-2, 0) -- (2, 0) node[above left]{$e$};
\draw[->] (0, -0.5) -- (0, 2) node[below right]{$p(e)$};
\node[below] at (1, 0){$\frac{q}{2}$};
\node[below] at (-1, 0){$-\frac{q}{2}$};
\node[right] at (1, 1){$\frac{1}{q}$};
\end{tikzpicture}Now, we can calculate the time average power of the quantization noise as
\begin{equation} P_q = \int_{-q/2}^{q/2} e^2 p(e) de = \frac{q^2}{12} \end{equation}The other important parameter of a noise source is the power spectral density (PSD), which indicates how the noise power spreads in different frequency bands. To find the power spectral density, we need to calculate the Fourier transform of the autocorrelation function of the noise.
Assuming that the noise samples are not correlated with one another, we can approximate the autocorrelation function with a delta function in the time domain. Since the Fourier transform of a delta function is equal to one, the power spectral density will be frequency independent. Therefore, the quantization noise is white noise with total power equal to $P_q = \frac{q^2}{12}$.
Thus, the two-sided PSD (from $\frac{-f_s}{2}$ to $\frac{f_s}{2}$), we should divide the noise power $P_q$ by $f_s$:
\begin{equation} \int_{-f_s/2}^{f_s/2} \Gamma(f) d f = f_s \Gamma = \frac{q^2}{12} \end{equation}Finally, the Power Spectral Density of the quantization noise of an ADC is equal to:
\begin{equation} \begin{aligned} \Gamma &= \frac{q^2}{12 f_s} \\ &= \frac{\left(\frac{\Delta V}{2^n}\right)^2}{12 f_s} \text{ in } \left[ \frac{V^2}{Hz} \right] \end{aligned} \end{equation}Let's take a 16bits ADC with a range of +/-10V and a sample frequency of 10kHz.
The quantization is: \[ q = \frac{20}{2^{16}} \approx 0.3\,mV \]
\[ \Gamma_Q = \frac{q^2}{12 f_N} = 7.5 \cdot 10^{-13} \quad [V^2/Hz] \]
ASD: \[ 0.88\,\mu V/\sqrt{Hz} \]
Speedgoat - IO131 board
Internally uses the AD7609 ADC from Analog Devices. 200kSPS 16 bits +/-10V
oversampling: Analog to Digital Converters
cite:lab13_improv_adc
To have additional $w$ bits of resolution, the oversampling frequency $f_{os}$ should be:
\begin{equation} f_{os} = 4^w \cdot f_s \end{equation}cite:hauser91_princ_overs_conver
Key points to consider are:
- The noise must approximate white noise with uniform power spectral density over the frequency band of interest.
- The noise amplitude must be sufficient to cause the input signal to change randomly from sample to sample by amounts comparable to at least the distance between two adjacent codes (i.e., 1 LSB).
- The input signal can be represented as a random variable that has equal probability of existing at any value between two adjacent ADC codes.
- Check noise and compare with quantization noise
- See is oversampling increase performances, and how much compared to the prediction Seems to increase the perf too much
Measured Noise
adc_noise = load("2023-08-23_15-42_io131_adc_noise.mat");
adc_noise_os8 = load("2023-08-23_16-00_io131_adc_noise_os8.mat");
adc_noise_os16 = load("2023-08-23_16-02_io131_adc_noise_os16.mat");% Spectral Analysis parameters
Ts = 1e-4;
Nfft = floor(1/Ts);
win = hanning(Nfft);
Noverlap = floor(Nfft/2);
% Identification of the transfer function from Va to di
[pxx_adc, f] = pwelch(detrend(adc_noise.adc_1, 0), win, Noverlap, Nfft, 1/Ts);
[pxx_adc_os8, ~] = pwelch(detrend(adc_noise_os8.adc_1, 0), win, Noverlap, Nfft, 1/Ts);
[pxx_adc_os16, ~] = pwelch(detrend(adc_noise_os16.adc_1, 0), win, Noverlap, Nfft, 1/Ts);figure;
hold on;
plot(f, sqrt(pxx_adc), 'DisplayName', 'NOS')
plot(f, sqrt(pxx_adc_os8), 'DisplayName', '8 OS')
plot(f, sqrt(pxx_adc_os16), 'DisplayName', '16 OS')
plot([f(2), f(end)], [q_asd, q_asd], 'k--', 'DisplayName', 'Quantization noise')
hold off;
set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log');
xlabel('Frequency [Hz]'); ylabel('ASD [V/$\sqrt{Hz}$]');
ylim([1e-7, 1e-4])Instrumentation Amplifier
Because the ADC noise may be too large to measure noise of other instruments, a low noise instrumentation amplifier may be used.
Different instrumentation amplifiers were used:
- EG&G 5113, 4nV/sqrt(Hz), gain up to 100000 (100dB)
- Femto DLPVA-101-B-S 2nV/sqrt(Hz), gain from 20 to 80dB
- Koheron AMP200, 2.4nV/sqrt(Hz), gain up to 100
Here, the Femto amplifier is used. To measure its noise, the gain is set to xxdB, …
\begin{tikzpicture}
\node[block={0.6cm}{0.6cm}] (const) {$0$};
% Pre Amp
\node[addb, right=0.6 of const] (addna) {};
\node[block, right=0.4 of addna] (Ga) {$G_a(s)$};
% ADC
\node[addb, right=1.2 of Ga] (addqad){};
\node[ADC, right=0.4 of addqad] (ADC) {ADC};
\draw[->] (const.east) -- (addna.west);
\draw[->] (addna.east) -- (Ga.west);
\draw[->] (Ga.east) -- (addqad.west);
\draw[->] (addqad.east) -- (ADC.west);
\draw[->] (ADC.east) -- node[sloped]{$/$} ++(1.0, 0) node[above left]{$n$};
\draw[<-] (addna.north) -- ++(0, 0.6) node[below right](na){$n_{a}$};
\draw[<-] (addqad.north) -- ++(0, 0.6) node[below right](qad){$q_{ad}$};
\coordinate[] (top) at (na.north);
\coordinate[] (bot) at (Ga.south);
% 5113
\begin{scope}[on background layer]
\node[fit={(addna.west|-bot) (Ga.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {Pre Amp};
\end{scope}
% ADC
\begin{scope}[on background layer]
\node[fit={(addqad.west|-bot) (ADC.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {ADC};
\end{scope}
\end{tikzpicture}Digital to Analog Converters
Noise Measurement
In order not to have any quantization noise and only measure the output voltage noise of the DAC, we "ask" the DAC to output a zero voltage.
The measurement setup is schematically represented in Figure ref:fig:noise_measure_setup_dac. The gain of the pre-amplifier is adjusted such that the measured amplified noise is much larger than the quantization noise of the ADC.
The Amplitude Spectral Density $\Gamma_n(\omega)$ of the measured signal is computed. The Amplitude Spectral Density of the DAC output voltage noise $n_{da}$ can be computed taking into account the gain of the pre-amplifier:
\begin{equation} \Gamma_{n_{da}}(\omega) = \frac{\Gamma_m(\omega)}{|G_a(\omega)|} \end{equation}And it is verified that the Amplitude Spectral Density of $n_{da}$ is much larger than the one of $n_a$:
\begin{equation} \Gamma_{n_{da}} \gg \Gamma_{n_a} \end{equation}\begin{tikzpicture}
\node[block={0.6cm}{0.6cm}] (const) {$0$};
% DAC
\node[DAC, right=0.6 of const] (DAC) {DAC};
\node[addb, right=0.4 of DAC] (addnda){};
% Pre Amp
\node[addb, right=1.2 of addnda] (addna) {};
\node[block, right=0.4 of addna] (Ga) {$G_a(s)$};
% ADC
\node[addb, right=1.2 of Ga] (addqad){};
\node[ADC, right=0.4 of addqad] (ADC) {ADC};
\draw[->] (const.east) -- node[sloped]{$/$} (DAC.west);
\draw[->] (DAC.east) -- (addnda.west);
\draw[->] (addnda.east) -- (addna.west);
\draw[->] (addna.east) -- (Ga.west);
\draw[->] (Ga.east) -- (addqad.west);
\draw[->] (addqad.east) -- (ADC.west);
\draw[->] (ADC.east) -- node[sloped]{$/$} ++(1.0, 0);
\draw[<-] (addnda.north) -- ++(0, 0.6) node[below right](nda){$n_{da}$};
\draw[<-] (addna.north) -- ++(0, 0.6) node[below right](na){$n_{a}$};
\draw[<-] (addqad.north) -- ++(0, 0.6) node[below right](qad){$q_{ad}$};
\coordinate[] (top) at (na.north);
\coordinate[] (bot) at (Ga.south);
% DAC
\begin{scope}[on background layer]
\node[fit={(DAC.west|-bot) (addnda.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {DAC};
\end{scope}
% 5113
\begin{scope}[on background layer]
\node[fit={(addna.west|-bot) (Ga.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {Pre Amp};
\end{scope}
% ADC
\begin{scope}[on background layer]
\node[fit={(addqad.west|-bot) (ADC.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {ADC};
\end{scope}
\end{tikzpicture}The obtained Amplitude Spectral Density of the DAC's output voltage is shown in Figure ref:fig:asd_noise_dac.
Bandwidth
DAC is directly wired to the ADC. The transfer function from DAC to ADC is computed.
It corresponds to 1 sample delay.
data_dac_adc = ("2023-08-22_15-52_io131_dac_to_adc.mat");Piezoelectric Voltage Amplifier
Noise
PD200 - Low frequency noise measurement
The measurement setup is shown in Figure ref:fig:noise_measure_setup_pd200. The input of the PD200 amplifier is shunted with a 50 Ohm resistor such that there in no voltage input expected the PD200 input voltage noise. The gain of the pre-amplifier is increased in order to measure a signal much larger than the quantization noise of the ADC.
\begin{tikzpicture}
\node[block={0.6cm}{0.6cm}] (const) {$0$};
% PD200
\node[addb, right=0.6 of const] (addnp){};
\node[block, right=0.4 of addnp] (Gp){$G_p(s)$};
% Pre Amp
\node[addb, right=1.2 of Gp] (addna) {};
\node[block, right=0.4 of addna] (Ga) {$G_a(s)$};
% ADC
\node[addb, right=1.2 of Ga] (addqad){};
\node[ADC, right=0.4 of addqad] (ADC) {ADC};
\draw[->] (const.east) -- (addnp.west);
\draw[->] (addnp.east) -- (Gp.west);
\draw[->] (Gp.east) -- (addna.west);
\draw[->] (addna.east) -- (Ga.west);
\draw[->] (Ga.east) -- (addqad.west);
\draw[->] (addqad.east) -- (ADC.west);
\draw[->] (ADC.east) -- node[sloped]{$/$} ++(1.0, 0) node[above left]{$n$};
\draw[<-] (addnp.north) -- ++(0, 0.6) node[below right](np){$n_{p}$};
\draw[<-] (addna.north) -- ++(0, 0.6) node[below right](na){$n_{a}$};
\draw[<-] (addqad.north) -- ++(0, 0.6) node[below right](qad){$q_{ad}$};
\coordinate[] (top) at (na.north);
\coordinate[] (bot) at (Ga.south);
% PD200
\begin{scope}[on background layer]
\node[fit={(addnp.west|-bot) (Gp.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {PD200};
\end{scope}
% 5113
\begin{scope}[on background layer]
\node[fit={(addna.west|-bot) (Ga.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {Pre Amp};
\end{scope}
% ADC
\begin{scope}[on background layer]
\node[fit={(addqad.west|-bot) (ADC.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {ADC};
\end{scope}
\end{tikzpicture}The measured low frequency (<20Hz) output noise of one of the PD200 amplifiers is shown in Figure ref:fig:pd200_noise_time_lpf. It is very similar to the one specified in the datasheet in Figure ref:fig:pd200_expected_noise.
The obtained RMS and peak to peak values of the measured output noise are shown in Table ref:tab:rms_pkp_noise and found to be very similar to the specified ones.
| RMS [$\mu V$] | Peak to Peak [$mV$] | |
|---|---|---|
| Specification [$10\,\mu F$] | 714.0 | 4.3 |
| PD200 1 | 565.1 | 3.7 |
| PD200 2 | 767.6 | 3.5 |
| PD200 3 | 479.9 | 3.0 |
| PD200 4 | 615.7 | 3.5 |
| PD200 5 | 651.0 | 2.4 |
| PD200 6 | 473.2 | 2.7 |
| PD200 7 | 423.1 | 2.3 |
PD200 - High frequency noise measurement
The measurement setup is the same as in Figure ref:fig:noise_measure_setup_pd200.
The Amplitude Spectral Density $\Gamma_n(\omega)$ of the measured signal by the ADC is computed. The Amplitude Spectral Density of the input voltage noise of the PD200 amplifier $n_p$ is then computed taking into account the gain of the pre-amplifier and the gain of the PD200 amplifier:
\begin{equation} \Gamma_{n_p}(\omega) = \frac{\Gamma_n(\omega)}{|G_p(j\omega) G_a(j\omega)|} \end{equation}And we verify that we are indeed measuring the noise of the PD200 and not the noise of the pre-amplifier by checking that:
\begin{equation} \Gamma_{n_p}(\omega) |G_p(j\omega)| \ll \Gamma_{n_a} \end{equation}The Amplitude Spectral Density of the measured input noise is computed and shown in Figure ref:fig:asd_noise_pd200_10uF.
It is verified that the contribution of the PD200 noise is much larger than the contribution of the pre-amplifier noise of the quantization noise.
The Amplitude Spectral Density of the input noise of the PD200 amplifiers present sharp peaks. It is not clear yet what causes such peaks and if these peaks have high influence on the total RMS noise of the amplifiers.
Bandwidth
Maximum Frequency/Voltage to not overload the amplifier
<<sec:tf_meas_w_max>>
Then the maximum output current of the amplifier is reached, the amplifier automatically shuts down itself. We should then make sure that the output current does not reach this maximum specified current.
The maximum current is 1A [rms] which corresponds to 0.7A in amplitude of the sin wave.
The impedance of the capacitance is: \[ Z_C(\omega) = \frac{1}{jC\omega} \]
Therefore the relation between the output current amplitude and the output voltage amplitude for sinusoidal waves of frequency $\omega$: \[ V_{out} = \frac{1}{C\omega} I_{out} \]
Moreover, there is a gain of 20 between the input voltage and the output voltage: \[ 20 V_{in} = \frac{1}{C\omega} I_{out} \]
For a specified voltage input amplitude $V_{in}$, the maximum frequency at which the output current reaches its maximum value is:
\begin{equation} \boxed{\omega_{\text{max}} = \frac{1}{20 C V_{in}} I_{out,\text{max}}} \end{equation}with:
- $\omega_{\text{max}}$ the maximum input sinusoidal frequency in Radians per seconds
- $C$ the load capacitance in Farads
- $V_{in}$ the input voltage sinusoidal amplitude in Volts
- $I_{out,\text{max}}$ the specified maximum output current in Amperes
$\omega_{\text{max}}/2\pi$ as a function of $V_{in}$ is shown in Figure ref:fig:max_frequency_voltage.
When doing sweep sine excitation, we make sure not to reach this maximum excitation frequency.
Small Signal Bandwidth
<<sec:meas_small_signal_bandwidth>>
Here the small signal dynamics of all the 7 PD200 amplifiers are identified.
A (logarithmic) sweep sine excitation voltage is generated by the Speedgoat DAC with an amplitude of 0.1V and a frequency going from 1Hz up to 5kHz.
The output voltage of the PD200 amplifier is measured thanks to the monitor voltage of the PD200 amplifier. The input voltage of the PD200 amplifier (the generated voltage by the DAC) is measured with another ADC of the Speedgoat. This way, the time delay related to the ADC will not be apparent in the results.
The obtained transfer functions from $V_{in}$ to $V_{out}$ are shown in Figure ref:fig:pd200_small_signal_tf.
We can see the very well matching between all the 7 amplifiers. The amplitude is constant over a wide frequency band and the phase drop is limited to less than 1 degree up to 500Hz.
Model of the amplifier small signal dynamics
<<sec:model_small_signal_bandwidth>>
The identified dynamics in Figure ref:fig:pd200_small_signal_tf can very well be modeled this dynamics with a first order low pass filter (even a constant could work fine).
Below is the defined transfer function $G_p(s)$.
Gp = 20/(1 + s/2/pi/25e3);Comparison of the model with the identified dynamics is shown in Figure ref:fig:pd200_small_signal_tf_model.
#+caption:Bode plot of $G_d(s)$ as well as the identified transfer functions of all 7 amplifiers
And finally this model is saved.
save('mat/pd200_model.mat', 'Gp');Large Signal Bandwidth
<<sec:bandwidth_amplitude>>
The PD200 amplifiers will most likely not be used for large signals, but it is still nice to see how the amplifier dynamics is changing with the input voltage amplitude.
Several identifications using sweep sin were performed with input voltage amplitude ranging from 0.1V to 4V. The maximum excitation frequency for each amplitude was limited from the estimation in Section ref:sec:tf_meas_w_max.
The obtained transfer functions for the different excitation amplitudes are shown in Figure ref:fig:pd200_large_signal_tf. It is shown that the input voltage amplitude does not affect that much the amplifier dynamics.
Output Impedance
The goal of this experimental setup is to estimate the output impedance $R_\text{out}$ of the PD200 voltage amplifiers. A DAC with a constant output voltage (here 0.1V) is connected to the input of the PD200 amplifier.
Then, the output voltage of the PD200 amplifier is measured in two conditions:
- $V$ when the output is not connected to any load
- $V_p$ when a load $R = 10\,\Omega$ is connected at the output of the amplifier
The load and the output impedance form a voltage divider, and thus: \[ V^\prime = \frac{R}{R + R_\text{out}} V \]
From the two values of voltage, the output impedance of the amplifier can be estimated: \[ R_\text{out} = R \frac{V - V^\prime}{V^\prime} \]
A schematic of the setup is shown in Figure ref:fig:setup_output_impedance.

Below are defined the measured output voltages with and without the 10Ohm load:
R = 10; % Load [Ohm]
% V Vp
meas = [1.988, 1.794; % PD200 - 1
1.990, 1.789; % PD200 - 2
1.982, 1.795; % PD200 - 3
1.984, 1.789; % PD200 - 4
1.998, 1.810; % PD200 - 5
1.984, 1.799; % PD200 - 6
2.004, 1.812] % PD200 - 7The output impedance of the amplifier can then be estimated using:
\begin{equation} R_{\text{out}} = R_{\text{load}} \frac{V - V_p}{V} \end{equation}meas(:, 3) = R * (meas(:,1) - meas(:,2))./meas(:,2)The obtained output impedances are shown in Table ref:tab:pd200_output_impedance.
| PD200 | $V\ [V]$ | $V_p\ [V]$ | $R_\text{out}\ [\Omega]$ |
|---|---|---|---|
| 1 | 1.988 | 1.794 | 1.081 |
| 2 | 1.99 | 1.789 | 1.124 |
| 3 | 1.982 | 1.795 | 1.042 |
| 4 | 1.984 | 1.789 | 1.09 |
| 5 | 1.998 | 1.81 | 1.039 |
| 6 | 1.984 | 1.799 | 1.028 |
| 7 | 2.004 | 1.812 | 1.06 |
The output impedance of the PD200 Amplifier is estimated to be $\approx 1\,\Omega$.
Model
PD200 Amplifier noise model
<<sec:pd200_noise_model>>
Let's design a transfer function $G_n(s)$ whose norm represent the Amplitude Spectral Density of the input voltage noise of the PD200 amplifier as shown in Figure fig:pd200-model-schematic-normalized-bis.

A simple transfer function that allows to obtain a good fit is defined below.
%% Model of the PD200 Input Voltage Noise
Gn = 1e-5 * ((1 + s/2/pi/20)/(1 + s/2/pi/2))^2 /(1 + s/2/pi/5e3);The comparison between the measured ASD of the modeled ASD is done in Figure ref:fig:pd200_asd_noise_model.
Let's now compute the Cumulative Amplitude Spectrum corresponding to the measurement and the model and compare them.
The integration from low to high frequency and from high to low frequency are both shown in Figure ref:fig:pd200_cas_noise_model.
The fit between the model and the measurements is rather good considering the complex shape of the measured ASD and the simple model used.
The obtained RMS noise of the model is
ans = 1e6*20*sqrt(CPS_Gn(end))Finally the model of the amplifier noise is saved.
save('mat/pd200_model.mat', 'Gn', '-append');Voltage Amplifier Model
<<sec:amplifier_model>>
The Amplifier is characterized by its dynamics $G_p(s)$ from voltage inputs $V_{in}$ to voltage output $V_{out}$. Ideally, the gain from $V_{in}$ to $V_{out}$ is constant over a wide frequency band with very small phase drop.
It is also characterized by its input noise $n$.
The objective is therefore to determine the transfer function $G_p(s)$ from the input voltage to the output voltage as well as the Power Spectral Density $S_n(\omega)$ of the amplifier input noise.
As $G_p$ depends on the load capacitance, it should be measured when loading the amplifier with a $10\,\mu F$ capacitor.
\begin{tikzpicture}
\node[addb] (add) at (0,0) {};
\node[block, right=0.8 of add] (G) {$G_p(s)$};
\draw[<-] (add.west) -- ++(-1.2, 0) node[above right]{$V_{in}$};
\draw[->] (add.east) -- (G.west);
\draw[<-] (add.north) -- ++(0, 0.6) node[below right](n){$n$};
\draw[->] (G.east) -- ++(1.2, 0) node[above left]{$V_{out}$};
\begin{scope}[on background layer]
\node[fit={(G.south-|add.west) (n.north-|G.east)}, inner sep=8pt, draw, dashed, fill=black!20!white] (P) {};
\node[below] at (P.north) {PD-200};
\end{scope}
\end{tikzpicture}The input noise of the amplifier $n$ can be further modeled by shaping a white noise with unitary PSD $\tilde{n}$ with a transfer function $G_n(s)$ as shown in Figure …
The Amplitude Spectral Density $\Gamma_n$ is then:
\begin{equation} \Gamma_n(\omega) = |G_n(j\omega)| \Gamma_{\tilde{n}}(\omega) \end{equation}with $\Gamma_{\tilde{n}}(\omega) = 1$.
\begin{tikzpicture}
\node[addb] (add) at (0,0) {};
\node[block, above=0.5 of add] (Gn) {$G_n(s)$};
\node[block, right=0.8 of add] (G) {$G_p(s)$};
\draw[<-] (add.west) -- ++(-1.2, 0) node[above right]{$V_{in}$};
\draw[->] (add.east) -- (G.west);
\draw[->] (Gn.south) -- (add.north) node[above right]{$n$};
\draw[<-] (Gn.north) -- ++(0, 0.6) node[below right](n){$\tilde{n}$};
\draw[->] (G.east) -- ++(1.2, 0) node[above left]{$V_{out}$};
\begin{scope}[on background layer]
\node[fit={(G.south east) (n.north-|Gn.west)}, inner sep=8pt, draw, dashed, fill=black!20!white] (P) {};
\node[below] at (P.north) {PD-200};
\end{scope}
\end{tikzpicture}Conclusion
| Characteristics | Measurement | Manual | Specification |
|---|---|---|---|
| Input Voltage Range | - | +/- 10 [V] | +/- 10 [V] |
| Output Voltage Range | - | -50/150 [V] | -20/150 [V] |
| Gain | 20 [V/V] | - | |
| Maximum RMS current | 0.9 [A] | > 50 [mA] | |
| Maximum Pulse current | 10 [A] | - | |
| Slew Rate | 150 [V/us] | - | |
| Noise (10uF load) | 0.7 [mV RMS] | < 2 [mV rms] | |
| Small Signal Bandwidth (10uF load) | 7.4 [kHz] | > 5 [kHz] | |
| Large Signal Bandwidth (150V, 10uF) | 300 [Hz] | - |
Noise of the full setup with 16bits DAC
Let's now measure the noise of the full setup in Figure ref:fig:noise_meas_procedure_bis and analyze the results.
The Amplitude Spectral Density of the measured noise is computed and the shown in Figure ref:fig:asd_noise_tot.
We can very well see that to total measured noise is the sum of the DAC noise and the PD200 noise.
The input noise of the PD200 amplifier is limited by the output voltage noise of the DAC. Having a DAC with lower output voltage noise could lower the overall noise of the setup. SSI2V 20bits DACs are used in the next section to verify that.
Linear Encoders
- Section ref:sec:noise_bench: the measurement bench is described
- Section ref:sec:thermal_drifts: long measurement is performed to estimate the low frequency drifts in the measurement
- Section ref:sec:vionic_noise_time: high frequency measurements are performed to estimate the high frequency noise
- Section ref:sec:noise_asd: the Spectral density of the measurement noise is estimated
- Section ref:sec:vionic_noise_model: finally, the measured noise is modeled
Test Bench
<<sec:noise_bench>>
To measure the noise $n$ of the encoder, one can rigidly fix the head and the ruler together such that no motion should be measured. Then, the measured signal $y_m$ corresponds to the noise $n$.
The measurement bench is shown in Figures ref:fig:meas_bench_top_view and ref:fig:meas_bench_side_view. Note that the bench is then covered with a "plastic bubble sheet" in order to keep disturbances as small as possible.
Thermal drifts
<<sec:thermal_drifts>> Measured displacement were recording during approximately 40 hours with a sample frequency of 100Hz. A first order low pass filter with a corner frequency of 1Hz
enc_l = load('mat/noise_meas_40h_100Hz_1.mat', 't', 'x');The measured time domain data are shown in Figure ref:fig:vionic_drifts_time.
The measured data seems to experience a constant drift after approximately 20 hour. Let's estimate this drift.
The mean drift is approximately 60.9 [nm/hour] or 1.0 [nm/min]
Comparison between the data and the linear fit is shown in Figure ref:fig:vionic_drifts_linear_fit.
Let's now estimate the Power Spectral Density of the measured displacement. The obtained low frequency ASD is shown in Figure ref:fig:vionic_noise_asd_low_freq.
Time Domain signals
<<sec:vionic_noise_time>>
Then, and for all the 7 encoders, we record the measured motion during 100s with a sampling frequency of 20kHz.
The raw measured data as well as the low pass filtered data (using a first order low pass filter with a cut-off at 10Hz) are shown in Figure ref:fig:vionic_noise_raw_lpf.
The time domain data for all the encoders are compared in Figure ref:fig:vionic_noise_time.
We can see some drifts that are in the order of few nm to 20nm per minute. As shown in Section ref:sec:thermal_drifts, these drifts should diminish over time down to 1nm/min.
Noise Spectral Density
<<sec:noise_asd>>
The amplitude spectral densities for all the encoder are computed and shown in Figure ref:fig:vionic_noise_asd.
We can combine these measurements with the low frequency noise computed in Section ref:sec:thermal_drifts. The obtained ASD is shown in Figure ref:fig:vionic_noise_asd_combined.
Noise Model
<<sec:vionic_noise_model>>
Let's create a transfer function that approximate the measured noise of the encoder.
Gn_e = 1.8e-11/(1 + s/2/pi/1e4);The amplitude of the transfer function and the measured ASD are shown in Figure ref:fig:vionic_noise_asd_model.
The cumulative amplitude spectrum is now computed and shown in Figure ref:fig:vionic_noise_cas_model.
We can see that the Root Mean Square value of the measurement noise is $\approx 1.6 \, nm$ as advertise in the datasheet.
Automatic Gain Control
agc = load('noise_meas_80h_100Hz_1.mat', 't', 'x');
no_agc = load('noise_meas_100Hz_without_AGC.mat', 't', 'x');figure;
hold on;
plot(agc.t/3600, 1e9*agc.x)
plot(no_agc.t/3600, 1e9*no_agc.x)External Metrology
Different options:
- Attocube: issue of non-linearity estimated from the encoders
- Smaract
- QuDIS
For the final tests, QuDIS were used.
Conclusion
<<sec:detail_instrumentation_conclusion>>