140 KiB
Optimization using Finite Element Models
- Introduction
- Reduced order flexible bodies
- Actuator Selection
- Flexible Joint Design
- Conclusion
- Bibliography
- Footnotes
Introduction ignore
During the detailed design phase of the nano-hexapod, optimizing individual components while ensuring their dynamic compatibility with the complete system presents significant challenges. While Finite Element Analysis (FEA) serves as a powerful tool for component-level optimization, understanding how the dynamics of each element interacts within the complete nano-active stabilization system (NASS) becomes crucial. A full Finite Element Model (FEM) of the NASS, while theoretically possible, would prove impractical for simulating real-time control scenarios due to its computational complexity.
This chapter presents a hybrid modeling approach that combines finite element analysis with multi-body dynamics, enabling both detailed component optimization and efficient system-level simulation. The methodology employs reduced-order flexible bodies, whereby components whose dynamic properties are determined through FEA can be effectively integrated into the multi-body framework. The theoretical foundations and practical implementation of this approach are presented in Section ref:sec:detail_fem_super_element, where experimental validation using an Amplified Piezoelectric Actuator (APA) demonstrates the method's accuracy in predicting both open and closed-loop dynamic behavior.
This validated modeling framework is then applied to optimize two critical elements of the nano-hexapod: the actuators and the flexible joints. Section ref:sec:detail_fem_actuator examines the selection and characterization of the actuators, developing both high-fidelity and computationally efficient models that capture essential dynamic characteristics. Section ref:sec:detail_fem_joint addresses the design of flexible joints, where proper parasitic stiffness proves crucial for system performance. In both cases, the hybrid modeling approach enables detailed component optimization while maintaining the ability to predict system-level dynamic behavior, particularly under closed-loop control conditions.
Reduced order flexible bodies
<<sec:detail_fem_super_element>>
Introduction ignore
Components exhibiting complex dynamical behavior are frequently found to be unsuitable for direct implementation within multi-body models. These components are traditionally analyzed using Finite Element Analysis (FEA) software. However, a methodological bridge between these two analytical approaches has been established, whereby components whose dynamical properties have been determined through FEA can be successfully integrated into multi-body models cite:&hatch00_vibrat_matlab_ansys. This combined multibody-FEA modeling approach presents significant advantages, as it enables the accurate FE modeling to specific elements while maintaining the computational efficiency of multi-body analysis for the broader system cite:&rankers98_machin.
The investigation of this hybrid modeling approach is structured in three sections. First, the fundamental principles and methodological approaches of this modeling framework are introduced (Section ref:ssec:detail_fem_super_element_theory). It is then illustrated through its practical application to the modelling of an Amplified Piezoelectric Actuator (APA) (Section ref:ssec:detail_fem_super_element_example). Finally, the validity of this modeling approach is demonstrated through experimental validation, wherein the obtained dynamics from the hybrid modelling approach is compared with measurements (Section ref:ssec:detail_fem_super_element_validation).
Procedure
<<ssec:detail_fem_super_element_theory>>
In this modeling approach, some components within the multi-body framework are represented as reduced-order flexible bodies, wherein their modal behavior is characterized through reduced mass and stiffness matrices derived from finite element analysis (FEA) models. These matrices are generated via modal reduction techniques, specifically through the application of component mode synthesis (CMS), thus establishing this design approach as a combined multibody-FEA methodology.
Standard FEA implementations typically involve thousands or even hundreds of thousands of DoF, rendering direct integration into multi-body simulations computationally prohibitive. The objective of modal reduction is therefore to substantially decrease the number of DoF while preserving the essential dynamic characteristics of the component.
The procedure for implementing this reduction involves several distinct stages. Initially, the component is modeled in a finite element software with appropriate material properties and boundary conditions. Subsequently, interface frames are defined at locations where the multi-body model will establish connections with the component. These frames serve multiple functions, including connecting to other parts, applying forces and torques, and measuring relative motion between defined frames.
Following the establishment of these interface parameters, modal reduction is performed using the Craig-Bampton method cite:&craig68_coupl_subst_dynam_analy (also known as the "fixed-interface method"), a technique that significantly reduce the number of DoF while while still presenting the main dynamical characteristics. This transformation typically reduces the model complexity from hundreds of thousands to fewer than 100 DoF. The number of degrees of freedom in the reduced model is determined by eqref:eq:detail_fem_model_order where $n$ represents the number of defined frames and $p$ denotes the number of additional modes to be modeled. The outcome of this procedure is an $m \times m$ set of reduced mass and stiffness matrices, which can subsequently be incorporated into the multi-body model to represent the component's dynamic behavior.
\begin{equation}\label{eq:detail_fem_model_order} m = 6 × n + p
\end{equation}
Example with an Amplified Piezoelectric Actuator
<<ssec:detail_fem_super_element_example>>
Introduction ignore
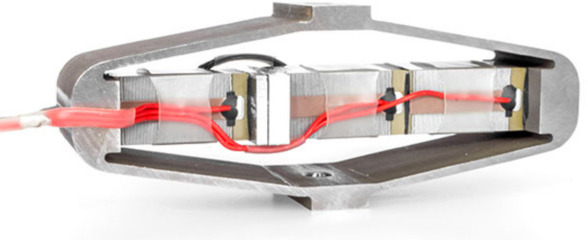
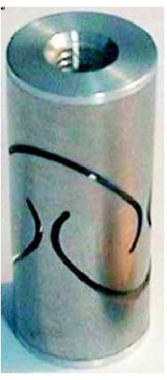
The presented modeling framework was first applied to an Amplified Piezoelectric Actuator (APA) for several reasons. Primarily, this actuator represents an excellent candidate for implementation within the nano-hexapod, as will be elaborated in Section ref:sec:detail_fem_actuator. Additionally, an Amplified Piezoelectric Actuator (the APA95ML shown in Figure ref:fig:detail_fem_apa95ml_picture) was available in the laboratory for experimental testing.
The APA consists of multiple piezoelectric stacks arranged horizontally (depicted in blue in Figure ref:fig:detail_fem_apa95ml_picture) and of an amplifying shell structure (shown in red) that serves two purposes: the application of pre-stress to the piezoelectric elements and the amplification of their displacement into the vertical direction cite:&claeyssen07_amplif_piezoel_actuat. The selection of the APA for validation purposes was further justified by its capacity to simultaneously demonstrate multiple aspects of the modeling framework. The specific design of the APA allows for the simultaneous modeling of a mechanical structure analogous to a flexible joint, piezoelectric actuation, and piezoelectric sensing, thereby encompassing the principal elements requiring validation.
\hfill
| Parameter | Value |
|---|---|
| Nominal Stroke | $100\,\mu m$ |
| Blocked force | $2100\,N$ |
| Stiffness | $21\,N/\mu m$ |
Finite Element Model
The development of the finite element model for the APA95ML necessitated the specification of appropriate material properties, as summarized in Table ref:tab:detail_fem_material_properties. The finite element mesh, shown in Figure ref:fig:detail_fem_apa95ml_mesh, was then generated.
| $E$ | $\nu$ | $\rho$ | |
|---|---|---|---|
| Stainless Steel | $190\,GPa$ | $0.31$ | $7800\,\text{kg}/m^3$ |
| Piezoelectric Ceramics (PZT) | $49.5\,GPa$ | $0.31$ | $7800\,\text{kg}/m^3$ |
The definition of interface frames, or "remote points", constitute a critical aspect of the model preparation. Seven frames were established: one frame at the two ends of each piezoelectric stack to facilitate strain measurement and force application, and additional frames at the top and bottom of the structure to enable connection with external elements in the multi-body simulation.
Six additional modes were considered, resulting in total model order of $48$. The modal reduction procedure was then executed, yielding the reduced mass and stiffness matrices that form the foundation of the component's representation in the multi-body simulation environment.
Super Element in the Multi-Body Model
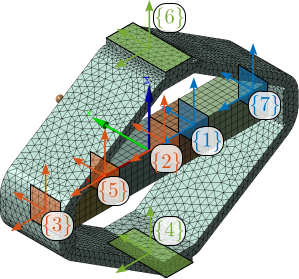
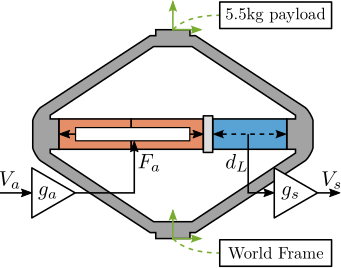
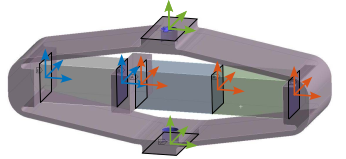
Previously computed reduced order mass and stiffness matrices were imported in a multi-body model block called "Reduced Order Flexible Solid". This block has several interface frames corresponding to the ones defined in the FEA software. Frame $\{4\}$ was connected to the "world" frame, while frame $\{6\}$ was coupled to a vertically guided payload. In this example, two piezoelectric stacks were used for actuation while one piezoelectric stack was used as a force sensor. Therefore, a force source $F_a$ operating between frames $\{3\}$ and $\{2\}$ was used, while a displacement sensor $d_L$ between frames $\{1\}$ and $\{7\}$ was used for the sensor stack. This is illustrated in Figure ref:fig:detail_fem_apa_model_schematic.
However, to have access to the physical voltage input of the actuators stacks $V_a$ and to the generated voltage by the force sensor $V_s$, conversion between the electrical and mechanical domains need to be determined.
Sensor and Actuator "constants"
To link the electrical domain to the mechanical domain, an "actuator constant" $g_a$ and a "sensor constant" $g_s$ were introduced as shown in Figure ref:fig:detail_fem_apa_model_schematic.
From cite:&fleming14_desig_model_contr_nanop_system p. 123, the relation between relative displacement $d_L$ of the sensor stack and generated voltage $V_s$ is given by eqref:eq:detail_fem_dl_to_vs.
\begin{equation}\label{eq:detail_fem_dl_to_vs} V_s = g_s ⋅ d_L, \quad g_s = \frac{d33}{ε^T s^D n}
\end{equation}
From cite:&fleming10_integ_strain_force_feedb_high the relation between the force $F_a$ and the applied voltage $V_a$ is given by eqref:eq:detail_fem_va_to_fa.
\begin{equation}\label{eq:detail_fem_va_to_fa} F_a = g_a ⋅ V_a, \quad g_a = d33 n k_a, \quad k_a = \frac{cE A}{L}
\end{equation}
Unfortunately, it is difficult to know exactly which material is used for the piezoelectric stacks1. Yet, based on the available properties of the stacks in the data-sheet (summarized in Table ref:tab:detail_fem_stack_parameters), the soft Lead Zirconate Titanate "THP5H" from Thorlabs seemed to match quite well the observed properties.
| Parameter | Unit | Value |
|---|---|---|
| Nominal Stroke | $\mu m$ | 20 |
| Blocked force | $N$ | 4700 |
| Stiffness | $N/\mu m$ | 235 |
| Voltage Range | $V$ | -20 to 150 |
| Capacitance | $\mu F$ | 4.4 |
| Length | $mm$ | 20 |
| Stack Area | $mm^2$ | 10x10 |
The properties of this "THP5H" material used to compute $g_a$ and $g_s$ are listed in Table ref:tab:test_apa_piezo_properties. From these parameters, $g_s = 5.1\,V/\mu m$ and $g_a = 26\,N/V$ were obtained.
| Parameter | Value | Description |
|---|---|---|
| $d_{33}$ | $680 \cdot 10^{-12}\,m/V$ | Piezoelectric constant |
| $\epsilon^{T}$ | $4.0 \cdot 10^{-8}\,F/m$ | Permittivity under constant stress |
| $s^{D}$ | $21 \cdot 10^{-12}\,m^2/N$ | Elastic compliance understand constant electric displacement |
| $c^{E}$ | $48 \cdot 10^{9}\,N/m^2$ | Young's modulus of elasticity |
| $L$ | $20\,mm$ per stack | Length of the stack |
| $A$ | $10^{-4}\,m^2$ | Area of the piezoelectric stack |
| $n$ | $160$ per stack | Number of layers in the piezoelectric stack |
%% Estimate "Sensor Constant" - (THP5H)
d33 = 680e-12; % Strain constant [m/V]
n = 160; % Number of layers per stack
eT = 4500*8.854e-12; % Permittivity under constant stress [F/m]
sD = 21e-12; % Compliance under constant electric displacement [m2/N]
gs = d33/(eT*sD*n); % Sensor Constant [V/m]
%% Estimate "Actuator Constant" - (THP5H)
d33 = 680e-12; % Strain constant [m/V]
n = 320; % Number of layers
cE = 1/sD; % Youngs modulus [N/m^2]
A = (10e-3)^2; % Area of the stacks [m^2]
L = 40e-3; % Length of the two stacks [m]
ka = cE*A/L; % Stiffness of the two stacks [N/m]
ga = d33*n*ka; % Actuator Constant [N/V]Identification of the APA Characteristics
Initial validation of the finite element model and its integration as a reduced-order flexible model within the multi-body model was accomplished through comparative analysis of key actuator characteristics against manufacturer specifications.
%% Load reduced order model
K = readmatrix('APA95ML_K.CSV'); % order: 48
M = readmatrix('APA95ML_M.CSV');
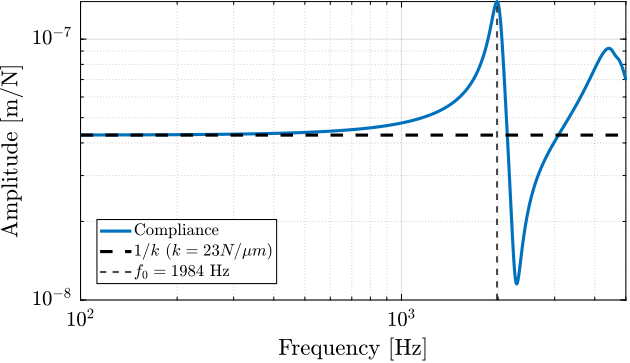
[int_xyz, int_i, n_xyz, n_i, nodes] = extractNodes('APA95ML_out_nodes_3D.txt');The stiffness of the APA95ML was estimated from the multi-body model by computing the axial compliance of the APA95ML (Figure ref:fig:detail_fem_apa95ml_compliance), which corresponds to the transfer function from a vertical force applied between the two interface frames to the relative vertical displacement between these two frames. The inverse of the DC gain this transfer function corresponds to the axial stiffness of the APA95ML. A value of $23\,N/\mu m$ was found which is close to the specified stiffness in the datasheet of $k = 21\,N/\mu m$.
%% Stiffness estimation
m = 0.0001; % block-free condition, no payload
k_support = 1e9;
c_support = 1e3;
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Fd'], 1, 'openinput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/y'], 1, 'openoutput'); io_i = io_i + 1;
G = linearize(mdl, io);
% The inverse of the DC gain of the transfer function
% from vertical force to vertical displacement is the axial stiffness of the APA
k_est = 1/dcgain(G); % [N/m]The multi-body model predicted a resonant frequency under block-free conditions of $\approx 2\,\text{kHz}$ (Figure ref:fig:detail_fem_apa95ml_compliance), which is in agreement with the nominal specification.
In order to estimate the stroke of the APA95ML, the mechanical amplification factor, defined as the ratio between vertical displacement and horizontal stack displacement, was first determined. This characteristic was quantified through analysis of the transfer function relating horizontal stack motion to vertical actuator displacement, from which an amplification factor of $1.5$ was derived.
The piezoelectric stacks, exhibiting a typical strain response of $0.1\,\%$ relative to their length (here equal to $20\,mm$), produce an individual nominal stroke of $20\,\mu m$ (see data-sheet of the piezoelectric stacks on Table ref:tab:detail_fem_stack_parameters, page pageref:tab:detail_fem_stack_parameters). As three stacks are used, the horizontal displacement is $60\,\mu m$. Through the established amplification factor of 1.5, this translates to a predicted vertical stroke of $90\,\mu m$ which falls within the manufacturer-specified range of $80\,\mu m$ and $120\,\mu m$.
The high degree of concordance observed across multiple performance metrics provides a first validation of the ability to include FEM into multi-body model.
Experimental Validation
<<ssec:detail_fem_super_element_validation>>
Introduction ignore
Further validation of the reduced-order flexible body methodology was undertaken through experimental investigation. The goal was to measure the dynamics of the APA95ML and to compare it with predictions derived from the multi-body model incorporating the actuator as a flexible element.
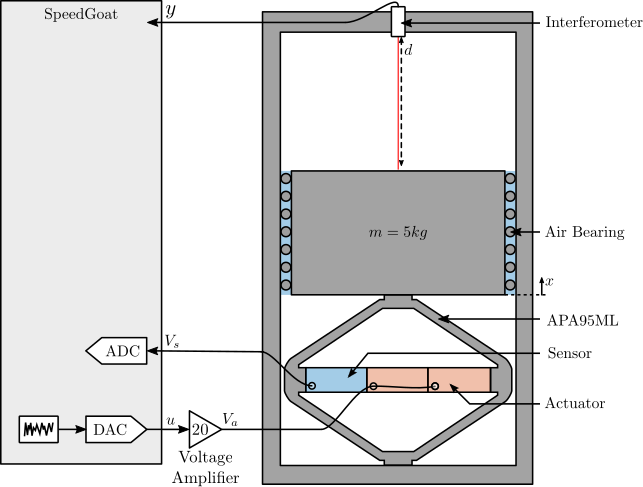
The test bench illustrated in Figure ref:fig:detail_fem_apa95ml_bench was used, which consists of a $5.7\,kg$ granite suspended on top of the APA95ML. The granite's motion was vertically guided with an air bearing system, and a fibered interferometer was used to measured its vertical displacement $y$. A digital-to-analog converter (DAC) was used to generate the control signal $u$, which was subsequently conditioned through a voltage amplifier with a gain of $20$, ultimately yielding the effective voltage $V_a$ across the two piezoelectric stacks. Measurement of the sensor stack voltage $V_s$ was performed using an analog-to-digital converter (ADC).
Comparison of the dynamics
Frequency domain system identification techniques were used to characterize the dynamic behavior of the APA95ML. The identification procedure necessitated careful choice of the excitation signal cite:&pintelon12_system_ident, chap. 5. Commonly employed excitation signals include impulses (which are particularly effective for modal analysis), steps, random noise signals, and multi-sine excitations During all this experimental work, random noise excitation was predominantly employed.
The designed excitation signal is then generated and both input and output signals are synchronously acquired. From the obtained input and output data, the frequency response functions were derived. To improve the quality of the obtained frequency domain data, averaging and windowing were used cite:&pintelon12_system_ident, chap. 13.
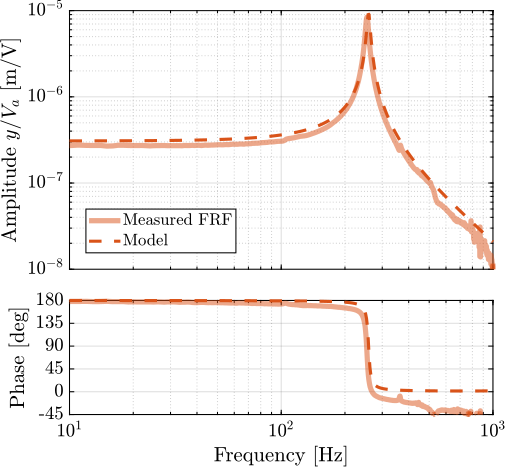
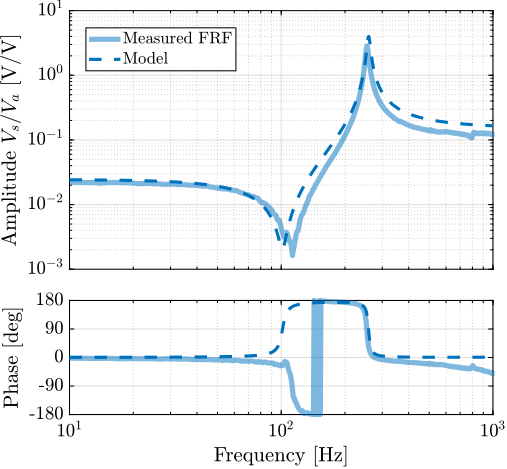
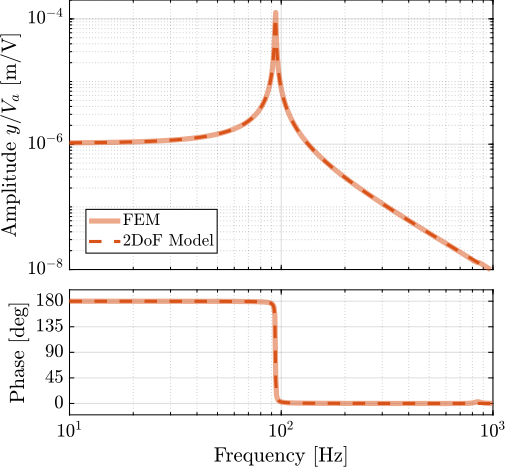
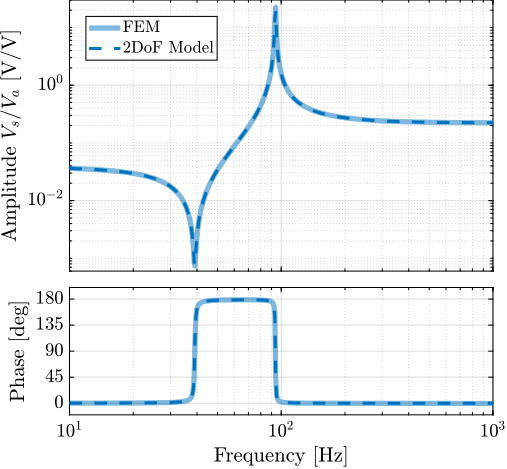
The obtained frequency response functions from $V_a$ to $V_s$ and to $y$ are compared with the theoretical predictions derived from the multi-body model in Figure ref:fig:detail_fem_apa95ml_comp_plant.
The difference in phase between the model and the measurements can be attributed to the sampling time of $0.1\,ms$ and to additional delays induced by electronic instrumentation related to the interferometer. The presence of a non-minimum phase zero in the measured system response (Figure ref:fig:detail_fem_apa95ml_comp_plant_sensor), shall be addressed during the experimental phase.
Regarding the amplitude characteristics, the constants $g_a$ and $g_s$ could be further refined through calibration against the experimental data.
%% Experimental plant identification
% with PD200 amplifier (gain of 20) - 2 stacks as an actuator, 1 as a sensor
load('apa95ml_5kg_2a_1s.mat')
Va = 20*u; % Voltage amplifier gain: 20
% Spectral Analysis parameters
Ts = t(end)/(length(t)-1);
Nfft = floor(1/Ts);
win = hanning(Nfft);
Noverlap = floor(Nfft/2);
% Identification of the transfer function from Va to di
[G_y, f] = tfestimate(detrend(Va, 0), detrend(y, 0), win, Noverlap, Nfft, 1/Ts);
[G_Vs, ~] = tfestimate(detrend(Va, 0), detrend(v, 0), win, Noverlap, Nfft, 1/Ts);
%% Plant Identification from Multi-Body model
% Load Reduced Order Matrices
K = readmatrix('APA95ML_K.CSV'); % order: 48
M = readmatrix('APA95ML_M.CSV');
[int_xyz, int_i, n_xyz, n_i, nodes] = extractNodes('APA95ML_out_nodes_3D.txt');
m = 5.5; % Mass of the suspended granite [kg]
k_support = 4e7;
c_support = 3e2;
% Compute transfer functions
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Va'], 1, 'openinput'); io_i = io_i + 1; % Voltage accros piezo stacks [V]
io(io_i) = linio([mdl, '/y'], 1, 'openoutput'); io_i = io_i + 1; % Vertical Displacement [m]
io(io_i) = linio([mdl, '/Vs'], 1, 'openoutput'); io_i = io_i + 1; % Sensor stack voltage [V]
Gm = linearize(mdl, io);
Gm.InputName = {'Va'};
Gm.OutputName = {'y', 'Vs'};Integral Force Feedback with APA
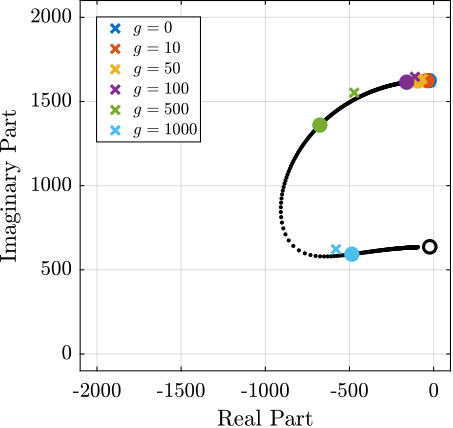
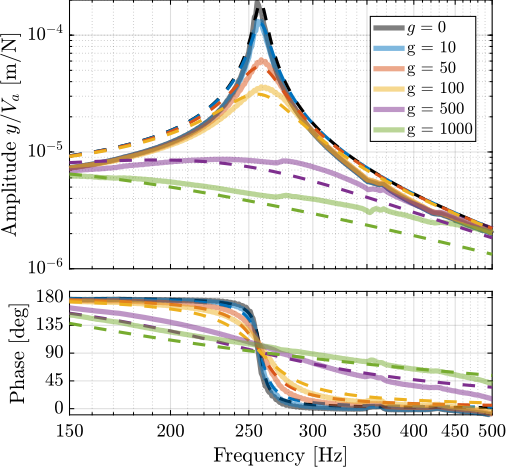
To further validate this modeling methodology, its ability to predict closed-loop behavior was verified experimentally. Integral Force Feedback (IFF) was implemented using the force sensor stack, and the measured dynamics of the damped system were compared with model predictions across multiple feedback gains.
The IFF controller implementation, defined in equation ref:eq:detail_fem_iff_controller, incorporated a tunable gain parameter $g$ and was designed to provide integral action near the system resonances and to limit the low frequency gain using an high pass filter.
\begin{equation}\label{eq:detail_fem_iff_controller} K_{\text{IFF}}(s) = \frac{g}{s + 2⋅ 2π} ⋅ \frac{s}{s + 0.5 ⋅ 2π}
\end{equation}
The theoretical damped dynamics of the closed-loop system was estimated using the model by computed the root locus plot shown in Figure ref:fig:detail_fem_apa95ml_iff_root_locus. For experimental validation, six gain values were tested: $g = [0,\,10,\,50,\,100,\,500,\,1000]$. The measured frequency responses for each gain configuration were compared with model predictions, as presented in Figure ref:fig:detail_fem_apa95ml_damped_plants.
The close agreement between experimental measurements and theoretical predictions across all gain configurations demonstrates the model's capability to accurately predict both open-loop and closed-loop system dynamics.
Conclusion
The experimental validation with an Amplified Piezoelectric Actuator confirms that this methodology accurately predicts both open-loop and closed-loop dynamic behaviors. This verification establishes its effectiveness for component design and system analysis applications.
The approach will be especially beneficial for optimizing actuators (Section ref:sec:detail_fem_actuator) and flexible joints (Section ref:sec:detail_fem_joint) for the nano-hexapod.
Actuator Selection
<<sec:detail_fem_actuator>>
Introduction ignore
The selection and modeling of actuators, that constitutes a critical step in the development of the nano-hexapod, is here presented. First, specifications for the nano-hexapod actuators are derived from previous analyses, leading to the selection of the actuator type and ultimately to a specific model (Section ref:ssec:detail_fem_actuator_specifications). Then, the chosen actuator is modeled using the reduced-order flexible body approach developed in the previous section, validating the choice of actuator through detailed dynamical analysis (Section ref:ssec:detail_fem_actuator_apa300ml). Finally, a simplified two-degree-of-freedom model is developed to facilitate time-domain simulations while maintaining accurate representation of the actuator's essential characteristics (Section ref:ssec:detail_fem_actuator_apa300ml_2dof).
Choice of the Actuator based on Specifications
<<ssec:detail_fem_actuator_specifications>>
The actuator selection process was driven by several critical requirements derived from previous dynamic analyses. A primary consideration is the actuator stiffness, which significantly impacts system dynamics through multiple mechanisms. The spindle rotation induces gyroscopic effects that modify plant dynamics and increase coupling, necessitating sufficient stiffness. Conversely, the actuator stiffness must be carefully limited to ensure the nano-hexapod's suspension modes remain below the problematic modes of the micro-station to limit the coupling between the two structures. These competing requirements suggest an optimal stiffness of approximately $1\,N/\mu m$.
Additional specifications arise from the control strategy and physical constraints. The implementation of the decentralized Integral Force Feedback (IFF) architecture necessitates force sensors to be collocated with each actuator. The system's geometric constraints limit the actuator height to 50mm, given the nano-hexapod's maximum height of 95mm and the presence of flexible joints at each strut extremity. Furthermore, the actuator stroke must exceed the micro-station positioning errors while providing additional margin for mounting adjustments and operational flexibility. An actuator stroke of $\approx 100\,\mu m$ is therefore required.
Three actuator technologies were evaluated (examples of such actuators are shown in Figure ref:fig:detail_fem_actuator_pictures): voice coil actuators, piezoelectric stack actuators, and amplified piezoelectric actuators. Variable reluctance actuators were not considered despite their superior efficiency compared to voice coil actuators, as their inherent nonlinearity would introduce unnecessary control complexity.
Voice coil actuators (shown in Figure ref:fig:detail_fem_voice_coil_picture), when combined with flexure guides of wanted stiffness ($\approx 1\,N/\mu m$), would require forces in the order of $100\,N$ to achieve the specified $100\,\mu m$ displacement. While these actuators offer excellent linearity and long strokes capabilities, the constant force requirement would result in significant steady-state current, leading to thermal loads that could compromise system stability. Their advantages (linearity and long stroke) were not considered adapted for this application, diminishing their benefits relative to piezoelectric solutions.
Conventional piezoelectric stack actuators (shown in Figure ref:fig:detail_fem_piezo_picture) present two significant limitations for the current application. Their stroke is inherently limited to approximately $0.1\,\%$ of their length, meaning that even with the maximum allowable height of $50\,mm$, the achievable stroke would only be $50\,\mu m$, insufficient for the application. Additionally, their extremely high stiffness, typically around $100\,N/\mu m$, exceeds the desired specifications by two orders of magnitude.
Amplified Piezoelectric Actuators (APAs) emerged as the optimal solution by addressing these limitations through a specific mechanical design. The incorporation of a shell structure serves multiple purposes: it provides mechanical amplification of the piezoelectric displacement, reduces the effective axial stiffness to more suitable levels for the application, and creates a compact vertical profile. Furthermore, the multi-stack configuration enables one stack to be dedicated to force sensing, ensuring excellent collocation with the actuator stacks, a critical feature for implementing robust decentralized IFF. Moreover, using APA for active damping has been successfully demonstrated in similar applications cite:&hanieh03_activ_stewar.
Several specific APA models were evaluated against the established specifications (Table ref:tab:detail_fem_piezo_act_models). The APA300ML emerged as the optimal choice. This selection was further reinforced by previous experience with APAs from the same manufacturer2, and particularly by the successful validation of the modeling methodology with a similar actuator (Section ref:ssec:detail_fem_super_element_example). The demonstrated accuracy of the modeling approach for the APA95ML provides confidence in the reliable prediction of the APA300ML's dynamic characteristics, thereby supporting both the selection decision and subsequent dynamical analyses.
| Specification | APA150M | APA300ML | APA400MML | FPA-0500E-P | FPA-0300E-S |
|---|---|---|---|---|---|
| Stroke $> 100\, [\mu m]$ | 187 | 304 | 368 | 432 | 240 |
| Stiffness $\approx 1\, [N/\mu m]$ | 0.7 | 1.8 | 0.55 | 0.87 | 0.58 |
| Resolution $< 2\, [nm]$ | 2 | 3 | 4 | ||
| Blocked Force $> 100\, [N]$ | 127 | 546 | 201 | 376 | 139 |
| Height $< 50\, [mm]$ | 22 | 30 | 24 | 27 | 16 |
APA300ML - Reduced Order Flexible Body
<<ssec:detail_fem_actuator_apa300ml>>
The validation of the APA300ML started by incorporating a "reduced order flexible body" into the multi-body model as explained in Section ref:sec:detail_fem_super_element. The FEA model was developed with particular attention to the placement of reference frames, as illustrated in Figure ref:fig:detail_fem_apa300ml_frames. Seven distinct frames were defined, with blue frames designating the force sensor stack interfaces for strain measurement, red frames denoting the actuator stack interfaces for force application and green frames for connecting to other elements. 120 additional modes were added during the modal reduction for a total order of 162. While this high order provides excellent accuracy for validation purposes, it proves computationally intensive for simulations.
The sensor and actuator "constants" ($g_s$ and $g_a$) derived in Section ref:ssec:detail_fem_super_element_example for the APA95ML were used for the APA300ML model, as both actuators employ identical piezoelectric stacks.
Simpler 2DoF Model of the APA300ML
<<ssec:detail_fem_actuator_apa300ml_2dof>>
To facilitate efficient time-domain simulations while maintaining essential dynamic characteristics, a simplified two-degree-of-freedom model, adapted from cite:&souleille18_concep_activ_mount_space_applic, was developed.
This model, illustrated in Figure ref:fig:detail_fem_apa_2dof_model, comprises three components. The mechanical shell is characterized by its axial stiffness $k_1$ and damping $c_1$. The actuator is modelled with stiffness $k_a$ and damping $c_a$, incorporating a force source $f$. This force is related to the applied voltage $V_a$ through the actuator constant $g_a$. The sensor stack is modeled with stiffness $k_e$ and damping $c_e$, with its deformation $d_L$ being converted to the output voltage $V_s$ through the sensor sensitivity $g_s$.
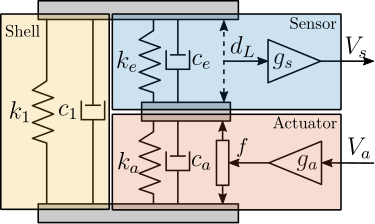
While providing computational efficiency, this simplified model has inherent limitations. It considers only axial behavior, treating the actuator as infinitely rigid in other directions. Several physical characteristics are not explicitly represented, including the mechanical amplification factor and the actual stress the piezoelectric stacks. Nevertheless, the model's primary advantage lies in its simplicity, adding only four states to the system model.
The model requires tuning of 8 parameters ($k_1$, $c_1$, $k_e$, $c_e$, $k_a$, $c_a$, $g_s$, and $g_a$) to match the dynamics extracted from the finite element analysis.
The shell parameters $k_1$ and $c_1$ were determined first through analysis of the zero in the $V_a$ to $V_s$ transfer function. The physical interpretation of this zero can be understood through Root Locus analysis: as controller gain increases, the poles of a closed-loop system converge to the open-loop zeros. The open-loop zero therefore corresponds to the poles of the system with a theoretical infinite-gain controller that ensures zero force in the sensor stack. This condition effectively represents the dynamics of an APA without the force sensor stack (i.e. an APA with only the shell). This physical interpretation enables straightforward parameter tuning: $k_1$ determines the frequency of the zero, while $c_1$ defines its damping characteristic.
The stack parameters ($k_a$, $c_a$, $k_e$, $c_e$) were then derived from the first pole of the $V_a$ to $y$ response. Given that identical piezoelectric stacks are used for both sensing and actuation, the relationships $k_e = 2k_a$ and $c_e = 2c_a$ were enforced, reflecting the series configuration of the dual actuator stacks. Finally, the sensitivities $g_s$ and $g_a$ were adjusted to match the DC gains of the respective transfer functions.
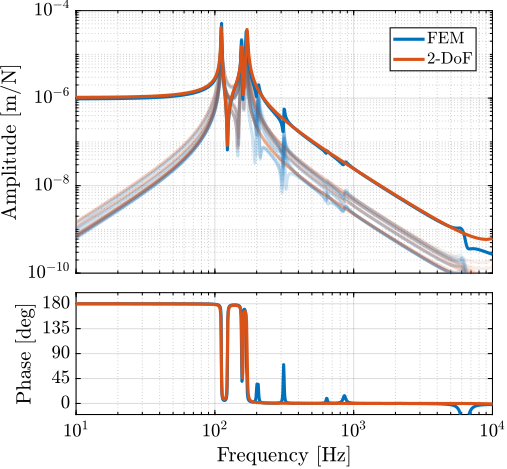
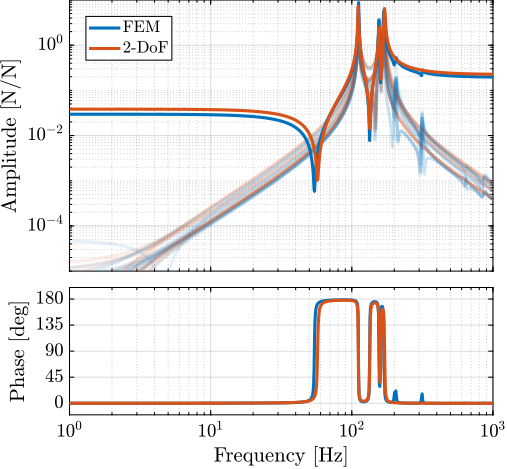
The resulting parameters, listed in Table ref:tab:detail_fem_apa300ml_2dof_parameters, yield dynamic behavior that closely matches the high-order finite element model, as demonstrated in Figure ref:fig:detail_fem_apa300ml_comp_fem_2dof_fem_2dof. While higher-order modes and non-axial flexibility are not captured, the model accurately represents the fundamental dynamics within the operational frequency range.
| Parameter | Value |
|---|---|
| $k_1$ | $0.30\,N/\mu m$ |
| $k_e$ | $4.3\, N/\mu m$ |
| $k_a$ | $2.15\,N/\mu m$ |
| $c_1$ | $18\,Ns/m$ |
| $c_e$ | $0.7\,Ns/m$ |
| $c_a$ | $0.35\,Ns/m$ |
| $g_a$ | $2.7\,N/V$ |
| $g_s$ | $0.53\,V/\mu m$ |
%% Identify dynamics with "Reduced Order Flexible Body"
K = readmatrix('APA300ML_mat_K.CSV');
M = readmatrix('APA300ML_mat_M.CSV');
[int_xyz, int_i, n_xyz, n_i, nodes] = extractNodes('APA300ML_out_nodes_3D.txt');
m = 5; % [kg]
ga = 25.9; % [N/V]
gs = 5.08e6; % [V/m]
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Va'], 1, 'openinput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/Fd'], 1, 'openinput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/z'], 1, 'openoutput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/Vs'], 1, 'openoutput'); io_i = io_i + 1;
G_fem = linearize(mdl, io);
G_fem_z = G_fem('z','Va');
G_fem_Vs = G_fem('Vs', 'Va');
G_fem_comp = G_fem('z', 'Fd');
%% Determine c1 and k1 from the zero
G_zeros = zero(minreal(G_fem_Vs));
G_zeros = G_zeros(imag(G_zeros)>0);
[~, i_sort] = sort(imag(G_zeros));
G_zeros = G_zeros(i_sort);
G_zero = G_zeros(1);
% Solving 2nd order equations
c1 = -2*m*real(G_zero);
k1 = m*(imag(G_zero)^2 + real(G_zero)^2);
%% Determine ka, ke, ca, ce from the first pole
G_poles = pole(minreal(G_fem_z));
G_poles = G_poles(imag(G_poles)>0);
[~, i_sort] = sort(imag(G_poles));
G_poles = G_poles(i_sort);
G_pole = G_poles(1);
% Solving 2nd order equations
ce = 3*(-2*m*real(G_pole(1)) - c1);
ca = 1/2*ce;
ke = 3*(m*(imag(G_pole)^2 + real(G_pole)^2) - k1);
ka = 1/2*ke;
%% Matching sensor/actuator constants
% ga = dcgain(G_fem_z) / (1/(ka + k1*ke/(k1 + ke)));
clear io; io_i = 1;
io(io_i) = linio([mdl, '_2dof', '/Fa'], 1, 'openinput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '_2dof', '/z'], 1, 'openoutput'); io_i = io_i + 1;
ga = dcgain(G_fem_z)/dcgain(linearize([mdl, '_2dof'], io));
clear io; io_i = 1;
io(io_i) = linio([mdl, '_2dof', '/Va'], 1, 'openinput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '_2dof', '/dL'], 1, 'openoutput'); io_i = io_i + 1;
gs = dcgain(G_fem_Vs)/dcgain(linearize([mdl, '_2dof'], io));
%% Identify dynamics with tuned 2DoF model
clear io; io_i = 1;
io(io_i) = linio([mdl, '_2dof', '/Va'], 1, 'openinput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '_2dof', '/Fd'], 1, 'openinput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '_2dof', '/z'], 1, 'openoutput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '_2dof', '/Vs'], 1, 'openoutput'); io_i = io_i + 1;
G_2dof = linearize([mdl, '_2dof'], io);
G_2dof_z = G_2dof('z','Va');
G_2dof_Vs = G_2dof('Vs', 'Va');
G_2dof_comp = G_2dof('z', 'Fd');Electrical characteristics of the APA
<<ssec:detail_fem_actuator_apa300ml_electrical>>
The behavior of piezoelectric actuators is characterized by coupled constitutive equations that establish relationships between electrical properties (charges, voltages) and mechanical properties (stress, strain) cite:&schmidt20_desig_high_perfor_mechat_third_revis_edition, chapter 5.5.
To evaluate the impact of electrical boundary conditions on the system dynamics, experimental measurements were conducted using the APA95ML, comparing the transfer function from $V_a$ to $y$ under two distinct configurations. With the force sensor stack in open-circuit condition (analogous to voltage measurement with high input impedance) and in short-circuit condition (similar to charge measurement with low output impedance). As demonstrated in Figure ref:fig:detail_fem_apa95ml_effect_electrical_boundaries, short-circuiting the force sensor stack results in a minor decrease in resonance frequency. The developed models of the APA do not represent such behavior, but as this effect is quite small, this validates the simplifying assumption made in the models.
%% Effect of electrical boundaries on the
oc = load('detail_fem_apa95ml_open_circuit.mat', 't', 'encoder', 'u');
sc = load('detail_fem_apa95ml_short_circuit.mat', 't', 'encoder', 'u');
% Spectral Analysis parameters
Ts = sc.t(end)/(length(sc.t)-1);
Nfft = floor(2/Ts);
win = hanning(Nfft);
Noverlap = floor(Nfft/2);
% Identification of the transfer function from Va to di
[G_oc, f] = tfestimate(detrend(oc.u, 0), detrend(oc.encoder, 0), win, Noverlap, Nfft, 1/Ts);
[G_sc, f] = tfestimate(detrend(sc.u, 0), detrend(sc.encoder, 0), win, Noverlap, Nfft, 1/Ts);
% Find resonance frequencies
[~, i_oc] = max(abs(G_oc(f<300)));
[~, i_sc] = max(abs(G_sc(f<300)));However, the electrical characteristics of the APA remain crucial for instrumentation design. Proper consideration must be given to voltage amplifier specifications and force sensor signal conditioning requirements. These aspects will be addressed in the instrumentation chapter.
Validation with the Nano-Hexapod
<<ssec:detail_fem_actuator_apa300ml_validation>>
The integration of the APA300ML model within the nano-hexapod simulation framework served two validation objectives: to validate the APA300ML choice through analysis of system dynamics with APA modelled as flexible bodies, and to validate the simplified 2DoF model through comparative analysis with the full FEM implementation.
The dynamics predicted using the flexible body model align well with the design requirements established during the conceptual phase. The dynamics from $\bm{u}$ to $\bm{V}_s$ exhibits the desired alternating pole-zero pattern (Figure ref:fig:detail_fem_actuator_fem_vs_perfect_hac_plant), a critical characteristic for implementing robust decentralized Integral Force Feedback. Additionally, the model predicts no problematic high-frequency modes in the dynamics from $\bm{u}$ to $\bm{\epsilon}_{\mathcal{L}}$ (Figure ref:fig:detail_fem_actuator_fem_vs_perfect_iff_plant), maintaining consistency with earlier conceptual simulations. These findings suggest that the control performance targets established during the conceptual phase remain achievable with the selected actuator.
Comparative analysis between the high-order FEM implementation and the simplified 2DoF model (Figure ref:fig:detail_fem_actuator_fem_vs_perfect_plants) demonstrates remarkable agreement in the frequency range of interest. This validates the use of the simplified model for time-domain simulations. The reduction in model order is substantial: while the FEM implementation results in approximately 300 states (36 states per actuator plus 12 additional states), the 2DoF model requires only 24 states for the complete nano-hexapod.
These results validate both the selection of the APA300ML and the effectiveness of the simplified modeling approach for the nano-hexapod.
%% Compare Dynamics between "Reduced Order" flexible joints and "2-dof and 3-dof" joints
% Let's initialize all the stages with default parameters.
initializeGround('type', 'rigid');
initializeGranite('type', 'rigid');
initializeTy('type', 'rigid');
initializeRy('type', 'rigid');
initializeRz('type', 'rigid');
initializeMicroHexapod('type', 'rigid');
initializeSample('m', 50);
initializeSimscapeConfiguration();
initializeDisturbances('enable', false);
initializeLoggingConfiguration('log', 'none');
initializeController('type', 'open-loop');
initializeReferences();
mdl = 'detail_fem_nass';
% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Controller'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/Tracking Error'], 1, 'openoutput', [], 'EdL'); io_i = io_i + 1; % Errors in the frame of the struts
io(io_i) = linio([mdl, '/NASS'], 3, 'openoutput', [], 'fn'); io_i = io_i + 1; % Force Sensors
% Flexible actuators
initializeSimplifiedNanoHexapod('actuator_type', 'flexible', ...
'flex_type_F', '2dof', ...
'flex_type_M', '3dof');
G_flex = linearize(mdl, io);
G_flex.InputName = {'f1', 'f2', 'f3', 'f4', 'f5', 'f6'};
G_flex.OutputName = {'l1', 'l2', 'l3', 'l4', 'l5', 'l6', 'fm1', 'fm2', 'fm3', 'fm4', 'fm5', 'fm6'};
% Actuators modeled as 2DoF system
initializeSimplifiedNanoHexapod('actuator_type', 'apa300ml', ...
'flex_type_F', '2dof', ...
'flex_type_M', '3dof');
G_ideal = linearize(mdl, io);
G_ideal.InputName = {'f1', 'f2', 'f3', 'f4', 'f5', 'f6'};
G_ideal.OutputName = {'l1', 'l2', 'l3', 'l4', 'l5', 'l6', 'fm1', 'fm2', 'fm3', 'fm4', 'fm5', 'fm6'};Flexible Joint Design
<<sec:detail_fem_joint>>
Introduction ignore
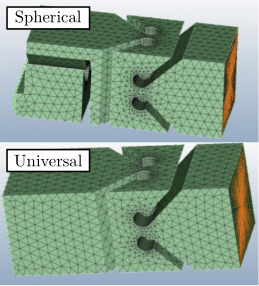
High-precision position control at the nanometer scale requires systems to be free from friction and backlash, as these nonlinear phenomena severely limit achievable positioning accuracy. This fundamental requirement prevents the use of conventional joints, necessitating instead the implementation of flexible joints that achieve motion through elastic deformation. For Stewart platforms requiring nanometric precision, numerous flexible joint designs have been developed and successfully implemented, as illustrated in Figure ref:fig:detail_fem_joints_examples. For design simplicity and component standardization, identical joints are employed at both ends of the nano-hexapod struts.
While ideally these joints would permit free rotation about defined axes while maintaining infinite rigidity in other degrees of freedom, practical implementations exhibit parasitic stiffness that can impact control performance cite:&mcinroy02_model_desig_flexur_joint_stewar. This section examines how these non-ideal characteristics affect system behavior, focusing particularly on bending/torsional stiffness (Section ref:ssec:detail_fem_joint_bending) and axial compliance (Section ref:ssec:detail_fem_joint_axial).
The analysis of bending and axial stiffness effects enables the establishment of comprehensive specifications for the flexible joints. These specifications guide the development and optimization of a flexible joint design through finite element analysis (Section ref:ssec:detail_fem_joint_specs). The validation process, detailed in Section ref:ssec:detail_fem_joint_validation, begins with the integration of the joints as "reduced order flexible bodies" in the nano-hexapod model, followed by the development of computationally efficient lower-order models that preserve the essential dynamic characteristics of the flexible joints.
Bending and Torsional Stiffness
<<ssec:detail_fem_joint_bending>>
The presence of bending stiffness in flexible joints causes the forces applied by the struts to deviate from the strut direction cite:&mcinroy02_model_desig_flexur_joint_stewar and can affect system dynamics.
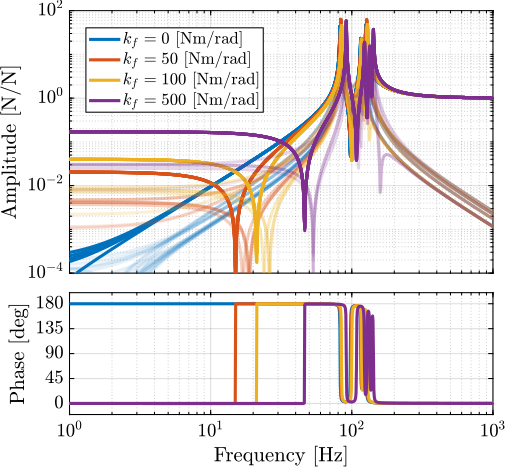
To quantify these effects, simulations were conducted with the micro-station considered rigid and using simplified 1DoF actuators (stiffness of $1\,N/\mu m$) without parallel stiffness to the force sensors. Flexible joint bending stiffness was varied from 0 (ideal case) to $500\,Nm/\text{rad}$.
Analysis of the plant dynamics reveals two significant effects. For the transfer function from $\bm{f}$ to $\bm{\epsilon}_{\mathcal{L}}$, bending stiffness increases low-frequency coupling, though this remains small for realistic stiffness values (Figure ref:fig:detail_fem_joints_bending_stiffness_hac_plant). In cite:&mcinroy02_model_desig_flexur_joint_stewar, it is established that forces remain effectively aligned with the struts when the flexible joint bending stiffness is much small than the actuator stiffness multiplied by the square of the strut length. For the nano-hexapod, this corresponds to having the bending stiffness much lower than 9000 Nm/rad. This condition is more readily satisfied with the relatively stiff actuators selected, and could be problematic for softer Stewart platforms.
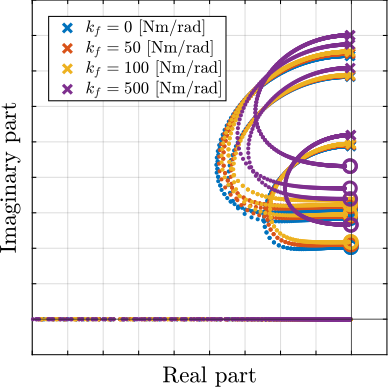
For the force sensor plant, bending stiffness introduces complex conjugate zeros at low frequency (Figure ref:fig:detail_fem_joints_bending_stiffness_iff_plant). This behavior resembles having parallel stiffness to the force sensor as was the case with the APA300ML (see Figure ref:fig:detail_fem_actuator_fem_vs_perfect_iff_plant). However, this time the parallel stiffness does not comes from the considered strut, but from the bending stiffness of the flexible joints of the other five struts. This characteristic impacts the achievable damping using decentralized Integral Force Feedback cite:&preumont07_six_axis_singl_stage_activ. This is confirmed by the Root Locus plot in Figure ref:fig:detail_fem_joints_bending_stiffness_iff_locus_1dof. This effect becomes less significant when using the selected APA300ML actuators (Figure ref:fig:detail_fem_joints_bending_stiffness_iff_locus_apa300ml), which already incorporate parallel stiffness by design which is higher than the one induced by flexible joint stiffness.
A parallel analysis of torsional stiffness revealed similar effects, though these proved less critical for system performance.
%% Identify the dynamics for several considered bending stiffnesses
% Let's initialize all the stages with default parameters.
initializeGround('type', 'rigid');
initializeGranite('type', 'rigid');
initializeTy('type', 'rigid');
initializeRy('type', 'rigid');
initializeRz('type', 'rigid');
initializeMicroHexapod('type', 'rigid');
initializeSample('m', 50);
initializeSimscapeConfiguration();
initializeDisturbances('enable', false);
initializeLoggingConfiguration('log', 'none');
initializeController('type', 'open-loop');
initializeReferences();
% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Controller'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/Tracking Error'], 1, 'openoutput', [], 'EdL'); io_i = io_i + 1; % Errors in the frame of the struts
io(io_i) = linio([mdl, '/NASS'], 3, 'openoutput', [], 'fn'); io_i = io_i + 1; % Force Sensors
% Effect of bending stiffness
Kf = [0, 50, 100, 500]; % [Nm/rad]
G_Kf = {zeros(length(Kf), 1)};
for i = 1:length(Kf)
% Limited joint axial compliance
initializeSimplifiedNanoHexapod('actuator_type', '1dof', ...
'flex_type_F', '2dof', ...
'flex_type_M', '3dof', ...
'actuator_k', 1e6, ...
'actuator_c', 1e1, ...
'actuator_kp', 0, ...
'actuator_cp', 0, ...
'Fsm', 56e-3, ... % APA300ML weight 112g
'Msm', 56e-3, ...
'Kf_F', Kf(i), ...
'Kf_M', Kf(i));
G_Kf(i) = {linearize(mdl, io)};
G_Kf{i}.InputName = {'f1', 'f2', 'f3', 'f4', 'f5', 'f6'};
G_Kf{i}.OutputName = {'l1', 'l2', 'l3', 'l4', 'l5', 'l6', 'fm1', 'fm2', 'fm3', 'fm4', 'fm5', 'fm6'};
end%% Identify the dynamics for several considered bending stiffnesses - APA300ML
G_Kf_apa300ml = {zeros(length(Kf), 1)};
for i = 1:length(Kf)
% Limited joint axial compliance
initializeSimplifiedNanoHexapod('actuator_type', 'apa300ml', ...
'flex_type_F', '2dof', ...
'flex_type_M', '3dof', ...
'Fsm', 56e-3, ... % APA300ML weight 112g
'Msm', 56e-3, ...
'Kf_F', Kf(i), ...
'Kf_M', Kf(i));
G_Kf_apa300ml(i) = {linearize(mdl, io)};
G_Kf_apa300ml{i}.InputName = {'f1', 'f2', 'f3', 'f4', 'f5', 'f6'};
G_Kf_apa300ml{i}.OutputName = {'l1', 'l2', 'l3', 'l4', 'l5', 'l6', 'fm1', 'fm2', 'fm3', 'fm4', 'fm5', 'fm6'};
endAxial Stiffness
<<ssec:detail_fem_joint_axial>>
The limited axial stiffness ($k_a$) of flexible joints introduces an additional compliance between the actuation point and the measurement point. As explained in cite:&preumont18_vibrat_contr_activ_struc_fourt_edition, chapter 6 and in cite:&rankers98_machin (effect called "actuator flexibility"), such intermediate flexibility invariably degrades control performance. Therefore, determining the minimum acceptable axial stiffness that maintains nano-hexapod performance becomes crucial.
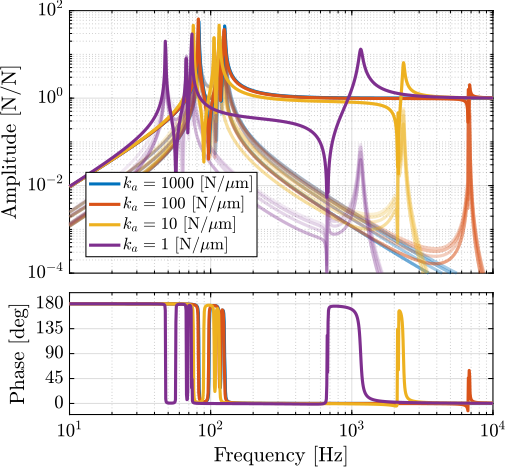
The analysis incorporates the strut mass (112g per APA300ML) to accurately model internal resonance effects. A parametric study was conducted by varying the axial stiffness from $1\,N/\mu m$ (matching actuator stiffness) to $1000\,N/\mu m$ (approximating rigid behavior). The resulting frequency responses (Figure ref:fig:detail_fem_joints_axial_stiffness_plants) reveal distinct effects on system dynamics.
The force-sensor (IFF) plant exhibits minimal sensitivity to axial compliance, as evidenced by both frequency response data (Figure ref:fig:detail_fem_joints_axial_stiffness_iff_plant) and root locus analysis (Figure ref:fig:detail_fem_joints_axial_stiffness_iff_locus).
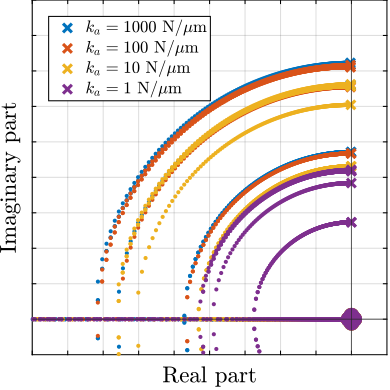
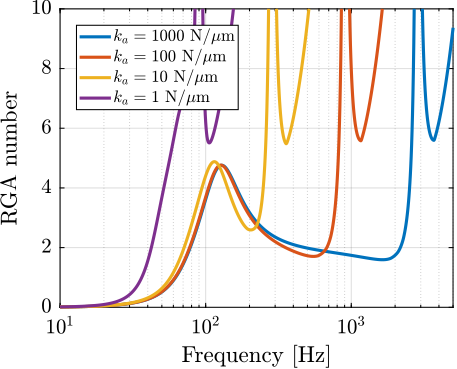
However, the transfer function from $\bm{f}$ to $\bm{\epsilon}_{\mathcal{L}}$ demonstrates significant effects: internal strut modes appear at high frequencies, introducing substantial cross-coupling between axes. This coupling is quantified through RGA analysis of the damped system (Figure ref:fig:detail_fem_joints_axial_stiffness_rga_hac_plant), which confirms increasing interaction between control channels at frequencies above the joint-induced resonance.
Above this resonance frequency, two critical limitations emerge. First, the system exhibits strong coupling between control channels, making decentralized control strategies ineffective. Second, control authority diminishes significantly near the resonant frequencies. These effects fundamentally limit achievable control bandwidth, making high axial stiffness essential for system performance.
Based on this analysis, an axial stiffness specification of $100\,N/\mu m$ was established for the nano-hexapod joints.
%% Identify the dynamics for several considered axial stiffnesses
% Let's initialize all the stages with default parameters.
initializeGround('type', 'rigid');
initializeGranite('type', 'rigid');
initializeTy('type', 'rigid');
initializeRy('type', 'rigid');
initializeRz('type', 'rigid');
initializeMicroHexapod('type', 'rigid');
initializeSample('m', 50);
initializeSimscapeConfiguration();
initializeDisturbances('enable', false);
initializeLoggingConfiguration('log', 'none');
initializeController('type', 'open-loop');
initializeReferences();
% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Controller'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/Tracking Error'], 1, 'openoutput', [], 'EdL'); io_i = io_i + 1; % Errors in the frame of the struts
io(io_i) = linio([mdl, '/NASS'], 3, 'openoutput', [], 'fn'); io_i = io_i + 1; % Force Sensors
% Effect of bending stiffness
Ka = 1e6*[1000, 100, 10, 1]; % [Nm/rad]
G_Ka = {zeros(length(Ka), 1)};
for i = 1:length(Ka)
% Limited joint axial compliance
initializeSimplifiedNanoHexapod('actuator_type', '1dof', ...
'flex_type_F', '2dof_axial', ...
'flex_type_M', '4dof', ...
'actuator_k', 1e6, ...
'actuator_c', 1e1, ...
'actuator_kp', 0, ...
'actuator_cp', 0, ...
'Fsm', 56e-3, ... % APA300ML weight 112g
'Msm', 56e-3, ...
'Ca_F', 1, ...
'Ca_M', 1, ...
'Ka_F', Ka(i), ...
'Ka_M', Ka(i));
G_Ka(i) = {linearize(mdl, io)};
G_Ka{i}.InputName = {'f1', 'f2', 'f3', 'f4', 'f5', 'f6'};
G_Ka{i}.OutputName = {'l1', 'l2', 'l3', 'l4', 'l5', 'l6', 'fm1', 'fm2', 'fm3', 'fm4', 'fm5', 'fm6'};
end%% Compute the damped plants
Kiff = -500 * ... % Gain
1/(s + 2*pi*0.1) * ... % LPF: provides integral action
eye(6); % Diagonal 6x6 controller (i.e. decentralized)
Kiff.InputName = {'fm1', 'fm2', 'fm3', 'fm4', 'fm5', 'fm6'};
Kiff.OutputName = {'u1iff', 'u2iff', 'u3iff', 'u4iff', 'u5iff', 'u6iff'};
% New damped plant input
S1 = sumblk("f1 = u1iff + u1");
S2 = sumblk("f2 = u2iff + u2");
S3 = sumblk("f3 = u3iff + u3");
S4 = sumblk("f4 = u4iff + u4");
S5 = sumblk("f5 = u5iff + u5");
S6 = sumblk("f6 = u6iff + u6");
G_Ka_iff = {zeros(1,length(Ka))};
for i=1:length(Ka)
G_Ka_iff(i) = {connect(G_Ka{i}, Kiff, S1, S2, S3, S4, S5, S6, {'u1', 'u2', 'u3', 'u4', 'u5', 'u6'}, {'l1', 'l2', 'l3', 'l4', 'l5', 'l6'})};
end
%% Interaction Analysis - RGA Number
rga = zeros(length(Ka), length(freqs));
for i = 1:length(Ka)
for j = 1:length(freqs)
rga(i,j) = sum(sum(abs(inv(evalfr(G_Ka_iff{i}({"l1", "l2", "l3", "l4", "l5", "l6"}, {"u1", "u2", "u3", "u4", "u5", "u6"}), 1j*2*pi*freqs(j)).').*evalfr(G_Ka_iff{i}({"l1", "l2", "l3", "l4", "l5", "l6"}, {"u1", "u2", "u3", "u4", "u5", "u6"}), 1j*2*pi*freqs(j)) - eye(6))));
end
endSpecifications and Design flexible joints
<<ssec:detail_fem_joint_specs>>
The design of flexible joints for precision applications requires careful consideration of multiple mechanical characteristics. Critical specifications include sufficient bending stroke to ensure long-term operation below yield stress, high axial stiffness for precise positioning, low bending and torsional stiffnesses to minimize parasitic forces, adequate load capacity, and well-defined rotational axes. Based on the dynamic analysis presented in previous sections, quantitative specifications were established and are summarized in Table ref:tab:detail_fem_joints_specs.
| Specification | FEM | |
|---|---|---|
| Axial Stiffness $k_a$ | $> 100\,N/\mu m$ | 94 |
| Shear Stiffness $k_s$ | $> 1\,N/\mu m$ | 13 |
| Bending Stiffness $k_f$ | $< 100\,Nm/\text{rad}$ | 5 |
| Torsion Stiffness $k_t$ | $< 500\,Nm/\text{rad}$ | 260 |
| Bending Stroke | $> 1\,\text{mrad}$ | 24.5 |
Among various possible flexible joint architectures, the design shown in Figure ref:fig:detail_fem_joints_design was selected for three key advantages. First, the geometry creates coincident $x$ and $y$ rotation axes, ensuring well-defined kinematic behavior, important for the precise definition of the nano-hexapod Jacobian matrix. Second, the design allows easy tuning of different directional stiffnesses through a limited number of geometric parameters. Third, the architecture inherently provides high axial stiffness while maintaining the required compliance in rotational degrees of freedom.
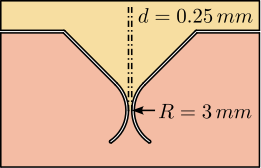
The joint geometry was optimized through parametric finite element analysis. The optimization process revealed an inherent trade-off between maximizing axial stiffness and achieving sufficiently low bending/torsional stiffness, while maintaining material stresses within acceptable limits. The final design, featuring a neck dimension of 0.25mm, achieves mechanical properties closely matching the target specifications, as verified through finite element analysis and summarized in Table ref:tab:detail_fem_joints_specs.
Validation with the Nano-Hexapod
<<ssec:detail_fem_joint_validation>>
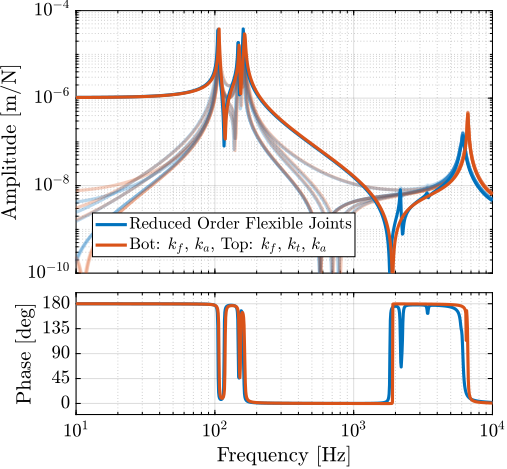
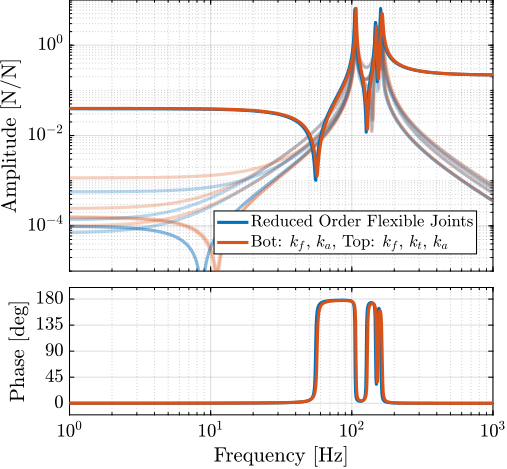
The designed flexible joint was first validated through integration into the nano-hexapod model using reduced-order flexible bodies derived from finite element analysis. This high-fidelity representation was created by defining two interface frames (Figure ref:fig:detail_fem_joints_frames) and extracting six additional modes, resulting in reduced-order mass and stiffness matrices of dimension $18 \times 18$. The computed transfer functions from actuator forces to both force sensor measurements ($\bm{f}$ to $\bm{f}_m$) and external metrology ($\bm{f}$ to $\bm{\epsilon}_{\mathcal{L}}$) demonstrate dynamics consistent with predictions from earlier analyses (Figure ref:fig:detail_fem_joints_fem_vs_perfect_plants), thereby validating the joint design.

%% Extract stiffness of the joint from the reduced order model
% We first extract the stiffness and mass matrices.
K = readmatrix('flex025_mat_K.CSV');
M = readmatrix('flex025_mat_M.CSV');
% Then, we extract the coordinates of the interface nodes.
[int_xyz, int_i, n_xyz, n_i, nodes] = extractNodes('flex025_out_nodes_3D.txt');
m = 1;
%% Name of the Simulink File
mdl = 'detail_fem_joint';
%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/T'], 1, 'openinput'); io_i = io_i + 1; % Forces and Torques
io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Translations and Rotations
G = linearize(mdl, io);
% Stiffness extracted from the Simscape model
k_a = 1/dcgain(G(3,3)); % Axial stiffness [N/m]
k_f = 1/dcgain(G(4,4)); % Bending stiffness [N/m]
k_t = 1/dcgain(G(6,6)); % Torsion stiffness [N/m]
% Stiffness extracted from the Stiffness matrix
k_s = K(1,1); % shear [N/m]
% k_s = K(2,2); % shear [N/m]
k_a = K(3,3); % axial [N/m]
k_f = K(4,4); % bending [Nm/rad]
% k_f = K(5,5); % bending [Nm/rad]
k_t = K(6,6); % torsion [Nm/rad]While this detailed modeling approach provides high accuracy, it results in a significant increase in system model order. The complete nano-hexapod model incorporates 240 states: 12 for the payload (6 DOF), 12 for the 2DOF struts, and 216 for the flexible joints (18 states for each of the 12 joints). To improve computational efficiency, a low order representation was developed using simplified joint elements with selective compliance DoF.
After evaluating various configurations, a compromise was achieved by modeling bottom joints with bending and axial stiffness ($k_f$ and $k_a$), and top joints with bending, torsional, and axial stiffness ($k_f$, $k_t$ and $k_a$). This simplification reduces the total model order to 48 states: 12 for the payload, 12 for the struts, and 24 for the joints (12 each for bottom and top joints). While additional degrees of freedom could potentially capture more dynamic features, the selected configuration preserves essential system characteristics while minimizing computational complexity.
%% Compare Dynamics between "Reduced Order" flexible joints and "2-dof and 3-dof" joints
% Let's initialize all the stages with default parameters.
initializeGround('type', 'rigid');
initializeGranite('type', 'rigid');
initializeTy('type', 'rigid');
initializeRy('type', 'rigid');
initializeRz('type', 'rigid');
initializeMicroHexapod('type', 'rigid');
initializeSample('m', 50);
initializeSimscapeConfiguration();
initializeDisturbances('enable', false);
initializeLoggingConfiguration('log', 'none');
initializeController('type', 'open-loop');
initializeReferences();
mdl = 'detail_fem_nass';
% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Controller'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/Tracking Error'], 1, 'openoutput', [], 'EdL'); io_i = io_i + 1; % Errors in the frame of the struts
io(io_i) = linio([mdl, '/NASS'], 3, 'openoutput', [], 'fn'); io_i = io_i + 1; % Force Sensors
% Fully flexible joints
initializeSimplifiedNanoHexapod('actuator_type', 'apa300ml', ...
'flex_type_F', 'flexible', ...
'flex_type_M', 'flexible', ...
'Fsm', 56e-3, ... % APA300ML weight 112g
'Msm', 56e-3);
G_flex = linearize(mdl, io);
G_flex.InputName = {'f1', 'f2', 'f3', 'f4', 'f5', 'f6'};
G_flex.OutputName = {'l1', 'l2', 'l3', 'l4', 'l5', 'l6', 'fm1', 'fm2', 'fm3', 'fm4', 'fm5', 'fm6'};
% Flexible joints modelled by 2DoF and 3DoF joints
initializeSimplifiedNanoHexapod('actuator_type', 'apa300ml', ...
'flex_type_F', '2dof_axial', ...
'flex_type_M', '4dof', ...
'Kf_F', k_f, ...
'Kt_F', k_t, ...
'Ka_F', k_a, ...
'Kf_M', k_f, ...
'Kt_M', k_t, ...
'Ka_M', k_a, ...
'Cf_F', 1e-2, ...
'Ct_F', 1e-2, ...
'Ca_F', 1e-2, ...
'Cf_M', 1e-2, ...
'Ct_M', 1e-2, ...
'Ca_M', 1e-2, ...
'Fsm', 56e-3, ... % APA300ML weight 112g
'Msm', 56e-3);
G_ideal = linearize(mdl, io);
G_ideal.InputName = {'f1', 'f2', 'f3', 'f4', 'f5', 'f6'};
G_ideal.OutputName = {'l1', 'l2', 'l3', 'l4', 'l5', 'l6', 'fm1', 'fm2', 'fm3', 'fm4', 'fm5', 'fm6'};Conclusion
<<sec:detail_fem_conclusion>>
In this chapter, the methodology of combining finite element analysis with multi-body modeling has been demonstrated and validated, proving particularly valuable for the detailed design of nano-hexapod components. The approach was first validated using an amplified piezoelectric actuator, where predicted dynamics showed excellent agreement with experimental measurements for both open and closed-loop behavior. This validation established confidence in the method's ability to accurately predict component behavior within a larger system.
The methodology was then successfully applied to optimize two critical components. For the actuators, it enabled validation of the APA300ML selection while providing both high-fidelity and computationally efficient models for system simulation. Similarly, for the flexible joints, the analysis of bending and axial stiffness effects led to clear specifications and an optimized design that balances competing mechanical requirements. In both cases, the ability to seamlessly integrate finite element models into the multi-body framework proved essential for understanding component interactions and their impact on system-level dynamics.
A key outcome of this work is the development of reduced-order models that maintain prediction accuracy while enabling efficient time-domain simulation. Such model reduction, guided by detailed understanding of component behavior, provides the foundation for subsequent control system design and optimization.