34 KiB
Measurements On the Slip-Ring
- Effect of the Slip-Ring on the signal when turned ON - Geophone measurement
- Measure of the noise induced by the Slip-Ring using voltage amplifiers - Geophone
- New LPF at 1kHz
- Effect of the rotation of the Slip-Ring - Noise
- Measure of the noise induced by the Slip-Ring using voltage amplifiers - Noise
- Measure of the noise induced by the Slip-Ring rotation - LPF added
First, the noise induced by the slip-ring is measured when using geophones:
-
Section sec:meas_slip_ring_geophone:
- A geophone located at the sample location is measured with its signal going directly to the ADC and going through the slip-ring
- The voltage amplifiers where saturating due to high frequency noise
-
Section sec:meas_sr_geophone:
- A Low Pass Filter is added before the voltage amplifiers
- Using a Oscilloscope, high frequency noise at 40kHz generated by the slip-ring has been identified
- With the additional low pass filter at the input of the voltage amplifiers, the slip-ring don't add any measurable noise to the signal
Then, we determine is the slip-ring add some noise to the signal when it is turning:
-
Section sec:meas_effect_sr:
- Noise is generated by the Speedgoat DAC and goes trough the slip-ring two times
- We measure the signal when it is OFF, ON but not turning and ON and turning
- However, the measurement is limited by the ADC noise
-
Section sec:meas_slip_ring:
- Voltage amplifiers are added, and the same measurements are done
- However, the voltage amplifiers are saturating because of high frequency noise
-
Section sec:meas_slip_ring_lpf:
- Low pass filter are added at the input of the voltage amplifier and the same measurement is done
Effect of the Slip-Ring on the signal when turned ON - Geophone measurement
<<sec:meas_slip_ring_geophone>>
All the files (data and Matlab scripts) are accessible here.
Experimental Setup
Goal: The goal is to determine if some noise is added to a signal passing through the slip-ring.
Setup: Two measurements are made with the control systems of all the stages turned OFF.
One geophone is located on the marble while the other is located at the sample location (figure fig:setup_slipring).
The two signals from the geophones are amplified with voltage amplifiers with the following settings:
- Gain: 60dB
- AC/DC switch: AC
- Low pass filter at the output set at 1kHz

Measurements: Two measurements are done:
| Measurement File | Description |
|---|---|
mat/meas_018.mat |
Signal goes through the Slip-ring (as shown on the figure above) |
mat/meas_019.mat |
Signal from the top geophone does not goes through the Slip-ring |
Each of the measurement mat file contains one data array with 3 columns:
| Column number | Description |
|---|---|
| 1 | Geophone - Marble |
| 2 | Geophone - Sample |
| 3 | Time |
Load data
We load the data of the z axis of two geophones.
meas_sr = load('mat/data_018.mat', 'data'); meas_sr = meas_sr.data;
meas_di = load('mat/data_019.mat', 'data'); meas_di = meas_di.data;Analysis - Time Domain
First, we compare the time domain signals for the two experiments (figure fig:slipring_time).
figure;
hold on;
plot(meas_di(:, 3), meas_di(:, 2), 'DisplayName', 'Geophone - Direct');
plot(meas_sr(:, 3), meas_sr(:, 2), 'DisplayName', 'Geophone - Slip-Ring');
hold off;
xlabel('Time [s]'); ylabel('Voltage [V]');
xlim([0, 50]);
legend('location', 'northeast'); <<plt-matlab>>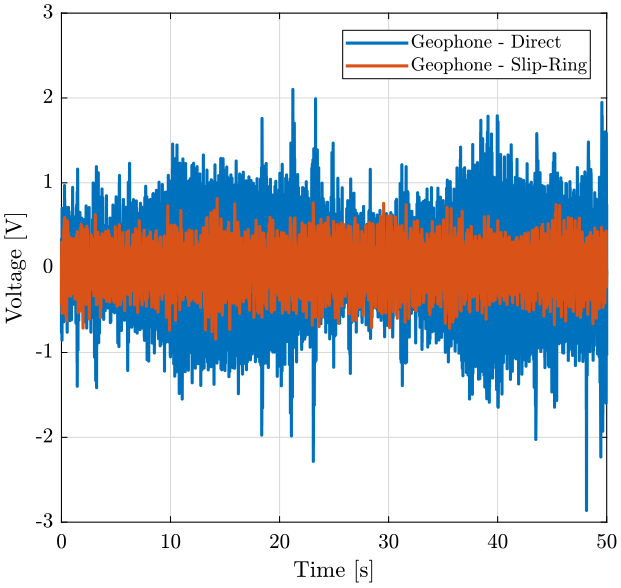
Analysis - Frequency Domain
We then compute the Power Spectral Density of the two signals and we compare them (figure fig:slipring_asd).
dt = meas_di(2, 3) - meas_di(1, 3);
Fs = 1/dt;
win = hanning(ceil(5*Fs)); [px_di, f] = pwelch(meas_di(:, 2), win, [], [], Fs);
[px_sr, ~] = pwelch(meas_sr(:, 2), win, [], [], Fs); figure;
hold on;
plot(f, sqrt(px_sr), 'DisplayName', 'Slip-Ring');
plot(f, sqrt(px_di), 'DisplayName', 'Wire');
hold off;
set(gca, 'xscale', 'log');
set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('Amplitude Spectral Density $\left[\frac{V}{\sqrt{Hz}}\right]$')
xlim([1, 500]);
legend('Location', 'southwest'); <<plt-matlab>>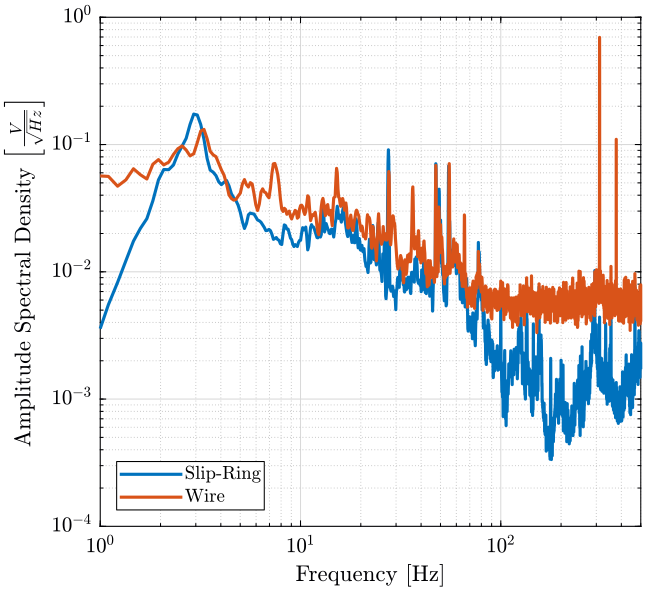
Conclusion
- The voltage amplifiers are saturating during the measurements (as shown by the LED on figure fig:setup_slipring)
- This saturation is mainly due to high frequency noise => a LPF will be added at the input of the voltage amplifiers in the further measurements
- The measurements will be redone
Measure of the noise induced by the Slip-Ring using voltage amplifiers - Geophone
<<sec:meas_sr_geophone>>
All the files (data and Matlab scripts) are accessible here.
First Measurement without LPF
Measurement Description
Goal:
- Determine if the noise induced by the slip-ring is a limiting factor when measuring the signal coming from a geophone
Setup:
- The geophone is located at the sample location
-
The two Voltage amplifiers have the same following settings:
- Gain: 60dB
- AC/DC option: AC
- Low pass filter at the output set to 1kHz
-
The signal from the geophone is split into two using a T-BNC:
- One part goes directly to the voltage amplifier and then to the ADC
- The other part goes to the slip-ring=>voltage amplifier=>ADC
Measurements: Two measurements are done:
| Measurement File | Description |
|---|---|
data_012 |
Slip-Ring OFF |
data_013 |
Slip-Ring ON |
Each of the measurement mat file contains one data array with 3 columns:
| Column number | Description |
|---|---|
| 1 | Measure of the geophone at the sample position with a direct wire |
| 2 | Measure of the geophone at the sample position going through the slip-ring |
| 3 | Time |
Load data
We load the data of the z axis of two geophones.
sr_off = load('mat/data_012.mat', 'data'); sr_off = sr_off.data;
sr_on = load('mat/data_013.mat', 'data'); sr_on = sr_on.data;Time Domain
We compare the signal when the Slip-Ring is OFF (figure fig:sr_geophone_time_off) and when it is ON (figure fig:sr_geophone_time_on).
<<plt-matlab>>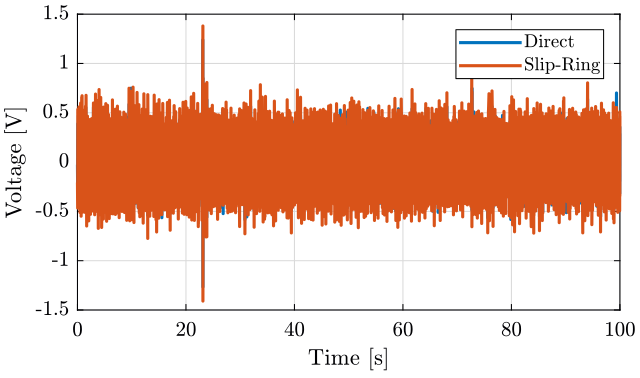
<<plt-matlab>>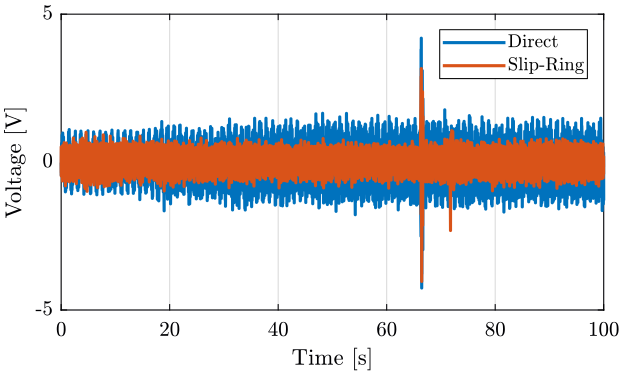
Frequency Domain
We first compute some parameters that will be used for the PSD computation.
dt = sr_off(2, 3)-sr_off(1, 3);
Fs = 1/dt; % [Hz]
win = hanning(ceil(10*Fs));
Then we compute the Power Spectral Density using pwelch function.
% Direct measure
[pxdoff, ~] = pwelch(sr_off(:, 1), win, [], [], Fs);
[pxdon, ~] = pwelch(sr_on(:, 1), win, [], [], Fs);
% Slip-Ring measure
[pxsroff, f] = pwelch(sr_off(:, 2), win, [], [], Fs);
[pxsron, ~] = pwelch(sr_on(:, 2), win, [], [], Fs);Finally, we compare the Amplitude Spectral Density of the signals (figure fig:sr_geophone_asd);
figure;
hold on;
plot(f, sqrt(pxdoff), 'DisplayName', 'Direct - OFF');
plot(f, sqrt(pxsroff), 'DisplayName', 'Slip-Ring - OFF');
plot(f, sqrt(pxdon), 'DisplayName', 'Direct - ON');
plot(f, sqrt(pxsron), 'DisplayName', 'Slip-Ring - ON');
hold off;
set(gca, 'xscale', 'log');
set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('ASD of the measured Voltage $\left[\frac{V}{\sqrt{Hz}}\right]$')
legend('Location', 'northeast');
xlim([0.1, 500]); <<plt-matlab>>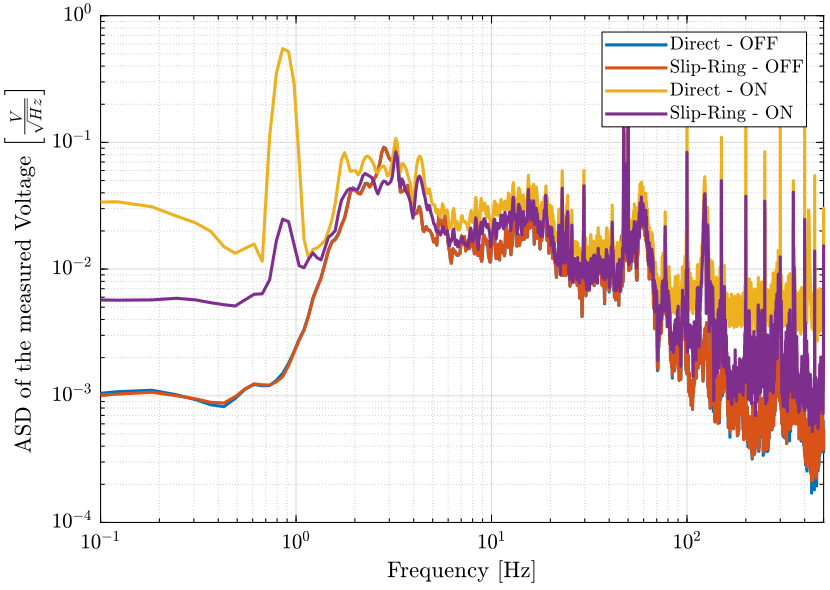
<<plt-matlab>>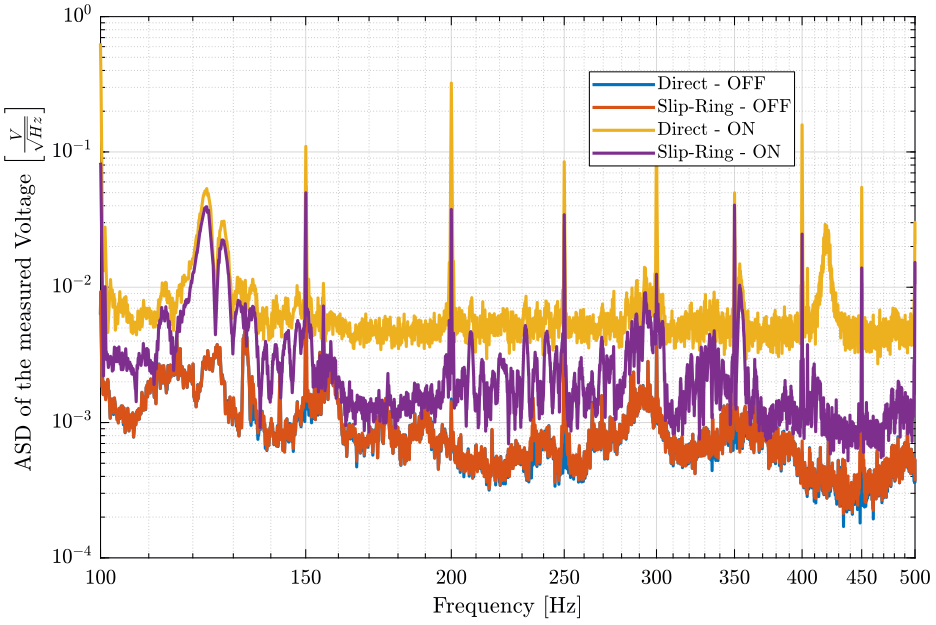
Conclusion
- The fact that the Slip-Ring is turned ON adds some noise to the signals
- The signal going through the Slip-Ring is less noisy than the one going directly to the ADC
- This could be due to better electromagnetic isolation in the slip-ring
Questions:
- Can the sharp peak on figure fig:sr_geophone_asd_zoom be due to the Aliasing?
Measurement using an oscilloscope
Measurement Setup
We are now measuring the same signals than in the previous section, but with an oscilloscope instead of with the Speedgoat ADC.
Observations
Then the Slip-Ring is ON (figure fig:oscilloscope_sr_on), we observe a signal at 40kHz with a peak-to-peak amplitude of 200mV for the direct measure and 100mV for the signal going through the Slip-Ring.
Then the Slip-Ring is OFF, we don't observe this noise at 40kHz anymore (figure fig:oscilloscope_sr_off).
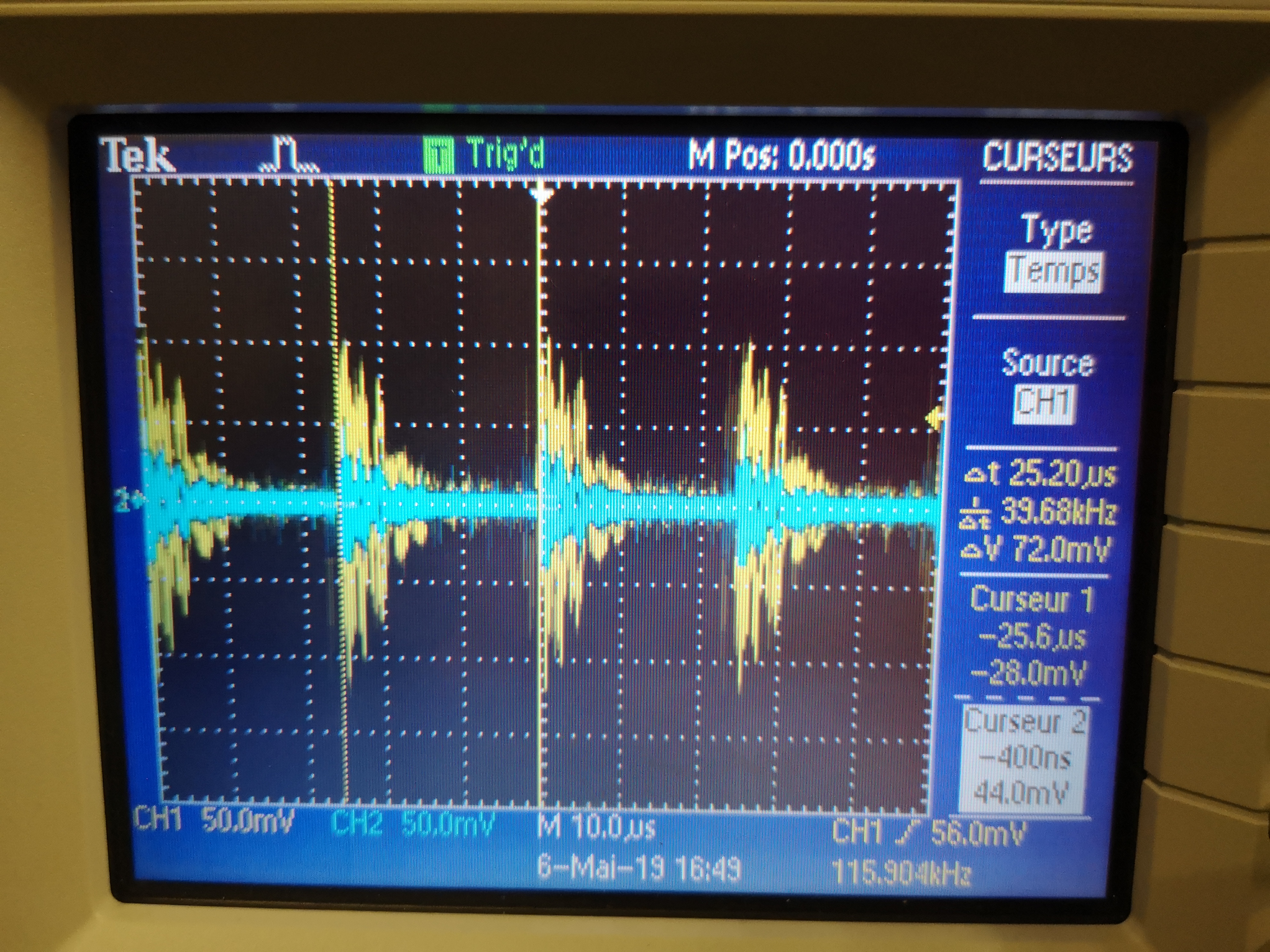
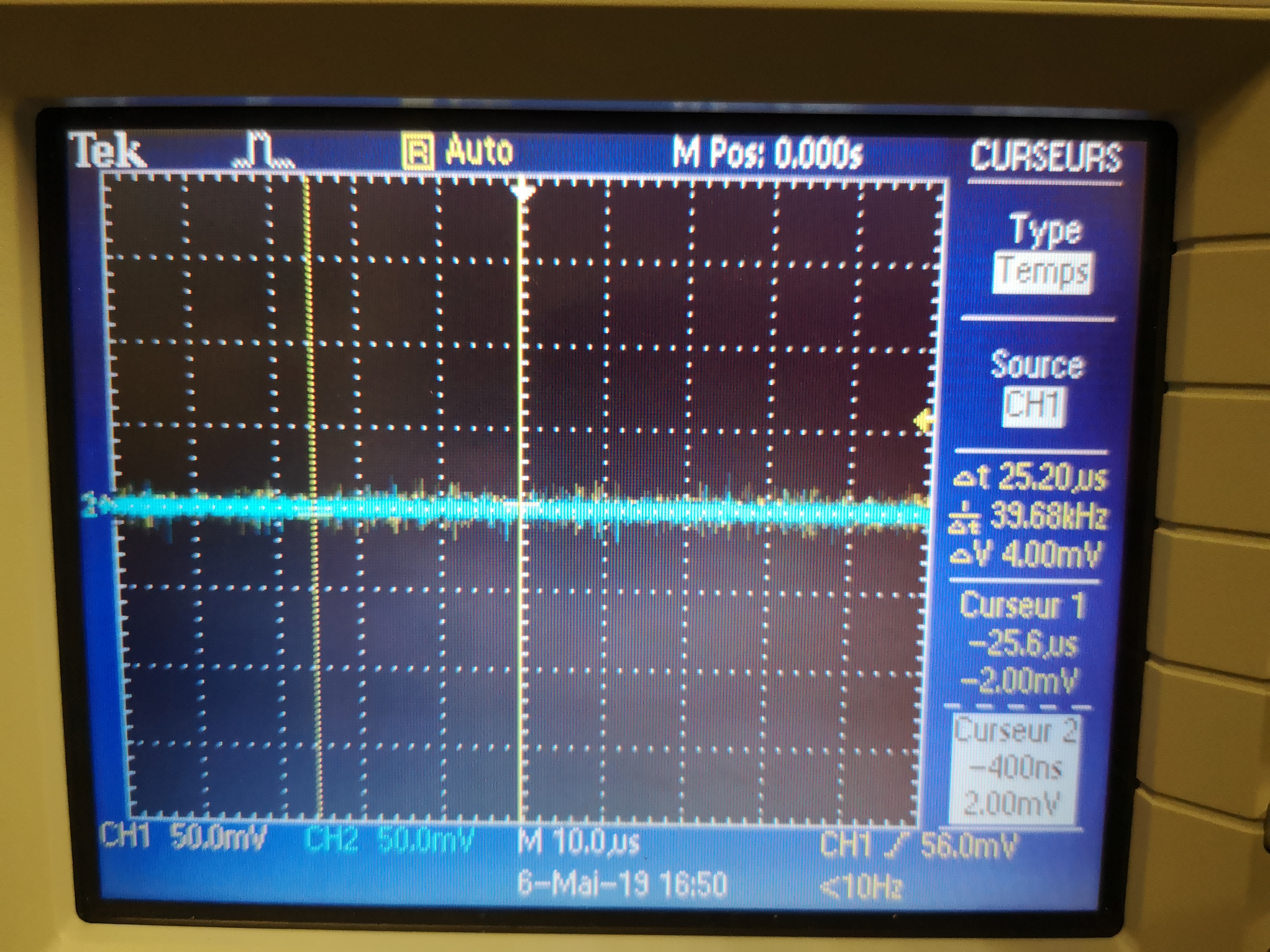
Conclusion
- By looking at the signals using an oscilloscope, there is a lot of high frequency noise when turning on the Slip-Ring
- This can eventually saturate the voltage amplifiers (seen by a led indicating saturation)
- The choice is to add a Low pass filter before the voltage amplifiers to not saturate them and filter the noise.
New measurements with a LPF before the Voltage Amplifiers
Setup description
Goal: The goal is to see if we can remove high frequency noise from the signals before the voltage amplifiers in order to not saturate them.
Setup: We are measuring the signal from a geophone put at the sample position. Using a BNC slitter, one part is going directly to the Low pass filter, voltage amplifier and ADC (first column), the other part is going through the slip ring before the low pass filter and the voltage amplifier (second column).
The two voltage amplifiers have the same following settings:
- Gain: 60dB
- AC/DC option: DC
- Low pass filter at the output set to 1kHz
The low pass filter is a first order low pass filter RC circuit. It is added before the Voltage Amplifiers and has the following values:
\begin{aligned} R &= 1k\Omega \\ C &= 1\mu F \end{aligned}And the cut-off frequency is $f_c = \frac{1}{RC} = 160Hz$.
Measurements: Two measurements are done:
| Measurement File | Description |
|---|---|
mat/data_016.mat |
Signal from the geophone at the sample location - Slip-Ring OFF |
mat/data_017.mat |
Signal from the geophone at the sample location - Slip-Ring ON |
Each of the measurement mat file contains one data array with 3 columns:
| Column number | Description |
|---|---|
| 1 | Direct measurement |
| 2 | Signal going through the slip-ring |
| 3 | Time |
Load data
We load the data of the z axis of two geophones.
sr_lpf_off = load('mat/data_016.mat', 'data'); sr_lpf_off = sr_lpf_off.data;
sr_lpf_on = load('mat/data_017.mat', 'data'); sr_lpf_on = sr_lpf_on.data;Time Domain
We compare the signal when the Slip-Ring is OFF (figure fig:sr_lpf_geophone_time_off) and when it is ON (figure fig:sr_lpf_geophone_time_on).
<<plt-matlab>>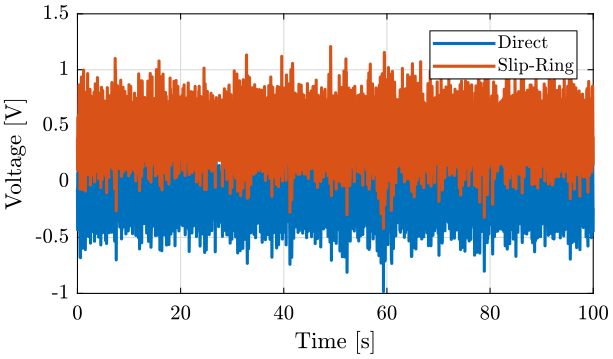
<<plt-matlab>>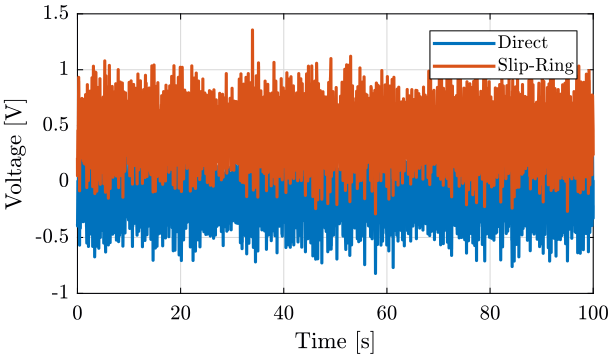
Frequency Domain
We first compute some parameters that will be used for the PSD computation.
dt = sr_lpf_off(2, 3)-sr_lpf_off(1, 3);
Fs = 1/dt; % [Hz]
win = hanning(ceil(10*Fs));
Then we compute the Power Spectral Density using pwelch function.
% Direct measure
[pxd_lpf_off, ~] = pwelch(sr_lpf_off(:, 1), win, [], [], Fs);
[pxd_lpf_on, ~] = pwelch(sr_lpf_on(:, 1), win, [], [], Fs);
% Slip-Ring measure
[pxsr_lpf_off, f] = pwelch(sr_lpf_off(:, 2), win, [], [], Fs);
[pxsr_lpf_on, ~] = pwelch(sr_lpf_on(:, 2), win, [], [], Fs);Finally, we compare the Amplitude Spectral Density of the signals (figure fig:sr_lpf_geophone_asd);
figure;
hold on;
plot(f, sqrt(pxd_lpf_off), 'DisplayName', 'Direct - OFF');
plot(f, sqrt(pxsr_lpf_off), 'DisplayName', 'Slip-Ring - OFF');
plot(f, sqrt(pxd_lpf_on), 'DisplayName', 'Direct - ON');
plot(f, sqrt(pxsr_lpf_on), 'DisplayName', 'Slip-Ring - ON');
hold off;
xlim([0.1, 500]);
set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('ASD of the measured Voltage $\left[\frac{V}{\sqrt{Hz}}\right]$')
legend('Location', 'soutwest'); <<plt-matlab>>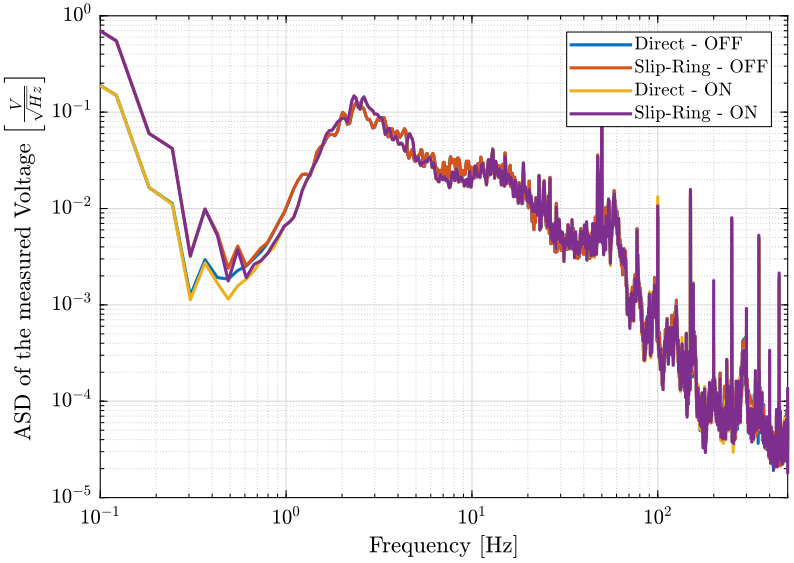
<<plt-matlab>>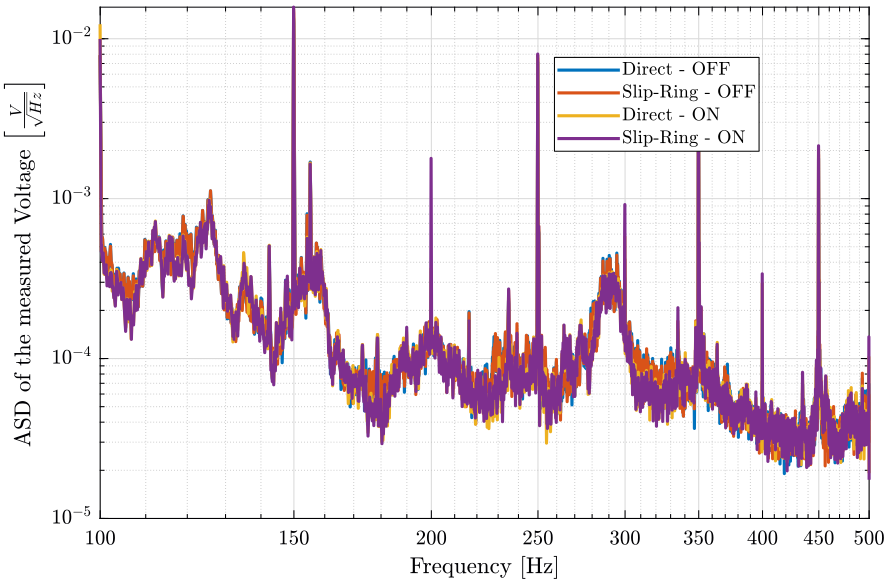
Conclusion
- Using the LPF, we don't see any additional noise coming from the slip-ring when it is turned ON
- However, we should use a smaller value of the capacitor to have a cut-off frequency at $1kHz$
- We here observe a signal at $50Hz$ and its harmonics
TODO New LPF at 1kHz
Effect of the rotation of the Slip-Ring - Noise
<<sec:meas_effect_sr>>
All the files (data and Matlab scripts) are accessible here.
Measurement Description
Goal: The goal is to determine if the signal is altered when the spindle is rotating.
Setup: Random Signal is generated by one SpeedGoat DAC.
The signal going out of the DAC is split into two:
- one BNC cable is directly connected to one ADC of the SpeedGoat
- one BNC cable goes two times in the Slip-Ring (from bottom to top and then from top to bottom) and then is connected to one ADC of the SpeedGoat
All the stages are turned OFF except the Slip-Ring.
Measurements:
| Data File | Description |
|---|---|
mat/data_001.mat |
Slip-ring not turning but ON |
mat/data_002.mat |
Slip-ring turning at 1rpm |
For each measurement, the measured signals are:
| Variable | Description |
|---|---|
t |
Time vector |
x1 |
Direct signal |
x2 |
Signal going through the Slip-Ring |
Load data
We load the data of the z axis of two geophones.
sr_off = load('mat/data_001.mat', 't', 'x1', 'x2');
sr_on = load('mat/data_002.mat', 't', 'x1', 'x2');Analysis
Let's first look at the signal produced by the DAC (figure fig:random_signal).
figure;
hold on;
plot(sr_on.t, sr_on.x1);
hold off;
xlabel('Time [s]'); ylabel('Voltage [V]');
xlim([0 10]); <<plt-matlab>>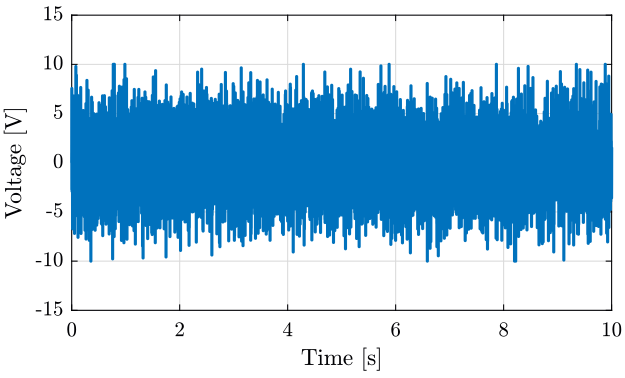
We now look at the difference between the signal directly measured by the ADC and the signal that goes through the slip-ring (figure fig:slipring_comp_signals).
figure;
hold on;
plot(sr_on.t, sr_on.x1 - sr_on.x2, 'DisplayName', 'Slip-Ring - $\omega = 1rpm$');
plot(sr_off.t, sr_off.x1 - sr_off.x2,'DisplayName', 'Slip-Ring off');
hold off;
xlabel('Time [s]'); ylabel('Voltage [V]');
xlim([0 10]);
legend('Location', 'northeast'); <<plt-matlab>>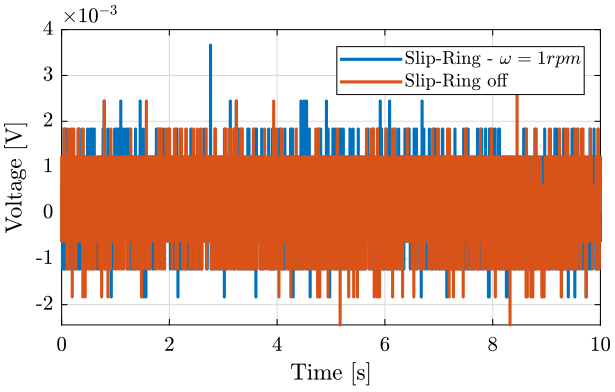
dt = sr_on.t(2) - sr_on.t(1);
Fs = 1/dt; % [Hz]
win = hanning(ceil(1*Fs)); [pxx_on, f] = pwelch(sr_on.x1 - sr_on.x2, win, [], [], Fs);
[pxx_off, ~] = pwelch(sr_off.x1 - sr_off.x2, win, [], [], Fs); <<plt-matlab>>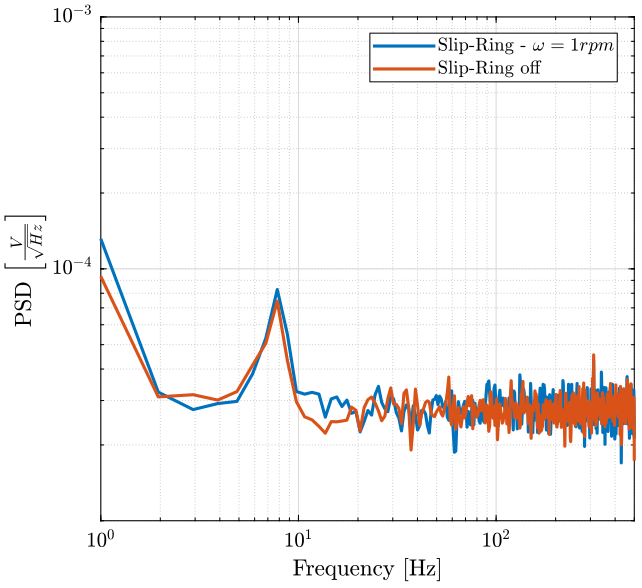
Conclusion
- The measurement is mostly limited by the resolution of the Speedgoat DAC (16bits over $\pm 10 V$)
- In section sec:meas_slip_ring, the same measurement is done but voltage amplifiers are added to amplify the noise
Measure of the noise induced by the Slip-Ring using voltage amplifiers - Noise
<<sec:meas_slip_ring>>
All the files (data and Matlab scripts) are accessible here.
Measurement Description
Goal:
- Determine the noise induced by the slip-ring when turned ON and when rotating
Setup:
- 0V is generated by one Speedgoat DAC
- Using a T, one part goes directly to one Speedgoat ADC
- The other part goes to the slip-ring 2 times and then to one voltage amplifier before going to the ADC
-
The parameters of the Voltage Amplifier are:
- gain of 80dB
- AC/DC option to AC (it adds an high pass filter at 1.5Hz at the input of the voltage amplifier)
- Output Low pass filter set at 1kHz
- Every stage of the station is OFF
First column: Direct measure Second column: Slip-ring measure
Measurements:
| Data File | Description |
|---|---|
mat/data_008.mat |
Slip-Ring OFF |
mat/data_009.mat |
Slip-Ring ON |
mat/data_010.mat |
Slip-Ring ON and omega=6rpm |
mat/data_011.mat |
Slip-Ring ON and omega=60rpm |
Each of the measurement mat file contains one data array with 3 columns:
| Column number | Description |
|---|---|
| 1 | Signal going directly to the ADC |
| 2 | Signal going through the Slip-Ring |
| 3 | Time |


Load data
We load the data of the z axis of two geophones.
sr_off = load('mat/data_008.mat', 'data'); sr_off = sr_off.data;
sr_on = load('mat/data_009.mat', 'data'); sr_on = sr_on.data;
sr_6r = load('mat/data_010.mat', 'data'); sr_6r = sr_6r.data;
sr_60r = load('mat/data_011.mat', 'data'); sr_60r = sr_60r.data;Time Domain
We plot the time domain data for the direct measurement (figure fig:sr_direct_time) and for the signal going through the slip-ring (figure fig:sr_slipring_time);
<<plt-matlab>>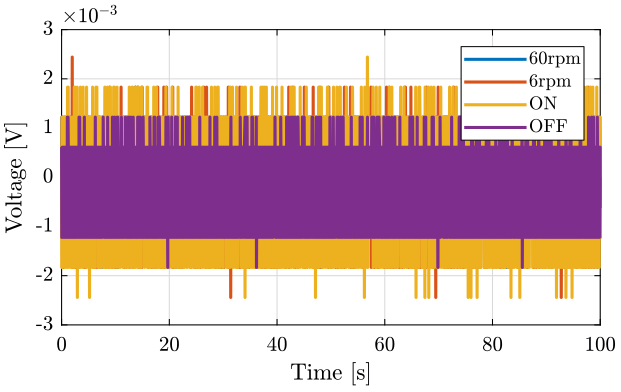
<<plt-matlab>>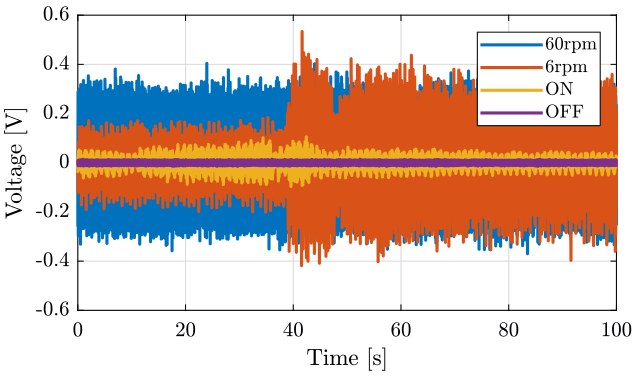
Frequency Domain
We first compute some parameters that will be used for the PSD computation.
dt = sr_off(2, 3)-sr_off(1, 3);
Fs = 1/dt; % [Hz]
win = hanning(ceil(10*Fs));
Then we compute the Power Spectral Density using pwelch function.
[pxdir, f] = pwelch(sr_off(:, 1), win, [], [], Fs);
[pxoff, ~] = pwelch(sr_off(:, 2), win, [], [], Fs);
[pxon, ~] = pwelch(sr_on(:, 2), win, [], [], Fs);
[px6r, ~] = pwelch(sr_6r(:, 2), win, [], [], Fs);
[px60r, ~] = pwelch(sr_60r(:, 2), win, [], [], Fs);And we plot the ASD of the measured signals (figure fig:sr_psd_compare);
figure;
hold on;
plot(f, sqrt(pxoff), 'DisplayName', 'OFF');
plot(f, sqrt(pxon), 'DisplayName', 'ON');
plot(f, sqrt(px6r), 'DisplayName', '6rpm');
plot(f, sqrt(px60r), 'DisplayName', '60rpm');
plot(f, sqrt(pxdir), 'k-', 'DisplayName', 'Direct');
hold off;
set(gca, 'xscale', 'log');
set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('ASD of the measured Voltage $\left[\frac{V}{\sqrt{Hz}}\right]$')
legend('Location', 'northeast');
xlim([0.1, 500]); <<plt-matlab>>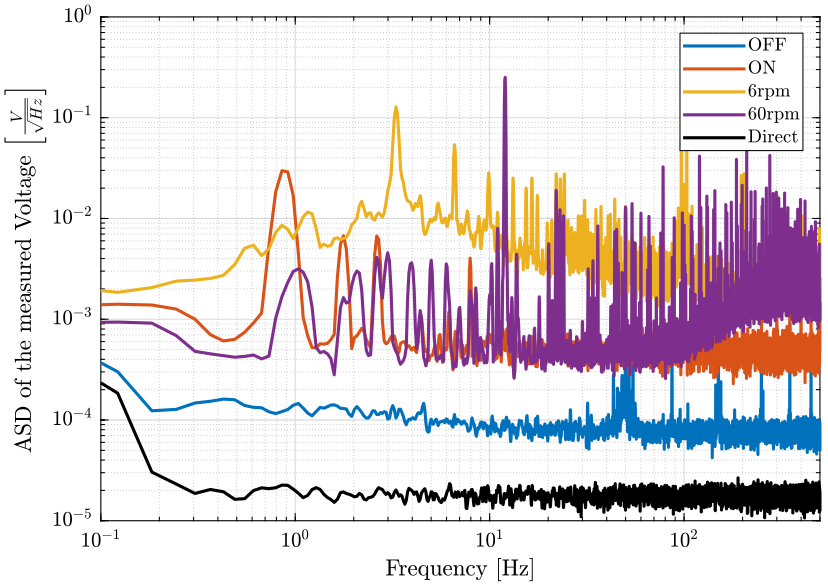
Questions:
- Why is there some sharp peaks? Can this be due to aliasing?
- It is possible that the amplifiers were saturating during the measurements. This saturation could be due to high frequency noise.
Conclusion
- The measurements are re-done using an additional low pass filter at the input of the voltage amplifier
TODO Measure of the noise induced by the Slip-Ring rotation - LPF added
<<sec:meas_slip_ring_lpf>>
All the files (data and Matlab scripts) are accessible here.