nass-micro-station-measurements/instrumentation/index.org

Measurements on the instrumentation

• Measure of the noise of the Voltage Amplifier
  • Measurement Description
  • Load data
  • Time Domain
  • Frequency Domain
  • Conclusion
• Measure of the influence of the AC/DC option on the voltage amplifiers
  • Measurement Description
  • Load data
  • Time Domain
  • Frequency Domain
  • Conclusion
• Transfer function of the Low Pass Filter
  • First LPF with a Cut-off frequency of 160Hz
    • Measurement Description
    • Load data
    • Transfer function of the LPF
    • Conclusion
  • Second LPF with a Cut-off frequency of 1000Hz
    • Measurement description
    • Load data
    • Transfer function of the LPF
    • Conclusion

Measure of the noise of the Voltage Amplifier

<<sec:meas_volt_amp>>

All the files (data and Matlab scripts) are accessible here.

Measurement Description

Goal:

• Determine the Voltage Amplifier noise

Setup:

• The two inputs (differential) of the voltage amplifier are shunted with 50Ohms
• The AC/DC option of the Voltage amplifier is on AC
• The low pass filter is set to 1hHz
• We measure the output of the voltage amplifier with a 16bits ADC of the Speedgoat

Measurements:

• data_003: Ampli OFF
• data_004: Ampli ON set to 20dB
• data_005: Ampli ON set to 40dB
• data_006: Ampli ON set to 60dB

Load data

  amp_off = load('mat/data_003.mat', 'data'); amp_off = amp_off.data(:, [1,3]);
  amp_20d = load('mat/data_004.mat', 'data'); amp_20d = amp_20d.data(:, [1,3]);
  amp_40d = load('mat/data_005.mat', 'data'); amp_40d = amp_40d.data(:, [1,3]);
  amp_60d = load('mat/data_006.mat', 'data'); amp_60d = amp_60d.data(:, [1,3]);

Time Domain

The time domain signals are shown on figure fig:ampli_noise_time.

  <<plt-matlab>>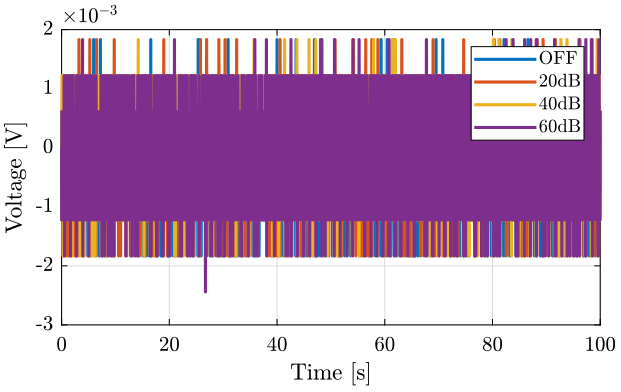

Output of the amplifier

Frequency Domain

We first compute some parameters that will be used for the PSD computation.

  dt = amp_off(2, 2)-amp_off(1, 2);

  Fs = 1/dt; % [Hz]

  win = hanning(ceil(10*Fs));

Then we compute the Power Spectral Density using pwelch function.

  [pxoff, f] = pwelch(amp_off(:,1), win, [], [], Fs);
  [px20d, ~] = pwelch(amp_20d(:,1), win, [], [], Fs);
  [px40d, ~] = pwelch(amp_40d(:,1), win, [], [], Fs);
  [px60d, ~] = pwelch(amp_60d(:,1), win, [], [], Fs);

We compute the theoretical ADC noise.

  q = 20/2^16; % quantization
  Sq = q^2/12/1000; % PSD of the ADC noise

Finally, the ASD is shown on figure fig:ampli_noise_psd.

  <<plt-matlab>>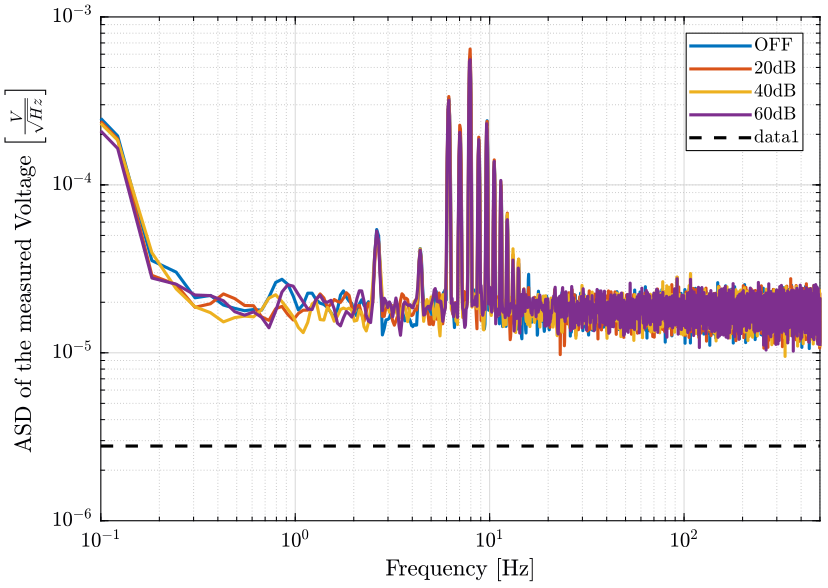

Amplitude Spectral Density of the measured voltage at the output of the voltage amplifier

Conclusion

Questions:

• Where does those sharp peaks comes from? Can this be due to aliasing?

Noise induced by the voltage amplifiers seems not to be a limiting factor as we have the same noise when they are OFF and ON.

Measure of the influence of the AC/DC option on the voltage amplifiers

<<sec:meas_noise_ac_dc>>

All the files (data and Matlab scripts) are accessible here.

Measurement Description

Goal:

• Measure the influence of the high-pass filter option of the voltage amplifiers

Setup:

• One geophone is located on the marble.
• It's signal goes to two voltage amplifiers with a gain of 60dB.
• One voltage amplifier is on the AC option, the other is on the DC option.

Measurements: First measurement (mat/data_014.mat file):

Column	Signal
1	Amplifier 1 with AC option
2	Amplifier 2 with DC option
3	Time

Second measurement (mat/data_015.mat file):

Column	Signal
1	Amplifier 1 with DC option
2	Amplifier 2 with AC option
3	Time

Picture of the two voltages amplifiers

Load data

We load the data of the z axis of two geophones.

  meas14 = load('mat/data_014.mat', 'data'); meas14 = meas14.data;
  meas15 = load('mat/data_015.mat', 'data'); meas15 = meas15.data;

Time Domain

The signals are shown on figure fig:ac_dc_option_time.

  <<plt-matlab>>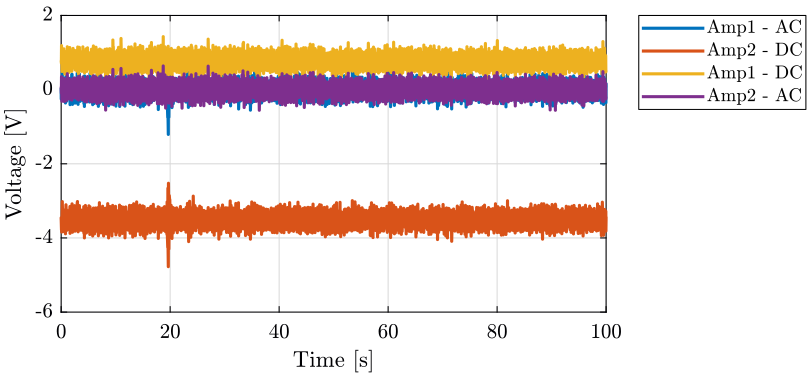

Comparison of the signals going through the Voltage amplifiers

Frequency Domain

We first compute some parameters that will be used for the PSD computation.

  dt = meas14(2, 3)-meas14(1, 3);

  Fs = 1/dt; % [Hz]

  win = hanning(ceil(10*Fs));

Then we compute the Power Spectral Density using pwelch function.

  [pxamp1ac, f] = pwelch(meas14(:, 1), win, [], [], Fs);
  [pxamp2dc, ~] = pwelch(meas14(:, 2), win, [], [], Fs);

  [pxamp1dc, ~] = pwelch(meas15(:, 1), win, [], [], Fs);
  [pxamp2ac, ~] = pwelch(meas15(:, 2), win, [], [], Fs);

The ASD of the signals are compare on figure fig:ac_dc_option_asd.

  <<plt-matlab>>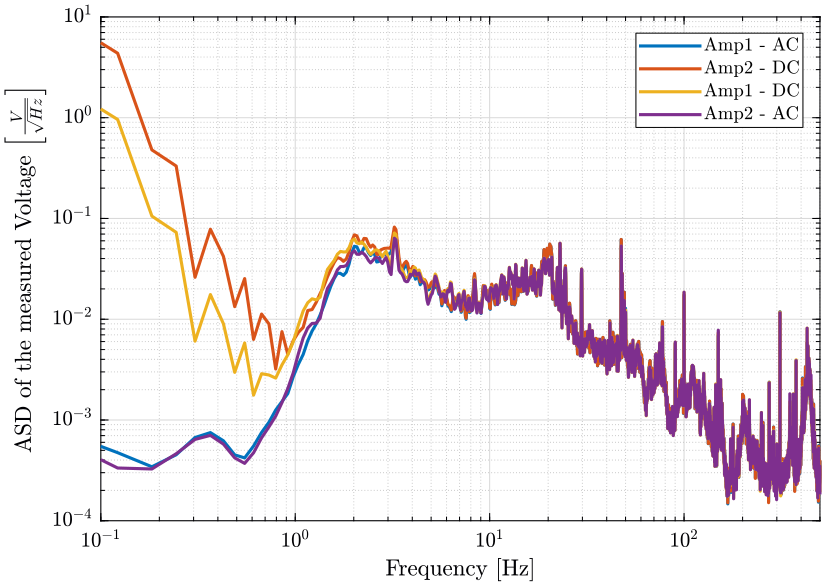

Amplitude Spectral Density of the measured signals

Conclusion

• The voltage amplifiers include some very sharp high pass filters at 1.5Hz (maybe 4th order)
• There is a DC offset on the time domain signal because the DC-offset knob was not set to zero

Transfer function of the Low Pass Filter

<<sec:low_pass_filter_measurements>>

The computation files for this section are accessible here.

First LPF with a Cut-off frequency of 160Hz

Measurement Description

Goal:

• Measure the Low Pass Filter Transfer Function

The values of the components are:

\begin{aligned} R &= 1k\Omega \\ C &= 1\mu F \end{aligned}

Which makes a cut-off frequency of $f_c = \frac{1}{RC} = 1000 rad/s = 160Hz$.

  \begin{tikzpicture}
    \draw (0,2)
          to [R=\(R\)] ++(2,0) node[circ]
          to ++(2,0)
          ++(-2,0)
          to [C=\(C\)] ++(0,-2) node[circ]
          ++(-2,0)
          to ++(2,0)
          to ++(2,0)
  \end{tikzpicture}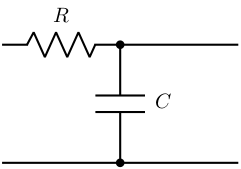

Schematic of the Low Pass Filter used

Setup:

• We are measuring the signal from from Geophone with a BNC T
• On part goes to column 1 through the LPF
• The other part goes to column 2 without the LPF

Measurements: mat/data_018.mat:

Column	Signal
1	Amplifier 1 with LPF
2	Amplifier 2
3	Time

Picture of the low pass filter used

Load data

We load the data of the z axis of two geophones.

  data = load('mat/data_018.mat', 'data'); data = data.data;

Transfer function of the LPF

We compute the transfer function from the signal without the LPF to the signal measured with the LPF.

  dt = data(2, 3)-data(1, 3);

  Fs = 1/dt; % [Hz]

  win = hanning(ceil(10*Fs));

  [Glpf, f] = tfestimate(data(:, 2), data(:, 1), win, [], [], Fs);

We compare this transfer function with a transfer function corresponding to an ideal first order LPF with a cut-off frequency of $1000rad/s$. We obtain the result on figure fig:Glpf_bode.

  Gth = 1/(1+s/1000)

  figure;
  ax1 = subplot(2, 1, 1);
  hold on;
  plot(f, abs(Glpf));
  plot(f, abs(squeeze(freqresp(Gth, f, 'Hz'))));
  hold off;
  set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
  set(gca, 'XTickLabel',[]);
  ylabel('Magnitude');

  ax2 = subplot(2, 1, 2);
  hold on;
  plot(f, mod(180+180/pi*phase(Glpf), 360)-180);
  plot(f, 180/pi*unwrap(angle(squeeze(freqresp(Gth, f, 'Hz')))));
  hold off;
  set(gca, 'xscale', 'log');
  ylim([-180, 180]);
  yticks([-180, -90, 0, 90, 180]);
  xlabel('Frequency [Hz]'); ylabel('Phase');

  linkaxes([ax1,ax2],'x');
  xlim([1, 500]);

  <<plt-matlab>>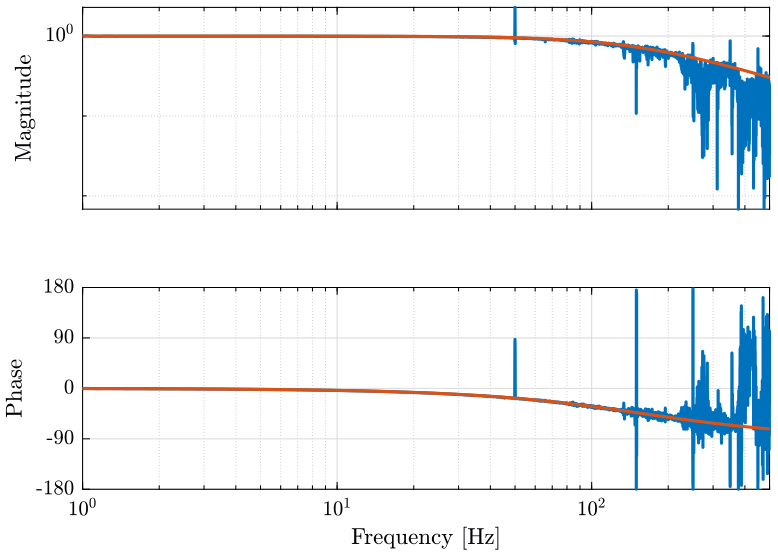

Bode Diagram of the measured Low Pass filter and the theoritical one

Conclusion

As we want to measure things up to $500Hz$, we chose to change the value of the capacitor to obtain a cut-off frequency of $1kHz$.

Second LPF with a Cut-off frequency of 1000Hz

Measurement description

This time, the value are

\begin{aligned} R &= 1k\Omega \\ C &= 150nF \end{aligned}

Which makes a low pass filter with a cut-off frequency of $f_c = 1060Hz$.

Load data

We load the data of the z axis of two geophones.

  data = load('mat/data_019.mat', 'data'); data = data.data;

Transfer function of the LPF

We compute the transfer function from the signal without the LPF to the signal measured with the LPF.

  dt = data(2, 3)-data(1, 3);

  Fs = 1/dt; % [Hz]

  win = hanning(ceil(10*Fs));

  [Glpf, f] = tfestimate(data(:, 2), data(:, 1), win, [], [], Fs);

We compare this transfer function with a transfer function corresponding to an ideal first order LPF with a cut-off frequency of $1060Hz$. We obtain the result on figure fig:Glpf_bode_bis.

  Gth = 1/(1+s/1060/2/pi);

  figure;
  ax1 = subplot(2, 1, 1);
  hold on;
  plot(f, abs(Glpf));
  plot(f, abs(squeeze(freqresp(Gth, f, 'Hz'))));
  hold off;
  set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
  set(gca, 'XTickLabel',[]);
  ylabel('Magnitude');

  ax2 = subplot(2, 1, 2);
  hold on;
  plot(f, mod(180+180/pi*phase(Glpf), 360)-180);
  plot(f, 180/pi*unwrap(angle(squeeze(freqresp(Gth, f, 'Hz')))));
  hold off;
  set(gca, 'xscale', 'log');
  ylim([-180, 180]);
  yticks([-180, -90, 0, 90, 180]);
  xlabel('Frequency [Hz]'); ylabel('Phase');

  linkaxes([ax1,ax2],'x');
  xlim([1, 500]);

  <<plt-matlab>>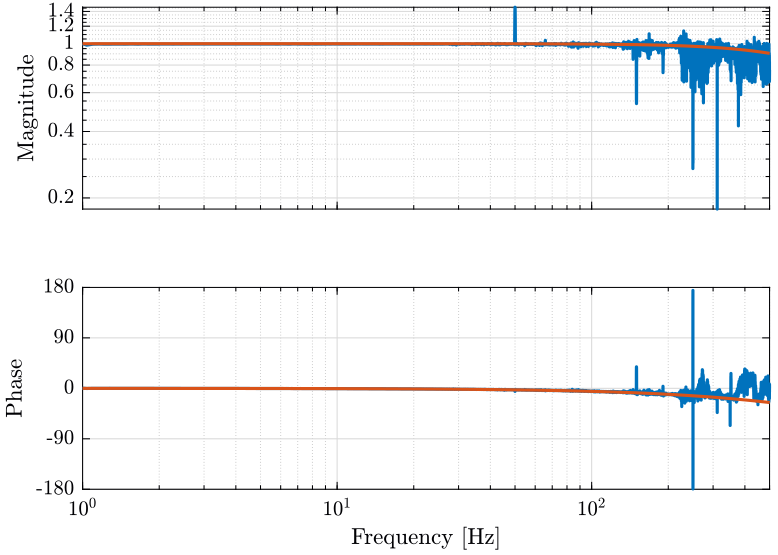

Bode Diagram of the measured Low Pass filter and the theoritical one

Conclusion

The added LPF has the expected behavior.