3.7 KiB
3.7 KiB
Modal Analysis of the ID31 Micro-Station
The goal is to experimentally extract a Spatial Model (mass, damping, stiffness) of the structure (shown on figure fig:nass_picture) in order to tune the Multi-Body model.

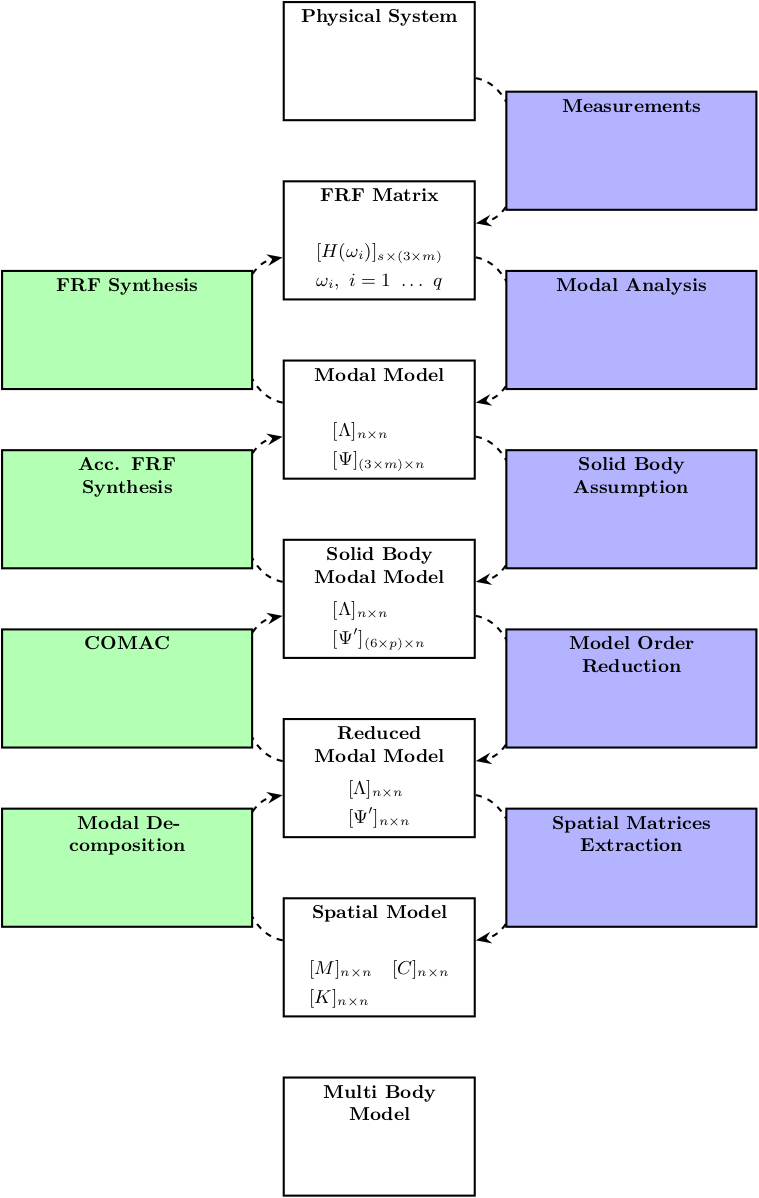
The procedure is represented on figure fig:vibration_analysis_procedure where we go from left to right.

The steps are:
- we obtain a Response Model (Frequency Response Functions) from measurements (described here)
- the response model is further converted into a Modal Model (Natural Frequencies and Mode Shapes) (described here)
- this is converted into a Spatial Model with the Mass/Damping/Stiffness matrices (described here)
Theses matrices will be used to tune the Simscape (multi-body) model.
The modes we want to identify are those in the frequency range between 0Hz and 150Hz.
| Symbol | Meaning | Value |
|---|---|---|
| $p$ | Number of solid body considered | 6 |
| $m$ | Number of accelerometers | 23 |
| $n$ | Number of identified modes | 21 |
| $q$ | Number of frequency points | 801 |
| $s$ | Number of excitation | 3 |
| Symbol | Meaning |
|---|---|
| $[\Lambda]$ | Complex eigen value matrix |
| $[\Psi]$ | Complex eigen vector matrix |
| $\omega_r$ | Eigen frequency of mode $r$ [rad/s] |
| $\xi_r$ | Modal damping for mode $r$ |
| $\{\psi\}_r$ | Complex mode shape of mode $r$ |
| $[M], [C], [K]$ | Mass, damping and stiffness matrices |
| $a_r$ | "Modal A" for mode $r$ |
The modal analysis of the ID31 Micro-station thus consists of several parts:
- Frequency Response Measurements
- Frequency Response Analysis and Processing
- Modal Parameter Extraction
- Derivation of Mathematical Model