18 KiB
Modal Analysis
- Goal
- Type of Model
- Instrumentation Used
- Structure Preparation and Test Planning
- Signal Processing
- Frequency Response Functions and Coherence Results
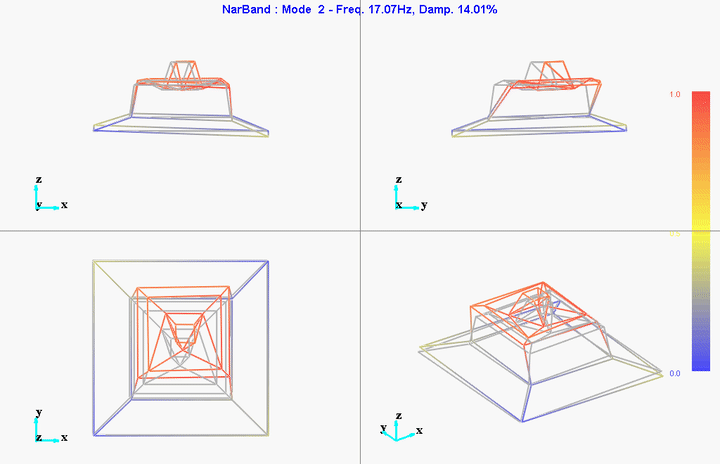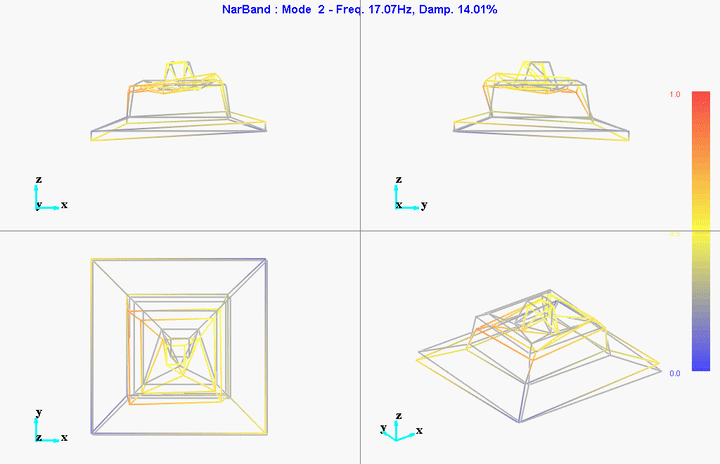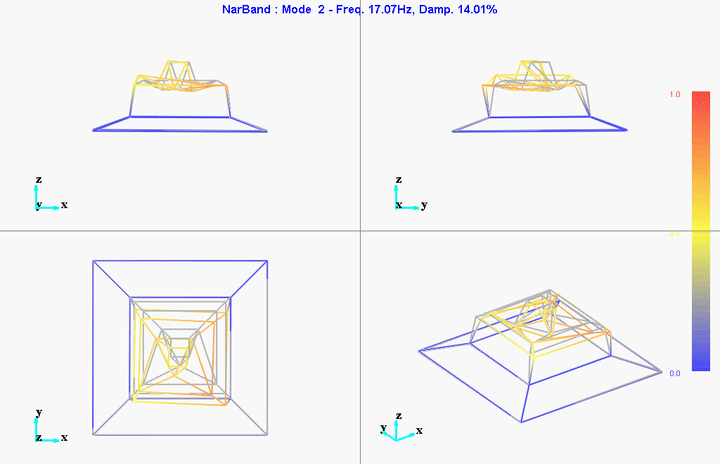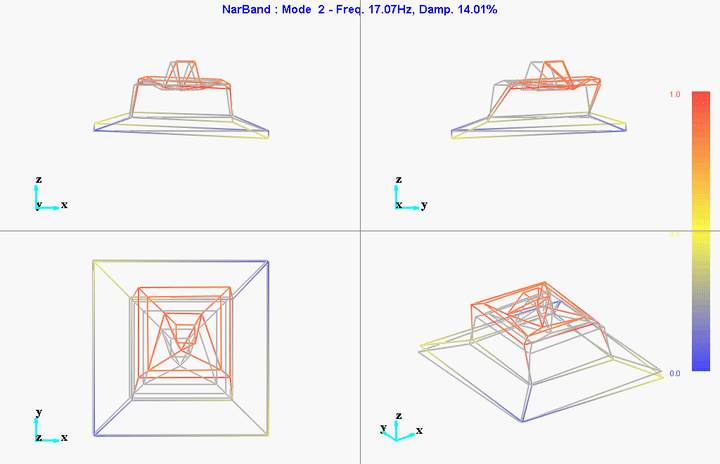
- Mode Shapes
- Obtained Modal Matrices
- Problem with AirLoc System
- Spatial Mode Extraction
Goal
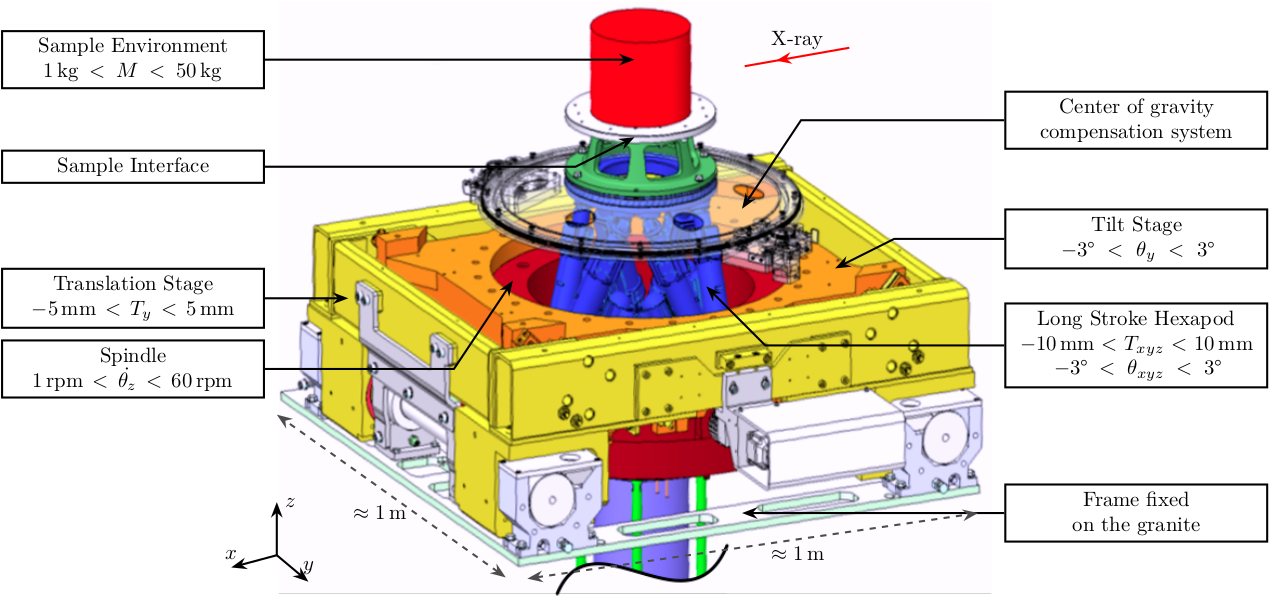
The goal is to experimentally extract a Spatial Model (mass, damping, stiffness) of the structure (shown on figure fig:nass_picture) in order to tune the Multi-Body model.
The procedure is represented on figure fig:vibration_analysis_procedure where we go from left to right.
First, we obtain a Response Model (Frequency Response Functions) from measurements. This is further converted into a Modal Model (Natural Frequencies and Mode Shapes). Finally, this is converted into a Spatial Model with the Mass/Damping/Stiffness matrices.
Theses matrices will be used to tune the Simscape (multi-body) model.
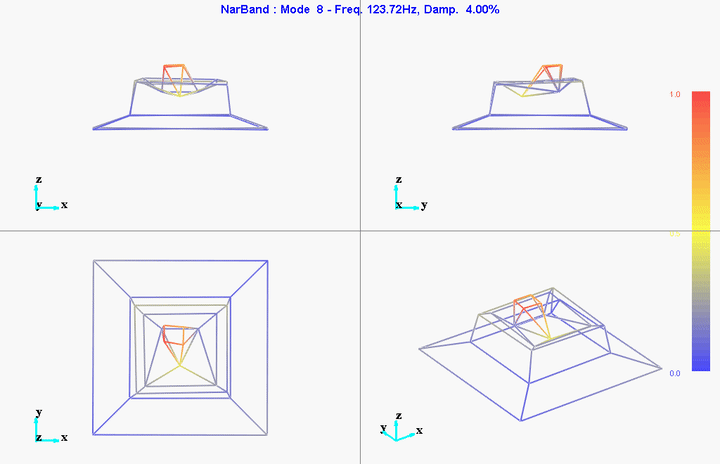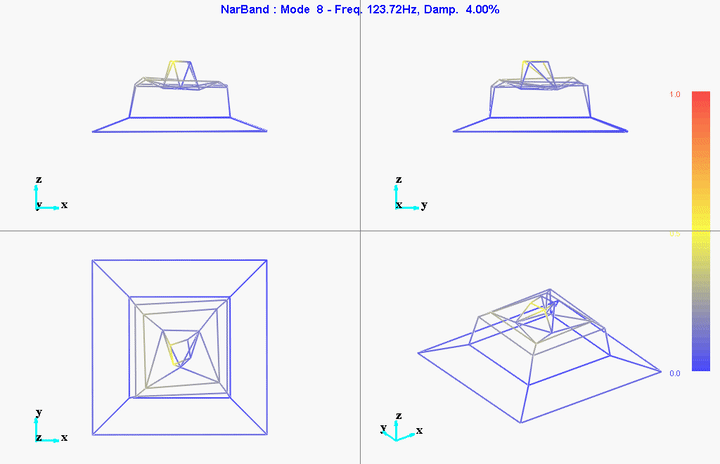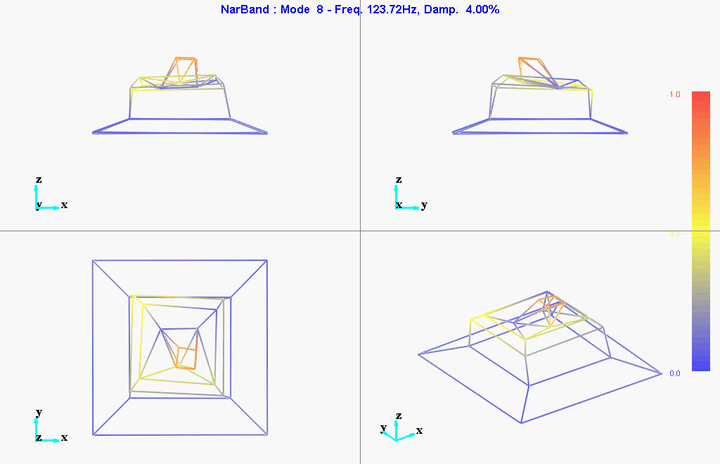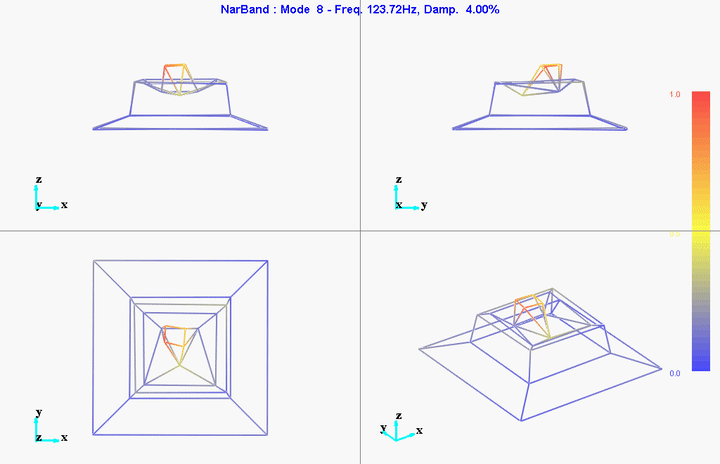
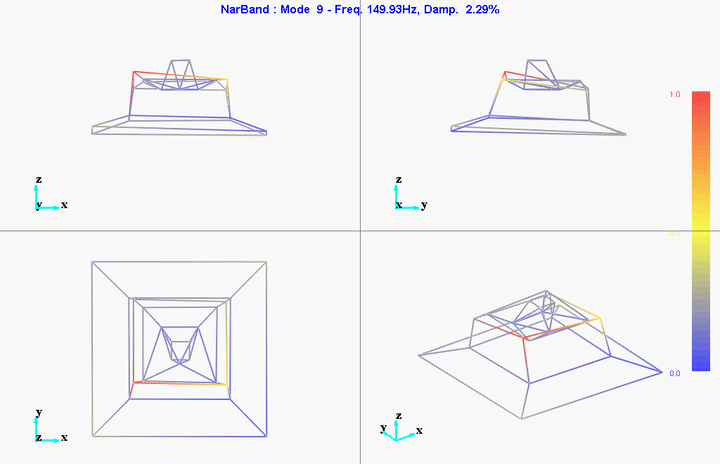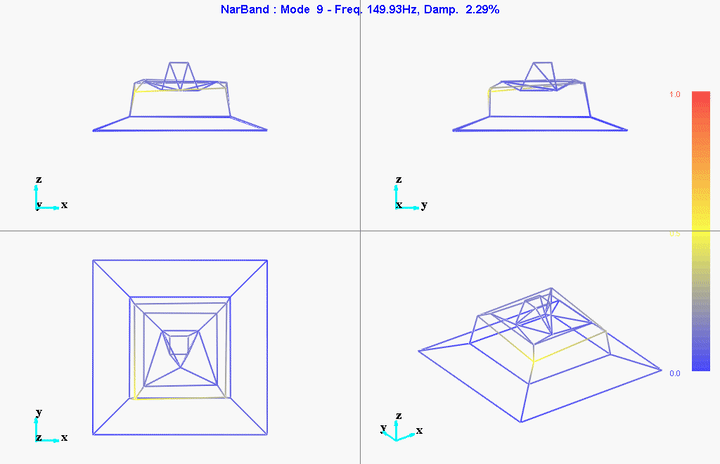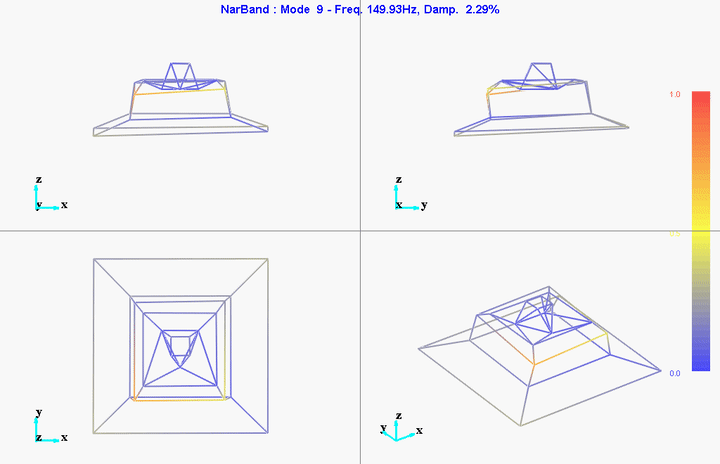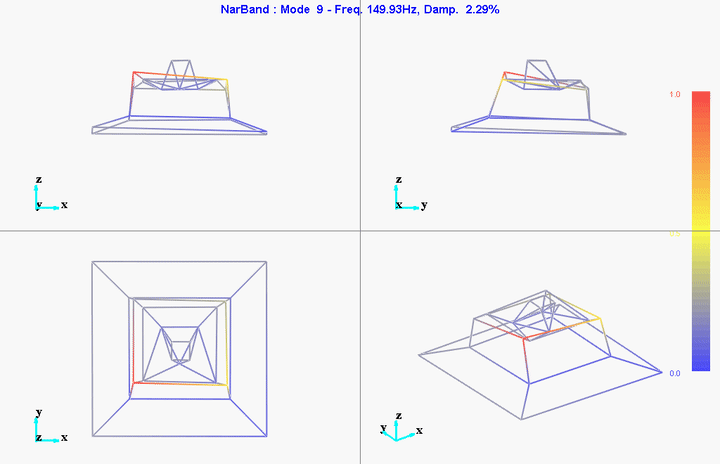
The modes we want to identify are those in the frequency range between 0Hz and 150Hz.
Type of Model
The model that we want to obtain is a multi-body model. It is composed of several solid bodies connected with springs and dampers. The solid bodies are represented with different colors on figure fig:nass_solidworks.
In the simscape model, the solid bodies are:
- the granite (1 or 2 solids)
- the translation stage
- the tilt stage
- the spindle and slip-ring
- the hexapod
However, each of the DOF of the system may not be relevant for the modes present in the frequency band of interest. For instance, the translation stage may not vibrate in the Z direction for all the modes identified. Then, we can block this DOF and this simplifies the model.
The modal identification done here will thus permit us to determine which DOF can be neglected.
Instrumentation Used
In order to perform to Modal Analysis and to obtain first a Response Model, the following devices are used:
- An acquisition system (OROS) with 24bits ADCs (figure fig:oros)
- 3 tri-axis Accelerometers (figure fig:accelero_M393B05) with parameters shown on table tab:accelero_M393B05
- An Instrumented Hammer with various Tips (figure fig:instrumented_hammer) (figure fig:hammer_tips)
The acquisition system permits to auto-range the inputs (probably using variable gain amplifiers) the obtain the maximum dynamic range. This is done before each measurement. Anti-aliasing filters are also included in the system.
| Sensitivity | 10V/g |
| Measurement Range | 0.5 g pk |
| Broadband Resolution | 0.000004 g rms |
| Frequency Range | 0.7 to 450Hz |
| Resonance Frequency | > 2.5kHz |
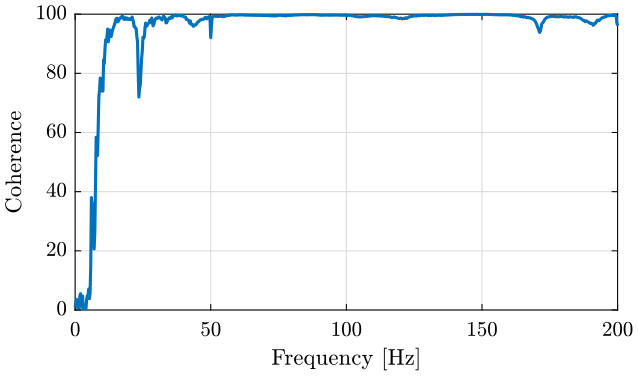
Tests have been conducted to determine the most suitable Hammer tip. This has been found that the softer tip gives the best results. It excites more the low frequency range where the coherence is low, the overall coherence was improved.
The accelerometers are glued on the structure.
Structure Preparation and Test Planning
Structure Preparation
All the stages are turned ON. This is done for two reasons:
- Be closer to the real dynamic of the station in used
- If the control system of stages are turned OFF, this would results in very low frequency modes un-identifiable with the current setup, and this will also decouple the dynamics which would not be the case in practice
This is critical for the translation stage and the spindle as their is no stiffness in the free DOF (air-bearing for the spindle for instance).
The alternative would have been to mechanically block the stages with screws, but this may result in changing the modes.
The stages turned ON are:
- Translation Stage
- Tilt Stage
- Spindle and Slip-Ring
- Hexapod
The top part representing the NASS and the sample platform have been removed in order to reduce the complexity of the dynamics and also because this will be further added in the model inside Simscape.
All the stages are moved to their zero position (Ty, Ry, Rz, Slip-Ring, Hexapod).
All other elements have been remove from the granite such as another heavy positioning system.
Test Planing
The goal is to identify the full $N \times N$ FRF matrix (where $N$ is the number of degree of freedom of the system).
However, the principle of reciprocity states that: \[ H_{jk} = \frac{X_j}{F_k} = H_{kj} = \frac{X_k}{F_j} \] Thus, only one column or one line of the matrix has to be identified.
Either we choose to identify $\frac{X_k}{F_i}$ or $\frac{X_i}{F_k}$ for any chosen $k$ and for $i = 1,\ ...,\ N$.
We here choose to identify $\frac{X_i}{F_k}$ for practical reasons:
- it is easier to glue the accelerometers on some stages than to excite this particular stage with the Hammer
The measurement thus consists of:
- always excite the structure at the same location with the Hammer
- Move the accelerometers to measure all the DOF of the structure
Location of the Accelerometers
4 tri-axis accelerometers are used for each solid body.
Only 2 could have been used as only 6DOF have to be measured, however, we have chosen to have some redundancy.
This could also help us identify measurement problems or flexible modes is present.
The position of the accelerometers are:
- 4 on the first granite
- 4 on the second granite (figure fig:accelerometers_granite2_overview)
- 4 on top of the translation stage (figure fig:accelerometers_ty_overview)
- 4 on top of the tilt stage
- 4 on top of the spindle
- 4 on top of the hexapod (figure fig:accelerometers_hexa_overview)
Hammer Impacts
Only 3 impact points are used.
The impact points are shown on figures fig:hammer_x, fig:hammer_y and fig:hammer_z.
Signal Processing
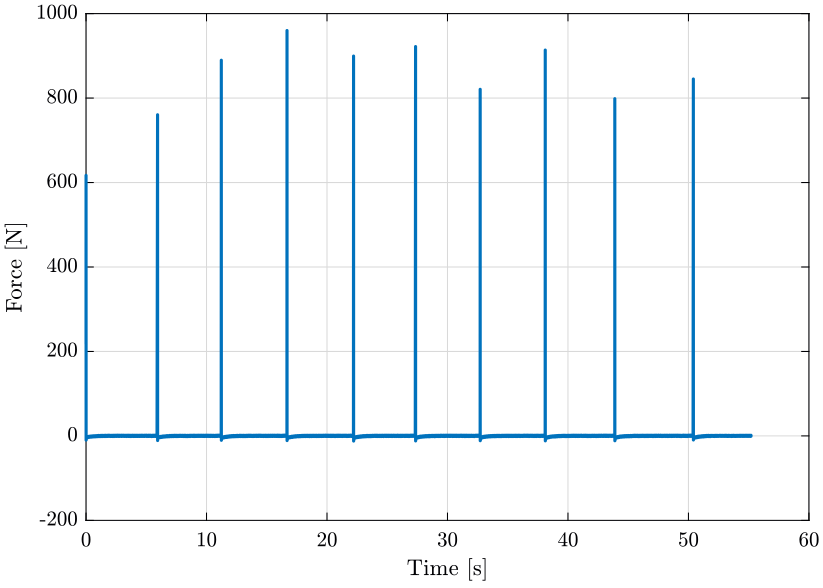
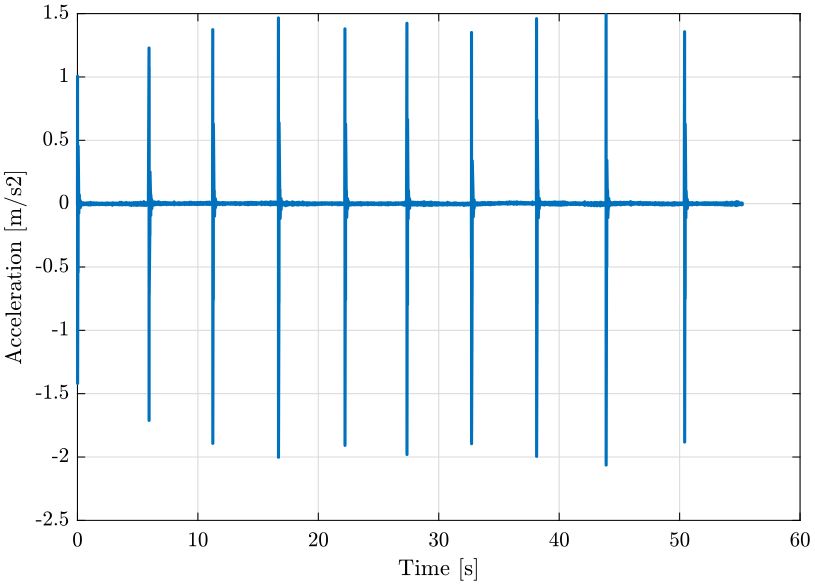
The measurements are averaged 10 times (figure fig:general_parameters) corresponding to 10 hammer impacts.
Windowing is used on the force response signals.
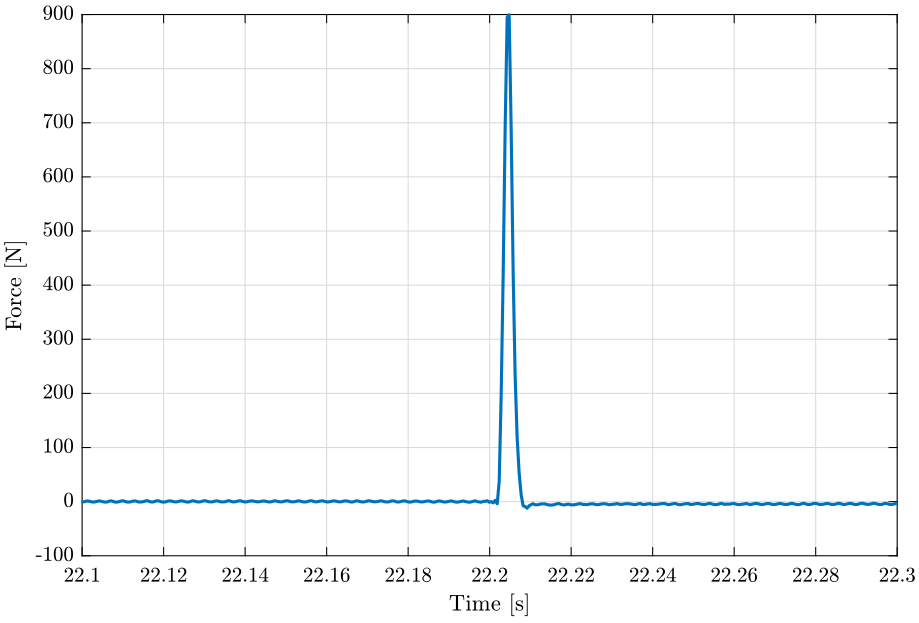
A boxcar window (figure fig:window_force) is used for the force signal as once the impact on the structure is done, the measured signal is meaningless.
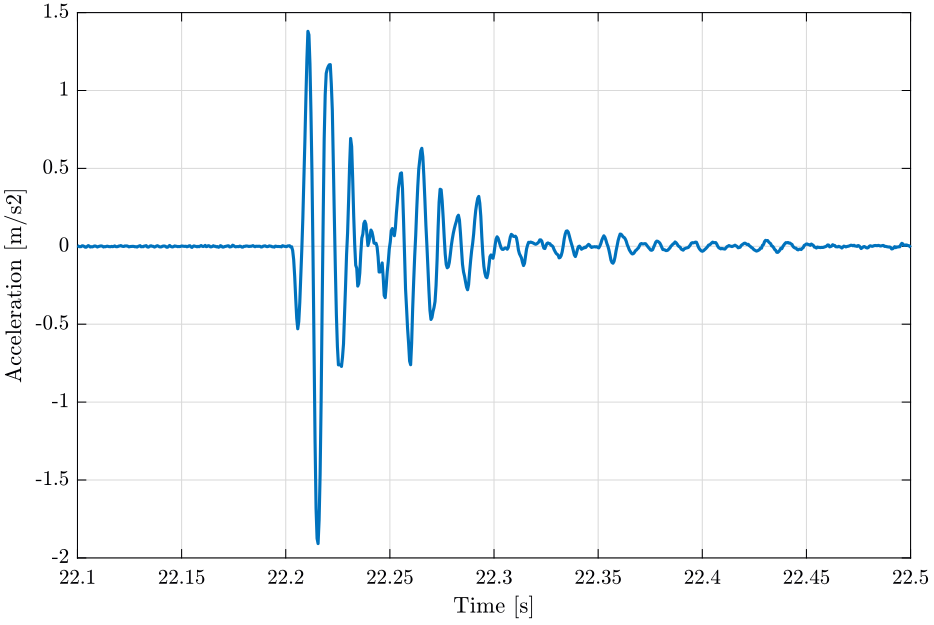
An exponential window (figure fig:window_response) is used for the response signal as we are measuring transient signals and most of the information is located at the beginning of the signal.
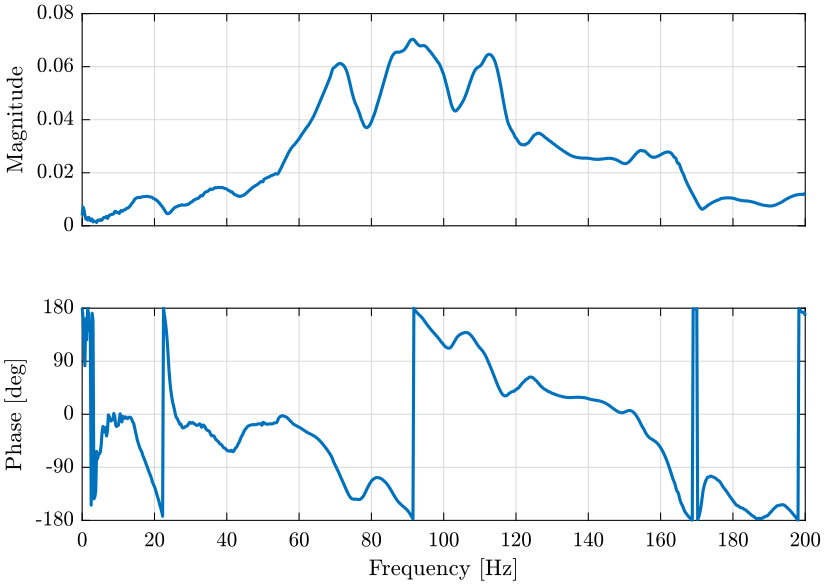
Frequency Response Functions and Coherence Results
Load Data
meas1_raw = load('modal_analysis/raw_data/Measurement1.mat');Raw Force Data
<<plt-matlab>>
<<plt-matlab>>
Raw Response Data
<<plt-matlab>>
<<plt-matlab>>
Load Data
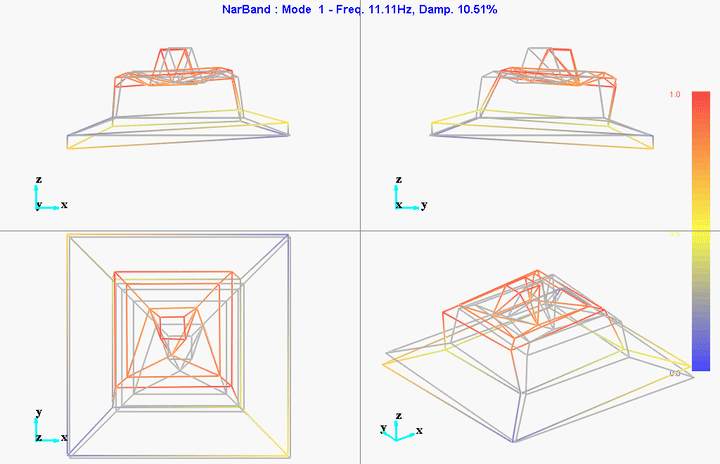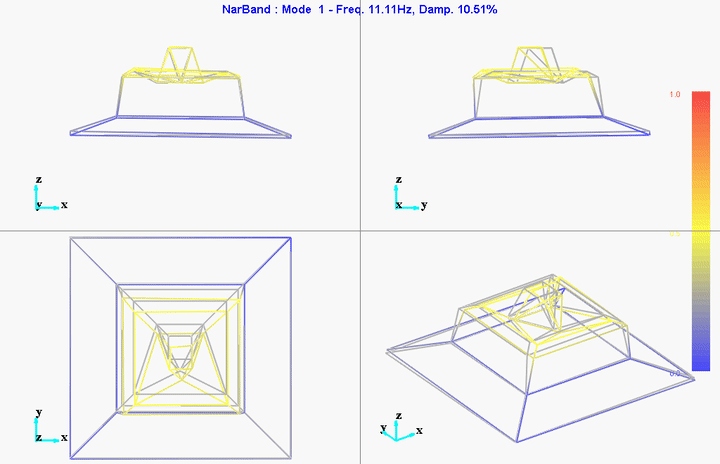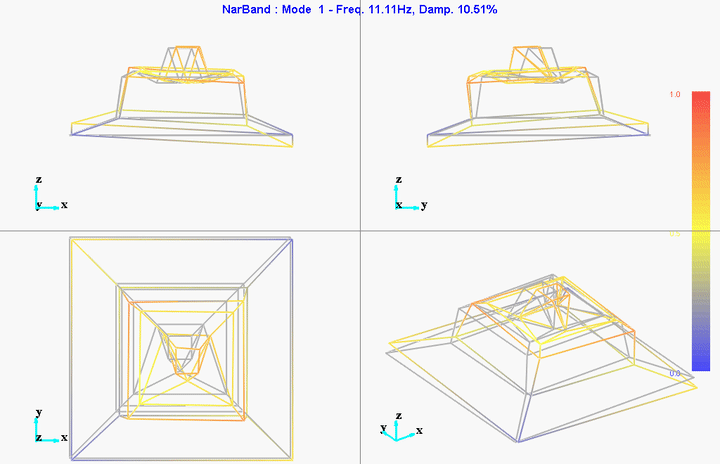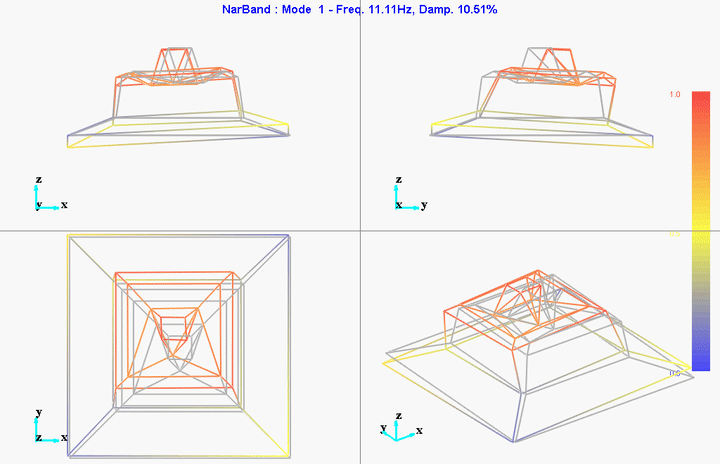
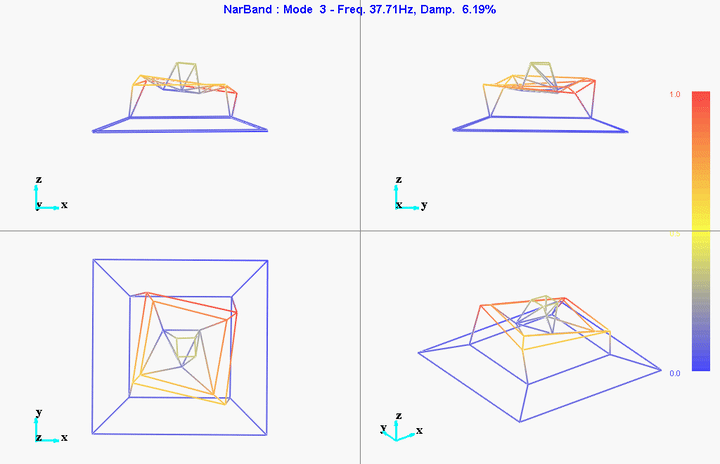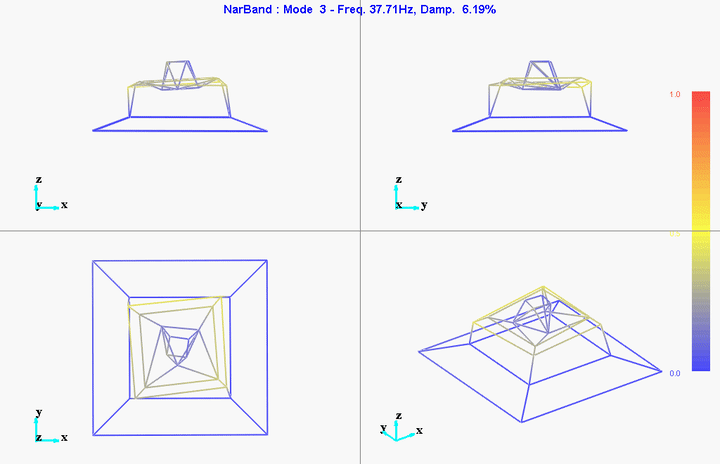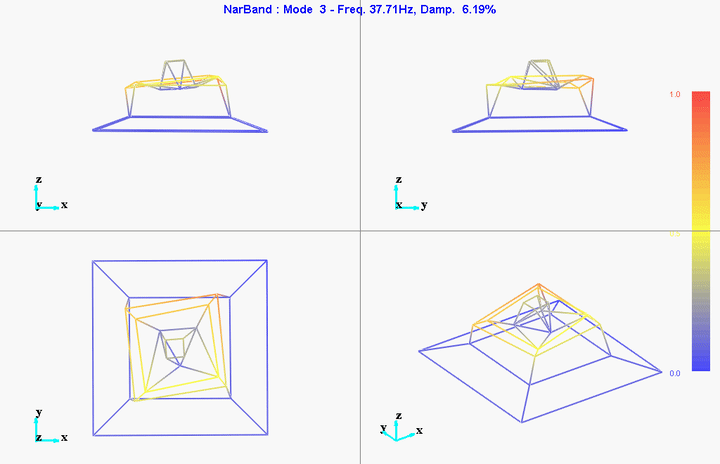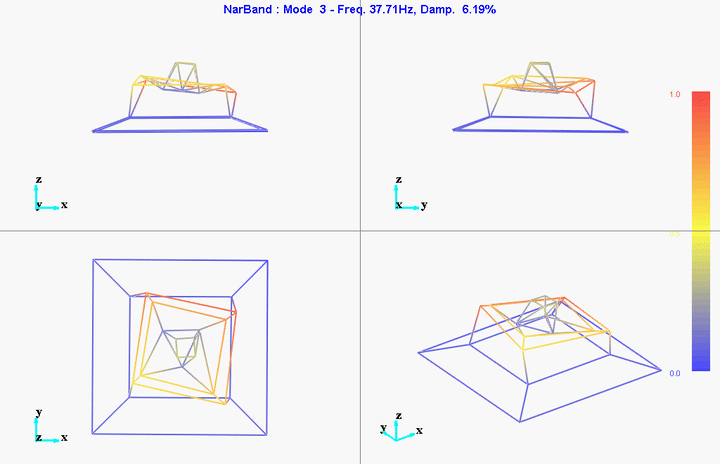
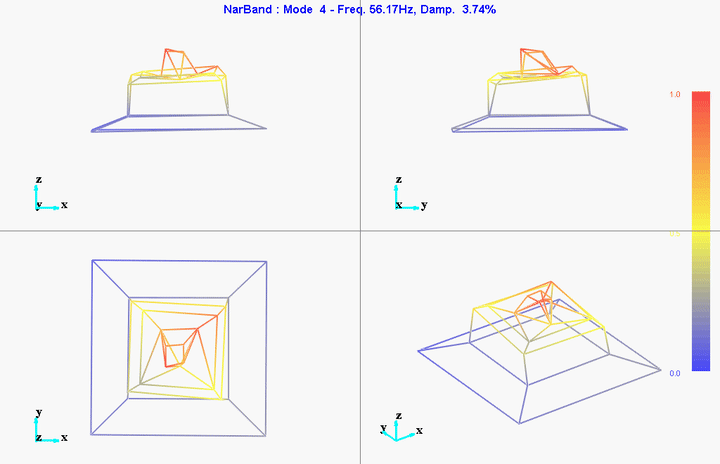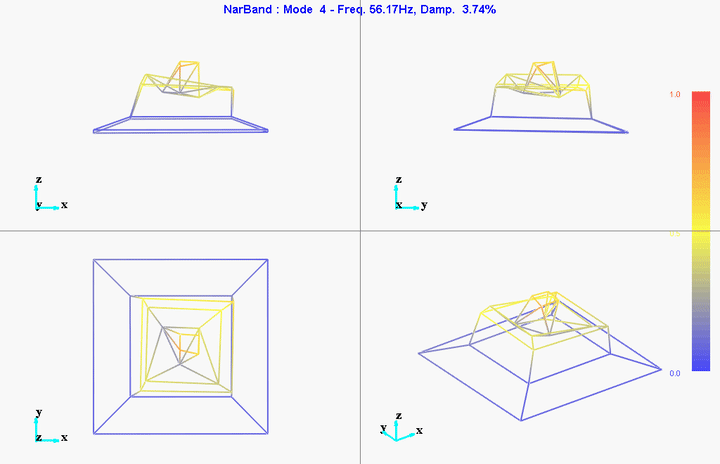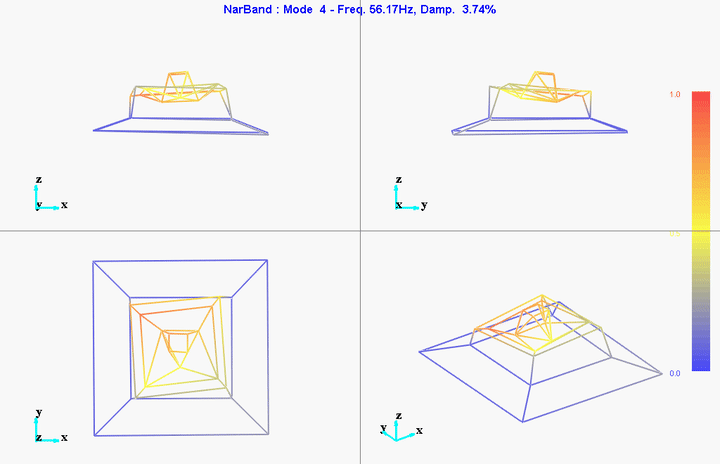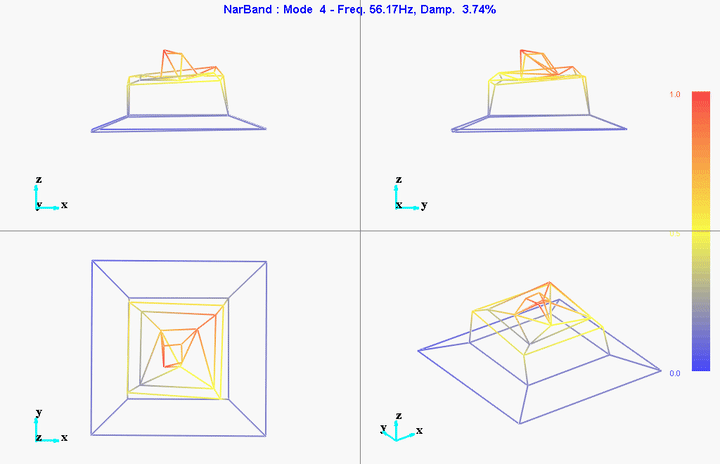
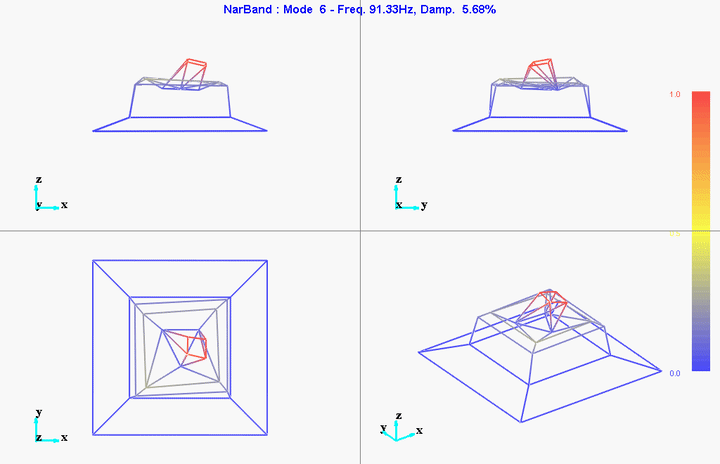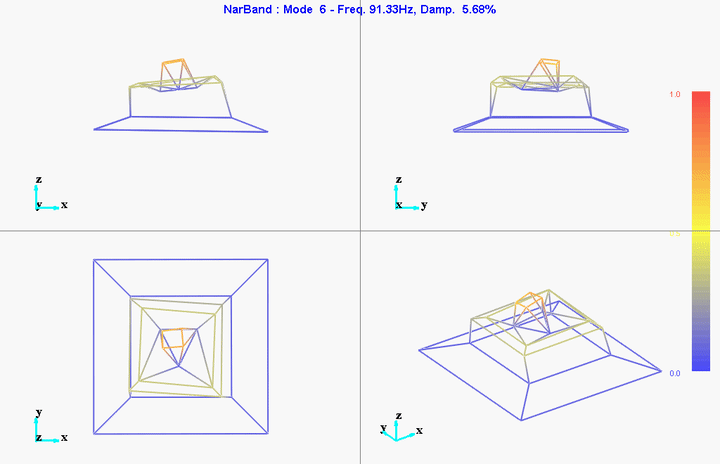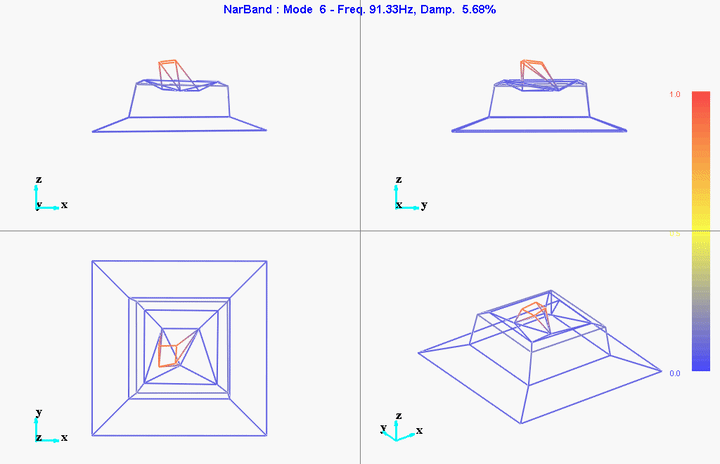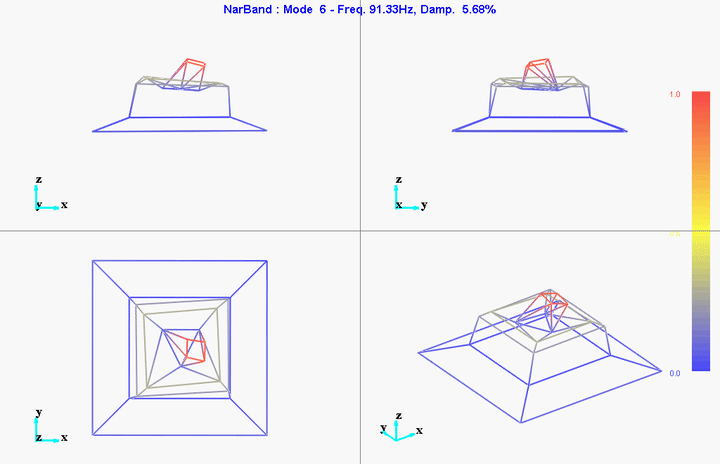
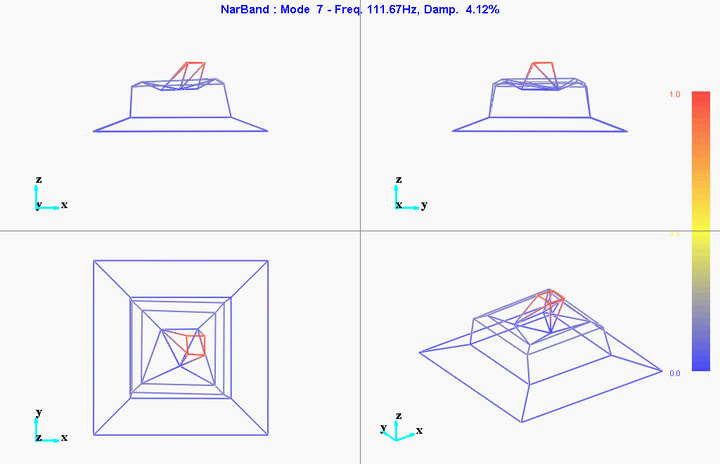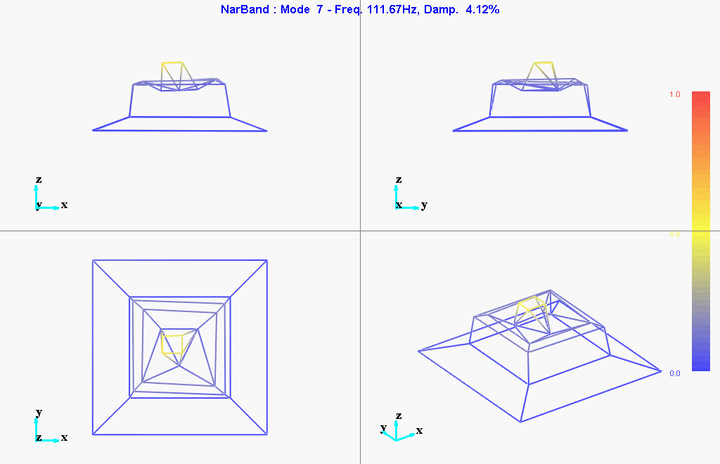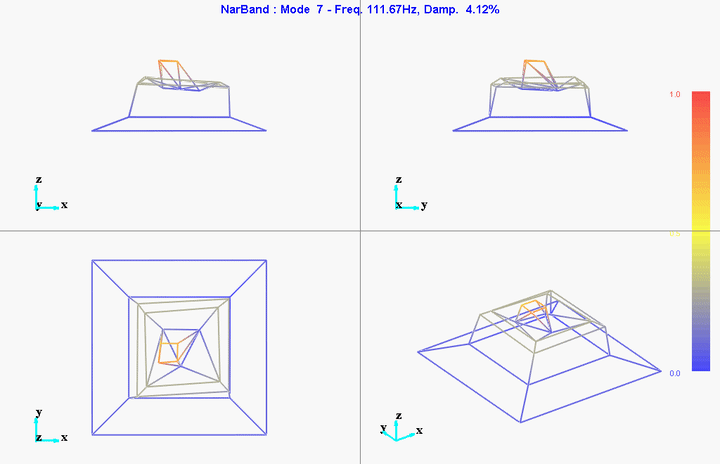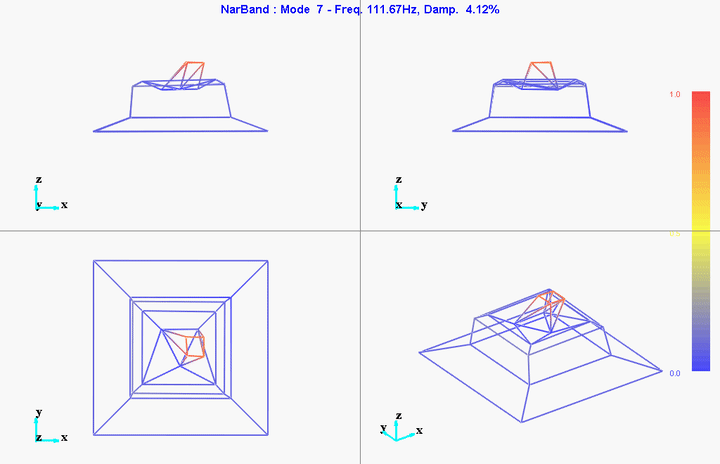
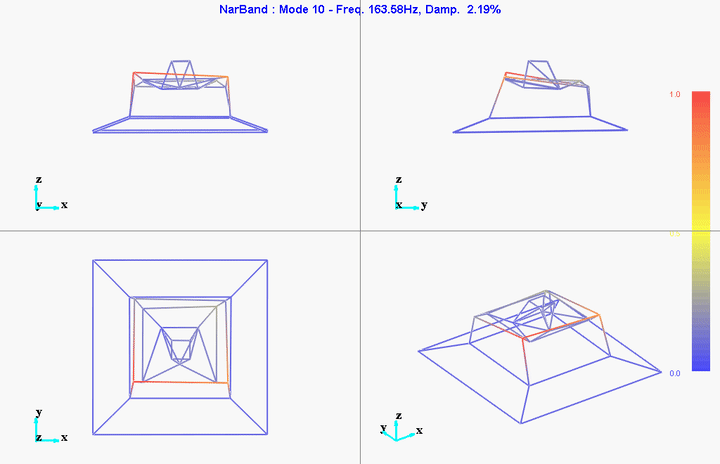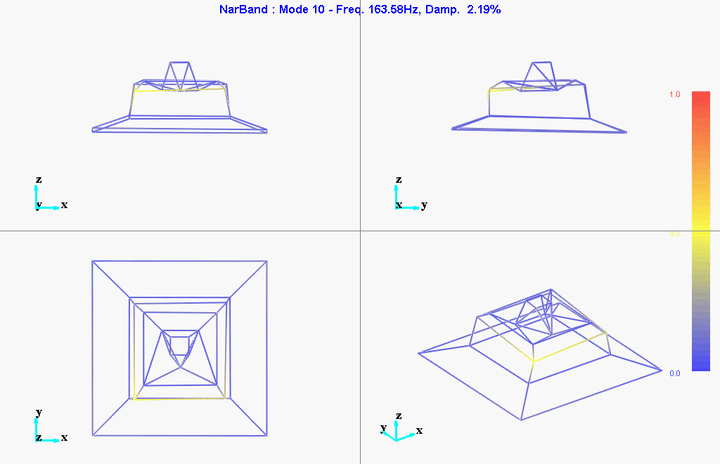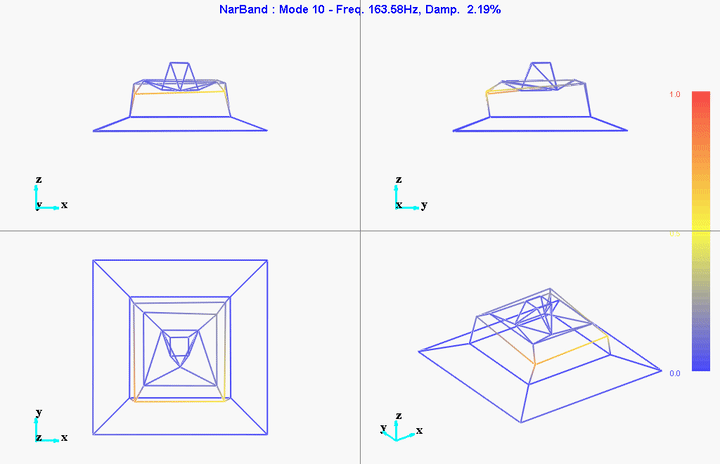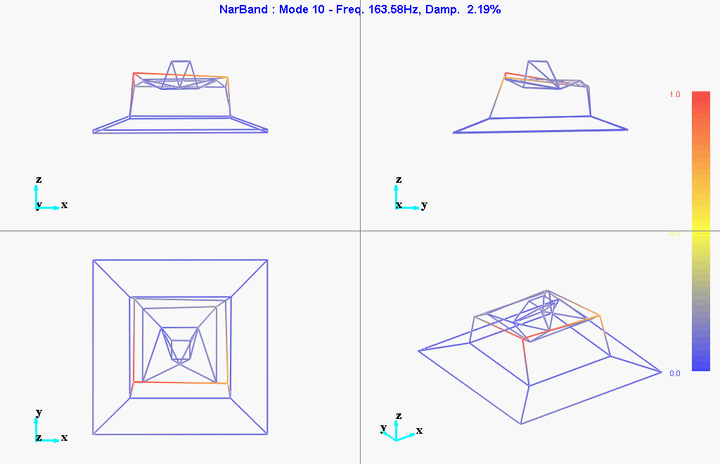
meas1 = load('modal_analysis/frf_coh/Measurement1.mat');FRF and Coherence Results
<<plt-matlab>>
<<plt-matlab>>
Mode Shapes
Multiple modal extraction techniques can be used (SIMO, MIMO, narrow band, wide band, …). First preliminary results on 10 identified modes are presented here.
Obtained Modal Matrices
From the modal analysis software, we can export the obtained eigen matrices: \[ \begin{bmatrix} \omega_1^2 & & 0 \\ & \ddots & \\ 0 & & \omega_n^2 \end{bmatrix}; \quad \Psi = \begin{bmatrix} & & \\ \{\psi_1\} & \dots & \{\psi_n\} \\ & & \end{bmatrix} \]
where $\bar{\omega}_r^2$ is the $r^\text{th}$ eigenvalue squared and $\{\phi\}_r$ is a description of the corresponding mode shape.
The file containing the eigen frequencies and mode shapes are shown below (for the first mode).
Created by N-Modal
Estimator: cmif
18-Jun-19 16:31:25
Mode 1
freq = 11.11191Hz
damp = 10.51401%
modal A = 8.52879e+003-2.29043e+003i
modal B = -9.64203e+004-6.08978e+005i
Mode matrix of local coordinate [DOF: Re IM]
1X+: -9.34637e-002 4.52445e-002
1Y+: 2.33790e-001 1.41439e-003
1Z+: -1.73754e-002 6.02449e-003
2X+: -7.42108e-002 3.91543e-002
2Y+: 2.41566e-001 -1.44869e-003
2Z+: -5.99285e-003 2.10370e-003
4X+: -1.02163e-001 2.79561e-002
4Y+: 2.29048e-001 2.89782e-002
4Z+: -2.85130e-002 1.77132e-004
5X+: -8.77132e-002 3.34081e-002
5Y+: 2.14182e-001 2.14655e-002
5Z+: -1.54521e-002 1.26682e-002
6X+: -7.90143e-002 2.42583e-002
6Y+: 2.20669e-001 2.12738e-002
6Z+: 4.60755e-002 4.96406e-003
7X+: -7.79654e-002 2.58385e-002
7Y+: 2.06861e-001 3.48019e-002
7Z+: -1.78311e-002 -1.29704e-002
8X+: -8.49357e-002 3.55200e-002
8Y+: 2.07470e-001 3.59745e-002
8Z+: -7.66974e-002 -3.19813e-003
9X+: -7.38565e-002 1.95146e-002
9Y+: 2.17403e-001 2.01550e-002
9Z+: -1.77073e-002 -3.46414e-003
10X+: -7.77587e-002 2.36700e-002
10Y+: 2.35654e-001 -2.14540e-002
10Z+: 7.94165e-002 -2.45897e-002
11X+: -8.17972e-002 2.20583e-002
11Y+: 2.20906e-001 -4.30164e-003
11Z+: -5.60520e-003 3.10187e-003
12X+: -8.64261e-002 3.66022e-002
12Y+: 2.15000e-001 -5.74661e-003
12Z+: -1.22622e-001 4.11767e-002
13X+: -4.25169e-002 1.56602e-002
13Y+: 5.31036e-002 -1.73951e-002
13Z+: -4.07130e-002 1.26884e-002
14X+: -3.85032e-002 1.29431e-002
14Y+: 5.36716e-002 -1.80868e-002
14Z+: 1.00367e-001 -3.48798e-002
15X+: -4.25524e-002 1.46363e-002
15Y+: 5.19668e-002 -1.69744e-002
15Z+: 5.89747e-003 -2.32428e-003
16X+: -4.31268e-002 1.38332e-002
16Y+: 5.07545e-002 -1.53045e-002
16Z+: -1.04172e-001 3.17984e-002
17X+: -2.69757e-002 9.07955e-003
17Y+: 3.07837e-002 -9.44663e-003
17Z+: -7.63502e-003 1.68203e-003
18X+: -3.00097e-002 9.23966e-003
18Y+: 2.83585e-002 -8.97747e-003
18Z+: 1.52467e-001 -4.78675e-002
19X+: -2.70223e-002 6.16478e-003
19Y+: 3.06149e-002 -6.25382e-003
19Z+: -4.84888e-003 1.93970e-003
20X+: -2.90976e-002 7.13184e-003
20Y+: 3.36738e-002 -7.30875e-003
20Z+: -1.66902e-001 3.93419e-002
3X+: -9.40720e-002 3.93724e-002
3Y+: 2.52307e-001 0.00000e+000
3Z+: -1.53864e-002 -9.25720e-004
21X+: -7.91940e-002 4.39648e-002
21Y+: 2.04567e-001 9.49987e-003
21Z+: -1.56087e-002 7.08838e-003
22X+: -1.01070e-001 3.13534e-002
22Y+: 1.92270e-001 1.80423e-002
22Z+: 2.93053e-003 -1.97308e-003
23X+: -8.86455e-002 4.29906e-002
23Z+: -3.38351e-002 1.81362e-003
23Y-: -1.90862e-001 -2.53414e-002
Problem with AirLoc System
4 Airloc Levelers are used for the granite (figure fig:airloc).
They are probably not well leveled so that could explain the first modes at 11Hz and 17Hz.