nass-micro-station-measurements/ground-motion/index.org

Ground Motion Measurements

• Experimental Setup
• Measurement Analysis
  • ZIP file containing the data and matlab files
  • Load data
  • Time domain plots of the measured voltage
  • Computation of the ASD of the measured voltage
  • Scaling to take into account the sensibility of the geophone and the voltage amplifier
  • Time domain plots of the ground motion
  • Computation of the ASD of the velocity and displacement
  • Save
  • Comparison with other measurements of ground motion
    • Load the measurement data
    • Compute PSD of the measurements
    • Compare PSD of Cern, ID09 and ID31

Experimental Setup

The goal here is to compare the ground motion at the location of the micro-station (ID31 beamline at ESRF) with other measurements of the ground motion.

This will also permit to confirm that the device use for the measurement (geophones, amplifiers, ADC) are working well and that the data processing is correct.

One L22 geophone is put on the ID31 floor. The signal is then filtered with a first order low pass filter with a cut-off frequency of $1kHz$. Then the signal is amplified by a Voltage Amplifier with the following settings:

• AC/DC option set to DC
• Amplification of 60dB (1000)
• Low pass filter at the output with a cut-off frequency of $1kHz$

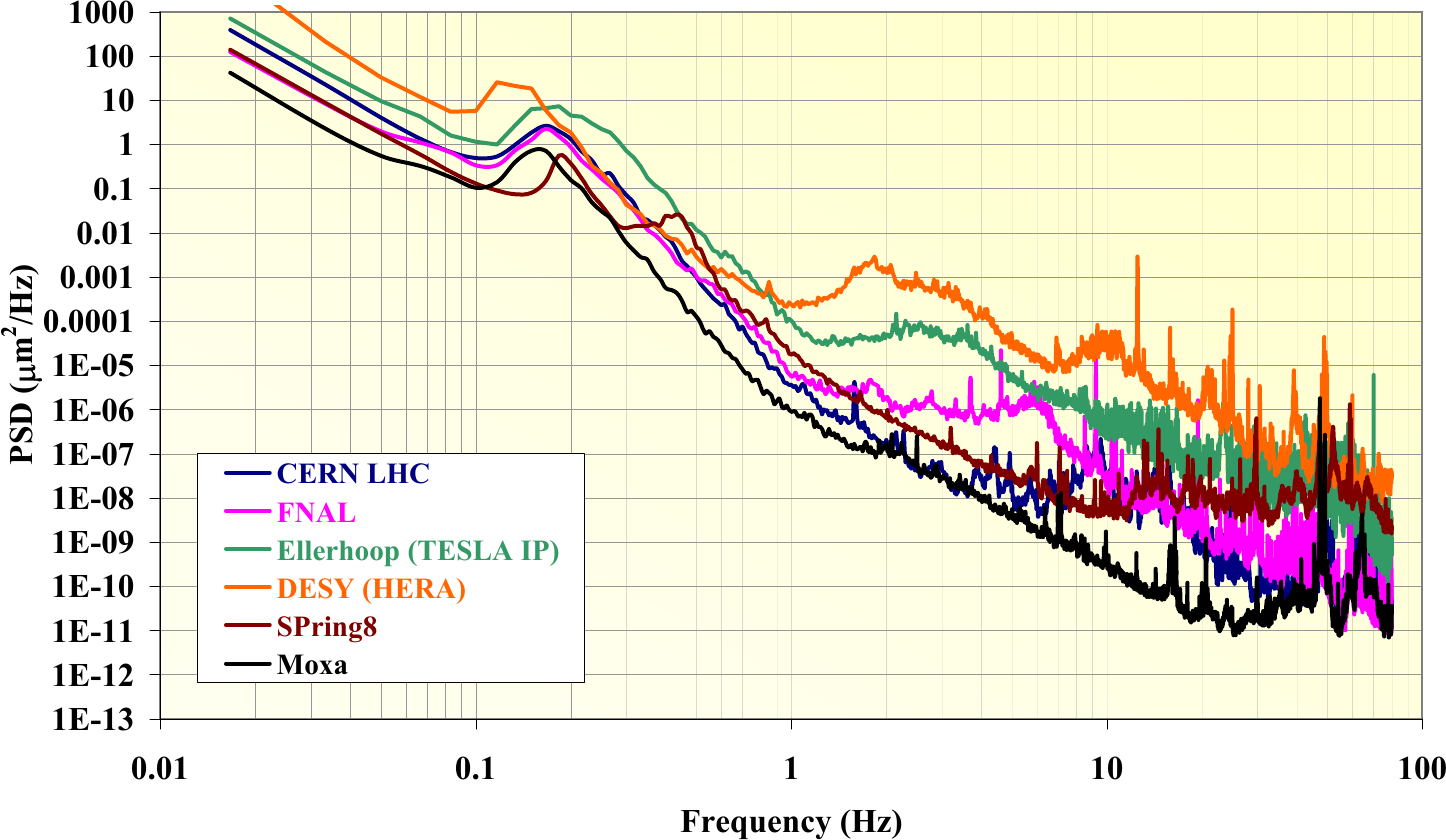
On figure fig:ground_motion_measurements is an overview of multiple measurements made at famous location.

Power spectral density of ground vibration in the vertical direction at multiple locations (source)

Measurement Analysis

<<sec:ground_meas_id31>>

ZIP file containing the data and matlab files   ignore

All the files (data and Matlab scripts) are accessible here.

Load data

  data = load('mat/data_028.mat', 'data'); data = data.data;

Time domain plots of the measured voltage

  figure;
  hold on;
  plot(data(:, 3), data(:, 1));
  hold off;
  xlabel('Time [s]'); ylabel('Voltage [V]');
  xlim([0, 100]);

  <<plt-matlab>>

Measurement of the ground motion - Time domain

Computation of the ASD of the measured voltage

  dt = data(2, 3) - data(1, 3);

  Fs = 1/dt;
  win = hanning(ceil(10*Fs));

  [px_dc, f] = pwelch(data(:, 1), win, [], [], Fs);

  figure;
  hold on;
  plot(f, sqrt(px_dc));
  hold off;
  set(gca, 'xscale', 'log');
  set(gca, 'yscale', 'log');
  xlabel('Frequency [Hz]'); ylabel('Amplitude Spectral Density $\left[\frac{V}{\sqrt{Hz}}\right]$')
  xlim([0.1, 500]);

  <<plt-matlab>>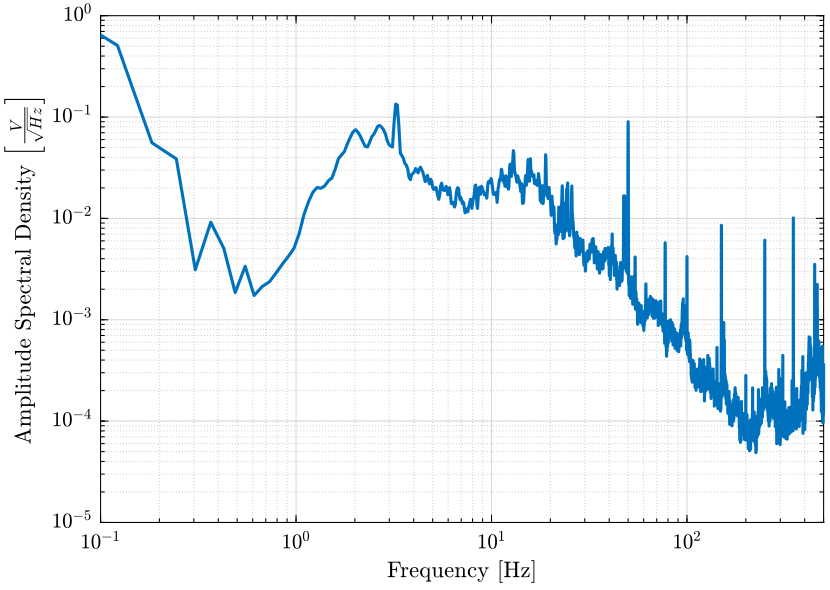

Amplitude Spectral Density of the measured Voltage

Scaling to take into account the sensibility of the geophone and the voltage amplifier

The Geophone used are L22. Their sensibility is shown on figure fig:geophone_sensibility.

  S0 = 88; % Sensitivity [V/(m/s)]
  f0 = 2; % Cut-off frequency [Hz]

  S = S0*(s/2/pi/f0)/(1+s/2/pi/f0);

  freqs = logspace(-1, 2, 1000);

  figure;
  hold on;
  plot(f, abs(squeeze(freqresp(S, f, 'Hz'))));
  hold off;
  set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
  xlabel('Frequency [Hz]'); ylabel('Magnitude $\left[\frac{V}{m/s}\right]$');
  xlim([0.1, 100]);

  <<plt-matlab>>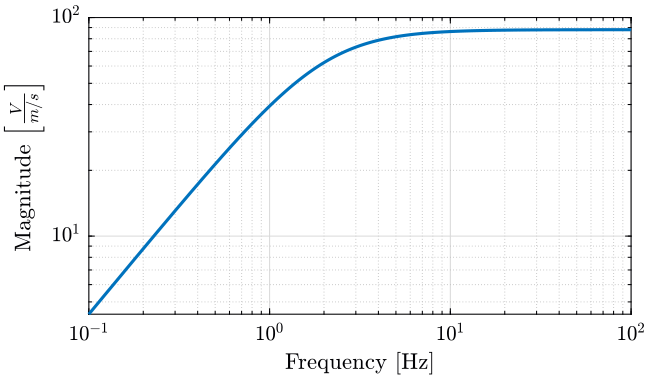

Sensibility of the Geophone

We also take into account the gain of the electronics which is here set to be $60dB$.

  G0_db = 60; % [dB]

  G0 = 10^(G0_db/20); % [abs]

We divide the PSD measured (in $\text{V^2}/\sqrt{Hz}$) by the square of the gain of the voltage amplifier to obtain the PSD of the voltage across the geophone. We further divide the result by the square of the magnitude of sensibility of the Geophone to obtain the PSD of the velocity in $(m/s)^2/Hz$.

  psd_gv = px_dc./abs(squeeze(freqresp(G0*S, f, 'Hz'))).^2;

Finally, we obtain the PSD of the ground motion in $m^2/Hz$ by dividing by the square of the frequency in $rad/s$.

  psd_gm = psd_gv./(2*pi*f).^2;

Time domain plots of the ground motion

We can inverse the dynamics of the geophone to convert the measured voltage into the estimated ground motion.

  est_vel = lsim(inv(G0*S)*(s/2/pi)/(1+s/2/pi), data(:, 1), data(:, 3)); % Estimated velocity above 1Hz
  est_vel = est_vel - mean(est_vel(data(:,3)>10)); % The mean value of the velocity if removed
  est_dis = lsim(1/(1+s/2/pi), est_vel, data(:, 3)); % The velocity is integrated above 1Hz

<<plt-matlab>>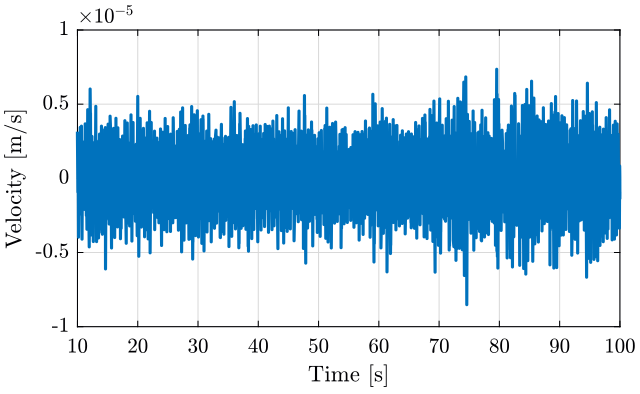

Time domain velocity (png, pdf)

<<plt-matlab>>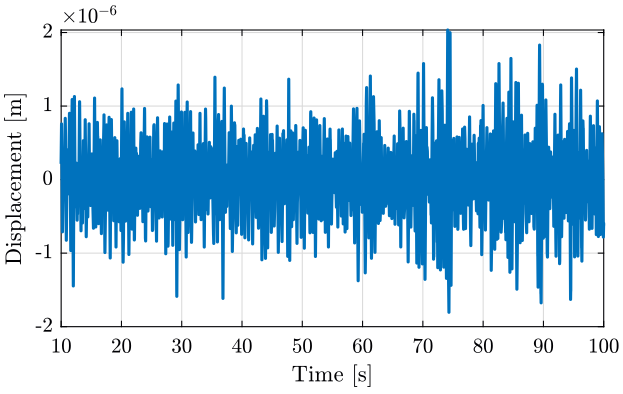

Time domain absolute displacement (png, pdf)

Computation of the ASD of the velocity and displacement

The ASD of the measured velocity is shown on figure fig:ground_motion_id31_asd_velocity.

  figure;
  hold on;
  plot(f, sqrt(psd_gv));
  hold off;
  set(gca, 'xscale', 'log');
  set(gca, 'yscale', 'log');
  xlabel('Frequency [Hz]'); ylabel('ASD of the measured Velocity $\left[\frac{m/s}{\sqrt{Hz}}\right]$')
  xlim([0.1, 500]);

  <<plt-matlab>>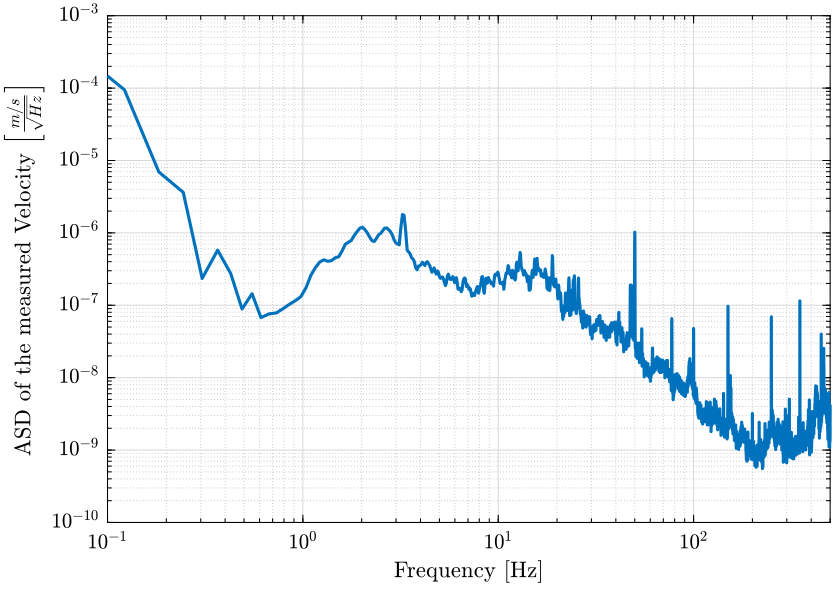

Amplitude Spectral Density of the Velocity

We also plot the ASD in displacement (figure fig:ground_motion_id31_asd_displacement);

  figure;
  hold on;
  plot(f, sqrt(psd_gm));
  hold off;
  set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
  xlabel('Frequency [Hz]'); ylabel('ASD of the displacement $\left[\frac{m}{\sqrt{Hz}}\right]$')
  xlim([0.1, 500]);

  <<plt-matlab>>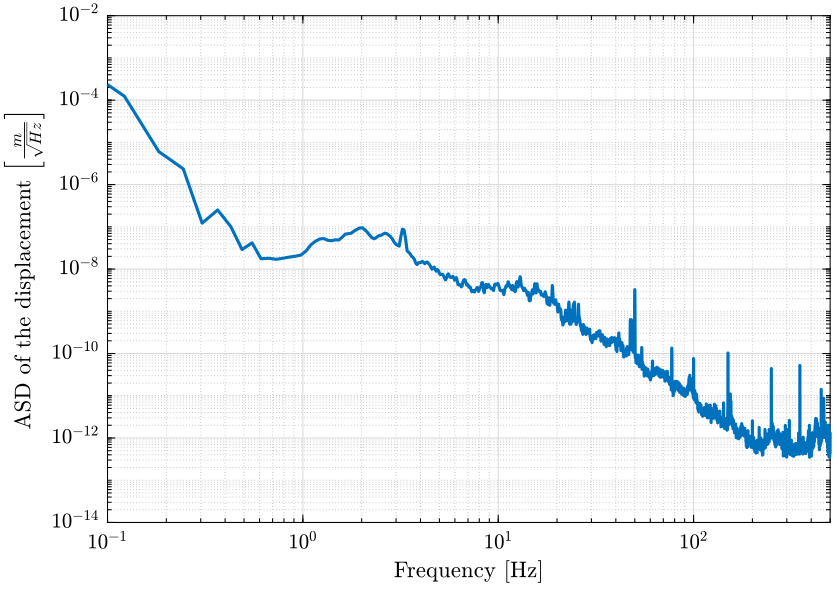

Amplitude Spectral Density of the Displacement

And we also plot the PSD of the displacement in $\frac{{\mu u}^2}{Hz}$ as it is a usual unit used (figure fig:ground_motion_id31_psd_displacement). One can then compare this curve with the figure fig:ground_motion_measurements.

  figure;
  hold on;
  plot(f, psd_gm.*1e12);
  hold off;
  set(gca, 'xscale', 'log');
  set(gca, 'yscale', 'log');
  xlabel('Frequency [Hz]'); ylabel('PSD of the measured displacement $\left[\frac{{ \mu m }^2}{Hz}\right]$')
  xlim([0.1, 500]); ylim([1e-13, 1e3]);

  <<plt-matlab>>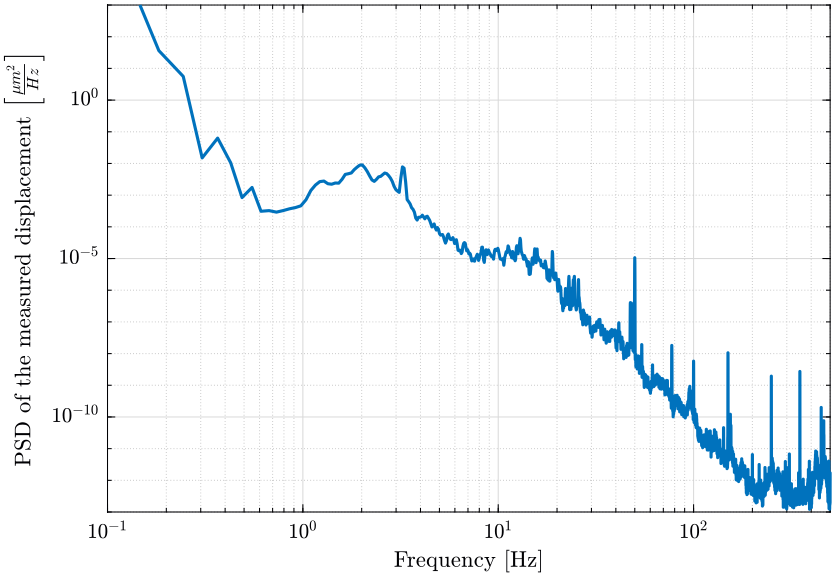

Power Spectral Density of the measured displacement

Save

We save the PSD of the ground motion for further analysis.

  save('./mat/psd_gm.mat', 'f', 'psd_gm', 'psd_gv');

Comparison with other measurements of ground motion

Now we will compare with other measurements.

Load the measurement data

First we load the measurement data. Here we have one measurement of the floor motion made at the ESRF in 2018, and one measurement made at CERN.

  id09 = load('./mat/id09_floor_september2018.mat');
  cern = load('./mat/ground_motion_dist.mat');

Compute PSD of the measurements

We compute the Power Spectral Densities of the measurements.

  Fs_id09 = 1/(id09.time3(2)-id09.time3(1));
  win_id09 = hanning(ceil(10*Fs_id09));
  [id09_pxx, id09_f] = pwelch(1e-6*id09.x_y_z(:, 3), win_id09, [], [], Fs_id09);

  Fs_cern = 1/(cern.gm.time(2)-cern.gm.time(1));
  win_cern = hanning(ceil(10*Fs_cern));
  [cern_pxx, cern_f] = pwelch(cern.gm.signal, win_cern, [], [], Fs_cern);

Compare PSD of Cern, ID09 and ID31

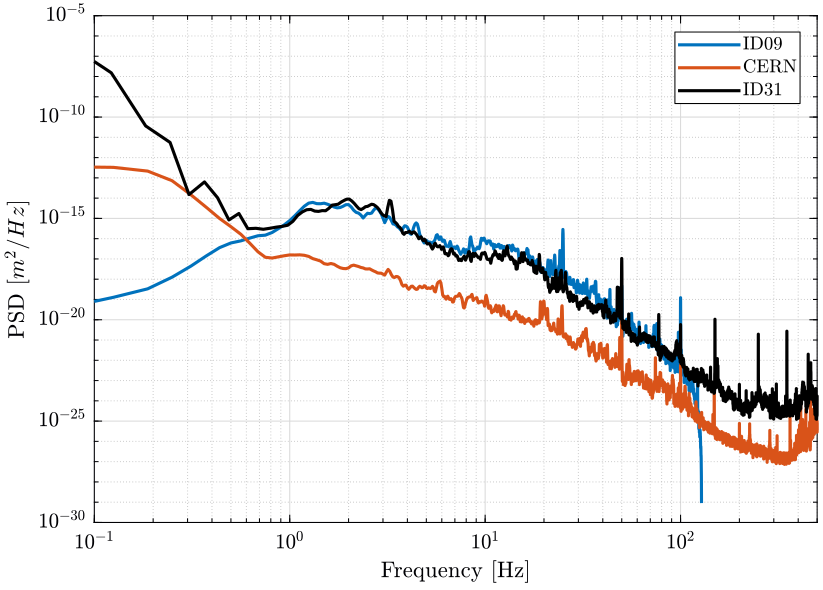
And we compare all the measurements (figure fig:ground_motion_compare).

  figure;
  hold on;
  plot(id09_f, id09_pxx, 'DisplayName', 'ID09');
  plot(cern_f, cern_pxx, 'DisplayName', 'CERN');
  plot(f, psd_gm, 'k', 'DisplayName', 'ID31');
  hold off;
  set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log');
  xlabel('Frequency [Hz]'); ylabel('PSD [$m^2/Hz$]');
  legend('Location', 'northeast');
  xlim([0.1, 500]);

  <<plt-matlab>>

Comparison of the PSD of the ground motion measured at different location