nass-fem/index.org

Finite Element Model with Simscape

• Amplified Piezoelectric Actuator - 3D elements
  • Introduction
  • Import Mass Matrix, Stiffness Matrix, and Interface Nodes Coordinates
  • Identification of the Dynamics
  • Comparison with Ansys
  • Force Sensor
  • Distributed Actuator
  • Distributed Actuator and Force Sensor
• Integral Force Feedback with Amplified Piezo
  • Import Mass Matrix, Stiffness Matrix, and Interface Nodes Coordinates
  • IFF Plant
  • IFF controller
  • Closed Loop System

Amplified Piezoelectric Actuator - 3D elements

Introduction   ignore

The idea here is to:

• export a FEM of an amplified piezoelectric actuator from Ansys to Matlab
• import it into a Simscape model
• compare the obtained dynamics
• add 10kg mass on top of the actuator and identify the dynamics
• compare with results from Ansys where 10kg are directly added to the FEM

Import Mass Matrix, Stiffness Matrix, and Interface Nodes Coordinates

We first extract the stiffness and mass matrices.

  K = extractMatrix('piezo_amplified_3d_K.txt');
  M = extractMatrix('piezo_amplified_3d_M.txt');

Then, we extract the coordinates of the interface nodes.

  [int_xyz, int_i, n_xyz, n_i, nodes] = extractNodes('piezo_amplified_3d.txt');

Total number of Nodes	168959
Number of interface Nodes	13
Number of Modes	30
Size of M and K matrices	108

Interface Nodes for the Amplified Piezo Actuator

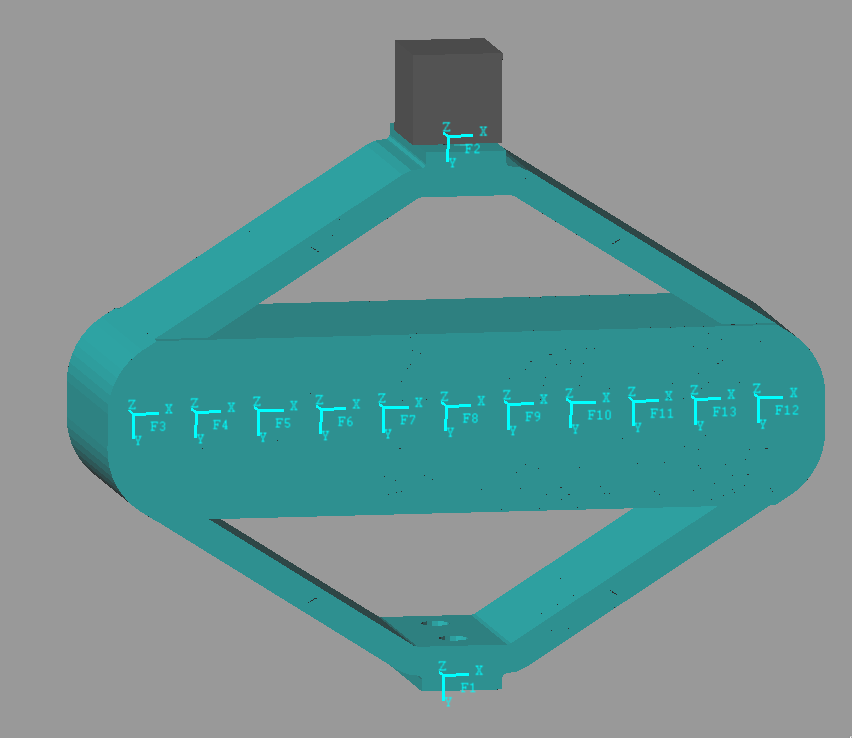
Node i	Node Number	x [m]	y [m]	z [m]
1.0	168947.0	0.0	0.03	0.0
2.0	168949.0	0.0	-0.03	0.0
3.0	168950.0	-0.035	0.0	0.0
4.0	168951.0	-0.028	0.0	0.0
5.0	168952.0	-0.021	0.0	0.0
6.0	168953.0	-0.014	0.0	0.0
7.0	168954.0	-0.007	0.0	0.0
8.0	168955.0	0.0	0.0	0.0
9.0	168956.0	0.007	0.0	0.0
10.0	168957.0	0.014	0.0	0.0
11.0	168958.0	0.021	0.0	0.0
12.0	168959.0	0.035	0.0	0.0
13.0	168960.0	0.028	0.0	0.0

Coordinates of the interface nodes

300000000.0	-30000.0	8000.0	-200.0	-30.0	-60000.0	20000000.0	-4000.0	500.0	8
-30000.0	100000000.0	400.0	30.0	200.0	-1	4000.0	-8000000.0	800.0	7
8000.0	400.0	50000000.0	-800000.0	-300.0	-40.0	300.0	100.0	5000000.0	40000.0
-200.0	30.0	-800000.0	20000.0	5	1	-10.0	-2	-40000.0	-300.0
-30.0	200.0	-300.0	5	40000.0	0.3	-4	-10.0	40.0	0.4
-60000.0	-1	-40.0	1	0.3	3000.0	7000.0	0.8	-1	0.0003
20000000.0	4000.0	300.0	-10.0	-4	7000.0	300000000.0	20000.0	3000.0	80.0
-4000.0	-8000000.0	100.0	-2	-10.0	0.8	20000.0	100000000.0	-4000.0	-100.0
500.0	800.0	5000000.0	-40000.0	40.0	-1	3000.0	-4000.0	50000000.0	800000.0
8	7	40000.0	-300.0	0.4	0.0003	80.0	-100.0	800000.0	20000.0

First 10x10 elements of the Stiffness matrix

0.03	2e-06	-2e-07	1e-08	2e-08	0.0002	-0.001	2e-07	-8e-08	-9e-10
2e-06	0.02	-5e-07	7e-09	3e-08	2e-08	-3e-07	0.0003	-1e-08	1e-10
-2e-07	-5e-07	0.02	-9e-05	4e-09	-1e-08	2e-07	-2e-08	-0.0006	-5e-06
1e-08	7e-09	-9e-05	1e-06	6e-11	4e-10	-1e-09	3e-11	5e-06	3e-08
2e-08	3e-08	4e-09	6e-11	1e-06	2e-10	-2e-09	2e-10	-7e-09	-4e-11
0.0002	2e-08	-1e-08	4e-10	2e-10	2e-06	-2e-06	-1e-09	-7e-10	-9e-12
-0.001	-3e-07	2e-07	-1e-09	-2e-09	-2e-06	0.03	-2e-06	-1e-07	-5e-09
2e-07	0.0003	-2e-08	3e-11	2e-10	-1e-09	-2e-06	0.02	-8e-07	-1e-08
-8e-08	-1e-08	-0.0006	5e-06	-7e-09	-7e-10	-1e-07	-8e-07	0.02	9e-05
-9e-10	1e-10	-5e-06	3e-08	-4e-11	-9e-12	-5e-09	-1e-08	9e-05	1e-06

First 10x10 elements of the Mass matrix

Using K, M and int_xyz, we can use the Reduced Order Flexible Solid simscape block.

Identification of the Dynamics

The flexible element is imported using the Reduced Order Flexible Solid simscape block.

To model the actuator, an Internal Force block is added between the nodes 3 and 12. A Relative Motion Sensor block is added between the nodes 1 and 2 to measure the displacement and the amplified piezo.

One mass is fixed at one end of the piezo-electric stack actuator, the other end is fixed to the world frame.

We first set the mass to be zero.

  m = 0;

The dynamics is identified from the applied force to the measured relative displacement.

  %% Name of the Simulink File
  mdl = 'piezo_amplified_3d';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/F'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/y'], 1, 'openoutput'); io_i = io_i + 1;

  Gh = linearize(mdl, io);

Then, we add 10Kg of mass:

  m = 10;

And the dynamics is identified.

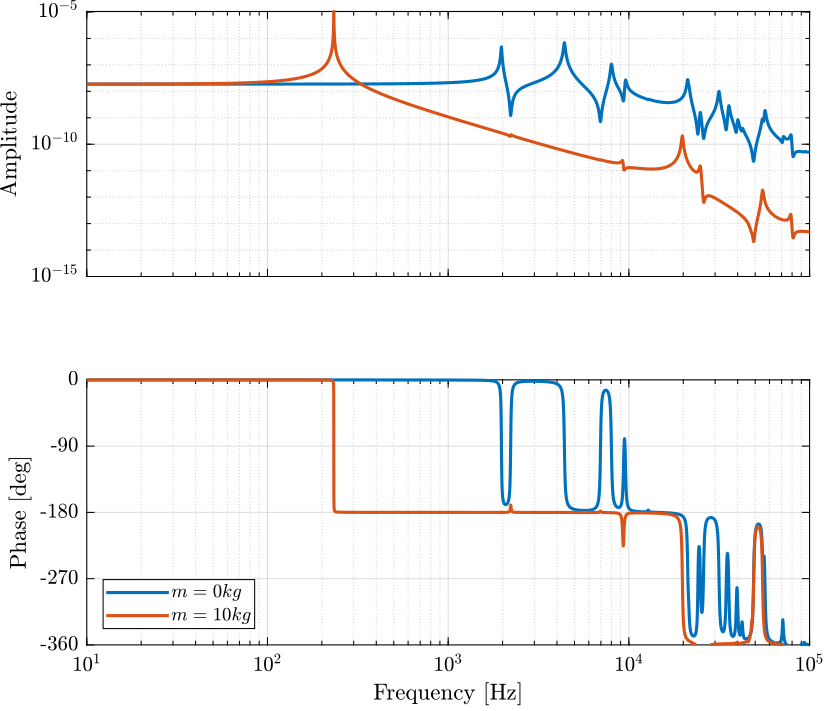
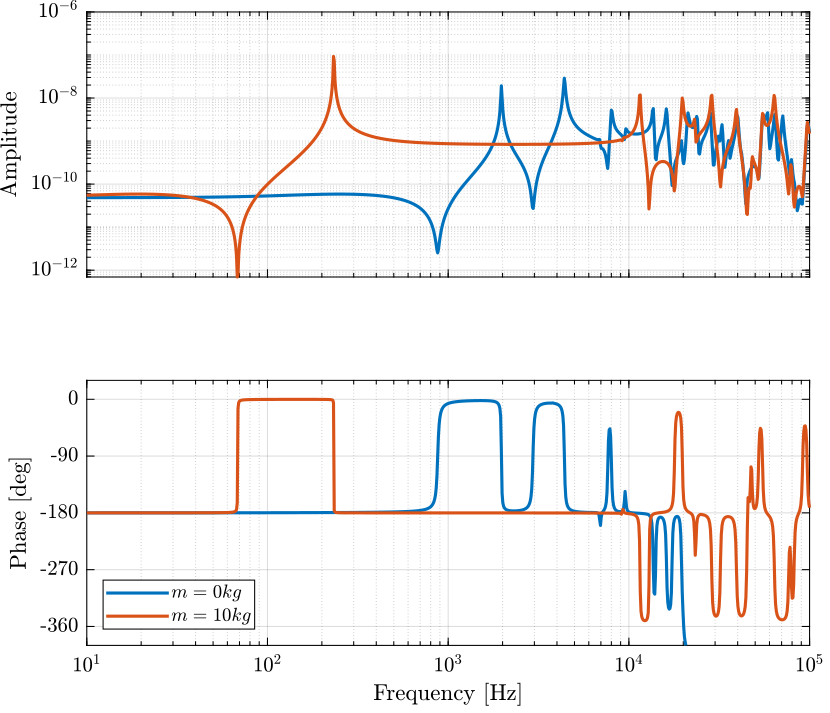
The two identified dynamics are compared in Figure fig:dynamics_act_disp_comp_mass.

  %% Name of the Simulink File
  mdl = 'piezo_amplified_3d';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/F'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/y'], 1, 'openoutput'); io_i = io_i + 1;

  Ghm = linearize(mdl, io);

Dynamics from $F$ to $d$ without a payload and with a 10kg payload

Comparison with Ansys

Let's import the results from an Harmonic response analysis in Ansys.

  Gresp0 = readtable('FEA_HarmResponse_00kg.txt');
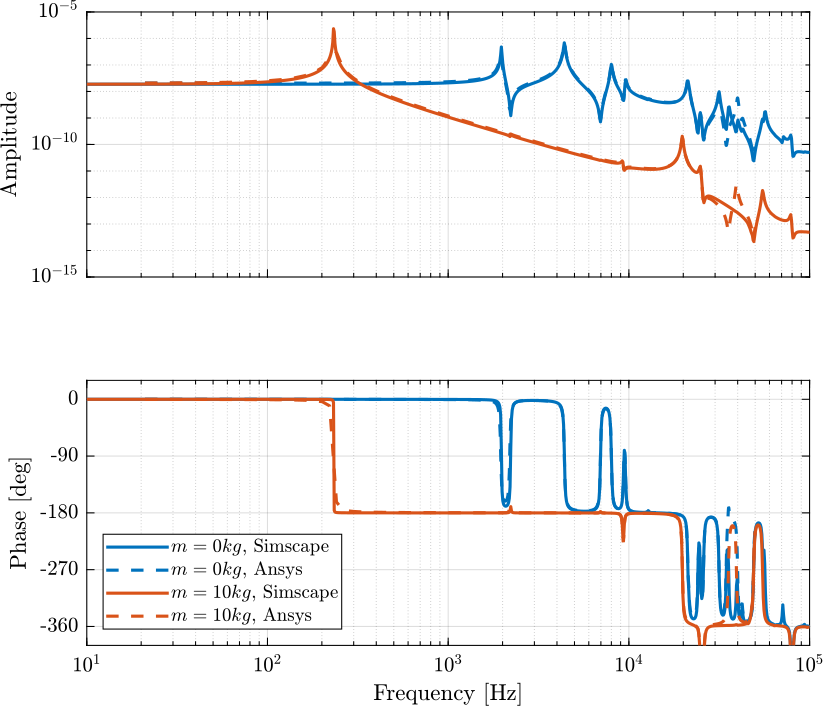
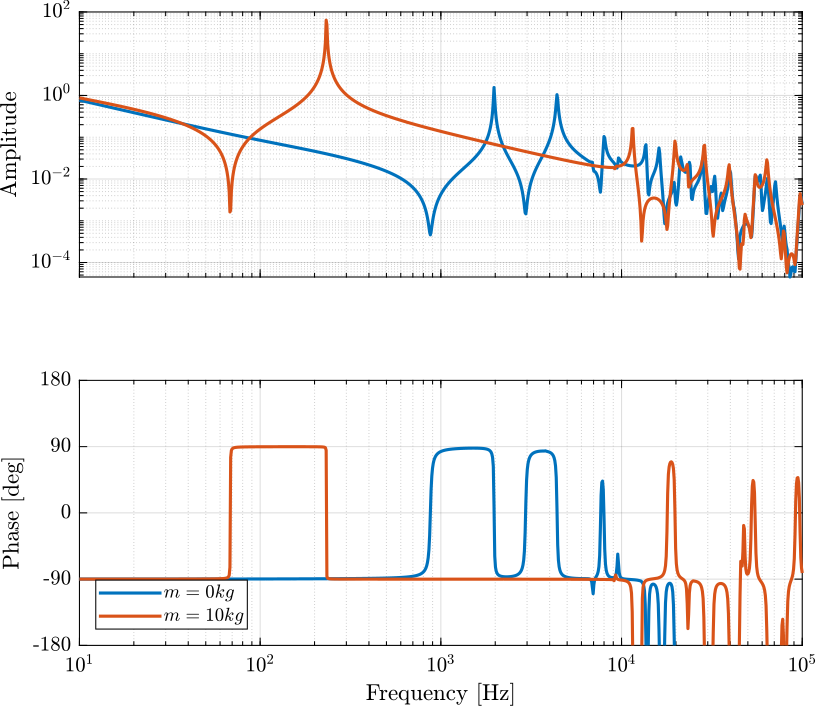
  Gresp10 = readtable('FEA_HarmResponse_10kg.txt');

The obtained dynamics from the Simscape model and from the Ansys analysis are compare in Figure fig:dynamics_force_disp_comp_anasys.

Comparison of the obtained dynamics using Simscape with the harmonic response analysis using Ansys

Force Sensor

The dynamics is identified from internal forces applied between nodes 3 and 11 to the relative displacement of nodes 11 and 13.

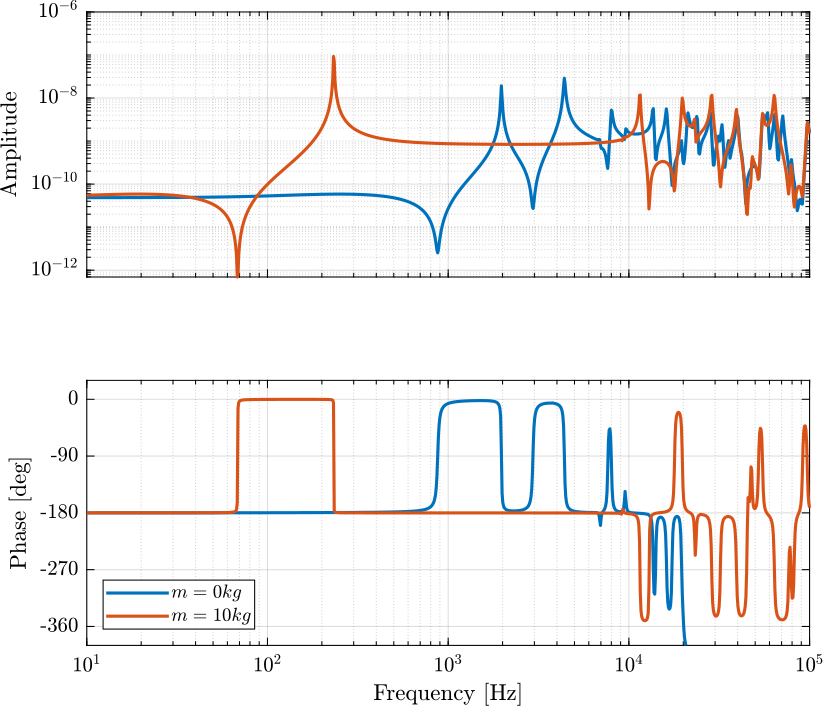
The obtained dynamics is shown in Figure fig:dynamics_force_force_sensor_comp_mass.

  m = 0;

  %% Name of the Simulink File
  mdl = 'piezo_amplified_3d';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/Fa'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Fs'], 1, 'openoutput'); io_i = io_i + 1;

  Gf = linearize(mdl, io);

  m = 10;

  %% Name of the Simulink File
  mdl = 'piezo_amplified_3d';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/Fa'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Fs'], 1, 'openoutput'); io_i = io_i + 1;

  Gfm = linearize(mdl, io);

Dynamics from $F$ to $F_m$ for $m=0$ and $m = 10kg$

Distributed Actuator

  m = 0;

The dynamics is identified from the applied force to the measured relative displacement.

  %% Name of the Simulink File
  mdl = 'piezo_amplified_3d_distri';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/F'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/y'], 1, 'openoutput'); io_i = io_i + 1;

  Gd = linearize(mdl, io);

Then, we add 10Kg of mass:

  m = 10;

And the dynamics is identified.

  %% Name of the Simulink File
  mdl = 'piezo_amplified_3d_distri';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/F'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/y'], 1, 'openoutput'); io_i = io_i + 1;

  Gdm = linearize(mdl, io);

Distributed Actuator and Force Sensor

  m = 0;

  %% Name of the Simulink File
  mdl = 'piezo_amplified_3d_distri_act_sens';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/F'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1;

  Gfd = linearize(mdl, io);

  m = 10;

  %% Name of the Simulink File
  mdl = 'piezo_amplified_3d_distri_act_sens';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/F'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1;

  Gfdm = linearize(mdl, io);

Integral Force Feedback with Amplified Piezo

Import Mass Matrix, Stiffness Matrix, and Interface Nodes Coordinates

We first extract the stiffness and mass matrices.

  K = extractMatrix('piezo_amplified_IFF_K.txt');
  M = extractMatrix('piezo_amplified_IFF_M.txt');

Then, we extract the coordinates of the interface nodes.

  [int_xyz, int_i, n_xyz, n_i, nodes] = extractNodes('piezo_amplified_IFF.txt');

IFF Plant

The transfer function from the force actuator to the force sensor is identified and shown in Figure fig:piezo_amplified_iff_plant.

  Kiff = tf(0);

  m = 0;

  %% Name of the Simulink File
  mdl = 'piezo_amplified_IFF';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/Kiff'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/G'],    1, 'openoutput'); io_i = io_i + 1;

  Gf = linearize(mdl, io);

  m = 10;

  Gfm = linearize(mdl, io);

IFF Plant

IFF controller

The controller is defined and the loop gain is shown in Figure fig:piezo_amplified_iff_loop_gain.

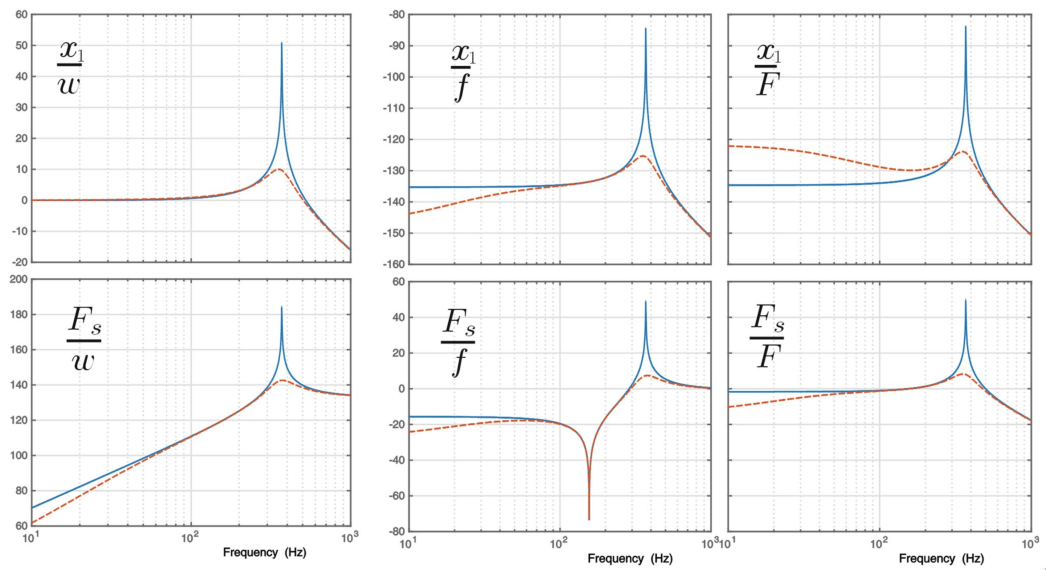
  Kiff = -1e12/s;

IFF Loop Gain

Closed Loop System

  m = 10;

  Kiff = -1e12/s;

  %% Name of the Simulink File
  mdl = 'piezo_amplified_IFF';

  %% Input/Output definition
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/Dw'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/F'],  1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/Fd'], 1, 'openinput');  io_i = io_i + 1;
  io(io_i) = linio([mdl, '/d'],  1, 'openoutput'); io_i = io_i + 1;
  io(io_i) = linio([mdl, '/G'],  1, 'output'); io_i = io_i + 1;

  Giff = linearize(mdl, io);
  Giff.InputName  = {'w', 'f', 'F'};
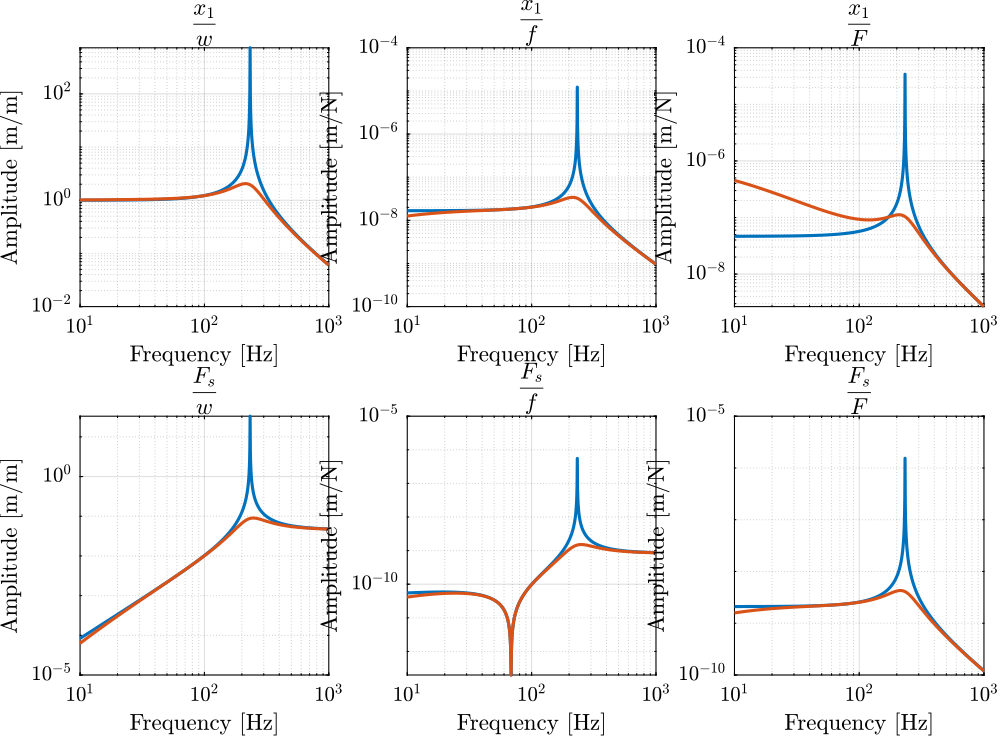
  Giff.OutputName  = {'x1', 'Fs'};

  Kiff = tf(0);

  G = linearize(mdl, io);
  G.InputName  = {'w', 'f', 'F'};
  G.OutputName  = {'x1', 'Fs'};

OL and CL transfer functions

Results obtained in cite:souleille18_concep_activ_mount_space_applic