lecture-h-infinity/index.org

Robust Control - $\mathcal{H}_\infty$ Synthesis

• Introduction to the Control Methodology - Model Based Control
• Some Background: From Classical Control to Robust Control
• The $\mathcal{H}_\infty$ Norm
• $\mathcal{H}_\infty$ Synthesis
• The Generalized Plant
• Problem Formulation
• Classical feedback control and closed loop transfer functions
• From a Classical Feedback Architecture to a Generalized Plant
• Modern Interpretation of the Control Specifications
  • Introduction
• Resources

Introduction to the Control Methodology - Model Based Control

The typical methodology when applying Model Based Control to a plant is schematically shown in Figure fig:control-procedure. It consists of three steps:

1. Identification or modeling: $\Longrightarrow$ mathematical model

2. Translate the specifications into mathematical criteria:

   • Specifications: Response Time, Noise Rejection, Maximum input amplitude, Robustness, …
   • Mathematical Criteria: Cost Function, Shape of TF
3. Synthesis: research of $K$ that satisfies the specifications for the model of the system

  \begin{tikzpicture}
    \node[addb={+}{}{}{}{-}] (addsub) at (0, 0){};

    \node[block, right=1.5 of addsub] (controller) {Controller};
    \node[block, right=1.5 of controller] (plant) {Plant};

    \node[block, above=1 of controller] (controller_design) {Synthesis};
    \node[block, above=1 of plant] (model_plant) {Model};

    \draw[<-] (addsub.west) -- ++(-1, 0) node[above right]{$r$};

    \draw[->] (addsub) -- (controller.west) node[above left]{$\epsilon$};
    \draw[->] (controller) -- (plant.west) node[above left]{$u$};
    \draw[->] (plant.east) -- ++(1, 0) node[above left]{$y$};
    \draw[] ($(plant.east) + (0.5, 0)$) -- ++(0, -1);
    \draw[->] ($(plant.east) + (0.5, -1)$) -| (addsub.south);

    \draw[->, dashed] (plant) -- node[midway, right, labelc, solid]{1} (model_plant);
    \draw[->, dashed] (controller_design) --node[midway, right, labelc, solid]{3} (controller);
    \draw[->, dashed] (model_plant) -- (controller_design);
    \draw[<-, dashed] (controller_design.west) -- node[midway, above, labelc, solid]{2} ++(-1, 0) node[left, style={align=center}]{Specifications};
  \end{tikzpicture}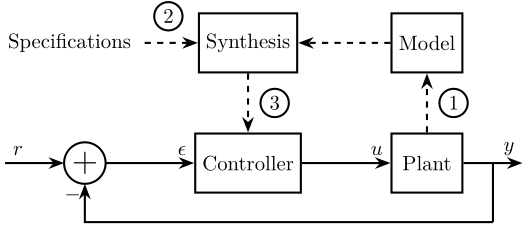

Typical Methodoly for Model Based Control

In this document, we will mainly focus on steps 2 and 3.

Some Background: From Classical Control to Robust Control

Classical Control (1930)

• Tools:

  • TF (input-output)
  • Nyquist, Bode, Black, \ldots
  • P-PI-PID, Phase lead-lag, \ldots

• Advantages:

  • Stability
  • Performances
  • Robustness

• Disadvantages:

  • Manual Method
  • Only SISO

Modern Control (1960)

• Tools:

  • State Space
  • Optimal Command
  • LQR, LQG

• Advantages:

  • Automatic Synthesis
  • MIMO
  • Optimisation problem

• Disadvantages:

  • Robustness
  • Rejection of Perturbations

Robust Control (1980)

• Tools:

  • Disk Margin
  • Systems and Signals norms ($\mathcal{H}_\infty$ and $\mathcal{H}_2$ norms)
  • Closed Loop Transfer Functions
  • Loop Shaping

• Advantages:

  • Stability
  • Performances
  • Robustness
  • Automatic Synthesis
  • MIMO
  • Optimization Problem

• Disadvantages:

  • Requires the knowledge of specific tools
  • Need a reasonably good model of the system

The $\mathcal{H}_\infty$ Norm

The $\mathcal{H}_\infty$ norm is defined as the peak of the maximum singular value of the frequency response

\begin{equation} \|G(s)\|_\infty = \max_\omega \bar{\sigma}\big( G(j\omega) \big) \end{equation}

For a SISO system $G(s)$, it is simply the peak value of $|G(j\omega)|$ as a function of frequency:

\begin{equation} \|G(s)\|_\infty = \max_{\omega} |G(j\omega)| \label{eq:hinf_norm_siso} \end{equation}

Let's define a plant dynamics:

   w0 = 2*pi; k = 1e6; xi = 0.04;

   G = 1/k/(s^2/w0^2 + 2*xi*s/w0 + 1);

And compute its $\mathcal{H}_\infty$ norm using the hinfnorm function:

  hinfnorm(G)

1.0013e-05

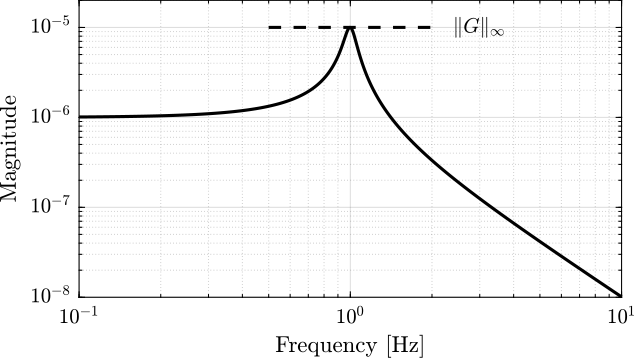
The magnitude $|G(j\omega)|$ of the plant $G(s)$ as a function of frequency is shown in Figure fig:hinfinity_norm_siso_bode. The maximum value of the magnitude over all frequencies does correspond to the $\mathcal{H}_\infty$ norm of $G(s)$ as Equation eqref:eq:hinf_norm_siso implies.

Example of the $\mathcal{H}_\infty$ norm of a SISO system

$\mathcal{H}_\infty$ Synthesis

Optimization problem: $\mathcal{H}_\infty$ synthesis is a method that uses an algorithm (LMI optimization, Riccati equation) to find a controller of the same order as the system so that the $\mathcal{H}_\infty$ norms of defined transfer functions are minimized.

Engineer work:

1. Write the problem as standard $\mathcal{H}_\infty$ problem
2. Translate the specifications as $\mathcal{H}_\infty$ norms
3. Make the synthesis and analyze the obtain controller
4. Reduce the order of the controller for implementation

Many ways to use the $\mathcal{H}_\infty$ Synthesis:

• Traditional $\mathcal{H}_\infty$ Synthesis
• Mixed Sensitivity Loop Shaping
• Fixed-Structure $\mathcal{H}_\infty$ Synthesis
• Signal Based $\mathcal{H}_\infty$ Synthesis

The Generalized Plant

  \begin{tikzpicture}
    \node[block={2.0cm}{2.0cm}] (P) {$P$};
    \node[above] at (P.north) {Generalized Plant};

    % Input and outputs coordinates
    \coordinate[] (inputw)  at ($(P.south west)!0.75!(P.north west)$);
    \coordinate[] (inputu)  at ($(P.south west)!0.25!(P.north west)$);
    \coordinate[] (outputz) at ($(P.south east)!0.75!(P.north east)$);
    \coordinate[] (outputv) at ($(P.south east)!0.25!(P.north east)$);

    % Connections and labels
    \draw[<-] (inputw) -- ++(-0.8, 0) node[above right]{$w$};
    \draw[<-] (inputu) -- ++(-0.8, 0) node[above right]{$u$};

    \draw[->] (outputz) -- ++(0.8, 0) node[above left]{$z$};
    \draw[->] (outputv) -- ++(0.8, 0) node[above left]{$v$};
  \end{tikzpicture}

Notation	Meaning
$P$	Generalized plant model
$w$	Exogenous inputs: commands, disturbances, noise
$z$	Exogenous outputs: signals to be minimized
$v$	Controller inputs: measurements
$u$	Control signals

Notations for the general configuration

\begin{equation} \begin{bmatrix} z \\ v \end{bmatrix} = P \begin{bmatrix} w \\ u \end{bmatrix} = \begin{bmatrix} P_{11} & P_{12} \\ P_{21} & P_{22} \end{bmatrix} \begin{bmatrix} w \\ u \end{bmatrix} \end{equation}

Problem Formulation

The $\mathcal{H}_\infty$ Synthesis objective is to find all stabilizing controllers $K$ which minimize

\begin{equation} \| F_l(P, K) \|_\infty = \max_{\omega} \overline{\sigma} \big( F_l(P, K)(j\omega) \big) \end{equation}

  \begin{tikzpicture}

    % Blocs
    \node[block={2.0cm}{2.0cm}] (P) {$P$};
    \node[block={1.5cm}{1.5cm}, below=0.7 of P] (K) {$K$};

    % Input and outputs coordinates
    \coordinate[] (inputw)  at ($(P.south west)!0.75!(P.north west)$);
    \coordinate[] (inputu)  at ($(P.south west)!0.25!(P.north west)$);
    \coordinate[] (outputz) at ($(P.south east)!0.75!(P.north east)$);
    \coordinate[] (outputv) at ($(P.south east)!0.25!(P.north east)$);

    % Connections and labels
    \draw[<-] (inputw) node[above left, align=right]{(weighted)\\exogenous inputs\\$w$} -- ++(-1.5, 0);
    \draw[<-] (inputu) -- ++(-0.8, 0) |- node[left, near start, align=right]{control signals\\$u$} (K.west);

    \draw[->] (outputz) node[above right, align=left]{(weighted)\\exogenous outputs\\$z$} -- ++(1.5, 0);
    \draw[->] (outputv) -- ++(0.8, 0) |- node[right, near start, align=left]{sensed output\\$v$} (K.east);
  \end{tikzpicture}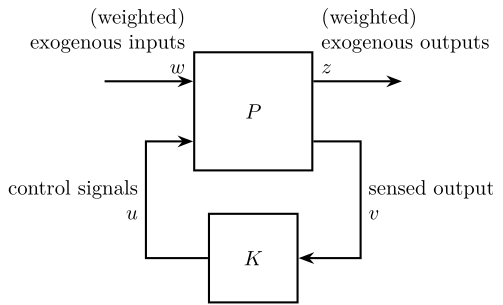

General Control Configuration

Classical feedback control and closed loop transfer functions

  \begin{tikzpicture}
    \node[addb={+}{}{}{}{-}] (addfb) at (0, 0){};
    \node[block, right=0.8 of addfb] (K){$K(s)$};
    \node[addb={+}{}{}{}{}, right=0.8 of K] (addu){};
    \node[block, right=0.8 of addu] (G){$G(s)$};

    \draw[<-] (addfb.west) -- ++(-0.8, 0) node[above right]{$r$};
    \draw[->] (addfb.east) -- (K.west) node[above left]{$\epsilon$};
    \draw[->] (K.east) -- (addu.west) node[above left]{$u$};
    \draw[->] (addu.east) -- (G.west);
    \draw[<-] (addu.north) -- ++(0, 0.8) node[below right]{$d$};
    \draw[->] (G.east) -- ++(1.2, 0);
    \draw[->] ($(G.east) + (0.6, 0)$) node[branch]{} node[above]{$y$} -- ++(0, -0.8) -| (addfb.south);
  \end{tikzpicture}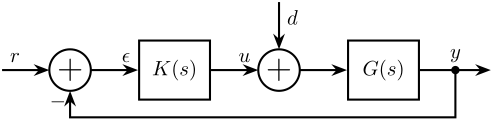

Classical Feedback Architecture

Notation	Meaning
$G$	Plant model
$K$	Controller
$r$	Reference inputs
$y$	Plant outputs
$u$	Control signals
$d$	Input Disturbance
$\epsilon$	Tracking Error

Notations for the Classical Feedback Architecture

From a Classical Feedback Architecture to a Generalized Plant

The procedure is:

1. define signals of the generalized plant
2. Remove $K$ and rearrange the inputs and outputs

  \begin{tikzpicture}
    \node[addb={+}{}{}{}{-}] (addfb) at (0, 0){};
    \node[block, right=0.8 of addfb] (K){$K(s)$};
    \node[block, right=0.8 of K] (G){$G(s)$};

    \draw[<-] (addfb.west) -- ++(-0.8, 0) node[above right]{$r$};
    \draw[->] (addfb.east) -- (K.west) node[above left]{$\epsilon$};
    \draw[->] (K.east) -- (G.west) node[above left]{$u$};
    \draw[->] (G.east) -- ++(1.2, 0);
    \draw[->] ($(G.east) + (0.6, 0)$) node[branch]{} node[above]{$y$} -- ++(0, -0.8) -| (addfb.south);
  \end{tikzpicture}

  \begin{tikzpicture}
    \node[block] (G) {$G(s)$};
    \node[addb={+}{-}{}{}{}, right=0.6 of G] (addw) {};
    \coordinate[above right=0.6 and 1.4 of addw] (u);
    \coordinate[above=0.6 of u] (epsilon);

    \coordinate[] (w) at ($(epsilon-|G.west)+(-1.4, 0)$);

    \node[block, below left=0.8 and 0 of addw] (K) {$K(s)$};

    % Connections
    \draw[->] (G.east) -- (addw.west);
    \draw[->] ($(addw.east)+(0.4, 0)$)node[branch]{} |- (epsilon) node[above left](z1){$\epsilon$};
    \draw[->] ($(G.west)+(-0.4, 0)$)node[branch](start){} |- (u) node[above left](z2){$u$};

    \draw[->] (addw.east) -- (addw-|z1) |- node[near start, right]{$v$} (K.east);
    \draw[->] (K.west) -| node[near end, left]{$u$} ($(G-|w)+(0.4, 0)$) -- (G.west);

    \draw[->] (w) node[above]{$w = r$} -| (addw.north);

    \draw [decoration={brace, raise=5pt}, decorate] (z1.north east) -- node[right=6pt]{$z$} (z2.south east);

    \begin{scope}[on background layer]
      \node[fit={(G.south-|start.west) ($(z1.north west)+(-0.4, 0)$)}, inner sep=6pt, draw, dashed, fill=black!20!white] (P) {};
      \node[below right] at (P.north west) {Generalized Plant $P(s)$};
    \end{scope}
  \end{tikzpicture}

Let's find the Generalized plant of corresponding to the tracking control architecture shown in Figure fig:classical_feedback_tracking

Classical Feedback Control Architecture (Tracking)

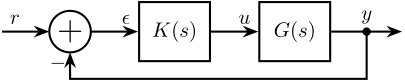
First, define the signals of the generalized plant:

• Exogenous inputs: $w = r$
• Signals to be minimized: $z_1 = \epsilon$, $z_2 = u$
• Control signals: $v = y$
• Control inputs: $u$

Then, Remove $K$ and rearrange the inputs and outputs. We obtain the generalized plant shown in Figure fig:mixed_sensitivity_ref_tracking.

Generalized plant of the Classical Feedback Control Architecture (Tracking)

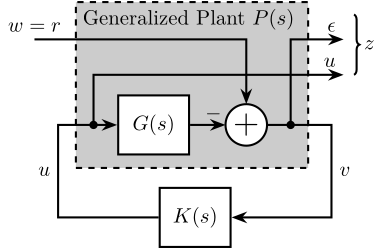
Using Matlab, the generalized plant can be defined as follows:

  P = [1 -G;
       0  1;
       1 -G]

Modern Interpretation of the Control Specifications

Introduction

• Reference tracking Overshoot, Static error, Setling time

  • $S(s) = T_{r \rightarrow \epsilon}$

• Disturbances rejection

  • $G(s) S(s) = T_{d \rightarrow \epsilon}$

• Measurement noise filtering

  • $T(s) = T_{n \rightarrow \epsilon}$

• Small command amplitude

  • $K(s) S(s) = T_{r \rightarrow u}$

• Stability

  • $S(s)$, $T(s)$, $K(s)S(s)$, $G(s)S(s)$
• Robustness to plant uncertainty (stability margins)
• Controller implementation

**

Resources

yt:?listType=playlist&list=PLn8PRpmsu08qFLMfgTEzR8DxOPE7fBiin

yt:?listType=playlist&list=PLsjPUqcL7ZIFHCObUU_9xPUImZ203gB4o