32 KiB
32 KiB
List of filters - Matlab Implementation
- Proportional - Integral - Derivative
- Low Pass
- High Pass
- Band Pass
- Notch
- Chebyshev
- Lead - Lag
- Complementary
- Combine Filters
Proportional - Integral - Derivative
Proportional
Integral
Derivative
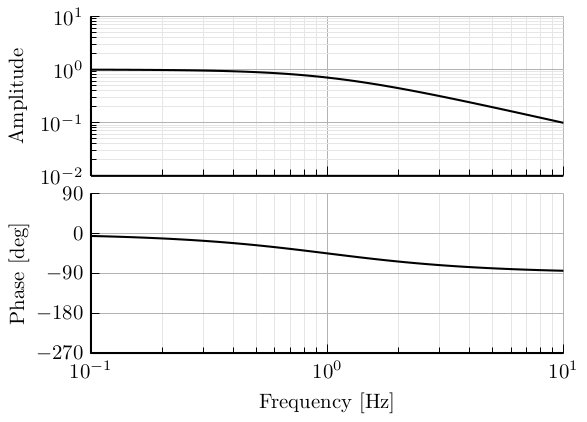
Low Pass
First Order
Second Order
Combine multiple filters
Nice combination
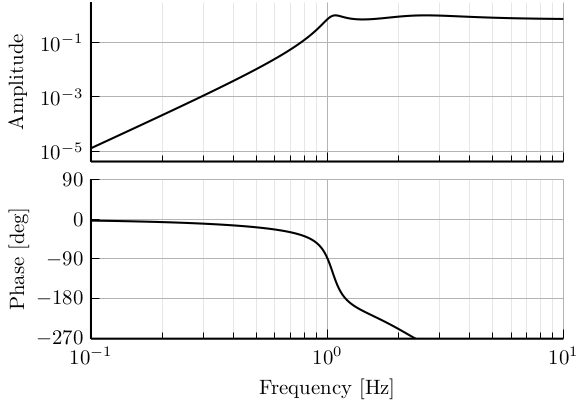
\begin{equation}
W(s) = G_c * \left(\frac{\frac{1}{\omega_0}\sqrt{\frac{1 - \left(\frac{G_0}{G_c}\right)^{\frac{2}{n}}}{1 - \left(\frac{G_c}{G_\infty}\right)^{\frac{2}{n}}}} s + \left(\frac{G_0}{G_c}\right)^{\frac{1}{n}}}{\frac{1}{\omega_0} \sqrt{\frac{1 - \left(\frac{G_0}{G_c}\right)^{\frac{2}{n}}}{\left(\frac{G_\infty}{G_c}\right)^{\frac{2}{n}} - 1}} s + 1}\right)^n
\end{equation}
n = 2; w0 = 2*pi*11; G0 = 1/10; G1 = 1000; Gc = 1/2;
wL = Gc*(((G1/Gc)^(1/n)/w0*sqrt((1-(G0/Gc)^(2/n))/((G1/Gc)^(2/n)-1))*s + (G0/Gc)^(1/n))/(1/w0*sqrt((1-(G0/Gc)^(2/n))/((G1/Gc)^(2/n)-1))*s + 1))^n;
n = 3; w0 = 2*pi*9; G0 = 10000; G1 = 0.1; Gc = 1/2;
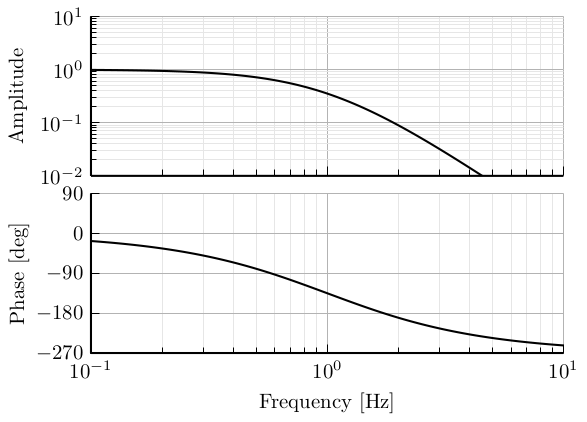
wH = Gc*(((G1/Gc)^(1/n)/w0*sqrt((1-(G0/Gc)^(2/n))/((G1/Gc)^(2/n)-1))*s + (G0/Gc)^(1/n))/(1/w0*sqrt((1-(G0/Gc)^(2/n))/((G1/Gc)^(2/n)-1))*s + 1))^n;High Pass
First Order
Second Order
Band Pass
Notch
Chebyshev
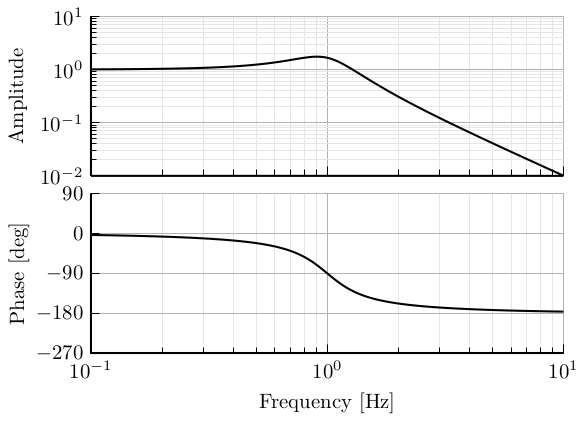
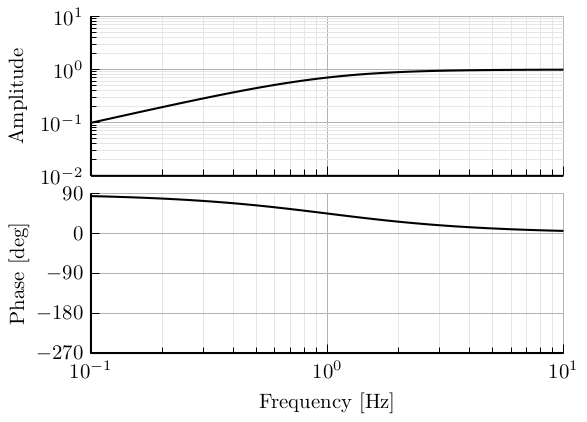
Lead - Lag
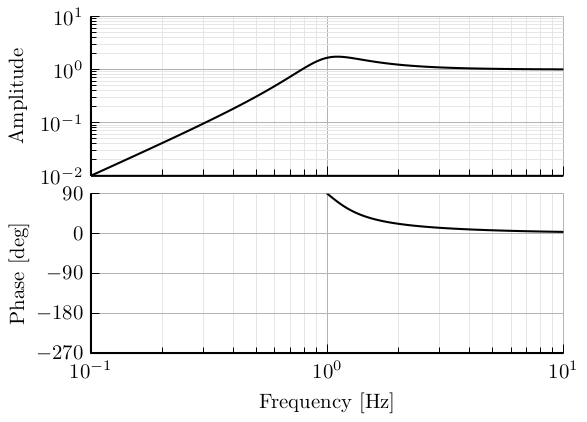
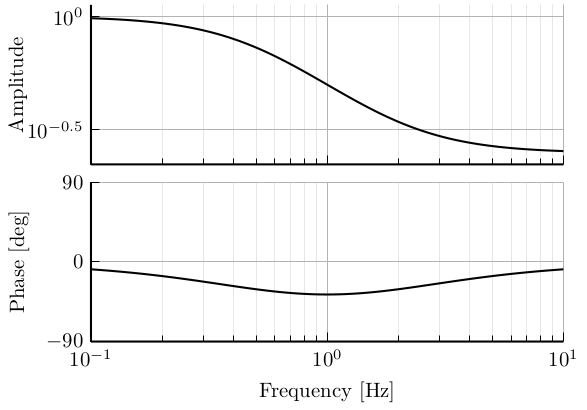
Lead
\[ H(s) = \frac{1 + s/\omega_z}{1 + s/\omega_p}, \quad \omega_z < \omega_p \]
- Find a nice parametrisation to be able to specify the center frequency and the phase added
- Compute also the change in magnitude
h = 2.0;
wz = 2*pi/h; % [rad/s]
wp = 2*pi*h; % [rad/s]
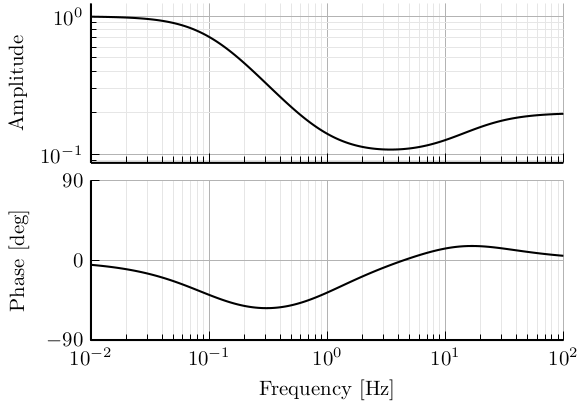
H = (1 + s/wz)/(1 + s/wp);Lag
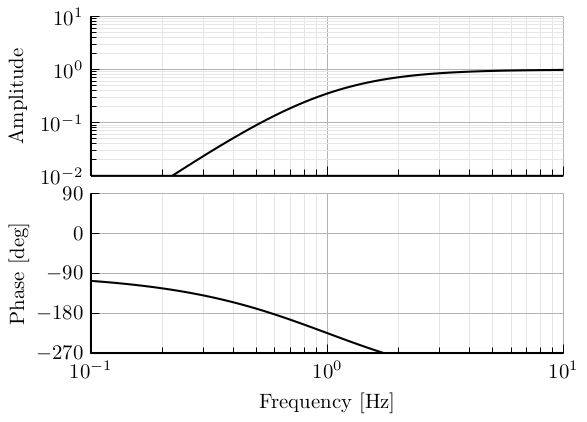
\[ H(s) = \frac{1 + s/\omega_z}{1 + s/\omega_p}, \quad \omega_z > \omega_p \]
- Find a nice parametrisation to be able to specify the center frequency and the phase added
- Compute also the change in magnitude
h = 2.0;
wz = 2*pi*h; % [rad/s]
wp = 2*pi/h; % [rad/s]
H = (1 + s/wz)/(1 + s/wp);Lead Lag
Complementary
Combine Filters
Additive
- Explain how phase and magnitude combine