55 KiB
EUSPEN
- Tutorial: Design concepts for sub-micrometer positioning
- Keynote: Mechatronic challenges in optical lithography
- Designing anti-aliasing-filters for control loops of mechatronic systems regarding the rejection of aliased resonances
- Flexure positioning stage based on delta technology for high precision and dynamic industrial machining applications
- Multivariable performance analysis of position-controlled payloads with flexible eigenmodes
- High-precision motion system design by topology optimization considering additive manufacturing
- A multivariable experiment design framework for accurate FRF identification of complex systems
- Keynote: High precision mechatronic approaches for advanced nanopositioning and nanomeasuring technologies
- Coordinate Measurement Machines (CMM)
- Difference between CMM and nano-CMM
- How to do nano-CMM
- Concept - Minimization of the Abbe Error
- Minimization of residual Abbe error
- Compare of long travel guiding systems
- Extended 6 DoF Abbe comparator principle
- Practical Realisation
- Tilt Compensation
- Comparison of long travail guiding systems - Bis
- Drive concept
- NPMM-200 with extended measuring volume
- measurement capability
- Extension of the measuring range (700mm)
- Inverse kinematic concept - Tetrahedrical concept
- Inverse kinematic concept - Scanning probe principle
- Inverse kinematic concept - Compact measuring head
- Inverse kinematic concept - Scanning probe principle
- Conclusion
- Reducing control delay times to enhance dynamic stiffness of magnetic bearings
- Digital twins in control: From fault detection to predictive maintenance in precision mechatronics
Tutorial: Design concepts for sub-micrometer positioning @huub_janssen
Positioning Terminology
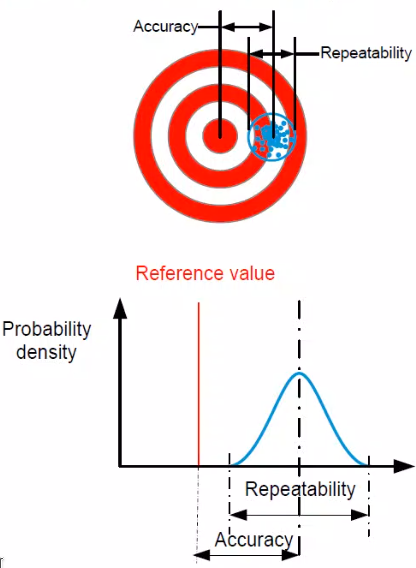
- Accuracy: Accuracy describes how close the mean result is to the reference value. (Figure fig:position_terminology)
- Repeatability: Repeatability describes the variation between results. (Figure fig:position_terminology)
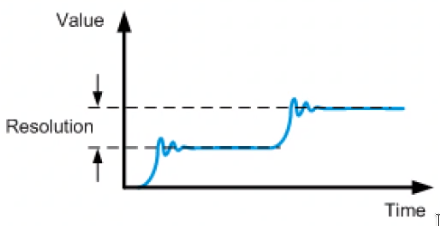
- Resolution: The resolution of a system is equal to the smallest incremental step that can be made (Figure fig:position_resolution)
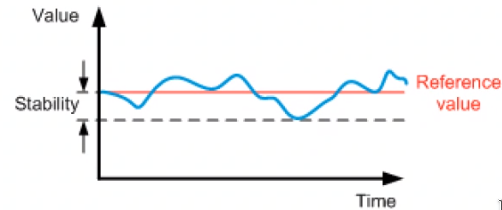
- Stability: The stability of a system is the maximum deviation from a constant reference value over time. The stability is always related to the time frame taken into account. (Figure fig:position_stability)
Principles of accuracy
Limited stiffness, play and friction will induce an hysteresis for a positioning system as shown in Figure fig:stiffness_friction.
The hysteresis can actually help estimating the play and friction present in the system.
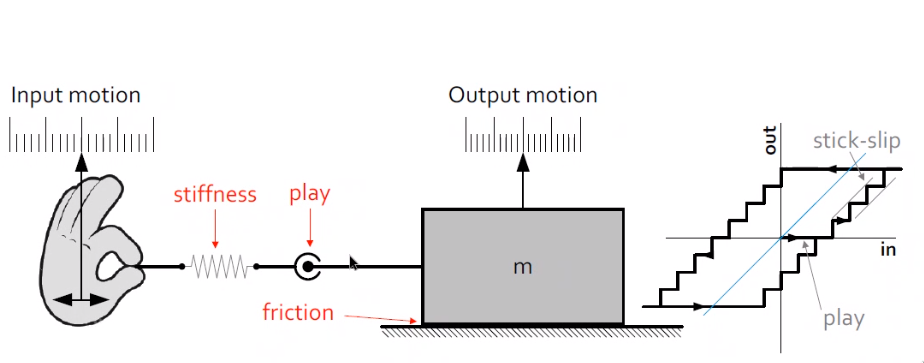
Ways to make the hysteresis smaller:
- avoid play (=> use compliant elements)
- minimize friction
- use high stiffness
The position uncertainty of a system can be estimated as follow (Figure fig:position_uncertainty):
\begin{equation} \text{Position Uncertainty} = \text{play} + 2 \times \text{Virtual Play} \end{equation}where the virtual play can be estimated as follow:
\begin{equation} \text{Virtual Play} = \frac{\text{Friction Force}}{\text{Actuator Stiffness}} = \frac{F_w}{c} \end{equation}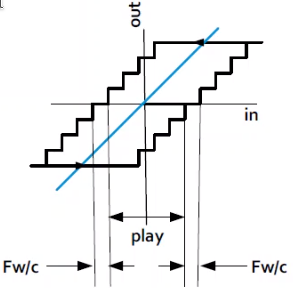
When considering dynamics, the goal is to make the first resonance frequency much higher than the frequency of the wanted motion. Thus, the general recommendation is then to minimize mass and to increase stiffness.
Moreover, we generally want things to be predictable:
- constant, preferably no friction. Note that it is very difficult to make a system with constant friction in practice, so better make a system with no friction.
- no play
- high stiffness
- low pass
Case 1 - Estimate the virtual play
Estimate the virtual play of the system in Figure fig:case_1 with following characteristics:
- Payload: $m = 20\,kg$
- Friction coefficient in drive direction: $f = 0.05$
- Table stroke: $L = 300\,mm$
- Screw spindle inner diameter: $d = 8\, mm$
- Spindle Material: Stainless steel

First the friction force can be calculated as the vertical mass times the friction coefficient:
\begin{equation} F_w = (mg) f \end{equation}Then, the axial stiffness of the screw spindle is computed:
\begin{equation} c = \frac{A}{L} E \end{equation}with:
- $A = \pi d^2$ is the screw section area
- $L = 300\,mm$ is the screw length
- $E$ is the Young modulus of stainless steel
And finally:
\begin{equation} \text{Virtual Play} = \frac{F_w}{c} \approx 0.6\,\mu m \end{equation}Conventional elements for constraining DoFs
There exist many conventional elements for constraining DoFs. Some of them are:
- Struts with ball joint: 1DoF constrained (Figure fig:ball_joint)
- Ball bearing: 5DoF constrained (Figure fig:ball_bearing)
- Guide with roller bearing: 4DoF constrained (Figure fig:roller_bearing)
- Roller rail guide: 5DoF constrained (Figure fig:roller_rail_guide)




Compliant elements for constraining DoFs
Basic leaf springs and folded leaf springs
An example of a complaint element is shown in Figure fig:compliant_leaf.

Other types of compliant elements include:
- Leaf spring: constrains 3 dof (Figure fig:leaf_springs)
- Folded leaf spring: constrains only 1dof (Figure fig:folded_leaf_springs) These are generally used in combination with other folded leaf springs.
- Flexure pivots: constrains 5 dofs (Figure fig:flexure_pivots)

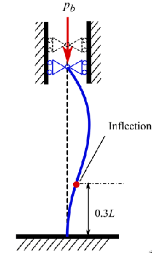
1dof Parallel Guiding
Parallel guiding can be made using two leaf springs (Figure fig:parallel_guiding):
- 2 parallel leaf springs
- Force actuator in center of parallelism (middle of the leaf springs) to avoid coupled rotation
-
Sag in vertical direction as a function as the horizontal displacement. This sag is predictible and reproducible:
\begin{equation} \delta z = 0.6 \frac{x^2}{L} \end{equation} - Vertical stiffness negatively affected by displacement
- Take care of maximum buckling (Figure fig:buckling)
- Improve buckling load and Z stiffness by reinforced mid-section (Figure fig:reinforced_leaf_springs)
Rotation Compliant Mechanism
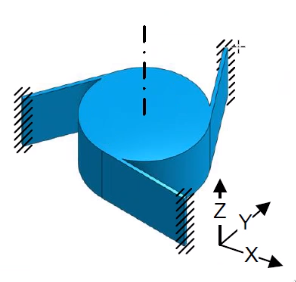
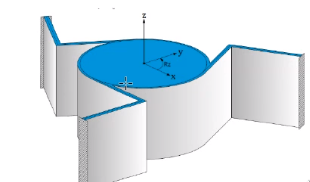
Figure fig:rotation_leaf_springs shows a rotation compliant mechanism:
- 3 leaf springs
- no sensitive for thermal load on the body: as the central part heat ups and expand, the center line of the rotation stays at the same position
Z translation
Figure fig:vertical_stage_compliant shows a Z translation mechanism:
- 5 struts ("needles")
- Not sensitive for thermal loads on body
The problem is that when it moves vertical, there will also be some z rotation because the length of the strut is fixed (stiff). This parasitic rotation is however predictable.

An alternative is to use folder leaf springs (Figure fig:vertical_stage_leafs), and this avoid the parasitic rotation.

X-Y-Rz Stage
An X-Y-Rz stage can be done either using 3 struts (Figure fig:x_y_rz_stage) or using 3 folded leaf springs (Figure fig:x_y_rz_leafs).

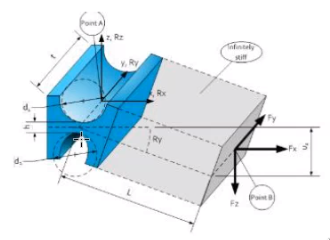
Compliant mechanism with only one fixed dof
The compliant mechanism shown in Figure fig:case_1_leaf_springs only constrain the rotation about the y-axis.

Summary
- compliant elements enable defined movements
- Hinges or guidings can be used for small movements
- No play, No friction, No wear, No contamination
- but limited rotation, need a constant force to hold in place
Examples
An example of a complex compliant mechanism is shown in Figure fig:compliant_example_1.

Figure fig:linear_bearing_leafs shown a reinforced part to avoid buckling and improve vertical stiffness.

Mechatronics positioning challenge
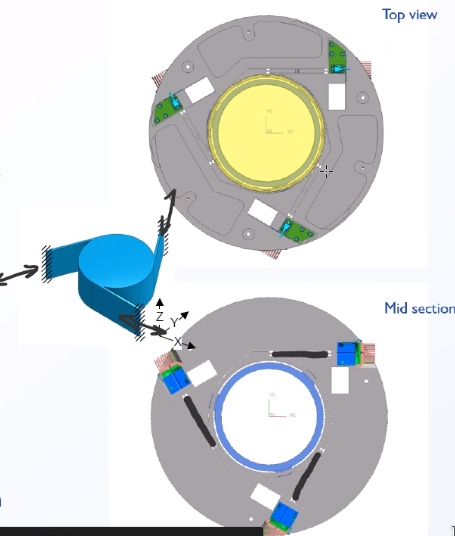
A X-Y-Rz stage is shown in Figure fig:xyRz_positioning_challenge. To make this stage usable for nano-metric positioning, the following ideas where used:
-
Use parallel mechanisms instead of serial one:
- no stacking of errors
- smaller, stiffer, in one plane
-
Symmetry:
- Use 3 identical voice coil actuators
- Use 3 identical sensors
- Center position insensitive for temperature change
-
Flexure only;
- no friction
- no play
- no wear
- no particule (important for clean rooms)
- no service
-
Continuously under control:
- no alignment / crosstalk issues between axes
- voice coil / sensors combination determines performance
yt:OjNnHa6O9A8
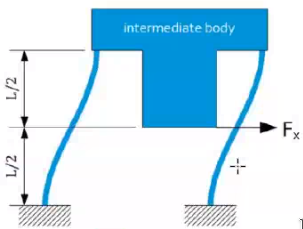
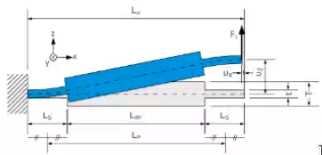
Case - Play Free parallel Stage
Figure fig:play_free_parallel_stage shows a parallel mechanism that should be converted to a compliant mechanism. Its characteristics are:
- 1mm stroke
- 1:5 lever arm
- 10kg payload
- distance between hinges: 5nmm
- thickness t: 40mm
- Material: aluminium

The goals are to:
- Make design using elastic hinges
- Maximize vertical stiffness
- Determine vertical stiffness
The solution is shown in Figure fig:play_free_parallel_stage_solution.

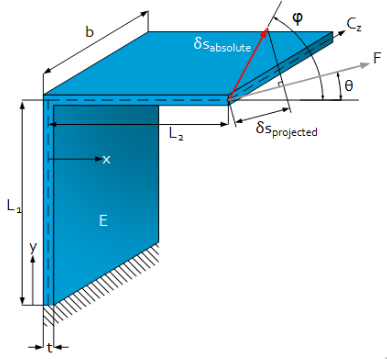
Thin plate design
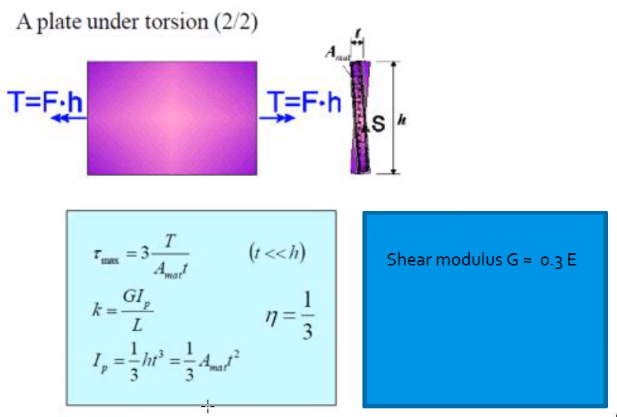
Thin plate in torsion
Thin plates are very important for compliant mechanisms.
The torsion stiffness of a thing plate is linear with the length of the thin plate:
\begin{equation} k = \frac{G I_p}{L} \end{equation}with $G$ the shear modulus:
\begin{equation} G \approx 0.3 E \end{equation}where $E$ is the young modulus
Then
\begin{equation} I_p = \frac{1}{3} h t^3 = \frac{1}{3} A t^2 \end{equation}where $A$ is the area of the cross section.
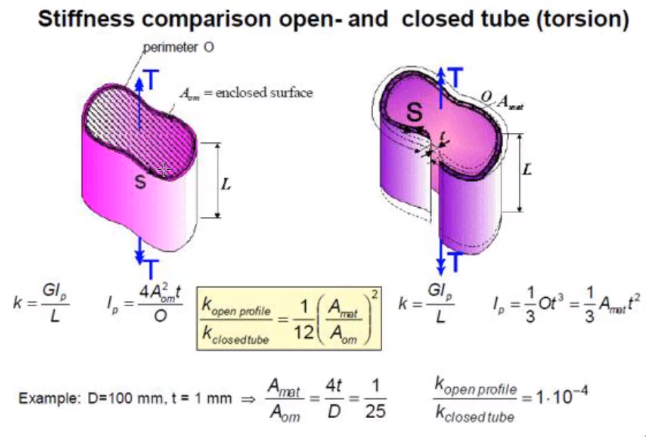
Difference between open and close profile
The close profile has much more torsional stiffness than the open profile.
Just by opening the tube, we have a much smaller torsional stiffness (but almost same axial stiffness for instance).
We have similar behavior with an open/closed box. If we remove one side of the cube shown in Figure fig:closed_box, we would have much smaller torsional stiffness along the axis perpendicular to the removed side.

If we use triangles, we obtain high torsional stiffness as shown in Figure fig:torsion_stiffness_box_double_triangle.

Frames are usually corresponding to open-boxes with have a small stiffness in torsion. On way to reinforce it is using triangles.
A nice way to have a 1dof flexure guiding with stiff frame is shown in Figure fig:z_stage_triangles.

Keynote: Mechatronic challenges in optical lithography @hans_butler
Introduction
Question: in chip manufacturing, how do developments in optical lithography impact the mechatronic design?
Main developments:
- Scanning & dual stage scanning
- Immersion
- Multiple patterning
- Extreme ultra violet lithography
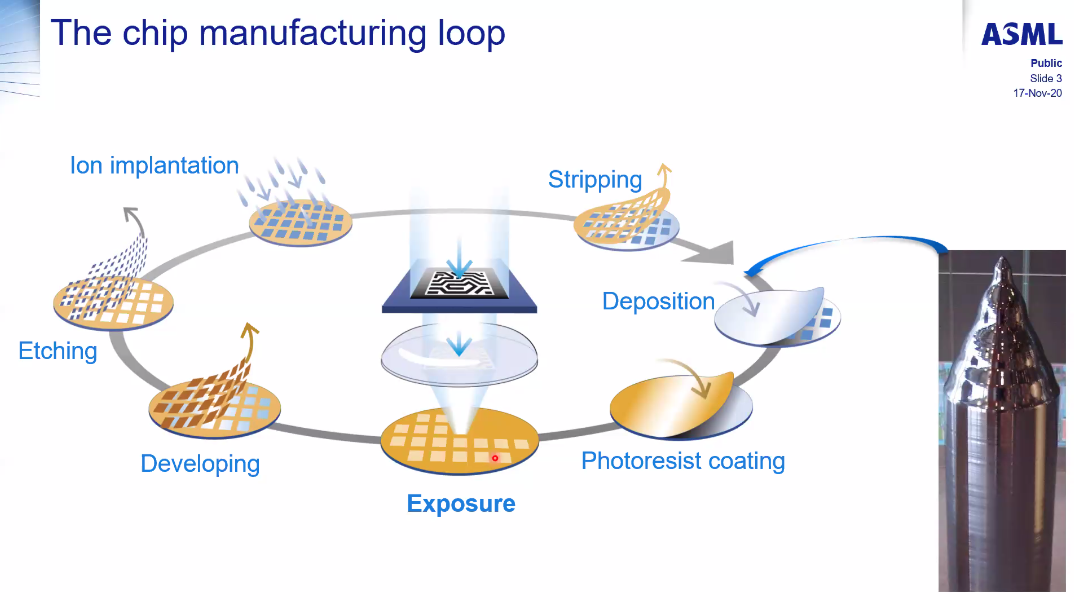
Chip manufacturing loop
In this presentation, only the exposure step is discussed (lithography).
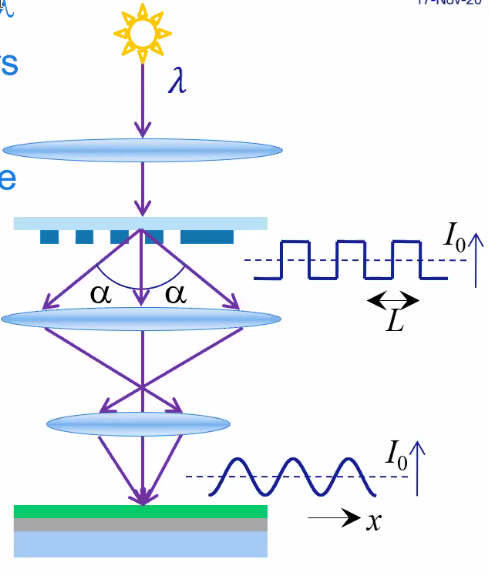
Imaging process - Basics
- An illuminator provides light at constant wavelength $\lambda$
- The pattern on the reticle diffracts the light into order
- At least +/-1st orders need to be captures. This will induce a sinusoidal wave on the wafer as shown in Figure fig:asml_imaging_process.
- Wafer and mast are placed on high accuracy moving stages
From stepper to scanner
Before, one chip was illumating at a time, but people wanted to make bigger chips. However, if was difficult to make larger lenses.
The solution was to use a scanner, were both the mask and wafer are on moving stages. This implied many requirements in dynamics and accuracy!
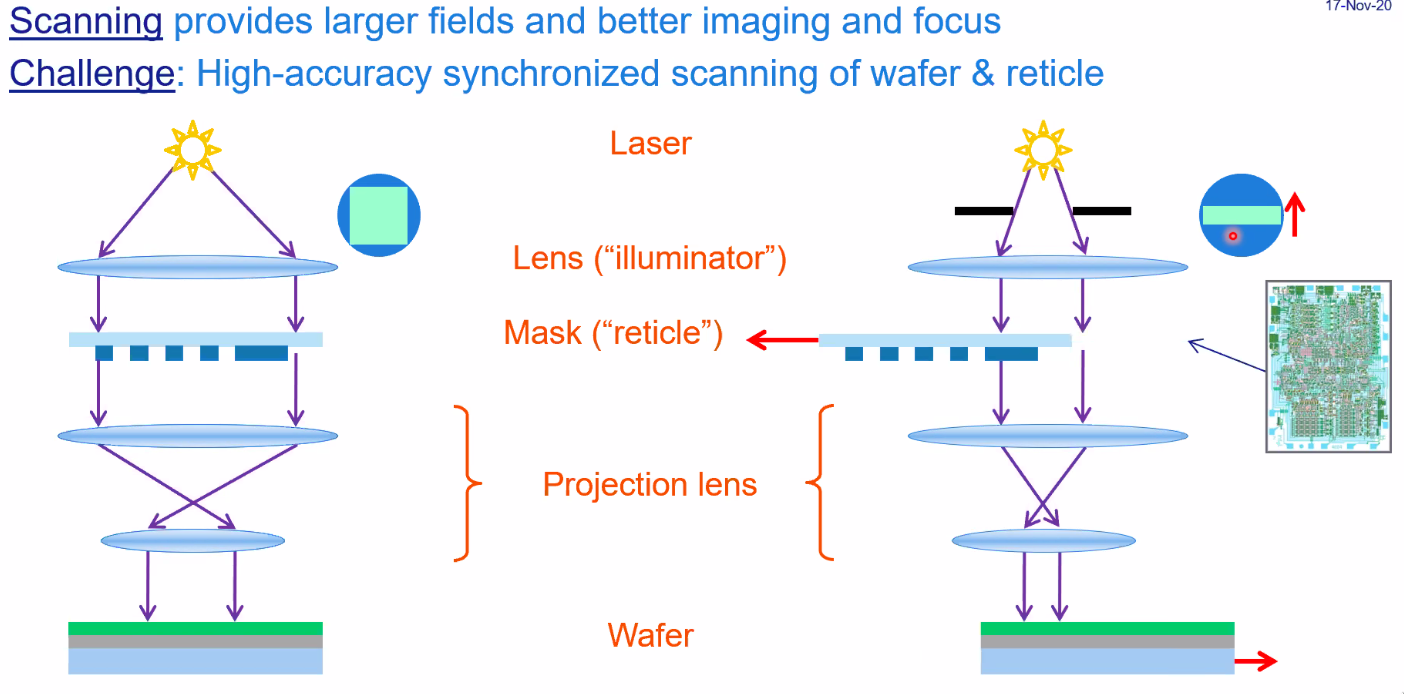
Dual stage scanners
Both the reticle stage and wafer stage are moving. In order to have the same throughput, higher stage accelerations are required.
This implies some mechatronics challenges:
- higher stage acceleration
- higher accuracy
- interaction between stages
Which are solved by:
- Larger forces => balance masses
- Stage dynamical design for high bandwidth control
- Control coupling between stages (one control system can act as a disturbance to another controlled system => feedforward)

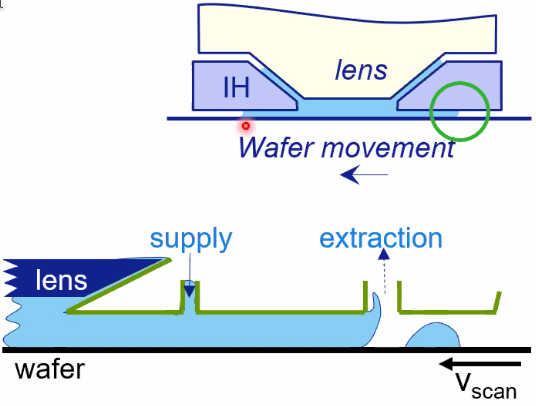
Immersion technology
Water is used between the lens and the wafer to increase the "NA" and thus decreasing the "critical dimension".
The "hood" is there to prevent any bubble to enter the illumination area (Figure fig:asml_hood_system). The position of the "hood" is actively control to follow the wafer stage (that can move in z direction and tilt).
Three solutions are used for the positioning control of the "hood" system (Figure fig:asml_immersion):
- Disturbance decoupling
- Iterative learning control
- Feed-forward control from the Wafer control signal
Multiple Patterning
The multiple patterning approach adds few mechatronics challenges:
- Position accuracy limited to ~4nm due to interferoemter position measurement (variation of temperature/pressure of air)
- Stage swap is complex and time-consuming
This was solved by:
- Using encoder instead of interferometers
- Use long stroke motor: h-stage => new wafer stage concept
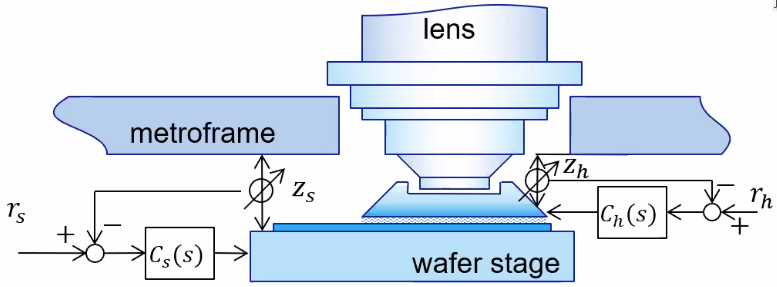
Machine layout
Each stage is controlled with 6dof lorentz short stroke actuators (Figure fig:asml_machine_layout_bis). The magnet stage can move horizontally (due to reaction forces of the wafer stages): it asks as a balance mass.
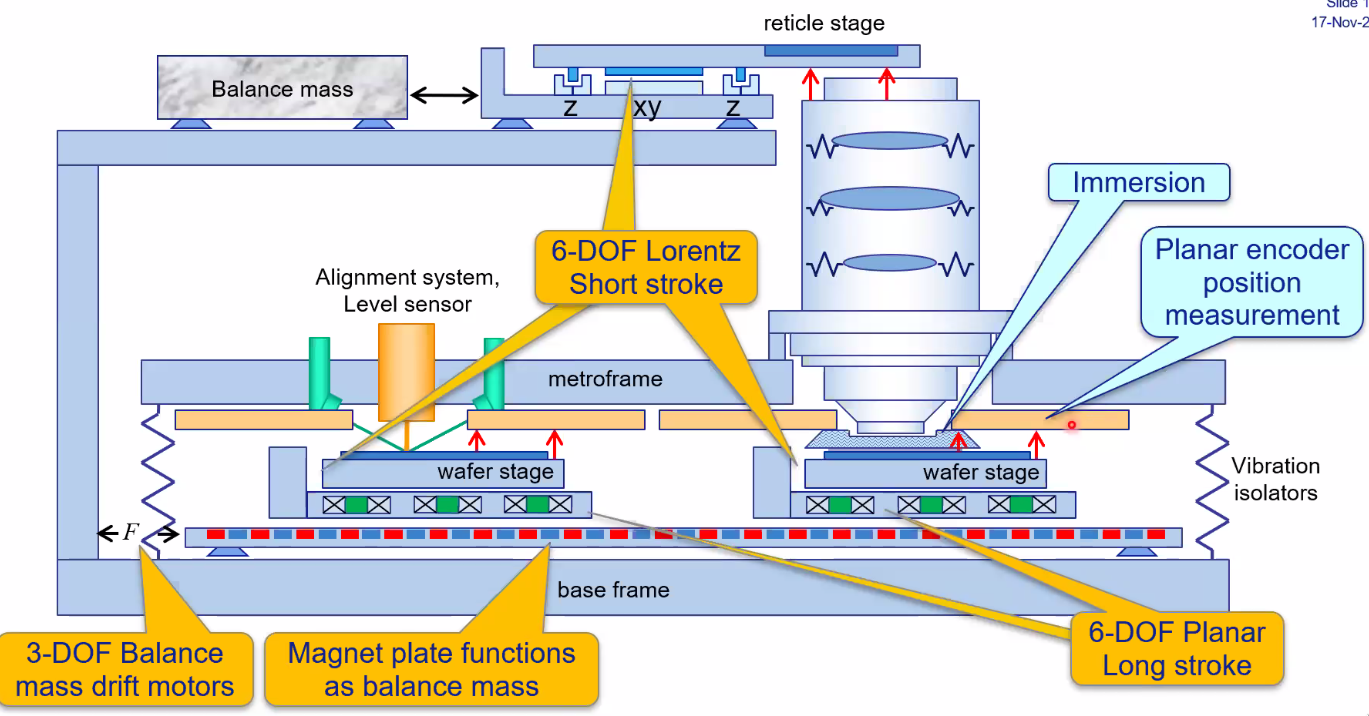
EUV Lithography
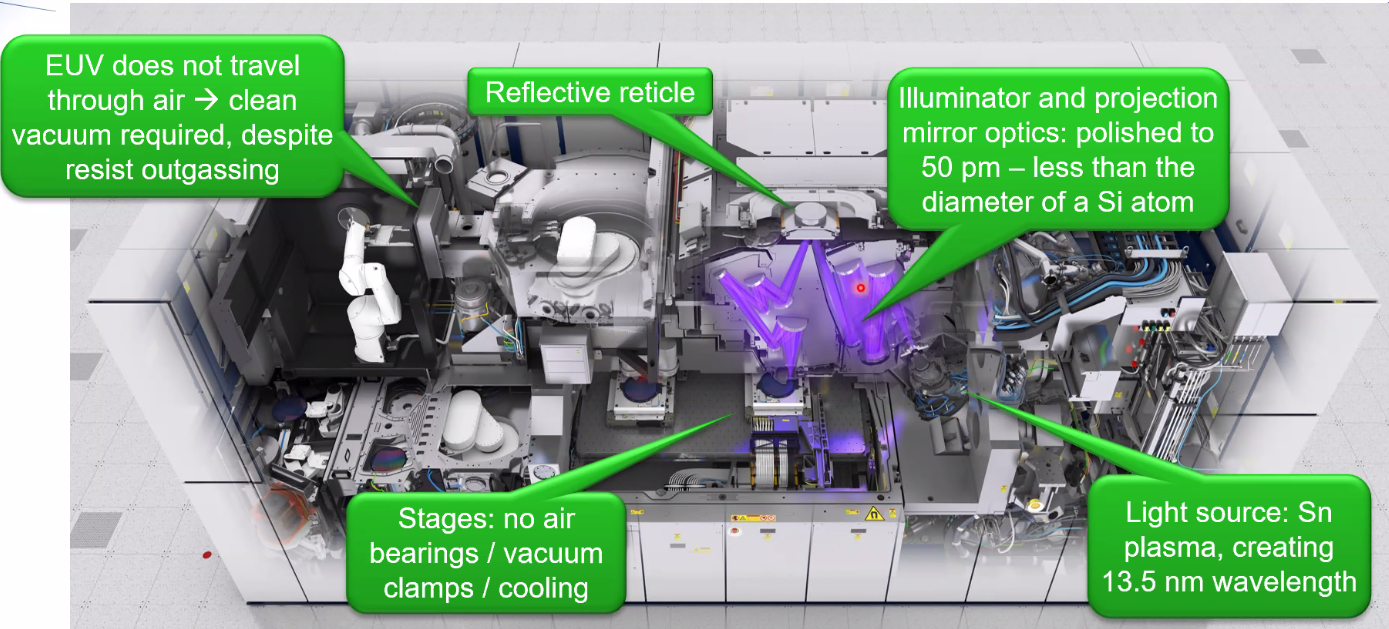
Vacuum is required which implies:
- no bearings
- no cooling
All the optics are reflective:
- extremely accurately polished
- challenge: keep mirrors optimally positioned
Wafer stage:
- Move at high speed and accelerations
- Challenge: in vaccum
- Solved by: machanically suspended balance mass, and interferoemter position meaured can be used because it is in vacuum now
The future: high-NA EUV
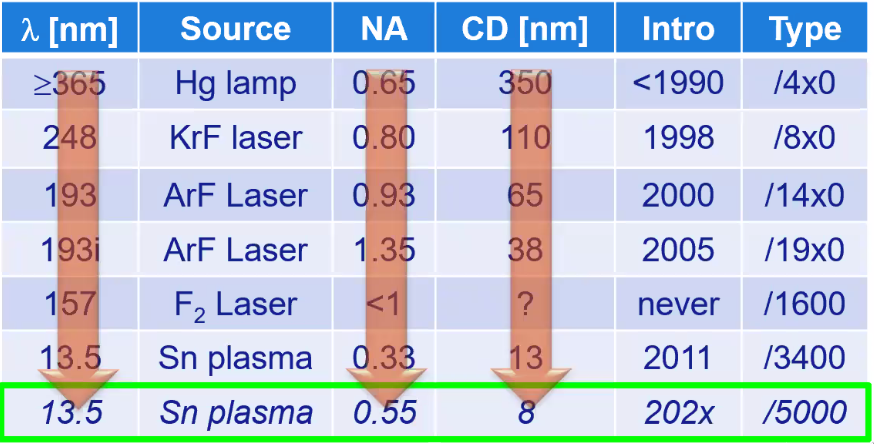
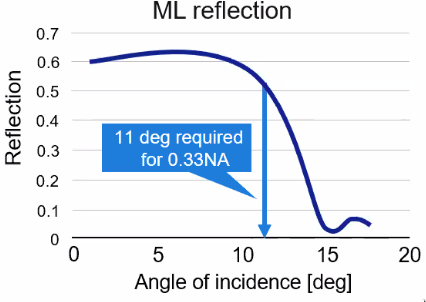
In order to do so, high "opening" of the optics is required which is very challenges because the reflectiveness of mirror is decreasing as high angle of incidence (Figure fig:asml_reflection_angle).
Challenges for future Optical Lithography machines
Challenges:
- Double wafer stage acceleration
- Much bigger mirrors
- Tighter accuracy specifications despite
Solutions:
- Stage and mirror dynamics, high bandwidth control
- Dynamics architecture: improved isolation, multiple isolate sets
- Heating compensation
Conclusion
The conclusions are:
- Lithographic tools are the main enabler for over shrinking device sizes
-
New (optical) requirements lead to new mechatronic challenges:
- Larger fields / better imaging: from stepping to scanning
- Larger wafer size: dual stage scanners
- Immersion: wafer stage & hood control
- Multiple patterning: planar motors and encoder technology
- EUV: all-vacuum stages
- High-NA EUV: new optics, much larger accelerations
Designing anti-aliasing-filters for control loops of mechatronic systems regarding the rejection of aliased resonances @ulrich_schonhoff
The phenomenon of aliasing of resonances
Weakly damped flexible modes of the mechanism can limit the performance of motion control systems.
For discrete time controlled systems, there can be an additional limitation: aliased resonances which are rarely discussed.

The aliasing of signals is well known (Figure fig:aliasing_signals).
However, aliasing in systems can also happens and is schematically shown in Figure fig:aliasing_system.

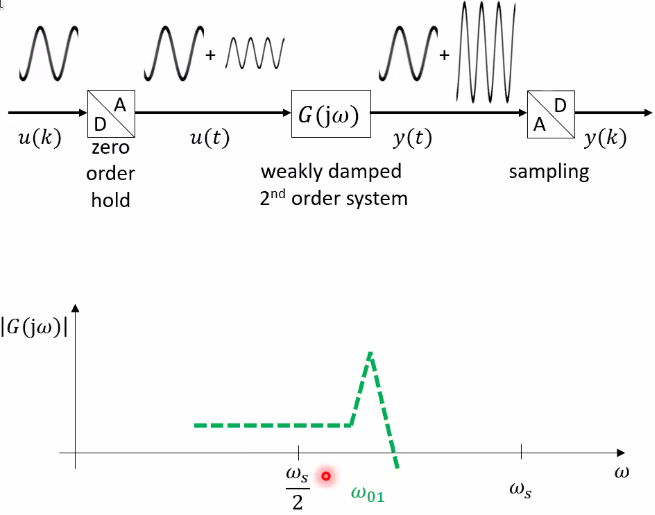
The poles of the system will be aliased and their location will change in the complex plane as shown in Figure fig:aliasing_poles.
More precisely:
- the imaginary parts of the poles mirror about the Nyquist frequency
- the real parts of the poles remain equal
Therefore, the damping of the aliased resonances are foreseen to have larger dampings.
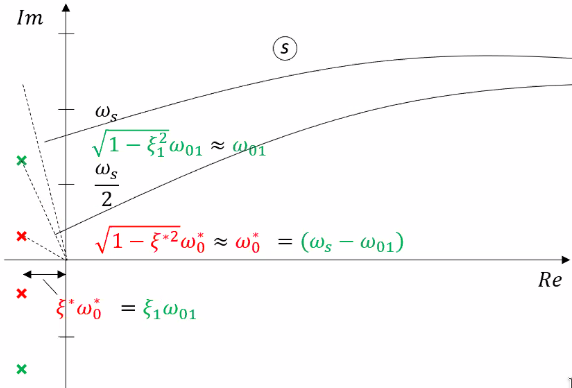
Let's consider two systems with a resonance:
- below the Nyquist frequency (blue dashed)
- above the Nyquist frequency (green dashed)
Then looking at the same systems in the digital domain, one can see thathen the resonance is above the Nyquist frequency (Figure fig:aliasing_above_nyquist):
- the resonance mirrors
- the damping is increased
Therefore, when identifying a low damped resonance, it could be that it comes form a high frequency low damped resonance.

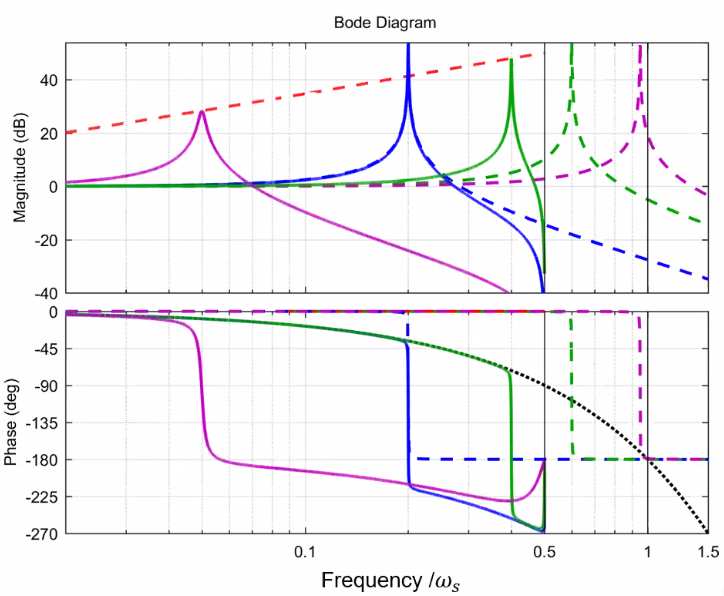
Nature, Modelling and Mitigation of potentially aliasing resonances
The aliased modes can for instance comes from local modes in the actuators that are lightly damped and at high frequency (Figure fig:alising_nature)

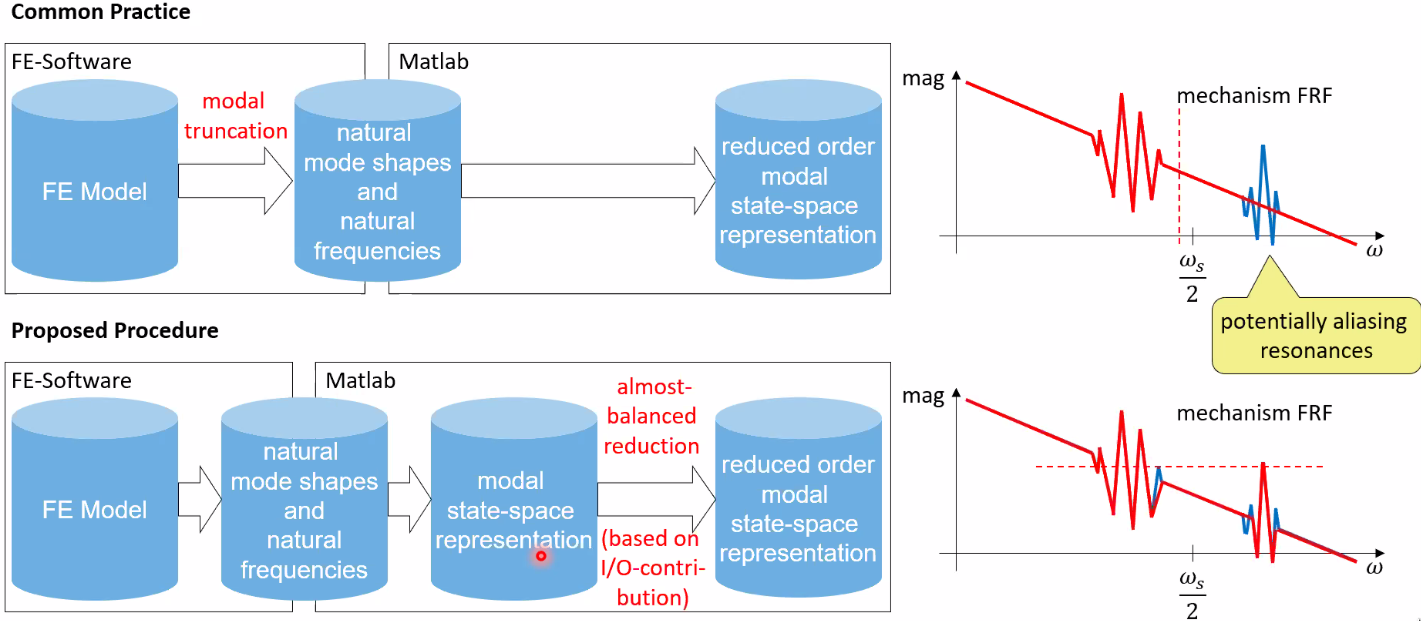
The proposed idea to better model aliasing resonances is to include more modes in the FEM software as shown in Figure fig:aliasing_modeling and then perform an order reduction in matlab.
Anti aliasing filter design
Introduction
- Anti-aliasing filtering can be used to reject aliasing of resonances and to maintain the stability of the control loop
-
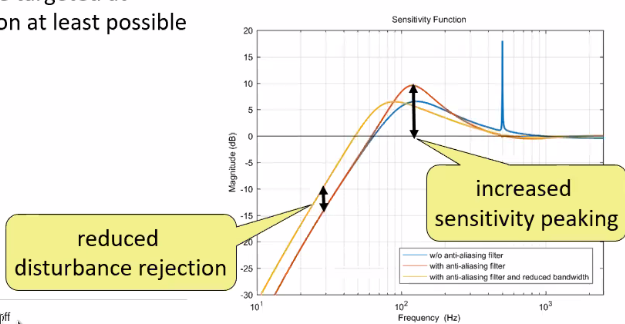
However, its phase lag deteriorates the control loop performances:
- phase margin decreases (Figure fig:alising_filter_introduction)
- sensitivity peak increases (Figure fig:aliasing_sensitivity_effect)
- Thus, the anti-aliasing filter should be targeted at sufficient rejection at least possible phase lag

Concept of equivalent delay
Concept:
-
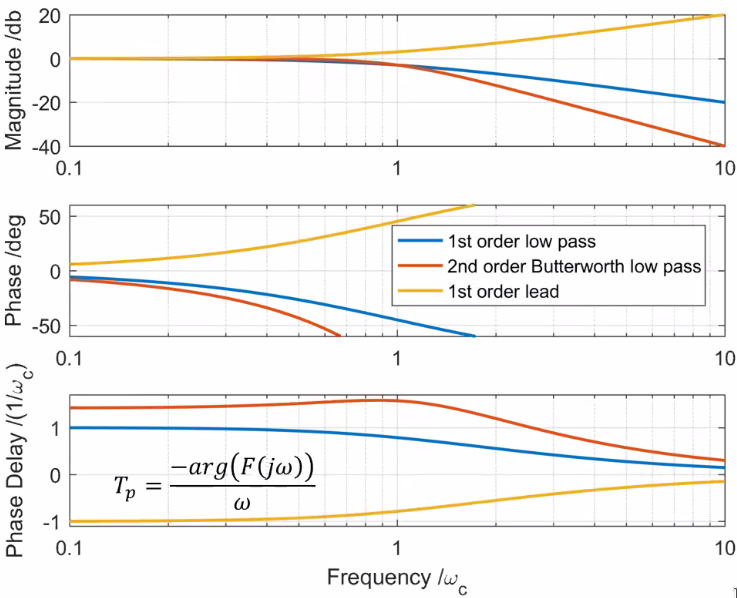
At frequencies well below its poles and zeros, a continuous time filter $F(j\omega)$ shows almost linear phase:
\begin{equation} \arg\big( F(j\omega) \big) \approx -T_e \omega \end{equation} -
Thus, the phase lag of the filter can be fairly correctly represented by a time delay (below the pole frequency). The equivalent delay is:
\begin{equation} T_e = \sum_{i=1}^{N_p} \frac{\xi_{pi}}{\omega_{0pi}} - \sum_{i=1}^{N_z} \frac{\xi_{zi}}{\omega_{0zi}} \end{equation} - where $\omega_{0pi}$ is the natural frequency $\xi_{pi}$ is the damping of the $N_p$ poles of $F(s)$. Similarly, $\omega_{0zi}$ is the natural frequency $\xi_{zi}$ is the damping of the $N_z$ zeros of $F(s)$.
Examples (Figure fig:aliasing_equivalent_delay):
- First order low pass filter: \[ \xi_p = 1 \Rightarrow T_e = \frac{1}{\omega_c} \]
- Second order Butterworth low pass filter: \[ \xi_p = \frac{1}{\sqrt{2}} \Rightarrow T_e = \sqrt{2} \frac{1}{\omega_c} \]
- First order lead: \[ \xi_z = 1 \Rightarrow T_e = - \frac{1}{\omega_c} \]
Budgeting of phase lag
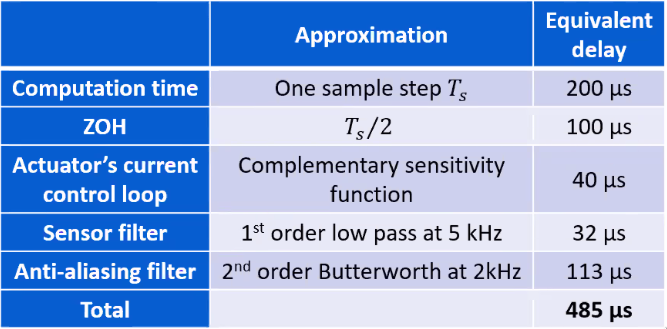
The budgeting of the phase lag is done by expressing the phase lag of each element by a time delay (Figure fig:aliasing_budget_phase)

The equivalent delay of each element are listed in Figure fig:aliasing_budget_table.
Selecting the filter order
The filter order can be chosen depending on the frequency of the resonance. Some example of Butterworth filters are shown in Figure fig:aliasing_filter_order_bode and summarized in Figure fig:aliasing_filter_order_table.


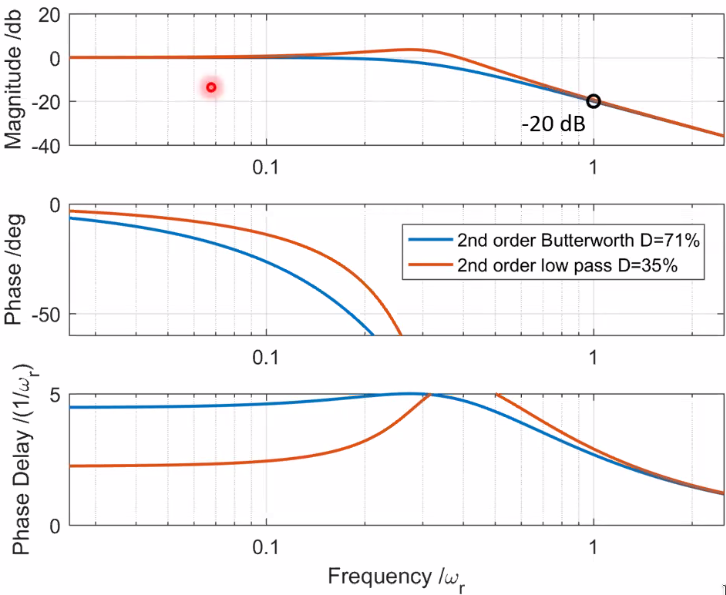
Reducing the phase lag
The equivalent delay of a low pass (here second order) depends on its damping, since: \[ T_e = -2 \frac{\xi_{zi}}{\omega_{0zi}} \]
Conclusion
The phenomenon of aliasing of resonances:
- Aliasing of resonances is an issue in discrete-time controlled mechatronic systems and can limit the performance and even render the closed loop system unstable
- Resonances above the Nyquist Frequency appear aliased at mirrored frequency for the discrete-time controller
- Aliased resonances show increased damping compared to the original resonances
- To find out if a resonance is an aliased one or not, change the sampling frequency and see if the frequency of the resonance is changing or not
Nature, modelling and mitigation of potentially aliasing resonances:
- The origin are typically local resonances of the sensor and actuator components
- Careful modelling and selecting dominant modes above the Nyquist frequency is commended
Anti-aliasing filter design:
- Anti-Aliasing filter design is the trade-off between rejection and phase-lag
- The concept of equivalent delay allows to budget and design the phase lag
- The order selection of anti alising-filter based on the required rejection is shown
- Several approaches to reduce overall phase lag are presented
Flexure positioning stage based on delta technology for high precision and dynamic industrial machining applications @mikael_bianchi
Introduction
- Goal: flexure positioning stage to do high precision and high dynamic/acceleration positioning. The control architecture should be as simple as possible.
- Application: micromachinign for fabrication of 3d structures
- Possible field: watch industry, electronics, optics, …
- Possible technologies: laser, milling, electro discharge machine
- Objectives: improve the productivity reaching high accelerations at high precision
Design
Description of the Delta robot
Technical choice: flexure based delta robot (Figure fig:flexure_delta_robot).
- Advantages: high mechanical precision without backlash
- Disadvantage: the motion is coupled, some transformations are required from motor coordinates to machine coordinates (Figure fig:flexure_delta_robot_schematic)

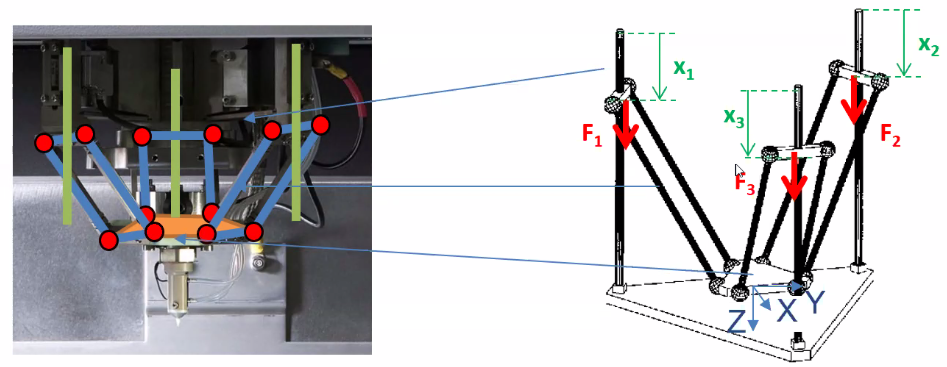
Modelling and validation of the delta robot
Lagrange equations are used to model the dynamics of the delta robot. The motor positions are used as the general coordinate system.
The system is then linearized around the working point (Figure fig:flexure_equations).

Then the parameters are identified from experiment (Figure fig:flexure_identification).
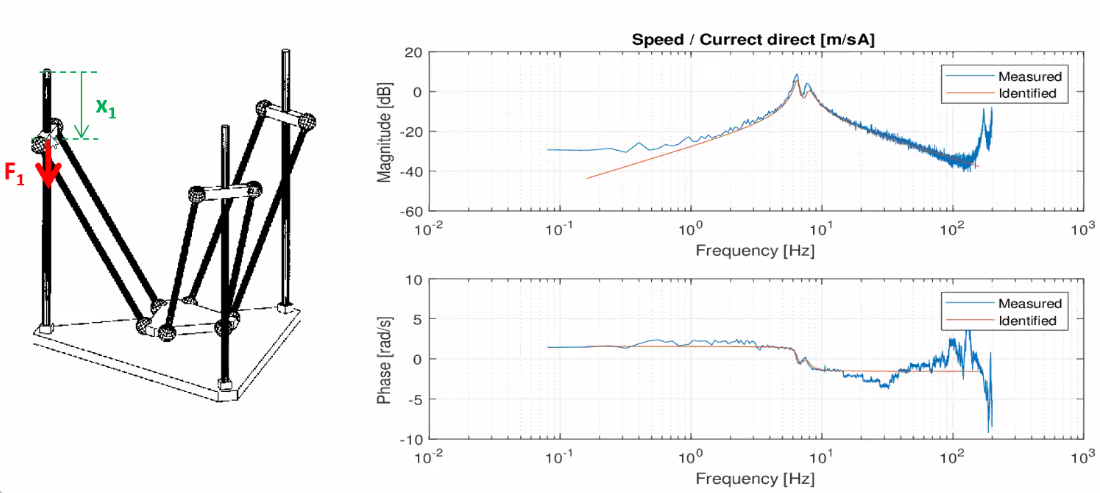
The measurement of the coupling is move complicated as shown in Figure fig:flexure_identification_coupling.

Control design for high trajectory tracking
Control requirements:
- Precise position control of the coupled system (+/-10nm steps)
- Minimal trajectory error at high frequency (+/- 100nm at +/- 1g acceleration)
- Higher resonances attenuation
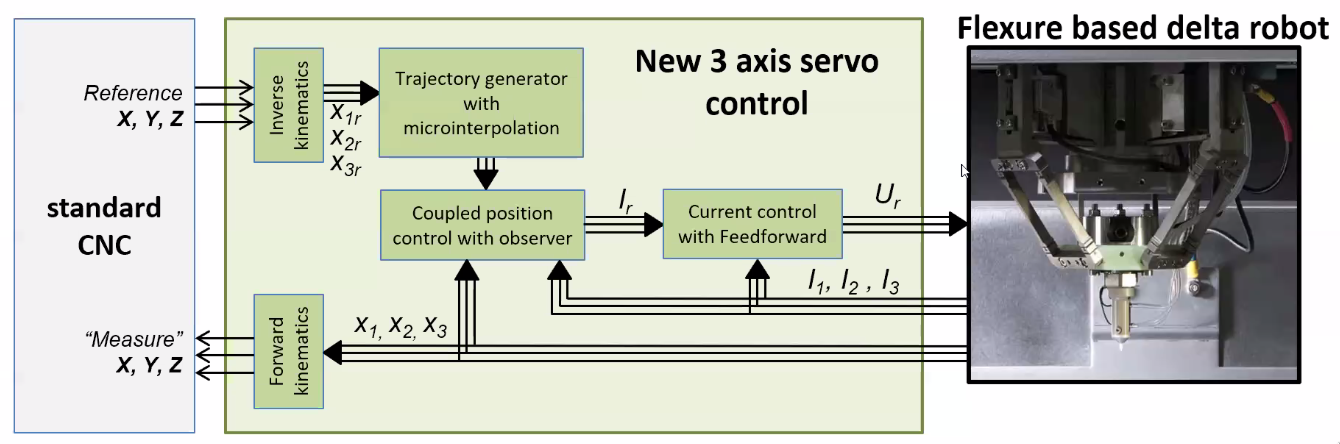
- Whole motion system is considered as a standard cartesian XYZ axes for the user (do the inverse/forward kinematics inside the control architecture)
Electronic board
A 3 axis servo control board as been developed (Figure fig:flexure_electronics_board) which includes:
- identification algorithm of the coupled system integrated in the board
- interpolator for sensors
 ]
]
Results
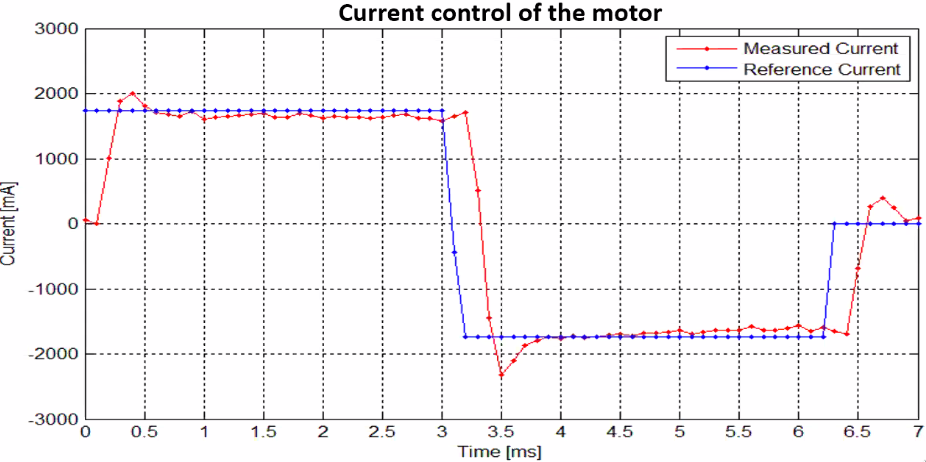
Current control
Step response of the current control loop is shown in Figure fig:flexure_current_control_results.
Trajectory tracking: results with laser interferometer and encoder
XY renishaw interferometers used to verify the performance of the system (Figure fig:flexure_sensors).

Some results are shown in Figures fig:flexure_results, fig:flexure_steps and fig:flexure_dynamics_errors.
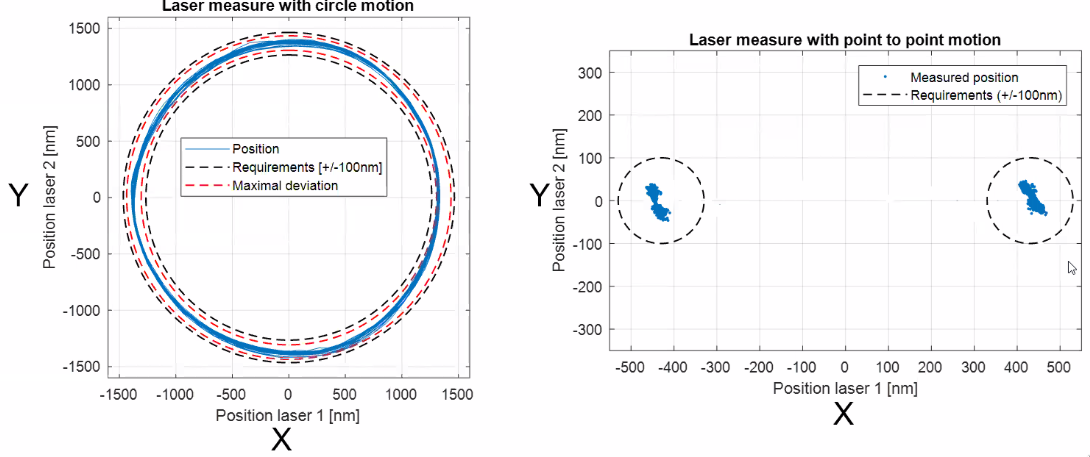
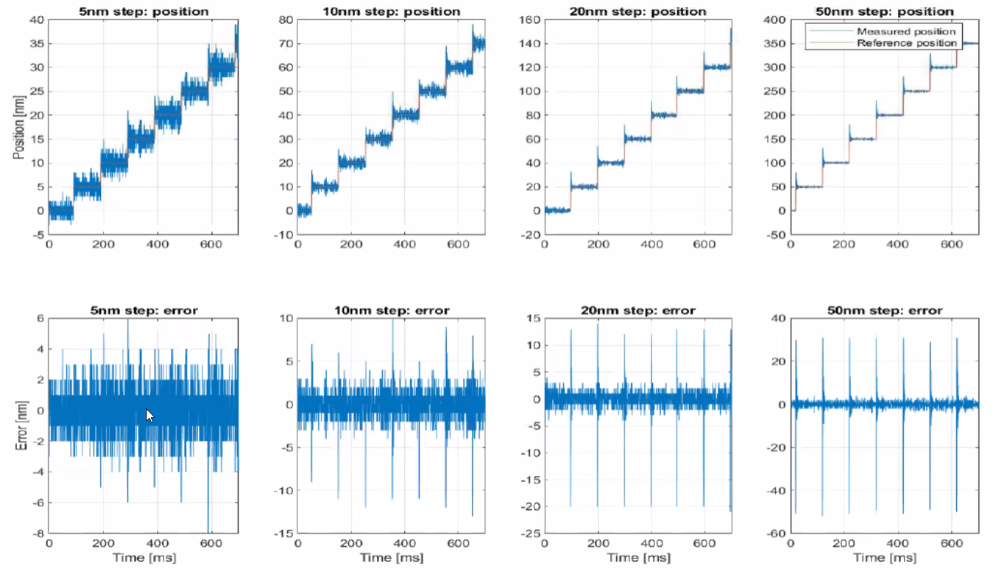
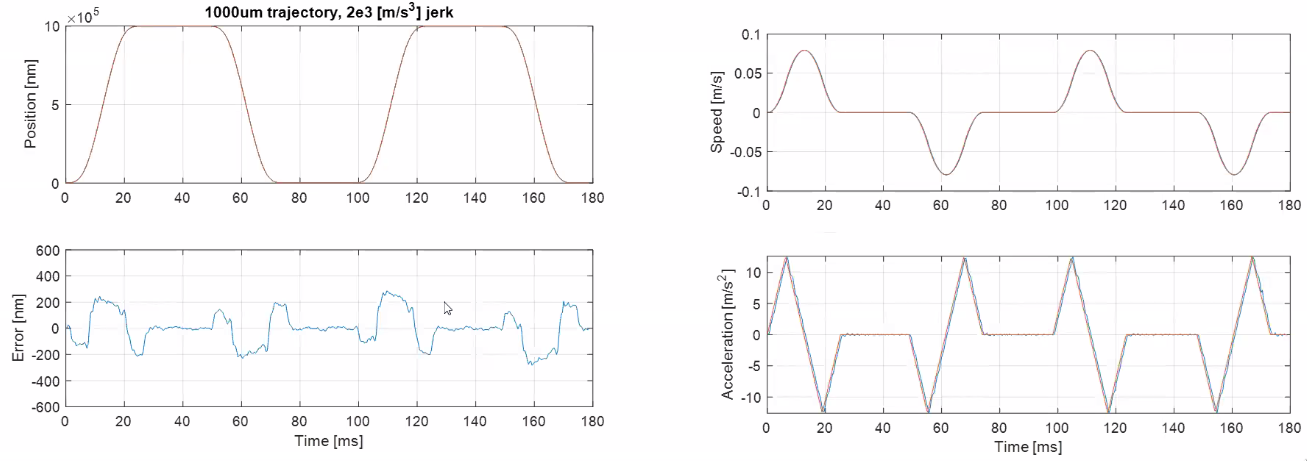
Conclusion
As a conclusion, here are the identified conditions for precise and high dynamic positioning:
- Mechanics without backlash and resonances in higher frequency
- Feedforward with correct parameters
- High bandwidth position control and precise encoder
- Low noise current sensors and high bandwidth current control
Resonances at mid frequencies are an issue for further improvements.
Multivariable performance analysis of position-controlled payloads with flexible eigenmodes @luca_mettenleiter
Motivation
Flexible eigenmodes are present in every system component and leads to::
- controller bandwidth limitation (Figure fig:mimo_flexible_modes)
- additional cross-coupling in the system behavior (Figure fig:mimo_flexible_modes_coupling)
=> can lead to stability problems
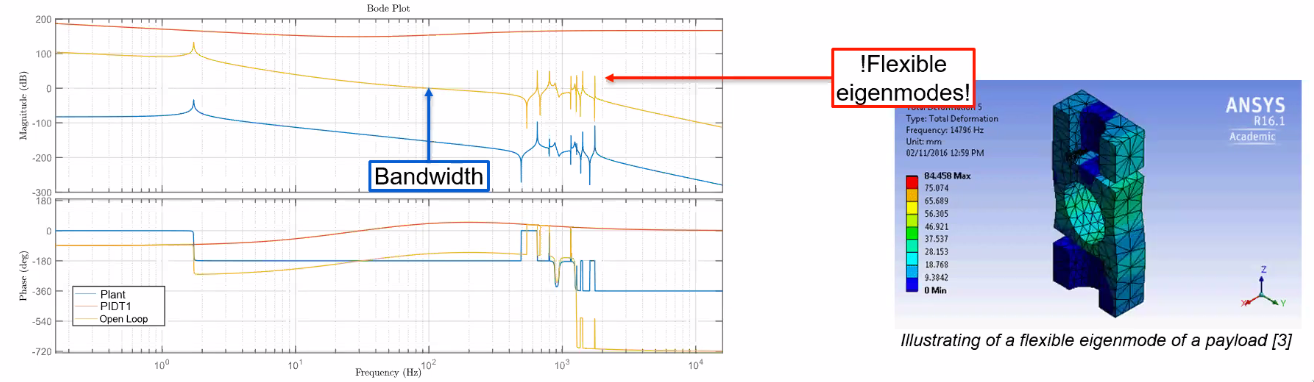
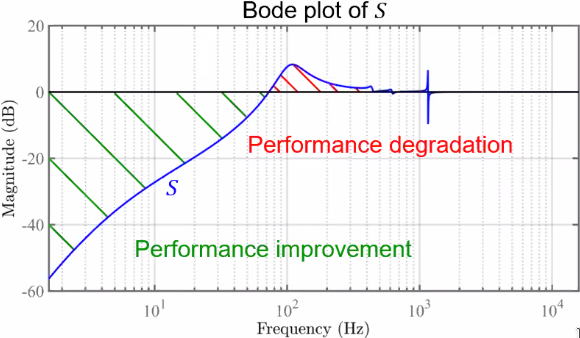
In order to estimate the performances of a system, the sensitivity function can be used (Figure fig:mimo_sensitivity_performance).
#+caption:Bode plot of a typical Sensitivity function
Performance analysis with different sensitivity functions
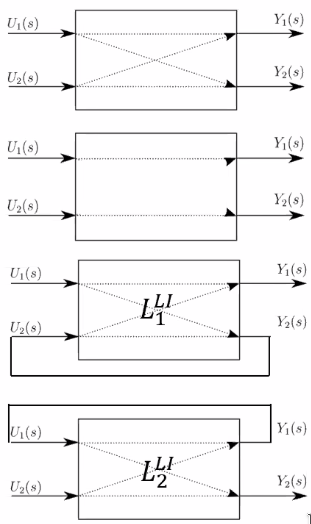
There are different way to analyse the sensitivity function base on different plants (Figure fig:mimo_sensitivity_functions):
- the full system (complicated): \[ L_{full} = \begin{bmatrix}L_{11} & L_{12} \\ L_{21} & L_{22} \end{bmatrix} \]
- the diagonal system (ignoring interaction) \[ L_{diag} = \begin{bmatrix}L_{11} & 0 \\ 0 & L_{22} \end{bmatrix} \]
- the loop interaction system (the one proposed here) \[ L^{LI} = \begin{bmatrix}L_1^{LI} & 0 \\ 0 & L_2^{LI} \end{bmatrix} \]
The loop interaction methods created a SISO system that also represents the coupling in the system. One loop is closed at a time, and the coupling effects are taken into account.
Example system
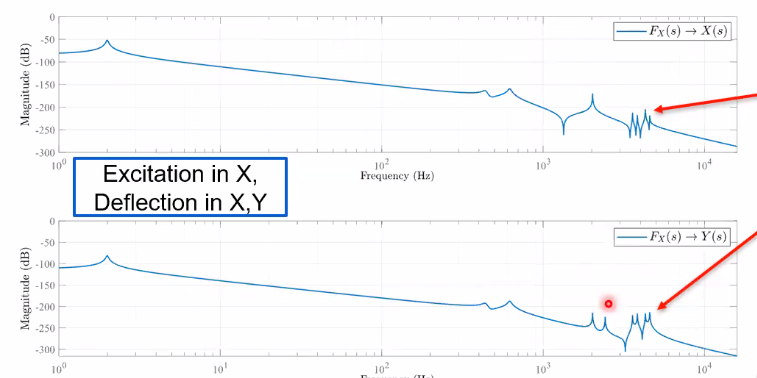
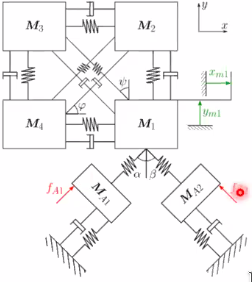
In order to compare the use of the three systems to estimate the performances of a MIMO system, the system shown in Figure fig:mimo_example_system is used. The 4 top masses are used to represent a payload that will add coupling in the system due to its resonances.
A diagonal PID controller is used.
The bode plot of the MIMO system is shown in Figure fig:mimo_example_bode where we can see the resonances in the off-diagonal elements.
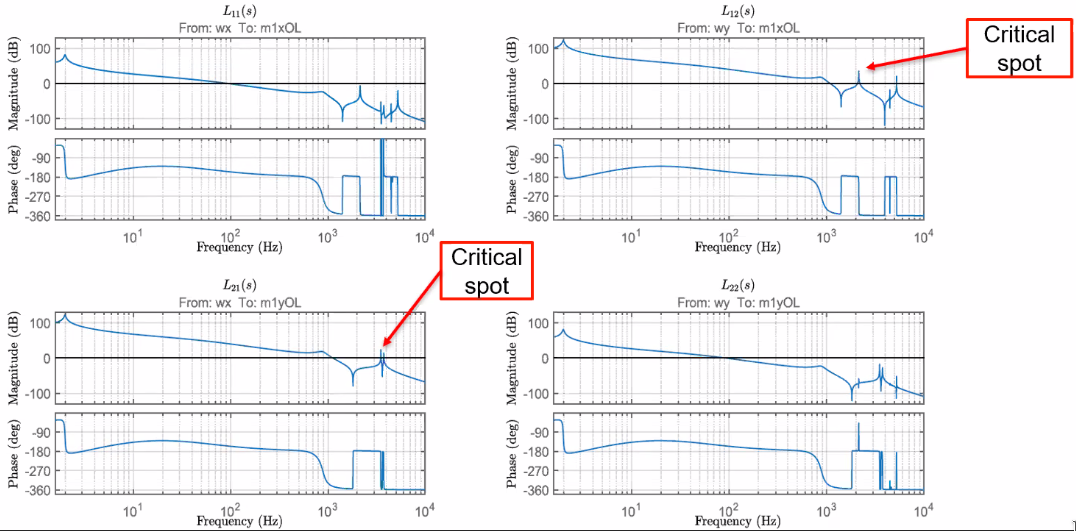
In Figure fig:mimo_example_sensitivity is shown that the sensitivity function computed from the SISO system is not correct. Whereas for the "interaction method" system, it is correct and almost match the full system sensibility. However, as expected, the off-diagonal sensibilities are not modelled.
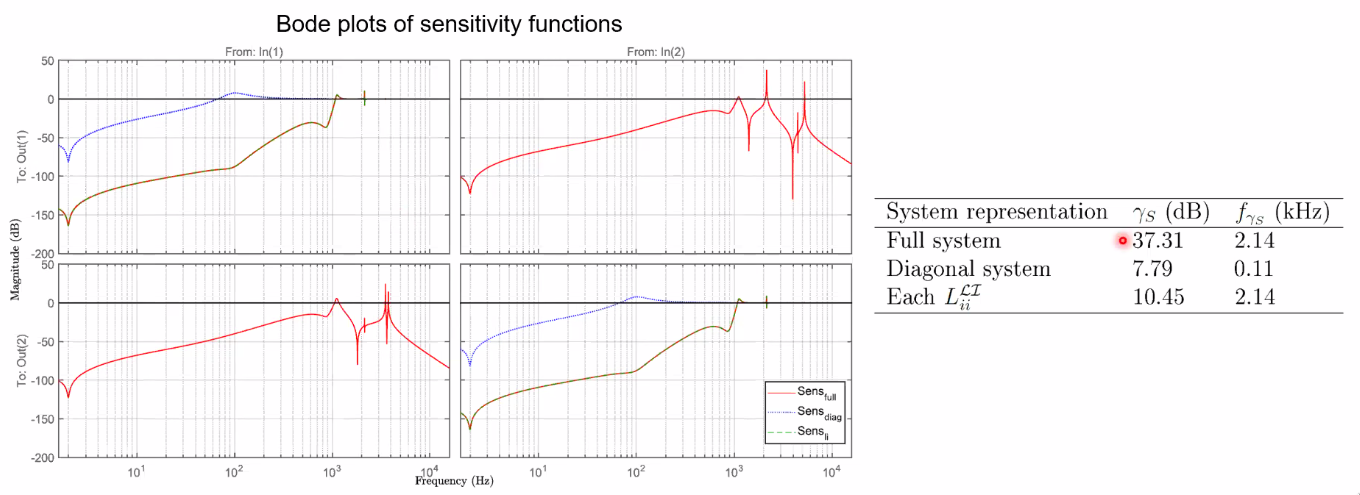
Conclusion
The conclusion are the following and summarized in Figure fig:mimo_results:
- Choice of suitable analysis method is key concept in mechatronics engineering
-
Various methods for analysis of multivariable systems available:
- Full system always delivers reliable information, but much analysis effort
- Loop interaction method delivers reliable information, only if the system is weakly or symmetrically coupled
- Diagonal system delivers unreliable information, as it does not take multivariable character into account

High-precision motion system design by topology optimization considering additive manufacturing @arnoud_delissen
Introduction
The goal of this project is to perform a topology optimization of a 6dof magnetic levitated stage suitable for vacuum.
For the current system (Figure fig:mimoopt_6dof_stage), the bandwidth is limited by the short-stroke dynamics (eigenfrequencies).
The goal here is to make the eigen-frequency higher as this will allow more bandwidth.

Case
More precisely, the goal is to automatically maximize the three eigen-frequencies of the system shown in Figure fig:mimoopt_case.

Manufacturing process
The manufacturing process must be embedded in the optimization such that the obtained design is producible. The process is shown in Figure fig:mimoopt_process.

Topology optimization
Problem: for a given volume, maximize the eigen-frequencies of the system.
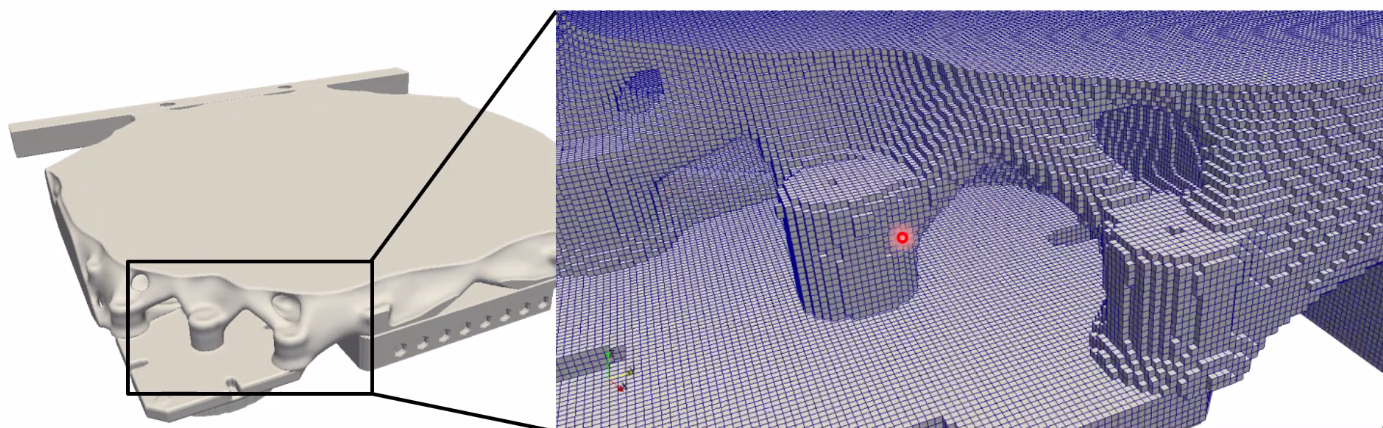
To do so, the system is discretized into small elements (Figure fig:mimoopt_3d_opti). Then, a Finite Element Analysis is performed to compute the eigen-frequencies of the system. Finally, for each element, the "gradient is computed" and we determine if material should be added or removed.
This is done in 3D. The individual 1mm x 1mm x 1mm elements are shown in Figure fig:mimoopt_3d_opti. The number of elements is 1 million (=> 15 minutes per iteration to compute the 3 eigen-frequencies).
Performance Comparison
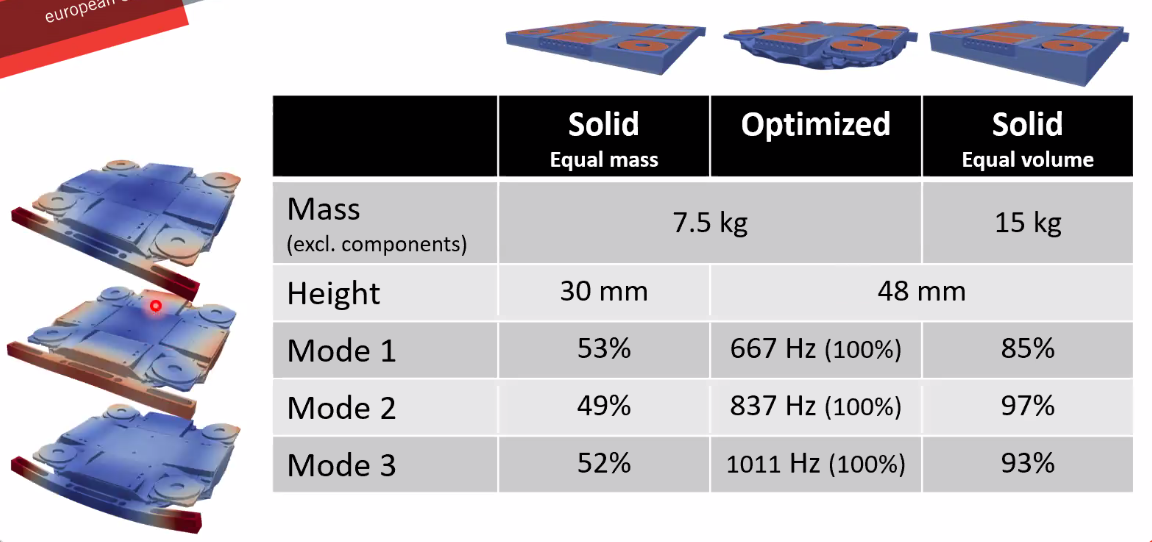
The obtained mass and eigen-frequencies of the optimized system and the solid equivalents are compared in Figure fig:mimoopt_performance.
Identification on the realized system shown that the obtained eigen-frequencies are very closed to the estimated ones (Figure fig:mimoopt_frf_identification).
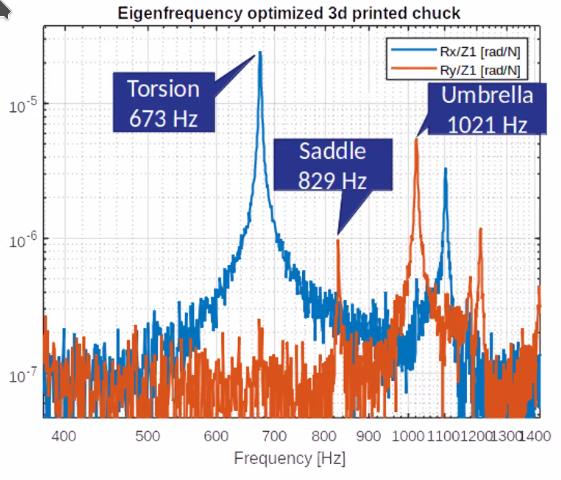
Conclusion
- Increase in performance (~2x) compared to solid designs
- A design is obtained in ~ 1 day
- Practical constraints are incorporated in the optimization
- The method is validated in practice by a demonstrator
A multivariable experiment design framework for accurate FRF identification of complex systems @nic_dirkx
Introduction
Goal: Need for higher quality FRF models that are used to:
- Controller design
- Observer design
- System diagnostics
- Parametric modelling
High quality FRFs requires careful design of excitation $w$.
Typical experimental identification of the FRFs is shown in Figure fig:frf_introduction.
The design trade-off is:
- Maximize input gain to minimize FRF uncertainty
- Bounded signal $u$ and $y$ to remain within operating limited (actuator/amplifier power limitations and limited move ranges)

For SISO systems:
- Only the frequency size of the excitation signal should be optimized
For MIMO systems:
- the gains and directions should be frequency wise optimized
Objective:
- establish optimal experiment design framework that optimize the excitation signal to obtain MIMO FRFs with low uncertainty
Role of directions and constrains in multivariable excitation design
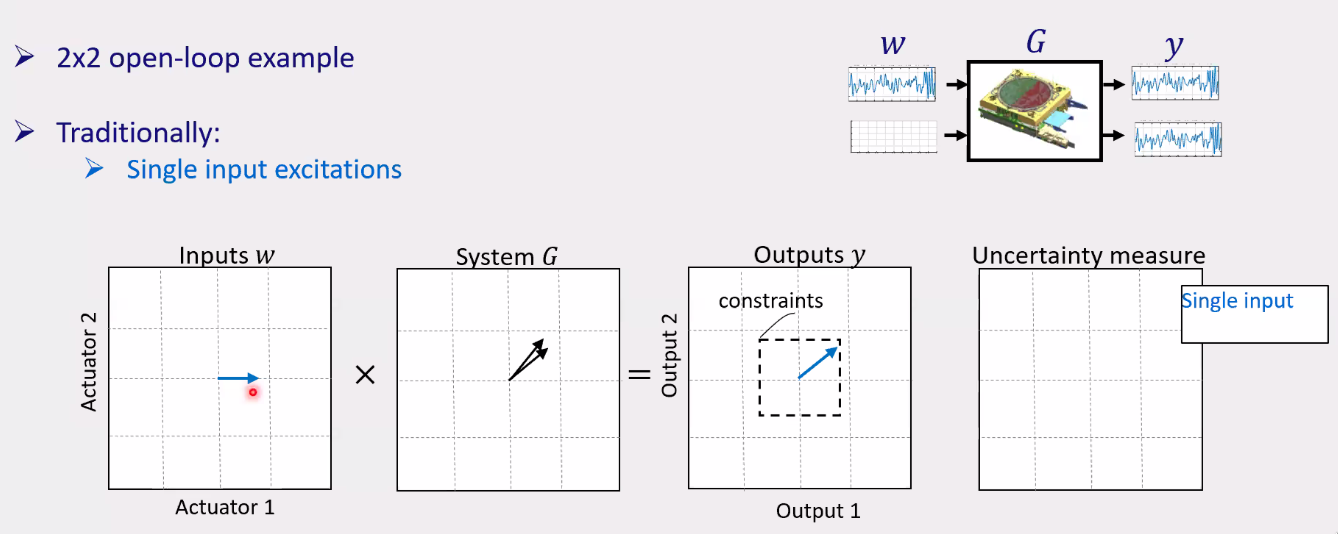
The classical way to estimate MIMO FRFs is the following:
- First start with one direction and increase the gain until constrains is attained (Figure fig:frf_direction_excitation)
- Do the same with the second input
This lead to non-optimal FRFs estimation.
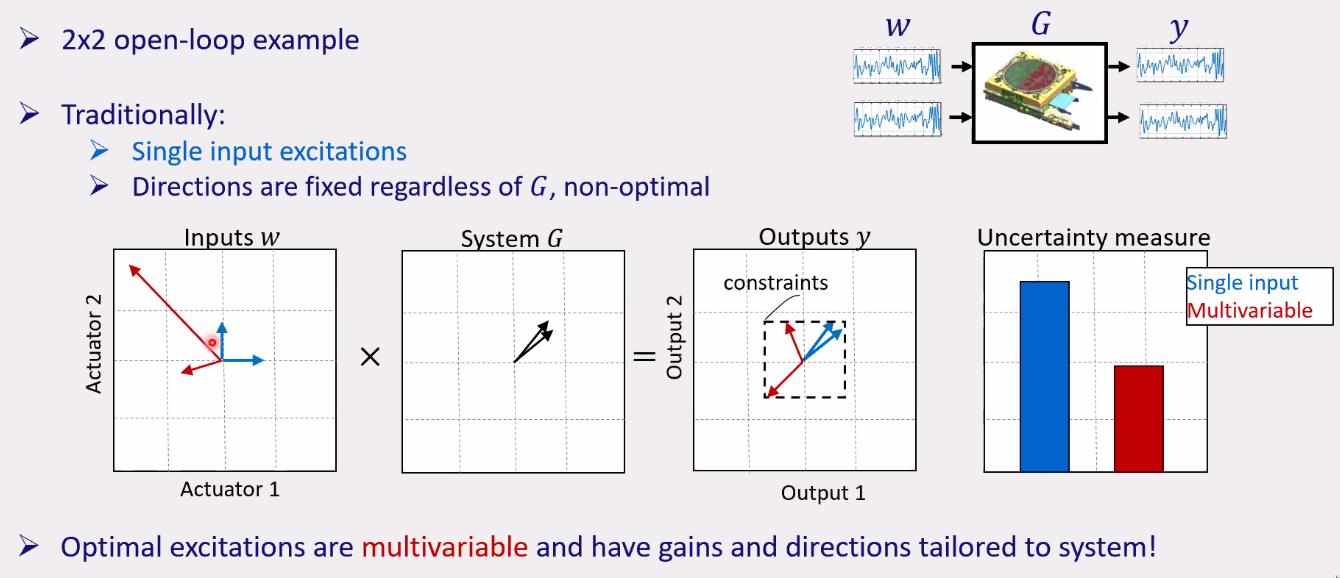
When having a MIMO approach and choosing both the direction and gain of the excitation inputs, we can obtained much better FRFs uncertainty while still fulfilling the constraints (Figure fig:frf_mimo).
Solving the optimization problem
The optimization problem is to minimize the model uncertainty by choosing the design variables which are the magnitude and direction of the inputs $w$.
The optimization is a two step process as shown in Figure fig:frf_optimization_steps:
- first identification without optimization that allows to have data to run the optimization process
- second identification with optimized input direction and gain
The problem with this optimization problem is that it is not convex in general and has a log of design variables. There is no general methods to solve this problem, a dedicated algorithm is required.
In this work, two algorithms are proposed and not further detailed here.

Experimental validation
Experimental identification of a 7x8 MIMO plant was performed in for different cases:
- non optimized SISO approach (grey)
- optimized SISO approach (blue)
- optimized MIMO approach using SSDR (first algorithm proposed) (green)
- optimized MIMO approach using RR (second algorithm proposed) (red)
The obtained FRFs are shown in Figure fig:frf_experiment.
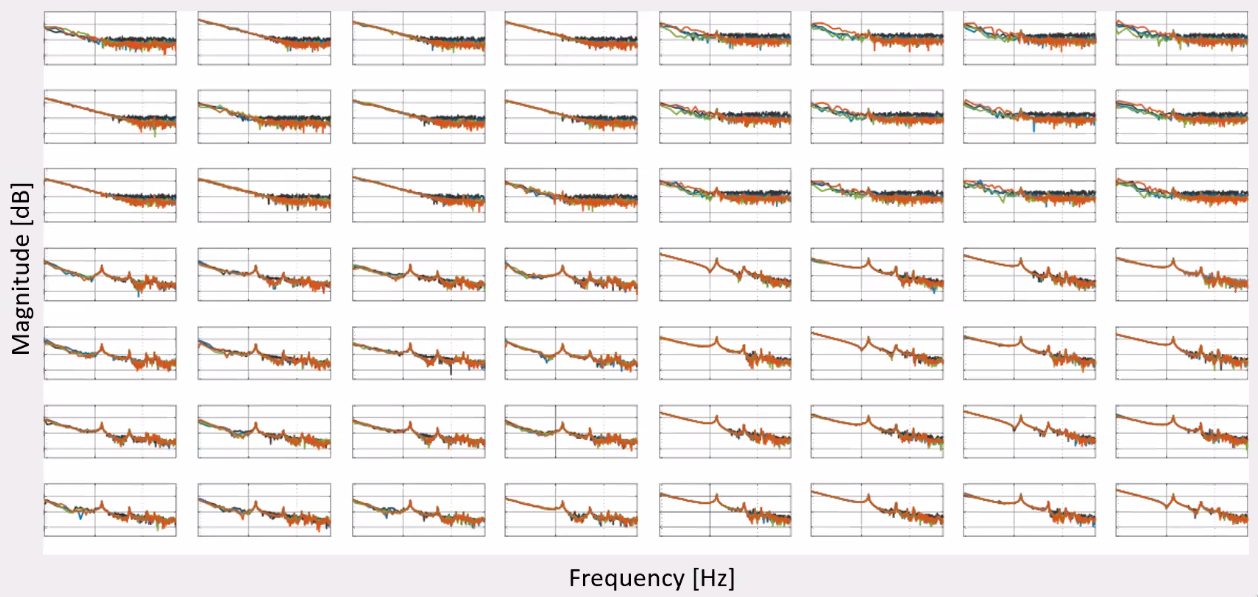
A comparison of one of the obtained FRFs is shown in Figure fig:frf_experiment_optimized. It is quite clear that the MIMO approach can give much lower FRF uncertainty. The RR proposed algorithm is giving the best results
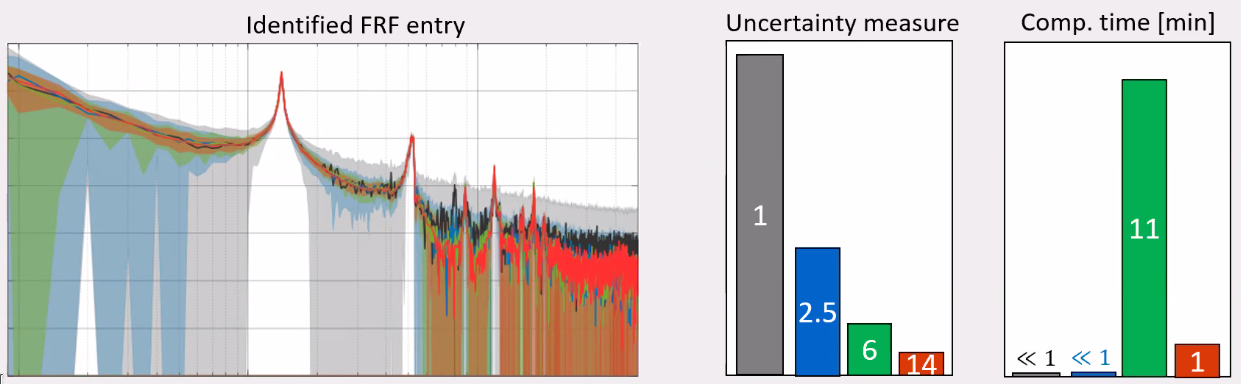
Conclusion
- The uncertainty of the obtained FRF are obtained by doing several experimental identification with a deterministic input signal. The FRF are computed multiple times, and the spread of the results at each frequency represents this uncertainty.
- Exploiting directionality in excitation design enables significant FRF quality improvement
- Multivariable design involves hard non-convex optimization problem
- Computationally tractable design framework for large scale MIMO systems established
- Near global optimal quality achieved on wafer stage setup using RR algorithm
Keynote: High precision mechatronic approaches for advanced nanopositioning and nanomeasuring technologies @eberhard_manske
Coordinate Measurement Machines (CMM)
Examples of Nano Coordinate Measuring Machines are shown in Figure fig:prec_cmm.

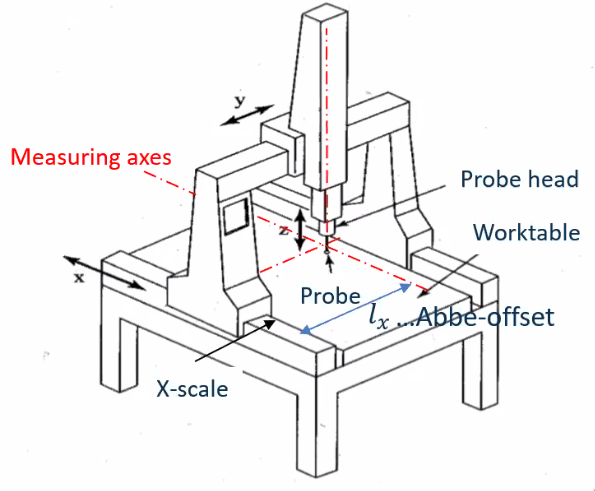
Difference between CMM and nano-CMM
With classical CMM, the Abbe-principle is not fulfilled in the x and y directions (Figure fig:prec_cmm_nano_cmm).
The Abbe error can be determined with:
\begin{equation} \Delta l_{x,y,z} = l_{x,y,z} \sin \Delta \phi_{x,y,z} \end{equation}Even with the best spindle: $l_{x,y} = 100 mm$ and $\Delta \phi = 2 \text{arcsec}$, we obtain an error of:
\begin{equation} \Delta l = 0.1 \mu m \end{equation}which is not compatible with nano-meter precisions.
Then, the classical CMM will not work for nano precision
How to do nano-CMM
High precision mechatronic approaches are required for advanced nano-positionign and nano-measuring technologies:
- High precision measurement concept
- High precision measurement systems
- High precision nano-sensors
Combined with:
- Advanced automatic control
- Advanced measuring strategies
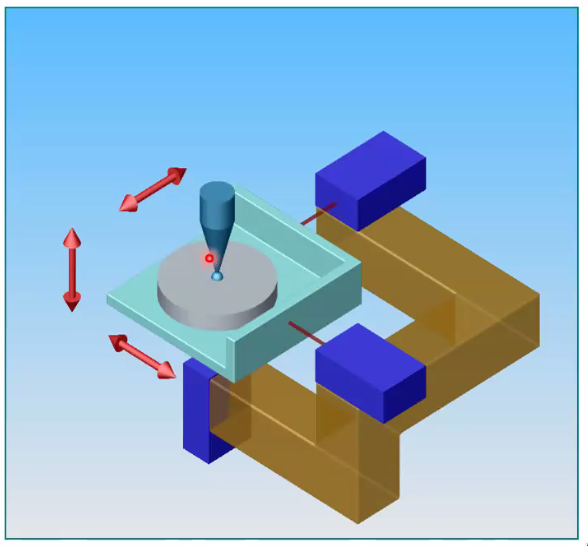
Concept - Minimization of the Abbe Error
In order to minimize the Abbe error, the measuring "lines" should have a common point of intersection (Figure fig:prec_nano_cmm_concept).
The 3D-realization of Abbe-principle is as follows:
- 3 interferometers: cartesian coordinate system
- probe located as the intersection point of the interferometers
Minimization of residual Abbe error
Still some residual Abbe error can happen as shown in Figure fig:prec_abbe_min due to both a change of angle and change of position.

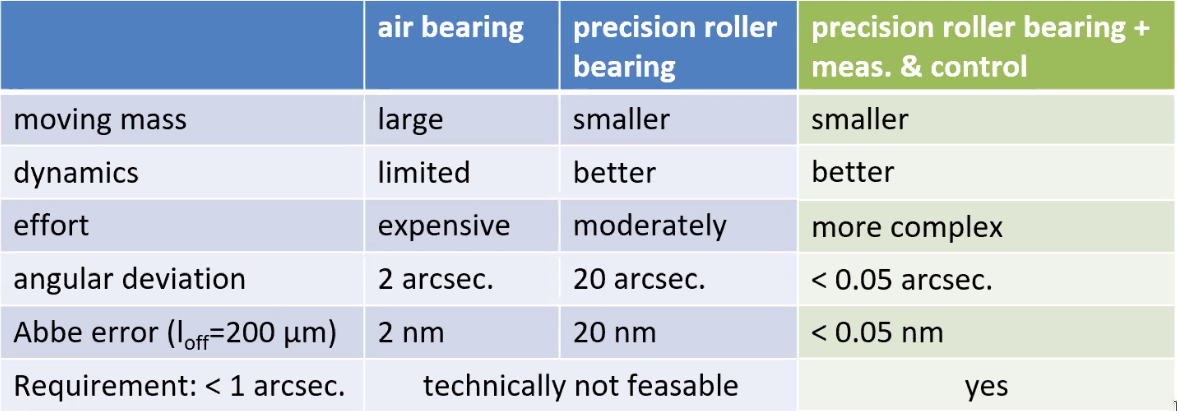
Compare of long travel guiding systems
In order to have the Abbe error compatible with nano-meter precision, the precision of the spindle should be less and one arcsec which is not easily feasible with air bearing of precision roller bearing technologies as shown in Figure fig:prec_comp_guid.

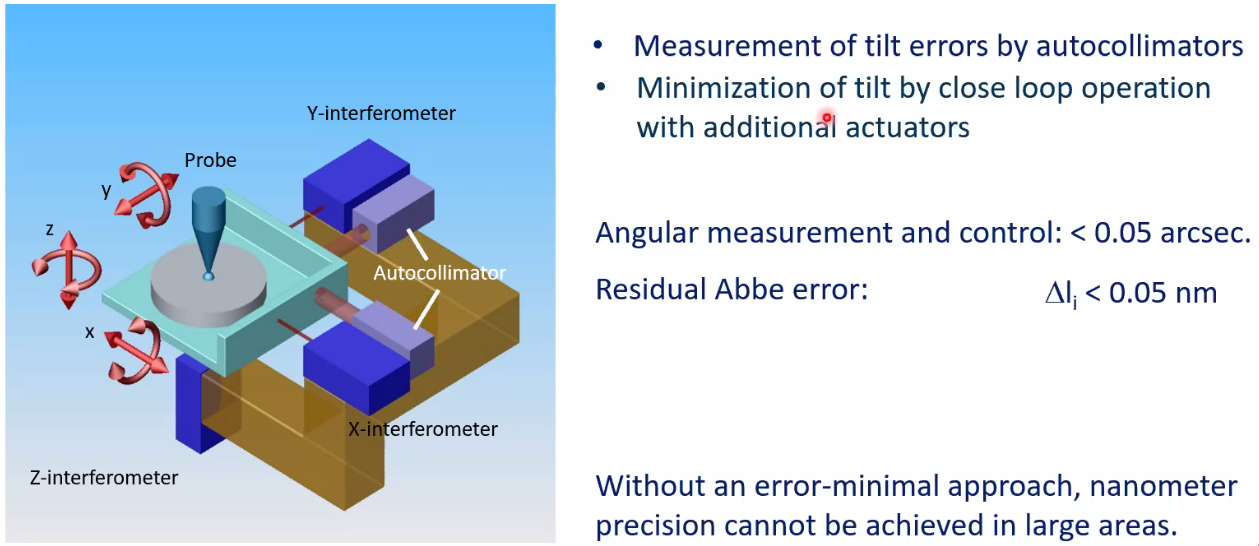
Extended 6 DoF Abbe comparator principle
The solution used was to measure in real time the angles of the frame using autocollimators as shown in Figure fig:prec_6dof_abbe and then to minimize this tilt by close loop operation with additional actuators.
The angular measurement error and control is less than $0.05 \text{arcses}$ which make the residual Abbe error:
\begin{equation} \Delta l < 0.05\,nm \end{equation}Without an error-minimal approach, nano-meter precision cannot be achieved in large areas.
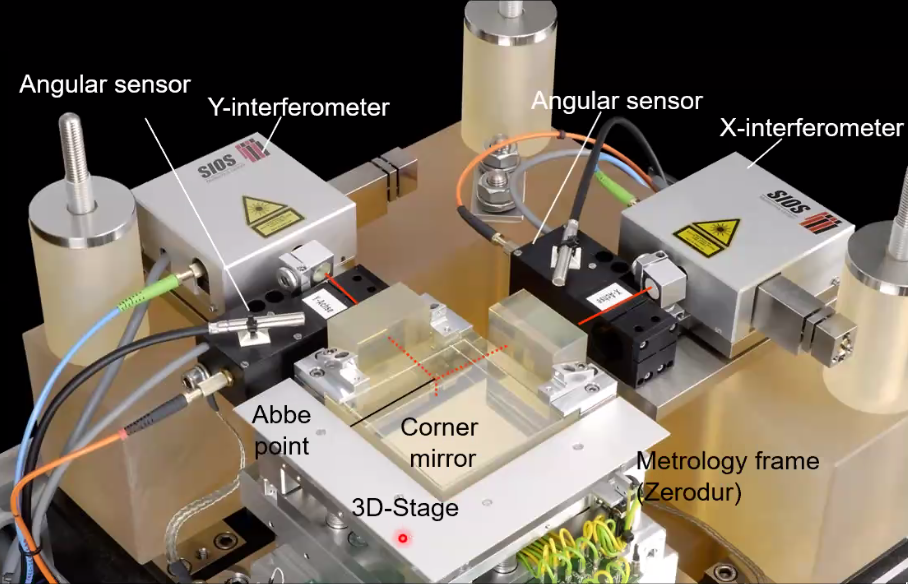
Practical Realisation
A practical realization of the Extended 6 DoF Abbe comparator principle is shown in Figure fig:prec_practical_6dof.
Tilt Compensation
To measure compensate for any tilt, two solutions are proposed:
-
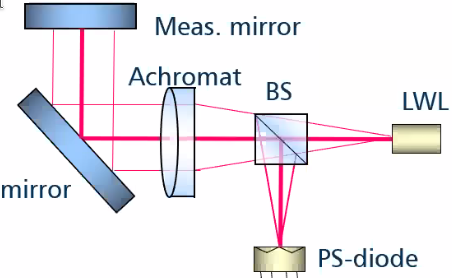
Use a zero point angular auto-collimator (Figure fig:prec_tilt_corection)
- Resolution: 0.005 arcsec
- Stability (1h): < 0.05 arcsec
-
6 DoF laser interferoemter (Figure fig:prec_tilt_corection_bis)
- Resolution: 0.00002 arcsec
- Stability (1h): < 0.00005 arcsec

Comparison of long travail guiding systems - Bis
Now, if we actively compensate the tilts are shown previously, we can fulfill the requirements as shown in Figure fig:prec_comp_guid_bis.
Measurement and control technology to minimize Abbe errors to achieve:
- sub-nanometer precision
- smaller moving mass
- better dynamics
Drive concept
Usually, in order to achieve a large range over small resolution, each axis of motion is a combination of a coarse motion and a fine motion stage. The coarse motion stage generally consist of a stepper motor while the fine motion is a piezoelectric actuator.
The approach here is to use an homogenous drive concept for increase dynamics (Figure fig:prec_drive_concept).
Only one linear voice coil actuator is used which with large moving range and sub-nanometer resolution can be achieve at one time.

NPMM-200 with extended measuring volume
The NPMM-200 machine can be seen in Figure fig:prec_mechanics.
Characteristics:
- Measuring range: 200 mm x 200 mm x 25 mm
- Resolution: 20 pm
- Abbe comparator principle
- 6 laser interferometers
- Active angular compensation
- Position uncertainty < 4 nm
- Measuring uncertainty up to 30 nm

The NPMM-200 actually operates inside a Vacuum chamber as shown in Figure fig:prec_vacuum_cham.

measurement capability
Some step responses are shown in Figure fig:prec_results_meas and show the nano-metric precision of the machine.
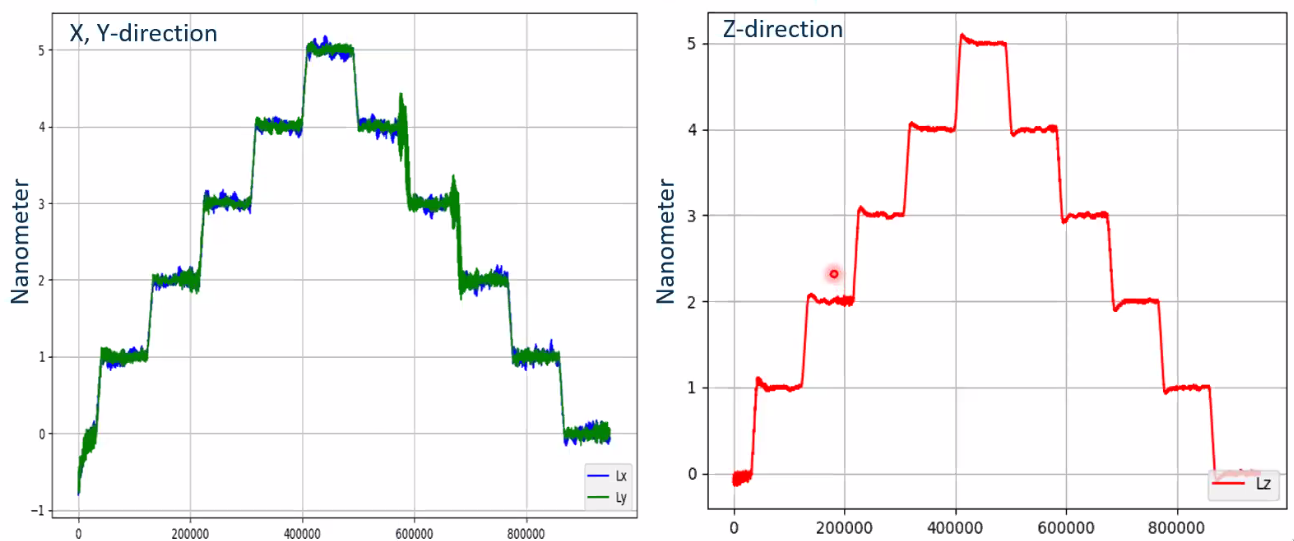
Picometer steps can even be achieved as shown in Figure fig:prec_results_pico.
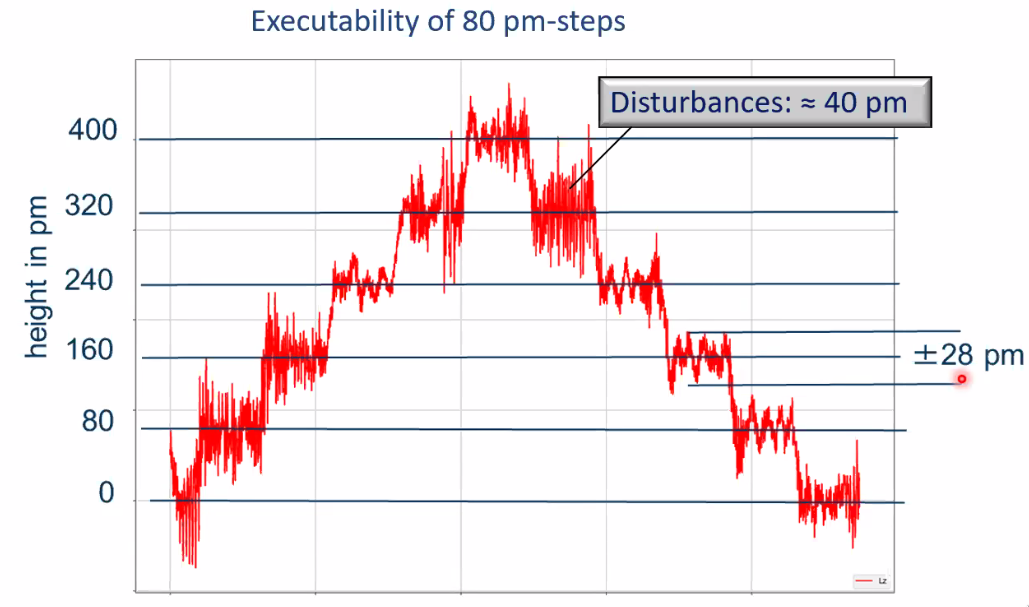
Extension of the measuring range (700mm)
If the measuring range is to be increase, there are some limits of the moving stage principle:
- large moving masses (~300kg)
- powerful drive systems required
- nano-meter position capability problematic
- large heat dissipation in the system
- dynamics and dynamic deformation
The proposed solution is to use inverse dynamic concept for minimization of moving masses.
Inverse kinematic concept - Tetrahedrical concept
The proposed concept is shown in Figure fig:prec_inverse_kin:
- mirrors and object to be measured are fixed
- probe and interferometer heads are moved
- laser beams virtually intersect in the probe tip
- Tetrahedrical measuring volume
This fulfills the Abbe principe but:
- large construction space
- difficult guide and drive concept
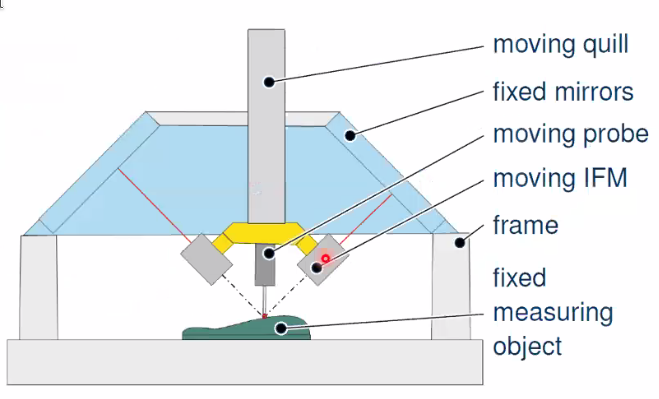
Inverse kinematic concept - Scanning probe principle
An other concept, the scanning probe principle is shown in Figure fig:prec_inverse_kin_scan:
- cuboidal measuring volume
- Fixed x-y-z mirrors
- moving measuring head
- guide and drive system outside measuring volume
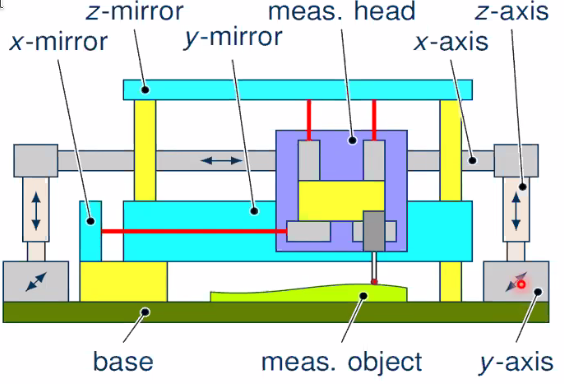
Inverse kinematic concept - Compact measuring head
In order to minimize the moving mass, compact measuring heads have been developed. The goal was to make a lightweight measuring head (<1kg)
The interferometer used are fiber coupled laser interferometers with a mass of 37g (Figure fig:prec_interferometers).

The concept is shown in Figure fig:prec_inverse_meas_head:
- 6dof interferometers are used
- one micro-probe
- the total mass of the head is less than 1kg
There is some abbe offset between measurement axis of probe and of interferometer but Abbe error compensation by closed loop control of angular deviations is used.
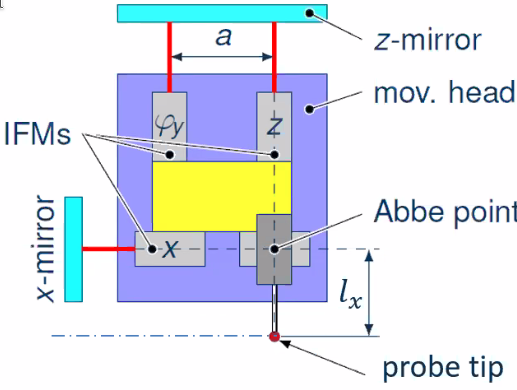
Inverse kinematic concept - Scanning probe principle
As shown in Figure fig:prec_abbe_compensation, the abbe error can be compensated from the two top interferometers as: \[ \text{for } l_x = a: \quad \Delta l_{\text{Abbe}} = \Delta l_{\text{int}} \] Thus the tilt and Abbe errors can be compensated for with sub-nm resolution.

Conclusion
Proposed approaches to push the nano-positioning and nano-measuring technology:
- Measurement and control technology to minimize Abbe errors
- Homogeneous drive concept for increased dynamics
- Inverse kinematic concept for minimization of moving mass
- Abbe-error compensation by closed loop control of angular deviations
Reducing control delay times to enhance dynamic stiffness of magnetic bearings @jan_philipp_schmidtmann
This projects focuses on reducing the control delay times of a magnetic bearing shown in Figure fig:magn_bear_intro.

Active magnetic bearings are unstable systems and require active control. However, the active control of magnet forces leads to a control delay that limits the performances (stiffness) of the bearing.
Typical contributors to the control delay time are shown in Figure fig:magn_bear_delay.
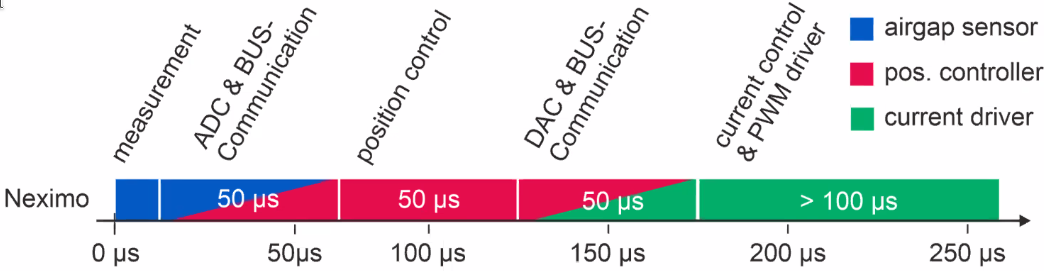
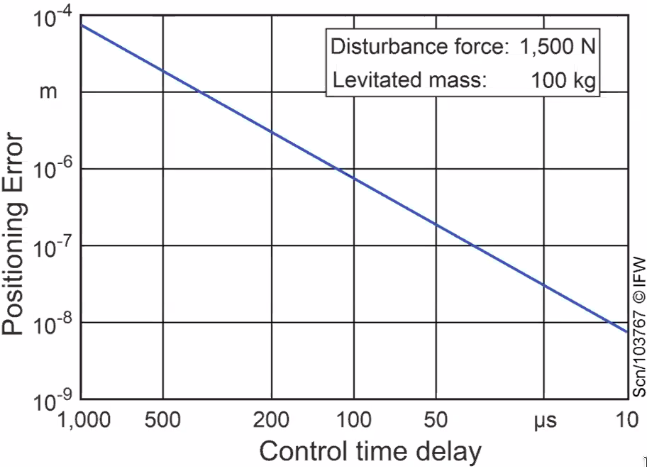
The reduction of the control time delay will increase the dynamic stiffness of the bearing as well as decrease the effects of external disturbances and hence improve the positioning errors (Figure fig:magn_bear_distur).
The steps to reduce the control delay time are:
- Eliminate BUSS-communication by merging position and current controller
- Reduce cycle time by using rapid prototyping system
- Reduce delay in PWM driver by using high PWM frequencies with SiC driver
Therefore, the position and current control have been merged into one controller (Figure fig:magn_controller).

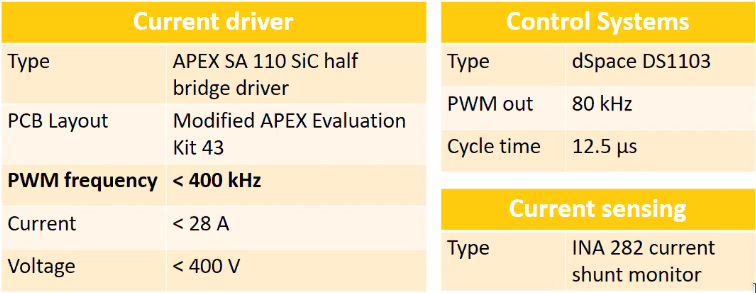
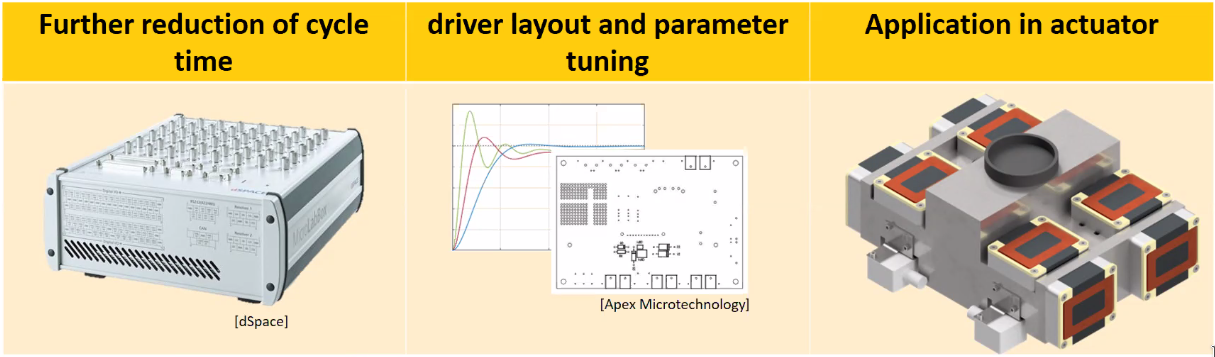
A dSpace rapid prototyping system is used for fast position and current control. Characteristics of the used elements are shown in Figure fig:magn_bear_setup.
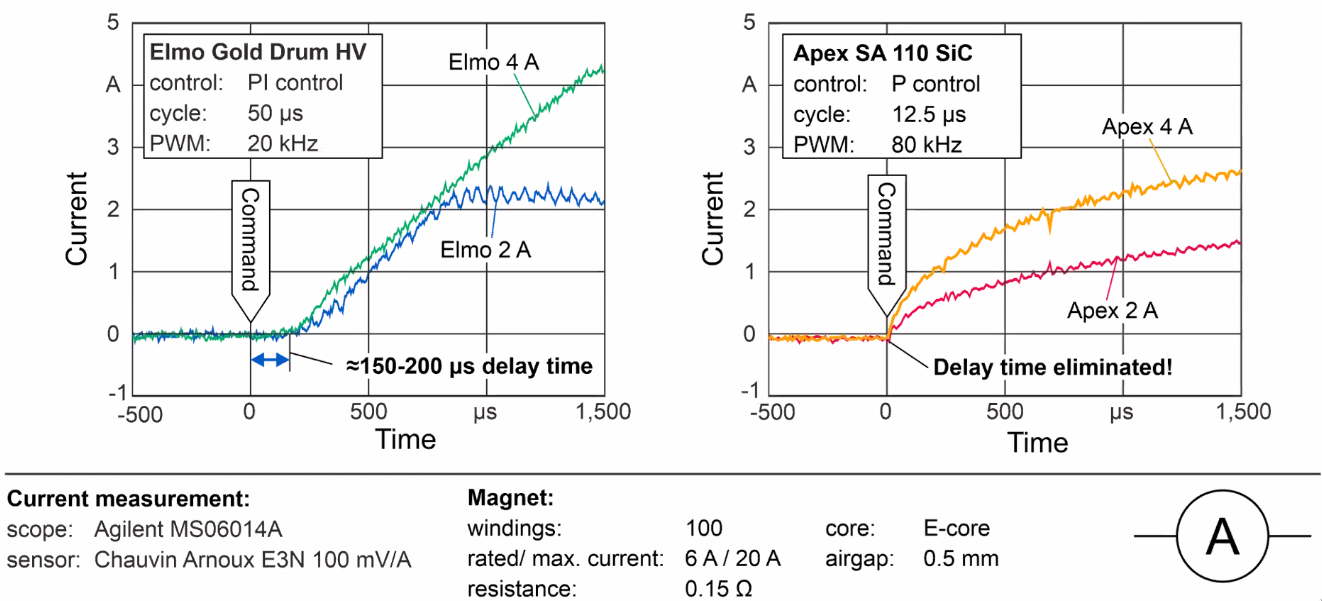
Differences between the previous PWM controller and the new SiC controller are shown in Figure fig:magn_bear_results. The delay time is almost completely eliminated.
Due to all the performed modifications, the control delay time could be reduced by 80%. The next steps for this project are shown in Figure fig:magn_bear_conclusion.
Digital twins in control: From fault detection to predictive maintenance in precision mechatronics @koen_classens
Motivation
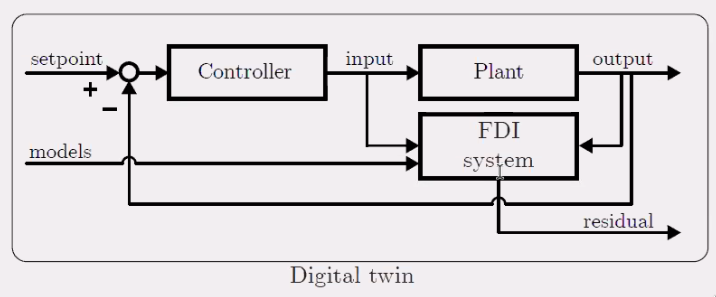
Models are usually for the control design part that can be either physical models (FEM, first principle) or data-driven models. However, these models are usually not used after control system is implemented (Figure fig:twins_motivation).

Here, the models are exploited to monitor the system and predict future possible failures in the system. Use models as digital twin for fault detection and Isolation for predictive maintenance in precision mechatronics (Figure fig:twing_fdi).
Predictive Maintenance
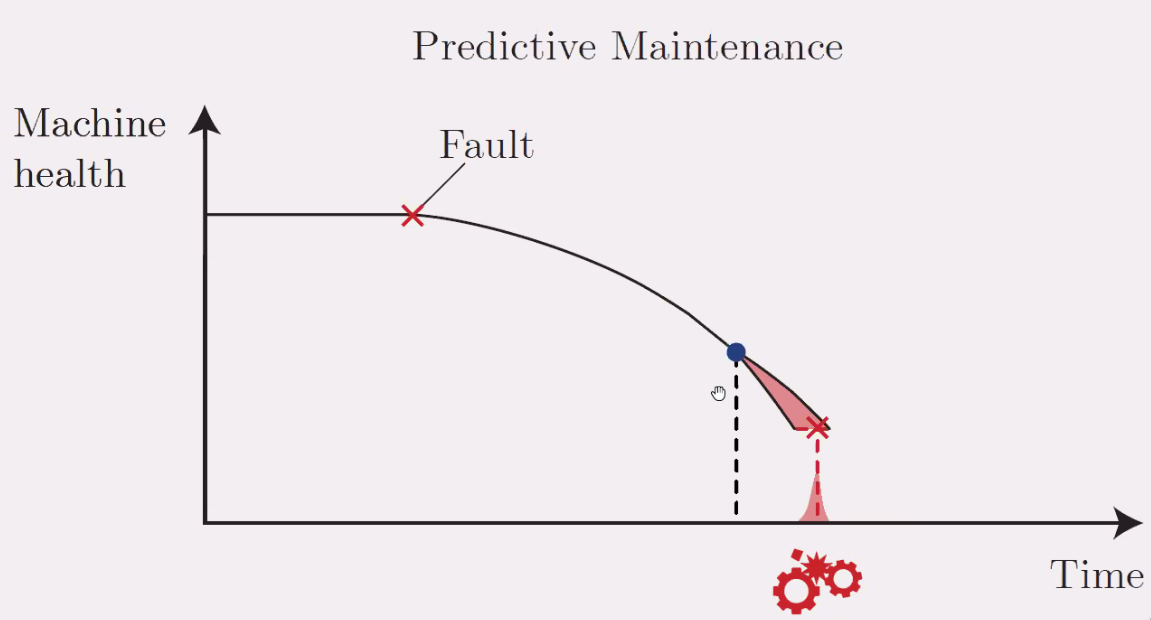
Classical maintenance happens when the system is not working anymore as shown in Figure fig:twins_predictive_maintenance.

It is possible to perform some preventive maintenance before a failure happens, but this is still not optimal.

The idea here is to predict when the failure will happen in order to only do maintenance only when really necessary. This will minimize the down time of the machine.
Objectives
The main objective is to develop a system monitoring approach for precision mechatronic systems, exploiting prior information (models) and integrating posterior information (real-time measured data).
Even though state of the art system monitoring are already in used in aerospace, process industry and automotive, there are few specificity for mechatronic systems:
- Control loops
- Large-scale MIMO systems (interaction)
- Accurate models: Frequency Response Functions
Null-space based FDI
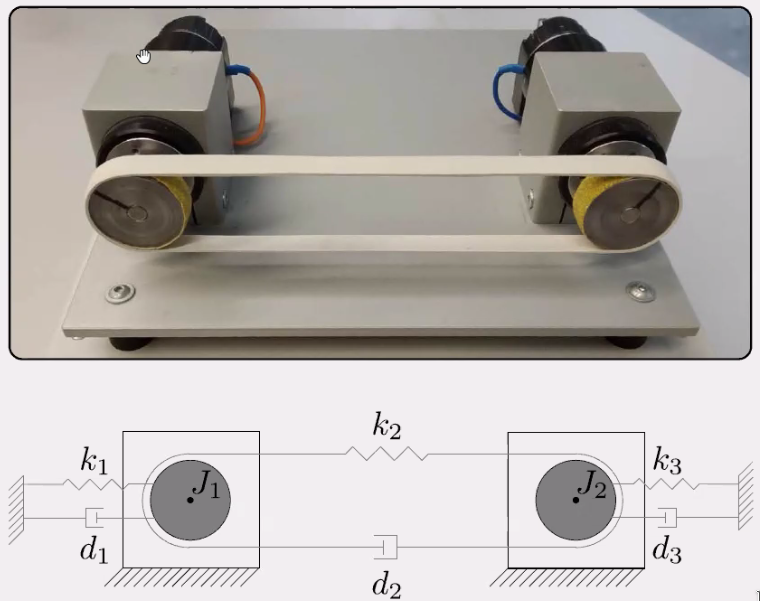
The goal is to applied a decentralized Fault Detection on the system shown in Figure fig:twings_fdi_test to detect actuator faults at $J_1$. This should take into account the control loop, interaction in the system and be FRF based.
The architecture to estimate faults in the system is shown in Figure fig:twins_null_space_fdi. The goal is to design $Q_u$ and $Q_y$ such that $\epsilon$ is a representation of faults in the system.

When a fault happens (Figure fig:twins_results_fdi), the outputs signals are not changing that much (because of feedback), however the system is able to find that there is a problem using the residual $\epsilon$.
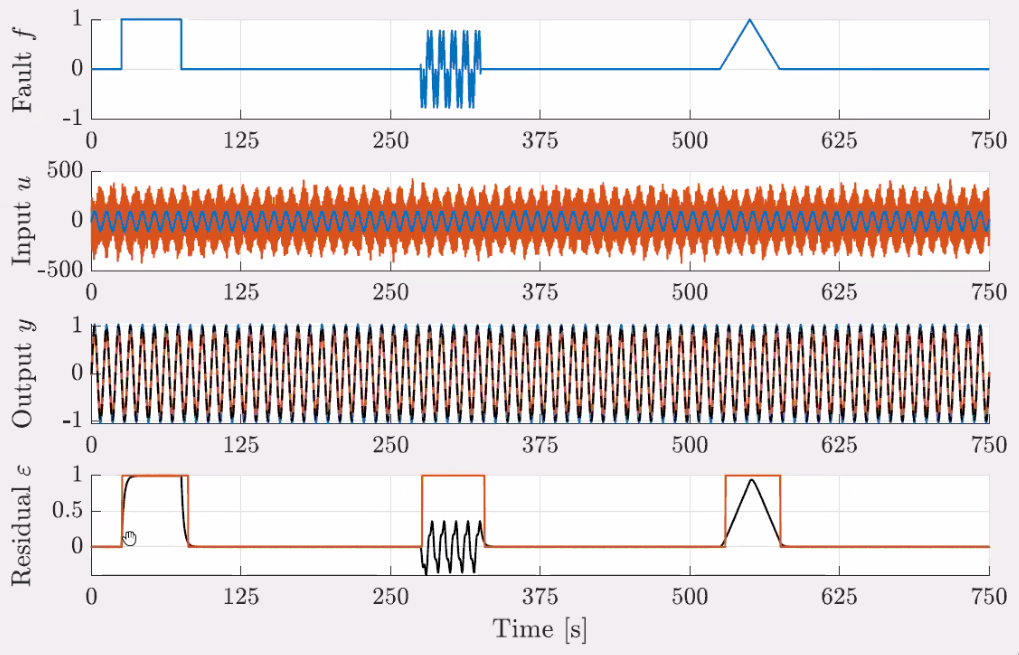
Procedure:
- Additive faults
- Closed-loop
- Interaction
- start from identification
Roadmap from fault detection to predictive maintenance
The proposed system can detect faults in the system (Figure fig:twins_roadmap). This proof of principle should now be applied on industrial systems. Moreover, from the fault detection, predictive maintenance should be performed (Figure fig:twins_roadmap).

