encoder-test-bench/index.org

Encoder - Test Bench

• Experimental Setup
• Huddle Test
  • Introduction
  • Load Data
  • Time Domain Results
  • Frequency Domain Noise
• Comparison Interferometer / Encoder
  • Introduction
  • Load Data
  • Time Domain Results
  • Difference between Encoder and Interferometer as a function of time
  • Difference between Encoder and Interferometer as a function of position
• Identification
  • Load Data
  • Identification

Experimental Setup

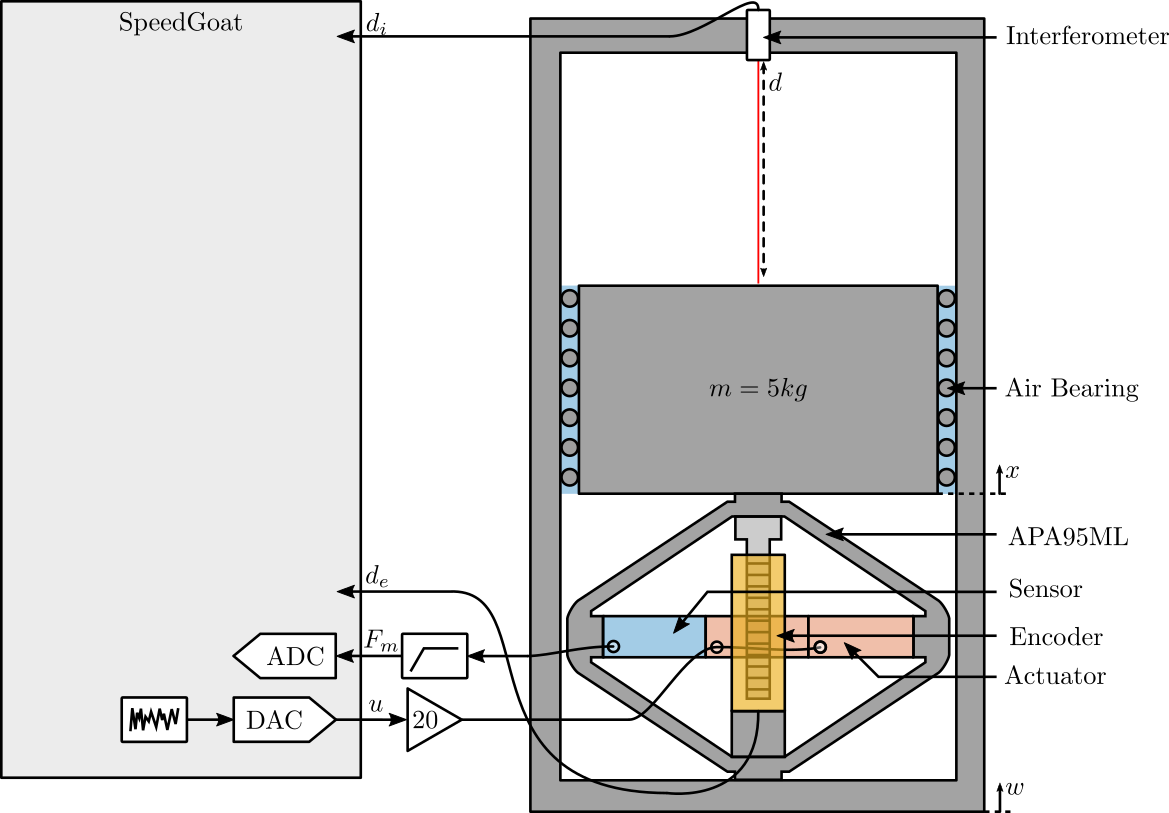
The experimental Setup is schematically represented in Figure fig:exp_setup_schematic.

The mass can be vertically moved using the amplified piezoelectric actuator. The displacement of the mass (relative to the mechanical frame) is measured both by the interferometer and by the encoder.

Schematic of the Experiment

Side View of the encoder

Front View of the encoder

Huddle Test

Introduction   ignore

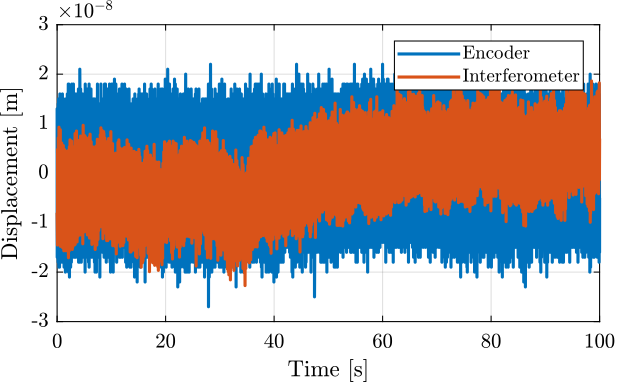
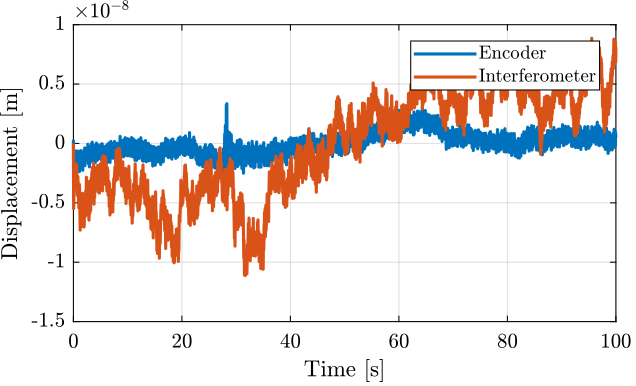
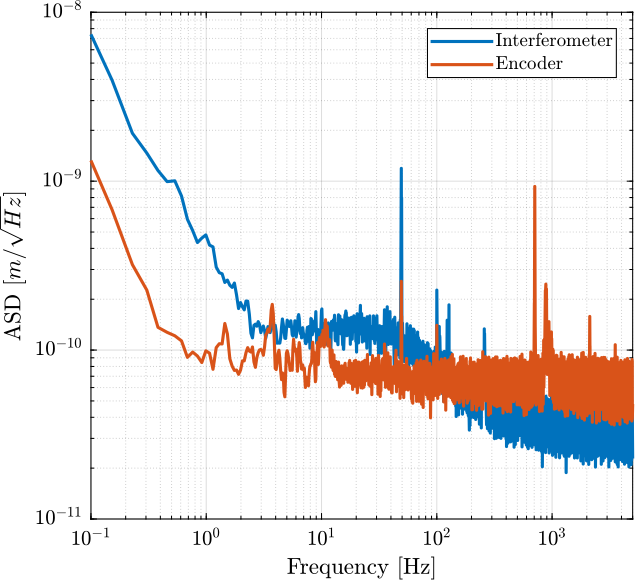
The goal in this section is the estimate the noise of both the encoder and the intereferometer.

Nothing is then to the actuator such that the relative motion between the mass and the frame is as small as possible. Ideally, a mechanical part would clamp the two together, we here suppose that the APA is still enough to clamp the two together.

Load Data

  load('mat/int_enc_huddle_test.mat', 'interferometer', 'encoder', 't');

  interferometer = detrend(interferometer, 0);
  encoder = detrend(encoder, 0);

Time Domain Results

Huddle test - Time domain signals

  G_lpf = 1/(1 + s/2/pi/10);

Huddle test - Time domain signals filtered with a LPF at 10Hz

Frequency Domain Noise

  Ts = 1e-4;
  win = hann(ceil(10/Ts));

  [p_i, f] = pwelch(interferometer, win, [], [], 1/Ts);
  [p_e, ~] = pwelch(encoder,        win, [], [], 1/Ts);

Amplitude Spectral Density of the signals during the Huddle test

Comparison Interferometer / Encoder

Introduction   ignore

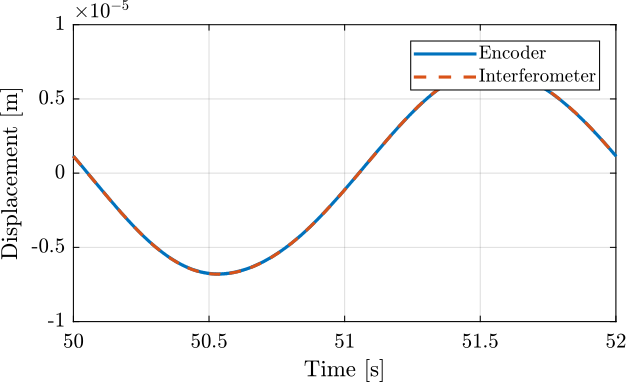
The goal here is to make sure that the interferometer and encoder measurements are coherent. We may see non-linearity in the interferometric measurement.

Load Data

  load('mat/int_enc_comp.mat', 'interferometer', 'encoder', 'u', 't');

  interferometer = detrend(interferometer, 0);
  encoder = detrend(encoder, 0);
  u = detrend(u, 0);

Time Domain Results

One cycle measurement

Difference between the Encoder and the interferometer during one cycle

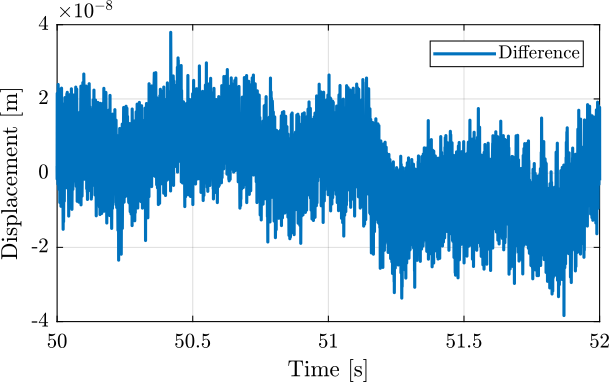
Difference between Encoder and Interferometer as a function of time

  Ts = 1e-4;
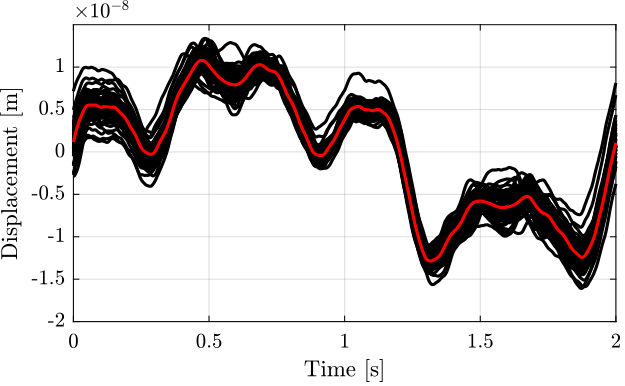
  d_i_mean = reshape(interferometer, [2/Ts floor(Ts/2*length(interferometer))]);
  d_e_mean = reshape(encoder,        [2/Ts floor(Ts/2*length(encoder))]);

  w0 = 2*pi*5; % [rad/s]
  xi = 0.7;

  G_lpf = 1/(1 + 2*xi/w0*s + s^2/w0^2);

  d_err_mean = reshape(lsim(G_lpf, encoder - interferometer, t), [2/Ts floor(Ts/2*length(encoder))]);
  d_err_mean = d_err_mean - mean(d_err_mean);

Difference between the two measurement in the time domain, averaged for all the cycles

Difference between Encoder and Interferometer as a function of position

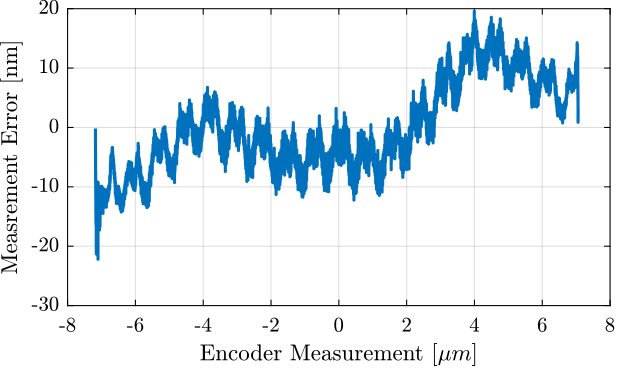
Compute the mean of the interferometer measurement corresponding to each of the encoder measurement.

  [e_sorted, ~, e_ind] = unique(encoder);

  i_mean = zeros(length(e_sorted), 1);
  for i = 1:length(e_sorted)
    i_mean(i) = mean(interferometer(e_ind == i));
  end

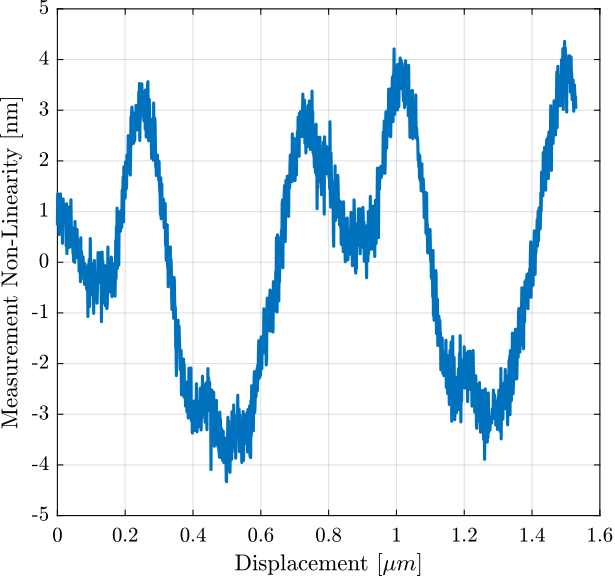
  i_mean_error = (i_mean - e_sorted);

Difference between the two measurement as a function of the measured position by the encoder, averaged for all the cycles

The period of the non-linearity seems to be $1.53 \mu m$ which corresponds to the wavelength of the Laser.

  win_length = 1530; % length of the windows (corresponds to 1.53 um)
  num_avg = floor(length(e_sorted)/win_length); % number of averaging

  i_init = ceil((length(e_sorted) - win_length*num_avg)/2); % does not start at the extremity

  e_sorted_mean_over_period = mean(reshape(i_mean_error(i_init:i_init+win_length*num_avg-1), [win_length num_avg]), 2);

Non-Linearity of the Interferometer over the period of the wavelength

Identification

Load Data

  load('mat/int_enc_id_noise_bis.mat', 'interferometer', 'encoder', 'u', 't');

  interferometer = detrend(interferometer, 0);
  encoder = detrend(encoder, 0);
  u = detrend(u, 0);

Identification

  Ts = 1e-4; % Sampling Time [s]
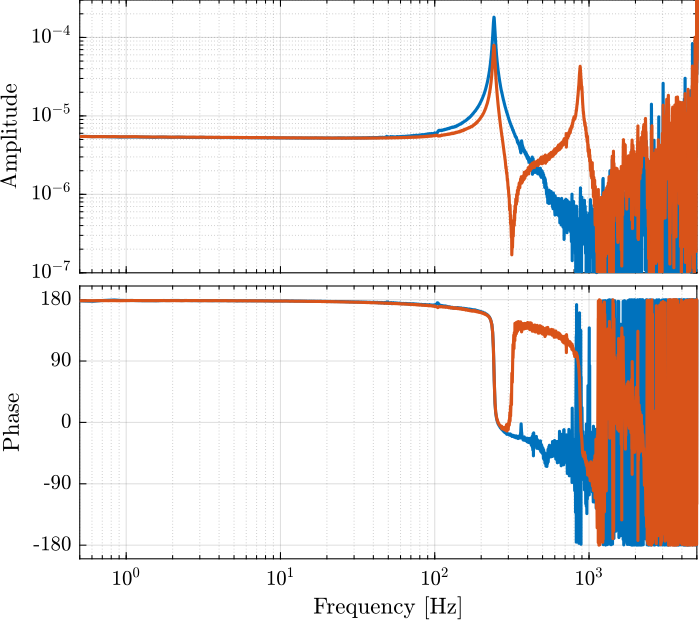
  win = hann(ceil(10/Ts));

  [tf_i_est, f] = tfestimate(u, interferometer, win, [], [], 1/Ts);
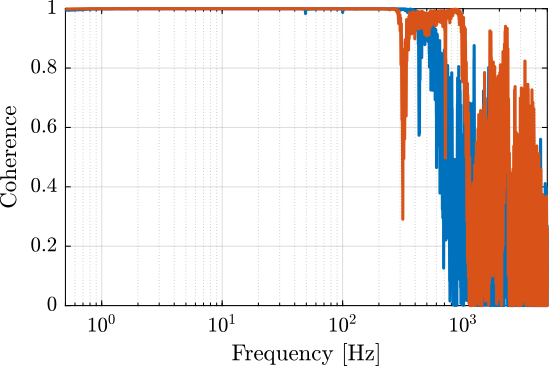
  [co_i_est, ~] = mscohere(u, interferometer, win, [], [], 1/Ts);

  [tf_e_est, ~] = tfestimate(u, encoder, win, [], [], 1/Ts);
  [co_e_est, ~] = mscohere(u, encoder, win, [], [], 1/Ts);