37 KiB
- Introduction
- Complementary filters requirements
- Design formulation using $\mathcal{H}_\infty$ synthesis
- Application: Complementary Filter Design for Active Vibration
- Concluding remarks
- Acknowledgment
Sensor fusion , Optimal filters , $\mathcal{H}_\infty$ synthesis , Vibration isolation , Precision
Introduction
The sensors used for measuring physical quantity often works well within a limited frequency range called as the bandwidth of the sensor. The signals recorded by the sensor beyond its bandwidth are often corrupt with noise and are not reliable. Many dynamical systems require measurements over a wide frequency range. Very often a variety of sensors are utilized to sense the same quantity. These sensors have different operational bandwidth and are reliable only in a particular frequency range. The signals from the different sensors are fused together in order to get the reliable measurement of the physical quantity over wider frequency band. The combining of signals from various sensor is called sensor fusion \cite{hua04_polyp_fir_compl_filter_contr_system}. The resulting sensor is referred as "super sensor" since it can have better noise characteristics and can operate over a wider frequency band as compared to the individual sensor used for merging \cite{shaw90_bandw_enhan_posit_measur_using_measur_accel}.
Sensor fusion is most commonly employed in the navigation systems to accurately measure the position of a vehicle. The GPS sensors, which are accurate in low frequency band, are merged with the high-frequency accelerometers. Zimmermann and Sulzer \cite{zimmermann92_high_bandw_orien_measur_contr} used sensor fusion to measure the orientation of a robot. They merged inclinometer and accelerometers for accurate angular measurements over large frequency band. Corke \cite{corke04_inert_visual_sensin_system_small_auton_helic} merged inertial measurement unit with the stereo vision system for measurement of attitude, height and velocity of an unmanned helicopter. Min and Jeung \cite{min15_compl_filter_desig_angle_estim} used accelerometer and gyroscope for angle estimations. Baerveldt and Klang \cite{baerveldt97} used an inclinometer and a gyroscope to measure the orientation of the autonomous helicopter. The measurement of the 3D orientation using a gyroscope and an accelerometer was demonstrated by Roberts et al. \cite{roberts03_low}. Cao et al. \cite{cao20_adapt_compl_filter_based_post} used sensor fusion to obtain the lateral and longitudinal velocities of the autonomous vehicle.
Sensor fusion is also used for enhancing the working range of the active isolation system. For example, the active vibration isolation system at the Laser Interferometer Gravitational-Wave Observatory (LIGO) \cite{matichard15_seism_isolat_advan_ligo} utilizes sensor fusion. The position sensors, seismometer and geophones are used for measuring the motion of the LIGO platform in different frequency bands \cite{hua05_low_ligo}. Tjepkema et al. \cite{tjepkema12_sensor_fusion_activ_vibrat_isolat_precis_equip} used sensor fusion to isolate precision equipment from the ground motion. The feedback from the accelerometer was used for active isolation at low frequency while force sensor was used at high frequency. Various configurations of sensor fusion for active vibration isolation systems are discussed by Collette and Matichard \cite{collette15_sensor_fusion_method_high_perfor}. Ma and Ghasemi-Nejhad \cite{ma04_frequen_weigh_adapt_contr_simul} used laser sensor and piezoelectric patches for simultaneous tracking and vibration control in smart structures. Recently, Verma et al. \cite{verma21_virtual_sensor_fusion_high_precis_contr} presented virtual sensor fusion for high precision control where the signals from a physical sensor are fused with a sensor simulated virtually.
Fusing signals from different sensors can typically be done using Kalman filtering \cite{odry18_kalman_filter_mobil_robot_attit_estim, ren19_integ_gnss_hub_motion_estim, faria19_sensor_fusion_rotat_motion_recon, liu18_innov_infor_fusion_method_with, abdel15_const_low_cost_gps_filter, biondi17_attit_recov_from_featur_track} or complementary filters \cite{brown72_integ_navig_system_kalman_filter}. A set of filters is said to be complementary if the sum of their transfer functions is equal to one at all frequencies. When two filters are complementary, usually one is a low pass filter while the other is an high pass filter. The complementary filters are designed in such a way that their magnitude is close to one in the bandwidth of the sensor they are combined with. This enables to measure the physical quantity over larger bandwidth. There are two different categories of complementary filters — frequency domain complementary filters and state space complementary filters. Earliest application of the the frequency domain complementary filters was seen in Anderson and Fritze \cite{anderson53_instr_approac_system_steer_comput}. A simple RC circuit was used to physically realize the complementary filters. Frequency domain complementary filters were also used in \cite{shaw90_bandw_enhan_posit_measur_using_measur_accel, zimmermann92_high_bandw_orien_measur_contr, baerveldt97, roberts03_low}. State space complementary filter finds application in tracking orientation of the flexible links in a robot \cite{bachmann03_desig_marg_dof, salcudean91_global_conver_angul_veloc_obser, mahony08_nonlin_compl_filter_special_orthog_group} and are particularly useful for multi-input multi-output systems. Pascoal et al. \cite{pascoal00_navig_system_desig_using_time} presented complementary filters which can adapt with time for navigation system capable of estimating position and velocity using GPS and SONAR sensors.
The noise characteristics of the super sensor are governed by the norms of the complementary filters. Therefore, the proper design of the complementary filters for sensor fusion is of immense importance. The design of complementary filters is a complex task as they need to tuned as per the specification of the sensor. In many applications, analytical formulas of first and second order complementary filters are used \cite{corke04_inert_visual_sensin_system_small_auton_helic,jensen13_basic_uas}. These filters are easy to tune and simple to implement using an analog circuit \cite{moore19_capac_instr_sensor_fusion_high_bandw_nanop,cite:yong16_high_speed_vertic_posit_stage}. However, these low order complementary filters are not optimal, and high order complementary filters can lead to better fusion \cite{jensen13_basic_uas,shaw90_bandw_enhan_posit_measur_using_measur_accel}.
Several design techniques have been proposed to design higher order complementary filters. Pascoal \cite{pascoal00_navig_system_desig_using_time} used linear matrix inequalities (LMIs) \cite{boyd94_linear} for the design of time varying complementary filters. LMIs were also used by Hua et al. \cite{hua04_polyp_fir_compl_filter_contr_system} to design finite impulse response (FIR) filters for the active vibration isolation system at LIGO. Plummer \cite{plummer06_optim_compl_filter_their_applic_motion_measur} proposed an optimal design method using the $\mathcal{H}_{\infty}$ synthesis and weighting functions representing the measurement noise of the sensors.
Although various methods have been presented in the literature for the design of complementary filters, there is a lack of general and simple framework that allows to shape the norm of complementary filters. Such a method would prove to be very useful as the noise of the "supper sensor" and its dynamical characteristics depend on the norm of the filters. This paper presents such a framework based on the $\mathcal{H}_\infty$ norm minimization. The proposed method is quite general and can be easily extended to a case where more than two complementary filters needs to be designed. The organization of this paper is as follows. Section 2 presents the design requirements of ideal complementary filters. It also demonstrates how the noise and robustness characteristics of the "super sensor" can be transformed into upper bounds on the norm of the complementary filters. The framework for the design of complementary filters is detailed in Section 3. This is followed by the application of the design method to complementary filter design for the active vibration isolation at LIGO in Section [[*Application: Complementary Filter Design for Active Vibration Isolation of LIGO][4]]. Finally, concluding remarks are presented in Section 5.
Complementary filters requirements
Introduction ignore
Complementary filters provides a framework for fusing signals from different sensors. As the effectiveness of the fusion depends on the proper design of the complementary filters, they are expected to fulfill certain requirements. These requirements are discussed in this section.
Complementary characteristics
Consider a case where two different sensors are used for measuring the same quantity, $x$ in different frequency range. The inherent dynamics of the sensors is represented by transfer functions $G_1(s)$ and $G_2(s)$. The two sensor also have uncorrelated noise characteristics given by $n_1$ and $n_2$. The signals from these two sensors are fused using complementary filters $H_1(s)$ and $H_2(s)$. The architecture of sensor fusion using complementary filters is shown in Figure 1. The resulting sensor, termed as "super sensor", can have larger bandwidth and better noise characteristics in comparison to the individual sensor. This means that the super sensor provides an estimate $\hat{x}$ of $x$ which can be more accurate over a larger frequency band than the outputs of the individual sensors. Based on Figure 1, the estimate of the physical quantity as measured by the super sensor can be written as $$\label{eq:comp_filter_estimate} \hat{x} = \left(G_1 H_1 + G_2 H_2\right) x + H_1 n_1 + H_2 n_2$$
complementary filters /tdehaeze/dehaeze21_desig_compl_filte/src/commit/1b0883024f57f2b5720cb4931d7dfb7e95943e1b/mohit/figs/fusion_super_sensor.pdf
The complementary property of filters $H_1(s)$ and $H_2(s)$ simply implies that the summation of their transfer functions is equal to unity. That is, unity magnitude and zero phase at all frequencies (filters which satisfies only the magnitude condition are referred as "magnitude complementary filter pair"). Therefore, a pair of strict complementary filter needs to satisfy the following condition.
$$\label{eq:comp_filter} H_1(s) + H_2(s) = 1$$
Noise characterization
In order to compute the noise characteristics associated with the estimate $\hat{x}$, it is first assumed that the dynamics of the individual sensors are perfect: $$\label{eq:perfect_dynamics} G_1(s) = G_2(s) = 1$$
The output of the super sensor, $\hat{x}$, based on the block diagram shown in Figure 1 can be written as $$\label{eq:estimate_perfect_dyn} \hat{x} = x + H_1 n_1 + H_2 n_2$$
The complementary are operating only on the noise component of the individual sensor. Thus, this sensor fusion architecture permits to filter the noise of both sensors without introducing any distortion in the physical quantity to be measured. The estimation error, $\delta x$, of the super sensor can be written as $$\label{eq:estimate_error} \delta x \triangleq \hat{x} - x = H_1 n_1 + H_2 n_2$$
The power spectral density (PSD) of the super sensor's estimation error is given by $$\label{eq:noise_filtering_psd} \Phi_{\delta x} = \left|H_1\right|^2 \Phi_{n_1} + \left|H_2\right|^2 \Phi_{n_2}$$ where, $\Phi_{\delta x}$ is the PSD of estimation error, $\Phi_{n_1}$ and $\Phi_{n_2}$ are the PSDs of the noise associated with the individual sensor. It can be seen that the estimation error's PSD depends on the PSD of the noise in individual sensor as well as the norm of the complementary filters. Therefore, by properly shaping the norm of the complementary filters, it is possible to minimize the noise of the super sensor noise.
Robustness requirements
In the previous subsection, the inherent sensor dynamics were ignored. However in the real system, the sensor dynamics is not equal to unity. In such cases, the output of the sensor is normalized using a filter whose transfer function is equal to the inverse of the sensor dynamics. There are two major concerns in using inversion. First being the sensors may not have been calibrated properly and the actual sensor dynamics is not exactly compensated by the inverse filter. The second problem is that the inversion of sensor dynamics can result in an improper transfer function and hence may not be physically realizable. We here suppose that the sensor dynamics can be inverted using a proper and stable transfer function $\hat{G}_i(s)$. However, we suppose there exists a normalization error since $\hat{G}_i^{-1}(s) G_i(s) \neq 1$. This normalization error can be represented using frequency dependent multiplicative uncertainty (Figure 2). In Figure 2, $\Delta_i(s)$ satisfies $\|\Delta_i(s)\|_\infty \le 1$ and $|w_i(s)|$ is a frequency dependent weighting function that represents the uncertainty corresponding to the normalization error.
normalization error in sensor fusion using multiplicative uncertainty /tdehaeze/dehaeze21_desig_compl_filte/src/commit/1b0883024f57f2b5720cb4931d7dfb7e95943e1b/mohit/figs/sensor_fusion_dynamic_uncertainty.pdf
Based on Figure 2, the super sensor dynamics can be written as $$\label{eq:super_sensor_dyn_uncertainty} \frac{\hat{x}}{x} = 1 + w_1(s) H_1(s) \Delta_1(s) + w_2(s) H_2(s) \Delta_2(s)$$
The dynamics of the super sensor now depends on the weighting functions ($w_1(s),w_2(s)$) and the complementary filters ($H_1(s),H_2(s)$).
The robust stability of the fusion can be studied graphically (refer Figure 3). The frequency response of the fusion output is plotted in a complex plane. The unity transfer function leads to a point $(1,0)$ located on the real axis. The uncertainty associated with first sensor at a particular frequency is represented by a circle with the center at (1,0) and radius $|w_1H_1|$. The uncertainty associated with the second is also represented using a circle centered at any point on the circle representing uncertainty associated with the first sensor and radius equal to $|w_2H_2|$. Therefore, the overall uncertainty of the fusion is represented with a circle centered at (1,0) and radius equal to $|w_1H_1|+|w_2H_2|$. The maximum phase difference that can result from the fusion is found by drawing a tangent from the origin to the uncertainty circle of super sensor. Mathematically, the maximum phase difference at frequency $\omega$ that can result from fusion is given by $$\label{eq:max_phase_uncertainty} \Delta\phi(\omega) = \arcsin\left( |w_1(j\omega) H_1(j\omega)| + |w_2(j\omega) H_2(j\omega)| \right)$$
sensor fusion in the complex plane. The uncertainty associated with the super sensor dynamics are represented with a solid circle while those associated with individual sensors are represented with dashed circles. /tdehaeze/dehaeze21_desig_compl_filte/src/commit/1b0883024f57f2b5720cb4931d7dfb7e95943e1b/mohit/figs/uncertainty_set_super_sensor.pdf
A constraint on the maximum phase difference at a given frequency can be incorporated in the design problem using the following equation: $$\label{eq:max_uncertainty_super_sensor} \max_\omega \big( \left|w_1 H_1\right| + \left|w_2 H_2\right|\big) < \sin\left( \Delta \phi_\text{max} \right)$$ where $\Delta \phi_\text{max}$ is the maximum allowable phase difference. It can also be inferred from the above equation that the magnitude of the complementary filter ($|H_i|$) should be tuned to a smaller value at the frequencies where the magnitude of weighing transfer functions ($|w_i|$) representing sensor uncertainty is large.
Design formulation using $\mathcal{H}_\infty$ synthesis
Introduction ignore
In this section, the shaping of complementary filters is expressed as an optimal $\mathcal{H}_{\infty}$ synthesis problem. The synthesis goal is to shape the frequency response of the filters such that they satisfy the design requirements presented in Section [[*Complementary filters requirements][2]].
Synthesis problem formulation
The first step is to formulate the filter design problem as a generalized plant-controller structure \cite{boyd91_linear}. The generalized plant and controller structure for complementary filters design is shown in Figure 4. In the figure, $P(s)$ is the generalized plant, $u$ is the "control input", $v$ is the "measured output" and $H_2(s)$ is the controller (filter) to be designed. The regulated outputs of the generalized plant, $z_1$ and $z_2$, are given by $$\begin{split} z_1 &= W_1(s)(1-H_2(s)) w = W_1(s) H_1(s) w \text{ by defining } H_{1}(s) \triangleq 1 - H_{2}(s)\\ z_2 &= W_2(s) H_2(s) w \end{split}$$ where $w$ is the "exogenous input" to the plant, $W_1(s), W_2(s)$ are the weighting functions for shaping the complementary filters.
The dynamics of the generalized plant can be written as $$\label{eq:generalized_plant} \begin{bmatrix} z_1 \\ z_2 \\ v \end{bmatrix} = P(s) \begin{bmatrix} w\\u \end{bmatrix}; \quad P(s) = \begin{bmatrix}W_1(s) & -W_1(s) \\ 0 & W_2(s) \\ 1 & 0 \end{bmatrix}$$
The weighting functions are chosen based on the specifications and requirements set for the complementary filters (discussed in Section 3.2). The objective of the optimization is to design a filter $H_2(s)$ such that the following conditions are satisfied $$\label{eq:comp_filter_problem_form}
\begin{split} \left| \frac{z_{1}}{w} \right| &= |1-H_2(s)| \le \frac{1}{|W_1(s)|} \\ \left| \frac{z_{1}}{w} \right| &= |H_2(s)| \le \frac{1}{|W_2(s)|} \end{split}, \quad \forall \omega \in \mathbb{R}^{+}$$ #+caption: [fig:h_infinity_robust_fusion]Generalized plant controller structure for the design of complementary filters file:figs/h_infinity_robust_fusion.pdf Based on Figure #fig:h_infinity_robust_fusion][4, the $\mathcal{H}_{\infty}$ synthesis problem for the complementary filters can be stated as #+begin_quote Find a stable transfer function, $H_2(s)$, which takes measured output, $v$, as input and generates a control input, $u$, such that the $\mathcal{H}_\infty$ norm of the generalized plant from exogenous input, $w$, to the regulated output, ${[z_1,z_2]}^T$ is less than unity. #+end_quote Mathematically, the synthesis objective can be written as $$\begin{split} &\left\|\begin{matrix} \left[1 - H_2(s)\right] W_1(s) \\ H_2(s) W_2(s) \end{matrix}\right\|_\infty \le 1 \\ \Longleftrightarrow & \left\|\begin{matrix} H_1(s) W_1(s) \\ H_2(s) W_2(s) \end{matrix}\right\|_\infty \le 1; \quad H_1(s) \triangleq 1 - H_2(s) \end{split}\label{eq:hinf_syn_obj}$$ The above optimization problem can be efficiently solved in Matlab \cite{MATLAB2009} using Riccati formulae, linear matrix inequality based method or maximum entropy method.
Design of weighting functions
The choice of weighting function governs the shape of the designed complementary filters. Therefore, it is very important that the design specifications are appropriately transformed into the weighting functions. The choice of weighting functions is also constrained by the following factors
- Only proper and stable transfer functions can be used as weighting functions
- As the order of the designed filter is equal to the sum of the orders of the weighting functions, the order of the weighting function needs to be reasonably small to ensure the physical implementation of the designed complementary filters. This also reduces the computational cost of the optimization problem.
- The complementary property of the filter imposes a fundamental limitations on the weighting functions. The imposes a restriction that the magnitude of the filters $H_1(s)$ and $H_2(s)$ cannot be made small simultaneously at the same frequency.
The specifications of the complementary filters are typically expressed using the following parameters — low frequency gain, high frequency gain, slope (order of the filter) and the crossover frequency. We propose a weighting function that allows to translate the above requirements by setting simple parameters: $$\label{eq:weight_formula} W(s) = \displaystyle\left( \frac{ \hfill{} \displaystyle\frac{1}{\omega_0} \sqrt{\frac{1 - \left(\displaystyle\frac{G_0}{G_c}\right)^{\displaystyle\frac{2}{n}}}{1 - {\left(\displaystyle\frac{G_c}{G_\infty}\right)}^{\displaystyle\frac{2}{n}}}} s + \left(\frac{G_0}{G_c}\right)^{\displaystyle\frac{1}{n}} }{ \left(\displaystyle\frac{1}{G_\infty}\right)^{\displaystyle\frac{1}{n}}\displaystyle \frac{1}{\omega_0} \sqrt{\displaystyle\frac{1 - \left(\displaystyle\frac{G_0}{G_c}\right)^{\displaystyle\frac{2}{n}}}{1 - \left(\displaystyle\frac{G_c}{G_\infty}\right)^{\displaystyle\frac{2}{n}}}} s + \left(\displaystyle\frac{1}{G_c}\right)^{\displaystyle\frac{1}{n}} }\right)^n$$ where, $G_0 = \lim_{\omega \to 0} |W(j\omega)|$ is the low frequency gain, $G_\infty = \lim_{\omega \to \infty} |W(j\omega)|$ is the high frequency gain, $\omega_c$ is the crossover frequency, $G_c = |W(j\omega_c)|$ is the absolute gain at the crossover frequency and $n$ is the order of the filter. As an illustration, the magnitude of the frequency response of the weighting function with the parameters $G_0 = 0.001$, $G_\infty = 10$, $\omega_c = \SI{10}{Hz}$, $G_c = 2$, $n = 3$ and having high pass characteristics is shown in Figure 5.
the weighting function obtained using equation [eq:weight_formula] with the parameters $G_0 = 0.001$, $G_\infty = 10$, $\omega_c = \SI{10}{Hz}$, $G_c = 2$, $n = 3$ /tdehaeze/dehaeze21_desig_compl_filte/src/commit/1b0883024f57f2b5720cb4931d7dfb7e95943e1b/mohit/figs/weight_formula.pdf
Verification
The proposed methodology for the design of complementary filters is now applied on the following example.
Example. Design complementary filters with the merging frequency around 10 Hz. The low pass filter should have DC gain of 0.001 and slope -2 above the merging frequency. The high pass filter should have a slope of 3 below the merging frequency and 0.001 high frequency gain.
The first step is to design the weighting functions that translate the above requirements. To do so, equation [eq:weight_formula] is used. The parameters corresponding to $W_1(s)$ and $W_2(s)$ are listed in Table 1. The obtained transfer functions of the weighting functions are $$\begin{split} W_1(s) &= \dfrac{1000 (s+34.55)^2}{(s+3455)^2}\\ W_2(s) &= \dfrac{0.1 (s+87.43)^3}{(s+4.058)^3} \end{split}$$
Using these weighting functions, the generalized plant is evaluated using equation [eq:generalized_plant]. The optimal complementary filters are obtained by solving the optimization problem given by equation [eq:hinf_syn_obj]. The complementary filters obtained after optimization are $$\begin{split} H_1(s) &= \frac{10^{-8} (s+6.6\times 10^9) (s+3450)^2 (s^2 + 49s + 895)}{(s+6.6e^4) (s^2 + 106 s + 3\times 10^3) (s^2 + 72s + 3580)}\\ H_2(s) &= \frac{(s+6.6\times 10^4) (s+160) (s+4)^3}{(s+6.6\times 10^4) (s^2 + 106 s + 3\times 10^3) (s^2 + 72s + 3580)} \end{split}$$
The obtained complementary filters are of order 5 which corresponds to the sum of the orders of the weighting functions used. The frequency responses of the designed complementary filters are shown in Figure 6. It can be seen that the designed filters fulfills all the design specifications and hence demonstrates the effectiveness of the designed methodology (more complex real life example is taken up in Section [[*Application: Complementary Filter Design for Active Vibration Isolation of LIGO][4]]).
<<tab:weights_params>>
| Parameter | $W_1(s)$ | $W_2(s)$ |
|---|---|---|
| $n$ | $2$ | $3$ |
| $G_c$ | $0.5$ | $0.5$ |
| $G_\infty$ | $1000$ | $0.1$ |
| $G_0$ | $0.1$ | $1000$ |
| $\omega_c$ [$\si{Hz}$] | $11$ | $10$ |
functions and designed complementary filters /tdehaeze/dehaeze21_desig_compl_filte/src/commit/1b0883024f57f2b5720cb4931d7dfb7e95943e1b/mohit/figs/hinf_filters_results.pdf
Extension to set of three complementary filters
In certain applications, more than two sensors are used to measure the same quantity and can be merged together to form a "super sensor". In such case, a set of three (or more) complementary filters is required. It is here shown that the proposed method can be generalized for the design of a set of arbitrary number of complementary filters. The control objective is now to design of a set of $n$ complementary filters ($H_i(s), i=1,\cdots,n$) which satisfy the following conditions $$\label{eq:hinf_problem_gen}
\begin{split} &\sum_{i=0}^n H_i(s) = 1 \\ &\left| H_i(s) \right| < \frac{1}{\left| W_i(s) \right|} \end{split}$$ Here, we extend the method to a case of three complementary filters. The generalized plant controller setup for this case is shown in Figure #fig:comp_filter_three_hinf][7. The synthesis objective is to design filters $H_2(s)$ and $H_3(s)$ such that the $\mathcal{H}_\infty$ norm from exogenous input $w$ to regulated output vector $[z_1,z_2,z_3]^T$ is less than unity. That is, $$\label{eq:hinf_syn_obj_three}
\begin{split} &\left\| \begin{matrix} \left[1 - H_2(s) - H_3(s)\right] W_1(s) \\ H_2(s) W_2(s) \\ H_3(s) W_3(s) \end{matrix} \right\|_\infty \le 1\\ \equiv &\left\| \begin{matrix} H_1(s) W_1(s) \\ H_2(s) W_2(s) \\ H_3(s) W_3(s) \end{matrix} \right\|_\infty \le 1; \quad H_1(s) \triangleq 1 - H_2(s) - H_3(s) \end{split}$$
setup for designing a set of three complementary filters using $\mathcal{H}_\infty$ synthesis /tdehaeze/dehaeze21_desig_compl_filte/src/commit/1b0883024f57f2b5720cb4931d7dfb7e95943e1b/mohit/figs/comp_filter_three_hinf.pdf
To validate this synthesis method, let's take an example where 3 sensors are merged together. The three sensors are working in the following three frequency range — below 1 Hz, between 1Hz to 10Hz and above 10Hz. The weighting functions used for the synthesis are $$\begin{split} W_1(s) &= \dfrac{1000 (s+3.141)^2}{(s+314.1)^2}\\ W_2(s) &= \dfrac{2200 (s+62.83)^2 (s+6.283)^2}{(s+6283)^2 (s+0.06283)^2}\\ W_3(s) &= \dfrac{0.1 (s+87.43)^3}{(s+4.058)^3} \end{split}$$ The complementary filters are obtained by solving the optimization problem given by equation [eq:hinf_syn_obj_three]. The frequency response of the designed filters and the weighting functions are shown in Figure 8.
weighting functions and designed set of three complementary filters /tdehaeze/dehaeze21_desig_compl_filte/src/commit/1b0883024f57f2b5720cb4931d7dfb7e95943e1b/mohit/figs/three_complementary_filters_results.pdf
Application: Complementary Filter Design for Active Vibration
Introduction ignore
Isolation of LIGO Gravitational waves can help in detection various astrophysical events occurring in our universe. This can also pave a path to validate theories built around the existence of gravitational waves. However, the detection of these waves is an arduous task owing to the extraordinary small strain experienced by the earth due to gravitational waves. Various methods have been proposed for their detection, out of which laser interferometers are the most popular ones. Laser interferometers offers large projection range and high displacement sensitivity. Among the existing detector, Laser interferometer gravitation-wave observatory (LIGO) is the most sensitive operational detector. LIGO consists of two longs arms, referred as beam tubes, that are placed orthogonal to each other. The arms of the LIGO accommodates a Michleson interferometer with a cavity (Fabry-Perot). The mirrors at the extremity of the cavity serve as inertial test masses which responds to the strain induced due to the gravitational waves. The optics of the LIGO are suspended like a pendulum. The schematics of the LIGO are shown in Figure 9.
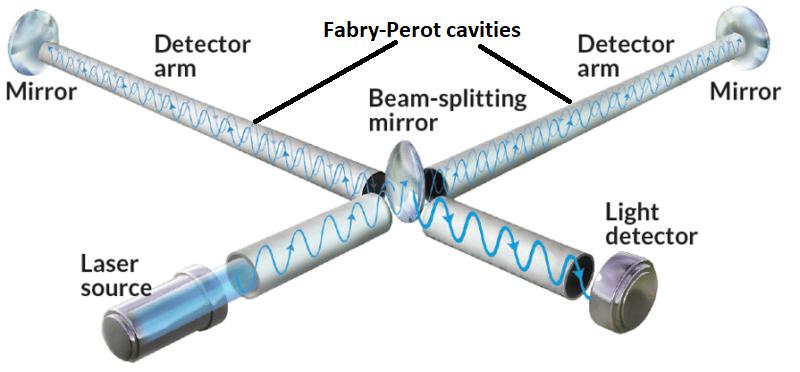
The isolation of the terrestrial interferometers is necessary in order to isolate the motion of the suspended inertial masses from the seismic ground motion. The vibration isolation system attenuates the effect of disturbances on the motion of the suspended masses in the gravitational wave band. The other sources that can affect the sensitivity of the LIGO are thermal noise, human activities, tidal motion etc. The suspensions of the LIGO needs to serve two purpose — isolation and alignment. The alignment is also important in order to ensure that the interferometer beam is targeted at the center of the suspended mass. The current vibration isolation system for LIGO has seven different stages. In the first stage, hydraulically actuated external pre-isolators are used for attenuating large ground motions. Two stages of active electromagnetic isolation system are placed next to pre-isolators. This is followed by four stages of pendulum based passive isolation system.
In the active isolation stage of LIGO, different sensors are used to sense the same physical signal in different frequency range. For example, seismometers are used to sense the position of the platform in the frequency band 0.5–10 Hz while geophones are employed above 10 Hz. The signals recorded from different sensor are fused using complementary filters \cite{hua05_low_ligo,hua04_polyp_fir_compl_filter_contr_system}. The stringent requirements on these filters complicate their design. Hua \cite{hua05_low_ligo} proposed complementary FIR filters which were synthesized using convex optimization. The designed FIR filters were found to be compliant with the design specifications. However, the order of the designed filter was very high, which limits its application to a practical system. In this section, we demonstrate the design of complementary filters with the same specification using the proposed method based on $\mathcal{H}_\infty$- synthesis.
Design specifications
The design specification of the complementary filters (as listed out in \cite{hua05_low_ligo}) are as follows:
- In the frequency range $0$-$\SI{0.008}{Hz}$: the high pass filter's magnitude should be less than $8 \times 10^{-4}$.
- For frequency range $\SI{0.008}{Hz}$-$\SI{0.04}{Hz}$: slope of the high pass filter is equal to three.
- Between $\SI{0.04}{Hz}$-$\SI{0.1}{Hz}$ frequency range: the high pass filter's magnitude should be less than $3$.
- For frequencies above $\SI{0.1}{Hz}$: the low pass filter's magnitude should be less than $0.045$.
The specification of the complementary filters are shown graphically by dashed black lines in Figure 10.
Weighting Functions Design
As the synthesis objective of the complementary filters is described by Eq. [eq:hinf_problem_gen], it is clear that the weighting functions should be chosen such that their inverse magnitude represent the maximum allowed norm of the complementary filters. This can be done manually using by combining poles and zeros or using useful formulas such as Eq. [eq:weight_formula]. It is important to note that the order of the filters should be kept reasonable small in order to keep the computational cost of the optimization reasonable. This will also ensure that the designed filters are realizable in the physical world. The transfer function representing weights should also be stable and minimum phase.
The weighting function corresponding to the low pass filter, $w_L(s)$, is here taken as Type I Chebyshev filter. The order of the weighting function for low pass filter is set as 20.
The weighting function for the high pass filter, $w_H(s)$, is designed in such a way that its magnitude response is as close as possible to the design specifications. This was achieved using a combination of high-, low- and band-pass filters in the particular frequency band. The overall order of the weighting function for high pass filter is 7.
The magnitude responses of the inverse of the designed weighting functions and their comparison with the specifications are shown in Figure 10. It can be seen that the inverse of the designed weights, shown in solid blue line for high pass filter and solid red line for low pass filter, are close to the specifications shown in black dotted line.
$\mathcal{H}_\infty$ synthesis of complementary filters
The complementary filters are designed using $\mathcal{H}_\infty$ synthesis based on the architecture shown in Figure 4. The generalized plant is obtained by substituting the transfer functions of the designed weighting functions in equation [eq:generalized_plant], i.e., $W_1(s)=w_H(s)$ and $W_2(s)=w_L(s)$. The objective of the $\mathcal{H}_\infty$ synthesis is given by equation [eq:hinf_syn_obj]. The optimization problem in solved in Matlab \cite{MATLAB2009} using Ricatti method. The frequency responses of the designed optimal complementary filters are shown in Figure 11. The order of the filters obtained using $\mathcal{H}_\infty$ optimization is $27$.
Now, we compare the designed complementary filters with the FIR filters designed by Hua \cite{hua05_low_ligo}. The transfer function of the FIR filter, $G(\omega)$, is the Fourier transform of its coefficients, $g(n)$. That is, $$G(\omega) = \sum_n g(n)e^{-j2n\pi\omega}$$ The FIR filter synthesis was formulated as a convex optimization problem. The objective of the optimization problem was to find the filter's coefficients such that their norm are below the specified upper bounds. The optimization problem was solved using SeDuMi \cite{sturm99_using_sedum} and the obtained order for the FIR filters is $512$. The bode plot of the FIR filters are shown with dotted lines in Figure 11. It can be seen that frequency responses of the designed complementary filters matches quite well with those of the FIR filters. The designed complementary filters are of much lower order and can be implemented with less computational cost can the FIR filters. The proposed methodology for the design of complementary filters can be effectively employed to obtain physically realizable filters.
using $\mathcal{H}_\infty$ synthesis and FIR filters \cite{hua05_low_ligo} /tdehaeze/dehaeze21_desig_compl_filte/src/commit/1b0883024f57f2b5720cb4931d7dfb7e95943e1b/mohit/figs/comp_fir_ligo_hinf.pdf
Concluding remarks
The measurements from the sensors are reliable only within its bandwidth. The signals from different sensors are usually fused in order to measure a physical quantity over larger bandwidth. The sensor obtained after fusion is called as super sensor as it has superior noise characteristics and wider bandwidth. Complementary filters are used for the combining the signals from different sensors. A new framework based on $\mathcal{H}_\infty$ synthesis has been presented in this paper to aid the design of complementary filters. The method presented allows to shape the complementary filters based on the design specifications. The task of filter design is posed as an $\mathcal{H}_{\infty}$ synthesis problem. The design specifications of the systems are transformed in the form of weighting functions. These weighting functions are used in the optimization problem to constraint the filter response in a frequency band. The method has also been demonstrated for designing a set of three complementary filters. The design frame is general, simple to implement and can easily be extended to difference scenarios of sensor fusion. The effectiveness of the method is demonstrated for a real life application where complementary filters are designed for active vibration isolation of Laser Interferometer Gravitational-Wave Observatory (LIGO). The filters designed with the proposed method have been with compared with the finite impulse response (FIR) filters. It was found that the filters designed using $\mathcal{H}_\infty$ have lower order compared to FIR filters. The designed filters are physically realizable and have lesser computational cost compared to FIR filters. The proposed method can be effectively used to shape complementary filters based on design specifications. The method can be further be extended for the design of robust complementary filters with desired noise characteristics considering uncertainties in the sensor dynamics. This is the focus of our future research.
Acknowledgment
The authors would like to acknowledge the help received from the French Community of Belgium for funding the FRIA Grant of Thomas Dehaeze (Grant No. FC 31597).