60 KiB
Robust and Optimal Sensor Fusion - Matlab Computation
- Introduction
- Sensor Description
- Introduction to Sensor Fusion
- Optimal Super Sensor Noise: $\mathcal{H}_2$ Synthesis
- Robust Sensor Fusion: $\mathcal{H}_\infty$ Synthesis
- Optimal and Robust Sensor Fusion: Mixed $\mathcal{H}_2/\mathcal{H}_\infty$ Synthesis
- Matlab Functions
- Bibliography
Introduction ignore
This document is arranged as follows:
- Section sec:sensor_description: the sensors are described (dynamics, uncertainty, noise)
- Section sec:introduction_sensor_fusion: the sensor fusion architecture is described and the super sensor noise and dynamical uncertainty are derived
- Section sec:optimal_comp_filters: the $\mathcal{H}_2$ synthesis is used to design complementary filters such that the RMS value of the super sensor's noise is minimized
- Section sec:comp_filter_robustness: the $\mathcal{H}_\infty$ synthesis is used to design complementary filters such that the super sensor's uncertainty is bonded to acceptable values
- Section sec:mixed_synthesis_sensor_fusion: the mixed $\mathcal{H}_2/\mathcal{H}_\infty$ synthesis is used to both limit the super sensor's uncertainty and to lower the RMS value of the super sensor's noise
- Section sec:matlab_functions: Matlab functions used for the analysis are described
Sensor Description
<<sec:sensor_description>>
Introduction ignore
In Figure fig:sensor_model_noise_uncertainty is shown a schematic of a sensor model that is used in the following study. In this example, the measured quantity $x$ is the velocity of an object.
| Notation | Meaning | Unit |
|---|---|---|
| $x$ | Physical measured quantity | $[m/s]$ |
| $\tilde{n}_i$ | White noise with unitary PSD | |
| $n_i$ | Shaped noise | $[m/s]$ |
| $v_i$ | Sensor output measurement | $[V]$ |
| $\hat{x}_i$ | Estimate of $x$ from the sensor | $[m/s]$ |
| $\Phi_n(\omega)$ | Power Spectral Density of $n$ | $[\frac{(m/s)^2}{Hz}]$ |
| $\phi_n(\omega)$ | Amplitude Spectral Density of $n$ | $[\frac{m/s}{\sqrt{Hz}}]$ |
| $\sigma_n$ | Root Mean Square Value of $n$ | $[m/s\ rms]$ |
| Notation | Meaning | Unit |
|---|---|---|
| $\hat{G}_i$ | Nominal Sensor Dynamics | $[\frac{V}{m/s}]$ |
| $W_i$ | Weight representing the size of the uncertainty at each frequency | |
| $\Delta_i$ | Any complex perturbation such that $\vert\vert\Delta_i\vert\vert_\infty < 1$ | |
| $N_i$ | Weight representing the sensor noise | $[m/s]$ |

Sensor Dynamics
<<sec:sensor_dynamics>> Let's consider two sensors measuring the velocity of an object.
The first sensor is an accelerometer. Its nominal dynamics $\hat{G}_1(s)$ is defined below.
m_acc = 0.01; % Inertial Mass [kg]
c_acc = 5; % Damping [N/(m/s)]
k_acc = 1e5; % Stiffness [N/m]
g_acc = 1e5; % Gain [V/m]
G1 = g_acc*m_acc*s/(m_acc*s^2 + c_acc*s + k_acc); % Accelerometer Plant [V/(m/s)]The second sensor is a displacement sensor, its nominal dynamics $\hat{G}_2(s)$ is defined below.
w_pos = 2*pi*2e3; % Measurement Banwdith [rad/s]
g_pos = 1e4; % Gain [V/m]
G2 = g_pos/s/(1 + s/w_pos); % Position Sensor Plant [V/(m/s)]These nominal dynamics are also taken as the model of the sensor dynamics. The true sensor dynamics has some uncertainty associated to it and described in section sec:sensor_uncertainty.
Both sensor dynamics in $[\frac{V}{m/s}]$ are shown in Figure fig:sensors_nominal_dynamics.

Sensor Model Uncertainty
<<sec:sensor_uncertainty>> The uncertainty on the sensor dynamics is described by multiplicative uncertainty (Figure fig:sensor_model_noise_uncertainty).
The true sensor dynamics $G_i(s)$ is then described by eqref:eq:sensor_dynamics_uncertainty.
\begin{equation} G_i(s) = \hat{G}_i(s) \left( 1 + W_i(s) \Delta_i(s) \right); \quad |\Delta_i(j\omega)| < 1 \forall \omega \label{eq:sensor_dynamics_uncertainty} \end{equation}The weights $W_i(s)$ representing the dynamical uncertainty are defined below and their magnitude is shown in Figure fig:sensors_uncertainty_weights.
W1 = createWeight('n', 2, 'w0', 2*pi*3, 'G0', 2, 'G1', 0.1, 'Gc', 1) * ...
createWeight('n', 2, 'w0', 2*pi*1e3, 'G0', 1, 'G1', 4/0.1, 'Gc', 1/0.1);
W2 = createWeight('n', 2, 'w0', 2*pi*1e2, 'G0', 0.05, 'G1', 4, 'Gc', 1);The bode plot of the sensors nominal dynamics as well as their defined dynamical spread are shown in Figure fig:sensors_nominal_dynamics_and_uncertainty.


Sensor Noise
<<sec:sensor_noise>> The noise of the sensors $n_i$ are modelled by shaping a white noise with unitary PSD $\tilde{n}_i$ eqref:eq:unitary_noise_psd with a LTI transfer function $N_i(s)$ (Figure fig:sensor_model_noise_uncertainty).
\begin{equation} \Phi_{\tilde{n}_i}(\omega) = 1 \label{eq:unitary_noise_psd} \end{equation}The Power Spectral Density of the sensor noise $\Phi_{n_i}(\omega)$ is then computed using eqref:eq:sensor_noise_shaping and expressed in $[\frac{(m/s)^2}{Hz}]$.
\begin{equation} \Phi_{n_i}(\omega) = \left| N_i(j\omega) \right|^2 \Phi_{\tilde{n}_i}(\omega) \label{eq:sensor_noise_shaping} \end{equation}The weights $N_1$ and $N_2$ representing the amplitude spectral density of the sensor noises are defined below and shown in Figure fig:sensors_noise.
omegac = 0.15*2*pi; G0 = 1e-1; Ginf = 1e-6;
N1 = (Ginf*s/omegac + G0)/(s/omegac + 1)/(1 + s/2/pi/1e4);
omegac = 1000*2*pi; G0 = 1e-6; Ginf = 1e-3;
N2 = (Ginf*s/omegac + G0)/(s/omegac + 1)/(1 + s/2/pi/1e4);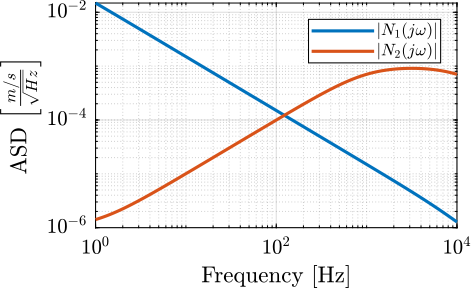
Save Model
All the dynamical systems representing the sensors are saved for further use.
save('./mat/model.mat', 'freqs', 'G1', 'G2', 'N2', 'N1', 'W2', 'W1');Introduction to Sensor Fusion
<<sec:introduction_sensor_fusion>>
Sensor Fusion Architecture
<<sec:sensor_fusion_architecture>>
The two sensors presented in Section sec:sensor_description are now merged together using complementary filters $H_1(s)$ and $H_2(s)$ to form a super sensor (Figure fig:sensor_fusion_noise_arch).

The complementary property of $H_1(s)$ and $H_2(s)$ means that the sum of their transfer function is equal to $1$ eqref:eq:complementary_property.
\begin{equation} H_1(s) + H_2(s) = 1 \label{eq:complementary_property} \end{equation}The super sensor estimate $\hat{x}$ is given by eqref:eq:super_sensor_estimate.
\begin{equation} \hat{x} = \left( H_1 \hat{G}_1^{-1} G_1 + H_2 \hat{G}_2^{-1} G_2 \right) x + \left( H_1 \hat{G}_1^{-1} G_1 N_1 \right) \tilde{n}_1 + \left( H_2 \hat{G}_2^{-1} G_2 N_2 \right) \tilde{n}_2 \label{eq:super_sensor_estimate} \end{equation}Super Sensor Noise
<<sec:super_sensor_noise>>
If we first suppose that the models of the sensors $\hat{G}_i$ are very close to the true sensor dynamics $G_i$ eqref:eq:good_dynamical_model, we have that the super sensor estimate $\hat{x}$ is equals to the measured quantity $x$ plus the noise of the two sensors filtered out by the complementary filters eqref:eq:estimate_perfect_models.
\begin{equation} \hat{G}_i^{-1}(s) G_i(s) \approx 1 \label{eq:good_dynamical_model} \end{equation} \begin{equation} \hat{x} = x + \underbrace{\left( H_1 N_1 \right) \tilde{n}_1 + \left( H_2 N_2 \right) \tilde{n}_2}_{n} \label{eq:estimate_perfect_models} \end{equation}As the noise of both sensors are considered to be uncorrelated, the PSD of the super sensor noise is computed as follow:
\begin{equation} \Phi_n(\omega) = \left| H_1(j\omega) N_1(j\omega) \right|^2 + \left| H_2(j\omega) N_2(j\omega) \right|^2 \label{eq:super_sensor_psd_noise} \end{equation}And the Root Mean Square (RMS) value of the super sensor noise $\sigma_n$ is given by Equation eqref:eq:super_sensor_rms_noise.
\begin{equation} \sigma_n = \sqrt{\int_0^\infty \Phi_n(\omega) d\omega} \label{eq:super_sensor_rms_noise} \end{equation}Super Sensor Dynamical Uncertainty
<<sec:super_sensor_dynamical_uncertainty>>
If we consider some dynamical uncertainty (the true system dynamics $G_i$ not being perfectly equal to our model $\hat{G}_i$) that we model by the use of multiplicative uncertainty (Figure fig:sensor_model_uncertainty), the super sensor dynamics is then equals to:
\begin{equation} \begin{aligned} \frac{\hat{x}}{x} &= \Big( H_1 \hat{G}_1^{-1} \hat{G}_1 (1 + W_1 \Delta_1) + H_2 \hat{G}_2^{-1} \hat{G}_2 (1 + W_2 \Delta_2) \Big) \\ &= \Big( H_1 (1 + W_1 \Delta_1) + H_2 (1 + W_2 \Delta_2) \Big) \\ &= \left( 1 + H_1 W_1 \Delta_1 + H_2 W_2 \Delta_2 \right), \quad \|\Delta_i\|_\infty<1 \end{aligned} \end{equation}
The uncertainty set of the transfer function from $\hat{x}$ to $x$ at frequency $\omega$ is bounded in the complex plane by a circle centered on 1 and with a radius equal to $|W_1(j\omega) H_1(j\omega)| + |W_2(j\omega) H_2(j\omega)|$ as shown in Figure fig:uncertainty_set_super_sensor.

Optimal Super Sensor Noise: $\mathcal{H}_2$ Synthesis
<<sec:optimal_comp_filters>>
Introduction ignore
In this section, the complementary filters $H_1(s)$ and $H_2(s)$ are designed in order to minimize the RMS value of super sensor noise $\sigma_n$.
The RMS value of the super sensor noise is (neglecting the model uncertainty):
\begin{equation} \begin{aligned} \sigma_{n} &= \sqrt{\int_0^\infty |H_1(j\omega) N_1(j\omega)|^2 + |H_2(j\omega) N_2(j\omega)|^2 d\omega} \\ &= \left\| \begin{matrix} H_1 N_1 \\ H_2 N_2 \end{matrix} \right\|_2 \end{aligned} \end{equation}The goal is to design $H_1(s)$ and $H_2(s)$ such that $H_1(s) + H_2(s) = 1$ (complementary property) and such that $\left\| \begin{matrix} H_1 N_1 \\ H_2 N_2 \end{matrix} \right\|_2$ is minimized (minimized RMS value of the super sensor noise). This is done using the $\mathcal{H}_2$ synthesis in Section sec:H2_synthesis.
$\mathcal{H}_2$ Synthesis
<<sec:H2_synthesis>>
Consider the generalized plant $P_{\mathcal{H}_2}$ shown in Figure fig:h_two_optimal_fusion and described by Equation eqref:eq:H2_generalized_plant.

\begin{equation} \label{eq:H2_generalized_plant}
\begin{pmatrix} z_1 \\ z_2 \\ v \end{pmatrix} = \underbrace{\begin{bmatrix} N_1 & -N_1 \\ 0 & N_2 \\ 1 & 0 \end{bmatrix}}_{P_{\mathcal{H}_2}} \begin{pmatrix} w \\ u \end{pmatrix}\end{equation}
Applying the $\mathcal{H}_2$ synthesis on $P_{\mathcal{H}_2}$ will generate a filter $H_2(s)$ such that the $\mathcal{H}_2$ norm from $w$ to $(z_1,z_2)$ which is actually equals to $\sigma_n$ by defining $H_1(s) = 1 - H_2(s)$:
\begin{equation} \left\| \begin{matrix} z_1/w \\ z_2/w \end{matrix} \right\|_2 = \left\| \begin{matrix} N_1 (1 - H_2) \\ N_2 H_2 \end{matrix} \right\|_2 = \sigma_n \quad \text{with} \quad H_1(s) = 1 - H_2(s) \end{equation}We then have that the $\mathcal{H}_2$ synthesis applied on $P_{\mathcal{H}_2}$ generates two complementary filters $H_1(s)$ and $H_2(s)$ such that the RMS value of super sensor noise is minimized.
The generalized plant $P_{\mathcal{H}_2}$ is defined below
PH2 = [N1 -N1;
0 N2;
1 0];
The $\mathcal{H}_2$ synthesis using the h2syn command
[H2, ~, gamma] = h2syn(PH2, 1, 1);Finally, $H_1(s)$ is defined as follows
H1 = 1 - H2;The obtained complementary filters are shown in Figure fig:htwo_comp_filters.

Super Sensor Noise
<<sec:H2_super_sensor_noise>>
The Power Spectral Density of the individual sensors' noise $\Phi_{n_1}, \Phi_{n_2}$ and of the super sensor noise $\Phi_{n_{\mathcal{H}_2}}$ are computed below.
PSD_S1 = abs(squeeze(freqresp(N1, freqs, 'Hz'))).^2;
PSD_S2 = abs(squeeze(freqresp(N2, freqs, 'Hz'))).^2;
PSD_H2 = abs(squeeze(freqresp(N1*H1, freqs, 'Hz'))).^2 + ...
abs(squeeze(freqresp(N2*H2, freqs, 'Hz'))).^2;The obtained ASD are shown in Figure fig:psd_sensors_htwo_synthesis.
The RMS value of the individual sensors and of the super sensor are listed in Table tab:rms_noise_H2.
| RMS value $[m/s]$ | |
|---|---|
| $\sigma_{n_1}$ | 0.015 |
| $\sigma_{n_2}$ | 0.080 |
| $\sigma_{n_{\mathcal{H}_2}}$ | 0.003 |

A time domain simulation is now performed. The measured velocity $x$ is set to be a sweep sine with an amplitude of $0.1\ [m/s]$. The velocity estimates from the two sensors and from the super sensors are shown in Figure fig:super_sensor_time_domain_h2. The resulting noises are displayed in Figure fig:sensor_noise_H2_time_domain.


Discrepancy between sensor dynamics and model
If we consider sensor dynamical uncertainty as explained in Section sec:sensor_uncertainty, we can compute what would be the super sensor dynamical uncertainty when using the complementary filters obtained using the $\mathcal{H}_2$ Synthesis.
The super sensor dynamical uncertainty is shown in Figure fig:super_sensor_dynamical_uncertainty_H2.
It is shown that the phase uncertainty is not bounded between 100Hz and 200Hz. As a result the super sensor signal can not be used for feedback applications about 100Hz.

Robust Sensor Fusion: $\mathcal{H}_\infty$ Synthesis
<<sec:comp_filter_robustness>>
Introduction ignore
We initially considered perfectly known sensor dynamics so that it can be perfectly inverted.
We now take into account the fact that the sensor dynamics is only partially known. To do so, we model the uncertainty that we have on the sensor dynamics by multiplicative input uncertainty as shown in Figure fig:sensor_fusion_arch_uncertainty.

As explained in Section sec:sensor_uncertainty, at each frequency $\omega$, the dynamical uncertainty of the super sensor can be represented in the complex plane by a circle with a radius equals to $|H_1(j\omega) W_1(j\omega)| + |H_2(j\omega) W_2(j\omega)|$ and centered on 1.
In order to specify a wanted upper bound on the dynamical uncertainty, a weight $W_u(s)$ is used where $1/|W_u(j\omega)|$ represents the maximum allowed radius of the uncertainty circle corresponding to the super sensor dynamics at a frequency $\omega$ eqref:eq:upper_bound_uncertainty.
\begin{align} & |H_1(j\omega) W_1(j\omega)| + |H_2(j\omega) W_2(j\omega)| < \frac{1}{|W_u(j\omega)|}, \quad \forall \omega \label{eq:upper_bound_uncertainty} \\ \Leftrightarrow & |H_1(j\omega) W_1(j\omega) W_u(j\omega)| + |H_2(j\omega) W_2(j\omega) W_u(j\omega)| < 1, \quad \forall\omega \label{eq:upper_bound_uncertainty_bis} \end{align}$|W_u(j\omega)|$ is also linked to the gain uncertainty $\Delta G$ eqref:eq:gain_uncertainty_bound and phase uncertainty $\Delta\phi$ eqref:eq:phase_uncertainty_bound of the super sensor.
\begin{align} \Delta G (\omega) &\le \frac{1}{|W_u(j\omega)|}, \quad \forall\omega \label{eq:gain_uncertainty_bound} \\ \Delta \phi (\omega) &\le \arcsin\left(\frac{1}{|W_u(j\omega)|}\right), \quad \forall\omega \label{eq:phase_uncertainty_bound} \end{align}The choice of $W_u$ is presented in Section sec:weight_uncertainty.
Condition eqref:eq:upper_bound_uncertainty_bis can almost be represented by eqref:eq:hinf_norm_uncertainty (within a factor $\sqrt{2}$).
\begin{equation} \left\| \begin{matrix} H_1(s) W_1(s) W_u(s) \\ H_2(s) W_2(s) W_u(s) \end{matrix} \right\|_\infty < 1 \label{eq:hinf_norm_uncertainty} \end{equation}The objective is to design $H_1(s)$ and $H_2(s)$ such that $H_1(s) + H_2(s) = 1$ (complementary property) and such that eqref:eq:hinf_norm_uncertainty is verified (bounded dynamical uncertainty).
This is done using the $\mathcal{H}_\infty$ synthesis in Section sec:Hinfinity_synthesis.
Weighting Function used to bound the super sensor uncertainty
<<sec:weight_uncertainty>>
$W_u(s)$ is defined such that the super sensor phase uncertainty is less than 10 degrees below 100Hz eqref:eq:phase_uncertainy_bound_low_freq and is less than 180 degrees below 400Hz eqref:eq:phase_uncertainty_max.
\begin{align} \frac{1}{|W_u(j\omega)|} &< \sin\left(10 \frac{\pi}{180}\right), \quad \omega < 100\,\text{Hz} \label{eq:phase_uncertainy_bound_low_freq} \\ \frac{1}{|W_u(j 2 \pi 400)|} &< 1 \label{eq:phase_uncertainty_max} \end{align}The uncertainty bounds of the two individual sensor as well as the wanted maximum uncertainty bounds of the super sensor are shown in Figure fig:weight_uncertainty_bounds_Wu.
Dphi = 10; % [deg]
Wu = createWeight('n', 2, 'w0', 2*pi*4e2, 'G0', 1/sin(Dphi*pi/180), 'G1', 1/4, 'Gc', 1);
$\mathcal{H}_\infty$ Synthesis
<<sec:Hinfinity_synthesis>>
The generalized plant $P_{\mathcal{H}_\infty}$ used for the $\mathcal{H}_\infty$ Synthesis of the complementary filters is shown in Figure fig:h_infinity_robust_fusion and is described by Equation eqref:eq:Hinf_generalized_plant.

\begin{equation} \label{eq:Hinf_generalized_plant}
\begin{pmatrix} z_1 \\ z_2 \\ v \end{pmatrix} = \underbrace{\begin{bmatrix} W_u W_1 & -W_u W_1 \\ 0 & W_u W_2 \\ 1 & 0 \end{bmatrix}}_{P_{\mathcal{H}_\infty}} \begin{pmatrix} w \\ u \end{pmatrix}\end{equation}
The generalized plant is defined below.
P = [Wu*W1 -Wu*W1;
0 Wu*W2;
1 0];
And the $\mathcal{H}_\infty$ synthesis is performed using the hinfsyn command.
H2 = hinfsyn(P, 1, 1,'TOLGAM', 0.001, 'DISPLAY', 'on'); Test bounds: 0.7071 <= gamma <= 1.291
gamma X>=0 Y>=0 rho(XY)<1 p/f
9.554e-01 0.0e+00 0.0e+00 3.529e-16 p
8.219e-01 0.0e+00 0.0e+00 5.204e-16 p
7.624e-01 3.8e-17 0.0e+00 1.955e-15 p
7.342e-01 0.0e+00 0.0e+00 5.612e-16 p
7.205e-01 0.0e+00 0.0e+00 7.184e-16 p
7.138e-01 0.0e+00 0.0e+00 0.000e+00 p
7.104e-01 4.1e-16 0.0e+00 6.749e-15 p
7.088e-01 0.0e+00 0.0e+00 2.794e-15 p
7.079e-01 0.0e+00 0.0e+00 6.503e-16 p
7.075e-01 0.0e+00 0.0e+00 4.302e-15 p
Best performance (actual): 0.7071
The $\mathcal{H}_\infty$ is successful as the $\mathcal{H}_\infty$ norm of the "closed loop" transfer function from $(w)$ to $(z_1,\ z_2)$ is less than one.
$H_1(s)$ is then defined as the complementary of $H_2(s)$.
H1 = 1 - H2;The obtained complementary filters as well as the wanted upper bounds are shown in Figure fig:hinf_comp_filters.

Super sensor uncertainty
The super sensor dynamical uncertainty is displayed in Figure fig:super_sensor_dynamical_uncertainty_Hinf. It is confirmed that the super sensor dynamical uncertainty is less than the maximum allowed uncertainty defined by the norm of $W_u(s)$.
The $\mathcal{H}_\infty$ synthesis thus allows to design filters such that the super sensor has specified bounded uncertainty.

Super sensor noise
We now compute the obtain Power Spectral Density of the super sensor's noise. The Amplitude Spectral Densities are shown in Figure fig:psd_sensors_hinf_synthesis.
PSD_S2 = abs(squeeze(freqresp(N2, freqs, 'Hz'))).^2;
PSD_S1 = abs(squeeze(freqresp(N1, freqs, 'Hz'))).^2;
PSD_Hinf = abs(squeeze(freqresp(N1*H1, freqs, 'Hz'))).^2 + ...
abs(squeeze(freqresp(N2*H2, freqs, 'Hz'))).^2;The obtained RMS of the super sensor noise in the $\mathcal{H}_2$ and $\mathcal{H}_\infty$ case are shown in Table tab:rms_noise_comp_H2_Hinf. As expected, the super sensor obtained from the $\mathcal{H}_\infty$ synthesis is much noisier than the super sensor obtained from the $\mathcal{H}_2$ synthesis.

| RMS [m/s] | |
|---|---|
| Optimal: $\mathcal{H}_2$ | 0.0027 |
| Robust: $\mathcal{H}_\infty$ | 0.041 |
Conclusion
Using the $\mathcal{H}_\infty$ synthesis, the dynamical uncertainty of the super sensor can be bounded to acceptable values.
However, the RMS of the super sensor noise is not optimized as it was the case with the $\mathcal{H}_2$ synthesis
Optimal and Robust Sensor Fusion: Mixed $\mathcal{H}_2/\mathcal{H}_\infty$ Synthesis
<<sec:mixed_synthesis_sensor_fusion>>
Introduction ignore
The (optima) $\mathcal{H}_2$ synthesis and the (robust) $\mathcal{H}_\infty$ synthesis are now combined to form an Optimal and Robust synthesis of complementary filters for sensor fusion.
The sensor fusion architecture is shown in Figure fig:sensor_fusion_arch_full ($\hat{G}_i$ are omitted for space reasons).

The goal is to design complementary filters such that:
- the maximum uncertainty of the super sensor is bounded to acceptable values (defined by $W_u(s)$)
- the RMS value of the super sensor noise is minimized
To do so, we can use the Mixed $\mathcal{H}_2/\mathcal{H}_\infty$ Synthesis presented in Section sec:H2_Hinf_synthesis.
Mixed $\mathcal{H}_2$ / $\mathcal{H}_\infty$ Synthesis
<<sec:H2_Hinf_synthesis>>
The synthesis architecture that is used here is shown in Figure fig:mixed_h2_hinf_synthesis.
The filter $H_2(s)$ is synthesized such that it:
- keeps the $\mathcal{H}_\infty$ norm of the transfer function from $w$ to $z_{\mathcal{H}_\infty}$ bellow some specified value
- minimizes the $\mathcal{H}_2$ norm of the transfer function from $w$ to $z_{\mathcal{H}_2}$

Let's see that with $H_1(s)= 1 - H_2(s)$
\begin{align} \left\| \frac{z_\infty}{w} \right\|_\infty &= \left\| \begin{matrix}H_1(s) W_1(s) W_u(s)\\ H_2(s) W_2(s) W_u(s)\end{matrix} \right\|_\infty \\ \left\| \frac{z_2}{w} \right\|_2 &= \left\| \begin{matrix}H_1(s) N_1(s) \\ H_2(s) N_2(s)\end{matrix} \right\|_2 = \sigma_n \end{align}The generalized plant $P_{\mathcal{H}_2/\mathcal{H}_\infty}$ is defined below
W1u = ss(W2*Wu); W2u = ss(W1*Wu); % Weight on the uncertainty
W1n = ss(N2); W2n = ss(N1); % Weight on the noise
P = [Wu*W1 -Wu*W1;
0 Wu*W2;
N1 -N1;
0 N2;
1 0];And the mixed $\mathcal{H}_2/\mathcal{H}_\infty$ synthesis is performed.
[H2, ~] = h2hinfsyn(ss(P), 1, 1, 2, [0, 1], 'HINFMAX', 1, 'H2MAX', Inf, 'DKMAX', 100, 'TOL', 1e-3, 'DISPLAY', 'on'); H1 = 1 - H2;The obtained complementary filters are shown in Figure fig:htwo_hinf_comp_filters.

Obtained Super Sensor's noise
The Amplitude Spectral Density of the super sensor's noise is shown in Figure fig:psd_sensors_htwo_hinf_synthesis.
A time domain simulation is shown in Figure fig:super_sensor_time_domain_h2_hinf.
The RMS values of the super sensor noise for the presented three synthesis are listed in Table tab:rms_noise_comp.
PSD_S2 = abs(squeeze(freqresp(N2, freqs, 'Hz'))).^2;
PSD_S1 = abs(squeeze(freqresp(N1, freqs, 'Hz'))).^2;
PSD_H2Hinf = abs(squeeze(freqresp(N1*H1, freqs, 'Hz'))).^2 + ...
abs(squeeze(freqresp(N2*H2, freqs, 'Hz'))).^2;

| RMS [m/s] | |
|---|---|
| Optimal: $\mathcal{H}_2$ | 0.0027 |
| Robust: $\mathcal{H}_\infty$ | 0.041 |
| Mixed: $\mathcal{H}_2/\mathcal{H}_\infty$ | 0.0098 |
Obtained Super Sensor's Uncertainty
The uncertainty on the super sensor's dynamics is shown in Figure fig:super_sensor_dynamical_uncertainty_Htwo_Hinf.

Conclusion
The mixed $\mathcal{H}_2/\mathcal{H}_\infty$ synthesis of the complementary filters allows to:
- limit the dynamical uncertainty of the super sensor
- minimize the RMS value of the estimation
Matlab Functions
<<sec:matlab_functions>>
createWeight
<<sec:createWeight>>
This Matlab function is accessible here.
function [W] = createWeight(args)
% createWeight -
%
% Syntax: [in_data] = createWeight(in_data)
%
% Inputs:
% - n - Weight Order
% - G0 - Low frequency Gain
% - G1 - High frequency Gain
% - Gc - Gain of W at frequency w0
% - w0 - Frequency at which |W(j w0)| = Gc
%
% Outputs:
% - W - Generated Weight
arguments
args.n (1,1) double {mustBeInteger, mustBePositive} = 1
args.G0 (1,1) double {mustBeNumeric, mustBePositive} = 0.1
args.G1 (1,1) double {mustBeNumeric, mustBePositive} = 10
args.Gc (1,1) double {mustBeNumeric, mustBePositive} = 1
args.w0 (1,1) double {mustBeNumeric, mustBePositive} = 1
end
mustBeBetween(args.G0, args.Gc, args.G1);
s = tf('s');
W = (((1/args.w0)*sqrt((1-(args.G0/args.Gc)^(2/args.n))/(1-(args.Gc/args.G1)^(2/args.n)))*s + (args.G0/args.Gc)^(1/args.n))/((1/args.G1)^(1/args.n)*(1/args.w0)*sqrt((1-(args.G0/args.Gc)^(2/args.n))/(1-(args.Gc/args.G1)^(2/args.n)))*s + (1/args.Gc)^(1/args.n)))^args.n;
end
% Custom validation function
function mustBeBetween(a,b,c)
if ~((a > b && b > c) || (c > b && b > a))
eid = 'createWeight:inputError';
msg = 'Gc should be between G0 and G1.';
throwAsCaller(MException(eid,msg))
end
end
plotMagUncertainty
<<sec:plotMagUncertainty>>
This Matlab function is accessible here.
function [p] = plotMagUncertainty(W, freqs, args)
% plotMagUncertainty -
%
% Syntax: [p] = plotMagUncertainty(W, freqs, args)
%
% Inputs:
% - W - Multiplicative Uncertainty Weight
% - freqs - Frequency Vector [Hz]
% - args - Optional Arguments:
% - G
% - color_i
% - opacity
%
% Outputs:
% - p - Plot Handle
arguments
W
freqs double {mustBeNumeric, mustBeNonnegative}
args.G = tf(1)
args.color_i (1,1) double {mustBeInteger, mustBePositive} = 1
args.opacity (1,1) double {mustBeNumeric, mustBeNonnegative} = 0.3
args.DisplayName char = ''
end
% Get defaults colors
colors = get(groot, 'defaultAxesColorOrder');
p = patch([freqs flip(freqs)], ...
[abs(squeeze(freqresp(args.G, freqs, 'Hz'))).*(1 + abs(squeeze(freqresp(W, freqs, 'Hz')))); ...
flip(abs(squeeze(freqresp(args.G, freqs, 'Hz'))).*max(1 - abs(squeeze(freqresp(W, freqs, 'Hz'))), 1e-6))], 'w', ...
'DisplayName', args.DisplayName);
p.FaceColor = colors(args.color_i, :);
p.EdgeColor = 'none';
p.FaceAlpha = args.opacity;
end
plotPhaseUncertainty
<<sec:plotPhaseUncertainty>>
This Matlab function is accessible here.
function [p] = plotPhaseUncertainty(W, freqs, args)
% plotPhaseUncertainty -
%
% Syntax: [p] = plotPhaseUncertainty(W, freqs, args)
%
% Inputs:
% - W - Multiplicative Uncertainty Weight
% - freqs - Frequency Vector [Hz]
% - args - Optional Arguments:
% - G
% - color_i
% - opacity
%
% Outputs:
% - p - Plot Handle
arguments
W
freqs double {mustBeNumeric, mustBeNonnegative}
args.G = tf(1)
args.color_i (1,1) double {mustBeInteger, mustBePositive} = 1
args.opacity (1,1) double {mustBeNumeric, mustBePositive} = 0.3
args.DisplayName char = ''
end
% Get defaults colors
colors = get(groot, 'defaultAxesColorOrder');
% Compute Phase Uncertainty
Dphi = 180/pi*asin(abs(squeeze(freqresp(W, freqs, 'Hz'))));
Dphi(abs(squeeze(freqresp(W, freqs, 'Hz'))) > 1) = 360;
% Compute Plant Phase
G_ang = 180/pi*angle(squeeze(freqresp(args.G, freqs, 'Hz')));
p = patch([freqs flip(freqs)], [G_ang+Dphi; flip(G_ang-Dphi)], 'w', ...
'DisplayName', args.DisplayName);
p.FaceColor = colors(args.color_i, :);
p.EdgeColor = 'none';
p.FaceAlpha = args.opacity;
endBibliography ignore
bibliographystyle:unsrt bibliography:ref.bib