dcm-simscape-model/dcm-simscape-model.org

ESRF Double Crystal Monochromator - Dynamical Multi-Body Model

• Introduction
• System Kinematics
  • Introduction
  • General description of the system architecture - Terminology
  • Forward and Inverse Kinematics problems
  • Bragg Angle
  • Kinematics of "hall" Crystals
    • Introduction
    • Interferometers - Primary "Hall" Crystal
    • Interferometers - Secondary "Hall" Crystal
    • Piezo - hall Crystal
  • Kinematics of "ring" Crystals
    • Introduction
    • Interferometers - ring primary Crystal
    • Interferometers - ring secondary Crystal
    • Piezo - ring Crystal
  • Kinematics of the Metrology Frame
  • Computing relative position between Crystals
  • Summary - List of notations
  • Save Kinematics
• Open Loop System Identification
  • Introduction
  • Identification
  • Plant in the frame of the fastjacks
  • Plant in the frame of the crystal
• Open-Loop Noise Budgeting
  • Introduction
  • Power Spectral Density of signals
  • Open Loop disturbance and measurement noise
• Active Damping Plant (Strain gauges)
  • Introduction
  • Identification
  • Relative Active Damping
  • Damped Plant
• Active Damping Plant (Force Sensors)
  • Introduction
  • Identification
  • Controller - Root Locus
  • Damped Plant
• Feedback Control
• HAC-LAC (IFF) architecture
  • Introduction
  • System Identification
  • High Authority Controller
  • Performances
  • Close Loop noise budget
• Bibliography

---

This report is also available as a pdf.

---

Introduction   ignore

In this document, a Simscape (.e.g. multi-body) model of the ESRF Double Crystal Monochromator (DCM) is presented and used to develop and optimize the control strategy.

It is structured as follow:

• Section sec:dcm_kinematics: the kinematics of the DCM is presented, and Jacobian matrices which are used to solve the inverse and forward kinematics are computed.
• Section sec:open_loop_identification: the system dynamics is identified in the absence of control.
• Section sec:dcm_noise_budget: an open-loop noise budget is performed.
• Section sec:active_damping_strain_gauges: it is studied whether if the strain gauges fixed to the piezoelectric actuators can be used to actively damp the plant.
• Section sec:active_damping_iff: piezoelectric force sensors are added in series with the piezoelectric actuators and are used to actively damp the plant using the Integral Force Feedback (IFF) control strategy.
• Section sec:hac_iff: the High Authority Control - Low Authority Control (HAC-LAC) strategy is tested on the Simscape model.

System Kinematics

<<sec:dcm_kinematics>>

Introduction   ignore

In this section, the kinematics of the DCM is described. The elements (crystals, fast jacks, metrology frame, …) are all defined. The associated frames in which the motion of those elements are expressed will also be defined. Finally, the transformation necessary to compute the relative pose of the crystals from the metrology is computed.

General description of the system architecture - Terminology

In order to describe the motion of the different elements, reference frames are used.

One global frame is first defined with:

• the $x$ axis is aligned with the x-ray
• the $y$ axis aligned with the Bragg axis
• the $z$ axis is pointing up aligned with the gravity

The axis are shown in Figure fig:dcm_schematic_overview. The origin of this frame is usually taken at the intersection between the x-ray and the bragg axis.

The Bragg axis is therefore rotating around the $y$ axis. Two sets of two crystals are also rotating with the bragg axis. One set is positioned on the "hall" side (i.e toward $+y$) while the other set is positioned on the "ring" side (i.e. toward $-y$).

For each of these two sets, there is a "primary" crystal directly fixed to the bragg axis, and a "secondary" crystal fixed on top of three fastjacks. There are therefore 4 crystals in total for each Double Crystal Monochromator.

There is then a metrology frame that hold all the interferometers.

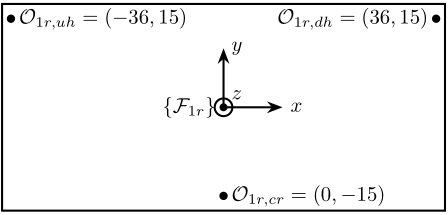
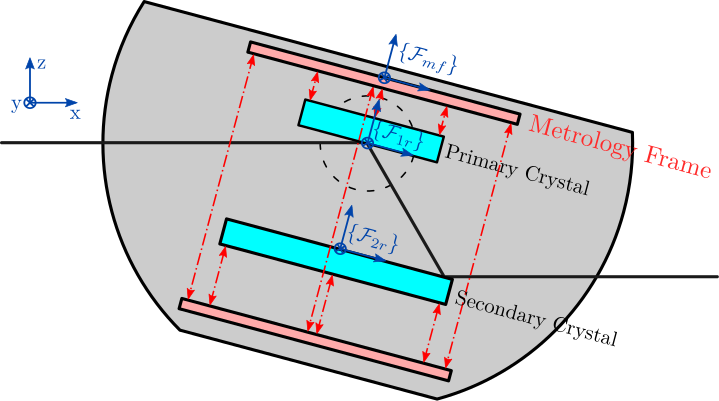
Several reference frame are used (displayed in Figure fig:dcm_schematic_overview for the "ring" crystals):

• $\{\mathcal{F}_{1r}\}$ and $\{\mathcal{F}_{1h}\}$: frames fixed to the bottom surface of first crystals with their origin at the intersection between the X-ray and the Bragg axis
• $\{\mathcal{F}_{2r}\}$ and $\{\mathcal{F}_{2h)}\}$: frames fixed to the top surface of second crystals. Their origin is at the crystal's center
• $\{\mathcal{F}_{mf}\}$: frame fixed to the center of the top part of the metrology frame

Schematic of the DCM with one set of first and second crystals with the associated frames

Here are the different letters used in the notations and there meaning:

• r: "ring" (i.e. toward $-y$)
• h: "hall" (i.e. toward $+y$)
• u: "upstream" (i.e. towards $-x$)
• d: "downstream" (i.e. towards $+x$)
• c: "center" (i.e. centered at $x=0$)
• 1: primary crystal
• 2: secondary crystal
• mf: metrology frame

Forward and Inverse Kinematics problems

Let's consider one plane initially orthogonal to the $z$ direction (Figure fig:schematic_measurement_plane). The pose of the plane, expressed in a frame $\{\mathcal{F}\}$ with origin $\mathcal{O}$ is defined by:

• its vertical motion: $d_z$
• its rotation around the $y$ axis: $r_y$
• its rotation around the $x$ axis: $r_x$

SChematic of a plane with three vertical interferometers

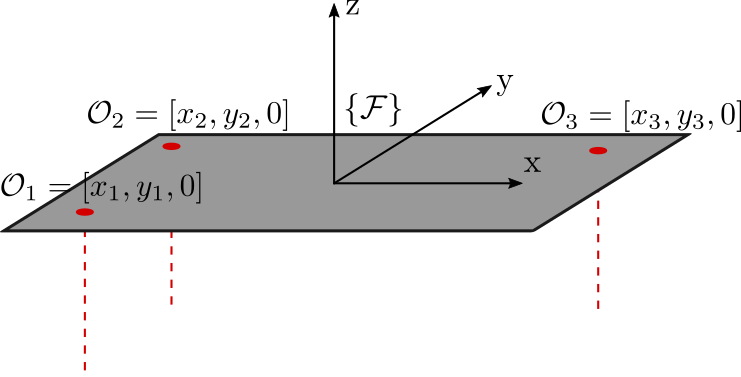
In order to measure the pose of the crystal, three interferometers are measuring the motion of the plane at three distinct positions $\mathcal{O}_1 = [x_1, y_1, 0]$, $\mathcal{O}_2 = [x_2, y_2, 0]$ and $\mathcal{O}_3 = [x_3, y_3, 0]$ (See Figure fig:schematic_measurement_plane). The interferometers can be pointed in the $z$ direction or in the opposite $z$ direction. The measured motion are noted $z_1$, $z_2$ and $z_3$.

The inverse kinematic problem consists of deriving the measured $[z_1, z_2, z_3]$ motions from the pose $[d_z, r_y, r_x]$ of the crystal. For small motion, this problem can be easily solved as follows:

\begin{equation} \boxed{ \begin{bmatrix} z_{1} \\ z_{2} \\ z_{3} \end{bmatrix} = \bm{J} \begin{bmatrix} d_{z} \\ r_{y} \\ r_{x} \end{bmatrix} } \end{equation}

with $\bm{J}$ called the Jacobian matrix.

The Jacobian matrix can be computed as follows in the case where the interferometers are pointing toward positive $z$: \begin{equation} \label{eq:jacobian_3dof_positive_z} \boxed{ \bm{J} = \begin{bmatrix} 1 & -x_1 & y_1
1 & -x_2 & y_2
1 & -x_3 & y_3

\end{bmatrix} }

\end{equation} and computed as follows if there are pointing torward negative $z$: \begin{equation} \label{eq:jacobian_3dof_negative_z} \boxed{ \bm{J} = \begin{bmatrix} -1 & x_1 & -y_1
-1 & x_2 & -y_2
-1 & x_3 & -y_3

\end{bmatrix} }

\end{equation}

The forward kinematic problem is then solved by inverting the Jacobian matrix:

\begin{equation} \boxed{ \begin{bmatrix} d_{z} \\ r_{y} \\ r_{x} \end{bmatrix} = \bm{J}^{-1} \begin{bmatrix} z_{1} \\ z_{2} \\ z_{3} \end{bmatrix} } \end{equation}

The same reasoning can be performed to convert the wanted motion of one plane to the motion of three vertical actuators fixed to the plane (tripod architecture).

Bragg Angle

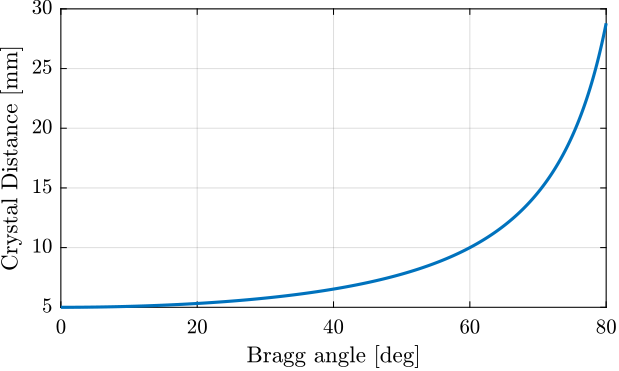
<<sec:kinematics_bragg>> In order to have a fix exit, the following relation must be verified: \begin{equation} \label{eq:bragg_angle_formula} \boxed{d_z = \frac{d_{\text{off}}}{2 cos θ_b}}

\end{equation} with:

• $d_{\text{off}}$ the wanted offset between the incident x-ray and the output x-ray
• $\theta_b$ the bragg angle
• $d_z$ the corresponding distance between the first and second crystal

This relation is shown in Figure fig:jack_motion_bragg_angle for a wanted fix exit offset of 10mm.

Jack motion as a function of Bragg angle ($d_z = 10\,mm$)

Kinematics of "hall" Crystals

<<sec:kinematics_hall_crystal>>

Introduction   ignore

There are two "hall" crystals, the primary one and the secondary one.

Interferometers - Primary "Hall" Crystal

Three interferometers fixed to the top metrology frame are pointed to the top surface (i.e. toward negative $z$) of the primary "hall" crystal. The measurements are performed along the $z$ direction.

The notations are:

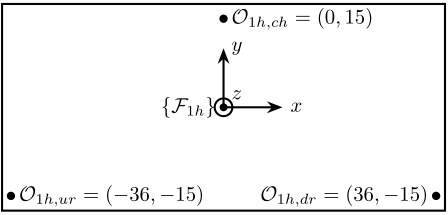
• $\{\mathcal{F}_{1h}\}$ is the frame in which motion of the crystal are expressed
• $\mathcal{O}_{1h,ur}$ measurement point for the "upstream-ring" interferometer
• $\mathcal{O}_{1h,ch}$ measurement point for the "center-hall" interferometer
• $\mathcal{O}_{1h,dr}$ measurement point for the "downstream-ring" interferometer

The measured displacements by the interferometers are noted $[z_{1h,ur},\ z_{1h,ch},\ z_{1h,dr}]$.

The corresponding motion of the crystal expressed in the frame as shown in Figure fig:sensor_hall_crystal_points_primary are:

• $d_{1h,z}$ motion in the $z$ direction
• $r_{1h,y}$ rotation around the $y$ axis
• $r_{1h,x}$ rotation around the $x$ axis

\begin{tikzpicture}
  % Crystal
  \draw (-7.5/2, -3.5/2) rectangle (7.5/2, 3.5/2);

  % Measurement Points
  \node[branch] (a1) at (-3.6, -1.5){};
  \node[branch] (a2) at ( 0,    1.5){};
  \node[branch] (a3) at ( 3.6, -1.5){};

  % Labels
  \node[right] at (a1) {$\mathcal{O}_{1h,ur} = (-36, -15)$};
  \node[right] at (a2) {$\mathcal{O}_{1h,ch} = ( 0,   15)$};
  \node[left]  at (a3) {$\mathcal{O}_{1h,dr} = ( 36, -15)$};

  % Origin
  \draw[->] (0, 0) node[] -- ++(1,  0) node[right]{$x$};
  \draw[->] (0, 0) -- ++(0, 1) node[right]{$y$};
  \draw[fill, color=black] (0, 0) circle (0.05);
  \draw[color=black] (0, 0) circle (0.15);
  \node[above right] at (0, 0){$z$};

  \node[left] at (0,0) {$\{\mathcal{F}_{1h}\}$};
\end{tikzpicture}

Top view of the primary crystal hall. Position of the measurement points. Units in [mm]

The inverse kinematics problem consists of deriving the measured displacement by the interferometer from the motion of the crystal (see Figure fig:schematic_sensor_jacobian_inverse_kinematics_hall_primary):

\begin{equation} \boxed{ \begin{bmatrix} z_{1h,ur} \\ z_{1h,ch} \\ z_{1h,dr} \end{bmatrix} = \bm{J}_{1h,s} \begin{bmatrix} d_{1h,z} \\ r_{1h,y} \\ r_{1h,x} \end{bmatrix} } \end{equation}

\begin{tikzpicture}
  % Blocs
  \node[block] (Js) {$\bm{J}_{1h,s}$};

  % Connections and labels
  \draw[->] ($(Js.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} d_{1h,z} \\ r_{1h,y} \\ r_{1h,x} \end{bmatrix}$} -- (Js.west);
  \draw[->] (Js.east)  -- ++(1.5, 0) node[above left]{$\begin{bmatrix} z_{1h,ur} \\ z_{1h,ch} \\ z_{1h,dr} \end{bmatrix}$};
\end{tikzpicture}

Inverse Kinematics - Interferometers

From the measurement coordinates in Figure fig:sensor_hall_crystal_points_primary and equation eqref:eq:jacobian_3dof_negative_z, the inverse kinematics the folowing Jacobian matrix is obtained:

\begin{equation} \boxed{\bm{J}_{1h,s} = \begin{bmatrix} -1 & -0.036 & 0.015 \\ -1 & 0 & -0.015 \\ -1 & 0.036 & 0.015 \end{bmatrix}} \end{equation}

The forward kinematics problem (computing the crystal motion from the 3 interferometers) is solved by inverting the Jacobian matrix (see Figure fig:schematic_sensor_jacobian_forward_kinematics_hall_primary).

\begin{equation} \boxed{ \begin{bmatrix} d_{1h,z} \\ r_{1h,y} \\ r_{1h,x} \end{bmatrix} = \bm{J}_{1h,s}^{-1} \begin{bmatrix} z_{1h,ur} \\ z_{1h,ch} \\ z_{1h,dr} \end{bmatrix} } \end{equation}

\begin{tikzpicture}
  % Blocs
  \node[block] (Js_inv) {$\bm{J}_{1h,s}^{-1}$};

  % Connections and labels
  \draw[->] ($(Js_inv.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} z_{1h,ur} \\ z_{1h,ch} \\ z_{1h,dr} \end{bmatrix}$} -- (Js_inv.west);
  \draw[->] (Js_inv.east)  -- ++(1.5, 0) node[above left]{$\begin{bmatrix} d_{1h,z} \\ r_{1h,y} \\ r_{1h,x} \end{bmatrix}$};
\end{tikzpicture}

Forward Kinematics - Interferometers

The obtained matrix is displayed in Table tab:inverse_jacobian_sensor_hall_primary.

-0.25	-0.5	-0.25
-13.89	0.0	13.89
16.67	-33.33	16.67

Interferometers - Secondary "Hall" Crystal

Three interferometers are pointed to the bottom surface (i.e. toward positive $z$) of the secondary "hall" crystal.

The position of the measurement points are shown in Figure fig:sensor_hall_secondary_crystal_points as well as the origin where the motion of the crystal is computed.

The notations are:

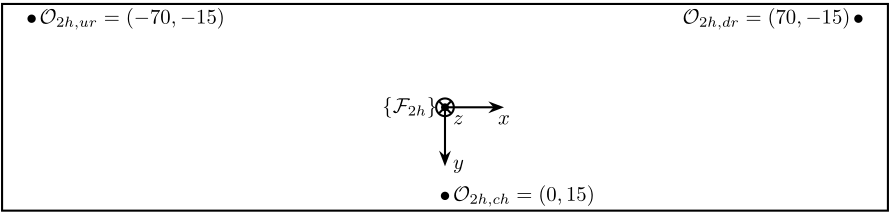
• $\{\mathcal{F}_{2h}\}$ is the frame in which motion of the crystal are expressed
• $\mathcal{O}_{2h,ur}$ measurement point for the "upstream-ring" interferometer
• $\mathcal{O}_{2h,ch}$ measurement point for the "center-hall" interferometer
• $\mathcal{O}_{2h,dr}$ measurement point for the "downstream-ring" interferometer

The measured displacements by the interferometers are noted $[z_{2h,ur},\ z_{2h,ch},\ z_{2h,dr}]$.

The corresponding motion of the crystal expressed in the frame as shown in Figure fig:sensor_hall_secondary_crystal_points are:

• $d_{2h,z}$ motion in the $z$ direction
• $r_{2h,y}$ rotation around the $y$ axis
• $r_{2h,x}$ rotation around the $x$ axis

\begin{tikzpicture}
  % Crystal
  \draw (-15/2, -3.5/2) rectangle (15/2, 3.5/2);

  % Measurement Points
  \node[branch] (a1) at (-7,  1.5){};
  \node[branch] (a2) at ( 0, -1.5){};
  \node[branch] (a3) at ( 7,  1.5){};

  % Labels
  \node[right] at (a1) {$\mathcal{O}_{2h,ur} = (-70, -15)$};
  \node[right] at (a2) {$\mathcal{O}_{2h,ch} = ( 0,   15)$};
  \node[left]  at (a3) {$\mathcal{O}_{2h,dr} = ( 70, -15)$};

  % Origin
  \draw[->] (0, 0) node[] -- ++(1,  0) node[below]{$x$};
  \draw[->] (0, 0) -- ++(0, -1) node[right]{$y$};
  \draw[fill, color=black] (0, 0) circle (0.05);
  \draw[color=black] (0, 0) circle (0.15);
  \draw[] (-0.1, 0.1) -- ( 0.1, -0.1);
  \draw[] (-0.1,-0.1) -- ( 0.1,  0.1);
  \node[below right] at (0,0) {$z$};

  \node[left] at (0,0) {$\{\mathcal{F}_{2h}\}$};
\end{tikzpicture}

Bottom view of the secondary "hall" crystal. Position of the measurement points. Coordinate values are in [mm]

The inverse kinematics consisting of deriving the interferometer measurements from the motion of the crystal (see Figure fig:schematic_sensor_jacobian_inverse_kinematics_hall_secondary):

\begin{equation} \boxed{ \begin{bmatrix} z_{2h,ur} \\ z_{2h,ch} \\ z_{2h,dr} \end{bmatrix} = \bm{J}_{2h,s} \begin{bmatrix} d_{2h,z} \\ r_{2h,y} \\ r_{2h,x} \end{bmatrix} } \end{equation}

\begin{tikzpicture}
  % Blocs
  \node[block] (Js) {$\bm{J}_{2h,s}$};

  % Connections and labels
  \draw[->] ($(Js.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} d_{2h,z} \\ r_{2h,y} \\ r_{2h,x} \end{bmatrix}$} -- (Js.west);
  \draw[->] (Js.east)  -- ++(1.5, 0) node[above left]{$\begin{bmatrix} z_{2h,ur} \\ z_{2h,ch} \\ z_{2h,dr} \end{bmatrix}$};
\end{tikzpicture}

Inverse Kinematics - Interferometers

From the measurement coordinates in Figure fig:sensor_hall_secondary_crystal_points and equation eqref:eq:jacobian_3dof_positive_z, the inverse kinematics the folowing Jacobian matrix is obtained:

\begin{equation} \boxed{\bm{J}_{2h,s} = \begin{bmatrix} 1 & 0.07 & -0.015 \\ 1 & 0 & 0.015 \\ 1 & -0.07 & -0.015 \end{bmatrix}} \end{equation}

The forward kinematics is solved by inverting the Jacobian matrix (see Figure fig:schematic_sensor_jacobian_forward_kinematics_hall_secondary).

\begin{equation} \boxed{ \begin{bmatrix} d_{2h,z} \\ r_{2h,y} \\ r_{2h,x} \end{bmatrix} = \bm{J}_{2h,s}^{-1} \begin{bmatrix} z_{2h,ur} \\ z_{2h,ch} \\ z_{2h,dr} \end{bmatrix} } \end{equation}

\begin{tikzpicture}
  % Blocs
  \node[block] (Js_inv) {$\bm{J}_{2h,s}^{-1}$};

  % Connections and labels
  \draw[->] ($(Js_inv.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} z_{2h,ur} \\ z_{2h,ch} \\ z_{2h,dr} \end{bmatrix}$} -- (Js_inv.west);
  \draw[->] (Js_inv.east)  -- ++(1.5, 0) node[above left]{$\begin{bmatrix} d_{2h,z} \\ r_{2h,y} \\ r_{2h,x} \end{bmatrix}$};
\end{tikzpicture}

Forward Kinematics - Interferometers

The results is shown in Table tab:inverse_jacobian_sensor_hall_secondary.

0.25	0.5	0.25
7.14	0.0	-7.14
-16.67	33.33	-16.67

Piezo - hall Crystal

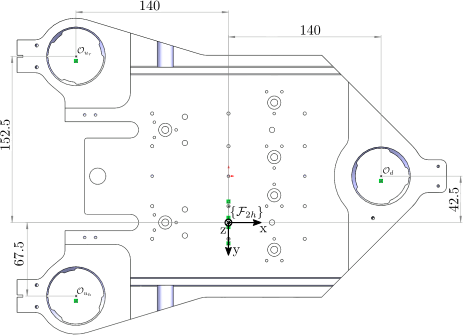
The locations of the actuators with respect with the center of the secondary "hall" crystal are shown in Figure fig:actuator_jacobian_hall_points.

Inverse Kinematics consist of deriving the corresponding z motion of the 3 actuators from the motion of the crystal expressed in $\{\mathcal{F}_{2h}\}$. As in the previous section, the motion of the secondary "hall" crystal is expressed by $[d_{2h,z},\ r_{2h,y},\ r_{2h,x}]$. The motion of the three fast jacks are expressed by $[d_{u_r},\ d_{u_h},\ d_{d}]$ are are corresponding to a motion along the $z$ axis toward positive values.

The inverse kinematics can therefore be solved as follows:

\begin{equation} \boxed{ \begin{bmatrix} d_{u_r} \\ d_{u_h} \\ d_{d} \end{bmatrix} = \bm{J}_{h,a} \begin{bmatrix} d_{2h,z} \\ r_{2h,y} \\ r_{2h,x} \end{bmatrix} } \end{equation}

\begin{tikzpicture}
  % Blocs
  \node[block] (Ja) {$\bm{J}_{h,a}$};

  % Connections and labels
  \draw[->] ($(Ja.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} d_{2h,z} \\ r_{2h,y} \\ r_{2h,x} \end{bmatrix}$} -- (Ja.west);
  \draw[->] (Ja.east)  -- ++(1.5, 0) node[above left]{$\begin{bmatrix} d_{u_r} \\ d_{u_h} \\ d_d \end{bmatrix}$};
\end{tikzpicture}

Inverse Kinematics - Actuators

Based on the geometry in Figure fig:actuator_jacobian_hall_points, the following Jacobian matrix is obtained (see Eq. eqref:eq:jacobian_3dof_positive_z):

\begin{equation} \boxed{\bm{J}_{h,a} = \begin{bmatrix} 1 & 0.14 & -0.1525 \\ 1 & 0.14 & 0.0675 \\ 1 & -0.14 & -0.0425 \end{bmatrix}} \end{equation}

The forward Kinematics is solved by inverting the Jacobian matrix:

\begin{equation} \boxed{ \begin{bmatrix} d_{2h,z} \\ r_{2h,y} \\ r_{2h,x} \end{bmatrix} = \bm{J}_{h,a}^{-1} \begin{bmatrix} d_{u_r} \\ d_{u_h} \\ d_{d} \end{bmatrix} } \end{equation}

\begin{tikzpicture}
  % Blocs
  \node[block] (Ja_inv) {$\bm{J}_{h,a}^{-1}$};

  % Connections and labels
  \draw[->] ($(Ja_inv.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} d_{u_r} \\ d_{u_h} \\ d_d \end{bmatrix}$} -- (Ja_inv.west);
  \draw[->] (Ja_inv.east)  -- ++(1.5, 0) node[above left]{$\begin{bmatrix} d_{2h,z} \\ r_{2h,y} \\ r_{2h,x} \end{bmatrix}$};
\end{tikzpicture}

The obtained inverse Jacobian matrix is shown in Table tab:inverse_jacobian_actuator_hall.

Forward Kinematics - Actuators for hall crystal

0.0568	0.4432	0.5
1.7857	1.7857	-3.5714
-4.5455	4.5455	0.0

Kinematics of "ring" Crystals

<<sec:kinematics_ring_crystal>>

Introduction   ignore

The same reasoning is now done for the "ring" crystals.

Interferometers - ring primary Crystal

Three interferometers fixed to the top metrology frame are pointed to the top surface (i.e. toward negative $z$) of the primary "hall" crystal. The measurements are perform along the $z$ direction.

The notations are:

• $\{\mathcal{F}_{1r}\}$ is the frame in which motion of the crystal are expressed
• $\mathcal{O}_{1r,uh}$ measurement point for the "upstream-hall" interferometer
• $\mathcal{O}_{1r,cr}$ measurement point for the "center-ring" interferometer
• $\mathcal{O}_{1r,dh}$ measurement point for the "downstream-hall" interferometer

The measured displacements by the interferometers are noted $[z_{1r,ur},\ z_{1r,ch},\ z_{1r,dr}]$.

The corresponding motion of the crystal expressed in the frame as shown in Figure fig:sensor_hall_crystal_points_primary are:

• $d_{1r,z}$ motion in the $z$ direction
• $r_{1r,y}$ rotation around the $y$ axis
• $r_{1r,x}$ rotation around the $x$ axis

\begin{tikzpicture}
  % Crystal
  \draw (-7.5/2, -3.5/2) rectangle (7.5/2, 3.5/2);

  % Measurement Points
  \node[branch] (a1) at (-3.6,  1.5){};
  \node[branch] (a2) at ( 0, -1.5){};
  \node[branch] (a3) at ( 3.6,  1.5){};

  % Labels
  \node[right] at (a1) {$\mathcal{O}_{1r,uh} = (-36,  15)$};
  \node[right] at (a2) {$\mathcal{O}_{1r,cr} = ( 0,  -15)$};
  \node[left]  at (a3) {$\mathcal{O}_{1r,dh} = ( 36,  15)$};

  % Origin
  \draw[->] (0, 0) node[] -- ++(1,  0) node[right]{$x$};
  \draw[->] (0, 0) -- ++(0, 1) node[right]{$y$};
  \draw[fill, color=black] (0, 0) circle (0.05);
  \draw[color=black] (0, 0) circle (0.15);
  \node[above right] at (0, 0){$z$};

  \node[left] at (0,0) {$\{\mathcal{F}_{1r}\}$};
\end{tikzpicture}

Top view of the primary crystal ring. Position of the measurement points in [mm].

The inverse kinematics consisting of deriving the interferometer measurements from the motion of the crystal (see Figure fig:schematic_sensor_jacobian_inverse_kinematics_ring_primary):

\begin{equation} \boxed{ \begin{bmatrix} z_{1r,ur} \\ z_{1r,ch} \\ z_{1r,dr} \end{bmatrix} = \bm{J}_{1r,s} \begin{bmatrix} d_{1r,z} \\ r_{1r,y} \\ r_{1r,x} \end{bmatrix} } \end{equation}

\begin{tikzpicture}
  % Blocs
  \node[block] (Js) {$\bm{J}_{1r,s}$};

  % Connections and labels
  \draw[->] ($(Js.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} d_{1r,z} \\ r_{1r,y} \\ r_{1r,x} \end{bmatrix}$} -- (Js.west);
  \draw[->] (Js.east)  -- ++(1.5, 0) node[above left]{$\begin{bmatrix} z_{1r,ur} \\ z_{1r,ch} \\ z_{1r,dr} \end{bmatrix}$};
\end{tikzpicture}

Inverse Kinematics - Interferometers (primary "ring" crystal)

From the measurement coordinates in Figure fig:sensor_ring_crystal_points_primary and equation eqref:eq:jacobian_3dof_negative_z, the inverse kinematics the folowing Jacobian matrix is obtained:

\begin{equation} \boxed{\bm{J}_{1r,s} = \begin{bmatrix} -1 & -0.036 & -0.015 \\ -1 & 0 & 0.015 \\ -1 & 0.036 & -0.015 \end{bmatrix}} \end{equation}

The forward kinematics is solved by inverting the Jacobian matrix (see Figure fig:schematic_sensor_jacobian_forward_kinematics_ring_primary).

\begin{equation} \boxed{ \begin{bmatrix} d_{1r,z} \\ r_{1r,y} \\ r_{1r,x} \end{bmatrix} = \bm{J}_{1r,s}^{-1} \begin{bmatrix} z_{1r,ur} \\ z_{1r,ch} \\ z_{1r,dr} \end{bmatrix} } \end{equation}

\begin{tikzpicture}
  % Blocs
  \node[block] (Js_inv) {$\bm{J}_{1r,s}^{-1}$};

  % Connections and labels
  \draw[->] ($(Js_inv.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} z_{1r,ur} \\ z_{1r,ch} \\ z_{1r,dr} \end{bmatrix}$} -- (Js_inv.west);
  \draw[->] (Js_inv.east)  -- ++(1.5, 0) node[above left]{$\begin{bmatrix} d_{1r,z} \\ r_{1r,y} \\ r_{1r,x} \end{bmatrix}$};
\end{tikzpicture}

Forward Kinematics - Interferometers

The obtained inverse Jacobian matrix is shown in Table tab:inverse_jacobian_sensor_ring_primary.

-0.25	-0.5	-0.25
-13.89	0.0	13.89
-16.67	33.33	-16.67

Interferometers - ring secondary Crystal

Three interferometers are pointed to the bottom surface (i.e. toward positive $z$) of the secondary "ring" crystal.

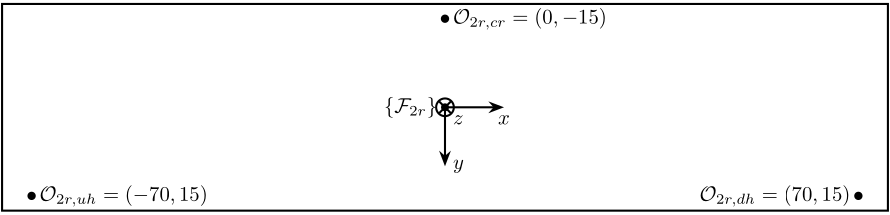
The position of the measurement points are shown in Figure fig:sensor_ring_secondary_crystal_points as well as the origin where the motion of the crystal is computed.

The notations are:

• $\{\mathcal{F}_{2r}\}$ is the frame in which motion of the crystal are expressed
• $\mathcal{O}_{2r,uh}$ measurement point for the "upstream-hall" interferometer
• $\mathcal{O}_{2r,cr}$ measurement point for the "center-ring" interferometer
• $\mathcal{O}_{2r,dh}$ measurement point for the "downstream-hall" interferometer

The measured displacements by the interferometers are noted $[z_{2r,ur},\ z_{2r,ch},\ z_{2r,dr}]$.

The corresponding motion of the crystal expressed in the frame as shown in Figure fig:sensor_hall_secondary_crystal_points are:

• $d_{2r,z}$ motion in the $z$ direction
• $r_{2r,y}$ rotation around the $y$ axis
• $r_{2r,x}$ rotation around the $x$ axis

The position of the measurement points are shown in Figure fig:sensor_ring_secondary_crystal_points as well as the origin where the motion of the crystal is computed.

\begin{tikzpicture}
  % Crystal
  \draw (-15/2, -3.5/2) rectangle (15/2, 3.5/2);

  % Measurement Points
  \node[branch] (a1) at (-7, -1.5){};
  \node[branch] (a2) at ( 0,  1.5){};
  \node[branch] (a3) at ( 7, -1.5){};

  % Labels
  \node[right] at (a1) {$\mathcal{O}_{2r,uh} = (-70,  15)$};
  \node[right] at (a2) {$\mathcal{O}_{2r,cr} = (  0, -15)$};
  \node[left]  at (a3) {$\mathcal{O}_{2r,dh} = ( 70,  15)$};

  % Origin
  \draw[->] (0, 0) node[] -- ++(1,  0) node[below]{$x$};
  \draw[->] (0, 0) -- ++(0, -1) node[right]{$y$};
  \draw[fill, color=black] (0, 0) circle (0.05);
  \draw[color=black] (0, 0) circle (0.15);
  \draw[] (-0.1, 0.1) -- ( 0.1, -0.1);
  \draw[] (-0.1,-0.1) -- ( 0.1,  0.1);
  \node[below right] at (0,0) {$z$};

  \node[left] at (0,0) {$\{\mathcal{F}_{2r}\}$};
\end{tikzpicture}

Bottom view of the second crystal ring. Position of the measurement points.

The inverse kinematics consisting of deriving the interferometer measurements from the motion of the crystal (see Figure fig:schematic_sensor_jacobian_inverse_kinematics_ring_secondary):

\begin{equation} \boxed{ \begin{bmatrix} z_{2r,uh} \\ z_{2r,cr} \\ z_{2r,dh} \end{bmatrix} = \bm{J}_{2r,s} \begin{bmatrix} d_{2r,z} \\ r_{2r,y} \\ r_{2r,x} \end{bmatrix} } \end{equation}

\begin{tikzpicture}
  % Blocs
  \node[block] (Js) {$\bm{J}_{2r,s}$};

  % Connections and labels
  \draw[->] ($(Js.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} d_{2r,z} \\ r_{2r,y} \\ r_{2r,x} \end{bmatrix}$} -- (Js.west);
  \draw[->] (Js.east)  -- ++(1.5, 0) node[above left]{$\begin{bmatrix} z_{2r,uh} \\ z_{2r,cr} \\ z_{2r,dh} \end{bmatrix}$};
\end{tikzpicture}

Inverse Kinematics - Interferometers

From the measurement coordinates in Figure fig:sensor_ring_secondary_crystal_points and equation eqref:eq:jacobian_3dof_positive_z, the inverse kinematics the folowing Jacobian matrix is obtained:

\begin{equation} \boxed{\bm{J}_{2r,s} = \begin{bmatrix} 1 & 0.07 & 0.015 \\ 1 & 0 & -0.015 \\ 1 & -0.07 & 0.015 \end{bmatrix}} \end{equation}

The forward kinematics is solved by inverting the Jacobian matrix (see Figure fig:schematic_sensor_jacobian_forward_kinematics_ring_secondary).

\begin{equation} \boxed{ \begin{bmatrix} d_{2r,z} \\ r_{2r,y} \\ r_{2r,x} \end{bmatrix} = \bm{J}_{2r,s}^{-1} \begin{bmatrix} z_{2r,uh} \\ z_{2r,cr} \\ z_{2r,dh} \end{bmatrix} } \end{equation}

\begin{tikzpicture}
  % Blocs
  \node[block] (Js_inv) {$\bm{J}_{s,r}^{-1}$};

  % Connections and labels
  \draw[->] ($(Js_inv.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} z_{2r,uh} \\ z_{2r,cr} \\ z_{2r,dh} \end{bmatrix}$} -- (Js_inv.west);
  \draw[->] (Js_inv.east)  -- ++(1.5, 0) node[above left]{$\begin{bmatrix} d_{2r,z} \\ r_{2r,y} \\ r_{2r,x} \end{bmatrix}$};
\end{tikzpicture}

Forward Kinematics - Interferometers

The obtained inverse Jacobian matrix is shown in Table tab:inverse_jacobian_sensor_ring_secondary.

0.25	0.5	0.25
7.14	0.0	-7.14
16.67	-33.33	16.67

Piezo - ring Crystal

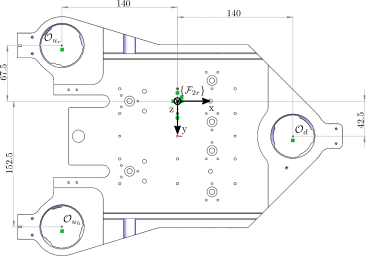
The location of the actuators with respect with the center of the secondary "ring" crystal are shown in Figure fig:actuator_jacobian_ring_points.

Inverse Kinematics consist of deriving the corresponding z motion of the 3 actuators from the motion of the crystal expressed in $\{\mathcal{F}_{2r}\}$. As in the previous section, the motion of the secondary "ring" crystal is expressed by $[d_{2r,z},\ r_{2r,y},\ r_{2r,x}]$. The motion of the three fast jacks are expressed by $[d_{u_r},\ d_{u_h},\ d_{d}]$ are are corresponding to a motion along the $z$ axis toward positive values.

The inverse kinematics can therefore be solved as follows:

\begin{equation} \boxed{ \begin{bmatrix} d_{u_r} \\ d_{u_h} \\ d_{d} \end{bmatrix} = \bm{J}_{h,a} \begin{bmatrix} d_{2r,z} \\ r_{2r,y} \\ r_{2r,x} \end{bmatrix} } \end{equation}

\begin{tikzpicture}
  % Blocs
  \node[block] (Ja) {$\bm{J}_{r,a}$};

  % Connections and labels
  \draw[->] ($(Ja.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} d_{2r,z} \\ r_{2r,y} \\ r_{2r,x} \end{bmatrix}$} -- (Ja.west);
  \draw[->] (Ja.east)  -- ++(1.5, 0) node[above left]{$\begin{bmatrix} d_{u_r} \\ d_{u_h} \\ d_d \end{bmatrix}$};
\end{tikzpicture}

Inverse Kinematics - Actuators

Based on the geometry in Figure fig:actuator_jacobian_ring_points, we obtain (see Eq. eqref:eq:jacobian_3dof_positive_z):

\begin{equation} \boxed{\bm{J}_{r,a} = \begin{bmatrix} 1 & 0.14 & -0.0675 \\ 1 & 0.14 & 0.1525 \\ 1 & -0.14 & 0.0425 \end{bmatrix}} \end{equation}

The forward Kinematics is solved by inverting the Jacobian matrix:

\begin{equation} \boxed{ \begin{bmatrix} d_{2r,z} \\ r_{2r,y} \\ r_{2r,x} \end{bmatrix} = \bm{J}_{r,a}^{-1} \begin{bmatrix} d_{u_r} \\ d_{u_h} \\ d_{d} \end{bmatrix} } \end{equation}

\begin{tikzpicture}
  % Blocs
  \node[block] (Ja_inv) {$\bm{J}_{r,a}^{-1}$};

  % Connections and labels
  \draw[->] ($(Ja_inv.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} d_{u_r} \\ d_{u_h} \\ d_d \end{bmatrix}$} -- (Ja_inv.west);
  \draw[->] (Ja_inv.east)  -- ++(1.5, 0) node[above left]{$\begin{bmatrix} d_{2r,z} \\ r_{2r,y} \\ r_{2r,x} \end{bmatrix}$};
\end{tikzpicture}

Forward Kinematics - Actuators for ring crystal

The obtained inverse Jacobian matrix is shown in Table tab:inverse_jacobian_actuator_ring_secondary.

0.4432	0.0568	0.5
1.7857	1.7857	-3.5714
-4.5455	4.5455	0.0

Kinematics of the Metrology Frame

<<sec:kinematics_metrology_frame>>

Three interferometers (aligned with the $z$ axis) are used to measure the relative motion between the bottom part and the top part of the metrology frame.

The location of the three interferometers are shown in Figure fig:jacobian_metrology_frame.

The measured displacements by the interferometers are are noted $[z_{mf,u},\ z_{mf,dh},\ z_{mf,dr}]$.

We here suppose that the bottom part of the metrology frame is fixed and only the top part is moving. The motion of the metrology top part expressed in the frame as shown in Figure fig:jacobian_metrology_frame are:

• $d_{mf,z}$ motion in the $z$ direction
• $r_{mf,y}$ rotation around the $y$ axis
• $r_{mf,x}$ rotation around the $x$ axis

Top View of the top part of the metrology frame

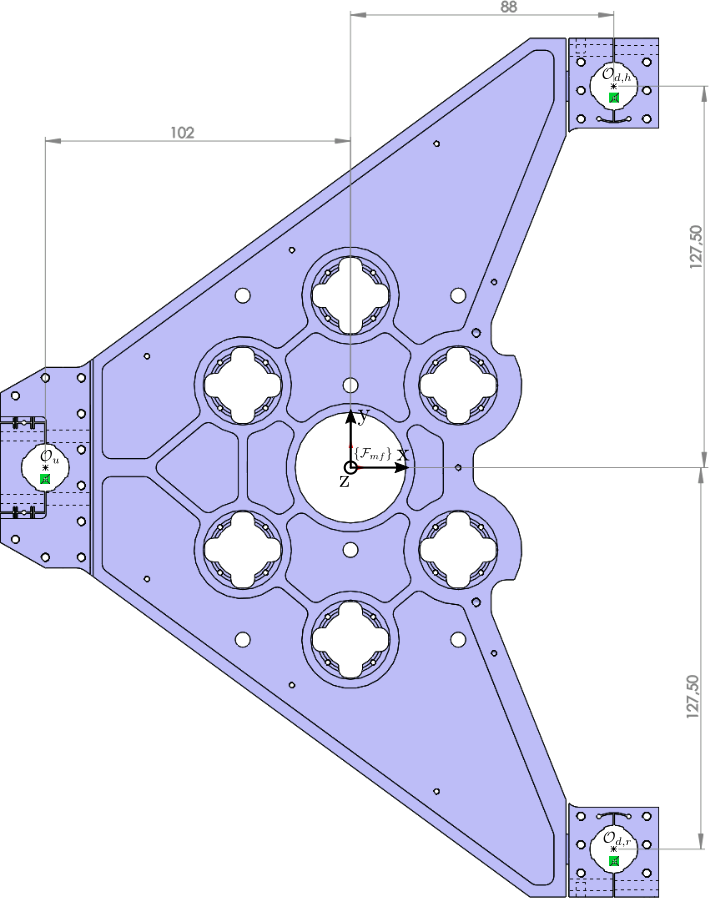
The inverse kinematics consisting of deriving the interferometer measurements from the motion of the metrology top part:

\begin{equation} \boxed{ \begin{bmatrix} z_{mf,u} \\ z_{mf,dh} \\ z_{mf,dr} \end{bmatrix} = \bm{J}_{mf,s} \begin{bmatrix} d_{mf,z} \\ r_{mf,y} \\ r_{mf,x} \end{bmatrix} } \end{equation}

From the coordinates in Figure fig:jacobian_metrology_frame and the equation eqref:eq:jacobian_3dof_positive_z, the following Jacobian matrix is obtained:

\begin{equation} \boxed{\bm{J}_{mf,r} = \begin{bmatrix} 1 & 0.102 & 0 \\ 1 & -0.088 & 0.1275 \\ 1 & -0.088 & -0.1275 \end{bmatrix}} \end{equation}

The forward kinematics is solved by inverting the Jacobian matrix:

\begin{equation} \boxed{ \begin{bmatrix} d_{mf,z} \\ r_{mf,y} \\ r_{mf,x} \end{bmatrix} = \bm{J}_{mf,s}^{-1} \begin{bmatrix} z_{mf,u} \\ z_{mf,dh} \\ z_{mf,dr} \end{bmatrix} } \end{equation}

The obtained inverse Jacobian matrix is shown in Table tab:inverse_jacobian_sensor_metrology_frame.

0.463	0.268	0.268
5.263	-2.632	-2.632
0.0	3.922	-3.922

Computing relative position between Crystals

In the previous sections, the motion of the individual crystals have been computed.

We wish to express the relative pose of the primary and secondary crystals $[d_{h,z},\ r_{h,y},\ r_{h,x}]$ or $[d_{r,z},\ r_{r,y},\ r_{r,x}]$.

The sign conventions for the relative crystal pose are:

• An increase of $d_{h,z}$ means the two crystals are further apart
• An increase of $r_{h,}$ means that the second crystals experiences a rotation around $y$ with respect to the primary crystal
• An increase of $r_{h,x}$ means that the second crystals experiences a rotation around $x$ with respect to the primary crystal

We therefore have the following relation (same for "hall" and "ring" crystals):

\begin{equation} \boxed{ \begin{bmatrix} d_{h,z} \\ r_{h,y} \\ r_{h,x} \end{bmatrix} = \begin{bmatrix} d_{2h,z} \\ r_{2h,y} \\ r_{2h,x} \end{bmatrix} - \begin{bmatrix} d_{1h,z} \\ r_{1h,y} \\ r_{1h,x} \end{bmatrix} - \begin{bmatrix} d_{mf,z} \\ r_{mf,y} \\ r_{mf,x} \end{bmatrix} } \end{equation}

The relative pose can be expressed as a function of the interferometers using the Jacobian matrices for the "hall" crystals:

\begin{equation} \boxed{ \begin{bmatrix} d_{h,z} \\ r_{h,y} \\ r_{h,x} \end{bmatrix} = \bm{J}_{2h,s}^{-1} \begin{bmatrix} z_{2h,ur} \\ z_{2h,ch} \\ z_{2h,dr} \end{bmatrix} - \bm{J}_{1h,s}^{-1} \begin{bmatrix} z_{1h,ur} \\ z_{1h,ch} \\ z_{1h,dr} \end{bmatrix} - \bm{J}_{mf,s}^{-1} \begin{bmatrix} z_{mf,u} \\ z_{mf,dh} \\ z_{mf,dr} \end{bmatrix} } \end{equation}

As well as for the "ring" crystals:

\begin{equation} \boxed{ \begin{bmatrix} d_{r,z} \\ r_{r,y} \\ r_{r,x} \end{bmatrix} = \bm{J}_{2r,s}^{-1} \begin{bmatrix} z_{2r,ur} \\ z_{2r,cr} \\ z_{2r,dr} \end{bmatrix} - \bm{J}_{1r,s}^{-1} \begin{bmatrix} z_{1r,ur} \\ z_{1r,cr} \\ z_{1r,dr} \end{bmatrix} - \bm{J}_{mf,s}^{-1} \begin{bmatrix} z_{mf,u} \\ z_{mf,dr} \\ z_{mf,dr} \end{bmatrix} } \end{equation}

Summary - List of notations

There are 5 Jacobian matrices that are used to convert the 15 interferometers to the relative pose between the primary and secondary crystals as well as 2 Jacobian matrices for the actuators. All Jacobian matrices are summarized in Table tab:jacobian_matrices.

Notation	Variable	Description
$\bm{J}_{1h,s}$	J_1h_s	Converts interferometers to the first "hall" crystal pose
$\bm{J}_{2h,s}$	J_2h_s	Converts interferometers to the second "hall" crystal pose
$\bm{J}_{1r,s}$	J_1r_s	Converts interferometers to the first "ring" crystal pose
$\bm{J}_{2r,s}$	J_2r_s	Converts interferometers to the second "ring" crystal pose
$\bm{J}_{mf,s}$	J_mf_s	Converts interferometers to the first "hall" crystal pose
$\bm{J}_{h,a}$	J_h_a	Converts Fastjack motion to the second "hall" crystal pose
$\bm{J}_{r,a}$	J_r_a	Converts Fastjack motion to the second "ring" crystal pose

The 15 interferometer measurements are summarized in Table tab:interferometer_list.

Notation	Variable	Interferometer
$z_{1h,ur}$	z_1h_ur	First "Hall" Crystal, "upstream-ring"
$z_{1h,ch}$	z_1h_ch	First "Hall" Crystal, "center-hall"
$z_{1h,dr}$	z_1h_dr	First "Hall" Crystal, "downstream-ring"
$z_{2h,ur}$	z_2h_ur	Second "Hall" Crystal, "upstream-ring"
$z_{2h,ch}$	z_2h_ch	Second "Hall" Crystal, "center-hall"
$z_{2h,dr}$	z_2h_dr	Second "Hall" Crystal, "downstream-ring"
$z_{1r,uh}$	z_1r_uh	First "Hall" Crystal, "upstream-hall"
$z_{1r,cr}$	z_1r_cr	First "Hall" Crystal, "center-ring"
$z_{1r,dh}$	z_1r_dh	First "Hall" Crystal, "downstream-hall"
$z_{2r,uh}$	z_2r_uh	Second "Hall" Crystal, "upstream-hall"
$z_{2r,cr}$	z_2r_cr	Second "Hall" Crystal, "center-ring"
$z_{2r,dh}$	z_2r_dh	Second "Hall" Crystal, "downstream-hall"
$z_{mf,u}$	z_mf_u	Metrology Frame, "upstream"
$z_{mf,dh}$	z_mf_dh	Metrology Frame, "downstream-hall"
$z_{mf,dr}$	z_mf_dr	Metrology Frame, "downstream-ring"

From the 15 interferometers, several crystal pose are computed. They are summarized in Table tab:crystal_pose_list.

Notation	Variable	Description
$d_{1h,z}$	d_1h_z	First "Hall" Crystal, z-translation
$r_{1h,y}$	r_1h_y	First "Hall" Crystal, y-rotation
$r_{1h,x}$	r_1h_x	First "Hall" Crystal, x-rotation
$d_{2h,z}$	d_2h_z	Second "Hall" Crystal, z-translation
$r_{2h,y}$	r_2h_y	Second "Hall" Crystal, y-rotation
$r_{2h,x}$	r_2h_x	Second "Hall" Crystal, x-rotation
$d_{1r,z}$	d_1r_z	First "Ring" Crystal, z-translation
$r_{1r,y}$	r_1r_y	First "Ring" Crystal, y-rotation
$r_{1r,x}$	r_1r_x	First "Ring" Crystal, x-rotation
$d_{2r,z}$	d_2r_z	Second "Ring" Crystal, z-translation
$r_{2r,y}$	r_2r_y	Second "Ring" Crystal, y-rotation
$r_{2r,x}$	r_2r_x	Second "Ring" Crystal, x-rotation
$d_{mf,z}$	d_mf_z	Metrology Frame, z-translation (top relative to bottom)
$r_{mf,y}$	r_mf_y	Metrology Frame, y-rotation (top relative to bottom)
$r_{mf,x}$	r_mf_x	Metrology Frame, x-rotation (top relative to bottom)

And finally, the relative pose between the first and second crystals are defined in Table tab:crystal_relative_pose_list.

Notation	Variable	Description
$d_{h,z}$	d_h_z	Relative distance between the "hall" crystals
$r_{h,y}$	r_h_y	Relative y-rotation of the 2nd "hall" crystal w.r.t. the primary
$r_{h,x}$	r_h_x	Relative x-rotation of the 2nd "hall" crystal w.r.t. the primary
$d_{r,z}$	d_r_z	Relative distance between the "ring" crystals
$r_{r,y}$	r_r_y	Relative y-rotation of the 2nd "ring" crystal w.r.t. the primary
$r_{r,x}$	r_r_x	Relative x-rotation of the 2nd "ring" crystal w.r.t. the primary

Save Kinematics

All the Jacobian matrix are exported so that there can be easily imported for computation purposes.

save('mat/dcm_kinematics.mat', 'J_1h_s', 'J_1r_s', 'J_2h_s', 'J_2r_s', 'J_mf_s', 'J_h_a', 'J_r_a')

Open Loop System Identification

<<sec:open_loop_identification>>

Introduction   ignore

Identification

Let's considered the system $\bm{G}(s)$ with:

• 3 inputs: force applied to the 3 fast jacks
• 3 outputs: measured displacement by the 3 interferometers pointing at the ring second crystal

It is schematically shown in Figure fig:schematic_system_inputs_outputs.

\begin{tikzpicture}
  % Blocs
  \node[block] (G) {$\bm{G}(s)$};

  % Connections and labels
  \draw[->] ($(G.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} u_{u_r} \\ u_{u_h} \\ u_d \end{bmatrix}$} -- (G.west);
  \draw[->] (G.east)  -- ++(1.5, 0) node[above left]{$\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}$};
\end{tikzpicture}

Dynamical system with inputs and outputs

The system is identified from the Simscape model.

%% Input/Output definition
clear io; io_i = 1;

%% Inputs
% Control Input {3x1} [N]
io(io_i) = linio([mdl, '/control_system'], 1, 'openinput');  io_i = io_i + 1;

%% Outputs
% Interferometers {3x1} [m]
io(io_i) = linio([mdl, '/DCM'], 1, 'openoutput'); io_i = io_i + 1;

%% Extraction of the dynamics
G = linearize(mdl, io);

size(G)

size(G)
State-space model with 3 outputs, 3 inputs, and 24 states.

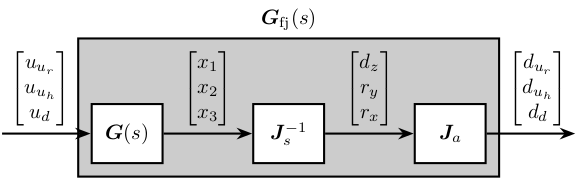
Plant in the frame of the fastjacks

load('dcm_kinematics.mat');

Using the forward and inverse kinematics, we can computed the dynamics from piezo forces to axial motion of the 3 fastjacks (see Figure fig:schematic_jacobian_frame_fastjack).

\begin{tikzpicture}
  % Blocs
  \node[block] (G) {$\bm{G}(s)$};
  \node[block, right=1.5 of G] (Js) {$\bm{J}_{s}^{-1}$};
  \node[block, right=1.5 of Js] (Ja) {$\bm{J}_{a}$};

  % Connections and labels
  \draw[->] ($(G.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} u_{u_r} \\ u_{u_h} \\ u_d \end{bmatrix}$} -- (G.west);
  \draw[->] (G.east)  -- node[midway, above]{$\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}$} (Js.west);
  \draw[->] (Js.east) -- node[midway, above]{$\begin{bmatrix} d_z \\ r_y \\ r_x \end{bmatrix}$} (Ja.west);
  \draw[->] (Ja.east) -- ++(1.5, 0) node[above left]{$\begin{bmatrix} d_{u_r} \\ d_{u_h} \\ d_{d} \end{bmatrix}$};

  \begin{scope}[on background layer]
    \node[fit={(G.south west) ($(Ja.east)+(0, 1.4)$)}, fill=black!20!white, draw, inner sep=6pt] (system) {};
    \node[above] at (system.north) {$\bm{G}_{\text{fj}}(s)$};
  \end{scope}
\end{tikzpicture}

Use of Jacobian matrices to obtain the system in the frame of the fastjacks

%% Compute the system in the frame of the fastjacks
G_pz = J_a_h*inv(J_2h_s)*G;

The DC gain of the new system shows that the system is well decoupled at low frequency.

dcgain(G_pz)

4.4407e-09	2.7656e-12	1.0132e-12
2.7656e-12	4.4407e-09	1.0132e-12
1.0109e-12	1.0109e-12	4.4424e-09

The bode plot of $\bm{G}_{\text{fj}}(s)$ is shown in Figure fig:bode_plot_plant_fj.

G_pz = diag(1./diag(dcgain(G_pz)))*G_pz;

Bode plot of the diagonal and off-diagonal elements of the plant in the frame of the fast jacks

Computing the system in the frame of the fastjack gives good decoupling at low frequency (until the first resonance of the system).

Plant in the frame of the crystal

\begin{tikzpicture}
  % Blocs
  \node[block] (G) {$\bm{G}(s)$};
  \node[block, left=1.5 of G] (Ja) {$\bm{J}_{a}^{-T}$};
  \node[block, right=1.5 of G] (Js) {$\bm{J}_{s}^{-1}$};

  % Connections and labels
  \draw[->] ($(Ja.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} \mathcal{F}_{z} \\ \mathcal{M}_{y} \\ \mathcal{M}_{x} \end{bmatrix}$} -- (Ja.west);
  \draw[->] (Ja.east)  -- node[midway, above]{$\begin{bmatrix} u_{u_r} \\ u_{u_h} \\ u_d \end{bmatrix}$} (G.west);
  \draw[->] (G.east) -- node[midway, above]{$\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}$} (Js.west);
  \draw[->] (Js.east) -- ++(1.5, 0) node[above left]{$\begin{bmatrix} d_z \\ r_y \\ r_x \end{bmatrix}$};

  \begin{scope}[on background layer]
    \node[fit={(Ja.south west) ($(Js.east)+(0, 1.4)$)}, fill=black!20!white, draw, inner sep=6pt] (system) {};
    \node[above] at (system.north) {$\bm{G}_{\text{cr}}(s)$};
  \end{scope}
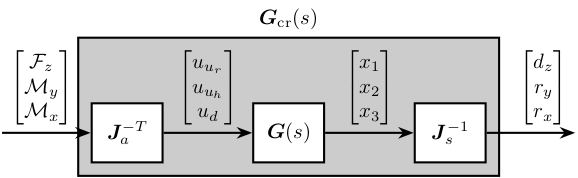
\end{tikzpicture}

Use of Jacobian matrices to obtain the system in the frame of the crystal

G_mr = inv(J_s_r)*G*inv(J_a_r');

dcgain(G_mr)

1.9978e-09	3.9657e-09	7.7944e-09
3.9656e-09	8.4979e-08	-1.5135e-17
7.7944e-09	-3.9252e-17	1.834e-07

This results in a coupled system. The main reason is that, as we map forces to the center of the ring crystal and not at the center of mass/stiffness of the moving part, vertical forces will induce rotation and torques will induce vertical motion.

Open-Loop Noise Budgeting

<<sec:dcm_noise_budget>>

Introduction   ignore

\begin{tikzpicture}
  % Blocs
  \node[block] (G) {$G(s)$};
  \node[addb,  left= of G] (adddu) {};
  \node[block, left= of adddu] (K) {$K(s)$};
  \node[addb={+}{}{}{}{-},  left= of K] (subL) {};
  \node[addb,  right= of G] (addd) {};
  \node[addb,  below right=0.8 and 0.6 of addd] (adddn) {};

  % Connections and labels
  \draw[->] (subL.east) -- (K.west);
  \draw[->] (K.east) -- (adddu.west);
  \draw[->] (adddu.east) -- (G.west);
  \draw[->] (G.east) -- (addd.west);
  \draw[->] (addd-|adddn)node[branch]{}node[above]{$y_{\text{fj}}$} -- (adddn.north);
  \draw[->] (adddn.west) -| (subL.south) node[below right]{$y_{\text{fj},m}$};
  \draw[<-] (adddu.north) -- ++(0, 1) node[below right]{$d_u$};
  \draw[<-] (addd.north) -- ++(0, 1) node[below right]{$d_{\text{fj}}$};
  \draw[<-] (adddn.east) -- ++(1, 0)coordinate(dn) node[above left]{$n_{\text{fj}}$};
  \draw[->] (addd.east) -- (addd-|dn);
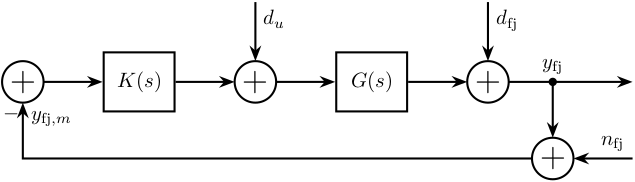
\end{tikzpicture}

Schematic representation of the control loop in the frame of one fast jack

Power Spectral Density of signals

Interferometer noise:

Wn = 6e-11*(1 + s/2/pi/200)/(1 + s/2/pi/60); % m/sqrt(Hz)

Measurement noise: 0.79 [nm,rms]

DAC noise (amplified by the PI voltage amplifier, and converted to newtons):

Wdac = tf(3e-8); % V/sqrt(Hz)
Wu = Wdac*22.5*10; % N/sqrt(Hz)

DAC noise: 0.95 [uV,rms]

Disturbances:

Wd = 5e-7/(1 + s/2/pi); % m/sqrt(Hz)

Disturbance motion: 0.61 [um,rms]

%% Save ASD of noise and disturbances
save('mat/asd_noises_disturbances.mat', 'Wn', 'Wu', 'Wd');

Open Loop disturbance and measurement noise

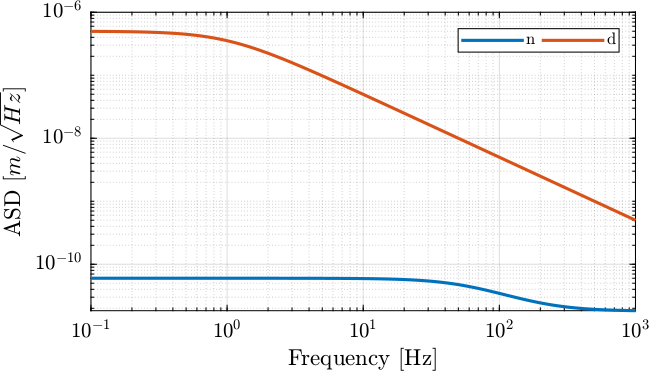
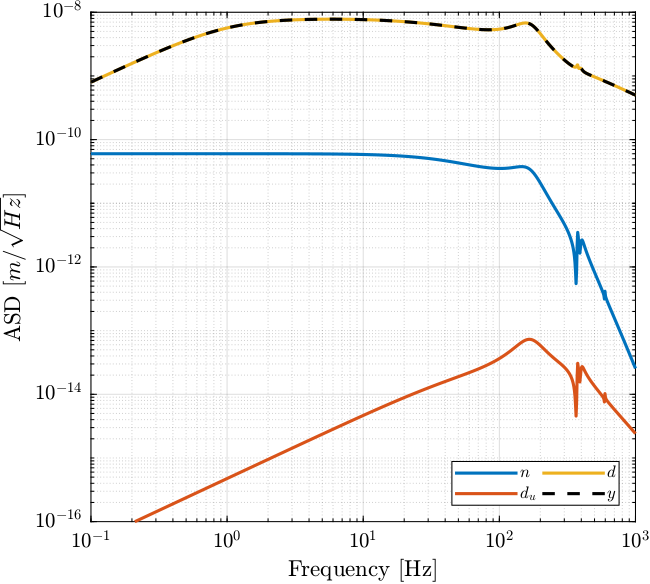
The comparison of the amplitude spectral density of the measurement noise and of the jack parasitic motion is performed in Figure fig:open_loop_noise_budget_fast_jack. It confirms that the sensor noise is low enough to measure the motion errors of the crystal.

Open Loop noise budgeting

Active Damping Plant (Strain gauges)

<<sec:active_damping_strain_gauges>>

Introduction   ignore

In this section, we wish to see whether if strain gauges fixed to the piezoelectric actuator can be used for active damping.

Identification

%% Input/Output definition
clear io; io_i = 1;

%% Inputs
% Control Input {3x1} [N]
io(io_i) = linio([mdl, '/control_system'], 1, 'openinput');  io_i = io_i + 1;

%% Outputs
% Strain Gauges {3x1} [m]
io(io_i) = linio([mdl, '/DCM'], 2, 'openoutput'); io_i = io_i + 1;

%% Extraction of the dynamics
G_sg = linearize(mdl, io);

dcgain(G_sg)

4.4443e-09	1.0339e-13	3.774e-14
1.0339e-13	4.4443e-09	3.774e-14
3.7792e-14	3.7792e-14	4.4444e-09

Bode Plot of the transfer functions from piezoelectric forces to strain gauges measuremed displacements

As the distance between the poles and zeros in Figure fig:iff_plant_bode_plot is very small, little damping can be actively added using the strain gauges. This will be confirmed using a Root Locus plot.

Relative Active Damping

Krad_g1 = eye(3)*s/(s^2/(2*pi*500)^2 + 2*s/(2*pi*500) + 1);

As can be seen in Figure fig:relative_damping_root_locus, very little damping can be added using relative damping strategy using strain gauges.

Root Locus for the relative damping control

Krad = -g*Krad_g1;

Damped Plant

The controller is implemented on Simscape, and the damped plant is identified.

%% Input/Output definition
clear io; io_i = 1;

%% Inputs
% Control Input {3x1} [N]
io(io_i) = linio([mdl, '/control_system'], 1, 'input');  io_i = io_i + 1;

%% Outputs
% Force Sensor {3x1} [m]
io(io_i) = linio([mdl, '/DCM'], 1, 'openoutput'); io_i = io_i + 1;

%% DCM Kinematics
load('dcm_kinematics.mat');

%% Identification of the Open Loop plant
controller.type = 0; % Open Loop
G_ol = J_a_r*inv(J_s_r)*linearize(mdl, io);
G_ol.InputName  = {'u_ur',  'u_uh',  'u_d'};
G_ol.OutputName = {'d_ur',  'd_uh',  'd_d'};

%% Identification of the damped plant with Relative Active Damping
controller.type = 2; % RAD
G_dp = J_a_r*inv(J_s_r)*linearize(mdl, io);
G_dp.InputName  = {'u_ur',  'u_uh',  'u_d'};
G_dp.OutputName = {'d_ur',  'd_uh',  'd_d'};

Bode plot of both the open-loop plant and the damped plant using relative active damping

Active Damping Plant (Force Sensors)

<<sec:active_damping_iff>>

Introduction   ignore

Force sensors are added above the piezoelectric actuators. They can consists of a simple piezoelectric ceramic stack. See for instance cite:fleming10_integ_strain_force_feedb_high.

Identification

%% Input/Output definition
clear io; io_i = 1;

%% Inputs
% Control Input {3x1} [N]
io(io_i) = linio([mdl, '/control_system'], 1, 'openinput');  io_i = io_i + 1;

%% Outputs
% Force Sensor {3x1} [m]
io(io_i) = linio([mdl, '/DCM'], 3, 'openoutput'); io_i = io_i + 1;

%% Extraction of the dynamics
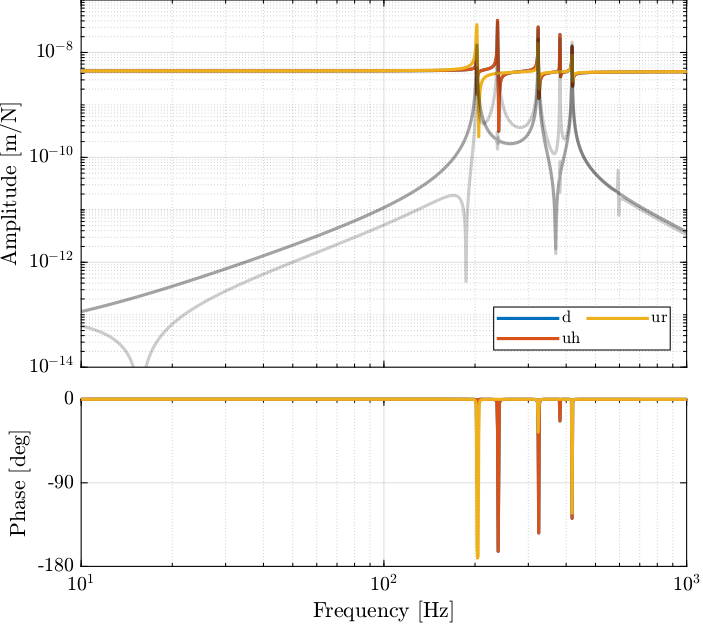
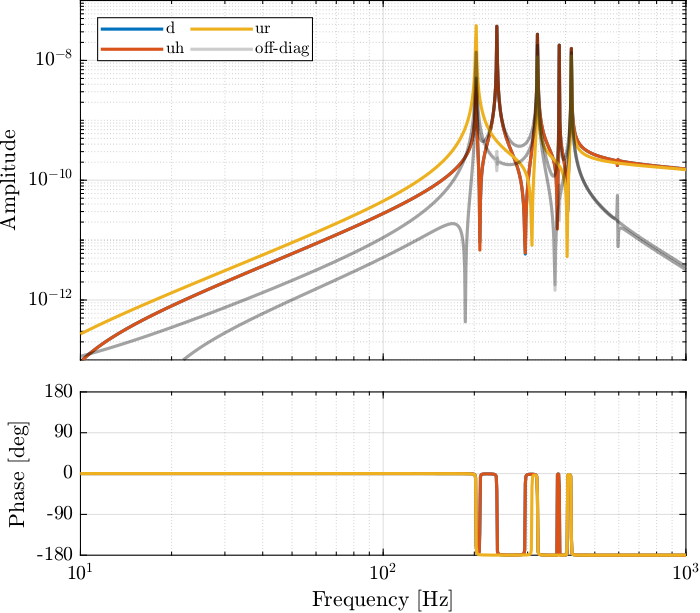
G_fs = linearize(mdl, io);

The Bode plot of the identified dynamics is shown in Figure fig:iff_plant_bode_plot. At high frequency, the diagonal terms are constants while the off-diagonal terms have some roll-off.

Bode plot of IFF Plant

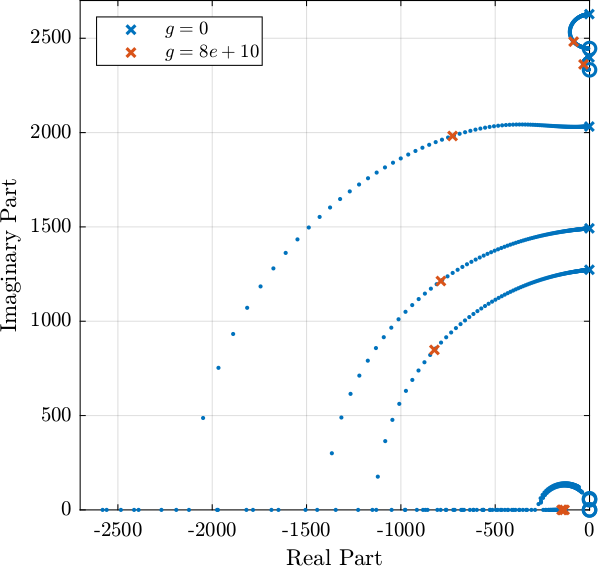
Controller - Root Locus

We want to have integral action around the resonances of the system, but we do not want to integrate at low frequency. Therefore, we can use a low pass filter.

%% Integral Force Feedback Controller
Kiff_g1 = eye(3)*1/(1 + s/2/pi/20);

Root Locus plot for the IFF Control strategy

%% Integral Force Feedback Controller with optimal gain
Kiff = g*Kiff_g1;

%% Save the IFF controller
save('mat/Kiff.mat', 'Kiff');

Damped Plant

Both the Open Loop dynamics (see Figure fig:schematic_jacobian_frame_fastjack) and the dynamics with IFF (see Figure fig:schematic_jacobian_frame_fastjack_iff) are identified.

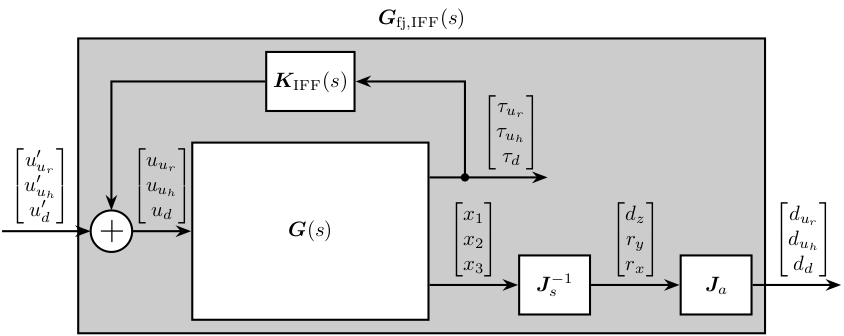
We are here interested in the dynamics from $\bm{u}^\prime = [u_{u_r}^\prime,\ u_{u_h}^\prime,\ u_d^\prime]$ (input of the damped plant) to $\bm{d}_{\text{fj}} = [d_{u_r},\ d_{u_h},\ d_d]$ (motion of the crystal expressed in the frame of the fast-jacks). This is schematically represented in Figure fig:schematic_jacobian_frame_fastjack_iff.

\begin{tikzpicture}
  % Blocs
  \node[block={4.0cm}{3.0cm}] (G) {$\bm{G}(s)$};
  \coordinate[] (inputF) at ($(G.south west)!0.5!(G.north west)$);
  \coordinate[] (outputF) at ($(G.south east)!0.8!(G.north east)$);
  \coordinate[] (outputL) at ($(G.south east)!0.2!(G.north east)$);

  \node[block, right=1.5 of outputL] (Js) {$\bm{J}_{s}^{-1}$};
  \node[block, right=1.5 of Js] (Ja) {$\bm{J}_{a}$};
  \node[addb,  left= of G] (addF) {};
  \node[block, above=0.5 of G] (Kiff) {$\bm{K}_{\text{IFF}}(s)$};

  % Connections and labels
  \draw[->] ($(addF.west)+(-1.5,0)$) node[above right]{$\begin{bmatrix} u_{u_r}^\prime \\ u_{u_h}^\prime \\ u_d^\prime \end{bmatrix}$} -- (addF.west);
  \draw[->] (addF.east) -- node[miday, above]{$\begin{bmatrix} u_{u_r} \\ u_{u_h} \\ u_d \end{bmatrix}$} (inputF);
  \draw[->] (outputF) -- ++(2.0, 0) node[above left]{$\begin{bmatrix} \tau_{u_r} \\ \tau_{u_h} \\ \tau_d \end{bmatrix}$};
  \draw[->] ($(outputF) + (0.6, 0)$)node[branch]{} |- (Kiff.east);
  \draw[->] (Kiff.west) -| (addF.north);
  \draw[->] (outputL) -- node[midway, above]{$\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}$} (Js.west);
  \draw[->] (Js.east) -- node[midway, above]{$\begin{bmatrix} d_z \\ r_y \\ r_x \end{bmatrix}$} (Ja.west);
  \draw[->] (Ja.east) -- ++(1.5, 0) node[above left]{$\begin{bmatrix} d_{u_r} \\ d_{u_h} \\ d_{d} \end{bmatrix}$};

  \begin{scope}[on background layer]
    \node[fit={(G.south -| addF.west) (Ja.east |- Kiff.north)}, fill=black!20!white, draw, inner sep=6pt] (system) {};
    \node[above] at (system.north) {$\bm{G}_{\text{fj,IFF}}(s)$};
  \end{scope}
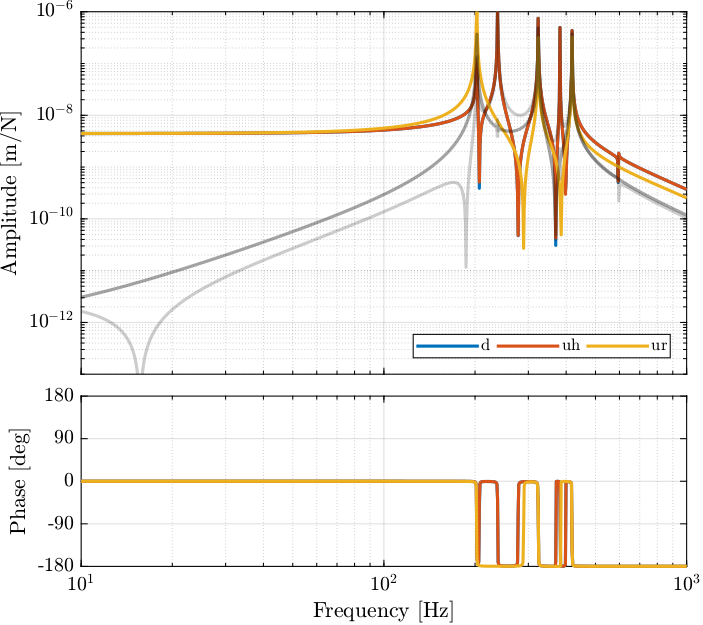
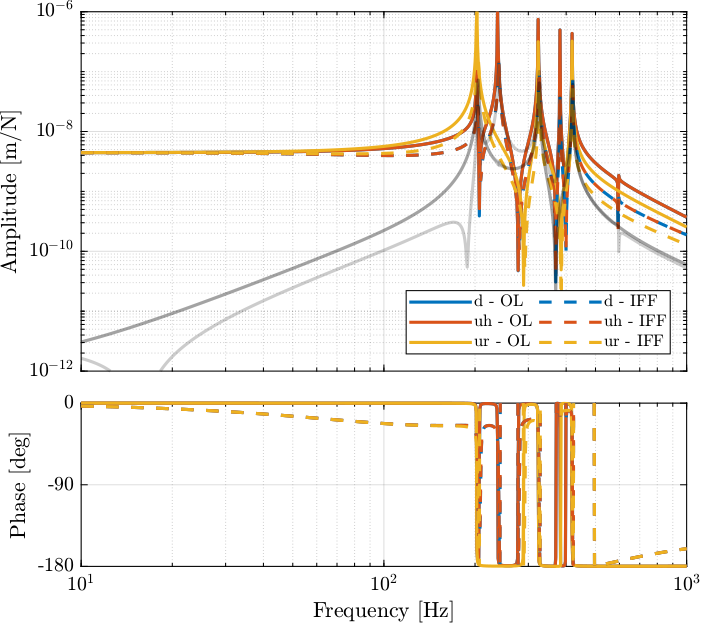
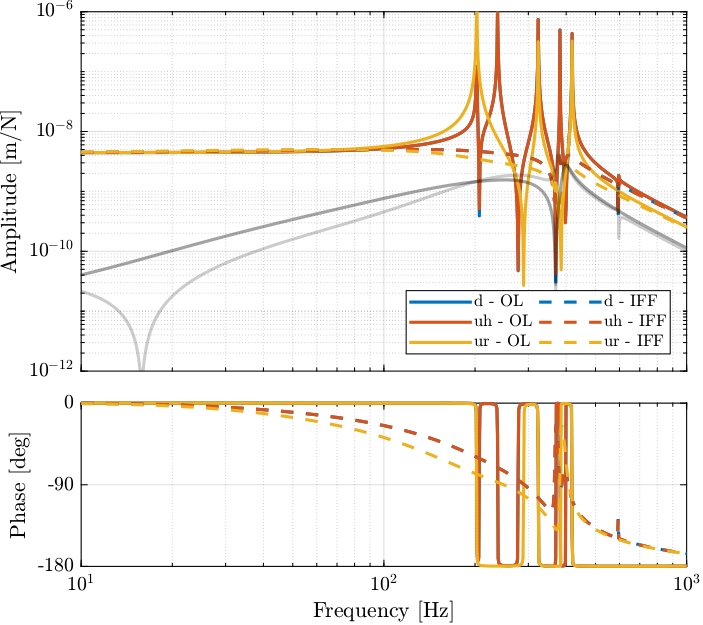
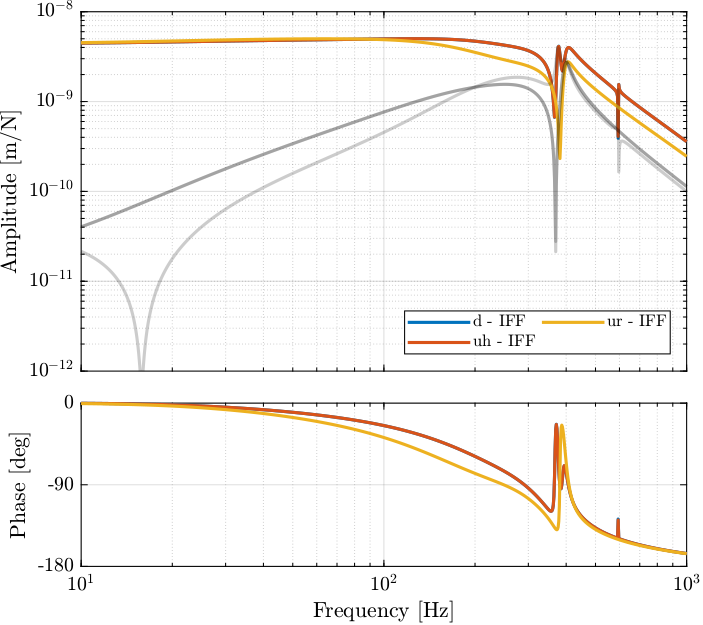
\end{tikzpicture}

Use of Jacobian matrices to obtain the system in the frame of the fastjacks

The dynamics from $\bm{u}$ to $\bm{d}_{\text{fj}}$ (open-loop dynamics) and from $\bm{u}^\prime$ to $\bm{d}_{\text{fs}}$ are compared in Figure fig:comp_damped_undamped_plant_iff_bode_plot. It is clear that the Integral Force Feedback control strategy is very effective in damping the resonances of the plant.

Bode plot of both the open-loop plant and the damped plant using IFF

The Integral Force Feedback control strategy is very effective in damping the modes present in the plant.

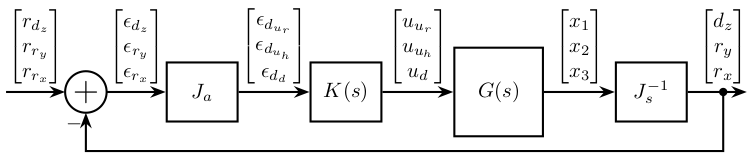
Feedback Control

\begin{tikzpicture}
  % Blocs
  \node[block={1.5cm}{1.5cm}] (G) at (0,0) {$\bm{G}(s)$};
  \node[block, right=1.2 of G] (Js) {$\bm{J}_{s}^{-1}$};

  \node[block, left=1.2 of G] (Khac) {$\bm{K}(s)$};
  \node[block, left=1.2 of Khac] (Ja) {$\bm{J}_{a}$};
  \node[addb={+}{}{}{}{-},  left=1.0 of Ja] (subL) {};

  % Connections and labels
  \draw[->] (Khac.east) -- node[midway, above]{$\begin{bmatrix} u_{u_r} \\ u_{u_h} \\ u_d \end{bmatrix}$} (G.west);
  \draw[->] (G.east) -- node[midway, above]{$\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}$} (Js.west);
  \draw[->] (Js.east) -- ++(1.0, 0);

  \draw[->] ($(subL.west) + (-1.0, 0)$) -- node[midway, above]{$\begin{bmatrix} r_{d_z} \\ r_{r_y} \\ r_{r_x} \end{bmatrix}$} (subL.west);
  \draw[->] (subL.east) -- node[midway, above]{$\begin{bmatrix} \epsilon_{d_z} \\ \epsilon_{r_y} \\ \epsilon_{r_x} \end{bmatrix}$} (Ja.west);
  \draw[->] (Ja.east) -- node[midway, above]{$\begin{bmatrix} \epsilon_{d_{u_r}} \\ \epsilon_{d_{u_h}} \\ \epsilon_{d_d} \end{bmatrix}$} (Khac.west);

  \draw[->] ($(Js.east) + (0.6, 0)$)node[branch]{}node[above]{$\begin{bmatrix} d_z \\ r_y \\ r_x \end{bmatrix}$} -- ++(0, -1.0) -| (subL.south);
\end{tikzpicture}

HAC-LAC (IFF) architecture

<<sec:hac_iff>>

Introduction   ignore

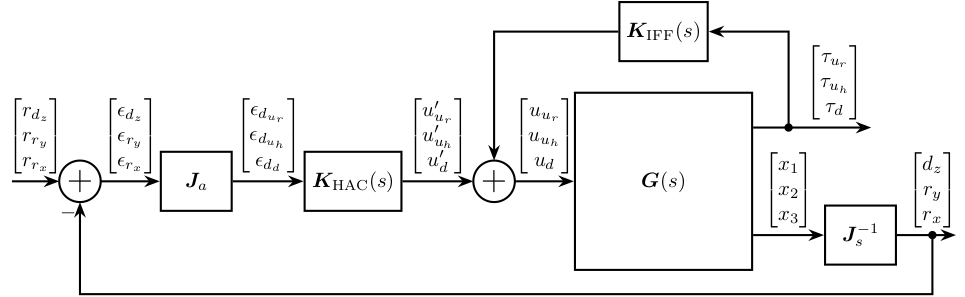
The HAC-LAC architecture is shown in Figure fig:schematic_jacobian_frame_fastjack_hac_iff.

\begin{tikzpicture}
  % Blocs
  \node[block={3.0cm}{3.0cm}] (G) {$\bm{G}(s)$};
  \coordinate[] (inputF) at ($(G.south west)!0.5!(G.north west)$);
  \coordinate[] (outputF) at ($(G.south east)!0.8!(G.north east)$);
  \coordinate[] (outputL) at ($(G.south east)!0.2!(G.north east)$);

  \node[block, right=1.2 of outputL] (Js) {$\bm{J}_{s}^{-1}$};

  \node[addb,  left= of G] (addF) {};
  \node[block, above=0.5 of G] (Kiff) {$\bm{K}_{\text{IFF}}(s)$};

  \node[block, left=1.2 of addF] (Khac) {$\bm{K}_{\text{HAC}}(s)$};
  \node[block, left=1.2 of Khac] (Ja) {$\bm{J}_{a}$};
  \node[addb={+}{}{}{}{-},  left=1.0 of Ja] (subL) {};


  % Connections and labels
  \draw[->] (Khac.east) -- node[midway, above]{$\begin{bmatrix} u_{u_r}^\prime \\ u_{u_h}^\prime \\ u_d^\prime \end{bmatrix}$} (addF.west);
  \draw[->] (addF.east) -- node[midway, above]{$\begin{bmatrix} u_{u_r} \\ u_{u_h} \\ u_d \end{bmatrix}$} (inputF);
  \draw[->] (outputF) -- ++(2.0, 0) node[above left]{$\begin{bmatrix} \tau_{u_r} \\ \tau_{u_h} \\ \tau_d \end{bmatrix}$};
  \draw[->] ($(outputF) + (0.6, 0)$)node[branch]{} |- (Kiff.east);
  \draw[->] (Kiff.west) -| (addF.north);
  \draw[->] (outputL) -- node[midway, above]{$\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}$} (Js.west);
  \draw[->] (Js.east) -- ++(1.0, 0);


  \draw[->] ($(subL.west) + (-0.8, 0)$) -- node[midway, above]{$\begin{bmatrix} r_{d_z} \\ r_{r_y} \\ r_{r_x} \end{bmatrix}$} (subL.west);
  \draw[->] (subL.east) -- node[midway, above]{$\begin{bmatrix} \epsilon_{d_z} \\ \epsilon_{r_y} \\ \epsilon_{r_x} \end{bmatrix}$} (Ja.west);
  \draw[->] (Ja.east) -- node[midway, above]{$\begin{bmatrix} \epsilon_{d_{u_r}} \\ \epsilon_{d_{u_h}} \\ \epsilon_{d_d} \end{bmatrix}$} (Khac.west);

  \draw[->] ($(Js.east) + (0.6, 0)$)node[branch]{}node[above]{$\begin{bmatrix} d_z \\ r_y \\ r_x \end{bmatrix}$} -- ++(0, -1.0) -| (subL.south);
\end{tikzpicture}

System Identification

Let's identify the damped plant.

Bode Plot of the plant for the High Authority Controller (transfer function from $\bm{u}^\prime$ to $\bm{\epsilon}_d$)

High Authority Controller

Let's design a controller with a bandwidth of 100Hz. As the plant is well decoupled and well approximated by a constant at low frequency, the high authority controller can easily be designed with SISO loop shaping.

%% Controller design
wc = 2*pi*100; % Wanted crossover frequency [rad/s]
a = 2; % Lead parameter

Khac = diag(1./diag(abs(evalfr(G_dp, 1j*wc)))) * ... % Diagonal controller
        wc/s * ... % Integrator
        1/(sqrt(a))*(1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a))) * ... % Lead
        1/(s^2/(4*wc)^2 + 2*s/(4*wc) + 1); % Low pass filter

%% Save the HAC controller
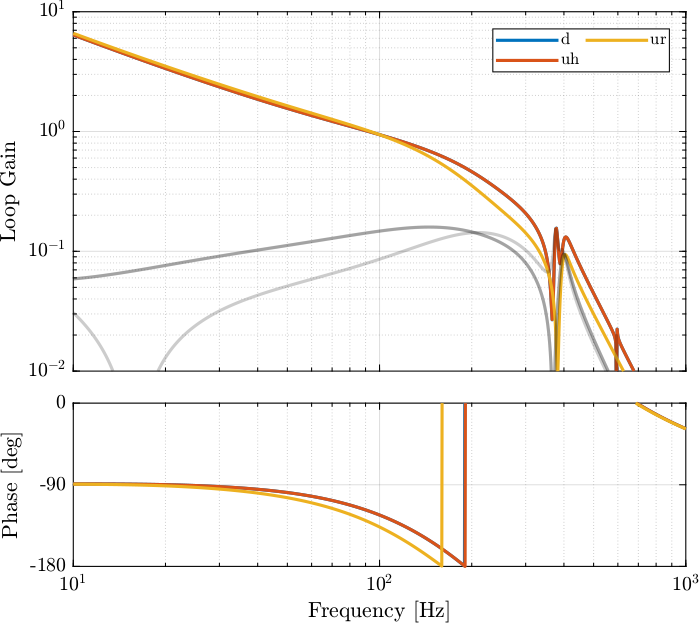
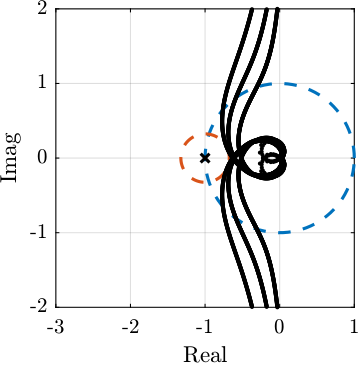
save('mat/Khac_iff.mat', 'Khac');

%% Loop Gain
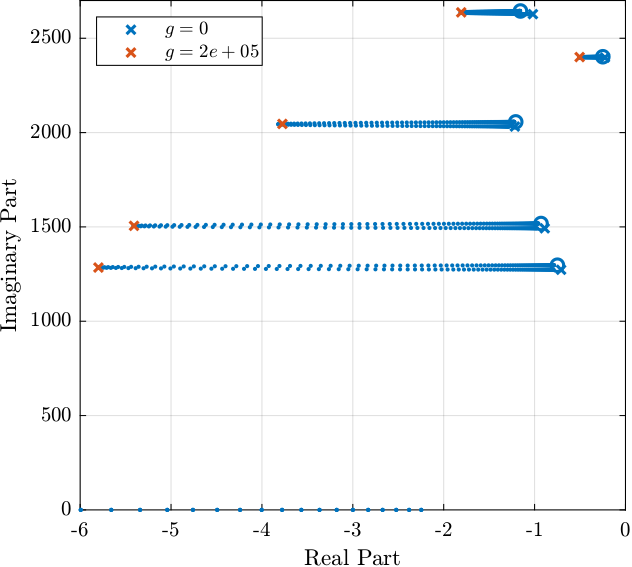
L_hac_lac = G_dp * Khac;

Bode Plot of the Loop gain for the High Authority Controller

As shown in the Root Locus plot in Figure fig:loci_hac_iff_fast_jack, the closed loop system should be stable.

Root Locus for the High Authority Controller

Performances

In order to estimate the performances of the HAC-IFF control strategy, the transfer function from motion errors of the stepper motors to the motion error of the crystal is identified both in open loop and with the HAC-IFF strategy.

It is first verified that the closed-loop system is stable:

isstable(T_hl)

1

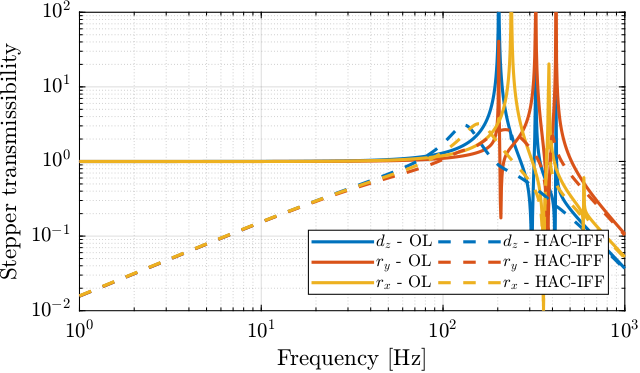
And both transmissibilities are compared in Figure fig:stepper_transmissibility_comp_ol_hac_iff.

Comparison of the transmissibility of errors from vibrations of the stepper motor between the open-loop case and the hac-iff case.

The HAC-IFF control strategy can effectively reduce the transmissibility of the motion errors of the stepper motors. This reduction is effective inside the bandwidth of the controller.

Close Loop noise budget

Let's compute the amplitude spectral density of the jack motion errors due to the sensor noise, the actuator noise and disturbances.

%% Computation of ASD of contribution of inputs to the closed-loop motion
% Error due to disturbances
asd_d = abs(squeeze(freqresp(Wd*(1/(1 + G_dp(1,1)*Khac(1,1))), f, 'Hz')));
% Error due to actuator noise
asd_u = abs(squeeze(freqresp(Wu*(G_dp(1,1)/(1 + G_dp(1,1)*Khac(1,1))), f, 'Hz')));
% Error due to sensor noise
asd_n = abs(squeeze(freqresp(Wn*(G_dp(1,1)*Khac(1,1)/(1 + G_dp(1,1)*Khac(1,1))), f, 'Hz')));

The closed-loop ASD is then:

%% ASD of the closed-loop motion
asd_cl = sqrt(asd_d.^2 + asd_u.^2 + asd_n.^2);

The obtained ASD are shown in Figure fig:close_loop_asd_noise_budget_hac_iff.

Closed Loop noise budget

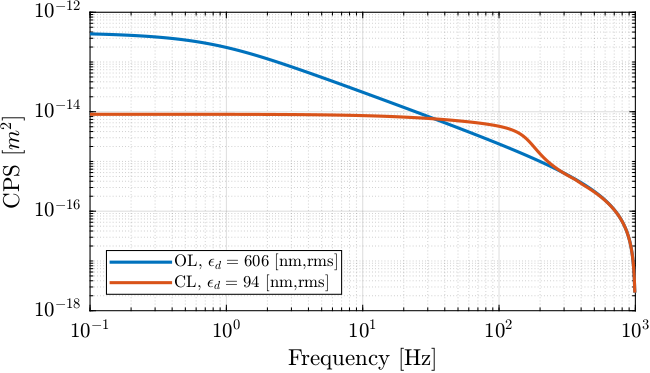
Let's compare the open-loop and close-loop cases (Figure fig:cps_comp_ol_cl_hac_iff).

Cumulative Power Spectrum of the open-loop and closed-loop motion error along one fast-jack

Bibliography   ignore