84 KiB
Voltage Amplifier PD200 - Test Bench
- Introduction
- Requirements PD200 Expected characteristics
- Voltage Amplifier Model
- Transfer Function measurement
- Noise measurement
- Introduction
- Measurement Setup
- Model of the setup
- Quantization Noise of the ADC
- EG&G - Amplifier noise measurement
- Femto - Amplifier noise measurement
- PD200 - Low frequency noise measurement
- PD200 - High frequency noise measurement
- 16bits DAC noise measurement
- Noise of the full setup with 16bits DAC
- 20bits DAC noise measurement
- Noise of the full setup with 20bits DAC
- PD200 Amplifier noise model
- Comparison to other commercial amplifiers
- Conclusion
This report is also available as a pdf.
\clearpage
Introduction ignore
The goal of this test bench is to characterize the Voltage amplifier PD200 from PiezoDrive.
This document is organized as follows:
- Section sec:requirements: the requirements for the amplifiers and the characteristics of the PD200 amplifiers as advertise in the datasheet are listed.
- Section sec:amplifier_model: a very simple amplifier model consisting of a transfer function and a noise source is described.
- Section sec:tf_meas: the transfer function from input voltage to output voltage is identified.
- Section sec:noise_meas: the power spectral density of the amplifier's noise is measured
- Section sec:comp_pi_cedrat: the characteristics of the PD200 amplifier are compared to the E.505 amplifier from PI and to the LA75 from cedrat
- Section sec:conclusion: the measured characteristics of the PD200 amplifier are compared with the requirements
Requirements PD200 Expected characteristics
<<sec:requirements>>
A picture of the PD200 amplifier is shown in Figure fig:amplifier_PD200.
The specifications as well as the amplifier characteristics as shown in the datasheet are summarized in Table tab:pd200_characteristics.
| Characteristics | Manual | Specification |
|---|---|---|
| Input Voltage Range | +/- 10 [V] | +/- 10 [V] |
| Output Voltage Range | -50/150 [V] | -20/150 [V] |
| Gain | 20 [V/V] | |
| Maximum RMS current | 0.9 [A] | > 50 [mA] |
| Maximum Pulse current | 10 [A] | |
| Slew Rate | 150 [V/us] | |
| Noise (10uF load) | 0.7 [mV RMS] | < 2 [mV rms] |
| Small Signal Bandwidth (10uF load) | 7.4 [kHz] | > 5 [kHz] |
| Large Signal Bandwidth (150V, 10uF) | 300 [Hz] |
The most important characteristics are the large (small signal) bandwidth > 5 [kHz] and the small noise (< 2 [mV RMS]).
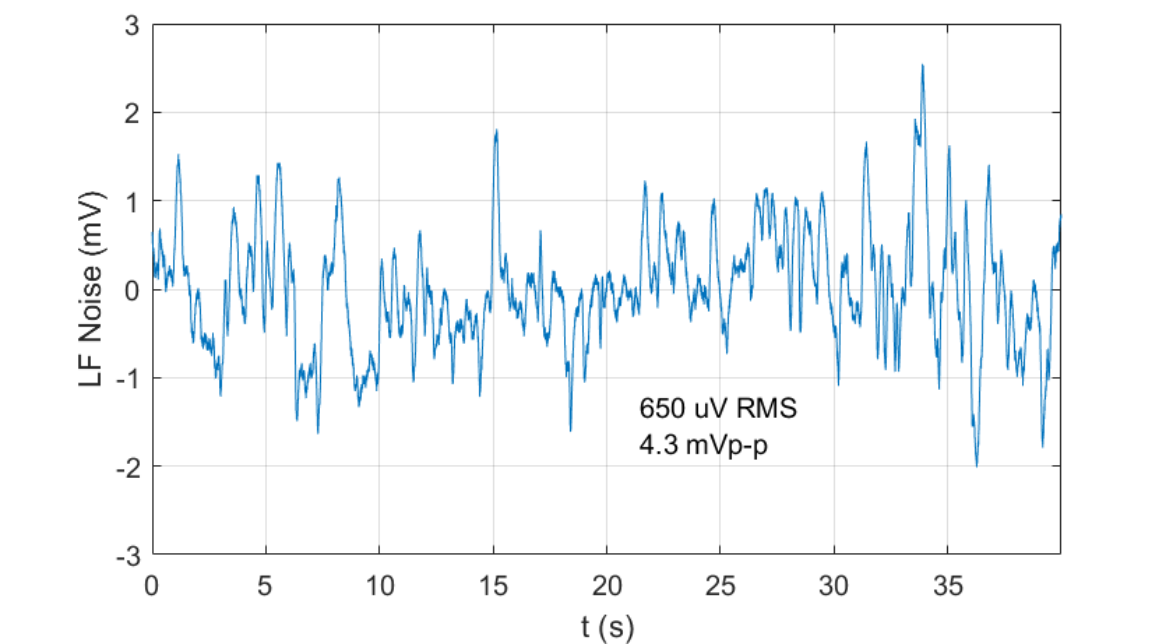
For a load capacitance of $10\,\mu F$, the expected $-3\,dB$ bandwidth is $6.4\,kHz$ (Figure fig:pd200_expected_small_signal_bandwidth) and the low frequency noise is $650\,\mu V\,\text{rms}$ (Figure fig:pd200_expected_noise).
These two characteristics are respectively measured in Section sec:tf_meas and Section sec:noise_meas.
#+caption:Expected small signal bandwidth
Voltage Amplifier Model
<<sec:amplifier_model>>
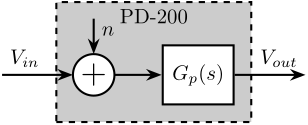
The Amplifier is characterized by its dynamics $G_p(s)$ from voltage inputs $V_{in}$ to voltage output $V_{out}$. Ideally, the gain from $V_{in}$ to $V_{out}$ is constant over a wide frequency band with very small phase drop.
It is also characterized by its input noise $n$.
The objective is therefore to determine the transfer function $G_p(s)$ from the input voltage to the output voltage as well as the Power Spectral Density $S_n(\omega)$ of the amplifier input noise.
As $G_p$ depends on the load capacitance, it should be measured when loading the amplifier with a $10\,\mu F$ capacitor.
\begin{tikzpicture}
\node[addb] (add) at (0,0) {};
\node[block, right=0.8 of add] (G) {$G_p(s)$};
\draw[<-] (add.west) -- ++(-1.2, 0) node[above right]{$V_{in}$};
\draw[->] (add.east) -- (G.west);
\draw[<-] (add.north) -- ++(0, 0.6) node[below right](n){$n$};
\draw[->] (G.east) -- ++(1.2, 0) node[above left]{$V_{out}$};
\begin{scope}[on background layer]
\node[fit={(G.south-|add.west) (n.north-|G.east)}, inner sep=8pt, draw, dashed, fill=black!20!white] (P) {};
\node[below] at (P.north) {PD-200};
\end{scope}
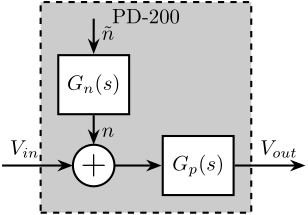
\end{tikzpicture}The input noise of the amplifier $n$ can be further modeled by shaping a white noise with unitary PSD $\tilde{n}$ with a transfer function $G_n(s)$ as shown in Figure fig:setup-dynamics-measurement.
The Amplitude Spectral Density $\Gamma_n$ is then:
\begin{equation} \Gamma_n(\omega) = |G_n(j\omega)| \Gamma_{\tilde{n}}(\omega) \end{equation}with $\Gamma_{\tilde{n}}(\omega) = 1$.
\begin{tikzpicture}
\node[addb] (add) at (0,0) {};
\node[block, above=0.5 of add] (Gn) {$G_n(s)$};
\node[block, right=0.8 of add] (G) {$G_p(s)$};
\draw[<-] (add.west) -- ++(-1.2, 0) node[above right]{$V_{in}$};
\draw[->] (add.east) -- (G.west);
\draw[->] (Gn.south) -- (add.north) node[above right]{$n$};
\draw[<-] (Gn.north) -- ++(0, 0.6) node[below right](n){$\tilde{n}$};
\draw[->] (G.east) -- ++(1.2, 0) node[above left]{$V_{out}$};
\begin{scope}[on background layer]
\node[fit={(G.south east) (n.north-|Gn.west)}, inner sep=8pt, draw, dashed, fill=black!20!white] (P) {};
\node[below] at (P.north) {PD-200};
\end{scope}
\end{tikzpicture}Transfer Function measurement
<<sec:tf_meas>>
Introduction ignore
In this section, the transfer function of the PD200 amplifier is measured:
- Section sec:tf_meas_setup: the measurement setup is described
- Section sec:tf_meas_w_max: the maximum sinusoidal excitation frequency is estimated in order to not overload the amplifier
- Section sec:meas_small_signal_bandwidth: the small signal bandwidth measurement results are shown
- Section sec:model_small_signal_bandwidth: a model of the small signal dynamics of the amplifier is obtained
- Section sec:bandwidth_amplitude: the amplifier's transfer function is estimated for several input amplitudes
Setup
<<sec:tf_meas_setup>>
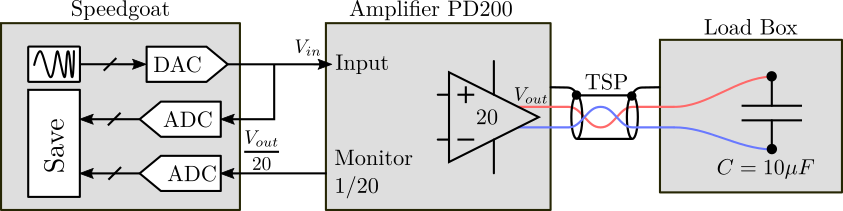
In order to measure the transfer function from the input voltage $V_{in}$ to the output voltage $V_{out}$, the test bench shown in Figure fig:setup-dynamics-measurement is used.
Here are the documentation of the equipment used for this test bench:
- Voltage Amplifier: PD200
- Load Capacitor: Film Capacitors 600V 10uF 5%
- DAC/ADC: IO313 Speedgoat Interface
For this measurement, the sampling frequency of the Speedgoat ADC should be as high as possible.
Maximum Frequency/Voltage to not overload the amplifier
<<sec:tf_meas_w_max>>
Then the maximum output current of the amplifier is reached, the amplifier automatically shuts down itself. We should then make sure that the output current does not reach this maximum specified current.
The maximum current is 1A [rms] which corresponds to 0.7A in amplitude of the sin wave.
The impedance of the capacitance is: \[ Z_C(\omega) = \frac{1}{jC\omega} \]
Therefore the relation between the output current amplitude and the output voltage amplitude for sinusoidal waves of frequency $\omega$: \[ V_{out} = \frac{1}{C\omega} I_{out} \]
Moreover, there is a gain of 20 between the input voltage and the output voltage: \[ 20 V_{in} = \frac{1}{C\omega} I_{out} \]
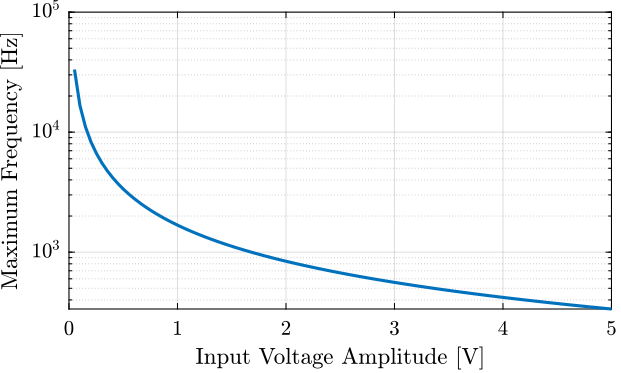
For a specified voltage input amplitude $V_{in}$, the maximum frequency at which the output current reaches its maximum value is:
\begin{equation} \boxed{\omega_{\text{max}} = \frac{1}{20 C V_{in}} I_{out,\text{max}}} \end{equation}with:
- $\omega_{\text{max}}$ the maximum input sinusoidal frequency in Radians per seconds
- $C$ the load capacitance in Farads
- $V_{in}$ the input voltage sinusoidal amplitude in Volts
- $I_{out,\text{max}}$ the specified maximum output current in Amperes
$\omega_{\text{max}}/2\pi$ as a function of $V_{in}$ is shown in Figure fig:max_frequency_voltage.
When doing sweep sine excitation, we make sure not to reach this maximum excitation frequency.
Small Signal Bandwidth
<<sec:meas_small_signal_bandwidth>>
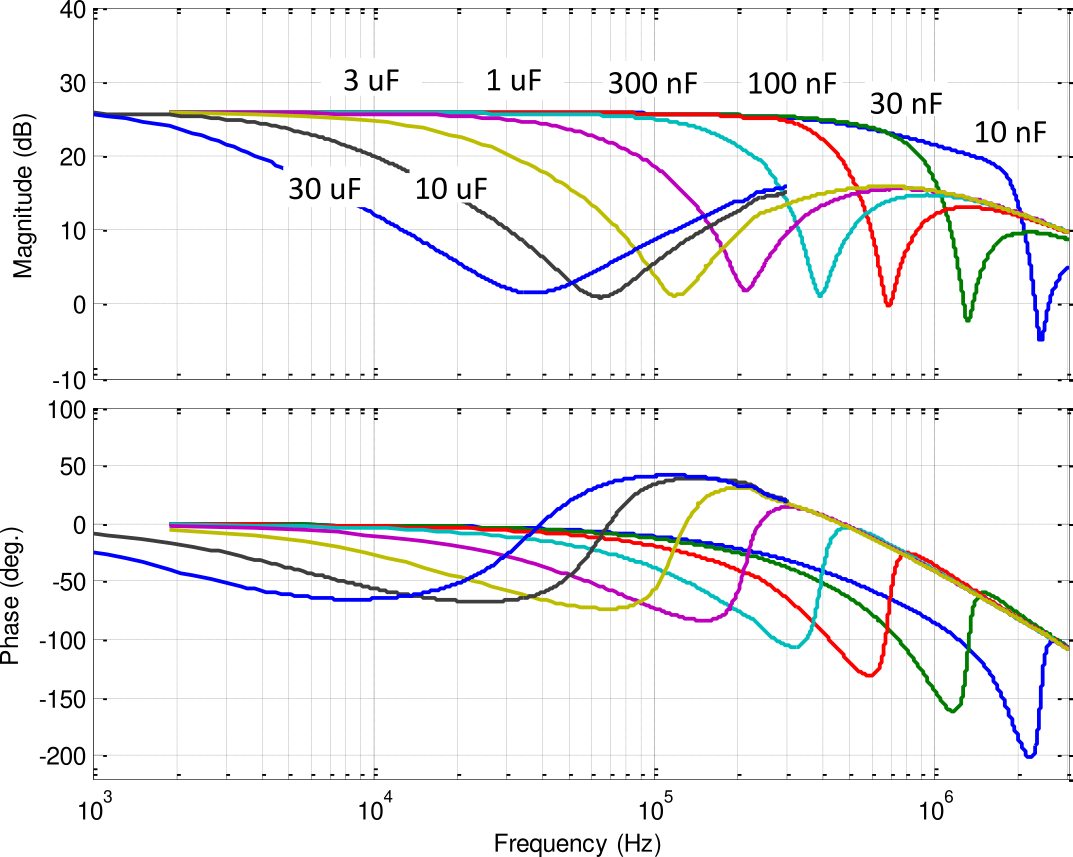
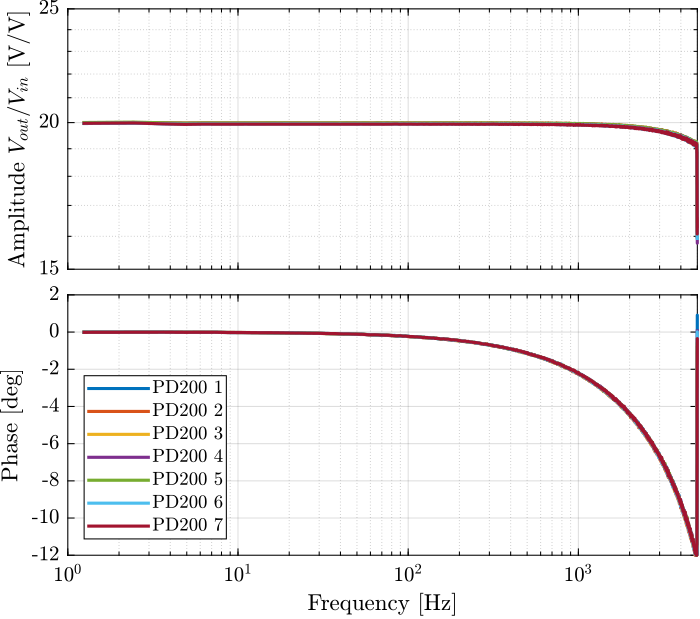
Here the small signal dynamics of all the 7 PD200 amplifiers are identified.
A (logarithmic) sweep sine excitation voltage is generated by the Speedgoat DAC with an amplitude of 0.1V and a frequency going from 1Hz up to 5kHz.
The output voltage of the PD200 amplifier is measured thanks to the monitor voltage of the PD200 amplifier. The input voltage of the PD200 amplifier (the generated voltage by the DAC) is measured with another ADC of the Speedgoat. This way, the time delay related to the ADC will not be apparent in the results.
The obtained transfer functions from $V_{in}$ to $V_{out}$ are shown in Figure fig:pd200_small_signal_tf.
We can see the very well matching between all the 7 amplifiers. The amplitude is constant over a wide frequency band and the phase drop is limited to less than 1 degree up to 500Hz.
Model of the amplifier small signal dynamics
<<sec:model_small_signal_bandwidth>>
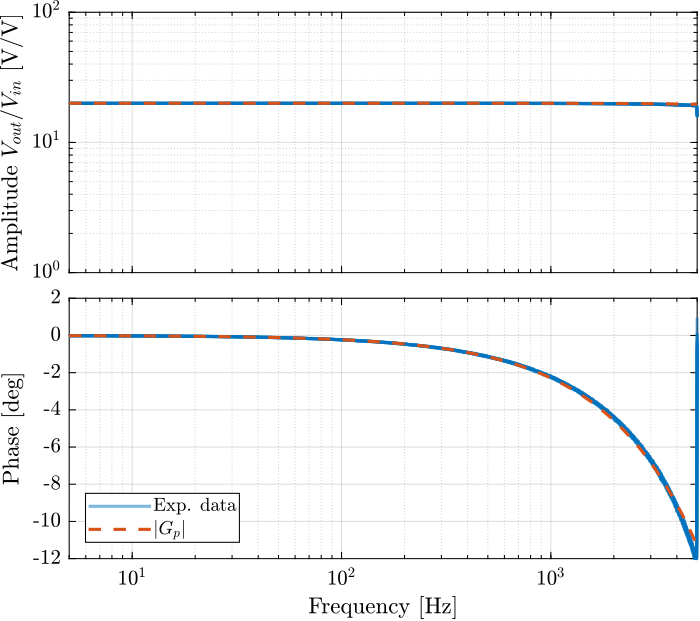
The identified dynamics in Figure fig:pd200_small_signal_tf can very well be modeled this dynamics with a first order low pass filter (even a constant could work fine).
Below is the defined transfer function $G_p(s)$.
Gp = 20/(1 + s/2/pi/25e3);Comparison of the model with the identified dynamics is shown in Figure fig:pd200_small_signal_tf_model.
#+caption:Bode plot of $G_d(s)$ as well as the identified transfer functions of all 7 amplifiers
And finally this model is saved.
save('mat/pd200_model.mat', 'Gp');Large Signal Bandwidth
<<sec:bandwidth_amplitude>>
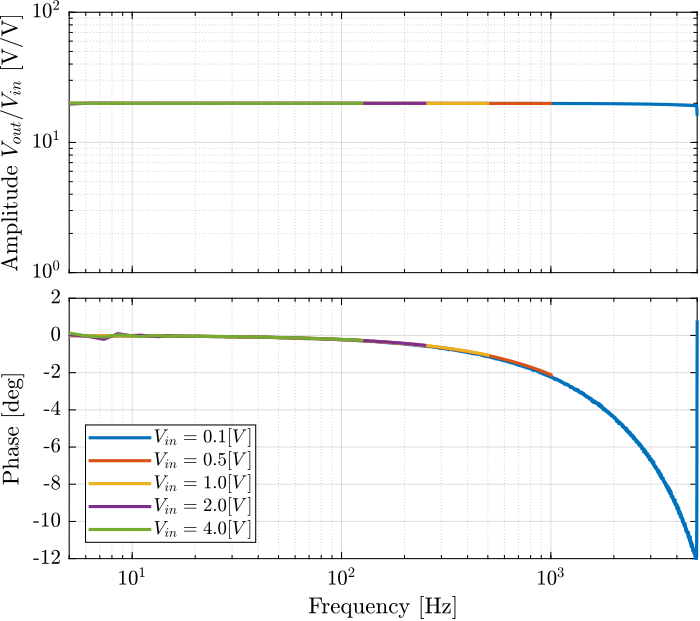
The PD200 amplifiers will most likely not be used for large signals, but it is still nice to see how the amplifier dynamics is changing with the input voltage amplitude.
Several identifications using sweep sin were performed with input voltage amplitude ranging from 0.1V to 4V. The maximum excitation frequency for each amplitude was limited from the estimation in Section sec:tf_meas_w_max.
The obtained transfer functions for the different excitation amplitudes are shown in Figure fig:pd200_large_signal_tf. It is shown that the input voltage amplitude does not affect that much the amplifier dynamics.
Noise measurement
<<sec:noise_meas>>
Introduction ignore
In this part, the goal is to measure the noise of the PD200 voltage amplifier. This noise can be separated into an input voltage noise and an input current noise. However, the input voltage noise has much larger effects than the input current noise and we will only try to measure the input voltage noise.
In section sec:noise_setup, the measurement setup is described and a model (block diagram) of the setup is given in section sec:noise_model.
Then, the noise contribution of each element is measured:
- Section sec:noise_quantization: the quantization noise of the ADC is estimated
- Sections sec:noise_egg and sec:noise_femto: the noise of the low-noise amplifiers are estimated
- Sections sec:low_freq_noise_pd200 and sec:high_freq_noise_pd200:: the input voltage noise of the PD200 amplifier is estimated
- Section sec:noise_dac: the output noise of the DAC is measured
- Section sec:noise_full_measurement: the noise of the full measurement chain (DAC to PD200 to pre-amplifier to ADC) is measured and it is found that the DAC is the main source of noise
- Section sec:noise_ssi2v: the noise of an 20bits DAC is measured
- Section sec:noise_full_measurement_ssi2v: it is shown if using the 20bits DAC could lower the overall noise of the setup
Finally in section sec:pd200_noise_model, a model of the PD200 amplifier's noise is developed.
Here are the documentation of the equipment used for this test bench:
- Voltage Amplifier PD200
- Load Capacitor: Film Capacitors 600V 10uF 5%
- Low Noise Voltage Amplifiers EG&G 5113 and Femto DLPVA
- ADC: IO313 Speedgoat card
- 16bits DAC: IO313 Speedgoat card
- 20bits DAC: SSI2V
Measurement Setup
<<sec:noise_setup>>
As the output noise of the PD200 voltage amplifier is foreseen to be around 1mV rms in a bandwidth from DC to 1MHz, it is not possible to directly measure it with an ADC. We need to amplify the noise before digitizing the signal. To do so, we need to use a low noise voltage amplifier with a noise density much smaller than the measured noise of the PD200 amplifier.
Let's first estimate the noise density of the PD200 amplifier. If we suppose a white noise, this correspond to an amplitude spectral density:
\begin{equation} \Gamma_{n}(\omega) \approx \frac{1\,mV}{\sqrt{1\,MHz}} = 1 \frac{\mu V}{\sqrt{Hz}} \end{equation}The input noise of the instrumentation amplifier should be then much smaller than the output noise of the PD200. We will use either the amplifier EG&G 5113 that has a noise of $\approx 4 nV/\sqrt{Hz}$ referred to its input or the Femto DLPVA amplifier with an input noise of $\approx 3nV/\sqrt{Hz}$.
The gain of the low-noise amplifier is then increased until the full range of the ADC is used. This gain should be around 1000 (60dB).
A representation of the measurement bench is shown in Figure fig:setup-noise-measurement.
Note that it is quite important to load the amplifier with the "Load Box" including a $10\,\mu F$ capacitor as the (high frequency) noise of the amplifier depends on the actual load being used.
Model of the setup
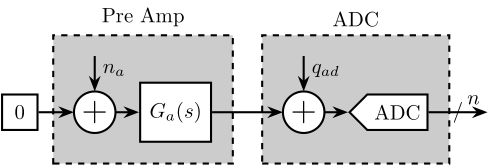
<<sec:noise_model>>
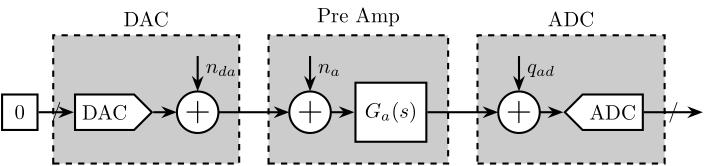
As shown in Figure fig:noise_meas_procedure, there are 4 elements involved in the measurement:
- a Digital to Analog Convert (DAC)
- the Voltage amplifier to be measured with a gain of 20 (PD200)
- a low noise voltage amplifier with a variable gain and integrated low pass filters and high pass filters
- an Analog to Digital Converter (ADC)
Each of these equipment has some noise:
- $q_{da}$: quantization noise of the DAC
- $n_{da}$: output noise of the DAC
- $n_p$: input noise of the PD200 (what we wish to characterize)
- $n_a$: input noise of the pre-amplifier
- $q_{ad}$: quantization noise of the ADC
\begin{tikzpicture}
% DAC
\node[DAC] (DAC) at (0,0) {DAC};
\node[addb, right=0.4 of DAC] (addqda){};
\node[addb, right=0.4 of addqda] (addnda){};
% PD200
\node[addb, right=1.2 of addnda] (addnp){};
\node[block, right=0.4 of addnp] (Gp){$G_p(s)$};
% Pre Amp
\node[addb, right=1.2 of Gp] (addna){};
\node[block, right=0.4 of addna] (Ga) {$G_a(s)$};
% ADC
\node[addb, right=1.2 of Ga] (addqad){};
\node[ADC, right=0.4 of addqad] (ADC) {ADC};
% \draw[->] (const.east) -- node[sloped]{$/$} (DAC.west);
\draw[<-] (DAC.west) -- node[sloped]{$/$} ++(-1.0, 0);
\draw[->] (DAC.east) -- (addqda.west);
\draw[->] (addqda.east) -- (addnda.west);
\draw[->] (addnda.east) -- (addnp.west);
\draw[->] (addnp.east) -- (Gp.west);
\draw[->] (Gp.east) -- (addna.west);
\draw[->] (addna.east) -- (Ga.west);
\draw[->] (Ga.east) -- (addqad.west);
\draw[->] (addqad.east) -- (ADC.west);
\draw[->] (ADC.east) -- node[sloped]{$/$} ++(1.0, 0) node[above left]{$n$};
\draw[<-] (addnda.north) -- ++(0, 0.6) node[below right](nda){$n_{da}$};
\draw[<-] (addqda.north) -- ++(0, 0.6) node[below right](qda){$q_{da}$};
\draw[<-] (addnp.north) -- ++(0, 0.6) node[below right](np){$n_{p}$};
\draw[<-] (addna.north) -- ++(0, 0.6) node[below right](na){$n_{a}$};
\draw[<-] (addqad.north) -- ++(0, 0.6) node[below right](qad){$q_{ad}$};
\coordinate[] (top) at (nda.north);
\coordinate[] (bot) at (Ga.south);
% DAC
\begin{scope}[on background layer]
\node[fit={(DAC.west|-bot) (addnda.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {DAC};
\end{scope}
% PD200
\begin{scope}[on background layer]
\node[fit={(addnp.west|-bot) (Gp.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {PD200};
\end{scope}
% 5113
\begin{scope}[on background layer]
\node[fit={(addna.west|-bot) (Ga.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {Pre Amp};
\end{scope}
% ADC
\begin{scope}[on background layer]
\node[fit={(addqad.west|-bot) (ADC.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {ADC};
\end{scope}
\end{tikzpicture}In the next sections, we wish to measure all these sources of noise and make sure that we can effectively characterize the noise $n_p$ of the PD200 amplifier.
Quantization Noise of the ADC
<<sec:noise_quantization>>
The quantization noise is something that can be predicted from the sampling frequency and the quantization of the ADC. Indeed, the Amplitude Spectral Density of the quantization noise of an ADC/DAC is equal to:
\begin{equation} \Gamma_q(\omega) = \frac{q}{\sqrt{12 f_s}} \end{equation}with:
- $q = \frac{\Delta V}{2^n}$ the quantization in [V], which is the corresponding value in [V] of the least significant bit
- $\Delta V$ is the full range of the ADC in [V]
- $n$ is the number of bits
- $f_s$ is the sample frequency in [Hz]
Let's estimate that with the ADC used for the measurements:
%% ADC Quantization noise
adc = struct();
adc.Delta_V = 20; % [V]
adc.n = 16; % number of bits
adc.Fs = 20e3; % [Hz]
adc.Gamma_q = adc.Delta_V/2^adc.n/sqrt(12*adc.Fs); % [V/sqrt(Hz)]The obtained Amplitude Spectral Density is
adc.Gamma_qEG&G - Amplifier noise measurement
<<sec:noise_egg>>
We now wish to measure the noise of the pre-amplifier. To do so, the input of the pre-amplifier is shunted with a 50Ohms resistor such that the pre-amplifier input voltage is just its input noise. Then, the gain of the amplifier is increased until the measured signal on the ADC is much larger than the quantization noise.
The Amplitude Spectral Density $\Gamma_n(\omega)$ of the measured signal $n$ is computed. Finally, the Amplitude Spectral Density of $n_a$ can be computed taking into account the gain of the pre-amplifier:
\begin{equation} \Gamma_{n_a}(\omega) \approx \frac{\Gamma_n(\omega)}{|G_a(\omega)|} \end{equation}\begin{tikzpicture}
\node[block={0.6cm}{0.6cm}] (const) {$0$};
% Pre Amp
\node[addb, right=0.6 of const] (addna) {};
\node[block, right=0.4 of addna] (Ga) {$G_a(s)$};
% ADC
\node[addb, right=1.2 of Ga] (addqad){};
\node[ADC, right=0.4 of addqad] (ADC) {ADC};
\draw[->] (const.east) -- (addna.west);
\draw[->] (addna.east) -- (Ga.west);
\draw[->] (Ga.east) -- (addqad.west);
\draw[->] (addqad.east) -- (ADC.west);
\draw[->] (ADC.east) -- node[sloped]{$/$} ++(1.0, 0) node[above left]{$n$};
\draw[<-] (addna.north) -- ++(0, 0.6) node[below right](na){$n_{a}$};
\draw[<-] (addqad.north) -- ++(0, 0.6) node[below right](qad){$q_{ad}$};
\coordinate[] (top) at (na.north);
\coordinate[] (bot) at (Ga.south);
% 5113
\begin{scope}[on background layer]
\node[fit={(addna.west|-bot) (Ga.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {Pre Amp};
\end{scope}
% ADC
\begin{scope}[on background layer]
\node[fit={(addqad.west|-bot) (ADC.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {ADC};
\end{scope}
\end{tikzpicture}The gain of the low noise amplifier is set to
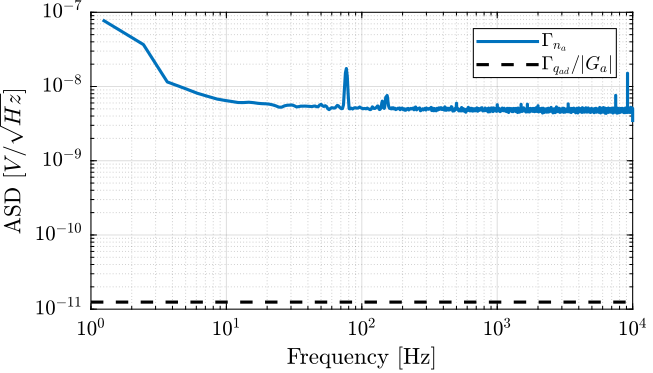
ans = egg.notes.pre_amp.gainThe obtained Amplitude Spectral Density of the Low Noise Voltage Amplifier is shown in Figure fig:asd_egg. The obtained noise amplitude is very closed to the one specified in the documentation of $4nV/\sqrt{Hz}$ at 1kHZ.
It is also verified that the quantization noise of the ADC is much smaller and what we are measuring is indeed the noise of the pre-amplifier.
Femto - Amplifier noise measurement
<<sec:noise_femto>>
Similarly to Section sec:noise_egg, the noise of the Femto amplifier is identified.
The obtained Amplitude spectral density is shown in Figure fig:asd_femto.
PD200 - Low frequency noise measurement
<<sec:low_freq_noise_pd200>>
The measurement setup is shown in Figure fig:noise_measure_setup_pd200. The input of the PD200 amplifier is shunted with a 50 Ohm resistor such that there in no voltage input expected the PD200 input voltage noise. The gain of the pre-amplifier is increased in order to measure a signal much larger than the quantization noise of the ADC.
\begin{tikzpicture}
\node[block={0.6cm}{0.6cm}] (const) {$0$};
% PD200
\node[addb, right=0.6 of const] (addnp){};
\node[block, right=0.4 of addnp] (Gp){$G_p(s)$};
% Pre Amp
\node[addb, right=1.2 of Gp] (addna) {};
\node[block, right=0.4 of addna] (Ga) {$G_a(s)$};
% ADC
\node[addb, right=1.2 of Ga] (addqad){};
\node[ADC, right=0.4 of addqad] (ADC) {ADC};
\draw[->] (const.east) -- (addnp.west);
\draw[->] (addnp.east) -- (Gp.west);
\draw[->] (Gp.east) -- (addna.west);
\draw[->] (addna.east) -- (Ga.west);
\draw[->] (Ga.east) -- (addqad.west);
\draw[->] (addqad.east) -- (ADC.west);
\draw[->] (ADC.east) -- node[sloped]{$/$} ++(1.0, 0) node[above left]{$n$};
\draw[<-] (addnp.north) -- ++(0, 0.6) node[below right](np){$n_{p}$};
\draw[<-] (addna.north) -- ++(0, 0.6) node[below right](na){$n_{a}$};
\draw[<-] (addqad.north) -- ++(0, 0.6) node[below right](qad){$q_{ad}$};
\coordinate[] (top) at (na.north);
\coordinate[] (bot) at (Ga.south);
% PD200
\begin{scope}[on background layer]
\node[fit={(addnp.west|-bot) (Gp.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {PD200};
\end{scope}
% 5113
\begin{scope}[on background layer]
\node[fit={(addna.west|-bot) (Ga.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {Pre Amp};
\end{scope}
% ADC
\begin{scope}[on background layer]
\node[fit={(addqad.west|-bot) (ADC.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {ADC};
\end{scope}
\end{tikzpicture}The measured low frequency (<20Hz) output noise of one of the PD200 amplifiers is shown in Figure fig:pd200_noise_time_lpf. It is very similar to the one specified in the datasheet in Figure fig:pd200_expected_noise.
The obtained RMS and peak to peak values of the measured output noise are shown in Table tab:rms_pkp_noise and found to be very similar to the specified ones.
| RMS [$\mu V$] | Peak to Peak [$mV$] | |
|---|---|---|
| Specification [$10\,\mu F$] | 714.0 | 4.3 |
| PD200 1 | 565.1 | 3.7 |
| PD200 2 | 767.6 | 3.5 |
| PD200 3 | 479.9 | 3.0 |
| PD200 4 | 615.7 | 3.5 |
| PD200 5 | 651.0 | 2.4 |
| PD200 6 | 473.2 | 2.7 |
| PD200 7 | 423.1 | 2.3 |
PD200 - High frequency noise measurement
<<sec:high_freq_noise_pd200>>
The measurement setup is the same as in Figure fig:noise_measure_setup_pd200.
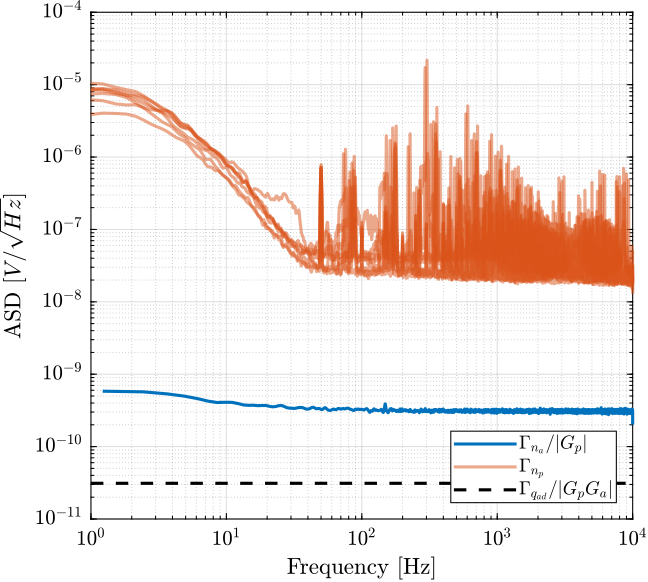
The Amplitude Spectral Density $\Gamma_n(\omega)$ of the measured signal by the ADC is computed. The Amplitude Spectral Density of the input voltage noise of the PD200 amplifier $n_p$ is then computed taking into account the gain of the pre-amplifier and the gain of the PD200 amplifier:
\begin{equation} \Gamma_{n_p}(\omega) = \frac{\Gamma_n(\omega)}{|G_p(j\omega) G_a(j\omega)|} \end{equation}And we verify that we are indeed measuring the noise of the PD200 and not the noise of the pre-amplifier by checking that:
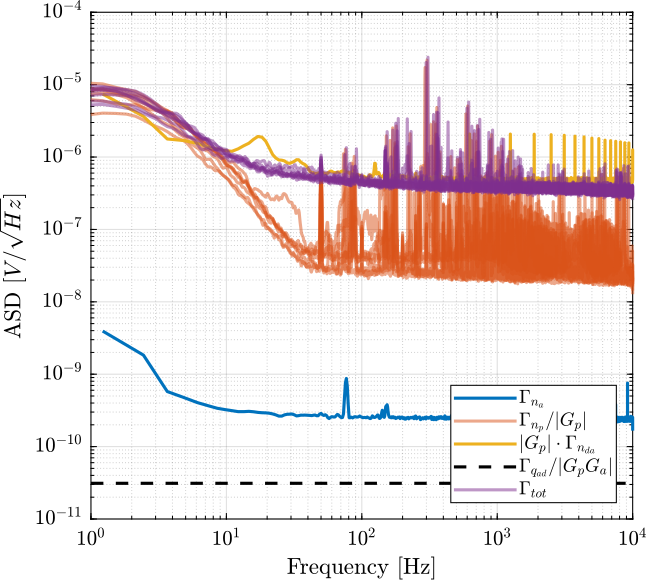
\begin{equation} \Gamma_{n_p}(\omega) |G_p(j\omega)| \ll \Gamma_{n_a} \end{equation}The Amplitude Spectral Density of the measured input noise is computed and shown in Figure fig:asd_noise_pd200_10uF.
It is verified that the contribution of the PD200 noise is much larger than the contribution of the pre-amplifier noise of the quantization noise.
The Amplitude Spectral Density of the input noise of the PD200 amplifiers present sharp peaks. It is not clear yet what causes such peaks and if these peaks have high influence on the total RMS noise of the amplifiers.
16bits DAC noise measurement
<<sec:noise_dac>>
In order not to have any quantization noise and only measure the output voltage noise of the DAC, we "ask" the DAC to output a zero voltage.
The measurement setup is schematically represented in Figure fig:noise_measure_setup_dac. The gain of the pre-amplifier is adjusted such that the measured amplified noise is much larger than the quantization noise of the ADC.
The Amplitude Spectral Density $\Gamma_n(\omega)$ of the measured signal is computed. The Amplitude Spectral Density of the DAC output voltage noise $n_{da}$ can be computed taking into account the gain of the pre-amplifier:
\begin{equation} \Gamma_{n_{da}}(\omega) = \frac{\Gamma_m(\omega)}{|G_a(\omega)|} \end{equation}And it is verified that the Amplitude Spectral Density of $n_{da}$ is much larger than the one of $n_a$:
\begin{equation} \Gamma_{n_{da}} \gg \Gamma_{n_a} \end{equation}\begin{tikzpicture}
\node[block={0.6cm}{0.6cm}] (const) {$0$};
% DAC
\node[DAC, right=0.6 of const] (DAC) {DAC};
\node[addb, right=0.4 of DAC] (addnda){};
% Pre Amp
\node[addb, right=1.2 of addnda] (addna) {};
\node[block, right=0.4 of addna] (Ga) {$G_a(s)$};
% ADC
\node[addb, right=1.2 of Ga] (addqad){};
\node[ADC, right=0.4 of addqad] (ADC) {ADC};
\draw[->] (const.east) -- node[sloped]{$/$} (DAC.west);
\draw[->] (DAC.east) -- (addnda.west);
\draw[->] (addnda.east) -- (addna.west);
\draw[->] (addna.east) -- (Ga.west);
\draw[->] (Ga.east) -- (addqad.west);
\draw[->] (addqad.east) -- (ADC.west);
\draw[->] (ADC.east) -- node[sloped]{$/$} ++(1.0, 0);
\draw[<-] (addnda.north) -- ++(0, 0.6) node[below right](nda){$n_{da}$};
\draw[<-] (addna.north) -- ++(0, 0.6) node[below right](na){$n_{a}$};
\draw[<-] (addqad.north) -- ++(0, 0.6) node[below right](qad){$q_{ad}$};
\coordinate[] (top) at (na.north);
\coordinate[] (bot) at (Ga.south);
% DAC
\begin{scope}[on background layer]
\node[fit={(DAC.west|-bot) (addnda.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {DAC};
\end{scope}
% 5113
\begin{scope}[on background layer]
\node[fit={(addna.west|-bot) (Ga.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {Pre Amp};
\end{scope}
% ADC
\begin{scope}[on background layer]
\node[fit={(addqad.west|-bot) (ADC.east|-top)}, inner sep=10pt, draw, dashed, fill=black!20!white] (P) {};
\node[above] at (P.north) {ADC};
\end{scope}
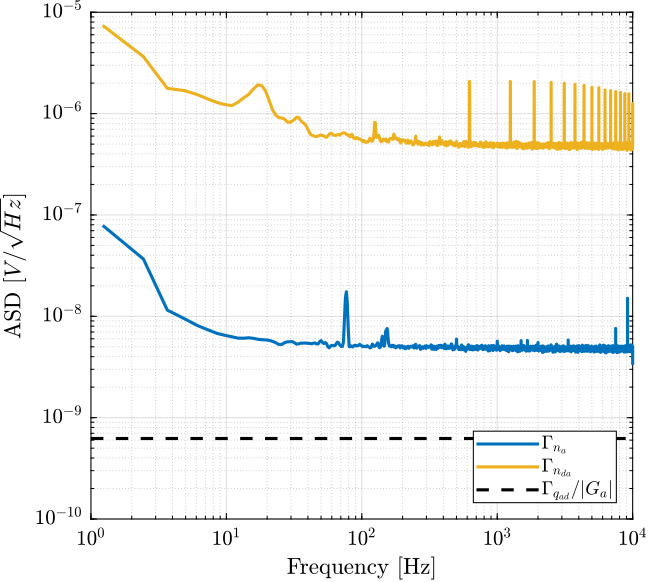
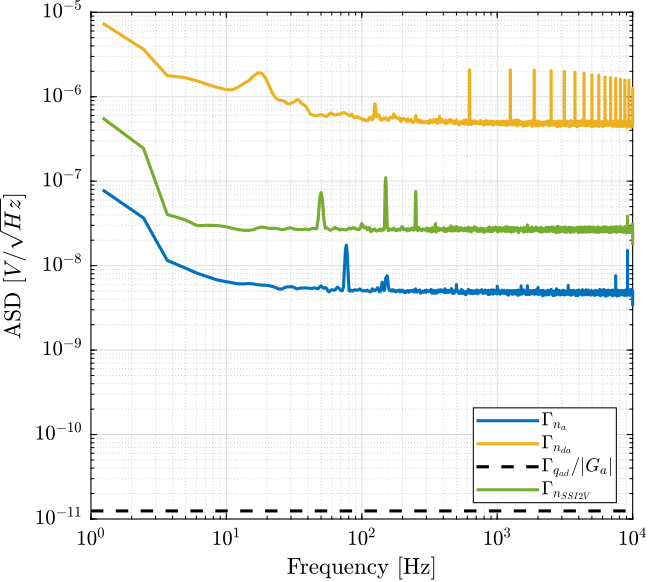
\end{tikzpicture}The obtained Amplitude Spectral Density of the DAC's output voltage is shown in Figure fig:asd_noise_dac.
Noise of the full setup with 16bits DAC
<<sec:noise_full_measurement>>
Let's now measure the noise of the full setup in Figure fig:noise_meas_procedure_bis and analyze the results.
The Amplitude Spectral Density of the measured noise is computed and the shown in Figure fig:asd_noise_tot.
We can very well see that to total measured noise is the sum of the DAC noise and the PD200 noise.
The input noise of the PD200 amplifier is limited by the output voltage noise of the DAC. Having a DAC with lower output voltage noise could lower the overall noise of the setup. SSI2V 20bits DACs are used in the next section to verify that.
20bits DAC noise measurement
<<sec:noise_ssi2v>>
Let's now measure the output voltage noise of another DAC called the "SSI2V" (doc). It is a 20bits DAC with an output voltage range of +/-10.48 V and a very low output voltage noise.
The measurement setup is the same as the one in Figure fig:noise_measure_setup_dac.
The obtained Amplitude Spectral Density of the output voltage noise of the SSI2V DAC is shown in Figure fig:asd_ssi2v_noise and compared with the output voltage noise of the 16bits DAC. It is shown to be much smaller (~1 order of magnitude).
Using the SSI2V as the DAC with the PD200 should give much better noise output than using the 16bits DAC. The limiting factor should then be the noise of the PD200 itself.
TODO Noise of the full setup with 20bits DAC
<<sec:noise_full_measurement_ssi2v>>
PD200 Amplifier noise model
<<sec:pd200_noise_model>>
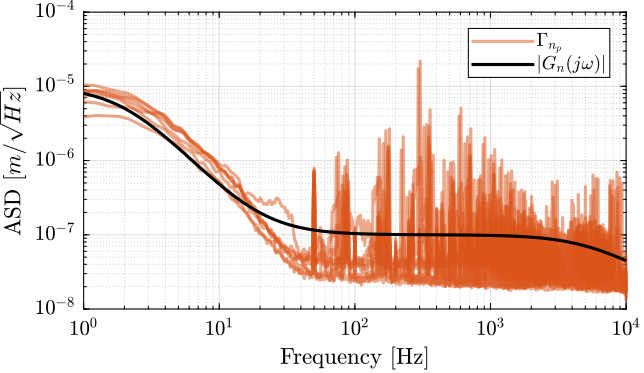
Let's design a transfer function $G_n(s)$ whose norm represent the Amplitude Spectral Density of the input voltage noise of the PD200 amplifier as shown in Figure fig:pd200-model-schematic-normalized-bis.
A simple transfer function that allows to obtain a good fit is defined below.
%% Model of the PD200 Input Voltage Noise
Gn = 1e-5 * ((1 + s/2/pi/20)/(1 + s/2/pi/2))^2 /(1 + s/2/pi/5e3);The comparison between the measured ASD of the modeled ASD is done in Figure fig:pd200_asd_noise_model.
Let's now compute the Cumulative Amplitude Spectrum corresponding to the measurement and the model and compare them.
The integration from low to high frequency and from high to low frequency are both shown in Figure fig:pd200_cas_noise_model.
The fit between the model and the measurements is rather good considering the complex shape of the measured ASD and the simple model used.
The obtained RMS noise of the model is
ans = 1e6*20*sqrt(CPS_Gn(end))Finally the model of the amplifier noise is saved.
save('mat/pd200_model.mat', 'Gn', '-append');Comparison to other commercial amplifiers
<<sec:comp_pi_cedrat>>
Introduction
In this section, three similar voltage amplifiers are compared:
These are compared in term of dynamic from input voltage to output voltage for a load of $10\,\mu F$ in Section sec:tf_comp and then in term of input voltage noise in Section sec:noise_comp.
The characteristics that I could find for the three amplifiers are summarized in Table tab:amplifiers_characteristics.
| Characteristics | PD200 | LA75B | E-505 |
|---|---|---|---|
| Gain | 20 [V/V] | 20 [V/V] | 10 [V/V] |
| Maximum RMS current | 0.9 [A] | 0.4 [A] | |
| Maximum Pulse current | 10 [A] | 1 [A] | 2 [A] |
| Slew Rate | 150 [V/us] | ||
| Noise (10uF load) | 0.7 [mV RMS] | 3.4 [mV RMS] | 0.6 [mV RMS] |
| Small Signal Bandwidth | 7.4 [kHz] (10uF) | 30 [kHz] (unloaded) |
Transfer functions
<<sec:tf_comp>>
la75 = load('tf_la75_10uF_small_signal.mat', 't', 'Vin', 'Vout');
pd200 = load('tf_pd200_1_10uF_small_signal.mat', 't', 'Vin', 'Vout', 'notes');Noise Characteristics
<<sec:noise_comp>>
pd200.Vout = pd200.Vout/pd200.notes.pre_amp.gain;
la75.Vout = la75.Vout/la75.notes.pre_amp.gain;figure;
hold on;
plot(pd200.t, 1e3*pd200.Vout)
plot(la75.t, 1e3*la75.Vout)
hold off;
xlabel('Time [s]');
ylabel('Voltage [mV]');
% ylim([-3, 3]);Conclusion
<<sec:conclusion>>
| Characteristics | Measurement | Manual | Specification |
|---|---|---|---|
| Input Voltage Range | - | +/- 10 [V] | +/- 10 [V] |
| Output Voltage Range | - | -50/150 [V] | -20/150 [V] |
| Gain | 20 [V/V] | - | |
| Maximum RMS current | 0.9 [A] | > 50 [mA] | |
| Maximum Pulse current | 10 [A] | - | |
| Slew Rate | 150 [V/us] | - | |
| Noise (10uF load) | 0.7 [mV RMS] | < 2 [mV rms] | |
| Small Signal Bandwidth (10uF load) | 7.4 [kHz] | > 5 [kHz] | |
| Large Signal Bandwidth (150V, 10uF) | 300 [Hz] | - |