Control of the Nano-Active-Stabilization-System

1. Control Configuration - Introduction
2. Tracking Control in the Frame of the Nano-Hexapod - Basic Architectures
- 2.1. Control in the frame of the Legs
- 2.2. Control in the Cartesian frame
3. Active Damping Architecture - Collocated Control (link)
- 3.1. Integral Force Feedback
- 3.2. Direct Relative Velocity Feedback
4. HAC-LAC Architectures (link)
5. Cascade Architectures (link)
- 5.1. Cascade Control with HAC-LAC Inner Loop and Primary Controller in the task space
- 5.2. Cascade Control with HAC-LAC Inner Loop and Primary Controller in the joint space
6. Force Control (link)

The system consist of the following inputs and outputs (Figure 1):

\(\bm{\tau}\): Forces applied in each leg
\(\bm{\tau}_m\): Force sensor located in each leg
\(\bm{\mathcal{X}}\): Measurement of the payload position with respect to the granite
\(d\bm{\mathcal{L}}\): Measurement of the (small) relative motion of each leg

Figure 1: Block diagram with the inputs and outputs of the system

In order to position the Sample with respect to the granite, we must use the measurement \(\bm{\mathcal{X}}\) in the control loop. The wanted position of the sample with respect to the granite is represented by \(\bm{r}_\mathcal{X}\). From \(\bm{r}_\mathcal{X}\) and \(\bm{\mathcal{X}}\), we can compute the required small change of pose of the nano-hexapod’s top platform expressed in the frame of the nano-hexapod’s base as shown in Figure 2.

This can we considered as:

the position error \(\bm{\epsilon}_{\mathcal{X}_n}\) expressed in a frame attach to the base of the nano-hexapod
the wanted (small) pose displacement \(\bm{r}_{d\mathcal{X}_n}\) of the nano-hexapod mobile platform with respect to its base

Figure 2: Block diagram corresponding to the computation of the position error in the frame of the nano-hexapod

In this document, we see how the different outputs of the system can be used to control of position \(\bm{\mathcal{X}}\).

1 Control Configuration - Introduction

In this section, we discuss the control configuration for the NASS.

From skogestad07_multiv_feedb_contr:

We define the control configuration to be the restrictions imposed on the overall controller \(K\) by decomposing it into a set of local controllers with predetermined links and with a possibly predetermined design sequence where subcontrollers are designed locally.

Some elements used to build up a specific control configuration are:

Cascade controllers. The output from one controller is the input to another

Decentralized controllers. The control system consists of independent feedback controllers which interconnect a subset of the output measurements with a subset of the manipulated inputs. These subsets should not be used by any other controller

Feedforward elements. Link measured disturbances and manipulated inputs

Decoupling elements. Link one set of manipulated inputs with another set of manipulated inputs. They are used to improve the performance of decentralized control systems.

Decoupling elements will be used to convert quantities from the joint space to the task space and vice-versa.

Decentralized controllers will be largely used both for Tracking control (Section 2) and for Active Damping techniques (Section 3)

Combining both can be done in an HAC-LAC topology presented in Section 4.

The use of decentralized controllers is proposed in Section 5.

2 Tracking Control in the Frame of the Nano-Hexapod - Basic Architectures

In this section, we suppose that we want to track some reference position \(\bm{r}_{\mathcal{X}_n}\) corresponding to the pose of the nano-hexapod’s mobile platform with respect to its fixed base.

To do so, we have to the use the leg’s length measurement \(d\bm{\mathcal{L}}\).

However, thanks to the forward and inverse kinematics, the controller can either be designed in the task space or in the joint space.

These to configuration are described in the next two sections.

2.1 Control in the frame of the Legs

From the wanted small change in pose of the nano-hexapod’s mobile platform \(\bm{r}_{d\mathcal{X}_n}\), we can use the Inverse Kinematics of the nano-hexapod to compute the corresponding small change of the leg length of the nano-hexapod \(\bm{r}_{d\mathcal{L}}\). Then, this is subtracted by the measurement of the leg relative displacement \(d\bm{\mathcal{L}}\) to obtain to displacement error of each leg \(\bm{\epsilon}_{d\mathcal{L}}\). Finally, a diagonal (Decentralized) controller \(\bm{K}_\mathcal{L}\) can be used.

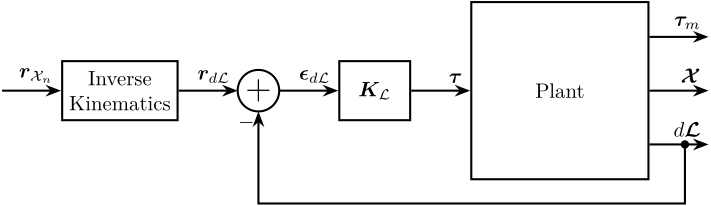
Figure 3: Control in the frame of the legs

2.2 Control in the Cartesian frame

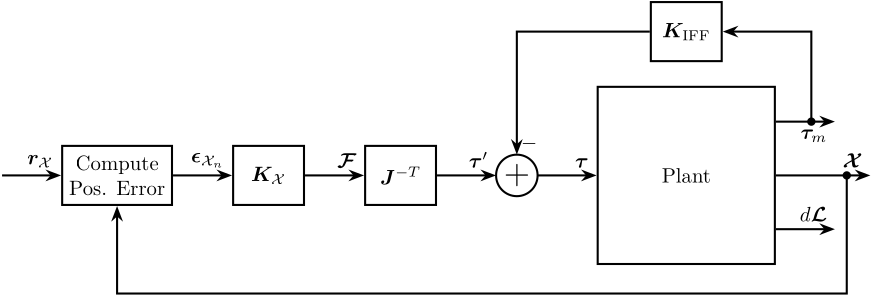
From the relative displacement of each leg \(d\bm{\mathcal{L}}\), the pose of the nano-hexapod’s mobile platform \(\bm{\mathcal{X}_n}\) is estimated. It is then subtracted from reference pose of the nano-hexapod \(\bm{r}_{\mathcal{X}_n}\) to obtain the pose error \(\bm{\epsilon}_{\mathcal{X}_n}\). A diagonal controller \(\bm{K}_\mathcal{X}\) is used to generate forces and torques applied on the payload in a frame attached to the nano-hexapod’s base. These forces are then converted to forces applied in each of the nano-hexapod’s actuators by the use of the Jacobian \(\bm{J}^{-T}\).

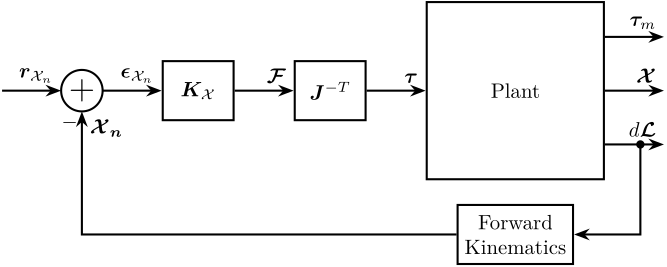
Figure 4: Control in the cartesian Frame (rotating frame attached to the nano-hexapod’s base)

3 Active Damping Architecture - Collocated Control (link)

From preumont18_vibrat_contr_activ_struc_fourt_edition:

Active damping is very effective in reducing the settling time of transient disturbances and the effect of steady state disturbances near the resonance frequencies of the system; however, away from the resonances, the active damping is completely ineffective and leaves the closed-loop response essentially unchanged. Such low-gain controllers are often called Low Authority Controllers (LAC), because they modify the poles of the system only slightly.

Two very well known active damping techniques are Integral Force Feedback and Direct Velocity Feedback.

These two active damping techniques are collocated control techniques.

The active damping techniques are studied in this document.

3.1 Integral Force Feedback

In this active damping technique, the force sensors in each leg is used.

The controller \(\bm{K}_\text{IFF}\) is a diagonal matrix, each of its diagonal element consists of:

an pure integrator
a gain \(g\) that can be tuned to achieve a maximum damping

\begin{equation} \bm{K}_\text{IFF}(s) = \frac{g}{s} \bm{I}_{6} \end{equation}

A lead-lag can also be used instead of a pure integrator.

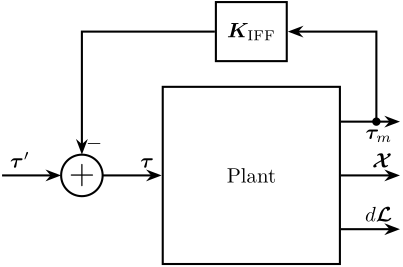
Figure 5: Integral Force Feedback

3.2 Direct Relative Velocity Feedback

The controller \(\bm{K}_\text{DVF}\) is a diagonal matrix. Each diagonal element consists of:

a derivative action up to some frequency \(\omega_0\)
a gain \(g\) that can be tuned to achieve a maximum damping

\begin{equation} \bm{K}_\text{DVF}(s) = \frac{g s}{\omega_0 + s} \bm{I}_{6} \end{equation}

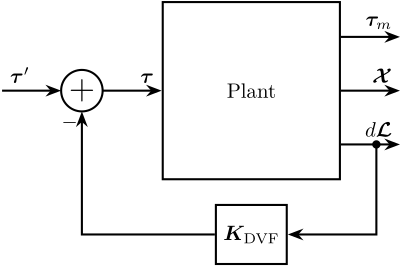
Figure 6: Direct Velocity Feedback

4 HAC-LAC Architectures (link)

Here we can combine Active Damping Techniques (Low authority control) with a tracking controller (high authority control). Usually, the low authority controller is designed first, and the high authority controller is designed based on the damped plant.

From preumont18_vibrat_contr_activ_struc_fourt_edition:

The HAC/LAC approach consist of combining the two approached in a dual-loop control as shown in Figure 7. The inner loop uses a set of collocated actuator/sensor pairs for decentralized active damping with guaranteed stability ; the outer loop consists of a non-collocated HAC based on a model of the actively damped structure. This approach has the following advantages:

The active damping extends outside the bandwidth of the HAC and reduces the settling time of the modes which are outsite the bandwidth

The active damping makes it easier to gain-stabilize the modes outside the bandwidth of the output loop (improved gain margin)

The larger damping of the modes within the controller bandwidth makes them more robust to the parmetric uncertainty (improved phase margin)

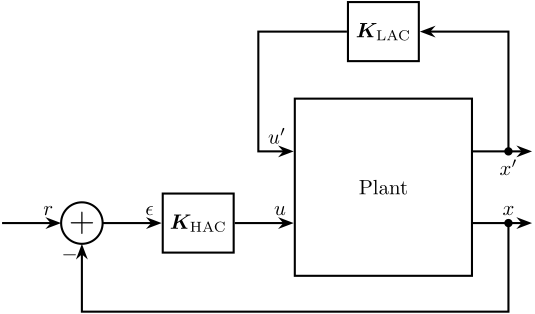
Figure 7: HAC-LAC Control Architecture

If there is only one input to the system, the HAC-LAC topology can be represented as depicted in Figure 8. Usually, the Low Authority Controller is first design, and then the High Authority Controller is designed based on the damped plant.

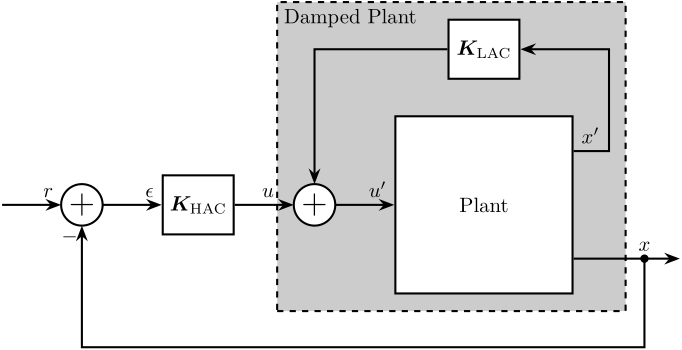
Figure 8: HAC-LAC Architecture with a system having only one input

4.1 HAC-LAC using IFF and Tracking control in the frame of the Legs

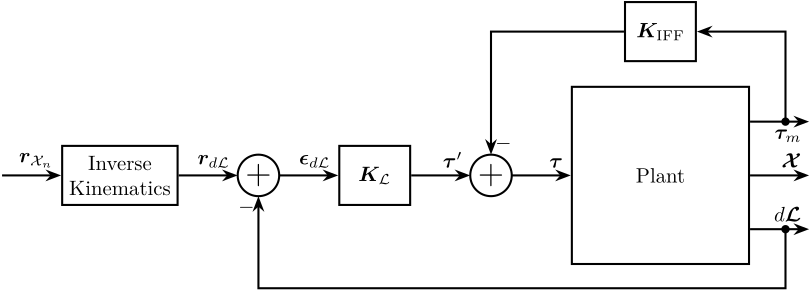
Figure 9: IFF + Control in the frame of the legs

4.2 HAC-LAC using IFF and Tracking control in the Cartesian frame

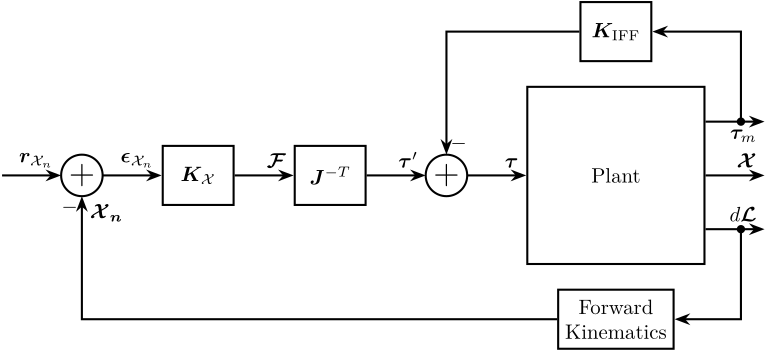
Figure 10: IFF + Control in the cartesian frame

4.3 HAC-LAC using IFF - the HAC controller is positioning the sample w.r.t. the granite

5 Cascade Architectures (link)

The principle of Cascade control is shown in Figure 12 and explained as follow:

To follow two objectives with different properties in one control system, usually a hierarchy of two feedback loops is used in practice. This kind of control topology is called cascade control, which is used when there are several measurements and one prime control variable. Cascade control is implemented by nesting the control loops, as shown in Figure 12. The output control loop is called the primary loop, while the inner loop is called the secondary loop and is used to fulfill a secondary objective in the closed-loop system. – taghirad13_paral

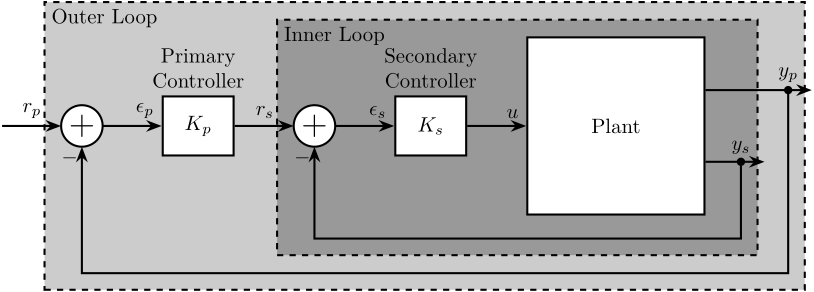
Figure 12: Cascade Control Architecture

This control topology seems adapted for the NASS, as indeed we have more inputs than outputs

In the NASS’s case:

The primary objective is to position the sample with respect to the granite, thus the outer loop (and primary controller) should corresponds to a motion control loop

The inner loop can be composed of the system controlled with the HAC-LAC topology.

5.1 Cascade Control with HAC-LAC Inner Loop and Primary Controller in the task space

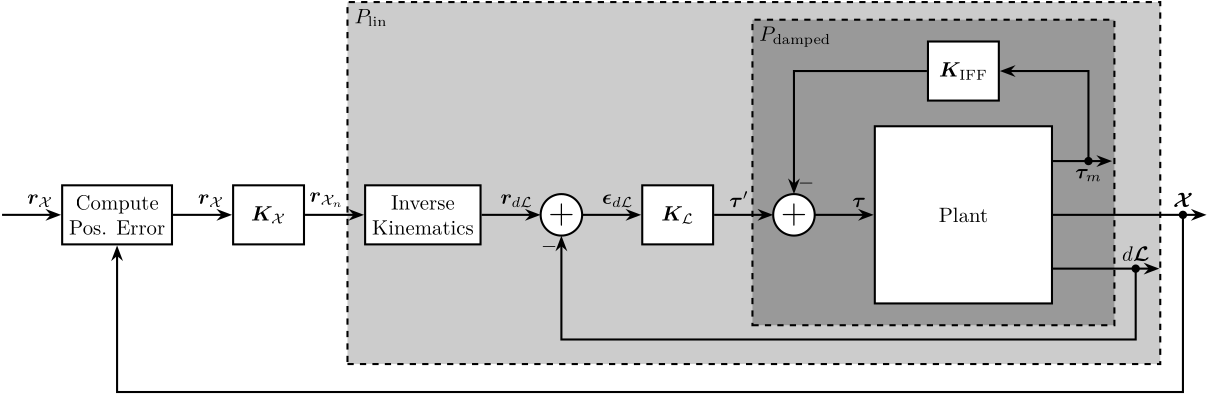
Figure 13: Cascaded Control consisting of (from inner to outer loop): IFF, Linearization Loop, Tracking Control in the frame of the Legs

5.2 Cascade Control with HAC-LAC Inner Loop and Primary Controller in the joint space

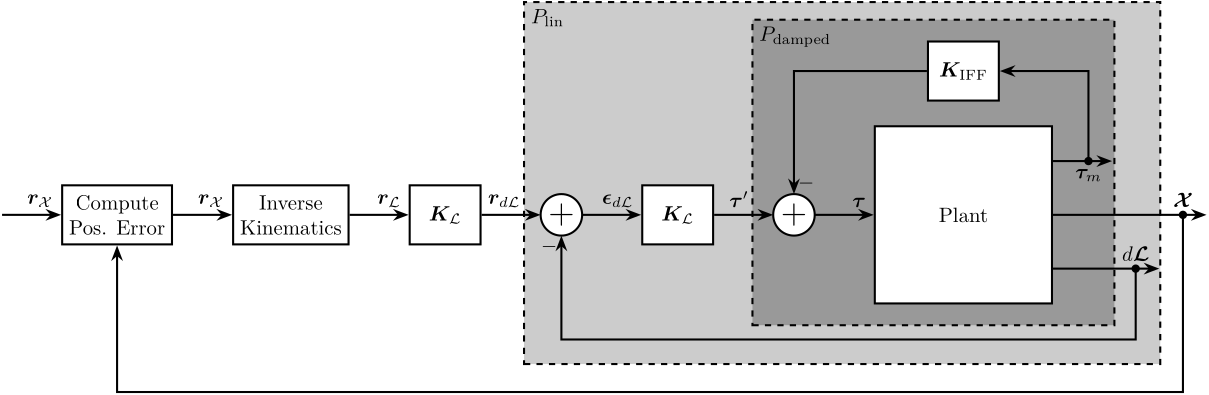
Figure 14: Cascaded Control consisting of (from inner to outer loop): IFF, Linearization Loop, Tracking Control in the Cartesian Frame

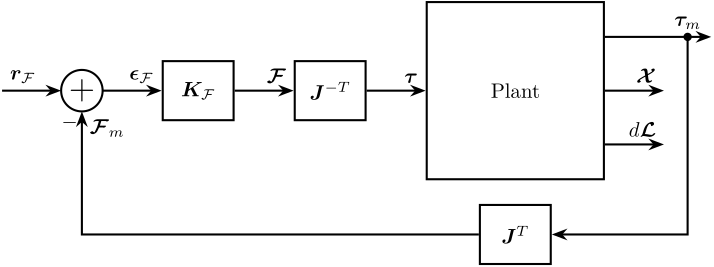
6 Force Control (link)

Signals:

\(\bm{r}_\mathcal{F}\) is the wanted total force/torque to be applied to the payload
\(\bm{\epsilon}_\mathcal{F}\) is the force/torque errors that should be applied to the payload
\(\bm{\tau}\) is the force applied in each actuator

Bibliography

[skogestad07_multiv_feedb_contr] Skogestad & Postlethwaite, Multivariable Feedback Control: Analysis and Design, John Wiley (2007).
[preumont18_vibrat_contr_activ_struc_fourt_edition] Andre Preumont, Vibration Control of Active Structures - Fourth Edition, Springer International Publishing (2018).
[taghirad13_paral] Taghirad, Parallel robots : mechanics and control, CRC Press (2013).