Design of the Nano-Hexapod and associated Control Architectures - Summary
Table of Contents
The overall objective is to design a nano-hexapod an the associated control architecture that allows the stabilization of samples down to \(\approx 10nm\) in presence of disturbances and system variability.
To understand the design challenges of such system, a short introduction to Feedback control is provided in Section 1. The mathematical tools (Power Spectral Density, Noise Budgeting, …) that will be used throughout this study are also introduced.
To be able to develop both the nano-hexapod and the control architecture in an optimal way, we need a good estimation of:
- the micro-station dynamics (Section 2)
- the frequency content of the important source of disturbances in play such as vibration of stages and ground motion (Section 3)
We then develop a model of the system that must represent all the important physical effects in play. Such model is presented in Section 4.
A modular model of the nano-hexapod is then included in the system. The effects of the nano-hexapod characteristics on the dynamics are then studied. Based on that, an optimal choice of the nano-hexapod stiffness is made (Section 5).
Finally, using the optimally designed nano-hexapod, a robust control architecture is developed. Simulations are performed to show that this design gives acceptable performance and the required robustness (Section 6).
1 Introduction to Feedback Systems and Noise budgeting
In this section, we first introduce some basics of feedback systems (Section 1.1). This should highlight the challenges in terms of combined performance and robustness.
In Section 1.2 is introduced the dynamic error budgeting which is a powerful tool that allows to derive the total error in a dynamic system from multiple disturbance sources. This tool will be widely used throughout this study to both predict the performances and identify the effects that do limit the performances.
1.1 Feedback System
The use of feedback control as several advantages and pitfalls that are listed below (taken from schmidt14_desig_high_perfor_mechat_revis_edition):
- Advantages:
- Reduction of the effect of disturbances: Disturbances affecting the sample vibrations are observed by the sensor signal, and therefore the feedback controller can compensate for them
- Handling of uncertainties: Feedback controlled systems can also be designed for robustness, which means that the stability and performance requirements are guaranteed even for parameter variation of the controller mechatronics system
- Pitfalls:
- Limited reaction speed: A feedback controller reacts on the difference between the reference signal (wanted motion) and the measurement (actual motion), which means that the error has to occur first before the controller can correct for it. The limited reaction speed means that the controller will be able to compensate the positioning errors only in some frequency band, called the controller bandwidth
- Feedback of noise: By closing the loop, the sensor noise is also fed back and will induce positioning errors
- Can introduce instability: Feedback control can destabilize a stable plant. Thus the robustness properties of the feedback system must be carefully guaranteed
1.1.1 Simplified Feedback Control Diagram for the NASS
Let’s consider the block diagram shown in Figure 1 where the signals are:
- \(y\): the relative position of the sample with respect to the granite (the quantity we wish to control)
- \(d\): the disturbances affecting \(y\) (ground motion, vibration of stages)
- \(n\): the noise of the sensor measuring \(y\)
- \(r\): the reference signal, corresponding to the wanted \(y\)
- \(\epsilon = r - y\): the position error
And the dynamical blocks are:
- \(G\): representing the dynamics from forces/torques applied by the nano-hexapod to the relative position sample/granite \(y\)
- \(G_d\): representing how the disturbances (e.g. ground motion) are affecting the relative position sample/granite \(y\)
- \(K\): representing the controller (to be designed)
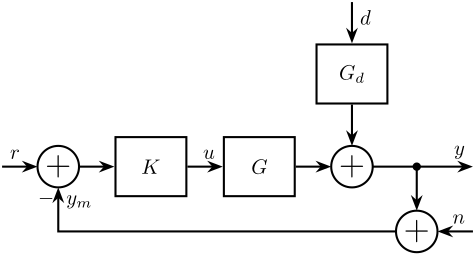
Figure 1: Block Diagram of a simple feedback system
Without the use of feedback (i.e. nano-hexapod), the disturbances will induce a sample motion error equal to:
\begin{equation} y = G_d d \label{eq:open_loop_error} \end{equation}which is out of the specifications (micro-meter range compare to the required \(\approx 10nm\)).
In the next section, we see how the use of the feedback system permits to lower the effect of the disturbances \(d\) on the sample motion error.
1.1.2 How does the feedback loop is modifying the system behavior?
If we write down the position error signal \(\epsilon = r - y\) as a function of the reference signal \(r\), the disturbances \(d\) and the measurement noise \(n\) (using the feedback diagram in Figure 1), we obtain: \[ \epsilon = \frac{1}{1 + GK} r + \frac{GK}{1 + GK} n - \frac{G_d}{1 + GK} d \]
We usually note:
\begin{align} S &= \frac{1}{1 + GK} \\ T &= \frac{GK}{1 + GK} \end{align}where \(S\) is called the sensibility transfer function and \(T\) the transmissibility transfer function.
And the position error can be rewritten as:
\begin{equation} \epsilon = S r + T n - G_d S d \label{eq:closed_loop_error} \end{equation}From Eq. \eqref{eq:closed_loop_error} representing the closed-loop system behavior, we can see that:
- the effect of disturbances \(d\) on \(\epsilon\) is multiplied by a factor \(S\) compared to the open-loop case
- the measurement noise \(n\) is injected and multiplied by a factor \(T\)
Ideally, we would like to design the controller \(K\) such that:
- \(|S|\) is small to limit the effect of disturbances
- \(|T|\) is small to limit the injection of sensor noise
As shown in the next section, there is a trade-off between the disturbance reduction and the noise injection.
1.1.3 Trade off: Disturbance Reduction / Noise Injection
We have from the definition of \(S\) and \(T\) that:
\begin{equation} S + T = \frac{1}{1 + GK} + \frac{GK}{1 + GK} = 1 \end{equation}meaning that we cannot have \(|S|\) and \(|T|\) small at the same time.
There is therefore a trade-off between the disturbance rejection and the measurement noise filtering.
Typical shapes of \(|S|\) and \(|T|\) as a function of frequency are shown in Figure 2. We can observe that \(|S|\) and \(|T|\) exhibit different behaviors depending on the frequency band:
- At low frequency (inside the control bandwidth):
- \(|S|\) can be made small and thus the effect of disturbances is reduced
- \(|T| \approx 1\) and all the sensor noise is transmitted
- At high frequency (outside the control bandwidth):
- \(|S| \approx 1\) and the feedback system does not reduce the effect of disturbances
- \(|T|\) is small and thus the sensor noise is filtered
- Near the crossover frequency (between the two frequency bands):
- The effect of disturbances is increased
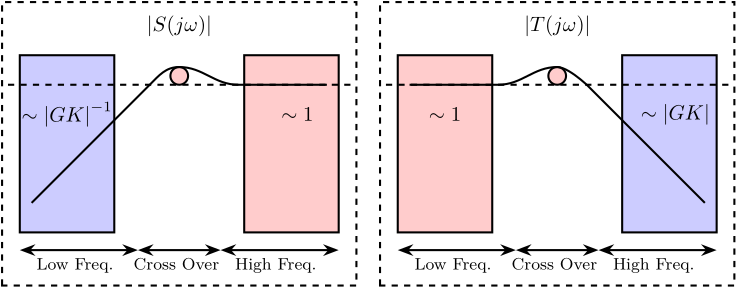
Figure 2: Typical shapes and constrain of the Sensibility and Transmibility closed-loop transfer functions
1.1.4 Trade off: Robustness / Performance
As shown in the previous section, the effect of disturbances is reduced inside the control bandwidth.
Moreover, the slope of \(|S(j\omega)|\) is limited for stability reasons (not explained here), and therefore a large control bandwidth is required to obtain sufficient disturbance rejection at lower frequencies (where the disturbances have large effects).
The next important question is what effects do limit the attainable control bandwidth?
The main issue it that for stability reasons, the behavior of the mechanical system must be known with only small uncertainty in the vicinity of the crossover frequency.
For mechanical systems, this generally means that control bandwidth should take place before any appearing of flexible dynamics (Right part of Figure 3).
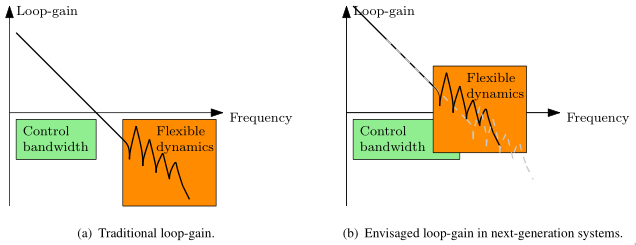
Figure 3: Envisaged developments in motion systems. In traditional motion systems, the control bandwidth takes place in the rigid-body region. In the next generation systemes, flexible dynamics are foreseen to occur within the control bandwidth. oomen18_advan_motion_contr_precis_mechat
This also means that any possible change in the system should have a small impact on the system dynamics in the vicinity of the crossover.
For the NASS, the possible changes in the system are:
- a modification of the payload mass and dynamics
- a change of experimental condition: spindle’s rotation speed, position of each micro-station’s stage
- a change in the micro-station dynamics (change of mechanical elements, aging effect, …)
The nano-hexapod and the control architecture have to be developed such that the feedback system remains stable and exhibit acceptable performance for all these possible changes in the system.
This problem of robustness represent one of the main challenge for the design of the NASS.
1.2 Dynamic error budgeting
The dynamic error budgeting is a powerful tool to study the effect of multiple error sources and to see how the feedback system does reduce the effect
To understand how to use and understand it, the Power Spectral Density and the Cumulative Power Spectrum are first introduced. Then, is shown how does multiple error sources are combined and modified by dynamical systems.
Finally,
1.2.1 Power Spectral Density
The Power Spectral Density (PSD) \(S_{xx}(f)\) of the time domain signal \(x(t)\) is defined as the Fourier transform of the autocorrelation function: \[ S_{xx}(\omega) = \int_{-\infty}^{\infty} R_{xx}(\tau) e^{-j \omega \tau} d\tau \ \frac{[\text{unit of } x]^2}{\text{Hz}} \]
The PSD \(S_{xx}(\omega)\) represents the distribution of the (average) signal power over frequency.
Thus, the total power in the signal can be obtained by integrating these infinitesimal contributions, the Root Mean Square (RMS) value of the signal \(x(t)\) is then:
\begin{equation} x_{\text{rms}} = \sqrt{\int_{0}^{\infty} S_{xx}(\omega) d\omega} \end{equation}One can also integrate the infinitesimal power \(S_{xx}(\omega)d\omega\) over a finite frequency band to obtain the power of the signal \(x\) in that frequency band:
\begin{equation} P_{f_1,f_2} = \int_{f_1}^{f_2} S_{xx}(\omega) d\omega \quad [\text{unit of } x]^2 \end{equation}1.2.2 Cumulative Power Spectrum
The Cumulative Power Spectrum is the cumulative integral of the Power Spectral Density starting from \(0\ \text{Hz}\) with increasing frequency:
\begin{equation} CPS_x(f) = \int_0^f S_{xx}(\nu) d\nu \quad [\text{unit of } x]^2 \end{equation}The Cumulative Power Spectrum taken at frequency \(f\) thus represent the power in the signal in the frequency band \(0\) to \(f\).
An alternative definition of the Cumulative Power Spectrum can be used where the PSD is integrated from \(f\) to \(\infty\):
\begin{equation} CPS_x(f) = \int_f^\infty S_{xx}(\nu) d\nu \quad [\text{unit of } x]^2 \end{equation}And thus \(CPS_x(f)\) represents the power in the signal \(x\) for frequencies above \(f\).
The Cumulative Power Spectrum will be used to determine in which frequency band the effect of disturbances should be reduced, and thus the approximate required control bandwidth.
1.2.3 Modification of a signal’s PSD when going through an LTI system
Let’s consider a signal \(u\) with a PSD \(S_{uu}\) going through a LTI system \(G(s)\) that outputs a signal \(y\) with a PSD (Figure 4).
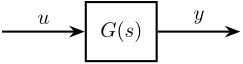
Figure 4: LTI dynamical system \(G(s)\) with input signal \(u\) and output signal \(y\)
The Power Spectral Density of the output signal \(y\) can be computed using:
\begin{equation} S_{yy}(\omega) = \left|G(j\omega)\right|^2 S_{uu}(\omega) \end{equation}1.2.4 PSD of combined signals
Let’s consider a signal \(y\) that is the sum of two uncorrelated signals \(u\) and \(v\) (Figure 5).
We have that the PSD of \(y\) is equal to sum of the PSD and \(u\) and the PSD of \(v\) (can be easily shown from the definition of the PSD): \[ S_{yy} = S_{uu} + S_{vv} \]

Figure 5: \(y\) as the sum of two signals \(u\) and \(v\)
1.2.5 Dynamic Noise Budgeting
Let’s consider the Feedback architecture in Figure 1 where the position error \(\epsilon\) is equal to: \[ \epsilon = S r + T n - G_d S d \]
If we suppose that the signals \(r\), \(n\) and \(d\) are uncorrelated (which is a good approximation in our case), the PSD of \(\epsilon\) is: \[ S_{\epsilon \epsilon}(\omega) = |S(j\omega)|^2 S_{rr}(\omega) + |T(j\omega)|^2 S_{nn}(\omega) + |G_d(j\omega) S(j\omega)|^2 S_{dd}(\omega) \]
And we can compute the RMS value of the residual motion using:
\begin{align*} \epsilon_\text{rms} &= \sqrt{ \int_0^\infty S_{\epsilon\epsilon}(\omega) d\omega} \\ &= \sqrt{ \int_0^\infty \Big( |S(j\omega)|^2 S_{rr}(\omega) + |T(j\omega)|^2 S_{nn}(\omega) + |G_d(j\omega) S(j\omega)|^2 S_{dd}(\omega) \Big) d\omega } \end{align*}To estimate the PSD of the position error \(\epsilon\) and thus the RMS residual motion (in closed-loop), we need to determine:
- The Power Spectral Densities of the signals affecting the system:
- \(S_{dd}\): disturbances, this will be done in Section 3
- \(S_{nn}\): sensor noise, this can be estimated from the sensor data-sheet
- \(S_{rr}\):
- The dynamics of the complete system comprising the micro-station and the nano-hexapod: \(G\), \(G_d\). To do so, we need to identify the dynamics of the micro-station (Section 2), include this dynamics in a model (Section 4) and add a model of the nano-hexapod to the model (Section 5)
- The controller \(K\) that will be designed in Section 6
2 Identification of the Micro-Station Dynamics
https://tdehaeze.github.io/meas-analysis/
Modal Analysis: https://tdehaeze.github.io/meas-analysis/modal-analysis/index.html
The obtained dynamics will allows us to compare the dynamics of the model.
2.1 Setup
In order to perform to Modal Analysis and to obtain first a response model, the following devices were used:
- An acquisition system (OROS) with 24bits ADCs
- 3 tri-axis Accelerometers
- An Instrumented Hammer
The measurement thus consists of:
- Exciting the structure at the same location with the Hammer (Figure 7)
- Move the accelerometers to measure all the DOF of the structure.
The position of the accelerometers are:
- 4 on the first granite
- 4 on the second granite
- 4 on top of the translation stage (figure 6)
- 4 on top of the tilt stage
- 3 on top of the spindle
- 4 on top of the hexapod
In total, 69 degrees of freedom are measured (23 tri axis accelerometers).

Figure 6: Figure caption

Figure 7: Figure caption
2.2 Results
From the measurements, we obtain
- Reduction of the
- solid body assumption
- verification of the assumption => ok
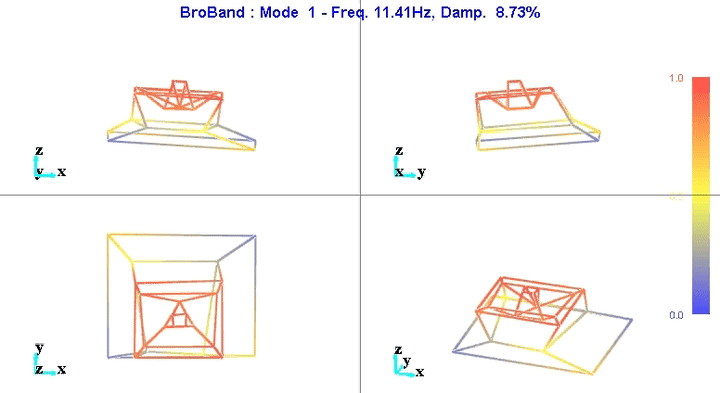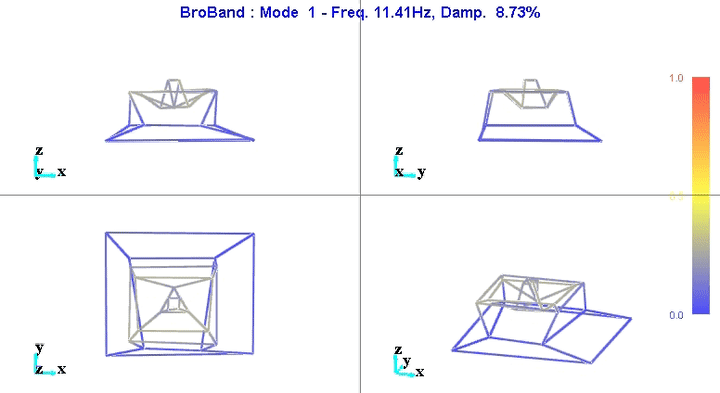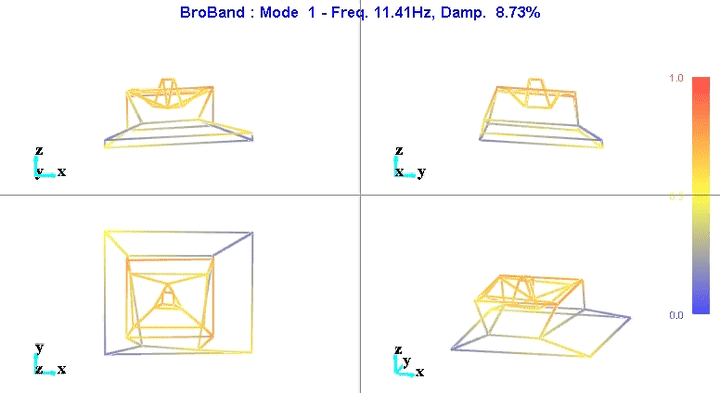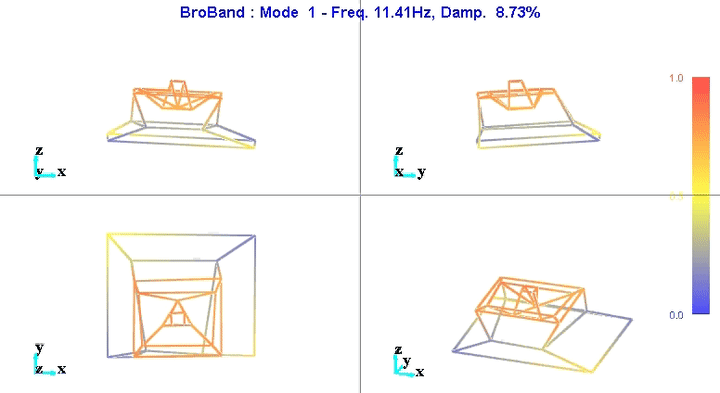
Figure 8: Figure caption
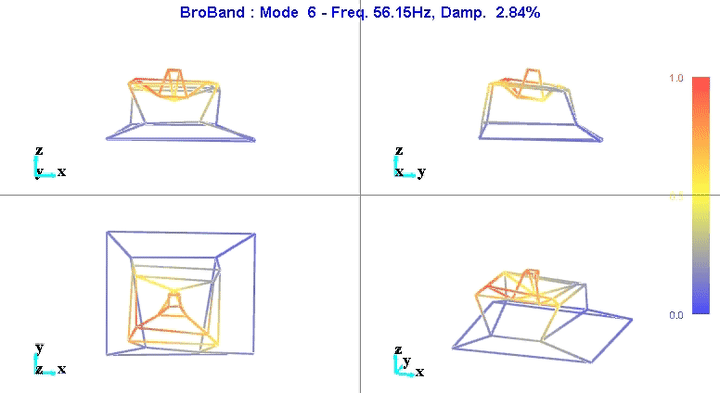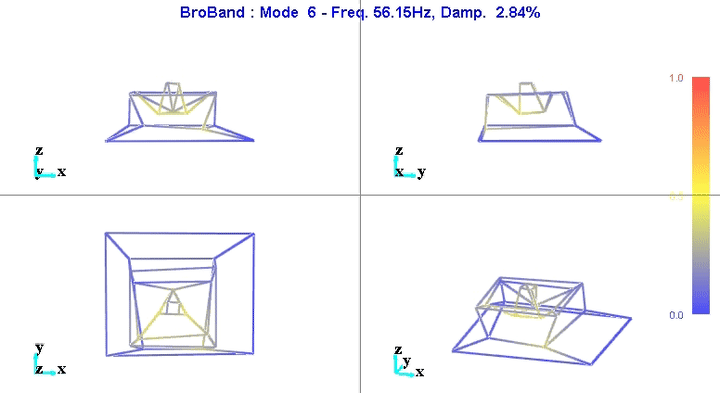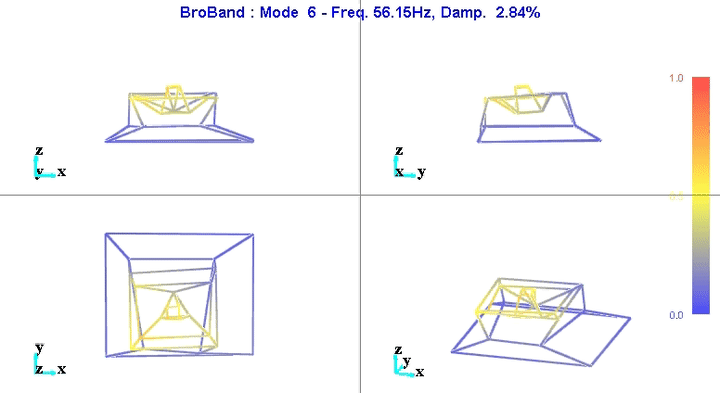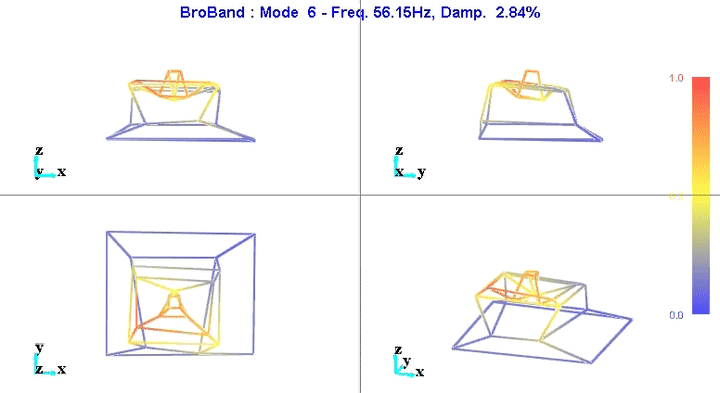
Figure 9: Figure caption
2.3 Conclusion
The reduction of the number of degrees of freedom from 69 (23 accelerometers with each 3DOF) to 36 (6 solid bodies with 6 DOF) seems to work well.
This confirms the fact that the stages are indeed behaving as a solid body in the frequency band of interest. This valid the fact that a multi-body model can be used to represent the dynamics of the micro-station.
3 Identification of the Disturbances
https://tdehaeze.github.io/meas-analysis/
Open Loop Noise budget: https://tdehaeze.github.io/nass-simscape/disturbances.html
Static Guiding errors:
- measured at the PEL
- low frequency errors, will thus be compensated
The problem are on the high frequency disturbances
3.2 Stage Vibration - Effect of Control systems
Control system of each stage has been tested https://tdehaeze.github.io/meas-analysis/disturbance-control-system/index.html https://tdehaeze.github.io/meas-analysis/2018-10-15%20-%20Marc/index.html
25Hz vertical motion when the Spindle is turned on (even when not rotating).
3.3 Stage Vibration - Effect of Motion
3.4 Sum of all disturbances
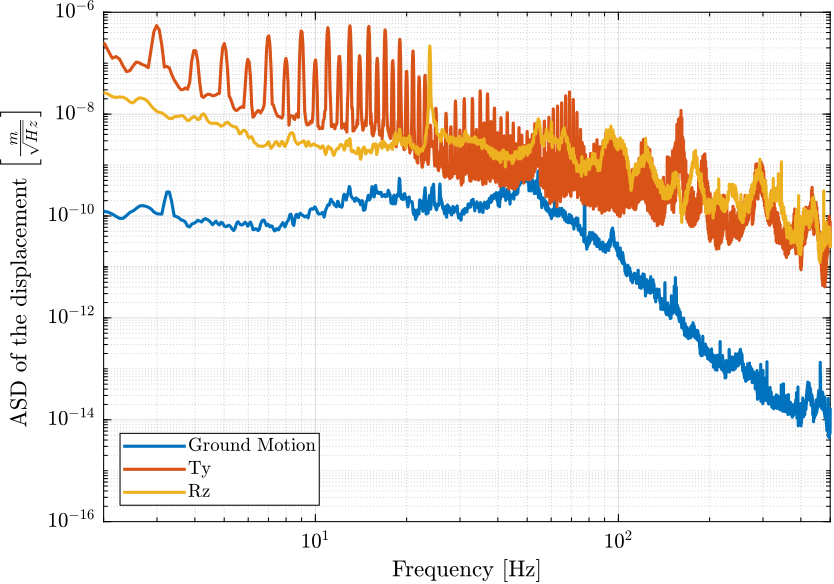
Figure 10: Amplitude Spectral Density fo the motion error due to disturbances
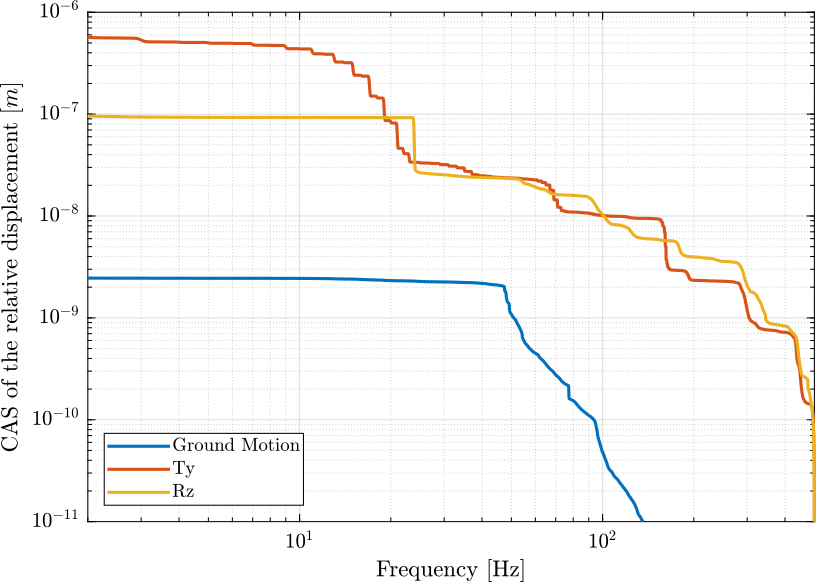
Figure 11: Cumulative Amplitude Spectrum of the motion error due to disturbances
Expected required bandwidth
3.5 Better measurement of the effect of disturbances
Here, the measurement were made with inertial sensors. However, we are interested in the relative motion of the sample with respect to the granite and not the absolute motion.
The best measurement of the disturbances would be to have the metrology already functioning.
We could perform a measurement using the X-ray.
Detector Requirement:
- Sample frequency above \(400Hz\)
- Resolution of \(\approx 20nm\)
3.6 Conclusion
4 Multi Body Model
4.1 Validity of the model
The mass/inertia of each stage is automatically computed from the geometry and the density of the materials.
The stiffness of each joint is first set to measured values or stiffness from data sheets.
Then, the values of the stiffness and damping of each joint is manually tuned until the obtained dynamics is sufficiently close to the measured dynamics.
We could, from the measurement, automatically extract the stiffness and damping values, we this would have required a lot of work and having a perfect match is not required here.
Comparison model - measurements : https://tdehaeze.github.io/nass-simscape/identification.html
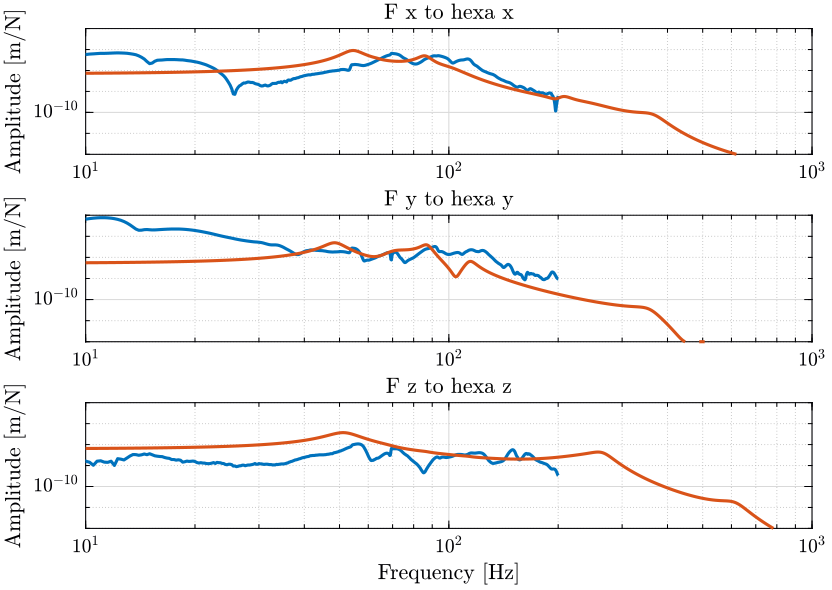
Figure 12: Figure caption
4.2 Wanted position of the sample and position error
From the reference position of each stage, we can compute the wanted pose of the sample with respect to the granite. This is done with multiple transformation matrices.
Then, from the measurement of the metrology corresponding to the position of the sample with respect to the granite, we can compute the position error of the sample expressed in a frame fixed to the nano-hexapod.
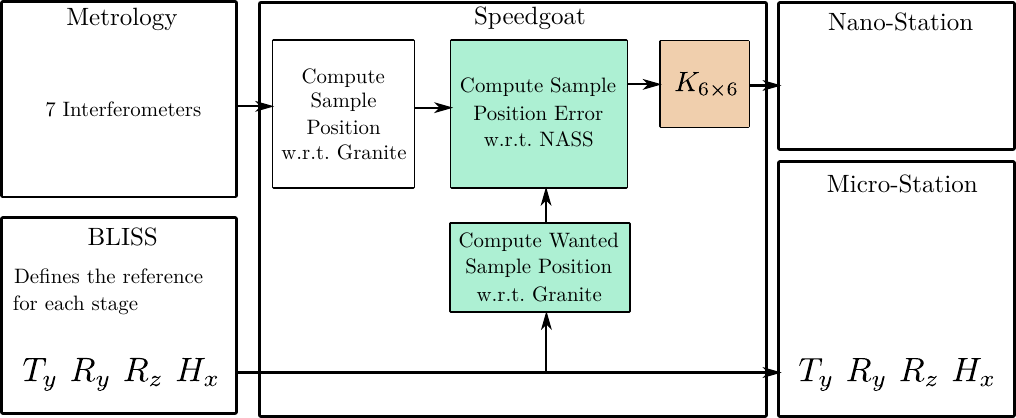
Figure 13: Figure caption
Measurement of the sample’s position - conversion of positioning error in the frame of the Nano-hexapod for control: https://tdehaeze.github.io/nass-simscape/positioning_error.html
4.3 Simulation of Experiments
Now that the
- dynamics of the model is tuned
- disturbances are included in the model
We can perform simulation of experiments.
https://tdehaeze.github.io/nass-simscape/experiments.html
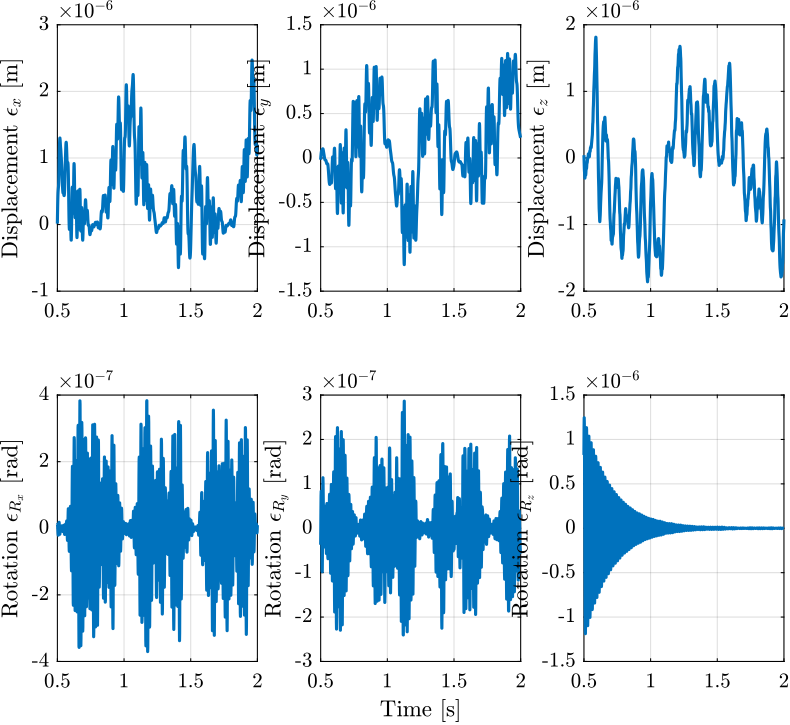
Figure 14: Position error of the Sample with respect to the granite during a Tomography Experiment with included disturbances
4.4 Conclusion
Possible to study many effects. Extraction of transfer function like \(G\) and \(G_d\).
Simulation of experiments to validate performance.
5 Optimal Nano-Hexapod Design
As explain before, the nano-hexapod properties (mass, stiffness, architecture, …) will influence:
- the plant dynamics \(G\)
- the effect of disturbances \(G_d\)
We which here to choose the nano-hexapod properties such that:
- has an easy
- minimize the
- minimize \(|G_d|\)
5.1 Optimal Stiffness to reduce the effect of disturbances
5.2 Optimal Stiffness
The goal is to design a system that is robust.
Thus, we have to identify the sources of uncertainty and try to minimize them.
Uncertainty in the system can be caused by:
- Effect of Support Compliance: https://tdehaeze.github.io/nass-simscape/uncertainty_support.html
- Effect of Payload Dynamics: https://tdehaeze.github.io/nass-simscape/uncertainty_payload.html
- Effect of experimental condition (micro-station pose, spindle rotation): https://tdehaeze.github.io/nass-simscape/uncertainty_experiment.html
All these uncertainty will limit the maximum attainable bandwidth.
Fortunately, the nano-hexapod stiffness have an influence on the dynamical uncertainty induced by the above effects.
Determination of the optimal stiffness based on all the effects:
The main performance limitation are payload variability
Main problem: heavy samples with small stiffness. The first resonance frequency of the sample will limit the performance.
The nano-hexapod stiffness will also change the sensibility to disturbances.
Effect of Nano-hexapod stiffness on the Sensibility to disturbances: https://tdehaeze.github.io/nass-simscape/optimal_stiffness_disturbances.html
5.3 Sensors to be included
Ways to damp:
- Force Sensor
- Relative Velocity Sensors
- Inertial Sensor
https://tdehaeze.github.io/rotating-frame/index.html
Sensors to be included:
6 Robust Control Architecture
6.1 Simulation of Tomography Experiments
6.2 Conclusion
7 Further notes
Soft granite
Sensible to detector motion?
Common metrology frame for the nano-focusing optics and the measurement of the sample position?
Cable forces?
Slip-Ring noise?