18 KiB
#+TITLE:SpeedGoat
Experimental Setup
Two L22 geophones are used. They are placed on the ID31 granite. They are leveled.
The signals are amplified using voltage amplifier with a gain of 60dB. The voltage amplifiers include a low pass filter with a cut-off frequency at 1kHz.
Signal Processing
The Matlab computing file for this part is accessible here.
The mat file containing the measurement data is accessible here.
Load data
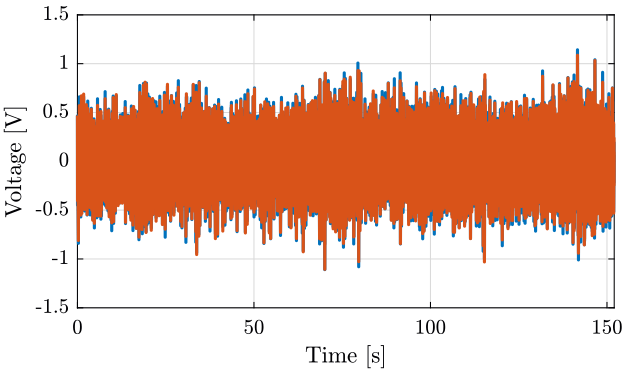
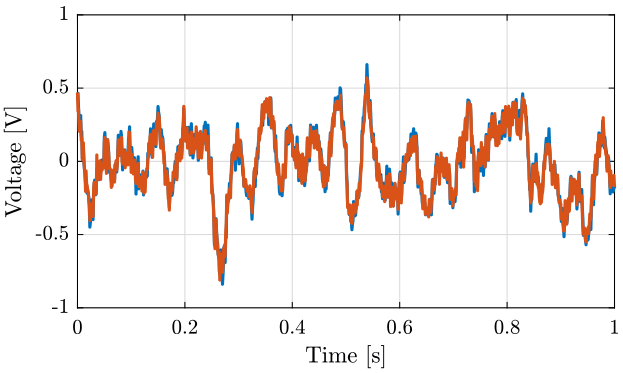
We load the data of the z axis of two geophones.
load('mat/data_001.mat', 't', 'x1', 'x2');
dt = t(2) - t(1);Time Domain Data
figure;
hold on;
plot(t, x1);
plot(t, x2);
hold off;
xlabel('Time [s]');
ylabel('Voltage [V]');
xlim([t(1), t(end)]); <<plt-matlab>>
figure;
hold on;
plot(t, x1);
plot(t, x2);
hold off;
xlabel('Time [s]');
ylabel('Voltage [V]');
xlim([0 1]); <<plt-matlab>>
Computation of the ASD of the measured voltage
We first define the parameters for the frequency domain analysis.
win = hanning(ceil(length(x1)/100));
Fs = 1/dt; [pxx1, f] = pwelch(x1, win, [], [], Fs);
[pxx2, ~] = pwelch(x2, win, [], [], Fs);Scaling to take into account the sensibility of the geophone and the voltage amplifier
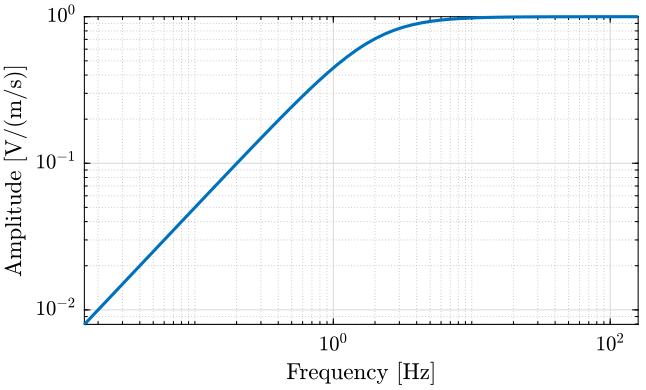
The Geophone used are L22. Their sensibility are shown on figure fig:geophone_sensibility.
S0 = 88; % Sensitivity [V/(m/s)]
f0 = 2; % Cut-off frequnecy [Hz]
S = (s/2/pi/f0)/(1+s/2/pi/f0); <<plt-matlab>>
We also take into account the gain of the electronics which is here set to be $60dB$. The amplifiers also include a low pass filter with a cut-off frequency set at 1kHz.
G0 = 60; % [dB]
G = 10^(G0/20)/(1+s/2/pi/1000);We divide the ASD measured (in $\text{V}/\sqrt{\text{Hz}}$) by the transfer function of the voltage amplifier to obtain the ASD of the voltage across the geophone. We further divide the result by the sensibility of the Geophone to obtain the ASD of the velocity in $m/s/\sqrt{Hz}$.
scaling = 1./squeeze(abs(freqresp(G*S, f, 'Hz')));Computation of the ASD of the velocity
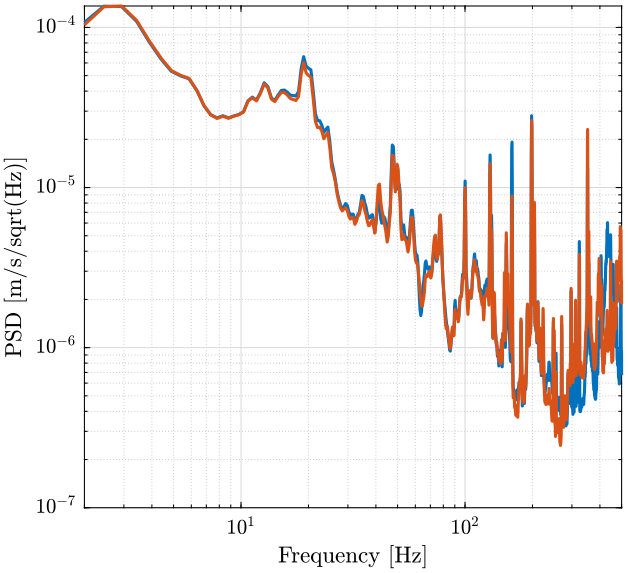
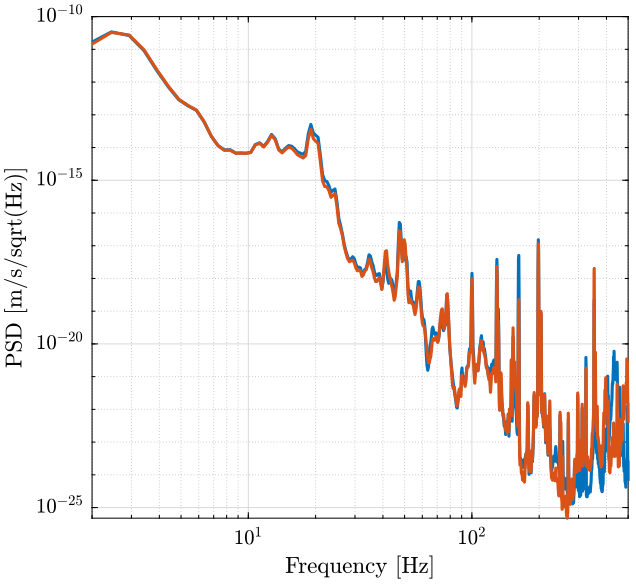
The ASD of the measured velocity is shown on figure fig:psd_velocity.
figure;
hold on;
plot(f, sqrt(pxx1).*scaling);
plot(f, sqrt(pxx2).*scaling);
hold off;
set(gca, 'xscale', 'log');
set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('PSD [m/s/sqrt(Hz)]')
xlim([2, 500]); <<plt-matlab>>
We also plot the ASD in displacement (figure fig:asd_displacement);
figure;
hold on;
plot(f, (pxx1.*scaling./f).^2);
plot(f, (pxx2.*scaling./f).^2);
hold off;
set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('PSD [m/s/sqrt(Hz)]')
xlim([2, 500]); <<plt-matlab>>
Transfer function between the two geophones
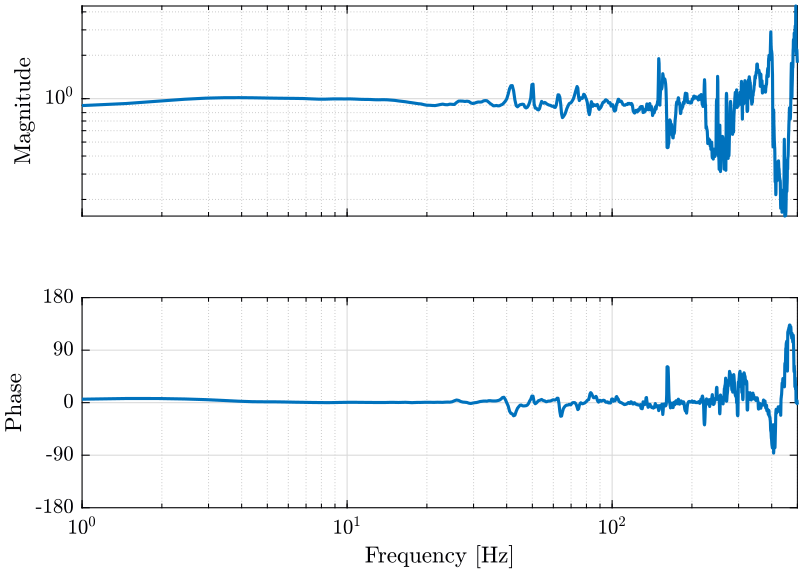
We here compute the transfer function from one geophone to the other. The result is shown on figure fig:tf_geophones.
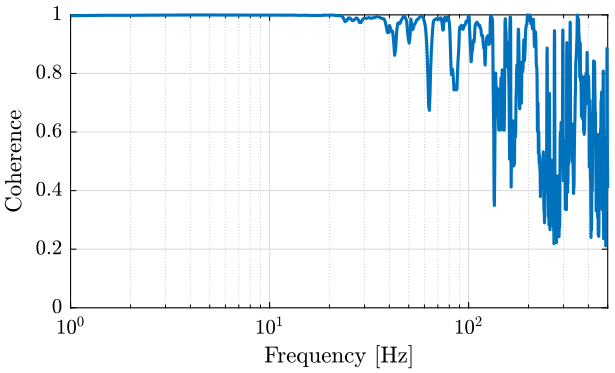
We also compute the coherence between the two signals (figure fig:coh_geophones).
[T12, ~] = tfestimate(x1, x2, win, [], [], Fs); <<plt-matlab>>
[coh12, ~] = mscohere(x1, x2, win, [], [], Fs); <<plt-matlab>>
Estimation of the sensor noise
The technique to estimate the sensor noise is taken from cite:barzilai98_techn_measur_noise_sensor_presen.
The coherence between signals $X$ and $Y$ is defined as follow \[ \gamma^2_{XY}(\omega) = \frac{|G_{XY}(\omega)|^2}{|G_{X}(\omega)| |G_{Y}(\omega)|} \] where $|G_X(\omega)|$ is the output Power Spectral Density (PSD) of signal $X$ and $|G_{XY}(\omega)|$ is the Cross Spectral Density (CSD) of signal $X$ and $Y$.
The PSD and CSD are defined as follow:
\begin{align} |G_X(\omega)| &= \frac{2}{n_d T} \sum^{n_d}_{n=1} \left| X_k(\omega, T) \right|^2 \\ |G_{XY}(\omega)| &= \frac{2}{n_d T} \sum^{n_d}_{n=1} [ X_k^*(\omega, T) ] [ Y_k(\omega, T) ] \end{align}where:
- $n_d$ is the number for records averaged
- $T$ is the length of each record
- $X_k(\omega, T)$ is the finite Fourier transform of the kth record
- $X_k^*(\omega, T)$ is its complex conjugate
The mscohere function is compared with this formula on Appendix (section sec:coherence), it is shown that it is identical.
Figure fig:huddle_test illustrate a block diagram model of the system used to determine the sensor noise of the geophone.
Two geophones are mounted side by side to ensure that they are exposed by the same motion input $U$.
Each sensor has noise $N$ and $M$.
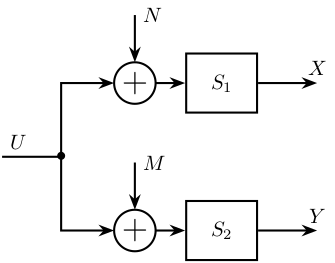
We here assume that each sensor has the same magnitude of instrumental noise ($N = M$). We also assume that $H_1 = H_2 = 1$.
We then obtain:
\begin{equation} \gamma_{XY}^2(\omega) = \frac{1}{1 + 2 \left( \frac{|G_N(\omega)|}{|G_U(\omega)|} \right) + \left( \frac{|G_N(\omega)|}{|G_U(\omega)|} \right)^2} \end{equation}Since the input signal $U$ and the instrumental noise $N$ are incoherent:
\begin{equation} |G_X(\omega)| = |G_N(\omega)| + |G_U(\omega)| \end{equation}From equations eq:coh_bis and eq:incoherent_noise, we finally obtain
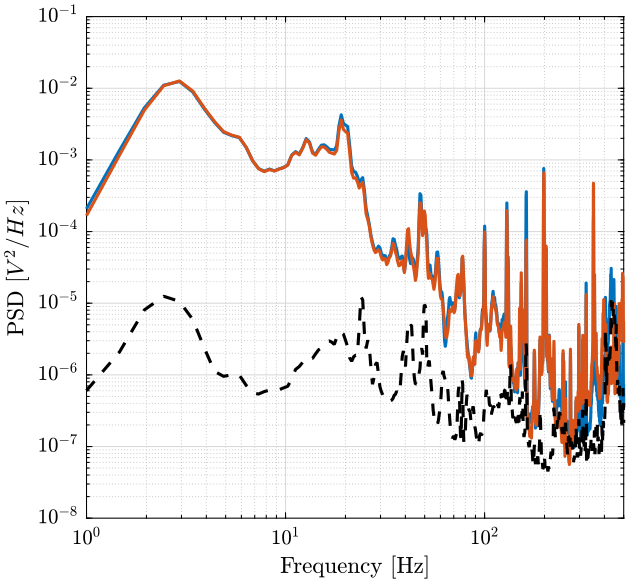
The instrumental noise is computed below. The result in V^2/Hz is shown on figure fig:intrumental_noise_V.
pxxN = pxx1.*(1 - coh12); figure;
hold on;
plot(f, pxx1, '-');
plot(f, pxx2, '-');
plot(f, pxxN, 'k--');
hold off;
set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('PSD [$V^2/Hz$]');
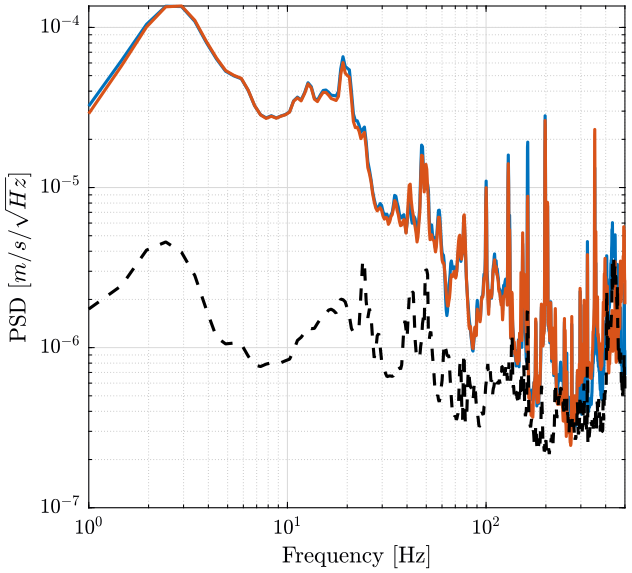
xlim([1, 500]); <<plt-matlab>>
This is then further converted into velocity and compared with the ground velocity measurement. (figure fig:intrumental_noise_velocity)
figure;
hold on;
plot(f, sqrt(pxx1).*scaling, '-');
plot(f, sqrt(pxx2).*scaling, '-');
plot(f, sqrt(pxxN).*scaling, 'k--');
hold off;
set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('PSD [$m/s/\sqrt{Hz}$]');
xlim([1, 500]); <<plt-matlab>>
Compare axis
The Matlab computing file for this part is accessible here.
The mat files containing the measurement data are accessible with the following links:
Load data
We first load the data for the three axis.
z = load('mat/data_001.mat', 't', 'x1', 'x2');
east = load('mat/data_002.mat', 't', 'x1', 'x2');
north = load('mat/data_003.mat', 't', 'x1', 'x2');Compare PSD
The PSD for each axis of the two geophones are computed.
[pz1, fz] = pwelch(z.x1, hanning(ceil(length(z.x1)/100)), [], [], 1/(z.t(2)-z.t(1)));
[pz2, ~] = pwelch(z.x2, hanning(ceil(length(z.x2)/100)), [], [], 1/(z.t(2)-z.t(1)));
[pe1, fe] = pwelch(east.x1, hanning(ceil(length(east.x1)/100)), [], [], 1/(east.t(2)-east.t(1)));
[pe2, ~] = pwelch(east.x2, hanning(ceil(length(east.x2)/100)), [], [], 1/(east.t(2)-east.t(1)));
[pn1, fn] = pwelch(north.x1, hanning(ceil(length(north.x1)/100)), [], [], 1/(north.t(2)-north.t(1)));
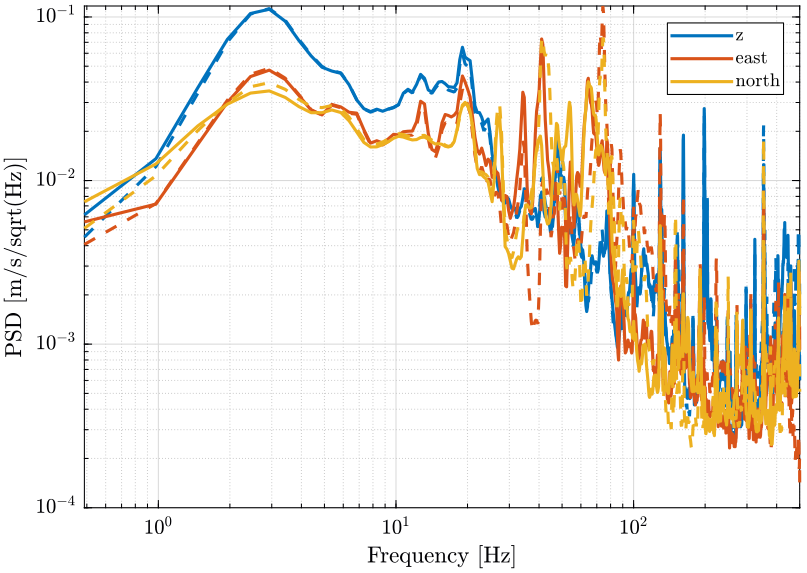
[pn2, ~] = pwelch(north.x2, hanning(ceil(length(north.x2)/100)), [], [], 1/(north.t(2)-north.t(1)));We compare them. The result is shown on figure fig:compare_axis_psd.
<<plt-matlab>>
Compare TF
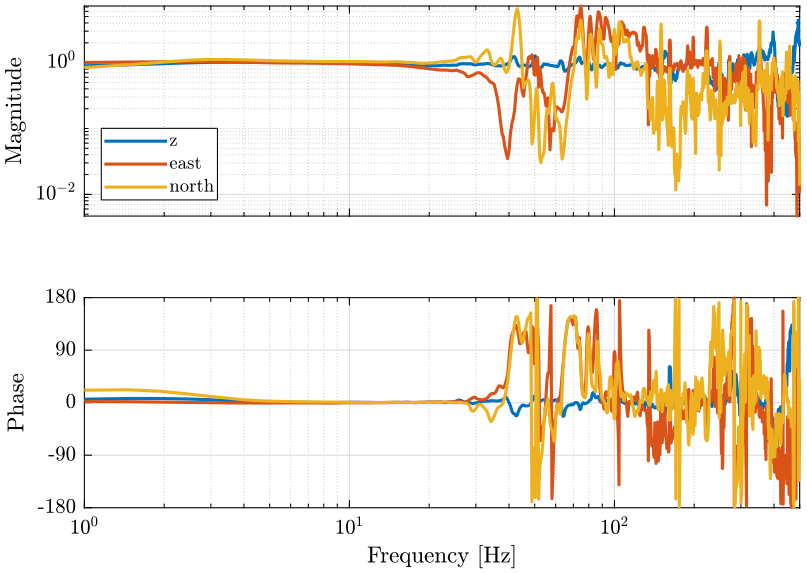
The transfer functions from one geophone to the other are also computed for each axis. The result is shown on figure fig:compare_tf_axis.
[Tz, fz] = tfestimate(z.x1, z.x2, hanning(ceil(length(z.x1)/100)), [], [], 1/(z.t(2)-z.t(1)));
[Te, fe] = tfestimate(east.x1, east.x2, hanning(ceil(length(east.x1)/100)), [], [], 1/(east.t(2)-east.t(1)));
[Tn, fn] = tfestimate(north.x1, north.x2, hanning(ceil(length(north.x1)/100)), [], [], 1/(north.t(2)-north.t(1))); <<plt-matlab>>
Appendix
Computation of coherence from PSD and CSD
<<sec:coherence>>
load('mat/data_001.mat', 't', 'x1', 'x2');
dt = t(2) - t(1);
Fs = 1/dt;
win = hanning(ceil(length(x1)/100)); pxy = cpsd(x1, x2, win, [], [], Fs);
pxx = pwelch(x1, win, [], [], Fs);
pyy = pwelch(x2, win, [], [], Fs);
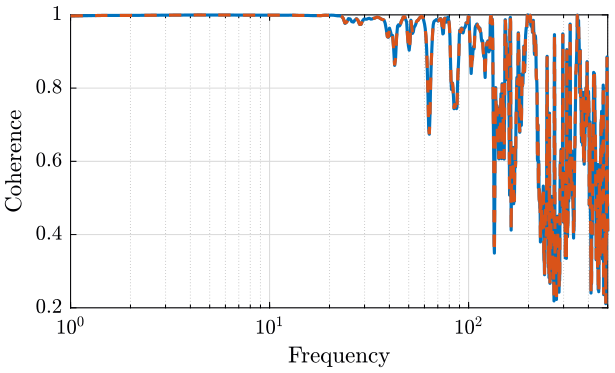
coh = mscohere(x1, x2, win, [], [], Fs); figure;
hold on;
plot(f, abs(pxy).^2./abs(pxx)./abs(pyy), '-');
plot(f, coh, '--');
hold off;
set(gca, 'xscale', 'log');
xlabel('Frequency'); ylabel('Coherence');
xlim([1, 500]); <<plt-matlab>>
mscohere and manual computation
Bibliography ignore
bibliographystyle:unsrt bibliography:ref.bib