Modal Analysis - Modal Parameter Extraction
Table of Contents
- 1. Load Data
- 2. Determine the number of modes
- 3. Modal parameter extraction
- 4. Obtained Mode Shapes animations
- 5. Modal Complexity
- 6. From local coordinates to global coordinates for the mode shapes
- 7. Some notes about constraining the number of degrees of freedom
- 8. Compare Mode Shapes
- 9. TODO Synthesis of FRF curves from the modal parameters
The goal here is to extract the modal parameters describing the modes of station being studied, namely:
- the eigen frequencies
- the modal damping
- the mode shapes (eigen vectors)
This is done from the FRF matrix previously extracted from the measurements.
In order to do the modal parameter extraction, we first have to estimate the order of the modal model we want to obtain. This corresponds to how many modes are present in the frequency band of interest. In section 2, we will use the Singular Value Decomposition and the Modal Indication Function to estimate the number of modes.
The modal parameter extraction methods generally consists of curve-fitting a theoretical expression for an individual FRF to the actual measured data. However, there are multiple level of complexity:
- works on a part of a single FRF curve
- works on a complete curve encompassing several resonances
- works on a set of many FRF plots all obtained from the same structure
The third method is the most complex but gives better results. This is the one we will use in section 3.
From the modal model, it is possible to obtain a graphic display of the mode shapes (section 4).
The modes of the structure are expected to be complex, however real modes are easier to work with when it comes to obtain a spatial model from the modal parameters. We will thus study the complexity of those modes, in section 5, and see if we can estimate real modes from the complex modes.
The mode obtained from the modal software describe the motion of the structure at the position of each accelerometer for all the modes. However, we would like to describe the motion of each stage (solid body) of the structure in its 6 DOFs. This in done in section 6.
All the files (data and Matlab scripts) are accessible here.
1 Load Data
load('mat/frf_coh_matrices.mat', 'FRFs', 'COHs', 'freqs'); load('mat/frf_o.mat', 'FRFs_O');
2 Determine the number of modes
2.1 Singular Value Decomposition - Modal Indication Function
The Mode Indicator Functions are usually used on \(n\times p\) FRF matrix where \(n\) is a relatively large number of measurement DOFs and \(p\) is the number of excitation DOFs, typically 3 or 4.
In these methods, the frequency dependent FRF matrix is subjected to a singular value decomposition analysis which thus yields a small number (3 or 4) of singular values, these also being frequency dependent.
These methods are used to determine the number of modes present in a given frequency range, to identify repeated natural frequencies and to pre process the FRF data prior to modal analysis.
From the documentation of the modal software:
The MIF consist of the singular values of the Frequency response function matrix. The number of MIFs equals the number of excitations. By the powerful singular value decomposition, the real signal space is separated from the noise space. Therefore, the MIFs exhibit the modes effectively. A peak in the MIFs plot usually indicate the existence of a structural mode, and two peaks at the same frequency point means the existence of two repeated modes. Moreover, the magnitude of the MIFs implies the strength of the a mode.
The Complex Mode Indicator Function is defined simply by the SVD of the FRF (sub) matrix:
\begin{align*} [H(\omega)]_{n\times p} &= [U(\omega)]_{n\times n} [\Sigma(\omega)]_{n\times p} [V(\omega)]_{p\times p}^H\\ [CMIF(\omega)]_{p\times p} &= [\Sigma(\omega)]_{p\times n}^T [\Sigma(\omega)]_{n\times p} \end{align*}We compute the Complex Mode Indicator Function. The result is shown on figure 1. The exact same curve is obtained when computed using the OROS software.
MIF = zeros(size(FRFs, 2), size(FRFs, 2), size(FRFs, 3)); for i = 1:length(freqs) [~,S,~] = svd(FRFs(:, :, i)); MIF(:, :, i) = S'*S; end
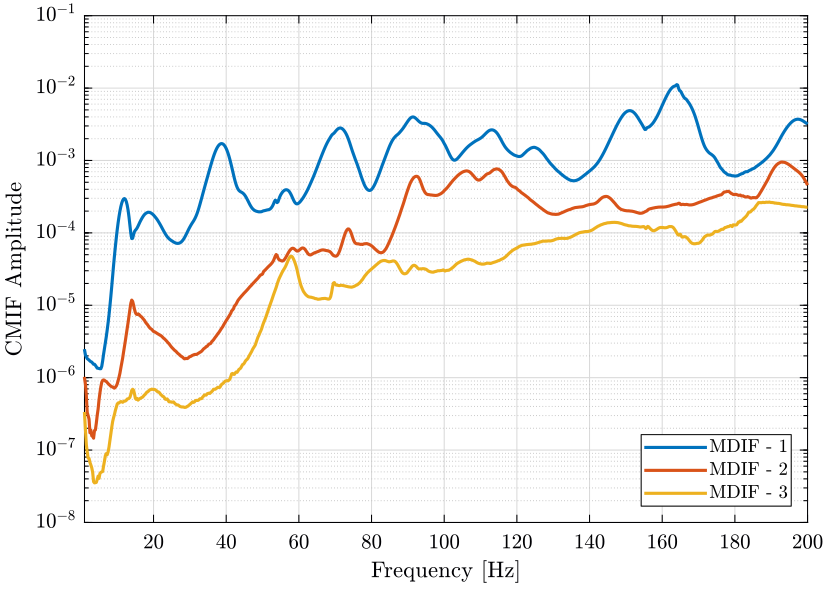
Figure 1: Complex Mode Indicator Function
We can also compute the CMIF using the FRF matrix expressed in the same global frame. We compare the two CMIF on figure 2.
They do not indicate the same resonance frequencies, especially around 110Hz.
MIF_O = zeros(size(FRFs_O, 2), size(FRFs_O, 2), size(FRFs_O, 3)); for i = 1:length(freqs) [~,S,~] = svd(FRFs_O(:, :, i)); MIF_O(:, :, i) = S'*S; end

Figure 2: Complex Mode Indicator Function - Original FRF: solid curves - Processed FRF: dashed curve
2.2 Composite Response Function
An alternative is the Composite Response Function \(HH(\omega)\) defined as the sum of all the measured FRF:
\begin{equation} HH(\omega) = \sum_j\sum_kH_{jk}(\omega) \end{equation}Instead, we choose here to use the sum of the norms of the measured FRFs:
\begin{equation} HH(\omega) = \sum_j\sum_k \left|H_{jk}(\omega) \right| \end{equation}The result is shown on figure 3.
figure; hold on; plot(freqs, squeeze(sum(sum(abs(FRFs)))), '-k'); plot(freqs, squeeze(sum(sum(abs(FRFs_O)))), '--k'); hold off; xlabel('Frequency [Hz]'); ylabel('Amplitude'); xlim([1, 200]);
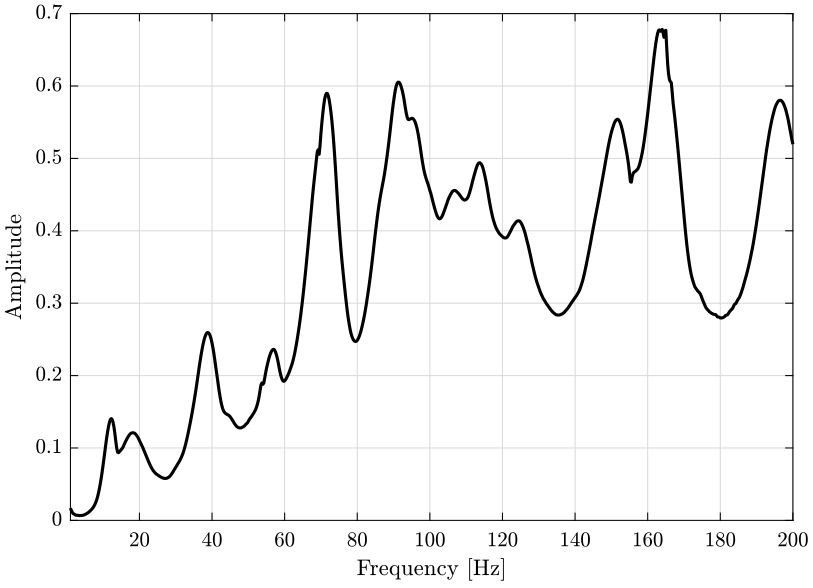
Figure 3: Composite Response Function. Solid curve: computed from the original FRFs. Dashed curve: computed from the FRFs expressed in the global frame.
3 Modal parameter extraction
3.1 OROS - Modal software
Modal identification can be done within the Modal software of OROS. The manual for the software is available here.
Several modal parameter extraction methods are available. We choose to use the "broad band method" as it permits to identify the modal parameters using all the FRF curves at the same times. It takes into account the fact the the properties of all the individual curves are related by being from the same structure: all FRF plots on a given structure should indicate the same values for the natural frequencies and damping factor of each mode.
Such method also have the advantage of producing a unique and consistent model as direct output.
In order to apply this method, we select the frequency range of interest and we give an estimate of how many modes are present.
Then, it shows a stabilization charts, such as the one shown on figure 4, where we have to manually select which modes to take into account in the modal model.

Figure 4: Stabilization Chart
We can then run the modal analysis, and the software will identify the modal damping and mode shapes at the selected frequency modes.
3.2 Exported modal parameters
The obtained modal parameters are:
- the resonance frequencies
- the modes shapes
- the modal damping
- the residues
They are all exported in a text file named modes.asc.
Its first 20 lines as shown below.
Created by N-Modal
Estimator: bbfd
01-Jul-19 16:44:11
Mode 1
freq = 11.41275Hz
damp = 8.72664%
modal A = -4.50556e+003-9.41744e+003i
modal B = -7.00928e+005+2.62922e+005i
Mode matrix of local coordinate [DOF: Re IM]
1X-: -1.04114e-001 3.50664e-002
1Y-: 2.34008e-001 5.04273e-004
1Z+: -1.93303e-002 5.08614e-003
2X-: -8.38439e-002 3.45978e-002
2Y-: 2.42440e-001 0.00000e+000
2Z+: -7.40734e-003 5.17734e-003
3Y-: 2.17655e-001 6.10802e-003
3X+: 1.18685e-001 -3.54602e-002
3Z+: -2.37725e-002 -1.61649e-003
We split this big modes.asc file into sub text files using bash. The obtained files are described one table 1.
sed '/^\s*[0-9]*[XYZ][+-]:/!d' mat/modes.asc > mat/mode_shapes.txt sed '/freq/!d' mat/modes.asc | sed 's/.* = \(.*\)Hz/\1/' > mat/mode_freqs.txt sed '/damp/!d' mat/modes.asc | sed 's/.* = \(.*\)\%/\1/' > mat/mode_damps.txt sed '/modal A/!d' mat/modes.asc | sed 's/.* =\s\+\([-0-9.e]\++[0-9]\+\)\([-+0-9.e]\+\)i/\1 \2/' > mat/mode_modal_a.txt sed '/modal B/!d' mat/modes.asc | sed 's/.* =\s\+\([-0-9.e]\++[0-9]\+\)\([-+0-9.e]\+\)i/\1 \2/' > mat/mode_modal_b.txt
| Filename | Content |
|---|---|
mat/mode_shapes.txt |
mode shapes |
mat/mode_freqs.txt |
resonance frequencies |
mat/mode_damps.txt |
modal damping |
mat/mode_modal_a.txt |
modal residues at low frequency (to be checked) |
mat/mode_modal_b.txt |
modal residues at high frequency (to be checked) |
3.3 Importation of the modal parameters on Matlab
Then we import the obtained .txt files on Matlab using readtable function.
shapes = readtable('mat/mode_shapes.txt', 'ReadVariableNames', false); % [Sign / Real / Imag] freqs = table2array(readtable('mat/mode_freqs.txt', 'ReadVariableNames', false)); % in [Hz] damps = table2array(readtable('mat/mode_damps.txt', 'ReadVariableNames', false)); % in [%] modal_a = table2array(readtable('mat/mode_modal_a.txt', 'ReadVariableNames', false)); % [Real / Imag] modal_b = table2array(readtable('mat/mode_modal_b.txt', 'ReadVariableNames', false)); % [Real / Imag] modal_a = complex(modal_a(:, 1), modal_a(:, 2)); modal_b = complex(modal_b(:, 1), modal_b(:, 2));
We guess the number of modes identified from the length of the imported data.
acc_n = 23; % Number of accelerometers dir_n = 3; % Number of directions dirs = 'XYZ'; mod_n = size(shapes,1)/acc_n/dir_n; % Number of modes
As the mode shapes are split into 3 parts (direction plus sign, real part and imaginary part), we aggregate them into one array of complex numbers.
T_sign = table2array(shapes(:, 1)); T_real = table2array(shapes(:, 2)); T_imag = table2array(shapes(:, 3)); modes = zeros(mod_n, acc_n, dir_n); for mod_i = 1:mod_n for acc_i = 1:acc_n % Get the correct section of the signs T = T_sign(acc_n*dir_n*(mod_i-1)+1:acc_n*dir_n*mod_i); for dir_i = 1:dir_n % Get the line corresponding to the sensor i = find(contains(T, sprintf('%i%s',acc_i, dirs(dir_i))), 1, 'first')+acc_n*dir_n*(mod_i-1); modes(mod_i, acc_i, dir_i) = str2num([T_sign{i}(end-1), '1'])*complex(T_real(i),T_imag(i)); end end end
The obtained mode frequencies and damping are shown below.
| Mode number | Frequency [Hz] | Damping [%] |
|---|---|---|
| 1.0 | 11.4 | 8.7 |
| 2.0 | 18.5 | 11.8 |
| 3.0 | 37.6 | 6.4 |
| 4.0 | 39.4 | 3.6 |
| 5.0 | 54.0 | 0.2 |
| 6.0 | 56.1 | 2.8 |
| 7.0 | 69.7 | 4.6 |
| 8.0 | 71.6 | 0.6 |
| 9.0 | 72.4 | 1.6 |
| 10.0 | 84.9 | 3.6 |
| 11.0 | 90.6 | 0.3 |
| 12.0 | 91.0 | 2.9 |
| 13.0 | 95.8 | 3.3 |
| 14.0 | 105.4 | 3.3 |
| 15.0 | 106.8 | 1.9 |
| 16.0 | 112.6 | 3.0 |
| 17.0 | 116.8 | 2.7 |
| 18.0 | 124.1 | 0.6 |
| 19.0 | 145.4 | 1.6 |
| 20.0 | 150.1 | 2.2 |
| 21.0 | 164.7 | 1.4 |
3.4 Modal Matrices
We arrange the obtained modal parameters into matrices: \[ \Omega = \begin{bmatrix} \omega_1^2 & & 0 \\ & \ddots & \\ 0 & & \omega_n^2 \end{bmatrix}; \quad \Psi = \begin{bmatrix} & & \\ \{\psi_1\} & \dots & \{\psi_n\} \\ & & \end{bmatrix} \] with \(n\) the number of identified modes and: \[ \{\psi_1\} = \begin{Bmatrix} \psi_{1_x} & \psi_{2_x} & \dots & \psi_{23_x} & \psi_{1_y} & \dots & \psi_{1_z} & \dots & \psi_{23_z} \end{Bmatrix}^T \]
eigen_value_M = diag(freqs*2*pi); eigen_vector_M = reshape(mode_shapes, [mod_n, 6*length(solid_names)])';
3.5 TODO Normalization of mode shapes?
We normalize each column of the eigen vector matrix.
Then, each eigenvector as a norm of 1.
eigen_vector_M = eigen_vector_M./vecnorm(eigen_vector_M);
Should we do such normalization?
4 Obtained Mode Shapes animations
From the modal parameters, it is possible to show the modal shapes with an animation.
Examples are shown on figures 5 and 6.
Animations of all the other modes are accessible using the following links: mode 1, mode 2, mode 3, mode 4, mode 5, mode 6, mode 7, mode 8, mode 9, mode 10, mode 11, mode 12, mode 13, mode 14, mode 15, mode 16, mode 17, mode 18, mode 19, mode 20, mode 21.
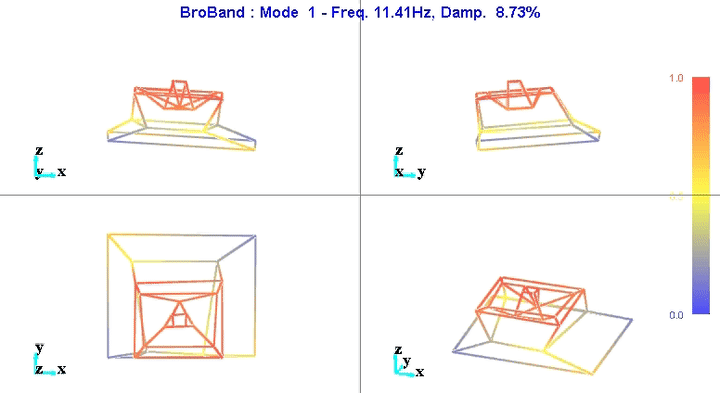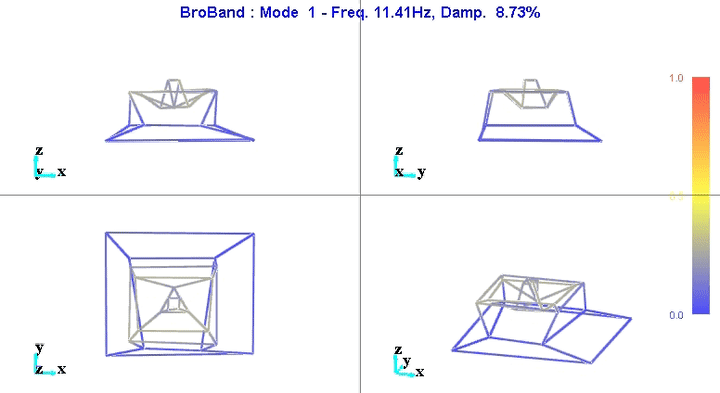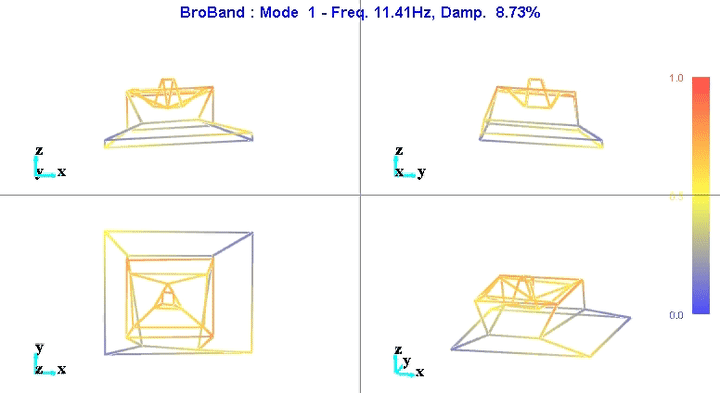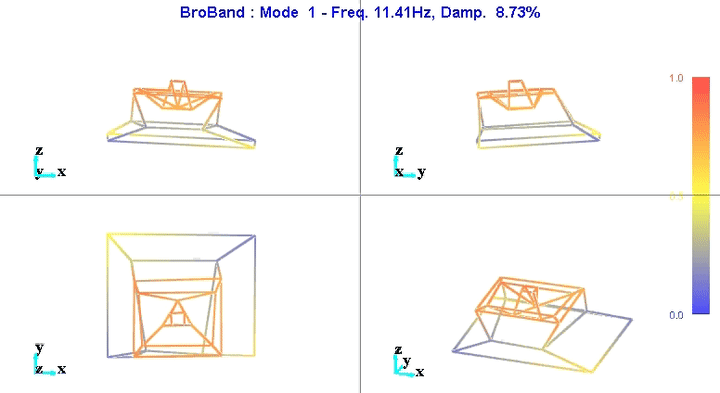
Figure 5: Mode 1
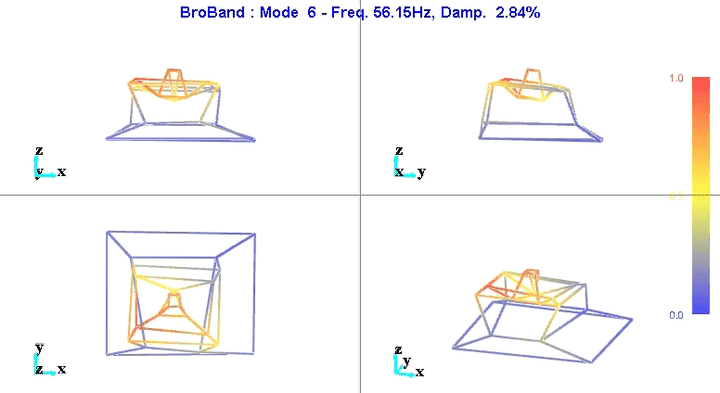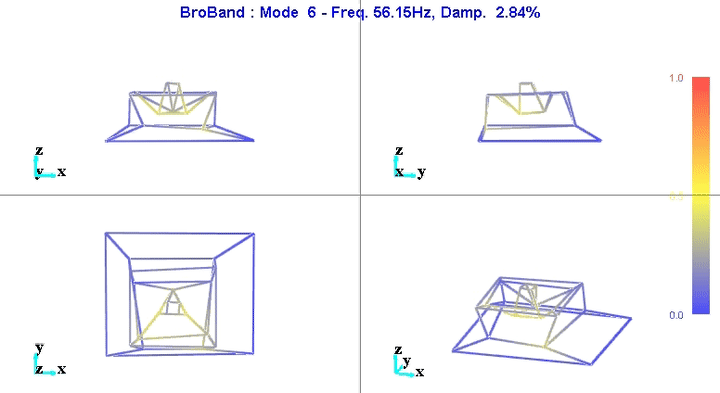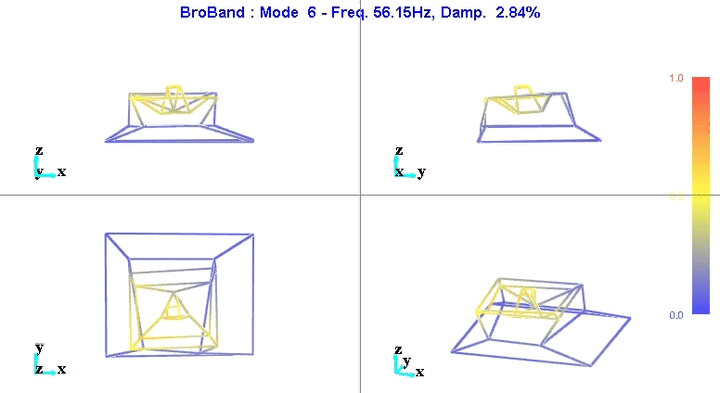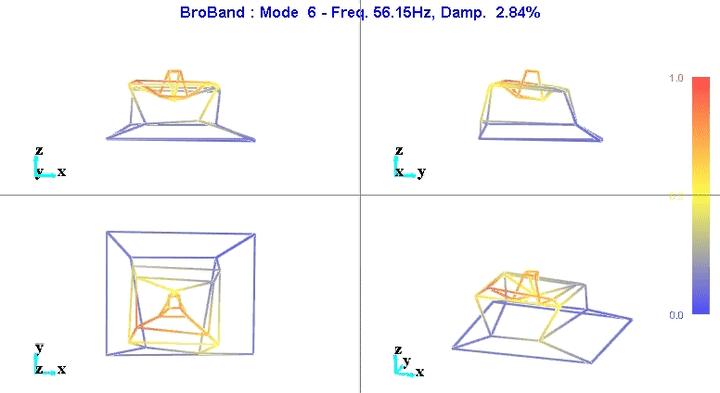
Figure 6: Mode 6
We can learn quite a lot from these mode shape animations.
For instance, the mode shape of the first mode at 11Hz (figure 5) seems to indicate that this corresponds to a suspension mode.
This could be due to the 4 Airloc Levelers that are used for the granite (figure 7).

Figure 7: AirLoc used for the granite (2120-KSKC)
They are probably not well leveled, so the granite is supported only by two Airloc.
5 Modal Complexity
A method of displaying modal complexity is by plotting the elements of the eigenvector on an Argand diagram (complex plane), such as the ones shown in figure 8.
To evaluate the complexity of the modes, we plot a polygon around the extremities of the individual vectors. The obtained area of this polygon is then compared with the area of the circle which is based on the length of the largest vector element. The resulting ratio is used as an indication of the complexity of the mode.
A mode with small complexity is shown on figure 8 whereas an highly complex mode is shown on figure 9. The complexity of all the modes are compared on figure 10.

Figure 8: Modal Complexity of one mode with small complexity
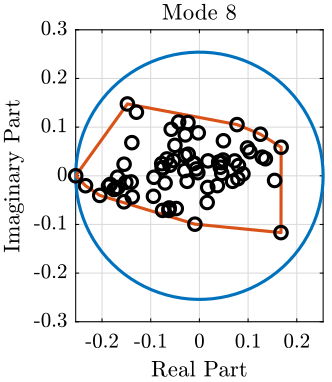
Figure 9: Modal Complexity of one higly complex mode

Figure 10: Modal complexity for each mode
6 From local coordinates to global coordinates for the mode shapes
6.1 Mathematical description
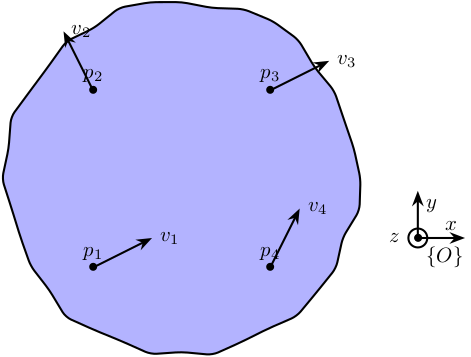
From the figure above, we can write:
\begin{align*} \vec{v}_1 &= \vec{v} + \Omega \vec{p}_1\\ \vec{v}_2 &= \vec{v} + \Omega \vec{p}_2\\ \vec{v}_3 &= \vec{v} + \Omega \vec{p}_3\\ \vec{v}_4 &= \vec{v} + \Omega \vec{p}_4 \end{align*}With
\begin{equation} \Omega = \begin{bmatrix} 0 & -\Omega_z & \Omega_y \\ \Omega_z & 0 & -\Omega_x \\ -\Omega_y & \Omega_x & 0 \end{bmatrix} \end{equation}\(\vec{v}\) and \(\Omega\) represent to velocity and rotation of the solid expressed in the frame \(\{O\}\).
We can rearrange the equations in a matrix form:
\begin{equation} \left[\begin{array}{ccc|ccc} 1 & 0 & 0 & 0 & p_{1z} & -p_{1y} \\ 0 & 1 & 0 & -p_{1z} & 0 & p_{1x} \\ 0 & 0 & 1 & p_{1y} & -p_{1x} & 0 \\ \hline & \vdots & & & \vdots & \\ \hline 1 & 0 & 0 & 0 & p_{4z} & -p_{4y} \\ 0 & 1 & 0 & -p_{4z} & 0 & p_{4x} \\ 0 & 0 & 1 & p_{4y} & -p_{4x} & 0 \end{array}\right] \begin{bmatrix} v_x \\ v_y \\ v_z \\ \hline \Omega_x \\ \Omega_y \\ \Omega_z \end{bmatrix} = \begin{bmatrix} v_{1x} \\ v_{1y} \\ v_{1z} \\\hline \vdots \\\hline v_{4x} \\ v_{4y} \\ v_{4z} \end{bmatrix} \end{equation}and then we obtain the velocity and rotation of the solid in the wanted frame \(\{O\}\):
\begin{equation} \begin{bmatrix} v_x \\ v_y \\ v_z \\ \hline \Omega_x \\ \Omega_y \\ \Omega_z \end{bmatrix} = \left[\begin{array}{ccc|ccc} 1 & 0 & 0 & 0 & p_{1z} & -p_{1y} \\ 0 & 1 & 0 & -p_{1z} & 0 & p_{1x} \\ 0 & 0 & 1 & p_{1y} & -p_{1x} & 0 \\ \hline & \vdots & & & \vdots & \\ \hline 1 & 0 & 0 & 0 & p_{4z} & -p_{4y} \\ 0 & 1 & 0 & -p_{4z} & 0 & p_{4x} \\ 0 & 0 & 1 & p_{4y} & -p_{4x} & 0 \end{array}\right]^{-1} \begin{bmatrix} v_{1x} \\ v_{1y} \\ v_{1z} \\\hline \vdots \\\hline v_{4x} \\ v_{4y} \\ v_{4z} \end{bmatrix} \end{equation}This inversion is equivalent to a mean square problem.
6.2 Matlab Implementation
mode_shapes_O = zeros(mod_n, length(solid_names), 6); for mod_i = 1:mod_n for solid_i = 1:length(solid_names) solids_i = solids.(solid_names{solid_i}); Y = reshape(squeeze(modes(mod_i, solids_i, :))', [], 1); A = zeros(3*length(solids_i), 6); for i = 1:length(solids_i) A(3*(i-1)+1:3*i, 1:3) = eye(3); A(3*(i-1)+1:3*i, 4:6) = [0 acc_pos(i, 3) -acc_pos(i, 2) ; -acc_pos(i, 3) 0 acc_pos(i, 1) ; acc_pos(i, 2) -acc_pos(i, 1) 0]; end mode_shapes_O(mod_i, solid_i, :) = A\Y; end end
6.3 Modal Matrices
We arrange the obtained modal parameters into matrices: \[ \Omega = \begin{bmatrix} \omega_1^2 & & 0 \\ & \ddots & \\ 0 & & \omega_n^2 \end{bmatrix}; \quad \Psi = \begin{bmatrix} & & \\ \{\psi_1\} & \dots & \{\psi_n\} \\ & & \end{bmatrix} \] with \[ \{\psi_1\} = \begin{Bmatrix} \psi_{1_x} & \psi_{2_x} & \dots & \psi_{6_x} & \psi_{1_y} & \dots & \psi_{1\Omega_x} & \dots & \psi_{6\Omega_z} \end{Bmatrix}^T \]
How to add damping to the eigen matrices?
eigen_value_M = diag(freqs*2*pi); eigen_vector_M = reshape(mode_shapes_O, [mod_n, 6*length(solid_names)])';
6.4 TODO Normalization of mode shapes?
We normalize each column of the eigen vector matrix.
Then, each eigenvector as a norm of 1.
eigen_vector_M = eigen_vector_M./vecnorm(eigen_vector_M);
Should we do such normalization?
7 Some notes about constraining the number of degrees of freedom
We want to have the two eigen matrices.
They should have the same size \(n \times n\) where \(n\) is the number of modes as well as the number of degrees of freedom. Thus, if we consider 21 modes, we should restrict our system to have only 21 DOFs.
Actually, we are measured 6 DOFs of 6 solids, thus we have 36 DOFs.
From the mode shapes animations, it seems that in the frequency range of interest, the two marbles can be considered as one solid. We thus have 5 solids and 30 DOFs.
In order to determine which DOF can be neglected, two solutions seems possible:
- compare the mode shapes
- compare the FRFs
The question is: in which base (frame) should be express the modes shapes and FRFs? Is it meaningful to compare mode shapes as they give no information about the amplitudes of vibration?
| Stage | Motion DOFs | Parasitic DOF | Total DOF | Description of DOF |
|---|---|---|---|---|
| Granite | 0 | 3 | 3 | |
| Ty | 1 | 2 | 3 | Ty, Rz |
| Ry | 1 | 2 | 3 | Ry, |
| Rz | 1 | 2 | 3 | Rz, Rx, Ry |
| Hexapod | 6 | 0 | 6 | Txyz, Rxyz |
| 9 | 9 | 18 |
8 Compare Mode Shapes
Let's say we want to see for the first mode which DOFs can be neglected. In order to do so, we should estimate the motion of each stage in particular directions. If we look at the z motion for instance, we will find that we cannot neglect that motion (because of the tilt causing z motion).
mode_i = 3; dof_i = 6; mode = eigen_vector_M(dof_i:6:end, mode_i); figure; hold on; for i=1:length(mode) plot([0, real(mode(i))], [0, imag(mode(i))], '-', 'DisplayName', solid_names{i}); end hold off; legend();
figure; subplot(2, 1, 1); hold on; for i=1:length(mode) plot(1, norm(mode(i)), 'o'); end hold off; ylabel('Amplitude'); subplot(2, 1, 2); hold on; for i=1:length(mode) plot(1, 180/pi*angle(mode(i)), 'o', 'DisplayName', solid_names{i}); end hold off; ylim([-180, 180]); yticks([-180:90:180]); ylabel('Phase [deg]'); legend();
test = mode_shapes_O(10, 1, :)/norm(squeeze(mode_shapes_O(10, 1, :))); test = mode_shapes_O(10, 2, :)/norm(squeeze(mode_shapes_O(10, 2, :)));