UP | HOME

Finite Element Model with Simscape

Table of Contents

1 Amplified Piezoelectric Actuator - 3D elements

The idea here is to:

  • export a FEM of an amplified piezoelectric actuator from Ansys to Matlab
  • import it into a Simscape model
  • compare the obtained dynamics
  • add 10kg mass on top of the actuator and identify the dynamics
  • compare with results from Ansys where 10kg are directly added to the FEM

1.1 Import Mass Matrix, Stiffness Matrix, and Interface Nodes Coordinates

We first extract the stiffness and mass matrices. 

K = extractMatrix('piezo_amplified_3d_K.txt');
M = extractMatrix('piezo_amplified_3d_M.txt');

Then, we extract the coordinates of the interface nodes. 

[int_xyz, int_i, n_xyz, n_i, nodes] = extractNodes('piezo_amplified_3d.txt');

save('./mat/piezo_amplified_3d.mat', 'int_xyz', 'int_i', 'n_xyz', 'n_i', 'nodes', 'M', 'K');

1.2 Output parameters

load('./mat/piezo_amplified_3d.mat', 'int_xyz', 'int_i', 'n_xyz', 'n_i', 'nodes', 'M', 'K');
Total number of Nodes 168959
Number of interface Nodes 13
Number of Modes 30
Size of M and K matrices 108

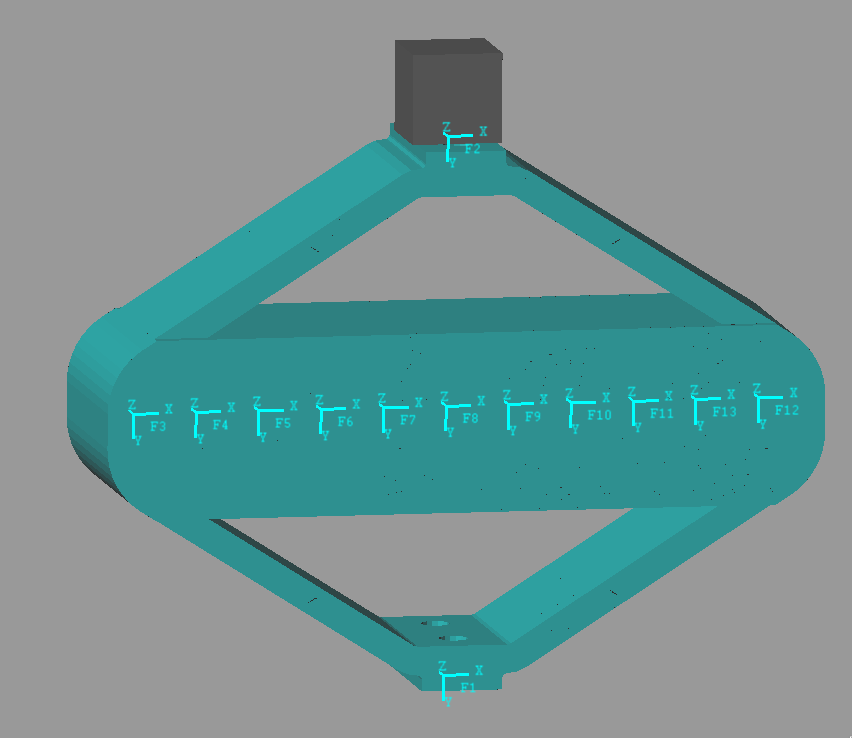
amplified_piezo_interface_nodes.png

Figure 1: Interface Nodes for the Amplified Piezo Actuator

Table 1: Coordinates of the interface nodes
Node i Node Number x [m] y [m] z [m]
1.0 168947.0 0.0 0.03 0.0
2.0 168949.0 0.0 -0.03 0.0
3.0 168950.0 -0.035 0.0 0.0
4.0 168951.0 -0.028 0.0 0.0
5.0 168952.0 -0.021 0.0 0.0
6.0 168953.0 -0.014 0.0 0.0
7.0 168954.0 -0.007 0.0 0.0
8.0 168955.0 0.0 0.0 0.0
9.0 168956.0 0.007 0.0 0.0
10.0 168957.0 0.014 0.0 0.0
11.0 168958.0 0.021 0.0 0.0
12.0 168959.0 0.035 0.0 0.0
13.0 168960.0 0.028 0.0 0.0
Table 2: First 10x10 elements of the Stiffness matrix
300000000.0 -30000.0 8000.0 -200.0 -30.0 -60000.0 20000000.0 -4000.0 500.0 8
-30000.0 100000000.0 400.0 30.0 200.0 -1 4000.0 -8000000.0 800.0 7
8000.0 400.0 50000000.0 -800000.0 -300.0 -40.0 300.0 100.0 5000000.0 40000.0
-200.0 30.0 -800000.0 20000.0 5 1 -10.0 -2 -40000.0 -300.0
-30.0 200.0 -300.0 5 40000.0 0.3 -4 -10.0 40.0 0.4
-60000.0 -1 -40.0 1 0.3 3000.0 7000.0 0.8 -1 0.0003
20000000.0 4000.0 300.0 -10.0 -4 7000.0 300000000.0 20000.0 3000.0 80.0
-4000.0 -8000000.0 100.0 -2 -10.0 0.8 20000.0 100000000.0 -4000.0 -100.0
500.0 800.0 5000000.0 -40000.0 40.0 -1 3000.0 -4000.0 50000000.0 800000.0
8 7 40000.0 -300.0 0.4 0.0003 80.0 -100.0 800000.0 20000.0
Table 3: First 10x10 elements of the Mass matrix
0.03 2e-06 -2e-07 1e-08 2e-08 0.0002 -0.001 2e-07 -8e-08 -9e-10
2e-06 0.02 -5e-07 7e-09 3e-08 2e-08 -3e-07 0.0003 -1e-08 1e-10
-2e-07 -5e-07 0.02 -9e-05 4e-09 -1e-08 2e-07 -2e-08 -0.0006 -5e-06
1e-08 7e-09 -9e-05 1e-06 6e-11 4e-10 -1e-09 3e-11 5e-06 3e-08
2e-08 3e-08 4e-09 6e-11 1e-06 2e-10 -2e-09 2e-10 -7e-09 -4e-11
0.0002 2e-08 -1e-08 4e-10 2e-10 2e-06 -2e-06 -1e-09 -7e-10 -9e-12
-0.001 -3e-07 2e-07 -1e-09 -2e-09 -2e-06 0.03 -2e-06 -1e-07 -5e-09
2e-07 0.0003 -2e-08 3e-11 2e-10 -1e-09 -2e-06 0.02 -8e-07 -1e-08
-8e-08 -1e-08 -0.0006 5e-06 -7e-09 -7e-10 -1e-07 -8e-07 0.02 9e-05
-9e-10 1e-10 -5e-06 3e-08 -4e-11 -9e-12 -5e-09 -1e-08 9e-05 1e-06

Using K, M and int_xyz, we can use the Reduced Order Flexible Solid simscape block.

1.3 Piezoelectric parameters

Parameters for the APA95ML: 

d33 = 3e-10; % Strain constant [m/V]
n = 80; % Number of layers per stack
eT = 1.6e-7; % Permittivity under constant stress [F/m]
sD = 2e-11; % Elastic compliance under constant electric displacement [m2/N]
ka = 235e6; % Stack stiffness [N/m]
C = 5e-6; % Stack capactiance [F]

na = 2; % Number of stacks used as actuator
ns = 1; % Number of stacks used as force sensor

The ratio of the developed force to applied voltage is \(d_{33} n k_a\) in [N/V]. We denote this constant by \(g_a\) and: \[ F_a = g_a V_a, \quad g_a = d_{33} n k_a \] 

d33*(na*n)*(ka/(na + ns)) % [N/V]

3.76

From (Fleming and Leang 2014) (page 123), the relation between relative displacement and generated voltage is: \[ V_s = \frac{d_{33}}{\epsilon^T s^D n} \Delta h \] where:

  • \(V_s\): measured voltage [V]
  • \(d_{33}\): strain constant [m/V]
  • \(\epsilon^T\): permittivity under constant stress [F/m]
  • \(s^D\): elastic compliance under constant electric displacement [m^2/N]
  • \(n\): number of layers
  • \(\Delta h\): relative displacement [m]
1e-6*d33/(eT*sD*ns*n) % [V/um]

1.1719

1.4 Identification of the Dynamics

The flexible element is imported using the Reduced Order Flexible Solid simscape block.

To model the actuator, an Internal Force block is added between the nodes 3 and 12. A Relative Motion Sensor block is added between the nodes 1 and 2 to measure the displacement and the amplified piezo.

One mass is fixed at one end of the piezo-electric stack actuator, the other end is fixed to the world frame.

We first set the mass to be zero. 

m = 0.01;

The dynamics is identified from the applied force to the measured relative displacement. 

%% Name of the Simulink File
mdl = 'piezo_amplified_3d';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/y'], 1, 'openoutput'); io_i = io_i + 1;

Gh = -linearize(mdl, io);

Then, we add 10Kg of mass: 

m = 5;

And the dynamics is identified.

The two identified dynamics are compared in Figure 2. 

%% Name of the Simulink File
mdl = 'piezo_amplified_3d';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/y'], 1, 'openoutput'); io_i = io_i + 1;

Ghm = -linearize(mdl, io);

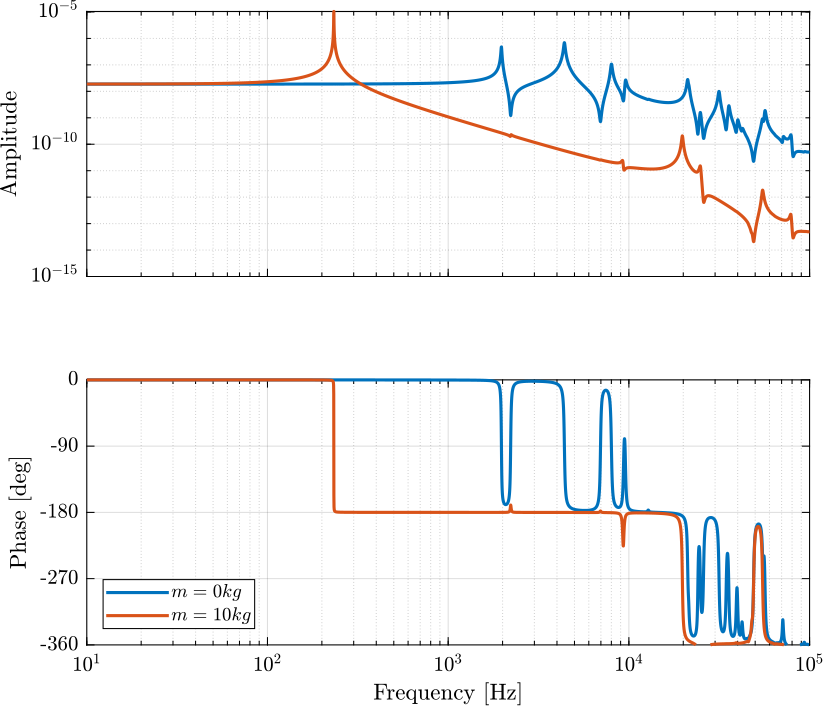
dynamics_act_disp_comp_mass.png

Figure 2: Dynamics from \(F\) to \(d\) without a payload and with a 10kg payload

1.5 Comparison with Ansys

Let’s import the results from an Harmonic response analysis in Ansys. 

Gresp0 = readtable('FEA_HarmResponse_00kg.txt');
Gresp10 = readtable('FEA_HarmResponse_10kg.txt');

The obtained dynamics from the Simscape model and from the Ansys analysis are compare in Figure 3.

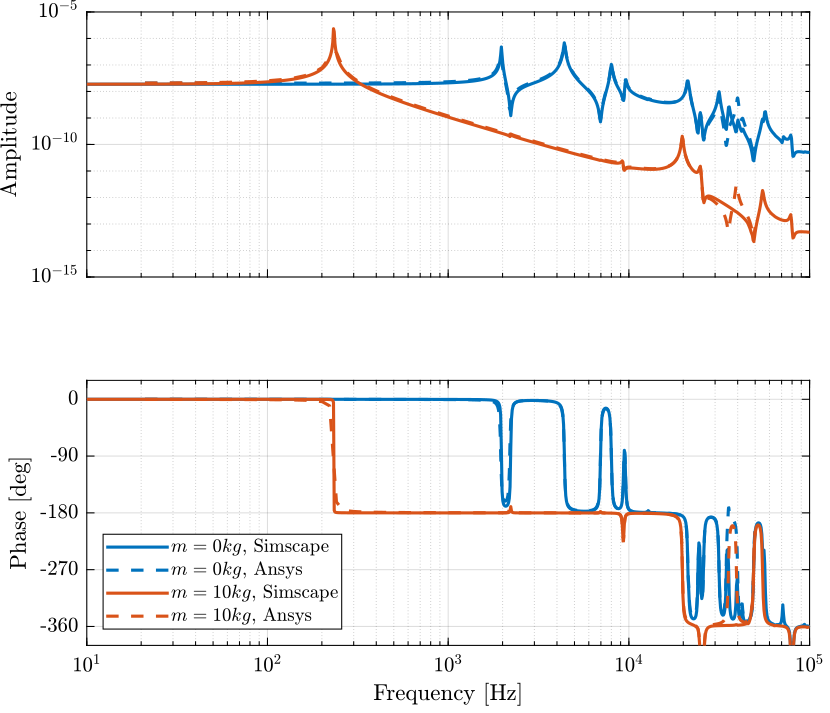
dynamics_force_disp_comp_anasys.png

Figure 3: Comparison of the obtained dynamics using Simscape with the harmonic response analysis using Ansys

1.6 Force Sensor

The dynamics is identified from internal forces applied between nodes 3 and 11 to the relative displacement of nodes 11 and 13.

The obtained dynamics is shown in Figure 4. 

m = 0;

%% Name of the Simulink File
mdl = 'piezo_amplified_3d';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Fa'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/Fs'], 1, 'openoutput'); io_i = io_i + 1;

Gf = linearize(mdl, io);

m = 10;

%% Name of the Simulink File
mdl = 'piezo_amplified_3d';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Fa'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/Fs'], 1, 'openoutput'); io_i = io_i + 1;

Gfm = linearize(mdl, io);

dynamics_force_force_sensor_comp_mass.png

Figure 4: Dynamics from \(F\) to \(F_m\) for \(m=0\) and \(m = 10kg\)

1.7 Distributed Actuator

m = 0;

The dynamics is identified from the applied force to the measured relative displacement. 

%% Name of the Simulink File
mdl = 'piezo_amplified_3d_distri';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/y'], 1, 'openoutput'); io_i = io_i + 1;

Gd = linearize(mdl, io);

Then, we add 10Kg of mass: 

m = 10;

And the dynamics is identified. 

%% Name of the Simulink File
mdl = 'piezo_amplified_3d_distri';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/y'], 1, 'openoutput'); io_i = io_i + 1;

Gdm = linearize(mdl, io);

1.8 Distributed Actuator and Force Sensor

m = 0;

%% Name of the Simulink File
mdl = 'piezo_amplified_3d_distri_act_sens';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1;

Gfd = linearize(mdl, io);

m = 10;

%% Name of the Simulink File
mdl = 'piezo_amplified_3d_distri_act_sens';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1;

Gfdm = linearize(mdl, io);

1.9 Dynamics from input voltage to displacement

m = 5;

And the dynamics is identified.

The two identified dynamics are compared in Figure 2. 

%% Name of the Simulink File
mdl = 'piezo_amplified_3d';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/V'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/y'], 1, 'openoutput'); io_i = io_i + 1;

G = -linearize(mdl, io);

save('../test-bench-apa/mat/fem_model_5kg.mat', 'G')

1.10 Dynamics from input voltage to output voltage

m = 5;

%% Name of the Simulink File
mdl = 'piezo_amplified_3d';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Va'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/Vs'], 1, 'openoutput'); io_i = io_i + 1;

G = -linearize(mdl, io);

2 APA300ML

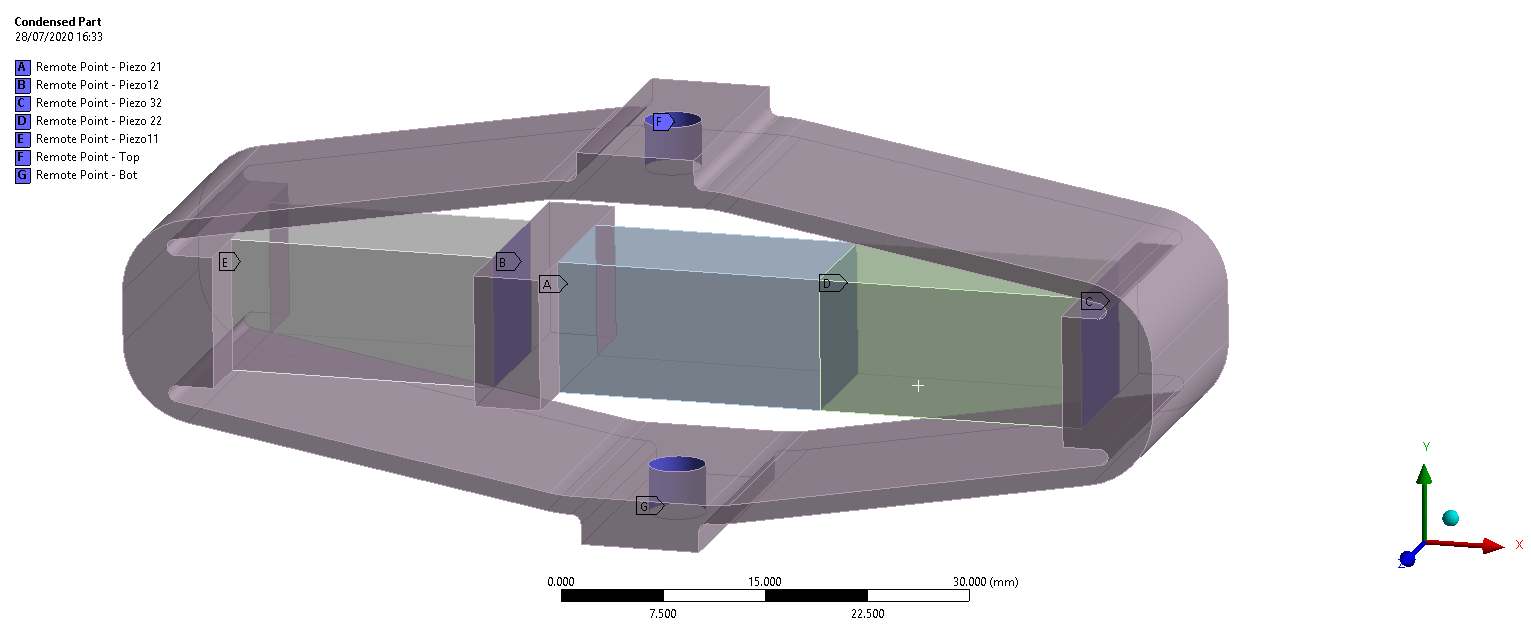
apa300ml_ansys.jpg

Figure 5: Ansys FEM of the APA300ML

2.1 Import Mass Matrix, Stiffness Matrix, and Interface Nodes Coordinates

We first extract the stiffness and mass matrices. 

K = extractMatrix('mat_K-48modes-7MDoF.matrix');
M = extractMatrix('mat_M-48modes-7MDoF.matrix');

K = extractMatrix('mat_K-80modes-7MDoF.matrix');
M = extractMatrix('mat_M-80modes-7MDoF.matrix');

Then, we extract the coordinates of the interface nodes. 

[int_xyz, int_i, n_xyz, n_i, nodes] = extractNodes('Nodes_MDoF_NLIST_MLIST.txt');

save('./mat/APA300ML.mat', 'int_xyz', 'int_i', 'n_xyz', 'n_i', 'nodes', 'M', 'K');

2.2 Output parameters

load('./mat/APA300ML.mat', 'int_xyz', 'int_i', 'n_xyz', 'n_i', 'nodes', 'M', 'K');
Total number of Nodes 7
Number of interface Nodes 7
Number of Modes 6
Size of M and K matrices 48
Table 4: Coordinates of the interface nodes
Node i Node Number x [m] y [m] z [m]
1.0 53917.0 0.0 -0.015 0.0
2.0 53918.0 0.0 0.015 0.0
3.0 53919.0 -0.0325 0.0 0.0
4.0 53920.0 -0.0125 0.0 0.0
5.0 53921.0 -0.0075 0.0 0.0
6.0 53922.0 0.0125 0.0 0.0
7.0 53923.0 0.0325 0.0 0.0
Table 5: First 10x10 elements of the Stiffness matrix
200000000.0 30000.0 50000.0 200.0 -100.0 -300000.0 10000000.0 -6000.0 20000.0 -60.0
30000.0 7000000.0 10000.0 30.0 -30.0 -70.0 7000.0 -500000.0 3000.0 -10.0
50000.0 10000.0 30000000.0 200000.0 -200.0 -100.0 20000.0 -2000.0 2000000.0 -9000.0
200.0 30.0 200000.0 1000.0 -0.8 -0.4 50.0 -6 9000.0 -30.0
-100.0 -30.0 -200.0 -0.8 10000.0 0.2 -40.0 10.0 20.0 -0.05
-300000.0 -70.0 -100.0 -0.4 0.2 900.0 -30000.0 10.0 -40.0 0.1
10000000.0 7000.0 20000.0 50.0 -40.0 -30000.0 200000000.0 -50000.0 30000.0 -50.0
-6000.0 -500000.0 -2000.0 -6 10.0 10.0 -50000.0 7000000.0 -4000.0 8
20000.0 3000.0 2000000.0 9000.0 20.0 -40.0 30000.0 -4000.0 30000000.0 -200000.0
-60.0 -10.0 -9000.0 -30.0 -0.05 0.1 -50.0 8 -200000.0 1000.0
Table 6: First 10x10 elements of the Mass matrix
0.01 7e-06 -5e-06 -6e-08 3e-09 -5e-05 -0.0005 -2e-07 -3e-06 1e-08
7e-06 0.009 4e-07 6e-09 -4e-09 -3e-08 -2e-07 6e-05 5e-07 -1e-09
-5e-06 4e-07 0.01 2e-05 2e-08 3e-08 -2e-06 -1e-07 -0.0002 9e-07
-6e-08 6e-09 2e-05 3e-07 1e-10 3e-10 -7e-09 2e-10 -9e-07 3e-09
3e-09 -4e-09 2e-08 1e-10 1e-07 -3e-12 6e-09 -2e-10 -3e-09 9e-12
-5e-05 -3e-08 3e-08 3e-10 -3e-12 6e-07 1e-06 -3e-09 2e-08 -7e-11
-0.0005 -2e-07 -2e-06 -7e-09 6e-09 1e-06 0.01 -8e-06 -2e-06 9e-09
-2e-07 6e-05 -1e-07 2e-10 -2e-10 -3e-09 -8e-06 0.009 1e-07 2e-09
-3e-06 5e-07 -0.0002 -9e-07 -3e-09 2e-08 -2e-06 1e-07 0.01 -2e-05
1e-08 -1e-09 9e-07 3e-09 9e-12 -7e-11 9e-09 2e-09 -2e-05 3e-07

Using K, M and int_xyz, we can use the Reduced Order Flexible Solid simscape block.

2.3 Piezoelectric parameters

Parameters for the APA300ML: 

d33 = 3e-10; % Strain constant [m/V]
n = 80; % Number of layers per stack
eT = 1.6e-8; % Permittivity under constant stress [F/m]
sD = 2e-11; % Elastic compliance under constant electric displacement [m2/N]
ka = 235e6; % Stack stiffness [N/m]
C = 5e-6; % Stack capactiance [F]

na = 2; % Number of stacks used as actuator
ns = 1; % Number of stacks used as force sensor

The ratio of the developed force to applied voltage is \(d_{33} n k_a\) in [N/V]. We denote this constant by \(g_a\) and: \[ F_a = g_a V_a, \quad g_a = d_{33} n k_a \] 

d33*(na*n)*(ka/(na + ns)) % [N/V]

0.42941

From (Fleming and Leang 2014) (page 123), the relation between relative displacement and generated voltage is: \[ V_s = \frac{d_{33}}{\epsilon^T s^D n} \Delta h \] where:

  • \(V_s\): measured voltage [V]
  • \(d_{33}\): strain constant [m/V]
  • \(\epsilon^T\): permittivity under constant stress [F/m]
  • \(s^D\): elastic compliance under constant electric displacement [m^2/N]
  • \(n\): number of layers
  • \(\Delta h\): relative displacement [m]
1e-6*d33/(eT*sD*ns*n) % [V/um]

5.8594

2.4 Identification of the APA Characteristics

2.4.1 Stiffness

The transfer function from vertical external force to the relative vertical displacement is identified.

The inverse of its DC gain is the axial stiffness of the APA: 

1e-6/dcgain(G) % [N/um]

1.8634

The specified stiffness in the datasheet is \(k = 1.8\, [N/\mu m]\).

2.4.2 Resonance Frequency

The resonance frequency is specified to be between 650Hz and 840Hz. This is also the case for the FEM model (Figure 6).

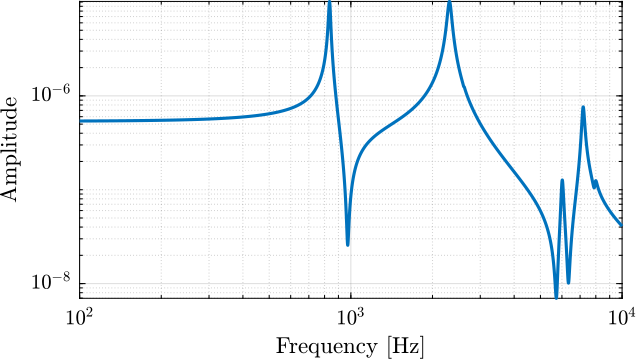
apa300ml_resonance.png

Figure 6: First resonance is around 800Hz

2.4.3 Amplification factor

The amplification factor is the ratio of the axial displacement to the stack displacement.

The ratio of the two displacement is computed from the FEM model. 

-dcgain(G(1,1))./dcgain(G(2,1))

4.936

If we take the ratio of the piezo height and length (approximation of the amplification factor): 

75/15

5

2.4.4 Stroke

Estimation of the actuator stroke: \[ \Delta H = A n \Delta L \] with:

  • \(\Delta H\) Axial Stroke of the APA
  • \(A\) Amplification factor (5 for the APA300ML)
  • \(n\) Number of stack used
  • \(\Delta L\) Stroke of the stack (0.1% of its length)
1e6 * 5 * 3 * 20e-3 * 0.1e-2

300

This is exactly the specified stroke in the data-sheet.

2.5 Identification of the Dynamics

The flexible element is imported using the Reduced Order Flexible Solid simscape block.

To model the actuator, an Internal Force block is added between the nodes 3 and 12. A Relative Motion Sensor block is added between the nodes 1 and 2 to measure the displacement and the amplified piezo.

One mass is fixed at one end of the piezo-electric stack actuator, the other end is fixed to the world frame.

We first set the mass to be zero. The dynamics is identified from the applied force to the measured relative displacement. The same dynamics is identified for a payload mass of 10Kg. 

m = 10;

apa300ml_plant_dynamics.png

Figure 7: Transfer function from forces applied by the stack to the axial displacement of the APA

2.6 IFF

Let’s use 2 stacks as actuators and 1 stack as force sensor.

The transfer function from actuator to sensors is identified and shown in Figure 8.

apa300ml_iff_plant.png

Figure 8: Transfer function from actuator to force sensor

For root locus corresponding to IFF is shown in Figure 9.

apa300ml_iff_root_locus.png

Figure 9: Root Locus for IFF

2.7 DVF

Now the dynamics from the stack actuator to the relative motion sensor is identified and shown in Figure 10.

apa300ml_dvf_plant.png

Figure 10: Transfer function from stack actuator to relative motion sensor

The root locus for DVF is shown in Figure 11.

apa300ml_dvf_root_locus.png

Figure 11: Root Locus for Direct Velocity Feedback

2.8 Identification for a simpler model

The goal in this section is to identify the parameters of a simple APA model from the FEM. This can be useful is a lower order model is to be used for simulations.

The presented model is based on (Souleille et al. 2018).

The model represents the Amplified Piezo Actuator (APA) from Cedrat-Technologies (Figure 12). The parameters are shown in the table below.

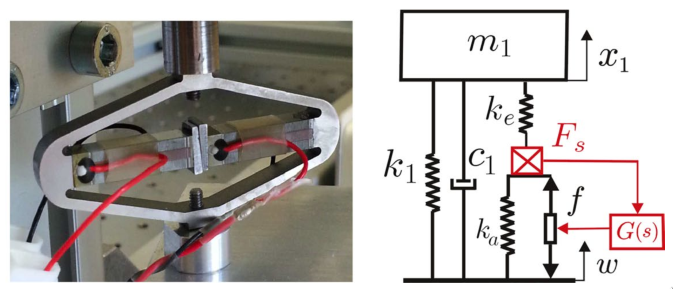
souleille18_model_piezo.png

Figure 12: Picture of an APA100M from Cedrat Technologies. Simplified model of a one DoF payload mounted on such isolator

Table 7: Parameters used for the model of the APA 100M
  Meaning
\(k_e\) Stiffness used to adjust the pole of the isolator
\(k_1\) Stiffness of the metallic suspension when the stack is removed
\(k_a\) Stiffness of the actuator
\(c_1\) Added viscous damping

The goal is to determine \(k_e\), \(k_a\) and \(k_1\) so that the simplified model fits the FEM model.

\[ \alpha = \frac{x_1}{f}(\omega=0) = \frac{\frac{k_e}{k_e + k_a}}{k_1 + \frac{k_e k_a}{k_e + k_a}} \] \[ \beta = \frac{x_1}{F}(\omega=0) = \frac{1}{k_1 + \frac{k_e k_a}{k_e + k_a}} \]

If we can fix \(k_a\), we can determine \(k_e\) and \(k_1\) with: \[ k_e = \frac{k_a}{\frac{\beta}{\alpha} - 1} \] \[ k_1 = \frac{1}{\beta} - \frac{k_e k_a}{k_e + k_a} \]

From the identified dynamics, compute \(\alpha\) and \(\beta\) 

alpha = abs(dcgain(G('y', 'Fa')));
beta  = abs(dcgain(G('y', 'Fd')));

\(k_a\) is estimated using the following formula: 

ka = 0.8/abs(dcgain(G('y', 'Fa')));

The factor can be adjusted to better match the curves.

Then \(k_e\) and \(k_1\) are computed. 

ke = ka/(beta/alpha - 1);
k1 = 1/beta - ke*ka/(ke + ka);
  Value [N/um]
ka 42.9
ke 1.5
k1 0.4

The damping in the system is adjusted to match the FEM model if necessary. 

c1 = 1e2;

Analytical model of the simpler system: 

Ga = 1/(m*s^2 + k1 + c1*s + ke*ka/(ke + ka)) * ...
     [ 1 ,              k1 + c1*s + ke*ka/(ke + ka)  , ke/(ke + ka) ;
      -ke*ka/(ke + ka), ke*ka/(ke + ka)*m*s^2 ,       -ke/(ke + ka)*(m*s^2 + c1*s + k1)];

Ga.InputName = {'Fd', 'w', 'Fa'};
Ga.OutputName = {'y', 'Fs'};

Adjust the DC gain for the force sensor: 

lambda = dcgain(Ga('Fs', 'Fd'))/dcgain(G('Fs', 'Fd'));

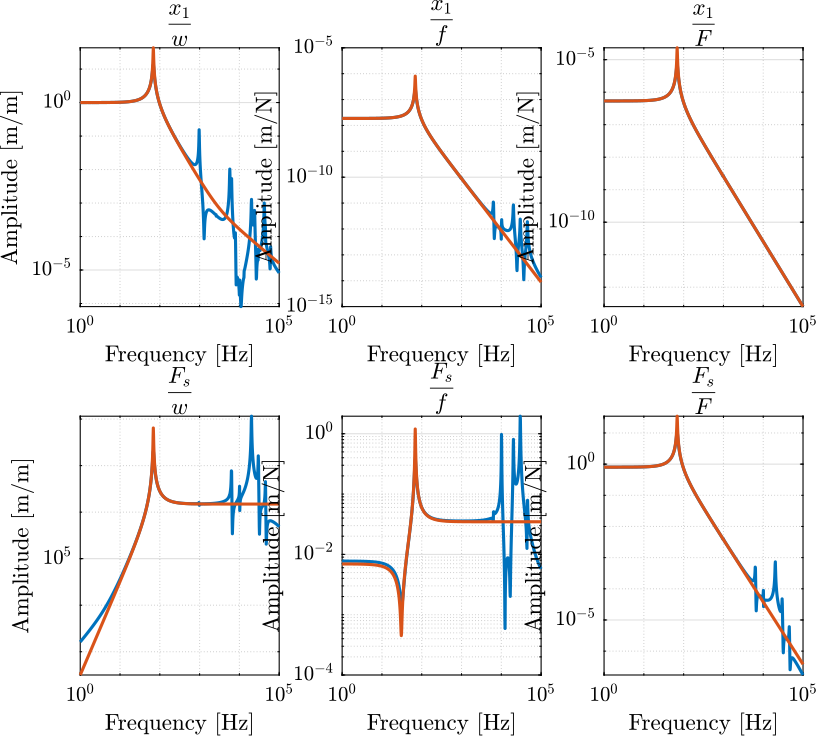
apa300ml_comp_simpler_model.png

Figure 13: Comparison of the Dynamics between the FEM model and the simplified one

3 Flexible Joint

flexor_id16_screenshot.png

Figure 14: Flexor studied

3.1 Import Mass Matrix, Stiffness Matrix, and Interface Nodes Coordinates

We first extract the stiffness and mass matrices. 

K = extractMatrix('mat_K_6modes_2MDoF.matrix');
M = extractMatrix('mat_M_6modes_2MDoF.matrix');

Then, we extract the coordinates of the interface nodes. 

[int_xyz, int_i, n_xyz, n_i, nodes] = extractNodes('out_nodes_3D.txt');

save('./mat/flexor_ID16.mat', 'int_xyz', 'int_i', 'n_xyz', 'n_i', 'nodes', 'M', 'K');

3.2 Output parameters

load('./mat/flexor_ID16.mat', 'int_xyz', 'int_i', 'n_xyz', 'n_i', 'nodes', 'M', 'K');
Total number of Nodes 2
Number of interface Nodes 2
Number of Modes 6
Size of M and K matrices 18
Table 8: Coordinates of the interface nodes
Node i Node Number x [m] y [m] z [m]
1.0 181278.0 0.0 0.0 0.0
2.0 181279.0 0.0 0.0 -0.0
Table 9: First 10x10 elements of the Stiffness matrix
11200000.0 195.0 2220.0 -0.719 -265.0 1.59 -11200000.0 -213.0 -2220.0 0.147
195.0 11400000.0 1290.0 -148.0 -0.188 2.41 -212.0 -11400000.0 -1290.0 148.0
2220.0 1290.0 119000000.0 1.31 1.49 1.79 -2220.0 -1290.0 -119000000.0 -1.31
-0.719 -148.0 1.31 33.0 0.000488 -0.000977 0.141 148.0 -1.31 -33.0
-265.0 -0.188 1.49 0.000488 33.0 0.00293 266.0 0.154 -1.49 0.00026
1.59 2.41 1.79 -0.000977 0.00293 236.0 -1.32 -2.55 -1.79 0.000379
-11200000.0 -212.0 -2220.0 0.141 266.0 -1.32 11400000.0 24600.0 1640.0 120.0
-213.0 -11400000.0 -1290.0 148.0 0.154 -2.55 24600.0 11400000.0 1290.0 -72.0
-2220.0 -1290.0 -119000000.0 -1.31 -1.49 -1.79 1640.0 1290.0 119000000.0 1.32
0.147 148.0 -1.31 -33.0 0.00026 0.000379 120.0 -72.0 1.32 34.7
Table 10: First 10x10 elements of the Mass matrix
0.02 1e-09 -4e-08 -1e-10 0.0002 -3e-11 0.004 5e-08 7e-08 1e-10
1e-09 0.02 -3e-07 -0.0002 -1e-10 -2e-09 2e-08 0.004 3e-07 1e-05
-4e-08 -3e-07 0.02 7e-10 -2e-09 1e-09 3e-07 7e-08 0.003 1e-09
-1e-10 -0.0002 7e-10 4e-06 -1e-12 -6e-13 2e-10 -7e-06 -8e-10 -1e-09
0.0002 -1e-10 -2e-09 -1e-12 3e-06 2e-13 9e-06 4e-11 2e-09 -3e-13
-3e-11 -2e-09 1e-09 -6e-13 2e-13 4e-07 8e-11 9e-10 -1e-09 2e-12
0.004 2e-08 3e-07 2e-10 9e-06 8e-11 0.02 -7e-08 -3e-07 -2e-10
5e-08 0.004 7e-08 -7e-06 4e-11 9e-10 -7e-08 0.01 -4e-08 0.0002
7e-08 3e-07 0.003 -8e-10 2e-09 -1e-09 -3e-07 -4e-08 0.02 -1e-09
1e-10 1e-05 1e-09 -1e-09 -3e-13 2e-12 -2e-10 0.0002 -1e-09 2e-06

Using K, M and int_xyz, we can use the Reduced Order Flexible Solid simscape block.

3.3 Flexible Joint Characteristics

Caracteristic Value Estimation by Francois
Axial Stiffness [N/um] 119 60
Bending Stiffness [Nm/rad] 33 15
Bending Stiffness [Nm/rad] 33 15
Torsion Stiffness [Nm/rad] 236 20

3.4 Identification

m = 10;

The dynamics is identified from the applied force to the measured relative displacement. 

%% Name of the Simulink File
mdl = 'flexor_ID16';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/T'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1;

G = linearize(mdl, io);
Caracteristic Value Identification
Axial Stiffness Dz [N/um] 119 119
Bending Stiffness Rx [Nm/rad] 33 34
Bending Stiffness Ry [Nm/rad] 33 126
Torsion Stiffness Rz [Nm/rad] 236 238

4 Integral Force Feedback with Amplified Piezo

In this section, we try to replicate the results obtained in (Souleille et al. 2018).

4.1 Import Mass Matrix, Stiffness Matrix, and Interface Nodes Coordinates

We first extract the stiffness and mass matrices. 

K = extractMatrix('piezo_amplified_IFF_K.txt');
M = extractMatrix('piezo_amplified_IFF_M.txt');

Then, we extract the coordinates of the interface nodes. 

[int_xyz, int_i, n_xyz, n_i, nodes] = extractNodes('piezo_amplified_IFF.txt');

4.2 IFF Plant

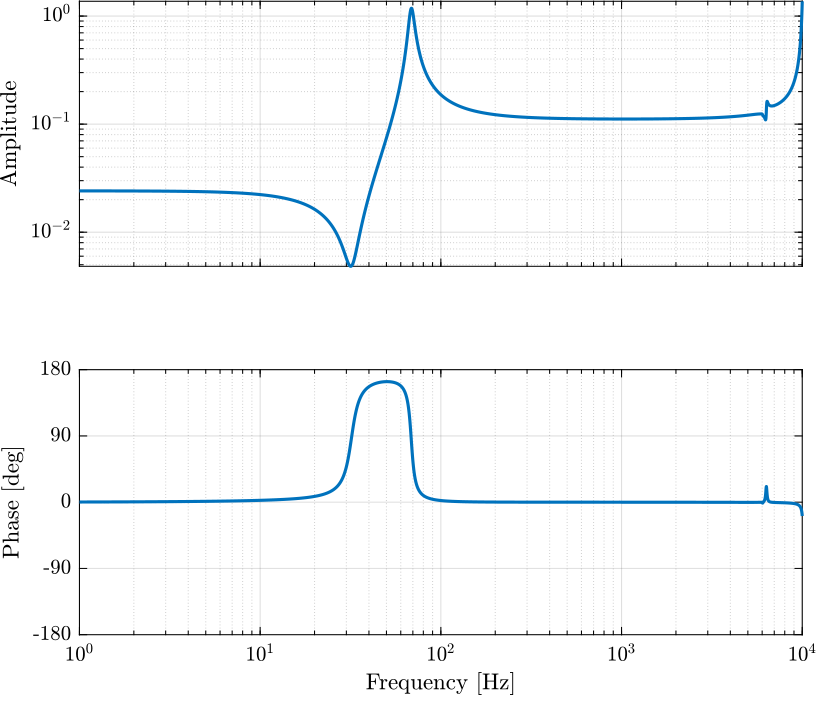
The transfer function from the force actuator to the force sensor is identified and shown in Figure 15. 

Kiff = tf(0);

m = 0;

%% Name of the Simulink File
mdl = 'piezo_amplified_IFF';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Kiff'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/G'],    1, 'openoutput'); io_i = io_i + 1;

Gf = linearize(mdl, io);

m = 10;

Gfm = linearize(mdl, io);

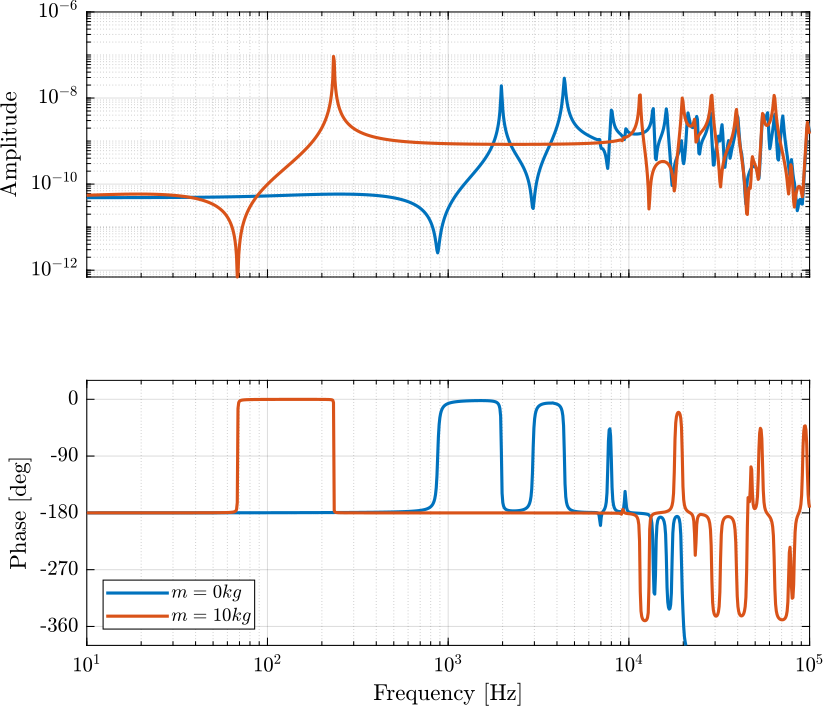
piezo_amplified_iff_plant.png

Figure 15: IFF Plant

4.3 IFF controller

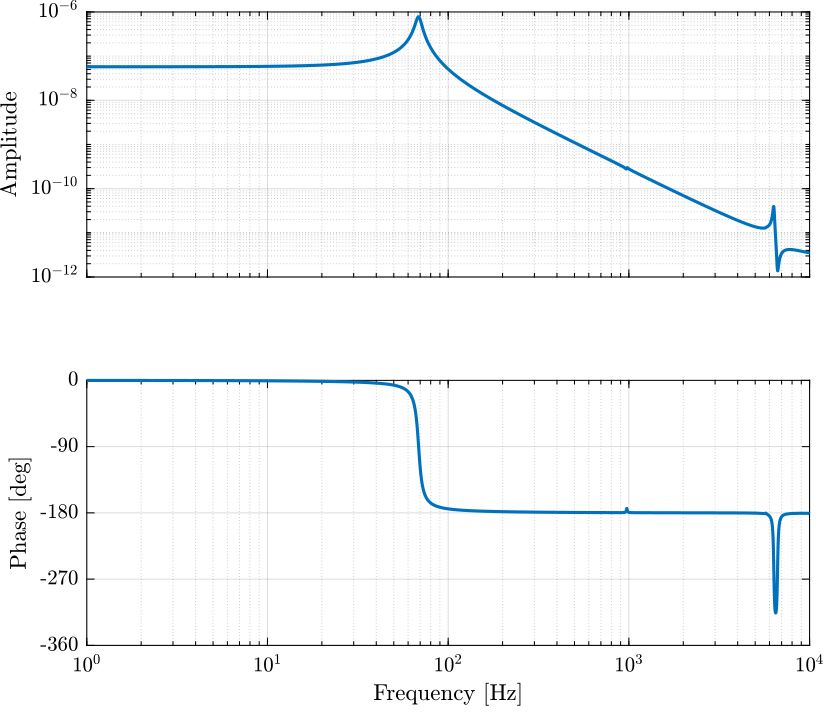
The controller is defined and the loop gain is shown in Figure 16. 

Kiff = -1e12/s;

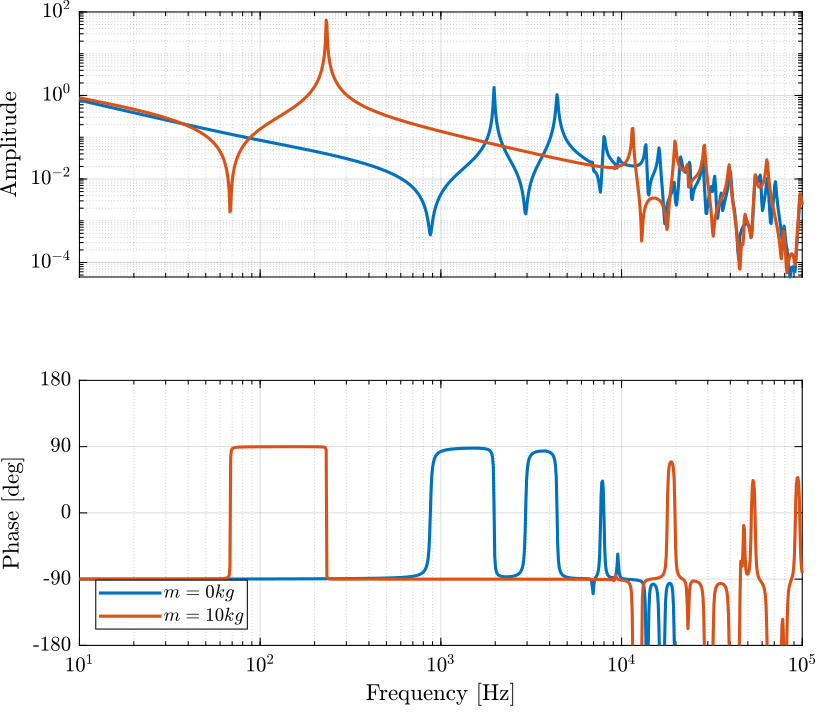
piezo_amplified_iff_loop_gain.png

Figure 16: IFF Loop Gain

4.4 Closed Loop System

m = 10;

Kiff = -1e12/s;

%% Name of the Simulink File
mdl = 'piezo_amplified_IFF';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Dw'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/F'],  1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/Fd'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/d'],  1, 'openoutput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/G'],  1, 'output'); io_i = io_i + 1;

Giff = linearize(mdl, io);
Giff.InputName  = {'w', 'f', 'F'};
Giff.OutputName  = {'x1', 'Fs'};

Kiff = tf(0);

G = linearize(mdl, io);
G.InputName  = {'w', 'f', 'F'};
G.OutputName  = {'x1', 'Fs'};

piezo_amplified_iff_comp.png

Figure 17: OL and CL transfer functions

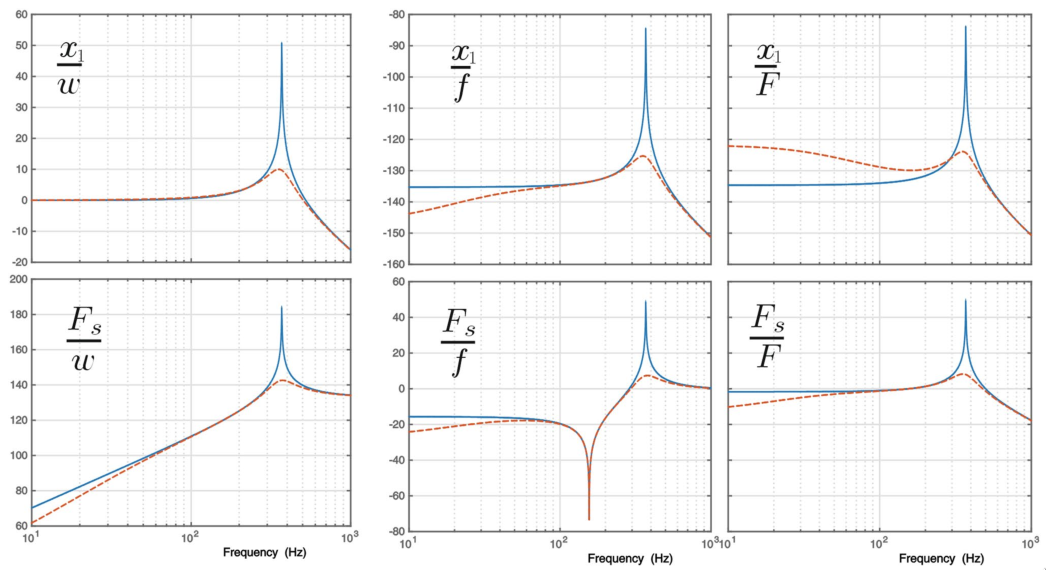
souleille18_results.png

Figure 18: Results obtained in souleille18_concep_activ_mount_space_applic

Bibliography

Fleming, Andrew J., and Kam K. Leang. 2014. Design, Modeling and Control of Nanopositioning Systems. Advances in Industrial Control. Springer International Publishing. https://doi.org/10.1007/978-3-319-06617-2.
Souleille, Adrien, Thibault Lampert, V Lafarga, Sylvain Hellegouarch, Alan Rondineau, Gonçalo Rodrigues, and Christophe Collette. 2018. “A Concept of Active Mount for Space Applications.” CEAS Space Journal 10 (2). Springer:157–65.

Author: Dehaeze Thomas

Created: 2020-08-04 mar. 11:53