DCM - Dynamical Multi-Body Model

1. System Kinematics
2. Open Loop System Identification
3. Active Damping Plant (Strain gauges)
- 3.1. Identification
4. Active Damping Plant (Force Sensors)
5. HAC-LAC (IFF) architecture

This report is also available as a pdf.

In this document, a Simscape (.e.g. multi-body) model of the ESRF Double Crystal Monochromator (DCM) is presented and used to develop and optimize the control strategy.

It is structured as follow:

Section 1: the kinematics of the DCM is presented, and Jacobian matrices which are used to solve the inverse and forward kinematics are computed.
Section 2: the system dynamics is identified in the absence of control.
Section 3: it is studied whether if the strain gauges fixed to the piezoelectric actuators can be used to actively damp the plant.
Section 4: piezoelectric force sensors are added in series with the piezoelectric actuators and are used to actively damp the plant using the Integral Force Feedback (IFF) control strategy.
Section 5: the High Authority Control - Low Authority Control (HAC-LAC) strategy is tested on the Simscape model.

1. System Kinematics

1.1. Bragg Angle

%% Tested bragg angles
bragg = linspace(5, 80, 1000); % Bragg angle [deg]
d_off = 10.5e-3; % Wanted offset between x-rays [m]

%% Vertical Jack motion as a function of Bragg angle
dz = d_off./(2*cos(bragg*pi/180));

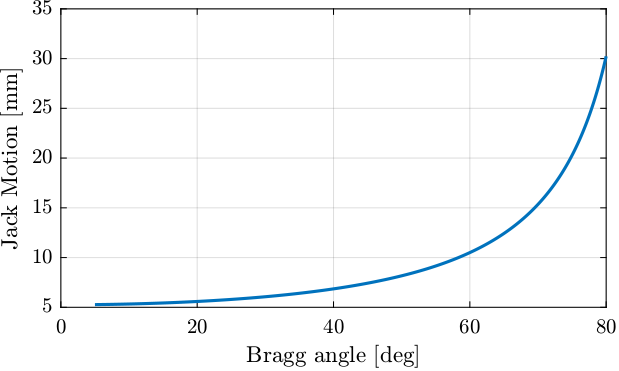
Figure 1: Jack motion as a function of Bragg angle

%% Required Jack stroke
ans = 1e3*(dz(end) - dz(1))

24.963

1.2. Kinematics (111 Crystal)

The reference frame is taken at the center of the 111 second crystal.

1.2.1. Interferometers - 111 Crystal

Three interferometers are pointed to the bottom surface of the 111 crystal.

The position of the measurement points are shown in Figure 2 as well as the origin where the motion of the crystal is computed.

Figure 2: Bottom view of the second crystal 111. Position of the measurement points.

The inverse kinematics consisting of deriving the interferometer measurements from the motion of the crystal (see Figure 3):

\begin{equation} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \bm{J}_{s,111} \begin{bmatrix} d_z \\ r_y \\ r_x \end{bmatrix} \end{equation}

Figure 3: Inverse Kinematics - Interferometers

From the Figure 2, the inverse kinematics can be solved as follow (for small motion):

\begin{equation} \bm{J}_{s,111} = \begin{bmatrix} 1 & 0.07 & -0.015 \\ 1 & 0 & 0.015 \\ 1 & -0.07 & -0.015 \end{bmatrix} \end{equation}

%% Sensor Jacobian matrix for 111 crystal
J_s_111 = [1,  0.07, -0.015
           1,  0,     0.015
           1, -0.07, -0.015];

Table 1: Sensor Jacobian \(\bm{J}_{s,111}\)
1.0	0.07	-0.015
1.0	0.0	0.015
1.0	-0.07	-0.015

The forward kinematics is solved by inverting the Jacobian matrix (see Figure 4).

\begin{equation} \begin{bmatrix} d_z \\ r_y \\ r_x \end{bmatrix} = \bm{J}_{s,111}^{-1} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \end{equation}

Figure 4: Forward Kinematics - Interferometers

Table 2: Inverse of the sensor Jacobian \(\bm{J}_{s,111}^{-1}\)
0.25	0.5	0.25
7.14	0.0	-7.14
-16.67	33.33	-16.67

1.2.2. Piezo - 111 Crystal

The location of the actuators with respect with the center of the 111 second crystal are shown in Figure 5.

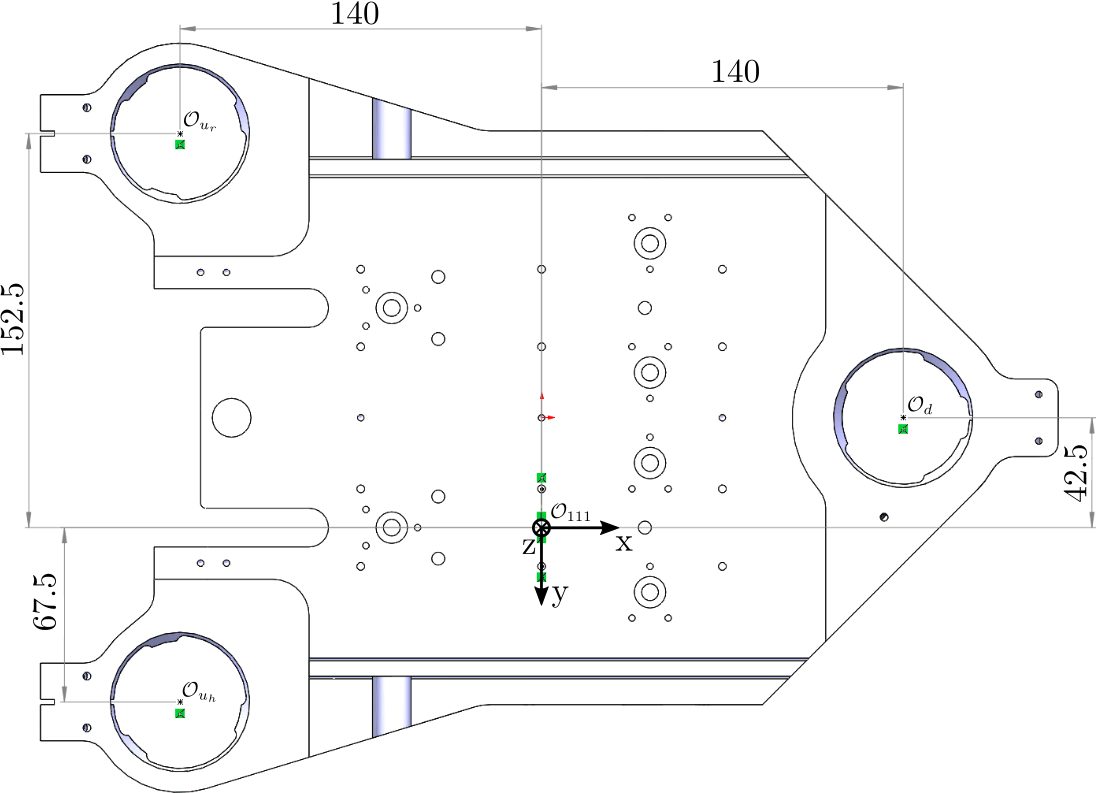
Figure 5: Location of actuators with respect to the center of the 111 second crystal (bottom view)

Inverse Kinematics consist of deriving the axial (z) motion of the 3 actuators from the motion of the crystal’s center.

\begin{equation} \begin{bmatrix} d_{u_r} \\ d_{u_h} \\ d_{d} \end{bmatrix} = \bm{J}_{a,111} \begin{bmatrix} d_z \\ r_y \\ r_x \end{bmatrix} \end{equation}

Figure 6: Inverse Kinematics - Actuators

Based on the geometry in Figure 5, we obtain:

\begin{equation} \bm{J}_{a,111} = \begin{bmatrix} 1 & 0.14 & -0.1525 \\ 1 & 0.14 & 0.0675 \\ 1 & -0.14 & -0.0425 \end{bmatrix} \end{equation}

%% Actuator Jacobian - 111 crystal
J_a_111 = [1,  0.14, -0.1525
           1,  0.14,  0.0675
           1, -0.14, -0.0425];

Table 3: Actuator Jacobian \(\bm{J}_{a,111}\)
1.0	0.14	-0.1525
1.0	0.14	0.0675
1.0	-0.14	-0.0425

The forward Kinematics is solved by inverting the Jacobian matrix:

\begin{equation} \begin{bmatrix} d_z \\ r_y \\ r_x \end{bmatrix} = \bm{J}_{a,111}^{-1} \begin{bmatrix} d_{u_r} \\ d_{u_h} \\ d_{d} \end{bmatrix} \end{equation}

Figure 7: Forward Kinematics - Actuators for 111 crystal

Table 4: Inverse of the actuator Jacobian \(\bm{J}_{a,111}^{-1}\)
0.0568	0.4432	0.5
1.7857	1.7857	-3.5714
-4.5455	4.5455	0.0

1.3. Save Kinematics

save('mat/dcm_kinematics.mat', 'J_a_111', 'J_s_111')

2. Open Loop System Identification

2.1. Identification

Let’s considered the system \(\bm{G}(s)\) with:

3 inputs: force applied to the 3 fast jacks
3 outputs: measured displacement by the 3 interferometers pointing at the 111 second crystal

It is schematically shown in Figure 8.

Figure 8: Dynamical system with inputs and outputs

The system is identified from the Simscape model.

%% Input/Output definition
clear io; io_i = 1;

%% Inputs
% Control Input {3x1} [N]
io(io_i) = linio([mdl, '/control_system'], 1, 'openinput');  io_i = io_i + 1;

%% Outputs
% Interferometers {3x1} [m]
io(io_i) = linio([mdl, '/DCM'], 1, 'openoutput'); io_i = io_i + 1;

%% Extraction of the dynamics
G = linearize(mdl, io);

size(G)

size(G)
State-space model with 3 outputs, 3 inputs, and 24 states.

2.2. Plant in the frame of the fastjacks

load('mat/dcm_kinematics.mat');

Using the forward and inverse kinematics, we can computed the dynamics from piezo forces to axial motion of the 3 fastjacks (see Figure 9).

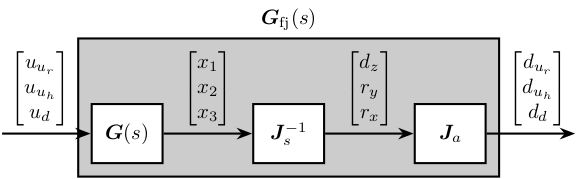
Figure 9: Use of Jacobian matrices to obtain the system in the frame of the fastjacks

%% Compute the system in the frame of the fastjacks
G_pz = J_a_111*inv(J_s_111)*G;

The DC gain of the new system shows that the system is well decoupled at low frequency.

dcgain(G_pz)

Table 5: DC gain of the plant in the frame of the fast jacks \(\bm{G}_{\text{fj}}\)
4.4407e-09	2.7656e-12	1.0132e-12
2.7656e-12	4.4407e-09	1.0132e-12
1.0109e-12	1.0109e-12	4.4424e-09

The bode plot of \(\bm{G}_{\text{fj}}(s)\) is shown in Figure 10.

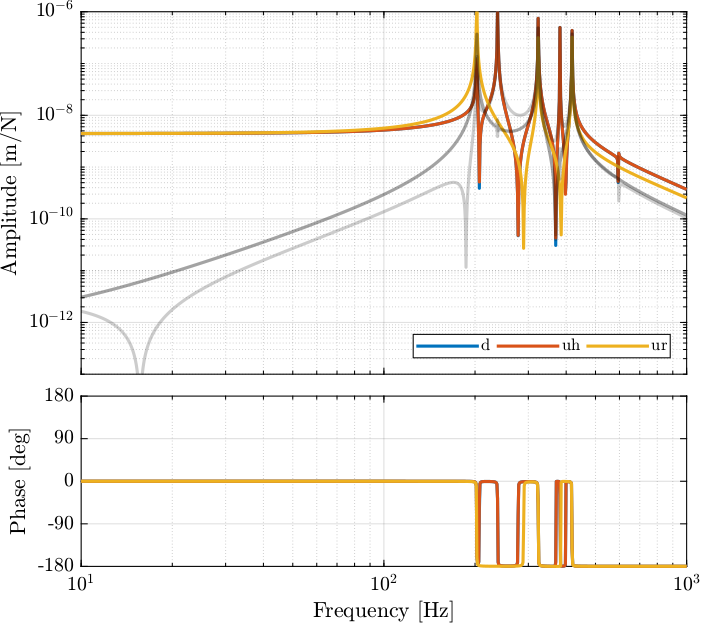
Figure 10: Bode plot of the diagonal and off-diagonal elements of the plant in the frame of the fast jacks

Computing the system in the frame of the fastjack gives good decoupling at low frequency (until the first resonance of the system).

2.3. Plant in the frame of the crystal

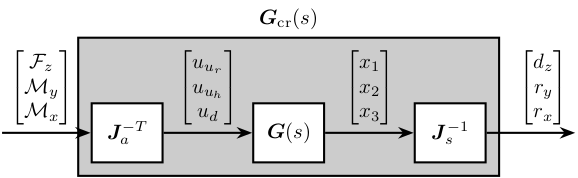
Figure 11: Use of Jacobian matrices to obtain the system in the frame of the crystal

G_mr = inv(J_s_111)*G*inv(J_a_111');

dcgain(G_mr)

1.9978e-09	3.9657e-09	7.7944e-09
3.9656e-09	8.4979e-08	-1.5135e-17
7.7944e-09	-3.9252e-17	1.834e-07

This results in a coupled system. The main reason is that, as we map forces to the center of the 111 crystal and not at the center of mass/stiffness of the moving part, vertical forces will induce rotation and torques will induce vertical motion.

3. Active Damping Plant (Strain gauges)

In this section, we wish to see whether if strain gauges fixed to the piezoelectric actuator can be used for active damping.

3.1. Identification

%% Input/Output definition
clear io; io_i = 1;

%% Inputs
% Control Input {3x1} [N]
io(io_i) = linio([mdl, '/u'], 1, 'openinput');  io_i = io_i + 1;
% % Stepper Displacement {3x1} [m]
% io(io_i) = linio([mdl, '/d'], 1, 'openinput');  io_i = io_i + 1;

%% Outputs
% Strain Gauges {3x1} [m]
io(io_i) = linio([mdl, '/sg'], 1, 'openoutput'); io_i = io_i + 1;

%% Extraction of the dynamics
G_sg = linearize(mdl, io);

dcgain(G_sg)

-1.4113e-13	1.0339e-13	3.774e-14
1.0339e-13	-1.4113e-13	3.774e-14
3.7792e-14	3.7792e-14	-7.5585e-14

4. Active Damping Plant (Force Sensors)

Force sensors are added above the piezoelectric actuators. They can consists of a simple piezoelectric ceramic stack. See for instance fleming10_integ_strain_force_feedb_high.

4.1. Identification

%% Input/Output definition
clear io; io_i = 1;

%% Inputs
% Control Input {3x1} [N]
io(io_i) = linio([mdl, '/control_system'], 1, 'openinput');  io_i = io_i + 1;

%% Outputs
% Force Sensor {3x1} [m]
io(io_i) = linio([mdl, '/DCM'], 3, 'openoutput'); io_i = io_i + 1;

%% Extraction of the dynamics
G_fs = linearize(mdl, io);

dcgain(G_fs)

-1.4113e-13	1.0339e-13	3.774e-14
1.0339e-13	-1.4113e-13	3.774e-14
3.7792e-14	3.7792e-14	-7.5585e-14

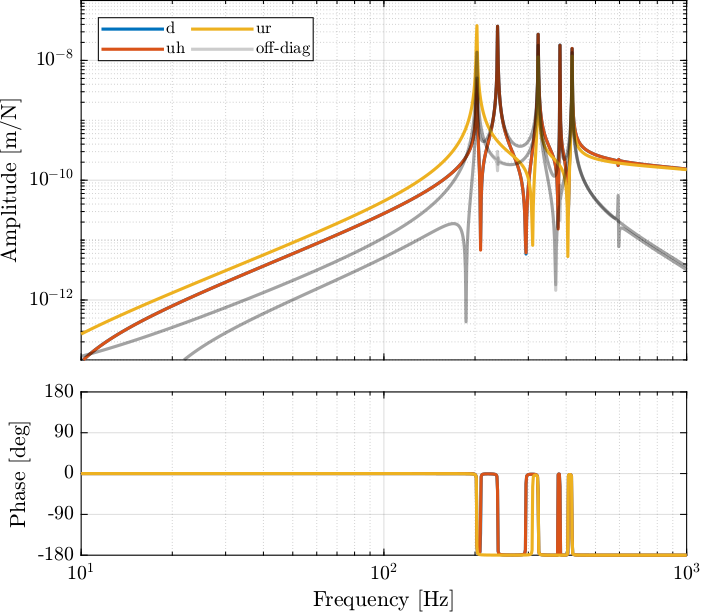
Figure 12: Bode plot of IFF Plant

4.2. Controller - Root Locus

Kiff_g1 = eye(3)*1/(1 + s/2/pi/20);

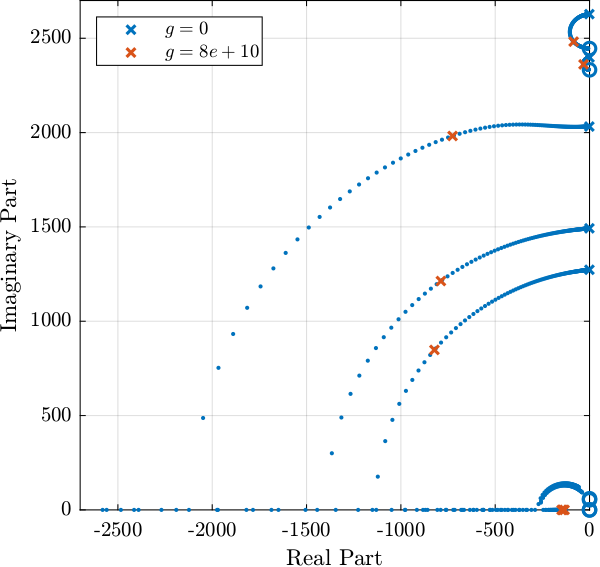
Figure 13: Root Locus plot for the IFF Control strategy

%% Integral Force Feedback Controller
Kiff = g*Kiff_g1;

4.3. Damped Plant

%% Input/Output definition
clear io; io_i = 1;

%% Inputs
% Control Input {3x1} [N]
io(io_i) = linio([mdl, '/control_system'], 1, 'input');  io_i = io_i + 1;

%% Outputs
% Force Sensor {3x1} [m]
io(io_i) = linio([mdl, '/DCM'], 1, 'openoutput'); io_i = io_i + 1;

%% DCM Kinematics
load('mat/dcm_kinematics.mat');

%% Identification of the Open Loop plant
controller.type = 0; % Open Loop
G_ol = J_a_111*inv(J_s_111)*linearize(mdl, io);
G_ol.InputName  = {'u_ur',  'u_uh',  'u_d'};
G_ol.OutputName = {'d_ur',  'd_uh',  'd_d'};

%% Identification of the damped plant with IFF
controller.type = 1; % IFF
G_dp = J_a_111*inv(J_s_111)*linearize(mdl, io);
G_dp.InputName  = {'u_ur',  'u_uh',  'u_d'};
G_dp.OutputName = {'d_ur',  'd_uh',  'd_d'};

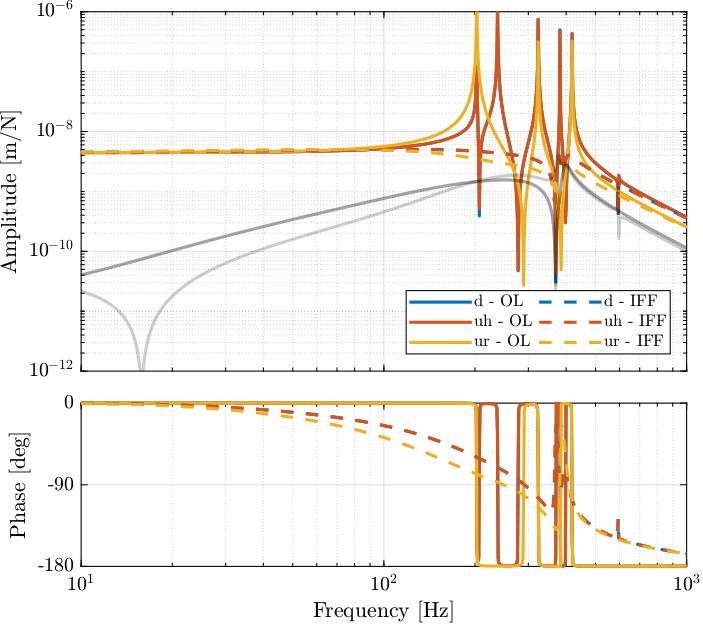
Figure 14: Bode plot of both the open-loop plant and the damped plant using IFF

The Integral Force Feedback control strategy is very effective in damping the suspension modes of the DCM.

4.4. Save

save('mat/Kiff.mat', 'Kiff');