attocube-test-bench/index.org

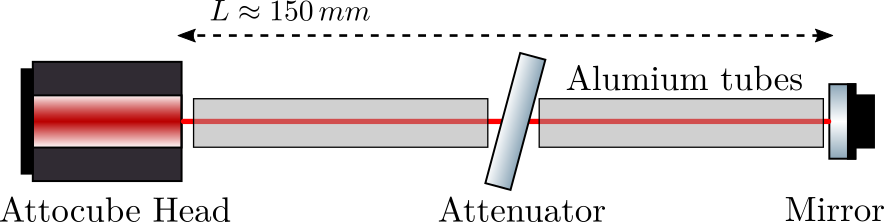
Attocube - Test Bench

• Estimation of the Spectral Density of the Attocube Noise
  • Introduction
  • Long and Slow measurement
  • Short and Fast measurement
  • Obtained Amplitude Spectral Density of the measured displacement
• Effect of the "bubble sheet" and Aluminium tube
  • Introduction
  • Aluminium Tube and Bubble Sheet
  • Only Aluminium Tube
  • Nothing
  • Comparison

Estimation of the Spectral Density of the Attocube Noise

Introduction   ignore

Test Bench Schematic

figs/IMG-7865.JPG

Picture of the test bench. The Attocube and mirror are covered by a "bubble sheet"

Long and Slow measurement

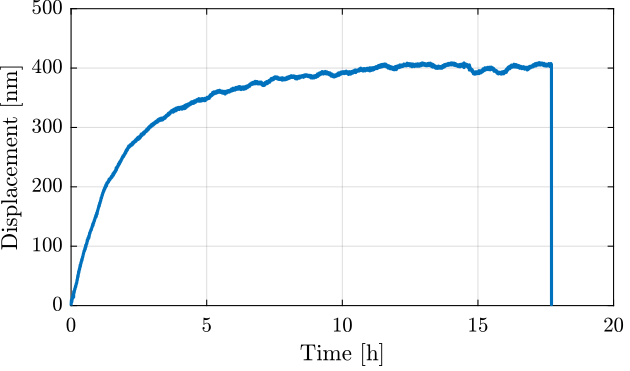
The first measurement was made during ~17 hours with a sampling time of $T_s = 0.1\,s$.

  load('./mat/long_test2.mat', 'x', 't')
  Ts = 0.1; % [s]

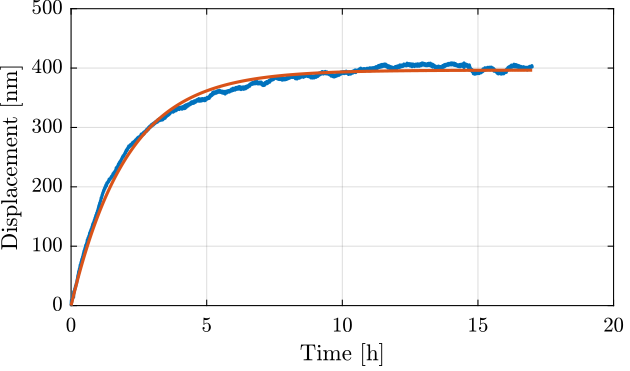
Long measurement time domain data

Let's fit the data with a step response to a first order low pass filter (Figure fig:long_meas_time_domain_fit).

  f = @(b,x) b(1)*(1 - exp(-x/b(2)));

  y_cur = x(t < 17*60*60);
  t_cur = t(t < 17*60*60);

  nrmrsd = @(b) norm(y_cur - f(b,t_cur)); % Residual Norm Cost Function
  B0 = [400e-9, 2*60*60];                        % Choose Appropriate Initial Estimates
  [B,rnrm] = fminsearch(nrmrsd, B0);     % Estimate Parameters ‘B’

The corresponding time constant is (in [h]):

2.0576

Fit of the measurement data with a step response of a first order low pass filter

We can see in Figure fig:long_meas_time_domain_full that there is a transient period where the measured displacement experiences some drifts. This is probably due to thermal effects. We only select the data between t1 and t2. The obtained displacement is shown in Figure fig:long_meas_time_domain_zoom.

  t1 = 11; t2 = 17; % [h]

  x = x(t > t1*60*60 & t < t2*60*60);
  x = x - mean(x);
  t = t(t > t1*60*60 & t < t2*60*60);
  t = t - t(1);

Kept data (removed slow drifts during the first hours)

The Power Spectral Density of the measured displacement is computed

  win = hann(ceil(length(x)/20));
  [p_1, f_1] = pwelch(x, win, [], [], 1/Ts);

As a low pass filter was used in the measurement process, we multiply the PSD by the square of the inverse of the filter's norm.

  G_lpf = 1/(1 + s/2/pi);
  p_1 = p_1./abs(squeeze(freqresp(G_lpf, f_1, 'Hz'))).^2;

Only frequencies below 2Hz are taken into account (high frequency noise will be measured afterwards).

  p_1 = p_1(f_1 < 2);
  f_1 = f_1(f_1 < 2);

Short and Fast measurement

An second measurement is done in order to estimate the high frequency noise of the interferometer. The measurement is done with a sampling time of $T_s = 0.1\,ms$ and a duration of ~100s.

  load('./mat/short_test_plastic.mat')
  Ts = 1e-4; % [s]

  x = detrend(x, 0);

The time domain measurement is shown in Figure fig:short_meas_time_domain.

Time domain measurement with the high sampling rate

The Power Spectral Density of the measured displacement is computed

  win = hann(ceil(length(x)/10));
  [p_2, f_2] = pwelch(x, win, [], [], 1/Ts);

Obtained Amplitude Spectral Density of the measured displacement

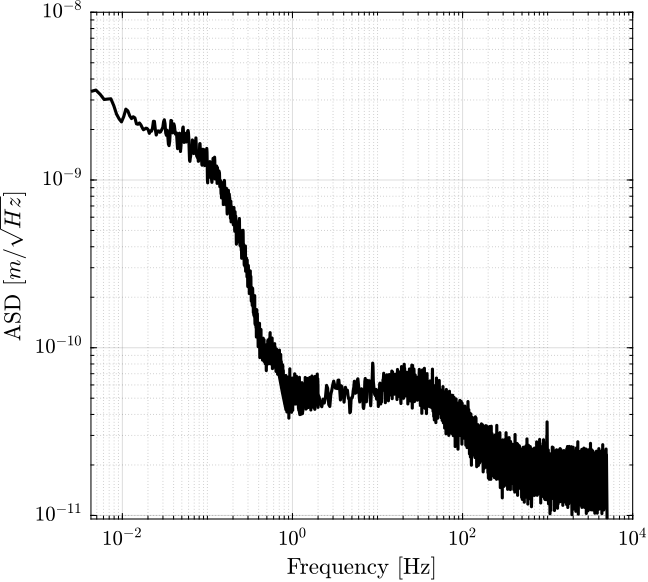
The computed ASD of the two measurements are combined in Figure fig:psd_combined.

Obtained Amplitude Spectral Density of the measured displacement

Effect of the "bubble sheet" and Aluminium tube

Introduction   ignore

figs/IMG-7864.JPG

Aluminium tube used to protect the beam path from disturbances

Aluminium Tube and Bubble Sheet

  load('./mat/long_test_plastic.mat');
  Ts = 1e-4; % [s]

  x = detrend(x, 0);

  win = hann(ceil(length(x)/10));
  [p_1, f_1] = pwelch(x, win, [], [], 1/Ts);

Only Aluminium Tube

  load('./mat/long_test_alu_tube.mat');
  Ts = 1e-4; % [s]

  x = detrend(x, 0);

The time domain measurement is shown in Figure fig:short_meas_time_domain.

  win = hann(ceil(length(x)/10));
  [p_2, f_2] = pwelch(x, win, [], [], 1/Ts);

Nothing

  load('./mat/long_test_without_material.mat');
  Ts = 1e-4; % [s]

  x = detrend(x, 0);

The time domain measurement is shown in Figure fig:short_meas_time_domain.

  win = hann(ceil(length(x)/10));
  [p_3, f_3] = pwelch(x, win, [], [], 1/Ts);

Comparison

Comparison of the noise ASD with and without bubble sheet